Prediction of the Freezing Temperature of Saline Soil Using Neural Network Methods
Abstract
1. Introduction
2. Methods
2.1. Databases
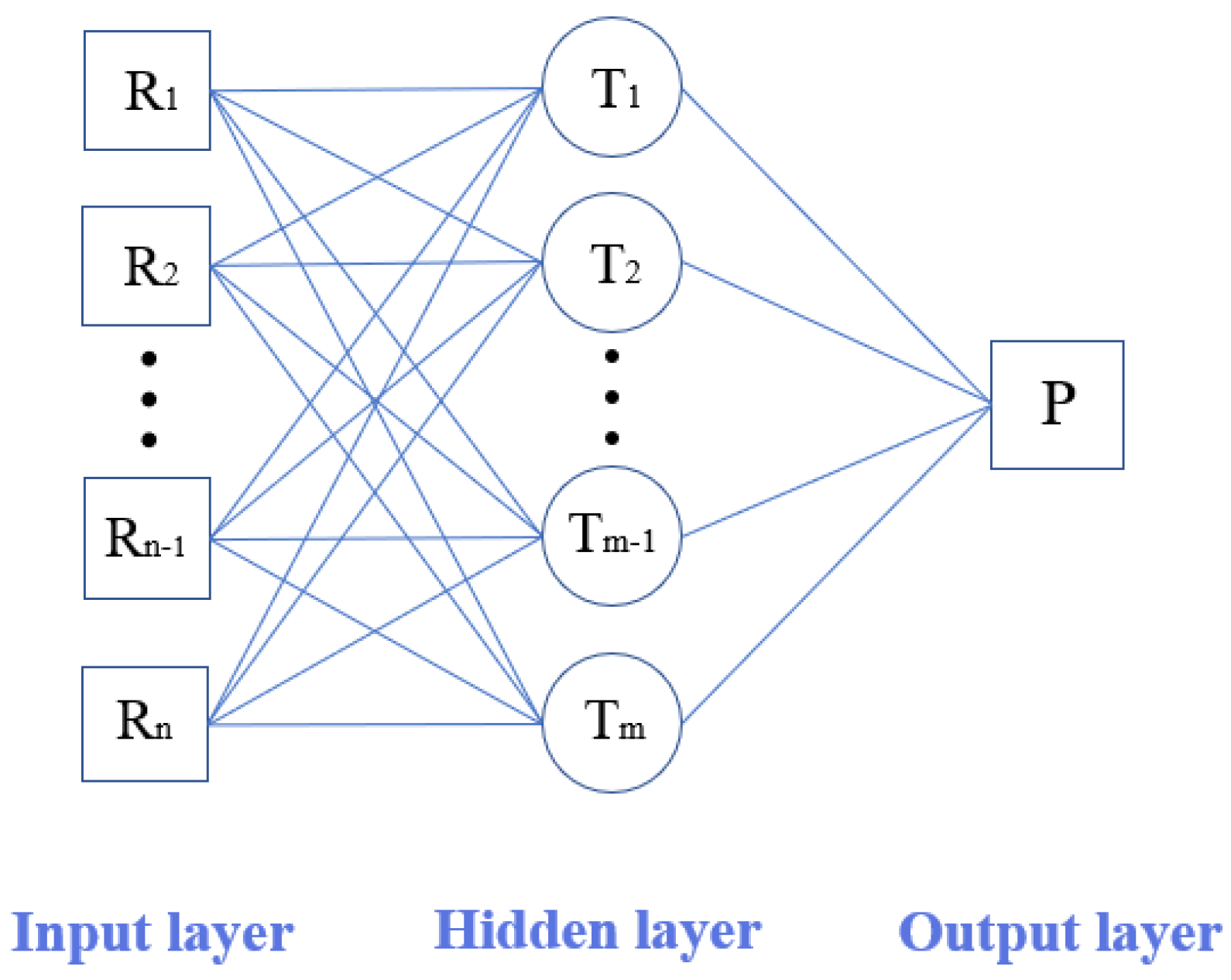
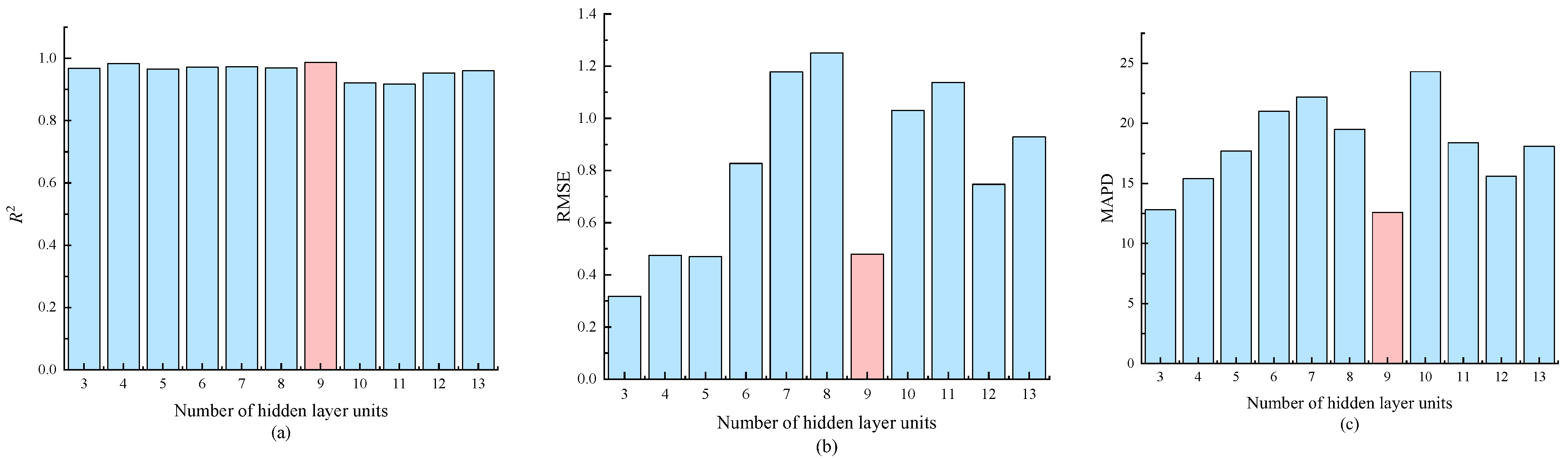
2.2. BPNN Method
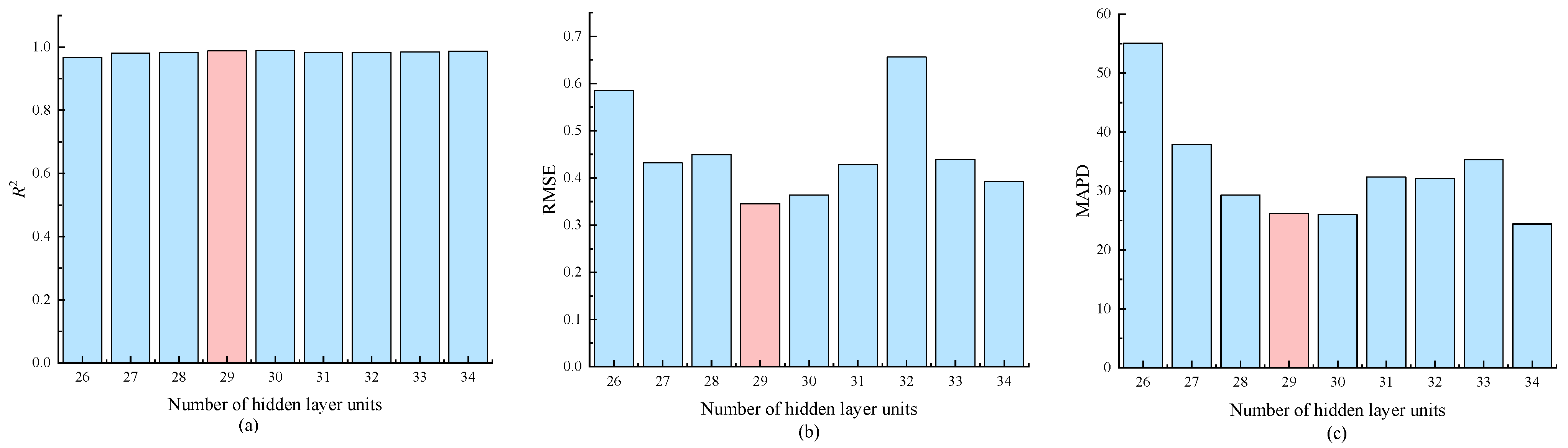
2.3. RBFNN Method
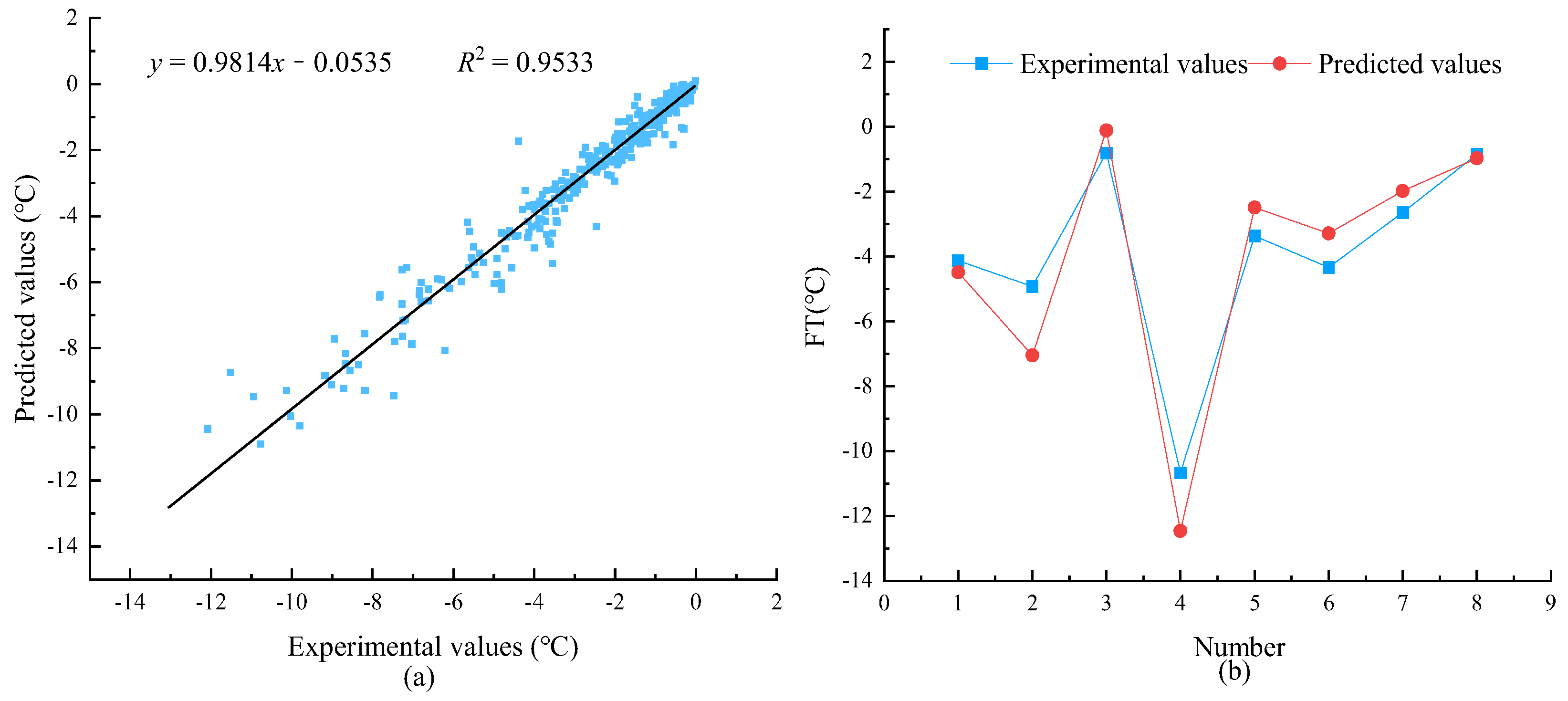
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, X.Z.; Wang, J.C.; Zhang, L.X.; Deng, Y.S. Mechanisms of Frost Heave and Soil Expansion of Soils; Science Press: Beijing, China, 1995. [Google Scholar]
- Xu, X.Z.; Wang, J.C.; Zhang, L.X. Frozen Soil Physics; Science Press: Beijing, China, 2010. [Google Scholar]
- Qiu, K.; Ding, L.; Yu, W.; Chen, K.; Huang, S.; Gao, K. Experimental Investigation of Shear Strength of Carbonate Saline Soil under Freeze-Thaw Cycles. Atmosphere 2022, 13, 2063. [Google Scholar] [CrossRef]
- Chun-lei, W.A.; Qiang, X.I.; Chong-xi, J.I. Analysis of thermal characteristics and mechanical properties of salty soil in frozen area of Qinghai-Tibet Railway. Rock Soil Mech. 2009, 3, 836–839. [Google Scholar]
- Tan, D.S.; Sun, Y.M.; Hu, L.X.; Jiang, F.Q.; Zhang, F.L. Salt expansion properties and mechanism of saline soil in Xinjiang section of Lanzhou–Xinjiang railway and preventive measures. J. China Railw. Soc. 2011, 33, 83–88. [Google Scholar]
- Cui, G.X. Determination of freezing temperature and thickness of frozen wall in wet soil with thick topsoil. J. China Univ. Min. Technol. 1997, 3, 3–6. [Google Scholar]
- Liu, J.K. Influence of nonuniform distribution of fine soil on mechanical properties of coarse-grained soil. Chin. J. Geotech. Eng. 2017, 39, 562–572. [Google Scholar]
- Hu, T.F.; Liu, J.; Fang, J. Experimental study on the effect of cyclic freezing-thawing on mechanical properties of silty clay under different cooling temperatures. Chin. J. Rock Mech. Eng. 2017, 33, 1496–1502. [Google Scholar]
- Wang, Z.J. Influence of freezing and thawing on collapsibility of loess. Chin. J. Undergr. Space Eng. 2016, 12, 1710–1716. [Google Scholar]
- Yingjun, S.O.; Lei, X.U.; Yang, L.U. Experimental studies on freeze-thaw cycles of expansive soil based on orthogonal design. J. Water Resour. Hydropower Eng. 2017, 2, 51–58. [Google Scholar]
- Xiao, Z.A.; Lai, Y.M.; You, Z.M. Water and salt migration and deformation mechanism of sodium chloride soil during unidirectional freezing process. Chin. J. Geotech. Eng. 2017, 39, 1992–2001. [Google Scholar]
- Li, G.; Li, N.; Liu, N.; Zhu, C. Practical algorithm of THM coupling process with ice-water phase change based on FLAC3D. Chin. J. Rock Mech. Eng. 2017, 36 (Suppl. 2), 3841–3851. [Google Scholar]
- Banin, A.; Anderson, D.M. Effects of salt concentration changes during freezing on the unfrozen water content of porous materials. Water Resour. Res. 1974, 10, 124–128. [Google Scholar] [CrossRef]
- Kozlowski, T. A comprehensive method of determining the soil unfrozen water curves: 2. stages of the phase change process in frozen soil–water system. Cold Reg. Sci. Technol. 2003, 36, 81–92. [Google Scholar] [CrossRef]
- Bing, H.; Ma, W. Laboratory investigation of the freezing point of saline soil. Cold Reg. Sci. Technol. 2011, 67, 79–88. [Google Scholar] [CrossRef]
- Low, P.F.; Anderson, D.M.; Hoekstra, P. Some thermodynamic relationships for soils at or below the freezing point: 1. Freezing point depression and heat capacity. Water Resour. Res. 1968, 4, 379–394. [Google Scholar] [CrossRef]
- Azmatch, T.F.; Sego, D.C.; Arenson, L.U.; Biggar, K.W. Using soil freezing characteristic curve to estimate the hydraulic conductivity function of partially frozen soils. Cold Reg. Sci. Technol. 2012, 83, 103–109. [Google Scholar] [CrossRef]
- Wan, X.S.; Lai, Y.M.; Wang, C. Experimental Study on freezing temperatures of Saline Silty Soils. Permafr. Periglac. Process. 2015, 26, 175–187. [Google Scholar] [CrossRef]
- Wan, X.S.; Lai, Y.M. Experimental study on freezing temperature and salt crystal precipitation of sodium sulphate soulotion and sodium sulphate saline soil. Chin. J. Geotech. Eng. 2013, 35, 2090–2096. [Google Scholar]
- Xiao, Z.A.; Lai, Y.M.; Zhang, M.Y. Study on freezing temperature of saline soil. Acta Geotech. 2018, 13, 195–205. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, J.; Wang, S.; Xu, J.; Yang, Y. Effect of freeze-thaw on freezing point of a saline loess. Cold Reg. Sci. Technol. 2020, 170, 102922. [Google Scholar] [CrossRef]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput. -Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Wu, X.; Ghaboussi, J.; Garrett, J.H., Jr. Use of neural networks in detection of structural damage. Comput. Struct. 1992, 42, 649–659. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Jahed Armaghani, D.; Momeni, E.; Alavi Nezhad Khalil Abad, S.V. Prediction of the unconfined compressive strength of soft rocks: A PSO-based ANN approach. Bull. Eng. Geol. Environ. 2015, 74, 745–757. [Google Scholar] [CrossRef]
- Hajihassani, M.; Armaghani, D.J.; Marto, A.; Mohamad, E.T. Ground vibration prediction in quarry blasting through an artificial neural network optimized by imperialist competitive algorithm. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Wang, B.; Man, T.; Jin, H. Prediction of expansion behavior of self-stressing concrete by artificial neural networks and fuzzy inference systems. Constr. Build. Mater. 2015, 84, 184–191. [Google Scholar] [CrossRef]
- Sun, J.Z. Study on Thaw Settlement Characteristics of Chloride Saline Soil Based on BP Neural Network. J. Lanzhou Jiaotong Univ. 2020, 39, 26–31. [Google Scholar]
- Moody, J.; Darken, C.J. Fast learning in networks of locally-tuned processing units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Sun, D.Y. Characteristics and Prediction of Frost Heave of Saline Soil in Western Jilin Province. Int. J. Heat Technol. 2016, 34, 709–714. [Google Scholar] [CrossRef]
- Fagerlund, G. Determination of pore-size distribution from freezing point depression. Mater. Struct. 1973, 6, 215–225. [Google Scholar] [CrossRef]
- Sun, Z.; Scherer, G.W. Pore size and shape in mortar by thermoporometry. Cem. Concr. Res. 2010, 40, 740–751. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Huo, Z.; Yu, T.; Wang, G.; Liu, T.; Wang, W. Prediction of Frost-Heaving Behavior of Saline Soil in Western Jilin Province, China, by Neural Network Methods. Math. Probl. Eng. 2017, 2017, 7689415. [Google Scholar] [CrossRef]
- Seshagiri, S.; Khalil, H.K. Output feedback control of nonlinear systems using RBF neural networks. IEEE Trans. Neural Netw. 2000, 11, 69–79. [Google Scholar] [CrossRef] [PubMed]




| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Number | 112 | 79 | 52 | 46 | 26 | 11 | 11 |
| Group | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Number | 11 | 8 | 3 | 5 | 1 | 1 | 1 |
| Net | Data | R2 | RMSE | MAPD |
|---|---|---|---|---|
| BPNN | Training data | 0.9533 | 0.533 | 24.1% |
| Testing data | 0.9632 | 0.479 | 12.6% | |
| RBFNN | Training data | 0.9796 | 0.352 | 27.3% |
| Testing data | 0.9883 | 0.345 | 26.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Xiao, Z.; Zhu, L.; Li, K. Prediction of the Freezing Temperature of Saline Soil Using Neural Network Methods. Atmosphere 2023, 14, 422. https://doi.org/10.3390/atmos14030422
Duan J, Xiao Z, Zhu L, Li K. Prediction of the Freezing Temperature of Saline Soil Using Neural Network Methods. Atmosphere. 2023; 14(3):422. https://doi.org/10.3390/atmos14030422
Chicago/Turabian StyleDuan, Jieyun, Zean Xiao, Linze Zhu, and Kangliang Li. 2023. "Prediction of the Freezing Temperature of Saline Soil Using Neural Network Methods" Atmosphere 14, no. 3: 422. https://doi.org/10.3390/atmos14030422
APA StyleDuan, J., Xiao, Z., Zhu, L., & Li, K. (2023). Prediction of the Freezing Temperature of Saline Soil Using Neural Network Methods. Atmosphere, 14(3), 422. https://doi.org/10.3390/atmos14030422





