Study on the Peak Factor of the Wind-Induced Response of Super-High-Rise Buildings
Abstract
:1. Introduction
2. Wind Tunnel Test of Aero-Elastic Model
2.1. Design of MDOF Model Skeleton
2.2. Wind Tunnel Test
3. Wind-Induced Response of the Aero-Elastic Model
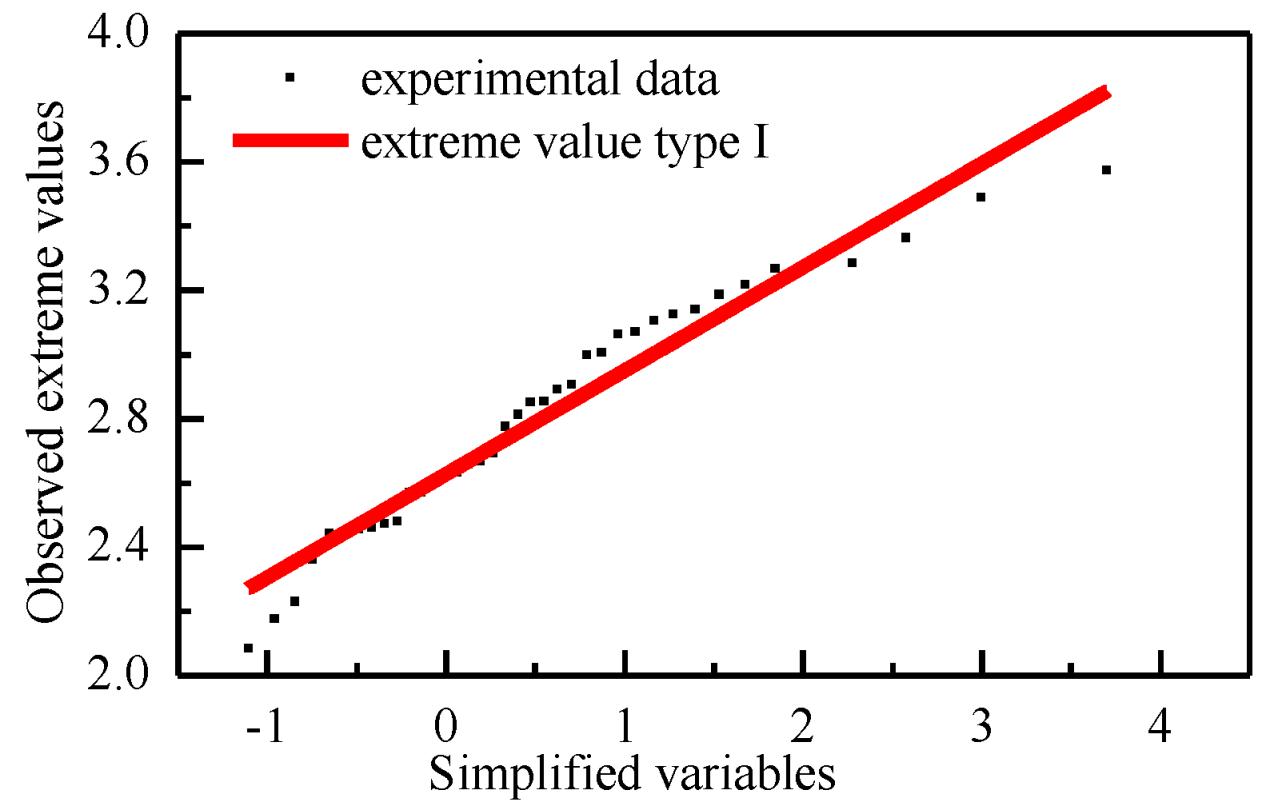
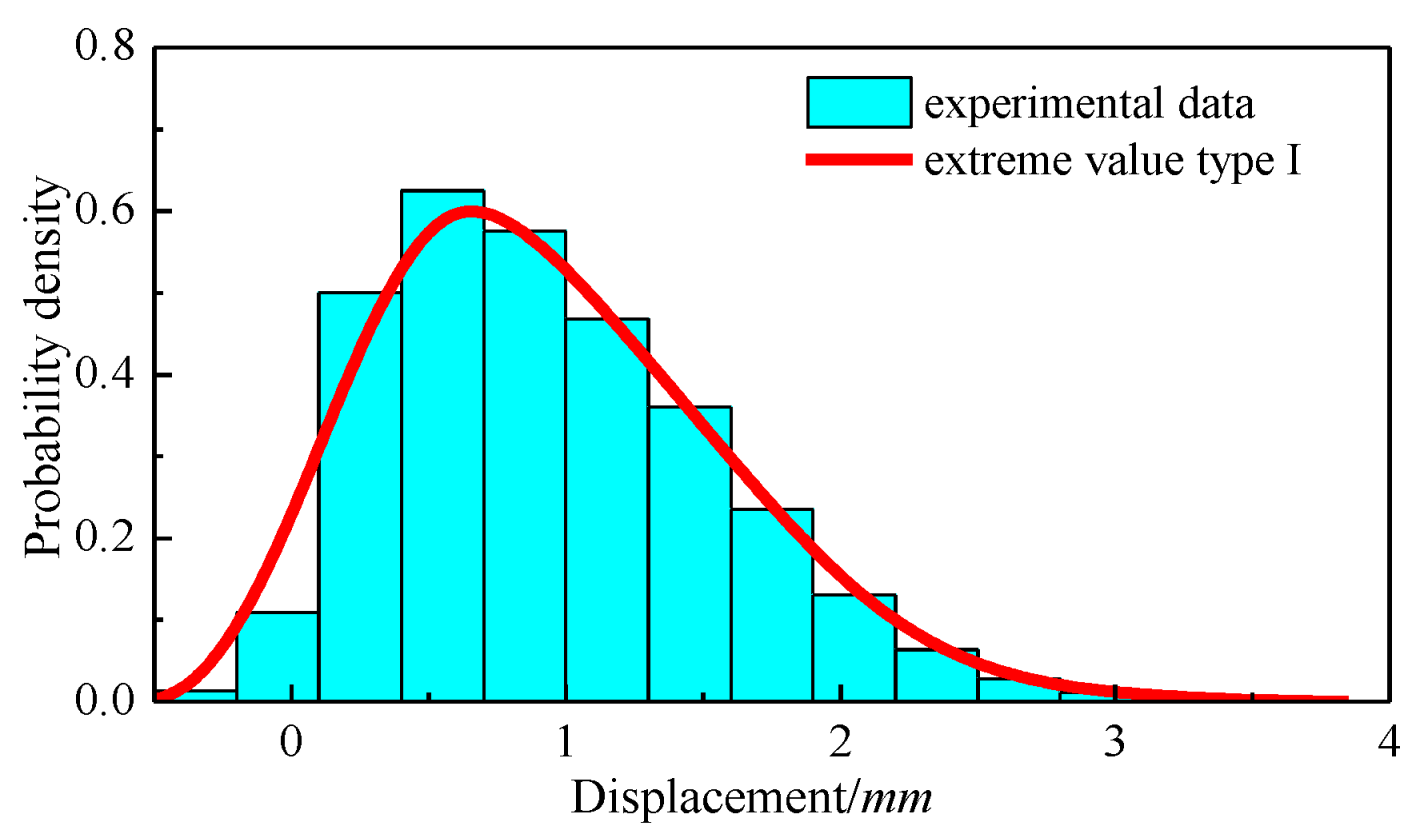
4. Calculation Method of the Peak Factor
4.1. Overview of the Calculation Method
- (1)
- Peak factor method
- (2)
- Improved peak factor method
- (3)
- Classical extreme value theory and method
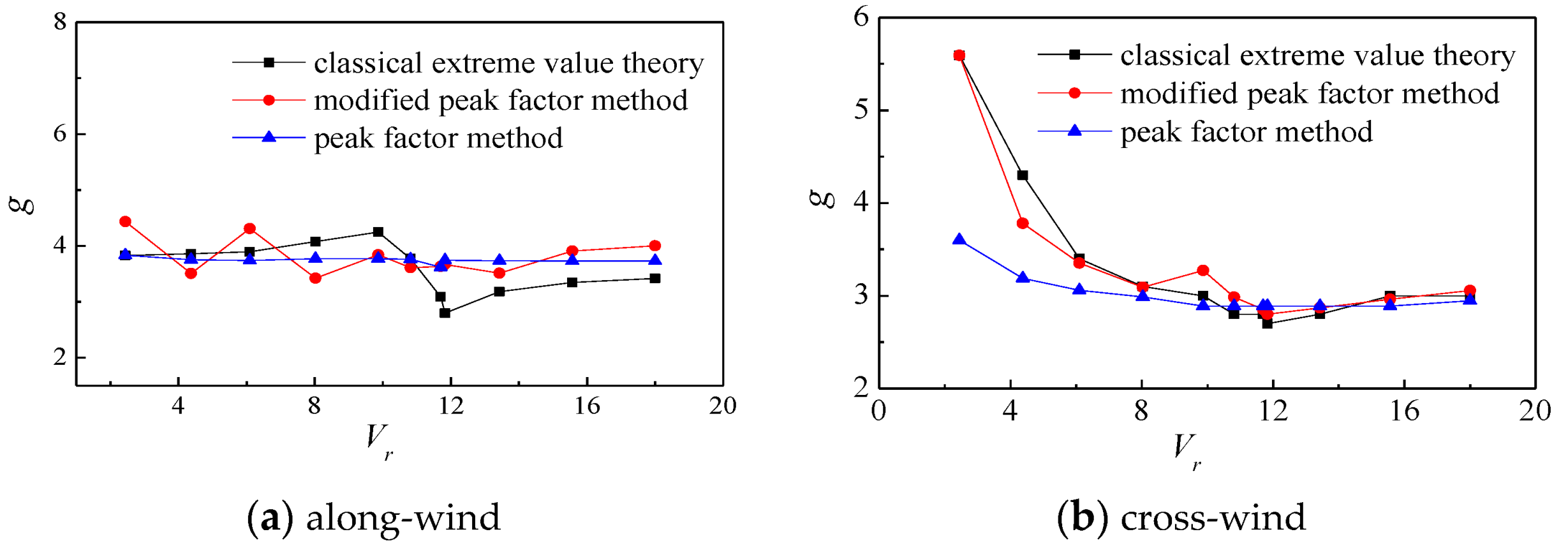
4.2. Comparison of the Calculation Results of the Two Methods
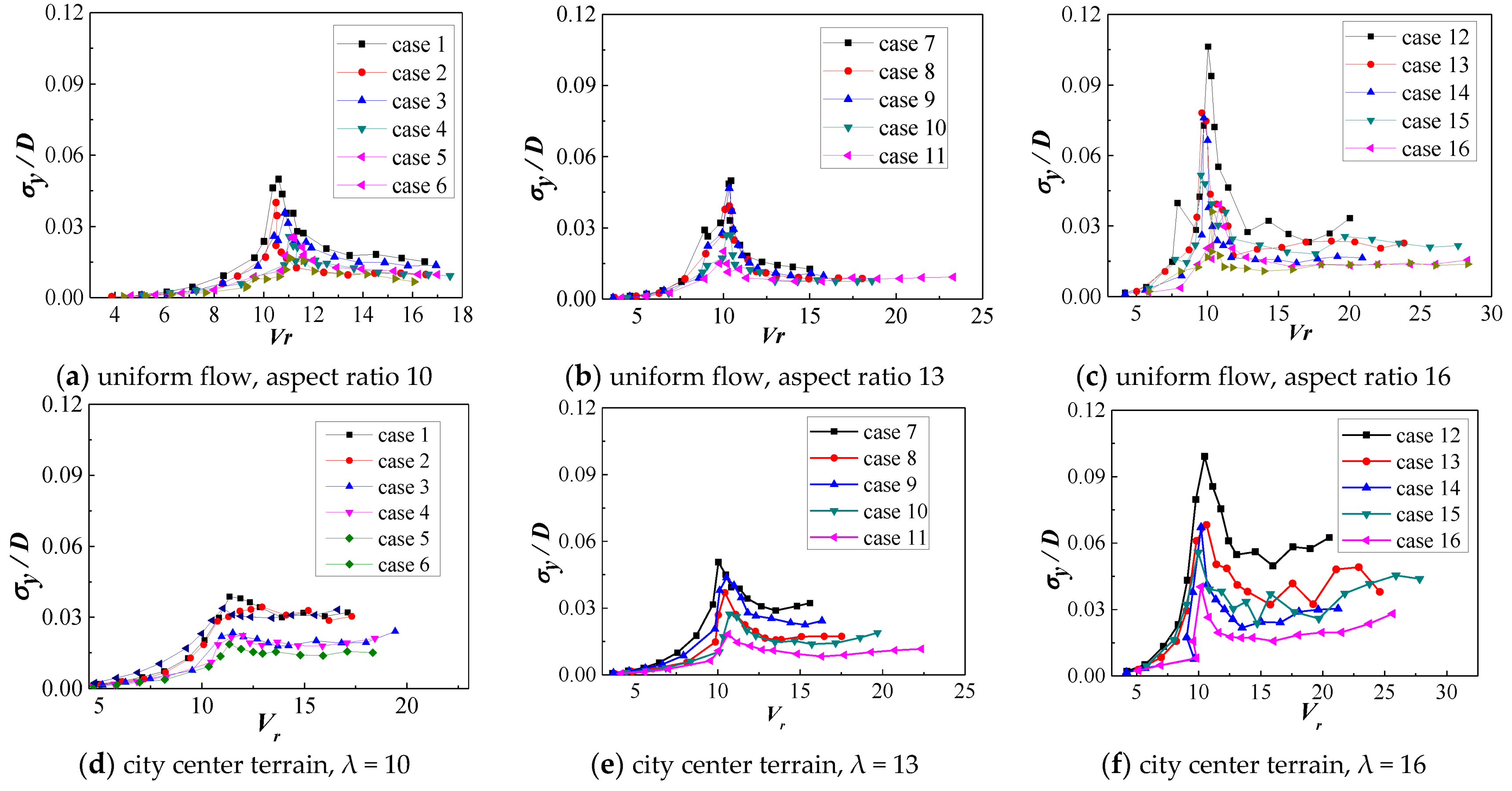
5. Peak Factor Analysis of the Wind-Induced Response
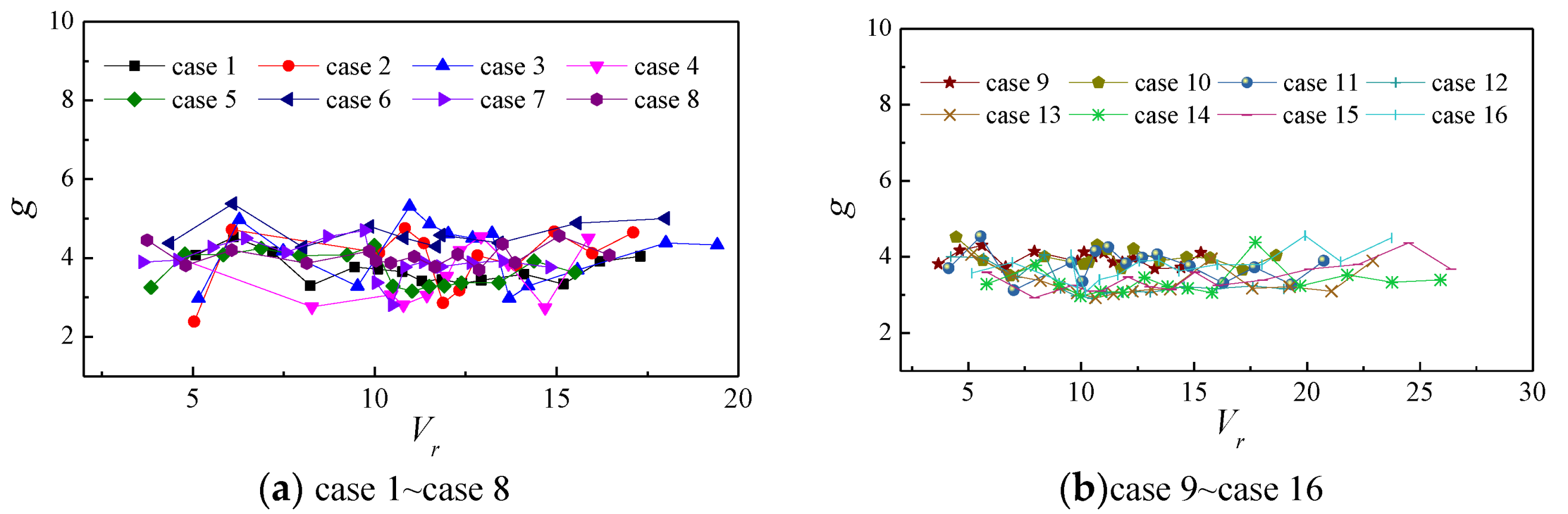
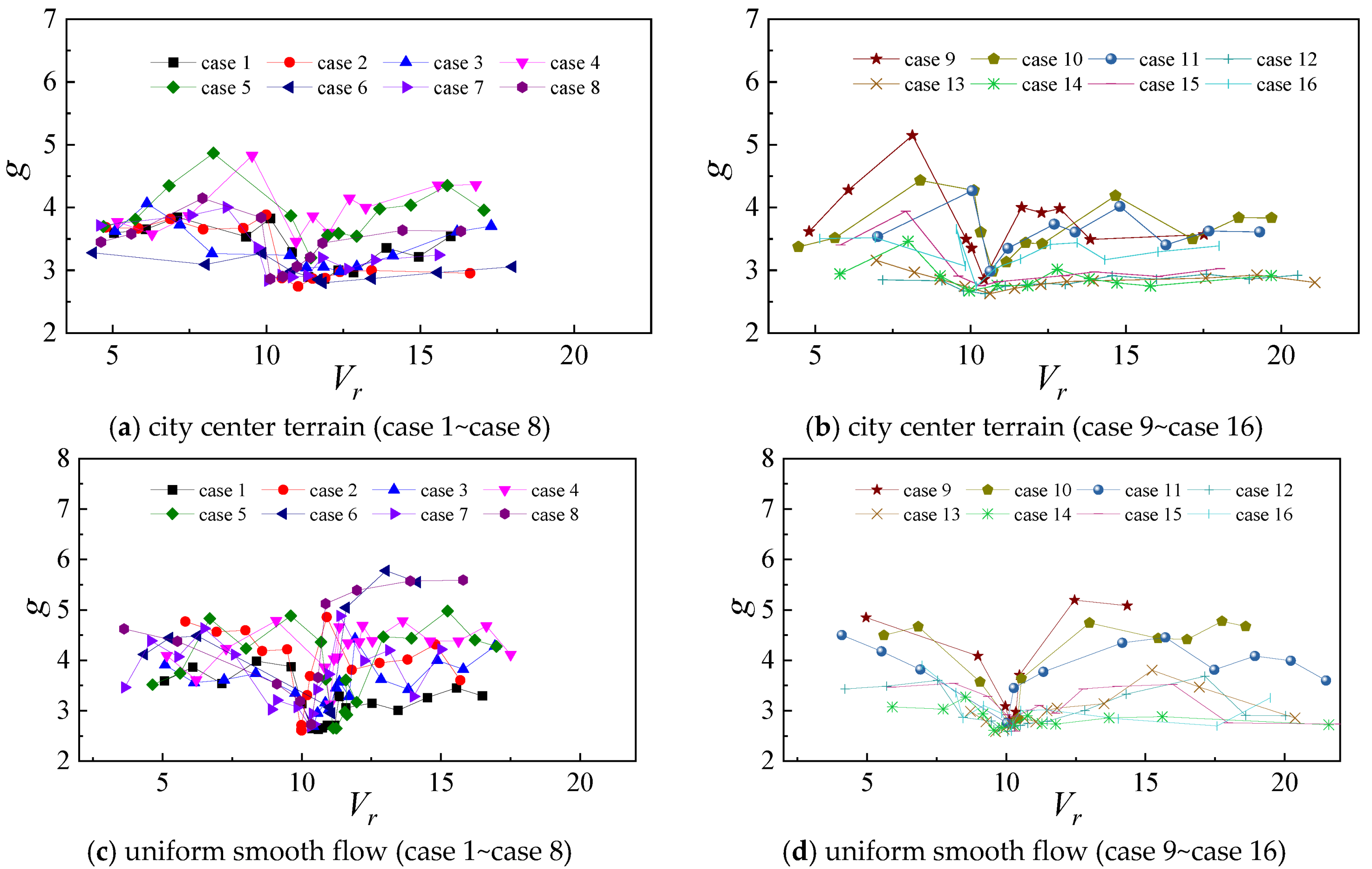
5.1. Preliminary Analysis
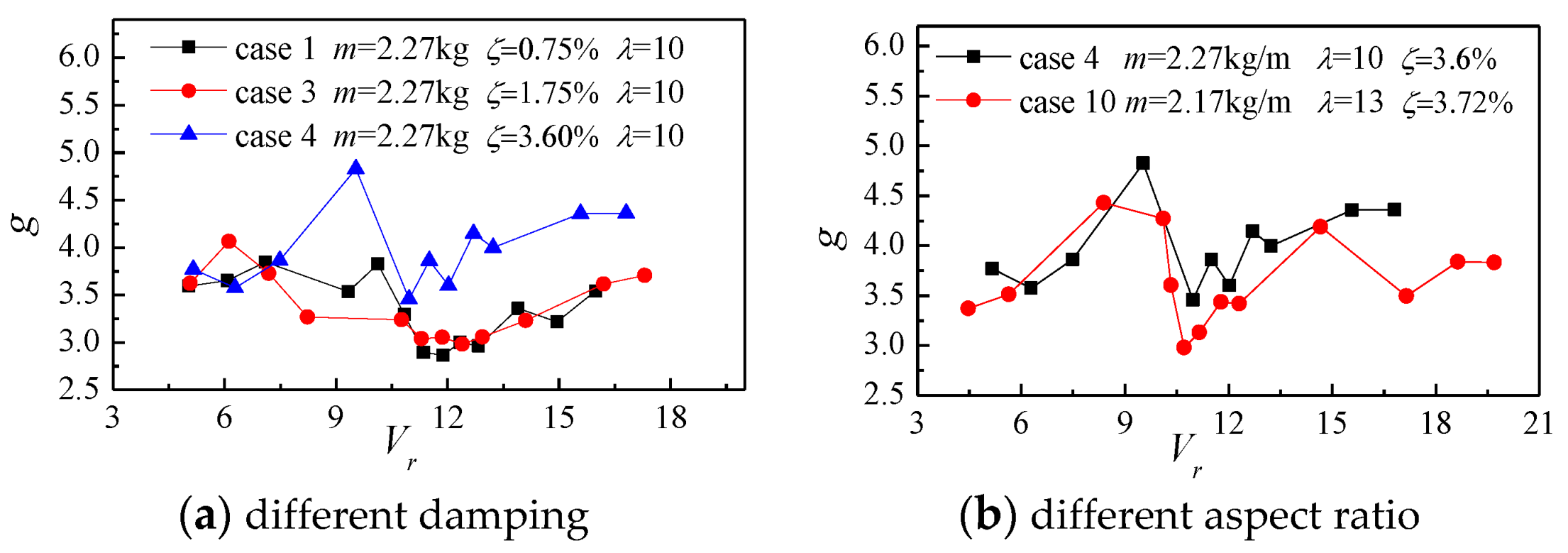
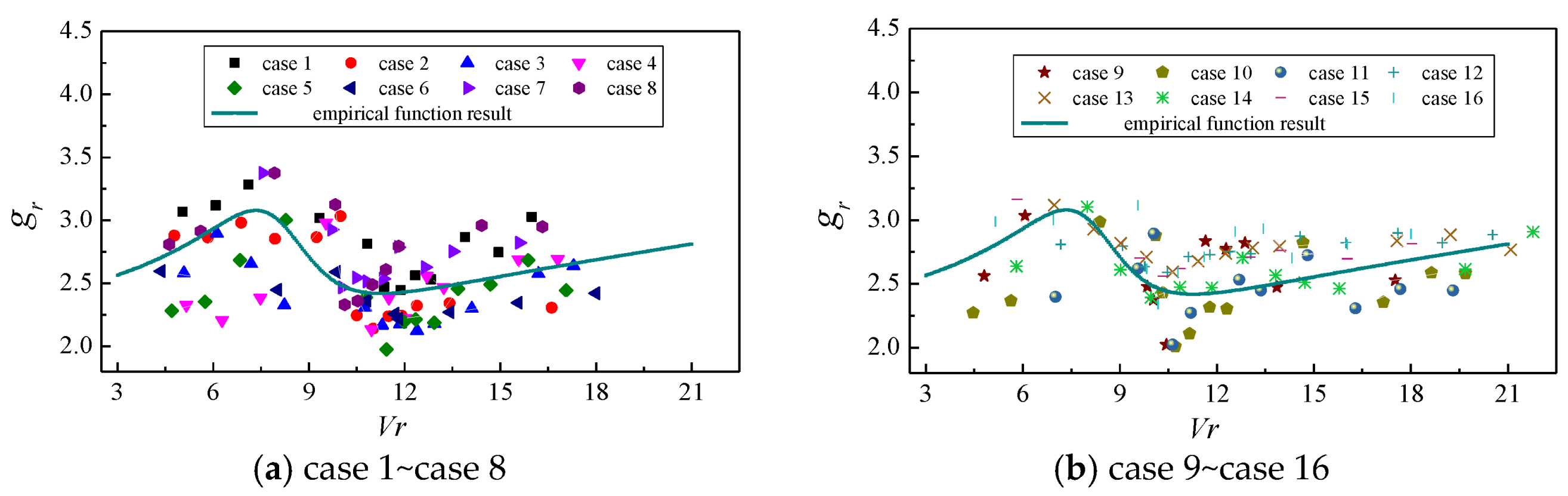
5.2. Empirical Formula
6. Conclusions
- (1)
- For the wind-induced response of super-high-rise buildings, the peak factor calculated by the improved peak factor method is consistent with that calculated by the classical extreme value theory, and the difference between the two calculation methods is approximately within 15%, indicating that the improved peak factor method is applicable to calculate the peak factor of the wind-induced response of high-rise buildings.
- (2)
- The peak factor of the along-wind response of super-high-rise buildings changes little with the reduced wind speed; therefore, the along-wind response peak factor at different wind speeds can be approximately taken as a constant in the wind-resistant design of actual tall buildings.
- (3)
- The peak factor of the cross-wind response of super-high-rise buildings varies greatly with wind speeds, varying from 2.5 to 5.5, and reaches the minimum near the critical wind speed of VIV. In the wind-resistant design of actual super tall buildings, the cross-wind peak factor should be taken as a relatively large value when the wind speed is far from the VIV wind speed, and as a relatively small value when the wind speed is close to the VIV wind speed.
- (4)
- The empirical formula proposed in this paper takes into account the effects of aspect ratio, structural damping, and reduced wind speed on the peak factor, which is an improvement of existing research work. The empirical formula can approximately reflect the variation characteristic of the cross-wind response peak factor. Although the accuracy of the formula is not good enough, it can provide a reference for the evaluation of the peak factor of the wind-induced response of super-high-rise buildings without wind tunnel test data, and the test data of this study can provide a reference for further research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davenport, A.G. Note on the distribution of the largest value of a random function with application to gust loading. Proc. Inst. Civ. Eng. 1964, 28, 187–196. [Google Scholar] [CrossRef]
- Yasushi, U.; Nicholas, I. Wind pressures acting on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. J. Int. Assoc. Wind. Eng. 1999, 82, 1–25. [Google Scholar]
- Kumar, K.S.; Stathopoulos, T. Wind Loads on Low Building Roofs: A Stochastic Perspective. J. Struct. Eng. 2000, 126, 944–956. [Google Scholar] [CrossRef]
- Yang, L.; Gurley, K.R.; Prevatt, D.O. Probabilistic modeling of wind pressure on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 2013, 114, 18–26. [Google Scholar] [CrossRef]
- Yang, Q.; Tian, Y. A model of probability density function of non-Gaussian wind pressure with multiple samples. J. Wind. Eng. Ind. Aerodyn. 2015, 140, 67–78. [Google Scholar] [CrossRef]
- Kareem, A.; Zhao, J. Analysis of Non-Gaussian surge response of tension leg platforms under wind loads. J. Offshore Mech. Arct. Eng. 1991, 116, 137–144. [Google Scholar] [CrossRef]
- Kwon, D.K.; Kareem, A. Peak Factors for Non-Gaussian Load Effects Revisited. J. Struct. Eng. 2011, 137, 1611–1619. [Google Scholar] [CrossRef]
- Winerstein, S.R. Nonlinear Vibration Models for Extremes and Fatigue. J. Eng. Mech. 1988, 114, 1772–1790. [Google Scholar] [CrossRef]
- Tognarelli, M.A.; Zhao, J.; Kareem, A. Equivalent Statistical Cubicization for System and Forcing Nonlinearities. J. Eng. Mech. 1997, 123, 890–893. [Google Scholar] [CrossRef]
- Winterstein, S.R.; Kleiven, G. Springing and slow-drift responses: Predicted extremes and fatigue vs. simulation. Processes 1994, 94, 1–15. [Google Scholar]
- Peng, L.; Liu, M.; Yang, Q.; Huang, G.; Chen, B. An analytical formula for Gaussian to non-Gaussian correlation relationship by moment-based piecewise Hermite polynomial model with application in wind engineering. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104094. [Google Scholar] [CrossRef]
- Huang, M.; Lou, W.; Chan, C.-M.; Bao, S. Peak factors of non-Gaussian wind forces on a complex-shaped tall building. Struct. Des. Tall Spec. Build. 2014, 22, 1105–1118. [Google Scholar] [CrossRef]
- Huang, M.F.; Lou, W.; Chan, C.M.; Lin, N.; Pan, X. Peak Distributions and Peak Factors of Wind-Induced Pressure Processes on Tall Buildings. J. Eng. Mech. 2013, 139, 1744–1756. [Google Scholar] [CrossRef]
- Sadek, F.; Simiu, E. Peak Non-Gaussing wind effects for database-assisted low-rise building design. J. Eng. Mech. 2002, 128, 530–539. [Google Scholar]
- Quan, Y.; Wang, F.; Gu, M. An Extreme-value Estimating Method of Non-Gaussian Wind Pressure Based on Generalized Extreme Value Theory. In Proceedings of the 13rd International Conference on Wind Engineering (ICWE13), Amsterdam, The Netherlands, 10–15 July 2011. [Google Scholar]
- Huang, G.; Luo, Y.; Yang, Q.; Tian, Y. A semi-analytical formula for estimating peak wind load effects based on Hermite polynomial model. Eng. Struct. 2017, 152, 856–864. [Google Scholar] [CrossRef]
- Melbourne, W.H. Predicting the cross-wind response of masts and structural members. J. Wind. Eng. Ind. Aerodyn. 1997, 69, 91–103. [Google Scholar] [CrossRef]
- Cheng, C.M.; Lu, P.C.; Tsaia, M.S. Acrosswind aerodynamic damping of isolated square-shaped buildings. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1743–1756. [Google Scholar] [CrossRef]
- Vickery, B.J.; Steckley, A. Aerodynamic Damping and Vortex Excitation on an Oscillating Prism in Turbulent Shear Flow. J. Wind. Eng. Ind. Aerodyn. 1993, 49, 121–140. [Google Scholar] [CrossRef]
- Wang, L.; Liang, S.; Huang, G.; Song, J.; Zou, L. Investigation on the unstability of vortex induced resonance of high-rise buildings. J. Wind. Eng. Ind. Aerodyn. 2018, 175, 17–31. [Google Scholar] [CrossRef]
- Li, Q.; Jia, H.; Qiu, Q.; Lu, Y.; Zhang, J.; Mao, J.; Fan, W.; Huang, M. Typhoon-Induced Fragility Analysis of Transmission Towers in Ningbo Area Considering the Effects of Long-Term Corrosion. Appl. Sci. 2022, 12, 4774. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Y.-J.; Wang, Z.-K.; Fan, Y.-H. A design method for multi-degree-of-freedom aeroelastic model of super tall buildings. Wind. Struct. 2021, 32, 219–225. [Google Scholar]
- Bearman, P.M. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012.
- Wang, L.; Liang, S.; Song, J.; Wang, S. Analysis of vortex induced vibration frequency of super tall building based on wind tunnel tests of mdof aero-elastic model. Wind. Struct. Int. J. 2015, 21, 523–536. [Google Scholar] [CrossRef]
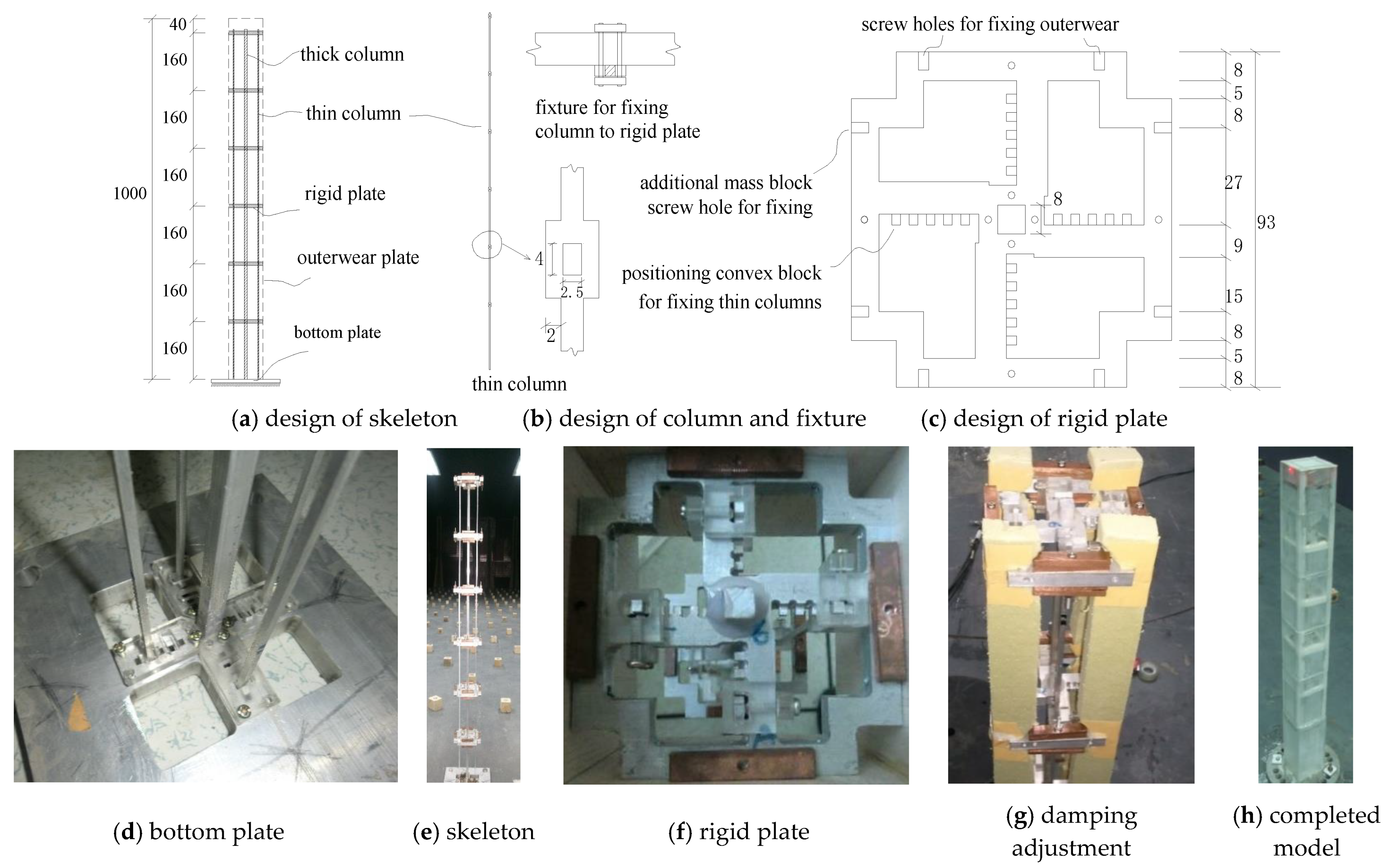




| Property | Model Parameters | Scale Ratio |
|---|---|---|
| Length | lm/lp | 1:600 |
| Time and frequency | nm/np | 100:1 |
| Velocity | Vm/Vp | 1:6 |
| Density | ρm/ρp | 1:1 |
| Test Case | Geometric Size | Aspect Ratio (λ) | 1st Natural Frequency (n1) | Equivalent Mass (m) | Damping Ratio (ζ) | Scruton Number (Sc) |
|---|---|---|---|---|---|---|
| 0 | 1.0 × 0.1 m | 10 | 7.00 Hz | 3.07 kg/m | 4.20% | 20.64 |
| 1 | 1.0 × 0.1 m | 10 | 9.89 Hz | 2.27 kg/m | 0.75% | 2.5 |
| 2 | 1.0 × 0.1 m | 10 | 10.18 Hz | 1.85 kg/m | 1.10% | 3.25 |
| 3 | 1.0 × 0.1 m | 10 | 9.64 Hz | 2.27 kg/m | 1.80% | 6.34 |
| 4 | 1.0 × 0.1 m | 10 | 9.27 Hz | 2.27 kg/m | 3.60% | 13.05 |
| 5 | 1.0 × 0.1 m | 10 | 9.40 Hz | 2.50 kg/m | 3.60% | 14.4 |
| 6 | 1.0 × 0.1 m | 10 | 7.01 Hz | 3.07 kg/m | 4.20% | 20.65 |
| 7 | 1.3 × 0.1 m | 13 | 10.83 Hz | 1.31 kg/m | 1.02% | 2.14 |
| 8 | 1.3 × 0.1 m | 13 | 9.02 Hz | 1.31 kg/m | 2.89% | 6.05 |
| 9 | 1.3 × 0.1 m | 13 | 10.6 Hz | 1.31 kg/m | 1.43% | 2.99 |
| 10 | 1.3 × 0.1 m | 13 | 8.70 Hz | 2.17 kg/m | 3.72% | 12.91 |
| 11 | 1.3 × 0.1 m | 13 | 7.17 Hz | 2.38 kg/m | 4.50% | 17.06 |
| 12 | 1.6 × 0.1 m | 16 | 7.14 Hz | 1.25 kg/m | 0.82% | 1.64 |
| 13 | 1.6 × 0.1 m | 16 | 5.98 Hz | 1.81 kg/m | 0.82% | 2.38 |
| 14 | 1.6 × 0.1 m | 16 | 7.02 Hz | 1.25 kg/m | 1.33% | 2.6 |
| 15 | 1.6 × 0.1 m | 16 | 5.19 Hz | 2.38 kg/m | 1.11% | 4.25 |
| 16 | 1.6 × 0.1 m | 16 | 5.68 Hz | 2.38 kg/m | 1.71% | 6.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-B.; Wang, Y.; Wang, L.; Liang, S.-G. Study on the Peak Factor of the Wind-Induced Response of Super-High-Rise Buildings. Atmosphere 2023, 14, 379. https://doi.org/10.3390/atmos14020379
Wang J-B, Wang Y, Wang L, Liang S-G. Study on the Peak Factor of the Wind-Induced Response of Super-High-Rise Buildings. Atmosphere. 2023; 14(2):379. https://doi.org/10.3390/atmos14020379
Chicago/Turabian StyleWang, Jun-Bo, Yu Wang, Lei Wang, and Shu-Guo Liang. 2023. "Study on the Peak Factor of the Wind-Induced Response of Super-High-Rise Buildings" Atmosphere 14, no. 2: 379. https://doi.org/10.3390/atmos14020379
APA StyleWang, J.-B., Wang, Y., Wang, L., & Liang, S.-G. (2023). Study on the Peak Factor of the Wind-Induced Response of Super-High-Rise Buildings. Atmosphere, 14(2), 379. https://doi.org/10.3390/atmos14020379








