Performance of Bayesian Model Averaging (BMA) for Short-Term Prediction of PM10 Concentration in the Peninsular Malaysia
Abstract
1. Introduction
2. Methods
2.1. Air Quality Monitoring Stations
2.2. The Air Quality Monitoring Data
2.3. The Bayesian Model
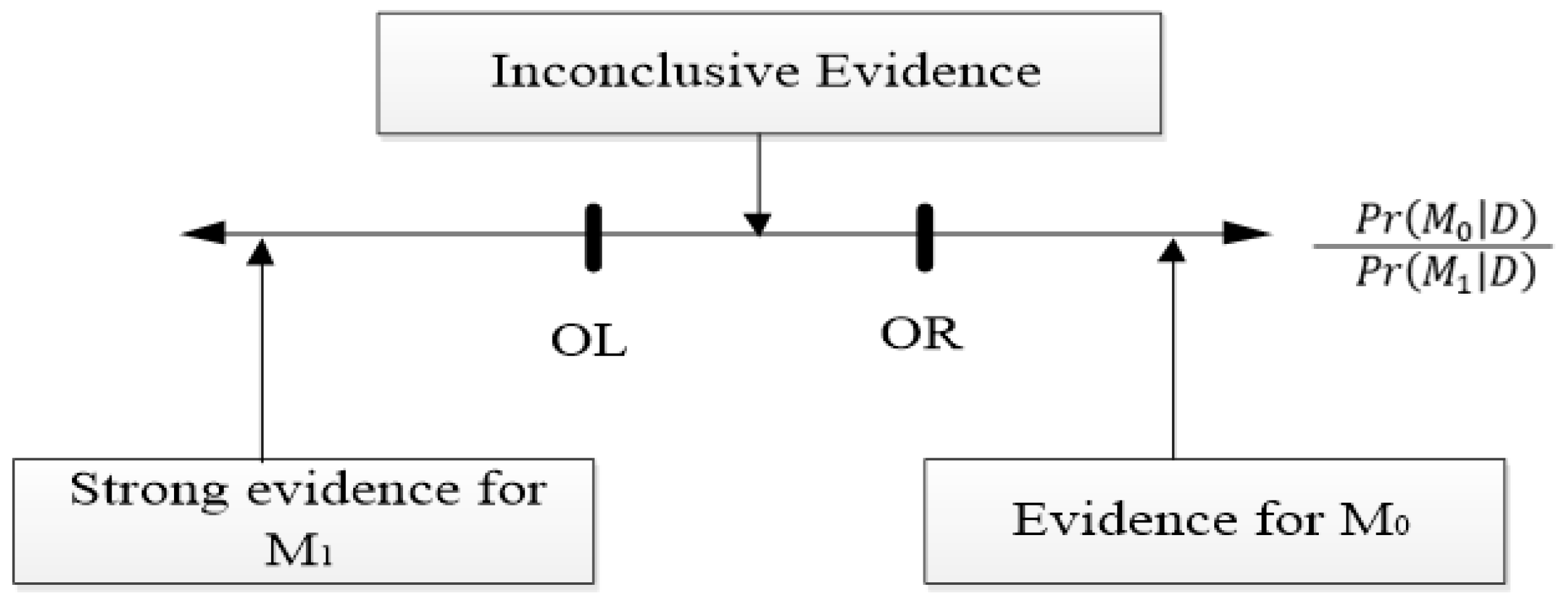
- 1.
- Consider instead of if the log posterior odd is positive (the data support the smaller model).
- 2.
- If the log posterior odd is small and negative, which indicates that the evidence is weaker against the smaller model, then both models should be taken into consideration.
- 3.
2.4. Performance Indicator
3. Results and Discussion
3.1. Descriptive Statistics of PM10 Level
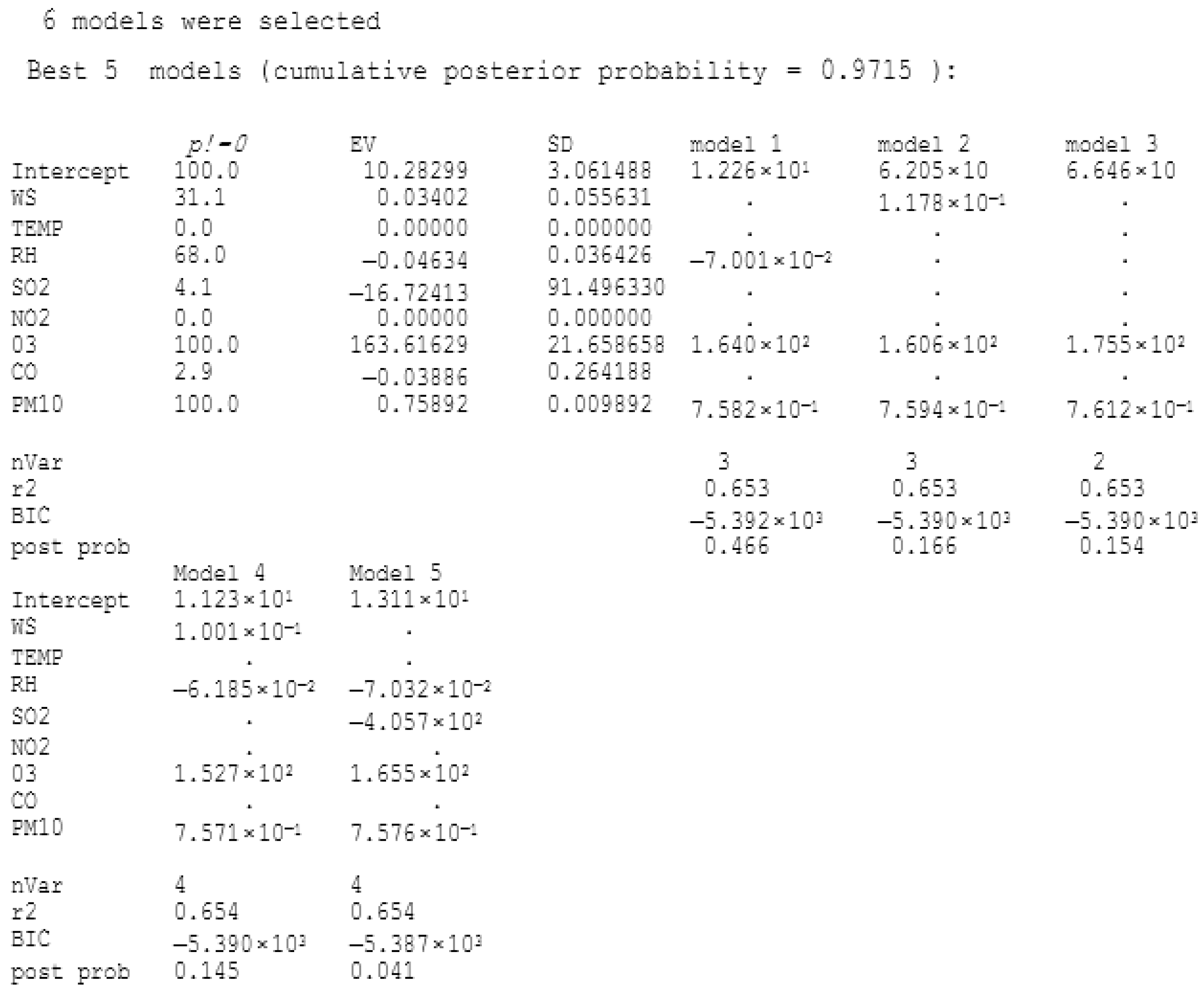
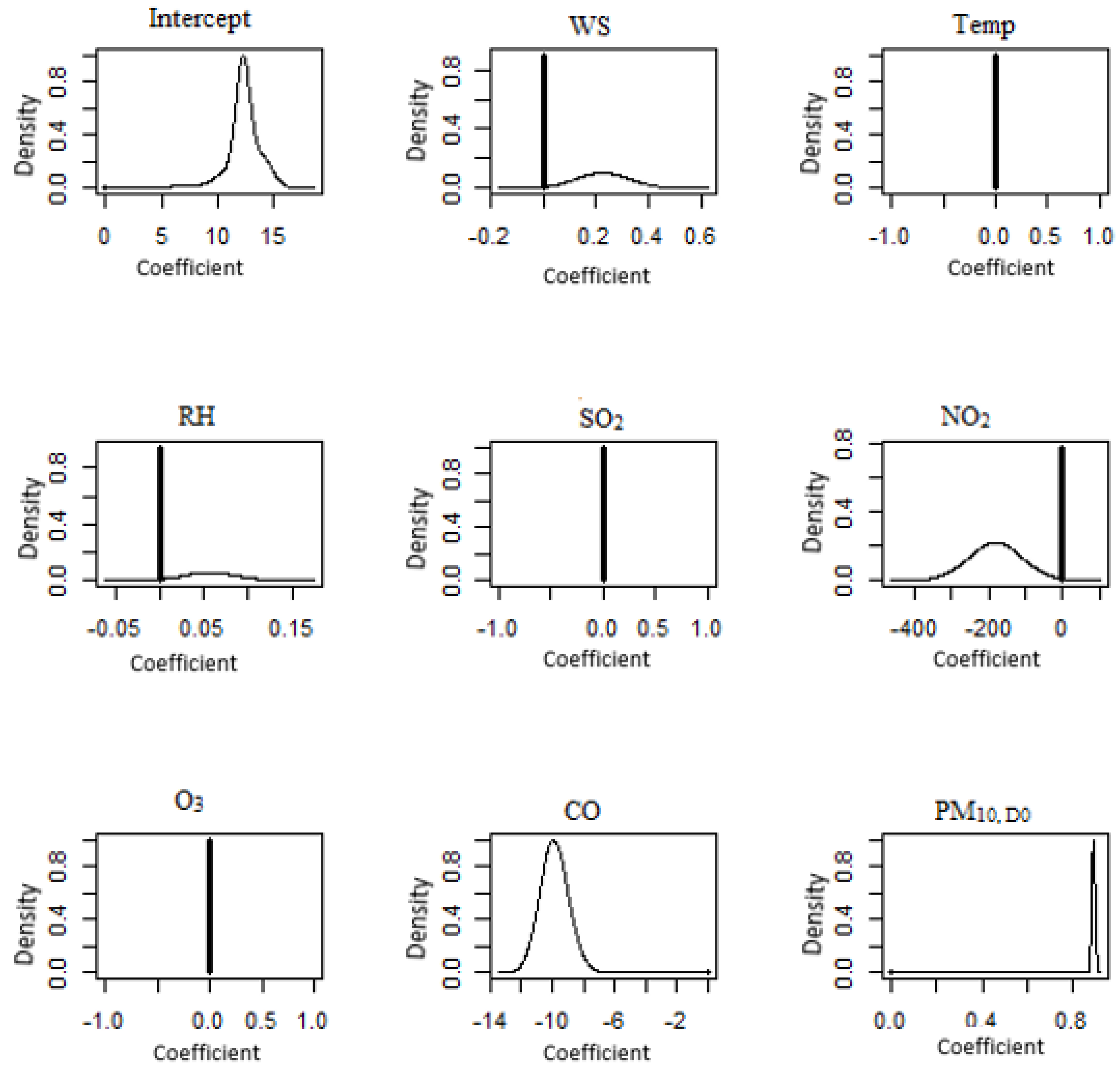
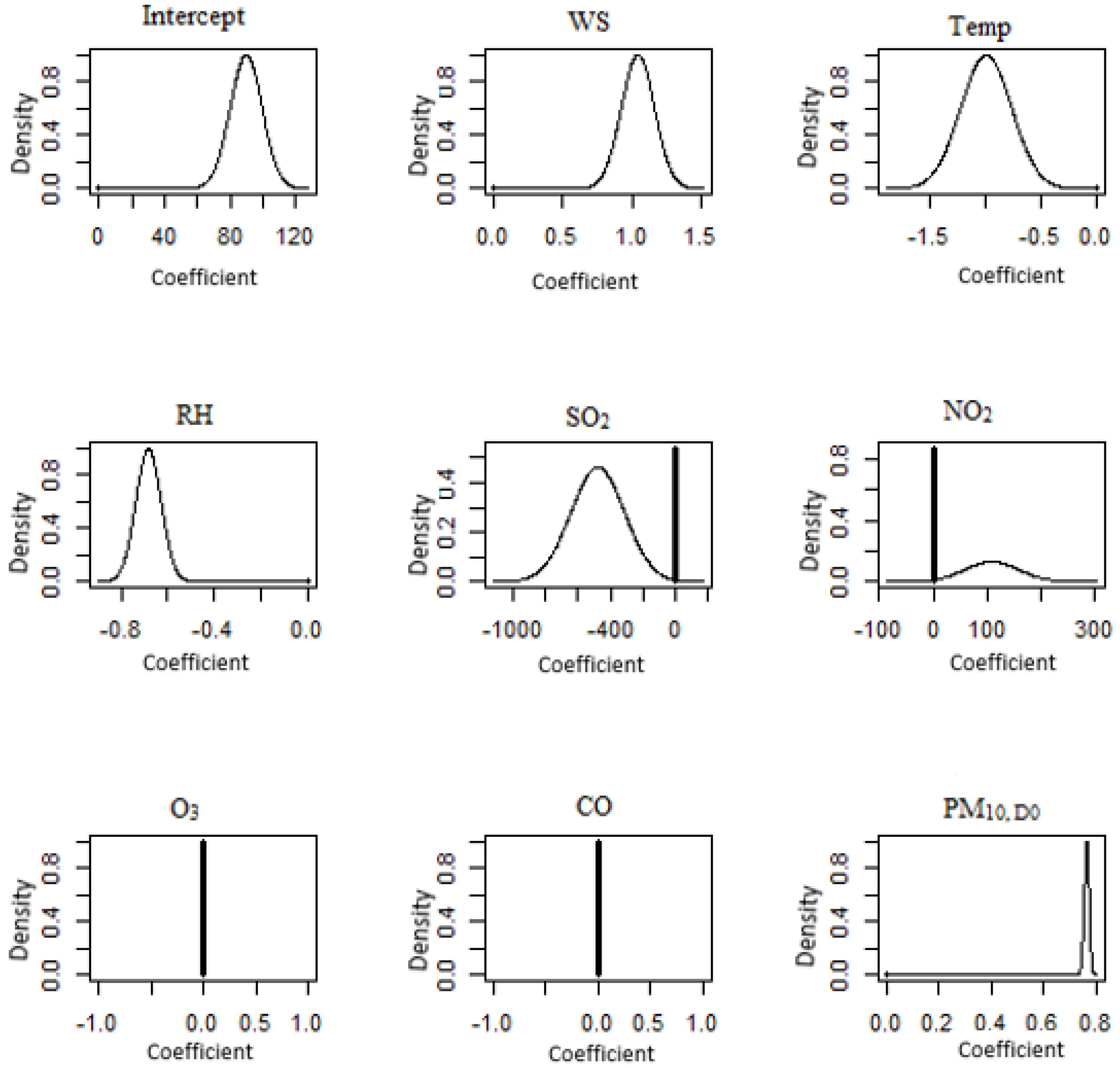
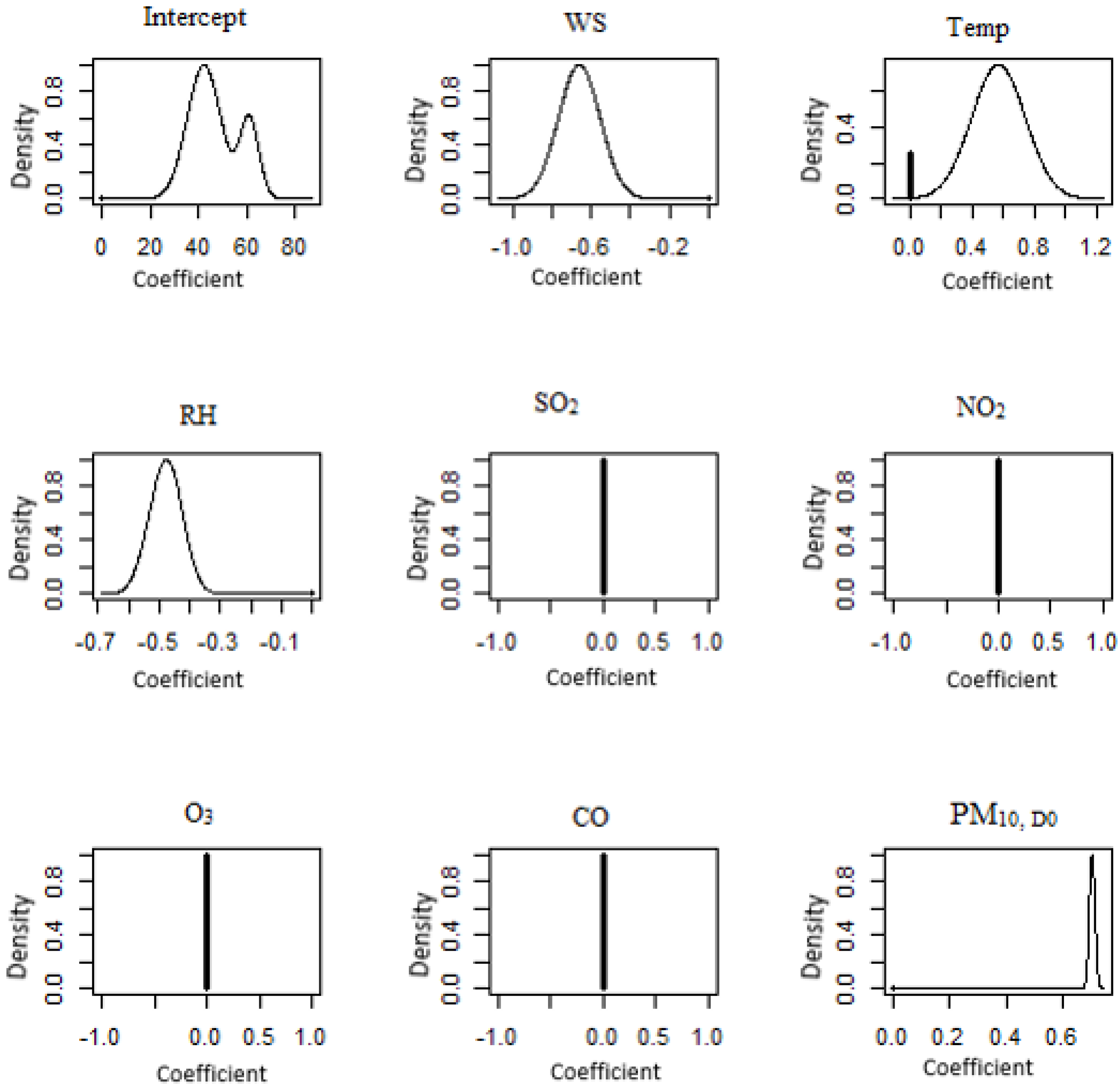
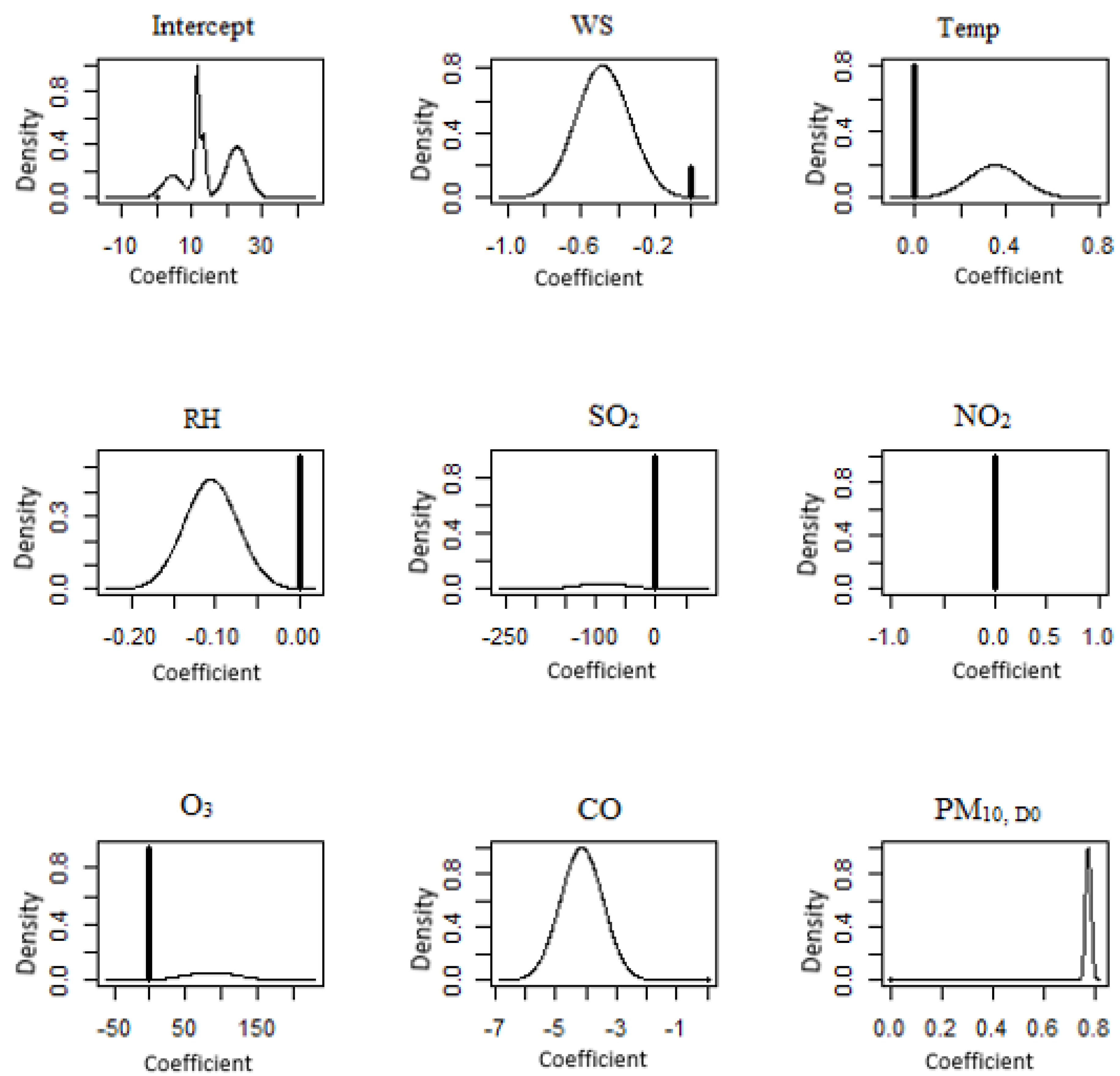
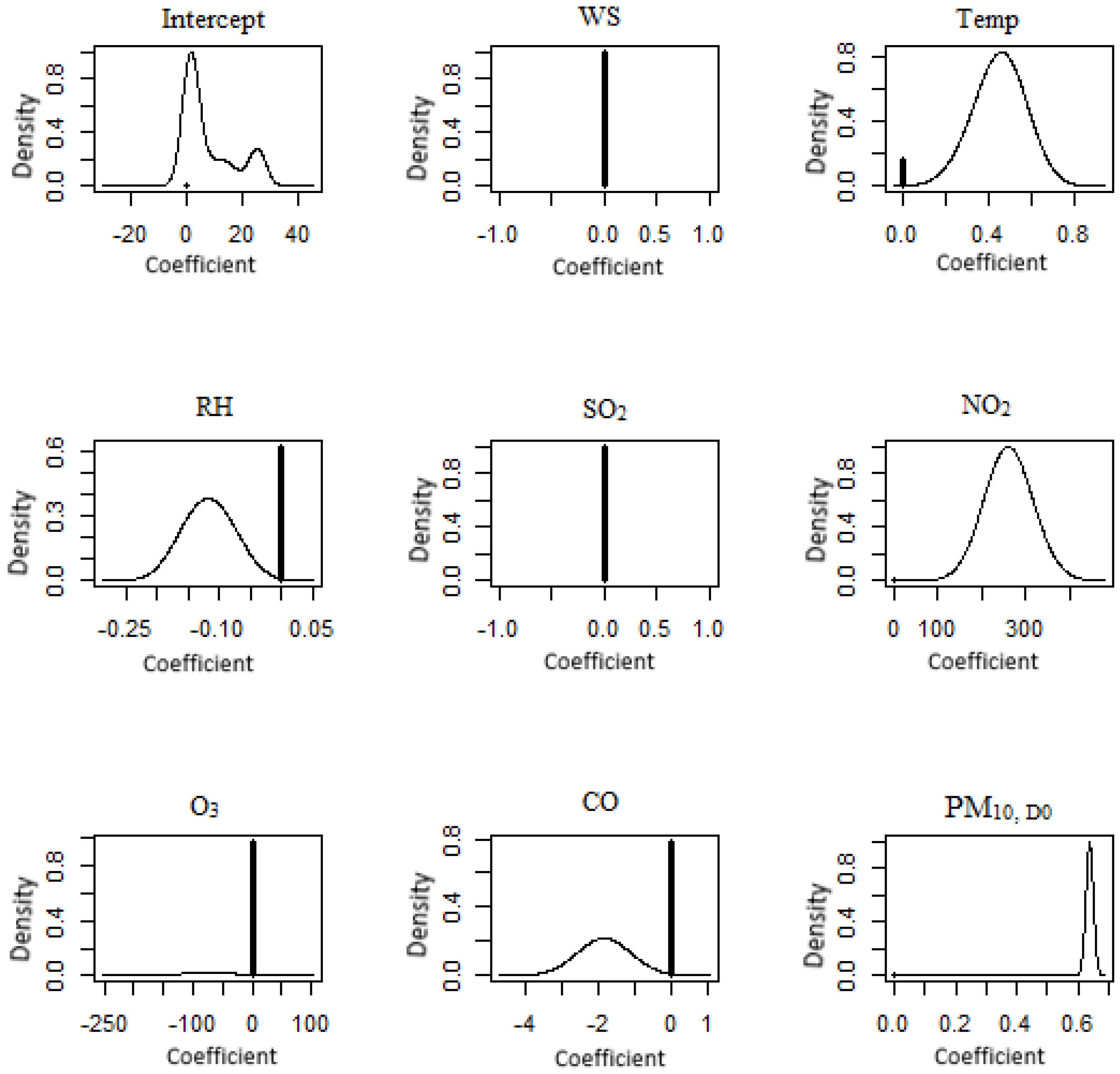
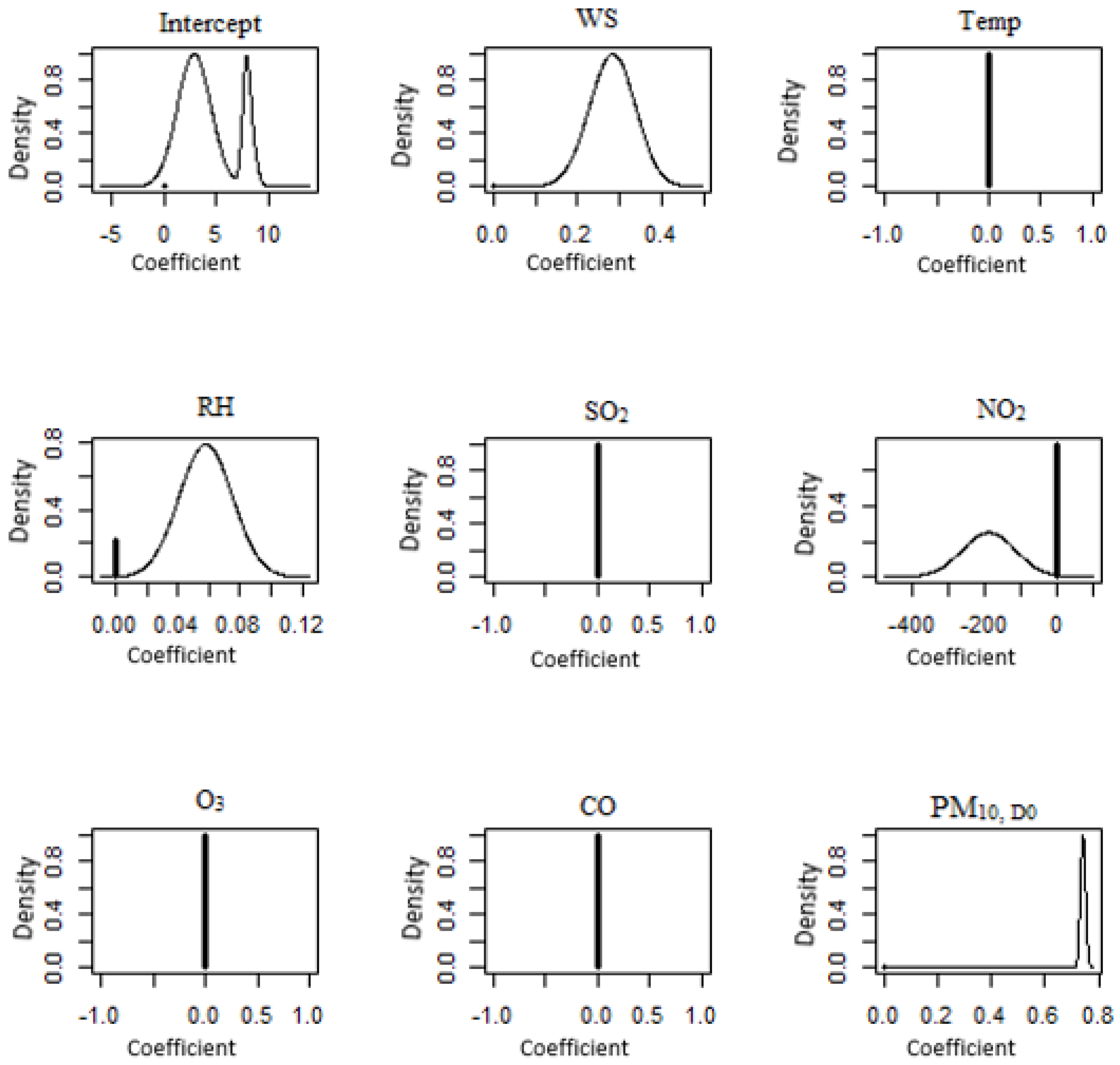
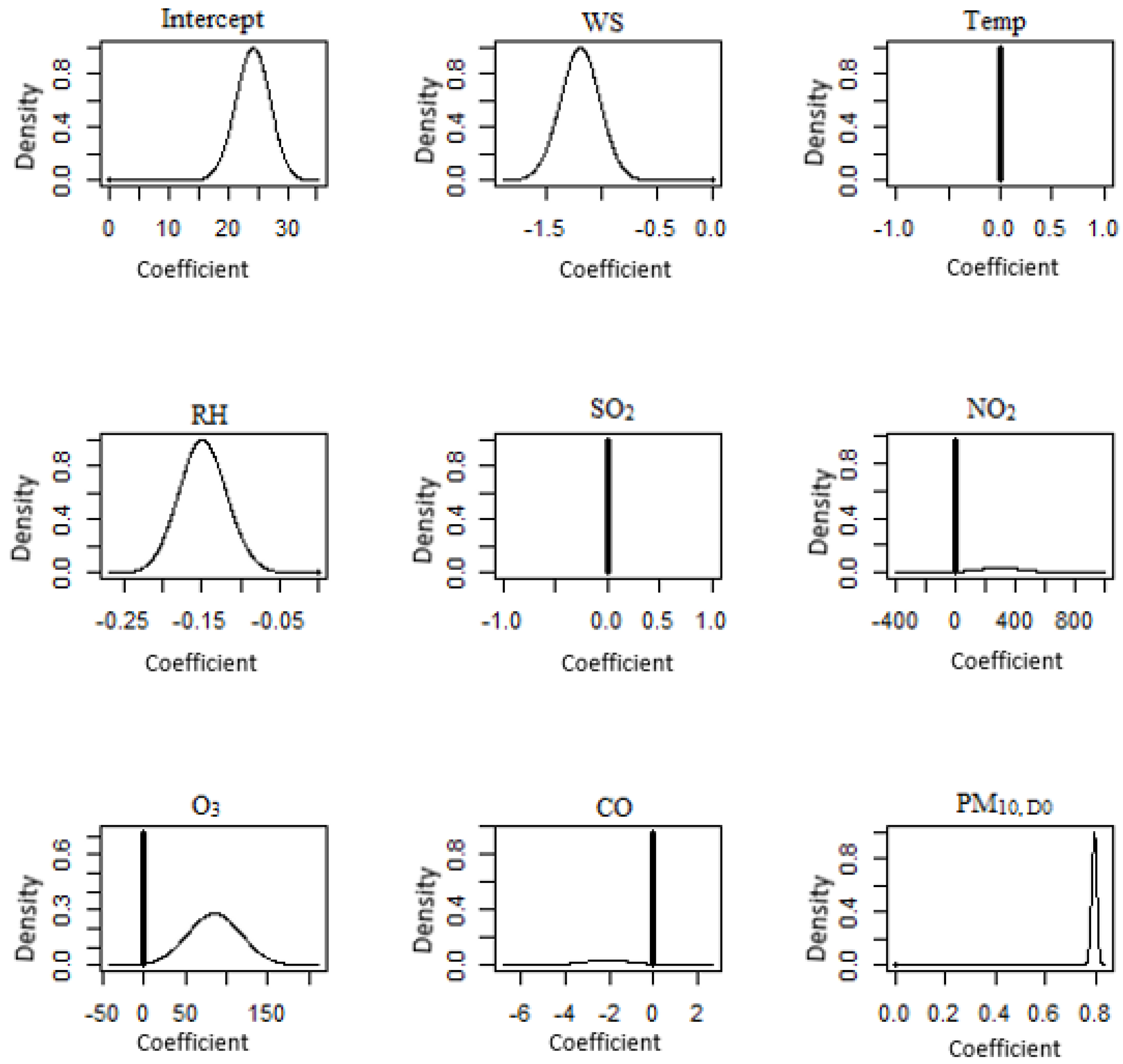
3.2. Bayesian Model Averaging (BMA)
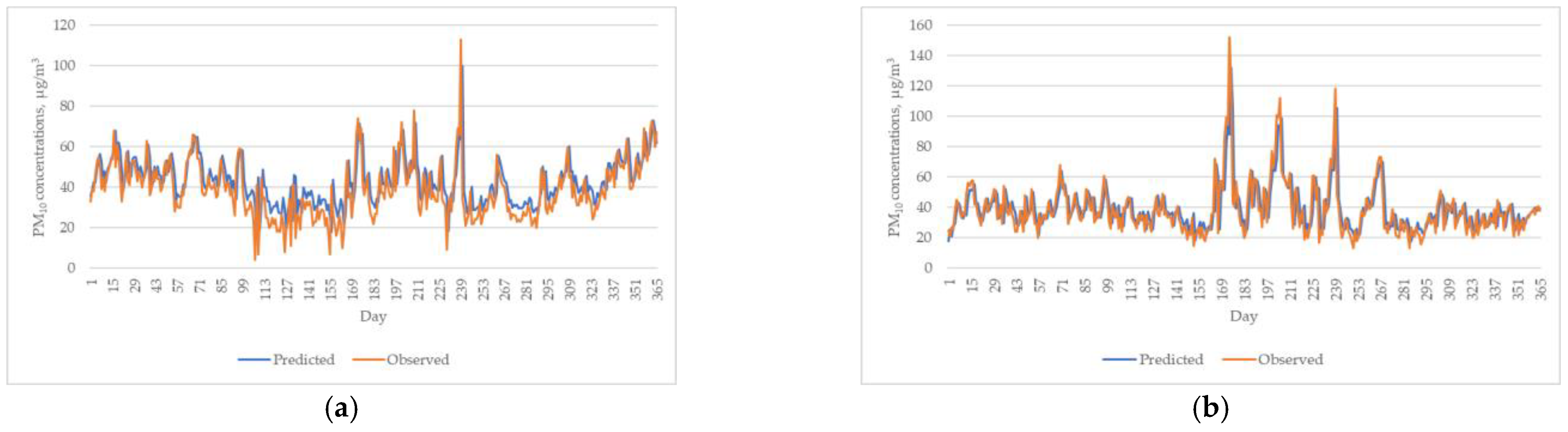
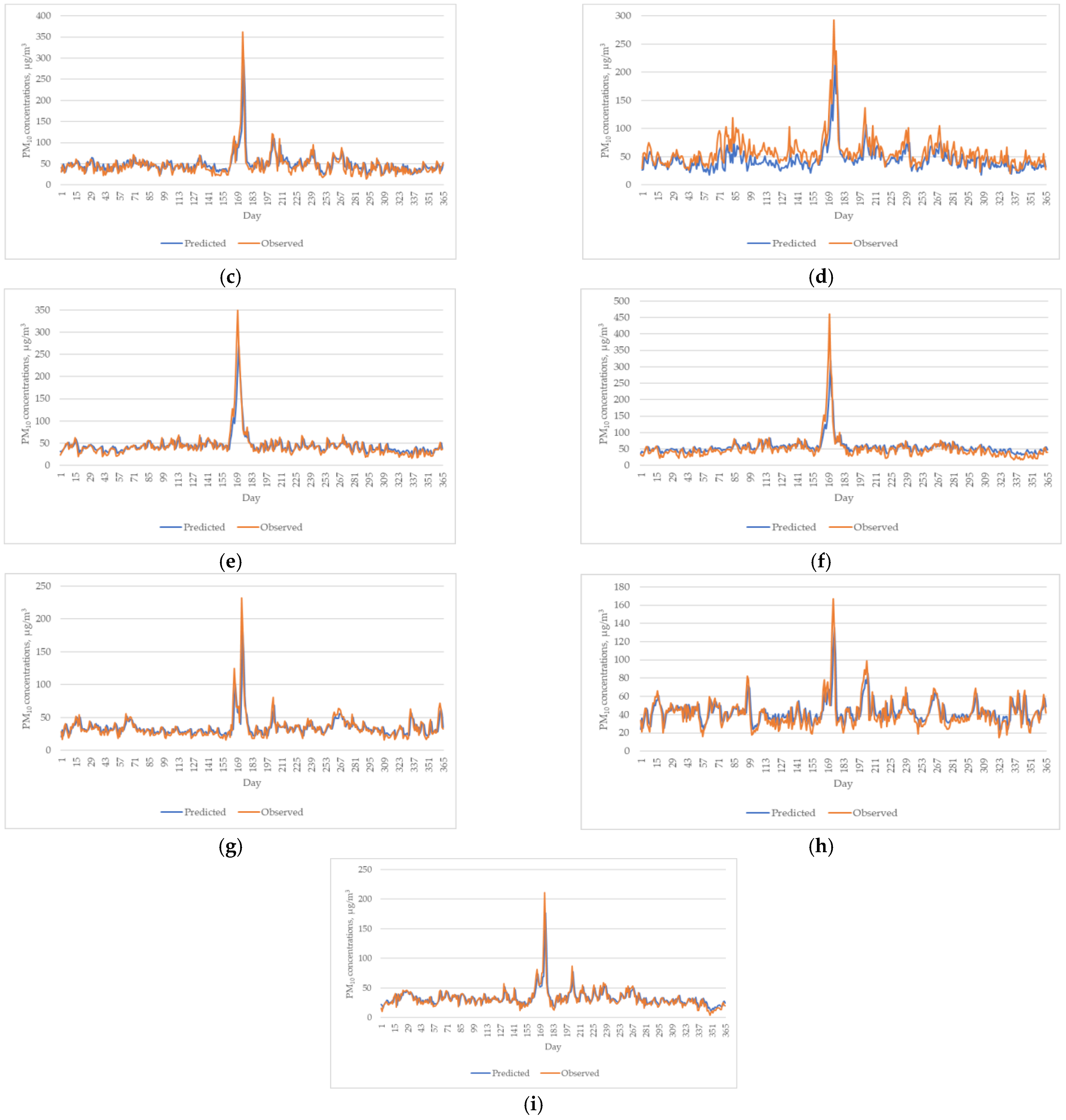
3.3. Performance of Bayesian Model Averaging (BMA)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. Air Pollution and Air Climate Change. In Statistical Yearbook for Asia and the Pacific; UN ESCAP: Beirut, Lebanon, 2011; pp. 79–84. [Google Scholar]
- Zhou, M.; Liu, Y.; Wang, L.; Kuang, X.; Xu, X.; Kan, H. Particulate Air Pollution and Mortality in a Cohort of Chinese Men. Environ. Pollut. 2014, 186, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Mohamed Noor, N.; Yahaya, A.S.; Abdullah, M.; Sandu, A.V. Variation of Air Pollutant (Particulate Matter-PM10) in Peninsular Malaysia Study in the Southwest Coast of Peninsular Malaysia. Rev. Chim. 2015, 66, 1443–1447. [Google Scholar]
- Latif, M.T.; Dominick, D.; Ahamad, F.; Khan, M.F.; Juneng, L.; Hamzah, F.M.; Nadzir, M.S.M. Long Term Assessment of Air Quality from a Background Station on the Malaysian Peninsula. Sci. Total Environ. 2014, 482–483, 336–348. [Google Scholar] [CrossRef] [PubMed]
- Jamalani, M.A.; Abdullah, A.M.; Azid, A.; Ramli, M.F.; Baharudin, M.R.; Chng, K.; Elhadi, R.E.; Yusof, K.M.K.K.; Gnadimzadeh, A.; Quality, A.; et al. PM10 emission inventory of industrial and road transport emission inventory of industrial and road transport vehicles in Klang Valley, Peninsular Malaysia. J. Fundam. Appl. Sci. 2018, 10, 313–324. [Google Scholar] [CrossRef]
- Wang, L.; Shi, T.; Chen, H. Air Pollution and Infant Mortality: Evidence from China. Econ. Hum. Biol. 2023, 49, 101229. [Google Scholar] [CrossRef]
- Azhari, A.; Halim, N.D.A.; Mohtar, A.A.A.; Aiyub, K.; Latif, M.T.; Ketzel, M. Evaluation and Prediction of PM10 and PM2.5 from Road Source Emissions in Kuala Lumpur City Centre. Sustainability 2021, 13, 5402. [Google Scholar] [CrossRef]
- Carugno, M.; Consonni, D.; Randi, G.; Catelan, D.; Grisotto, L.; Bertazzi, P.A.; Biggeri, A.; Baccini, M. Air Pollution Exposure, Cause-Specific Deaths and Hospitalizations in a Highly Polluted Italian Region. Environ. Res. 2016, 147, 415–424. [Google Scholar] [CrossRef]
- Zoran, M.A.; Savastru, R.S.; Savastru, D.M.; Tautan, M.N. Impacts of Exposure to Air Pollution, Radon and Climate Drivers on the COVID-19 Pandemic in Bucharest, Romania: A Time Series Study. Environ. Res. 2022, 212, 113437. [Google Scholar] [CrossRef]
- Hassan, N.A.; Hashim, Z.; Hashim, J.H. Impact of Climate Change on Air Quality and Public Health in Urban Areas. Asia Pac. J. Public Health 2014, 28, 38S–48S. [Google Scholar] [CrossRef]
- Samsuddin, N.A.C.; Khan, M.F.; Maulud, K.N.A.; Hamid, A.H.; Munna, F.T.; Rahim, M.A.A.; Latif, M.T.; Akhtaruzzaman, M. Local and Transboundary Factors’ Impacts on Trace Gases and Aerosol during Haze Episode in 2015 El Niño in Malaysia. Sci. Total Environ. 2018, 630, 1502–1514. [Google Scholar] [CrossRef]
- Latif, M.T.; Othman, M.; Idris, N.; Juneng, L.; Abdullah, A.M.; Hamzah, W.P.; Khan, M.F.; Nik Sulaiman, N.M.; Jewaratnam, J.; Aghamohammadi, N.; et al. Impact of Regional Haze towards Air Quality in Malaysia: A Review. Atmos. Environ. 2018, 177, 28–44. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Ahmed, A.N.; Abdullah, A.M. Forecasting Particulate Matter Concentration Using Linear and Non-Linear Approaches for Air Quality Decision Support. Atmosphere 2019, 10, 667. [Google Scholar] [CrossRef]
- Sulong, N.A.; Latif, M.T.; Khan, M.F.; Amil, N.; Ashfold, M.J.; Wahab, M.I.A.; Chan, K.M.; Sahani, M. Source Apportionment and Health Risk Assessment among Specific Age Groups during Haze and Non-Haze Episodes in Kuala Lumpur, Malaysia. Sci. Total Environ. 2017, 601–602, 556–570. [Google Scholar] [CrossRef]
- Akenji, L.; Bengtsson, M. Making Sustainable Consumption and Production the Core of Sustainable Development Goals. Sustainability 2014, 6, 513–529. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the Specific Heat Capacity of Water-Based Hybrid Nanofluids for Solar Energy Applications: A Comparative Evaluation of Modern Ensemble Machine Learning Techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Shaziayani, W.N.; Ahmat, H.; Razak, T.R.; Zainan Abidin, A.W.; Warris, S.N.; Asmat, A.; Noor, N.M.; Ul-Saufie, A.Z. A Novel Hybrid Model Combining the Support Vector Machine (SVM) and Boosted Regression Trees (BRT) Technique in Predicting PM10 Concentration. Atmosphere 2022, 13, 2046. [Google Scholar] [CrossRef]
- Plocoste, T.; Laventure, S. Forecasting PM10 Concentrations in the Caribbean Area Using Machine Learning Models. Atmosphere 2023, 14, 134. [Google Scholar] [CrossRef]
- Qiao, W.; Wang, Y.; Zhang, J.; Tian, W.; Tian, Y.; Yang, Q. An Innovative Coupled Model in View of Wavelet Transform for Predicting Short-Term PM10 Concentration. J. Environ. Manag. 2021, 289, 112438. [Google Scholar] [CrossRef]
- Sudharshan, K.; Naveen, C.; Vishnuram, P.; Krishna Rao Kasagani, D.V.S.; Nastasi, B. Systematic Review on Impact of Different Irradiance Forecasting Techniques for Solar Energy Prediction. Energies 2022, 15, 6267. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Zeng, H.; Yu, R. Haze Risk Assessment Based on Improved PCA-MEE and ISPO-LightGBM Model. Systems 2022, 10, 263. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Zeng, H.; Zhou, F. PM2.5 Volatility Prediction by XGBoost-MLP Based on GARCH Models. J. Clean Prod. 2022, 356, 131898. [Google Scholar] [CrossRef]
- Department of Statistics Malaysia. Monthly Statistical Bulletin Malaysia; Department of Statistics Malaysia: Putrajaya, Malaysia, 2018. [Google Scholar]
- Ul-Saufie, A.Z.; Yahaya, A.S.; Ramli, N.A.; Hamid, H.A. PM10 Concentrations Short Term Prediction Using Feedforward Backpropagation and General Regression Neural Network in a Sub-Urban Area. J. Environ. Sci. Technol. 2015, 8, 59–73. [Google Scholar] [CrossRef]
- Fong, S.Y.; Abdullah, S.; Ismail, M. Forecasting of Particulate Matter (PM10) Concentration Based on Gaseous Pollutants and Meteorological Factors for Different Monsoons of Urban Coastal Area in Terengganu. J. Sustain. Sci. Manag. Spec. Issue Number 2018, 5, 3–18. [Google Scholar]
- Abdullah, S.; Ismail, M.; Fong, S.Y.; Mahfoodh, A.; Ahmed, A.N. Evaluation for Long Term PM10 Concentration Forecasting Using Multi Linear Regression (MLR) and Principal Component Regression (PCR) Models. Environ. Asia 2016, 9, 101–110. [Google Scholar] [CrossRef]
- Dominick, D.; Juahir, H.; Latif, M.T.; Zain, S.M.; Aris, A.Z. Spatial Assessment of Air Quality Patterns in Malaysia Using Multivariate Analysis. Atmos. Environ. 2012, 60, 172–181. [Google Scholar] [CrossRef]
- Ul-Saufie, A.Z.; Yahaya, A.S.; Ramli, N.A.; Rosaida, N.; Hamid, H.A. Future Daily PM10 Concentrations Prediction by Combining Regression Models and Feedforward Backpropagation Models with Principle Component Analysis (PCA). Atmos. Environ. 2013, 77, 621–630. [Google Scholar] [CrossRef]
- Hamid, H.A. Probabilistic and Distribution Modelling for Predicting PM10 Concentration in Malaysia; Universiti Sains Malaysia: George Town, Malaysia, 2013. [Google Scholar]
- Bozdağ, A.; Dokuz, Y.; Gökçek, Ö.B. Spatial Prediction of PM10 Concentration Using Machine Learning Algorithms in Ankara, Turkey. Environ. Pollut. 2020, 263, 114635. [Google Scholar] [CrossRef]
- Kumar, K.; Pande, B.P. Air Pollution Prediction with Machine Learning: A Case Study of Indian Cities. Int. J. Environ. Sci. Technol. 2022, 1–16. [Google Scholar] [CrossRef]
- Suleiman, A.; Tight, M.R.; Quinn, A.D. Hybrid Neural Networks and Boosted Regression Tree Models for Predicting Roadside Particulate Matter. Environ. Model. Assess. 2016, 21, 731–750. [Google Scholar] [CrossRef]
- Qin, S.; Liu, F.; Wang, J.; Sun, B. Analysis and Forecasting of the Particulate Matter (PM) Concentration Levels over Four Major Cities of China Using Hybrid Models. Atmos. Environ. 2014, 98, 665–675. [Google Scholar] [CrossRef]
- Shahraiyni, H.T.; Sodoudi, S. Statistical Modeling Approaches for PM10 Prediction in Urban Areas; A Review of 21st-Century Studies. Atmosphere 2016, 7, 15. [Google Scholar] [CrossRef]
- Stadlober, E.; Hörmann, S.; Pfeiler, B. Quality and Performance of a PM10 Daily Forecasting Model. Atmos. Environ. 2008, 42, 1098–1109. [Google Scholar] [CrossRef]
- Brunelli, U.; Piazza, V.; Pignato, L.; Sorbello, F.; Vitabile, S. Two-Days Ahead Prediction of Daily Maximum Concentrations of SO2, O3, PM10, NO2, CO in the Urban Area of Palermo, Italy. Atmos. Environ. 2007, 41, 2967–2995. [Google Scholar] [CrossRef]
- Paschalidou, A.K.; Karakitsios, S.; Kleanthous, S.; Kassomenos, P.A. Forecasting Hourly PM10 Concentration in Cyprus through Artificial Neural Networks and Multiple Regression Models: Implications to Local Environmental Management. Environ. Sci. Pollut. Res. 2011, 18, 316–327. [Google Scholar] [CrossRef]
- Baklanov, A.; Hänninen, O.; Slørdal, L.H.; Kukkonen, J.; Bjergene, N.; Fay, B.; Finardi, S.; Hoe, S.C.; Jantunen, M.; Karppinen, A.; et al. Integrated Systems for Forecasting Urban Meteorology, Air Pollution and Population Exposure. Atmos. Chem. Phys. 2007, 7, 855–874. [Google Scholar] [CrossRef]
- Amini, S.M.; Parmeter, C.F. Bayesian Model Averaging in R. Comput. Stat. Data Anal. 2011, 56, 1–35. [Google Scholar] [CrossRef]
- Lee, Y.S. Management of a Periodic-Review Inventory System Using Bayesian Model Averaging When New Marketing Efforts Are Made. Int. J. Prod. Econ. 2014, 158, 278–289. [Google Scholar] [CrossRef]
- Gibbons, J.M.; Cox, G.M.; Wood, A.T.A.; Craigon, J.; Ramsden, S.J.; Tarsitano, D.; Crout, N.M.J. Applying Bayesian Model Averaging to Mechanistic Models: An Example and Comparison of Methods. Environ. Model. Softw. 2008, 23, 973–985. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J. Forecasting Natural Gas Consumption in China by Bayesian Model Averaging. Energy Rep. 2015, 1, 216–220. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. Application of Bayesian Model Averaging in Modeling Long-Term Wind Speed Distributions. Renew. Energy 2010, 35, 1192–1202. [Google Scholar] [CrossRef]
- Pannullo, F.; Lee, D.; Waclawski, E.; Leyland, A.H. How Robust Are the Estimated Effects of Air Pollution on Health? Accounting for Model Uncertainty Using Bayesian Model Averaging. Spat. Spatio-Temporal Epidemiol. 2016, 18, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Benke, K.K.; Lowell, K.E.; Hamilton, A.J. Parameter Uncertainty, Sensitivity Analysis and Prediction Error in a Water-Balance Hydrological Model. Math. Comput. Model. 2008, 47, 1134–1149. [Google Scholar] [CrossRef]
- Fragoso, T.M.; Bertoli, W.; Louzada, F. Bayesian Model Averaging: A Systematic Review and Conceptual Classification. Int. Stat. Rev. 2018, 86, 1–28. [Google Scholar] [CrossRef]
- Hinne, M.; Gronau, Q.F.; van den Bergh, D.; Wagenmakers, E.J. A Conceptual Introduction to Bayesian Model Averaging. Adv. Methods Pract. Psychol. Sci. 2020, 3, 200–215. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian Model Averaging: A Tutorial. Stat. Sci. 1999, 14, 382–417. [Google Scholar]
- Monteiro, A.; Ribeiro, I.; Tchepel, O.; Sá, E.; Ferreira, J.; Carvalho, A.; Martins, V.; Strunk, A.; Galmarini, S.; Elbern, H.; et al. Bias Correction Techniques to Improve Air Quality Ensemble Predictions: Focus on O3 and PM Over Portugal. Environ. Model. Assess. 2013, 18, 533–546. [Google Scholar] [CrossRef]
- Fang, X.; Li, R.; Kan, H.; Bottai, M.; Fang, F.; Cao, Y. Bayesian Model Averaging Method for Evaluating Associations between Air Pollution and Respiratory Mortality: A Time-Series Study. BMJ Open 2016, 6, e011487. [Google Scholar] [CrossRef]
- Cárdenas Rodríguez, M.; Dupont-Courtade, L.; Oueslati, W. Air Pollution and Urban Structure Linkages: Evidence from European Cities. Renew. Sustain. Energy Rev. 2016, 53, 1–9. [Google Scholar] [CrossRef]
- Qi, H.; Ma, S.; Chen, J.; Sun, J.; Wang, L.; Wang, N.; Wang, W.; Zhi, X.; Yang, H. Multi-Model Evaluation and Bayesian Model Averaging in Quantitative Air Quality Forecasting in Central China. Aerosol Air Qual. Res. 2022, 22, 210247. [Google Scholar] [CrossRef]
- Evans, S. Bayesian Regression Analysis; University of Louisville: Louisville, KY, USA, 2012. [Google Scholar]
- Ismail, A.S.; Abdullah, A.M.; Samah, M.A.A. Environmetric Study on Air Quality Pattern for Assessment in Northern Region of Peninsular Malaysia. J. Environ. Sci. Technol. 2017, 10, 186–196. [Google Scholar] [CrossRef]
- Mohtar, Z.A.; Faizah, N.; Yusof, F.; Ramli, N.A.; Yahya, A.S. Comparison of Particulate Matter (PM10) Monitoring Using Beta Attenuation Monitor (BAM) and Simple Instrument. Int. J. Eng. Technol. 2013, 3, 358–367. [Google Scholar]
- Mohd Zahid, A.Z.; Abdul Malik, N.N.A.; Kassim, J. Particulate Matter Study at Residential and Educational Areas in Shah Alam, Malaysia. MATEC Web Conf. 2018, 06010, 1–16. [Google Scholar] [CrossRef]
- Ahmat, H. Prediction of PM10 Concentrations Using Extreme Value Distributions (EVD): Classical and Bayesian Approaches; Universiti Sains Malaysia: George Town, Malaysia, 2016. [Google Scholar]
- Noor, N.M.; Abdullah, M.M.A.; Tan, C.Y.; Ramli, N.A.; Yahay, A.S.; Fitri, N.F.M.Y. Modelling of PM10 Concentration for Industrialized Area in Malaysia: A Case Study in Shah Alam. Phys. Procedia 2011, 22, 318–324. [Google Scholar] [CrossRef]
- Amin, N.A.M.; Adam, M.B.; Aris, A.Z. Bayesian Extreme for Modeling High PM10 Concentration in Johor. Procedia Environ. Sci. 2015, 30, 309–314. [Google Scholar] [CrossRef]
- AhmadIsiyaka, H.; Juahir, H.; Toriman, M.E.; Gasim, B.M.; Azid, A.; Amri, M.K.; Ibrahim, A.; Usman, U.N.; Rano, A.R.; Garba, M.A. Spatial Assessment of Air Pollution Index Using Environmetric Modeling Techniques. Adv. Environ. Biol. 2014, 8, 244–256. [Google Scholar]
- Ismail, A.S.; Latif, M.T.; Azmi, S.Z.; Juneng, L.; Jemain, A.A. Variation of Surface Ozone Recorded at the Eastern Coastal Region of the Malaysian Peninsula. Am. J. Environ. Sci. 2010, 6, 560–569. [Google Scholar] [CrossRef]
- Awang, N.R.; Elbayoumi, M.; Ramli, N.A.; Yahaya, A.S. The Influence of Spatial Variability of Critical Conversion Point (CCP) in Production of Ground Level Ozone in the Context of Tropical Climate. Aerosol Air Qual. Res. 2016, 16, 153–165. [Google Scholar] [CrossRef]
- Banan, N.; Latif, M.T.; Juneng, L.; Ahamad, F. Characteristics of Surface Ozone Concentrations at Stations with Different Backgrounds in the Malaysian Peninsula. Aerosol Air Qual. Res. 2013, 13, 1090–1106. [Google Scholar] [CrossRef]
- Awang, N.R.; Ramli, N.A.; Mohammed, N.I.; Yahaya, A.S. Time Series Evaluation of Ozone Concentrations in Malaysia Based on Location of Monitoring Stations Time Series Evaluation of Ozone Concentrations in Malaysia Based on Location of Monitoring Stations. Int. J. Eng. Technol. 2013, 3, 390–394. [Google Scholar]
- Kery, M. Introduction to WinBUGS for Ecologists: A Bayesian Approach to Regression, ANOVA, Mixed Models and Related Analyses, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2010; ISBN 978-0-12-378605-0. [Google Scholar]
- Kruschke, J.K. Doing Bayesian Data Analysis: A Tutorial with R and BUGS, 1st ed.; Academic Press: Cambridge, MA, USA, 2010; ISBN 0123814855. [Google Scholar]
- Leamer, E.E. Specification Searches: Ad Hoc Inference with Nonexperimental Data, 1st ed.; John Wiley & Sons: New York, NY, USA, 1978; ISBN 0471015202. [Google Scholar]
- Tzikas, D.G.; Likas, A.C.; Galatsanos, N.P. The Variational Approximation for Bayesian Inference. IEEE Signal Process. Mag. 2008, 25, 131–146. [Google Scholar] [CrossRef]
- Adrian Raftery, A.; Hoeting, J.; Volinsky, C.; Painter, I.; Yeung, K. Package “BMA”: Bayesian Model Averaging; 2015. Available online: https://cran.r-project.org/web/packages/BMA/BMA.pdf (accessed on 4 December 2020).
- Amini, S.M.; Parmeter, C.F. Bayesian Model Averaging in R. J. Econ. Soc. Meas. 2011, 36, 253–287. [Google Scholar] [CrossRef]
- Sloughter, J.M.; Gneiting, T.; Raftery, A.E. Probabilistic Wind Speed Forecasting Using Ensembles and Bayesian Model Averaging. J. Am. Stat. Assoc. 2010, 105, 25–35. [Google Scholar] [CrossRef]
- Madigan, D.; Raftery, A.E. Model Selection and Accounting in Graphical Models for Model Uncertainty Using Occam’s Window. J. Am. Stat. Assoc. 1994, 89, 1535–1546. [Google Scholar] [CrossRef]
- Department of Environment Malaysia. Malaysia Annual Report 2015; Department of Environment Malaysia: Putrajaya, Malaysia, 2015. [Google Scholar]
- Department of Environment Malaysia. Malaysia Environmental Quality Report 2006; Department of Environment Malaysia: Putrajaya, Malaysia, 2007. [Google Scholar]
- Department of Environment Malaysia. Malaysia Environmental Quality Report 2005; Department of Environment Malaysia: Putrajaya, Malaysia, 2006. [Google Scholar]
- Afroz, R.; Hassan, M.N.; Ibrahim, N.A. Review of Air Pollution and Health Impacts in Malaysia. Environ. Res. 2003, 92, 71–77. [Google Scholar] [CrossRef]
- Kamarul Zaman, N.A.F.; Kanniah, K.D.; Kaskaoutis, D.G. Estimating Particulate Matter Using Satellite Based Aerosol Optical Depth and Meteorological Variables in Malaysia. Atmos. Res. 2017, 193, 142–162. [Google Scholar] [CrossRef]
- Department of Environment Malaysia Chronology of Haze Episodes in Malaysia. Available online: www.doe.gov.my/en/2021/10/26/chronology-of-haze-episodes-in-malaysia-2/ (accessed on 15 January 2022).
- Rahman, A.S.R.; Ismail, S.N.S.; Ramli, M.F.; Latif, M.T.; Abidin, E.Z.; Praveena, S.M. The Assessment of Ambient Air Pollution Trend in Klang Valley. World Environ. 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Elbayoumi, M.; Ramli, N.A.; Yusof, N.F.F.; Yahaya, A.S.; Al Madhoun, W.; Ul-Saufie, A.Z. Multivariate Methods for Indoor PM10 and PM2.5 Modelling in Naturally Ventilated Schools Buildings. Atmos. Environ. 2014, 94, 11–21. [Google Scholar] [CrossRef]
- Wong, Y.K.; Mohamed Noor, N.; Mohamad Hashim, N.I. Temporal Variation of Ambient PM10 Concentration within an Urban-Industrial Environment. In Proceedings of the E3S Web of Conferences, Penang, Malaysia, 19 March 2018; EDP Sciences: Les Ulis, France, 2018; Volume 34. [Google Scholar]
- Kusumaningtyas, S.D.A.; Aldrian, E. Impact of the June 2013 Riau Province Sumatera Smoke Haze Event on Regional Air Pollution. Environ. Res. Lett. 2016, 11, 075007. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Li, T.; Shen, H.; Zhang, L. The Relationships between PM2.5 and Meteorological Factors in China: Seasonal and Regional Variations. Int. J. Environ. Res. Public Health 2017, 14, 1510. [Google Scholar] [CrossRef]
- Monteiro, A.; Ribeiro, I.; Tchepel, O.; Carvalho, A.; Martins, H.; Sá, E.; Ferreira, J.; Martins, V.; Galmarini, S.; Miranda, A.I.; et al. Ensemble Techniques to Improve Air Quality Assessment: Focus on O3 and PM. Environ. Model. Assess. 2013, 18, 249–257. [Google Scholar] [CrossRef]
- Tran, H.; Kim, J.; Kim, D.; Choi, M.; Choi, M. Impact of Air Pollution on Cause-Specific Mortality in Korea: Results from Bayesian Model Averaging and Principle Component Regression Approaches. Sci. Total Environ. 2018, 636, 1020–1031. [Google Scholar] [CrossRef]
- Wang, G.; Jia, R.; Liu, J.; Zhang, H. A Hybrid Wind Power Forecasting Approach Based on Bayesian Model Averaging and Ensemble Learning. Renew. Energy 2020, 145, 2426–2434. [Google Scholar] [CrossRef]
- Consonni, G.; Fouskakis, D.; Liseo, B.; Ntzoufras, I. Prior Distributions for Objective Bayesian Analysis. Bayesian Anal. 2018, 13, 627–679. [Google Scholar] [CrossRef]
- Vehtari, A.; Simpson, D.P.; Yao, Y.; Gelman, A. Limitations of “Limitations of Bayesian Leave-One-out Cross-Validation for Model Selection. ” Comput. Brain Behav. 2019, 2, 22–27. [Google Scholar] [CrossRef]
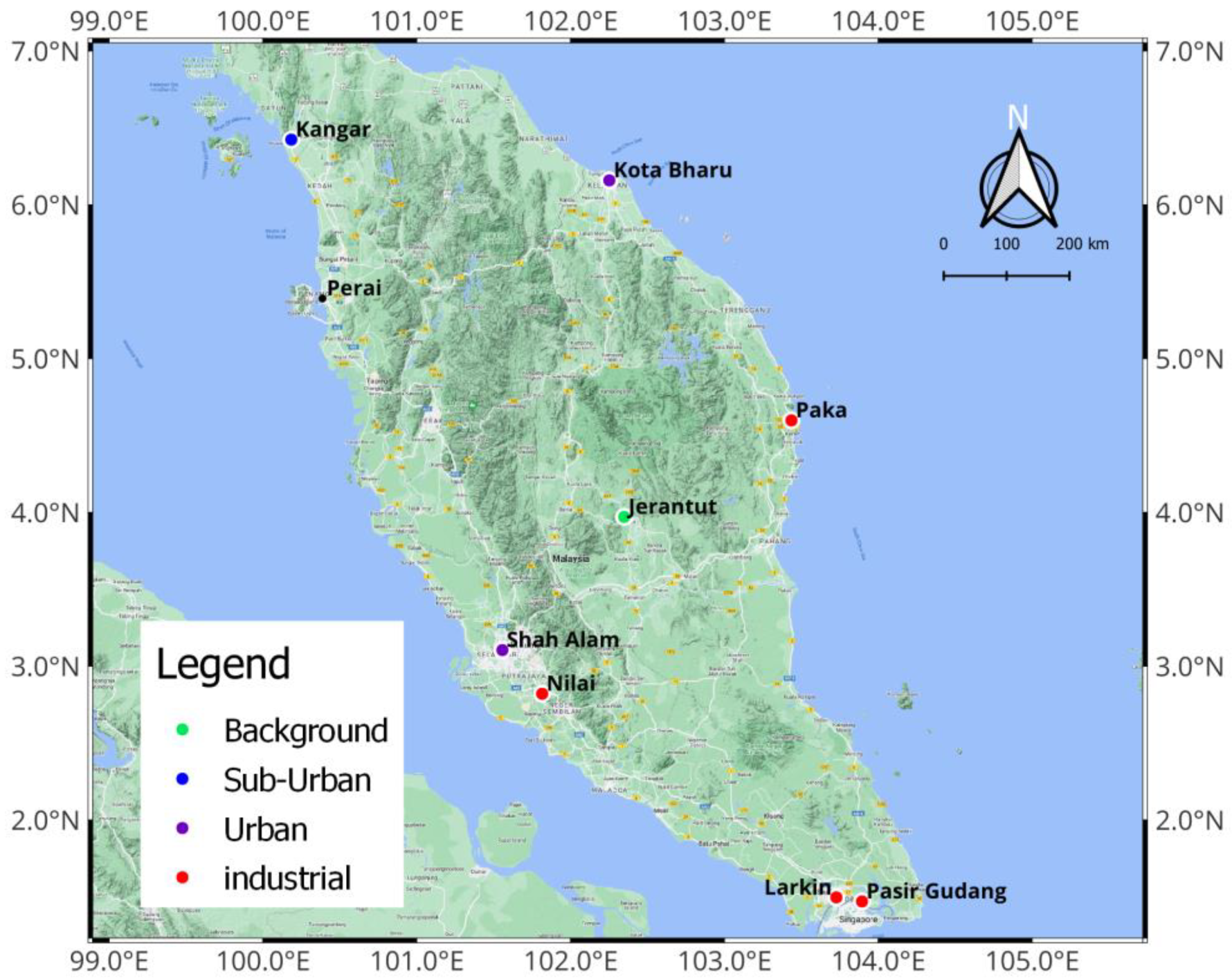


| Station | State | Location | Coordinate | Region | Classification |
|---|---|---|---|---|---|
| Kangar | Perlis | Institut Latihan Perindustrian (ILP) | 6°25.424′ N 100°11.046′ E | North | Sub-urban |
| Perai | Pulau Pinang | Sek. Keb. Cenderawasih, Taman Inderawasih | 5°23.470′ N 100°23.213′ E | Industrial | |
| Shah Alam | Selangor | Sek. Keb. Taman Tun Dr. Ismail Jaya | 3°06.287′ N 101°33.368′ E | Centre | Urban |
| Nilai | Negeri Sembilan | Taman Semarak (Phase II) | 2°49.246′ N 101°48.877′ E | Industrial | |
| Larkin | Johor | Teacher Education Temenggong Ibrahim Campus | 1°29.815′ N 103°43.617′ E | South | Industrial |
| Pasir Gudang | Johor | Sek. Men. Keb. Pasir Gudang 2 | 1°28.225′ N 103°53.637′ E | Industrial | |
| Paka | Terengganu | Tenaga Nasional Berhad Quarters, Paka-Kertih | 4°35.880′ N 103°26.096′ E | East | Industrial |
| Kota Bharu | Kelantan | Sek. Men. Keb. Tanjung Chat | 6°09.520′ N 102°15.059′ E | Urban | |
| Jerantut | Pahang | Meteorology Monitoring Station Batu Embun | 3°58.238′ N 102°20.863′ E | - | Background |
| Parameter | Symbol | Unit |
|---|---|---|
| Particulate matter | PM10 | µg/m3 |
| Nitrogen dioxide | NO2 | ppm |
| Sulphur dioxide | SO2 | ppm |
| Carbon monoxide | CO | ppm |
| Ground-level ozone | O3 | ppm |
| Temperature | T; Temp | °C |
| Relative humidity | RH | % |
| Wind speed | WS | km/h |
| Distributions | Formula | |
|---|---|---|
| Normal | ||
| cdf | ||
| Uniform | ||
| cdf | ||
| Gamma | ||
| cdf | ||
| Conjugate Prior Distribution | Likelihood | Posterior Distribution |
|---|---|---|
| BIC (Bayesian Information Criterion) Difference | Evidence |
|---|---|
| 0–2 | Weak |
| 3–6 | Positive |
| 7–10 | Strong |
| >10 | Very strong |
| Performance Indicator | Equation | Criteria |
|---|---|---|
| R2 | Range between [0, 1] with the best value of 1. | |
| IA | ||
| KGE | ||
| MAE | The best model has the values closer to zero (0) or the smallest values. | |
| RMSE | ||
| MAPE |
| Station | Kangar | Perai | Shah Alam | Nilai | Larkin | Pasir Gudang | Paka | Kota Bharu | Jerantut |
|---|---|---|---|---|---|---|---|---|---|
| Number of data set | 6209 | 6209 | 6209 | 6178 | 6209 | 6179 | 6209 | 6209 | 6209 |
| Minimum | 4 | 13 | 14 | 15 | 13 | 15 | 14 | 12 | 11 |
| Maximum | 363 | 317 | 587 | 327 | 349 | 461 | 238 | 189 | 271 |
| Mean | 40.74 | 53.77 | 53.61 | 59.19 | 43.17 | 51.21 | 37.34 | 42.06 | 38.35 |
| Std. Deviation | 16.50 | 24.80 | 26.89 | 23.39 | 18.54 | 19.54 | 13.81 | 15.63 | 15.99 |
| Coefficient of variation | 0.41 | 0.46 | 0.50 | 0.40 | 0.43 | 0.38 | 0.37 | 0.37 | 0.42 |
| Skewness | 3.09 | 1.67 | 4.64 | 3.15 | 4.05 | 4.65 | 4.30 | 1.82 | 3.19 |
| Kurtosis | 36.77 | 5.55 | 53.38 | 20.82 | 37.01 | 57.04 | 37.88 | 6.97 | 24.01 |
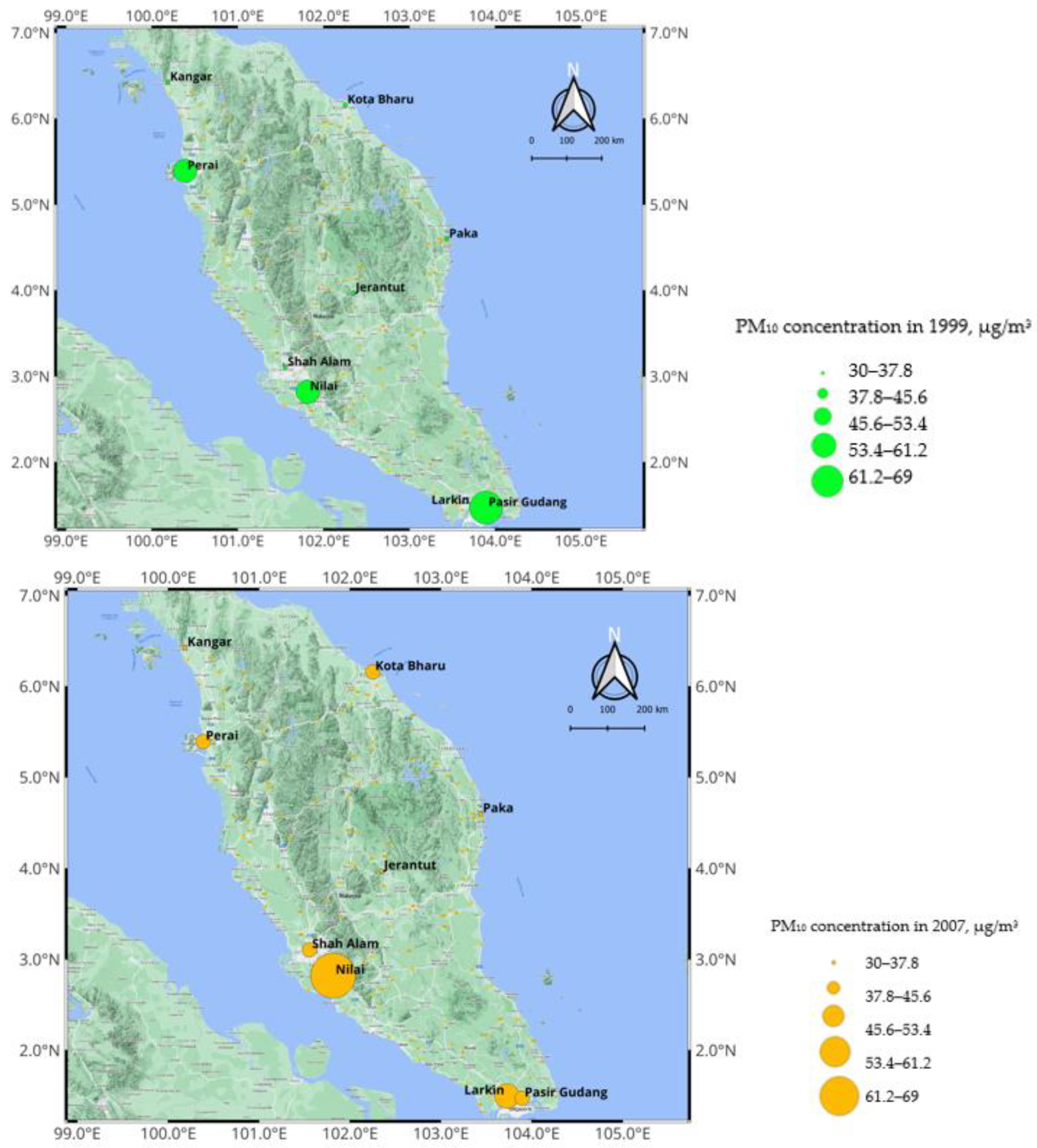
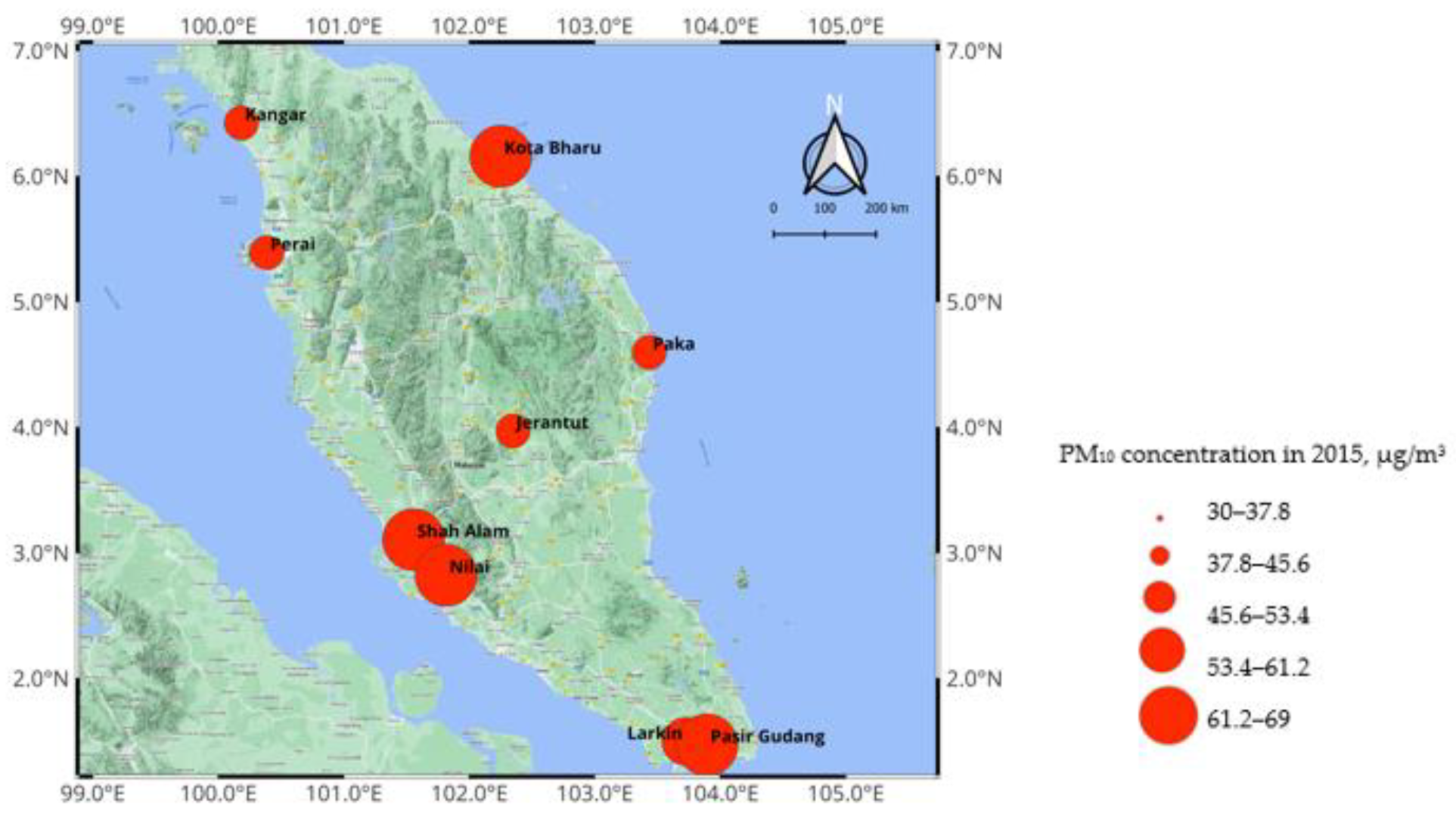
| Year | Kangar | Perai | Shah Alam | Nilai | Larkin | Pasir Gudang | Paka | Kota Bharu | Jerantut |
|---|---|---|---|---|---|---|---|---|---|
| 1999 | 33 | 52 * | 35 | 45 | 34 | 55 * | 38 | 34 | 37 |
| 2000 | 37 | 55 * | 39 | 59 * | 34 | 50 * | 37 | 40 | 32 |
| 2001 | 38 | 57 * | 43 | 54 * | 33 | 49 | 36 | 37 | 35 |
| 2002 | 44 | 74 * | 78 * | 59 * | 37 | 49 | 42 | 37 | 36 |
| 2003 | 43 | 79 * | 58 * | 55 * | 38 | 48 | 38 | 40 | 36 |
| 2004 | 54 * | 91 * | 67 * | 61 * | 50 * | 46 | 33 | 47 | 44 |
| 2005 | 59 * | 78 * | 64 * | 63 * | 36 | 46 | 32 | 43 | 50 * |
| 2006 | 43 | 50 * | 56 * | 63 * | 56 * | 47 | 34 | 40 | 45 |
| 2007 | 38 | 45 | 45 | 62 * | 55 * | 43 | 32 | 40 | 38 |
| 2008 | 34 | 38 | 54 * | 56 * | 40 | 51 * | 38 | 38 | 42 |
| 2009 | 35 | 39 | 53 * | 56 * | 44 | 57 * | 38 | 43 | 36 |
| 2010 | 36 | 40 | 48 | 56 * | 42 | 49 | 35 | 42 | 34 |
| 2011 | 38 | 46 | 54 * | 59 * | 44 | 45 | 38 | 46 | 36 |
| 2012 | 35 | 42 | 48 | 61 * | 41 | 51 * | 32 | 39 | 34 |
| 2013 | 39 | 39 | 47 | 58 * | 44 | 51 * | 35 | 42 | 34 |
| 2014 | 39 | 42 | 55 * | 64 * | 45 | 50 * | 44 | 41 | 33 |
| 2015 | 47 | 47 | 66 * | 70 * | 60 * | 65 * | 53 * | 67 * | 49 |
| Region | Station | BMA Model |
|---|---|---|
| North | Kangar | PM10,D1 = 10.283 + 163.616O3 + 0.759PM10,D0 |
| Perai | PM10,D1 = 12.272 − 9.879CO + 0.893PM10,D0 | |
| Centre | Shah Alam | PM10,D1 = 89.618 + 1.044WS − 0.987T − 0.682RH + 0.764PM10,D0 |
| Nilai | PM10,D1 = 46.79 − 0.664WS − 0.480RH + 0.705PM10,D0 | |
| South | Larkin | PM10,D1 = 15.450 − 0.392WS − 4.143CO + 0.775PM10,D0 |
| Pasir Gudang | PM10,D1 = 7.923 + 0.371T + 261.238NO2 + 0.639PM10,D0 | |
| East | Paka | PM10,D1 = 4.016 + 0.283WS + 0.045RH + 0.743PM10,D0 |
| Kota Bharu | PM10,D1 = 12.910 − 0.131RH + 698.4NO2 + 275O3 − 4.194CO + 0.731PM10,D0 | |
| Background station | Jerantut | PM10,D1 = 24.154 − 1.191WS − 0.148RH + 0.796PM10,D0 |
| Station | PI for Training | |||||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | KGE | IA | R2 | |
| Kangar | 7.290 | 12.355 | 17.699 | 0.730 | 0.898 | 0.699 |
| Perai | 7.878 | 13.555 | 18.105 | 0.728 | 0.889 | 0.667 |
| Shah Alam | 13.255 | 22.560 | 24.322 | 0.691 | 0.877 | 0.655 |
| Nilai | 13.522 | 21.180 | 21.652 | 0.669 | 0.871 | 0.654 |
| Larkin | 8.584 | 14.933 | 16.973 | 0.692 | 0.905 | 0.748 |
| Pasir Gudang | 9.747 | 18.091 | 17.726 | 0.609 | 0.877 | 0.749 |
| Paka | 8.874 | 15.764 | 22.704 | 0.638 | 0.857 | 0.632 |
| Kota Bharu | 9.127 | 13.247 | 20.701 | 0.706 | 0.887 | 0.677 |
| Jerantut | 7.164 | 13.012 | 18.204 | 0.740 | 0.897 | 0.696 |
| Station | PI for Validation | |||||
| MAE | RMSE | MAPE | KGE | IA | R2 | |
| Kangar | 8.028 | 12.790 | 18.406 | 0.732 | 0.889 | 0.696 |
| Perai | 8.581 | 14.508 | 19.361 | 0.732 | 0.883 | 0.638 |
| Shah Alam | 12.767 | 21.462 | 21.538 | 0.692 | 0.890 | 0.676 |
| Nilai | 16.011 | 23.725 | 31.718 | 0.666 | 0.843 | 0.661 |
| Larkin | 8.268 | 14.653 | 15.681 | 0.702 | 0.907 | 0.749 |
| Pasir Gudang | 10.373 | 17.473 | 16.963 | 0.614 | 0.884 | 0.752 |
| Paka | 7.736 | 14.505 | 17.328 | 0.636 | 0.875 | 0.663 |
| Kota Bharu | 8.933 | 12.714 | 18.763 | 0.706 | 0.883 | 0.703 |
| Jerantut | 6.911 | 12.823 | 16.690 | 0.737 | 0.897 | 0.692 |
| Case Study | Parameter and Data | Result |
|---|---|---|
| Northern China [50] | PM10, CO, NOx, temperature, relative humidity, wind speed and pressure (2009–2010) |
|
| Europe [51] | NO2, PM10 and SO2, number of fragments, shares of artificial, agricultural, wetland, forest areas, population density, population decentralization (2006) |
|
| West Central, Scotland [44] | NO2, 2089 disease data (2006–2012) |
|
| Portugal [84] | O3 and PM10 (July 2006) |
|
| Seoul, South Korea [85] | PM10, O3, NO2, CO and SO2 (2005–2015) |
|
| Henan Province, China [52] | PM2.5, PM10, O3, NO2, CO and SO2 (2017–2019) |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramli, N.; Abdul Hamid, H.; Yahaya, A.S.; Ul-Saufie, A.Z.; Mohamed Noor, N.; Abu Seman, N.A.; Kamarudzaman, A.N.; Deák, G. Performance of Bayesian Model Averaging (BMA) for Short-Term Prediction of PM10 Concentration in the Peninsular Malaysia. Atmosphere 2023, 14, 311. https://doi.org/10.3390/atmos14020311
Ramli N, Abdul Hamid H, Yahaya AS, Ul-Saufie AZ, Mohamed Noor N, Abu Seman NA, Kamarudzaman AN, Deák G. Performance of Bayesian Model Averaging (BMA) for Short-Term Prediction of PM10 Concentration in the Peninsular Malaysia. Atmosphere. 2023; 14(2):311. https://doi.org/10.3390/atmos14020311
Chicago/Turabian StyleRamli, Norazrin, Hazrul Abdul Hamid, Ahmad Shukri Yahaya, Ahmad Zia Ul-Saufie, Norazian Mohamed Noor, Nor Amirah Abu Seman, Ain Nihla Kamarudzaman, and György Deák. 2023. "Performance of Bayesian Model Averaging (BMA) for Short-Term Prediction of PM10 Concentration in the Peninsular Malaysia" Atmosphere 14, no. 2: 311. https://doi.org/10.3390/atmos14020311
APA StyleRamli, N., Abdul Hamid, H., Yahaya, A. S., Ul-Saufie, A. Z., Mohamed Noor, N., Abu Seman, N. A., Kamarudzaman, A. N., & Deák, G. (2023). Performance of Bayesian Model Averaging (BMA) for Short-Term Prediction of PM10 Concentration in the Peninsular Malaysia. Atmosphere, 14(2), 311. https://doi.org/10.3390/atmos14020311









