Abstract
This study aims to identify the optimal operating parameters for the carbon dioxide (CO2) capture process using a combination of artificial intelligence and metaheuristics techniques. The main objective of the study is to maximize CO2 capture capacity. The proposed method integrates fuzzy modeling with the RUNge Kutta optimizer (RUN) to analyze the impact of three operational factors: carbonation temperature, carbonation duration, and H2O-to-CO2 flow rate ratio. These factors are considered to maximize the CO2 capture. A fuzzy model was developed based on the measured data points to simulate the CO2 capture process in terms of the stated parameters. The model was then used to identify the optimal values of carbonation temperature, carbonation duration, and H2O-to-CO2 flow rate ratio using RUN. The results of the proposed method are then compared with an optimized performance using the response surface methodology (RSM) and measured data to demonstrate the superiority of the proposed strategy. The results of the study showed that the suggested technique increased the CO2 capture capacity from 6.39 to 6.99 by 10.08% and 9.39%, respectively, compared to the measured and RSM methods. This implies that the proposed method is an effective approach to maximize the CO2 capture capacity. The results of this study can be used to improve the performance of the CO2 capture process in various industrial applications.
1. Introduction
Massive fossil fuel consumption has severe environmental consequences, including global warming and accompanying anomalous droughts and floods [1,2]. Various approaches have been explored to prevent global warming, including waste heat recovery [3,4,5,6], the development of renewable energy sources [7,8], and carbon capture and storage [9,10]. Although waste heat recovery enhanced the efficiency of existing operations, it is still insufficient for reducing gas emissions. However, the development of renewable energy sources is still far from meeting global energy demands. As a result, carbon capture and storage are considered practical and tangible means of controlling global warming in the near future [11,12,13].
Carbon capture is classified into three types: post-combustion, oxyfuel combustion, and pre-combustion [14,15]. Post-combustion is the most widely used CO2 capture technology because it can simply be integrated into existing power facilities [16,17]. In this process, CO2 is extracted from flue gas using a variety of processes, such as adsorption, absorption, membrane separation, hydrate-based separation, and cryogenic distillation.
Amine solutions are widely used in CO2 capture. However, there are various drawbacks, such as poor capture efficiency, corrosion, and toxicity [18,19]. Using solid materials such as nanotubes, metal-organic frameworks, and metal oxides/hydroxides are well-known methods of CO2 capture [20,21,22]. Adsorption by solid sorbents offers various benefits, including high CO2 selectivity and high adsorption capacity [23,24]. Most of these methods involve the application of heat to the capturing agent during regeneration process, which is necessary to release CO2. Simultaneously, the optimal adsorbent material should be effective at low temperatures (500 K) to maximize capture efficiency [22,25]. Several studies have demonstrated the effectiveness of bulk metal oxides and alkali-earth metal hydroxides (e.g., Ca(OH)2 and Mg(OH)2) in adsorbing CO2 at low to intermediate temperatures (between 300 and 1000 K). It was also demonstrated that the CO2 capture process resulted in very stable carbonate products in the bulk crystals, which necessitate further heat treatment (between 600 and 1400 K) to release captured CO2. Ca(OH)2 and Mg(OH)2 powders were found to be efficient adsorbents, with the amount of CO2 adsorbed inversely proportional to the domain size of the specimen [22,26].
The chemical adsorption of CO2 over alkali-metal-based solid sorbents such as K2CO3 (reaction 1) is a potential method for selectively capturing diluted CO2 from a large quantity of nitrogen in the flue gas. The following equation expresses the CO2 adsorption over K2CO3,
K2CO3 + CO2 + H2O ↔ 2KHCO3
However, the presence of water caused the K2CO3 to hydrolyze according to the following equation, reducing the CO2 adsorption capacity.
K2CO3 + 1.5H2O ↔ K2CO3·1.5H2O
A hydrophobic K2CO3/boehmite/TiO2 was prepared by Bararpour et al. [27] to alleviate the hydrolysis of the K2CO3.
Numerous factors, including the length of time, temperature, and water vapor content of the CO2 stream, influence the CO2 adsorption process. One advantageous method for maximizing the effectiveness of the CO2 adsorption processes is to optimize different operating parameters. The experimental optimization of numerous processes, including CO2 adsorption, is restricted, time and effort consuming, and expensive. Although physical and mathematical modeling have made significant progress in simulating various processes, their accuracy is still constrained by the constants and parameters that are often presupposed [28,29]. Artificial intelligence has demonstrated high effectiveness in the accurate modeling and optimization of various processes, such as biodiesel production from palm kernel shell [30], electricity generation in fuel cells [31,32,33], microbial fuel cells [34,35,36], alternative fuels [37], heat transfer and waste heat recovery [38,39,40], biohydrogen production [41,42], etc. As a general rule, system identification and parameter identification applications, optimization is a critical technique [34,43]. Although there are several types of optimization methods, the group of metaheuristic algorithms (MHAs) has a significant position among all other types of approaches [44]. MHAs are distinguished by their simplicity and ease of implementation. Most of the MHAs were inspired by natural laws. RUNge Kutta (RUN) is a contemporary and efficient optimizer that is used to predict optimal system parameters. RUNge Kutta (RUN) is a contemporary and efficient optimizer used to predict optimal system parameters.
Integrating fuzzy logic and the metaheuristic optimization algorithm resulted in a satisfactory model with an accurate estimation of its optimal parameters. Therefore, the present work benefits from this cooperation by building a fuzzy model of the addressed system and then predicting the optimal set of regulating parameters using the RUN optimizer. This study utilizes fuzzy modeling in combination with the RUN optimizer to determine optimal the CO2 capture parameters. Furthermore, this study strives to optimize the effectiveness of CO2 capture. To the best of the authors knowledge, this is the first time that collaboration between the FIS and the RUNge Kutta optimizer has been used to maximize CO2 capture capacity. To demonstrate the superiority of the proposed strategy, a comparison between the performances of the proposed methodology, RSM tool, and the measured values was also investigated.
2. Experimental Data Sets
As shown in Figure 1, a mixture of N2, H2O, and CO2 was fed into the device, and the CO2 and water adsorbed on the surface of the catalyst were measured using a thermogravimetric analyzer (TGA, Thermax 500). The adsorbed masses of the individual CO2 and H2O were determined by accurately determining the quantity of the CO2 adsorbed using MA “mass spectrometer”. Each measurement was determined as the average of ten adsorption generation cycles, the influence of carbonation temperature (40, 60, and 80 °C), carbonation duration (15, 30, and 45 min), and H2O to CO2 ratio (0.5, 1.25, and 2). The regeneration was carried out by purging with pure N2 at 150 °C. The results are presented in Table 1.

Figure 1.
The schematic design of the experimental setup utilized for CO2 collection is reprinted with permission from [27].

Table 1.
The effect of the different operating parameters, i.e., carbonation temperature, carbonation time, and H2O to CO2 ratio, on the CO2 adsorption capacity, reproduced with permission from [27].
3. Proposed Strategy
The proposed strategy is divided into two stages: modeling and parameter identification. The first phase was performed utilizing the fuzzy logic (FL) approach as a fuzzy-based architecture, and the optimum parameters were identified in the second phase using a recent and efficient optimization algorithm, namely the RUNge Kutta optimizer (RUN).
3.1. Fuzzy-Modeling
FL has made development and implementation considerably easier since its introduction in the late 1960s. In particular, it does not use sophisticated mathematical models. Only a practical comprehension of the overall system behavior is required. Furthermore, it overcomes the shortcomings of formula-based modeling techniques that do not require the high number-crunching demands of formula-based solutions. In other words, FL detects all gradations between the clear-cut or black-and-white alternatives. The FL process includes fuzzification, inference engines, and defuzzification. The fuzzification process is based on mapping any variable from a crisp-valued number to a fuzzy-valued number using membership functions (MFs). Every MF corresponds to the variable domain-of-discourse to a value in the range of [0, 1]. For each MF, a fuzzy value of one indicates that the variable entirely belongs to that MF, whereas a value of zero indicates that it does not belong to that MF at all. However, any value between 0 and 1 means that this variable is partially related to the MF. The inference engine, which contains fuzzy rules, is responsible for generating (firing) the output of the rule based on the minimal (Min) operation. The Sugeno-type IF-THEN fuzzy rule is always used in system modeling, and its consequence (output) is regarded as a function of the antecedent (inputs). In data modeling, the Sugeno-type IF-THEN fuzzy rule is the most suitable, as its sequence part is a mathematical function of the inputs. Hence, it can efficiently capture the functional relationship (dependency) between the output of the system and its inputs using a training algorithm. It is worth mentioning that the other common type of the IF-THEN fuzzy rule is the Mamdani-type, which is more suitable in dealing with control systems applications where the rules are usually configured using an expert. The final crisp output was then aggregated from the whole rule-based set using the weighted average approach. The defuzzification process is the last step of the fuzzy modeling approach. The fuzzy inference system (FIS) can accurately capture the optimal model from the system’s input–output data by completing these processes. FIS employs a hybrid learning process that combines the gradient descent (GD) and least squares estimate (LSE) approaches to achieve the best network parameters. However, different training tools, such as convolutional and swarm optimization techniques, can be used to produce the optimal parameters of the membership functions, as well as the fuzzy rules [45,46]. Based on the collected data, a fuzzy model was developed in this study. A system should often include more than one rule to effectively design a system model. There are many methods for obtaining the output of a fuzzy rule [47]. However, in this work, the Min implication method was adopted. Every fuzzy rule output is aggregated to the whole rule base to yield one final fuzzy output. The actual final output is produced by defuzzing the fuzzy output. In the Sugeno-type rule, the optimal defuzzification approach is a weighted average (Wavg).
An example of Sugeno-type rule is as shown:
where, a and b are the inputs, c is the output; and A and B are the MFs of a and b, respectively;
IF a is A and b is B, THEN c = f (a, b)
The fuzzy rule demonstrates that the output c is a function of the inputs a and b.
3.2. RUNge Kutta Optimizer
Obtaining the optimal values of the operational variables that allow the system to operate perfectly is a critical challenge in many engineering applications. Accordingly, many scholars have been interested in the topic of optimization algorithms. Although the concept of optimization is not new, its methodology and procedures have garnered increasing research interest. Metaheuristic algorithms (MHAs) are a key component of this field. Unlike other traditional optimization techniques using the gradient descent methodology, MHAs use a stochastic search strategy to avoid premature convergence issues. Furthermore, MHAs can solve single or multi object problems in both linear and non-linear systems. Most of these algorithms were inspired by nature. The purpose of this is to emulate the behavior of specific organisms (particles/agents/solutions) in order to achieve the optimal goal (position/location/target) based on the interaction relationship between these organisms. Formulating the mathematical equations that imitate these relationships frequently results in an optimization method [48].
The MHA can be categorized according to the inspired creature movements to be emulated. These were basically classified into three categories. The first category of algorithms, such as Genetic Algorithms (GA) and Simulated Annealing (SA), mimics the evolution process of creatures. However, the second is the simulation of swarm social motion, such as Particle Swarm Optimization (PSO), Grey Wolf Optimization (GWO), and so on [49,50]. The third is motivated by physical or mathematical rules, such as the Gravitational Search Algorithm (GSA), Archimedes Optimization Algorithm (AOA), etc. All the preceding classes begin with a set of starting solutions that are randomly generated. Then, each solution is updated iteratively, depending on the inspired algorithm, until a final stopping condition is reached. Typically, the iterative procedure ends when either the updating change is infinitesimally small over an extended period of time, or the maximum number of iterations has been achieved.
The RUNge Kutta (RUN) optimizer is one of the most modern optimizers of the third class of MHAs, which was proposed by Ahmadianfar and his colleagues [51]. The Runge-Kutta (RK) technique was developed in the early twentieth century by mathematicians Carl Runge and Wilhelm Kutta. This is an iterative approach that offers an approximate solution to the ordinary differential equation using a numerical analysis methodology. In fact, the RK technique is the primary impetus behind the RUN optimizer. The RUN optimization technique is based on the variable slopes introduced in the classical RK4 approach to adjust the exploration and exploitation phases of the optimizer. In addition, the RUN used the improved solution quality (ESQ) mechanism to enhance convergence to the global optimum solution rather than to the local one. This enhancement improves not only the accuracy but also the speed of the convergence curve to the end target. The RUN algorithm consists of four operations: initialization, exploration and exploitation, solution updating, and enhanced solution quality. As a result, the RUN algorithm can be expressed as follows.
3.2.1. Initialization
Similar to most MHAs optimizers, the RUN starts by initializing the population pool with a set of stochastic solutions within the lower and higher bounds of the unknown variables. Every member of the population is denoted as with a D-dimensional solution to an optimization problem, where (n = 1, 2,..., N) and (l = 1, 2, …, D).
3.2.2. Search Mechanism
The coefficient that defined as follows, based on the first-order derivative.
Therefore, is defined as:
The worst and best solutions identified for each iteration are represented by and , respectively, and are computed using three randomly selected solutions from the swarm pool (,), and r1 ≠ r2 ≠ r3 ≠ n.
Consequently, three other coefficients (i.e.,,..., and ) can be defined as follows.
The two stochastic numbers that vary within the domain [0, 1] are represented by and . The Δt formula is defined as,
Stp = r ⋅((tb-r × xmean ) +γ)
Moreover, and are determined as follows:
else
end
where represents the best solution. Moreover, if the fitness of the current solution ) is better than that of , the best and worst solutions ( and ) are equal to and , respectively, in Equation (15). Then, they are equal to and , respectively. Subsequently, RUN’s leading search mechanism (SM) can be defined as follows:
where, = + 2 + 2 +
3.2.3. Solutions Update
The updating process can be executed as follows:
if r < 0.5
(Exploration phase)
else
(Exploitation phase)
end
In Equations (16) and (17), μ is a stochastic number, r is a stochastic number with a normal distribution. Consequently, μ = 0.5 + 0.1 r. Moreover, SF denotes an adaptive factor, which can be described as follows:
To execute the local search around solutions and , and thus exploring new regions in the searching domain, Equations (16) and (17) can be reformulated as follows:
if r < 0.5
else
end
where r is an integer number, which is 1 or −1. Changing this parameter from 1 to −1 and vice versa enhances the diversity of the searching mechanism; g is a stochastic number that varies in the domain [0, 2].
It is worth mentioning that in stochastic search optimization, a random generator is often used to extend the search area around the proposed solution in a form of circular region with a certain radius. In this case, the random generator in Equations (16), (17), (20), and (21) is denoted by the variable g, and the length of the radius is 2 to construct a stochastic search area in the range [0, 2] around the location of the addressed solution.
3.2.4. Enhanced Solution Quality
Enhanced solution quality (ESQ) is used in the RUN method using three random solutions () and mixed with the best position () to generate a new as follows:
if r < 0.5
if w < 1
else
tnew2 = tnew1 + r⋅w⋅|(tnew1 − tmean) + r|
end
end
The solution calculated in this part () may not have better fitness than the present solution (i.e., ). For the purpose of enhancing the likelihood of creating a better solution, another new solution () was produced and computed as follows:
if r < w
end
where v represents a stochastic number with the value 2 r.
4. Results and Discussion
4.1. Fuzzy-Based Results
Establishing a robust and accurate model is a vital task in parameter estimation applications, particularly when the optimization phase is highly dependent on it. Accordingly, the first step was to develop a fuzzy model. However, the 13 experimental data samples were utilized to substantially complete the model. The carbonation temperature (°C), carbonation duration (minutes), and H2O-to-CO2 flow rate ratio were all inputs for each sample. Meanwhile, the output was CO2 capture. In this study, the Gaussian-shape, subtractive clustering (SC), and weighted average (Wavg) parameters were assigned values ranging from 70 to 30. The fuzzy model was constructed and trained using MATLAB R2022b software. In particular, the code was written on an Intel CORE i7 with 8 GB RAM. The code starts by reading the data and splitting them into training and testing subsets with a predefined ratio. Subsequently, a 3-input single-output fuzzy model structure was constructed. In this phase, the fuzzy rules and the membership function shapes of the inputs were generated. The SC algorithm and the Gaussian-shape were applied for the fuzzy rules and the membership functions shapes, respectively. However, the Wavg method was applied for obtaining the final crisp output. Afterwards, the model was trained using the training data subset and the quality of the training phase was tested using the testing data subset.
Table 2 shows the MSE, RMSE, and R2 of the model predictions in relation to the experimental data for both processes. The table shows that the model performance was reliable due to the small values of 1.15 × 10−12 and 1.07 × 10−6 for the MSE and RMSE of the training phase, respectively, and 0.0962 and 0.3101 for the testing phase. Furthermore, the high R2 values show that the predicted patterns of the model are well-matched with the experimental data trends. The R2 of the training phase predictions in the present investigation reached one value, demonstrating that the perfections corresponded with their corresponding experimental values. Furthermore, the R2 value of the testing phase predictions was 0.9873, indicating that the perfections were exceptionally close to their related experimental values. The previous statistical findings have demonstrated the accuracy of the obtained fuzzy model. Figure 2 shows the configuration of the fuzzy model for the CO2 capture process. There were nine fuzzy rules. Figure 3 depicts the membership functions of the fuzzy model for the CO2 capture process. In the input space, each colored MF curve represents a cluster.

Table 2.
Numerical assessment of the fuzzy model.
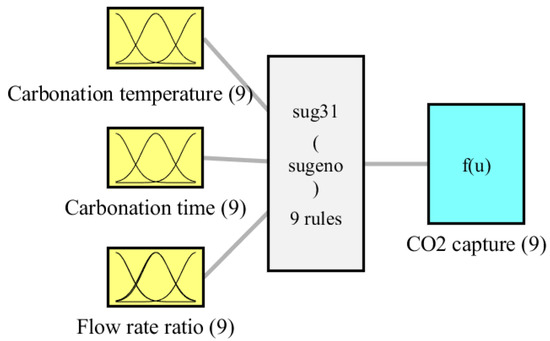
Figure 2.
Configuration of the fuzzy model of the CO2 capture process.

Figure 3.
Membership functions of the fuzzy model of the CO2 capture process.
Figure 4 represents the model predictions versus the relevant observed data. The fuzzy model performs precisely as expected, as evidenced by the low RMSE and high R2 values of 1.07 × 10−6 and 1, respectively. Figure 5 portrays the prediction accuracy of the fuzzy model. The model results were all on the same 100% accuracy line. All of the above demonstrations confirmed the accuracy of the fuzzy model.
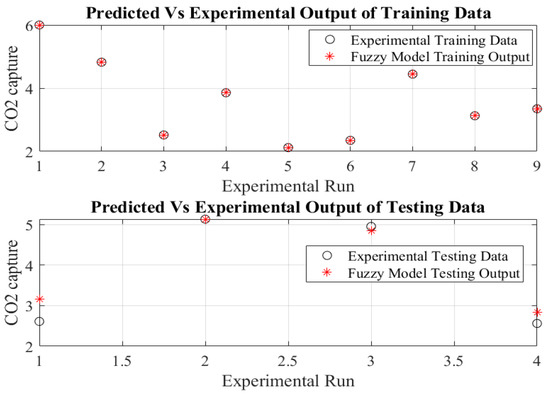
Figure 4.
Predicted versus measured data of fuzzy model of the CO2 capture process.
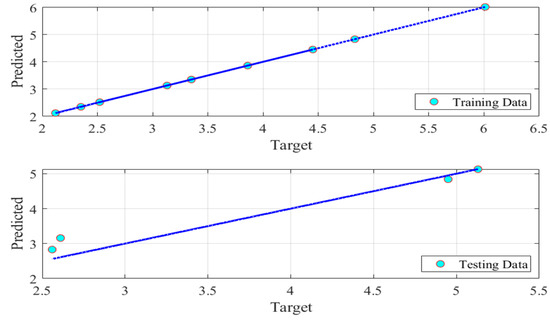
Figure 5.
Fuzzy model prediction accuracy of the CO2 capture process.
Examining the input–output relationship caused by the investigated system aids in comprehending the impact of the inputs on the output. As a result, Figure 6 depicts the 3-D surfaces that connect each of the two inputs to the output. The surface level contours are plotted to indicate the regions of low, moderate, and high CO2 capture. The dark blue color has a very low value, whereas the dark red color has a very high value. However, the contour colors between them reflect the intermediate levels. By evaluating the three graphs in Figure 6, it is clear that CO2 capture increases at high carbonation temperatures, medium flow rate ratios, and long carbonation times. However, the CO2 capture was reduced when the carbonation temperature was high, the flow rate ratio was low, and the carbonation period was short.
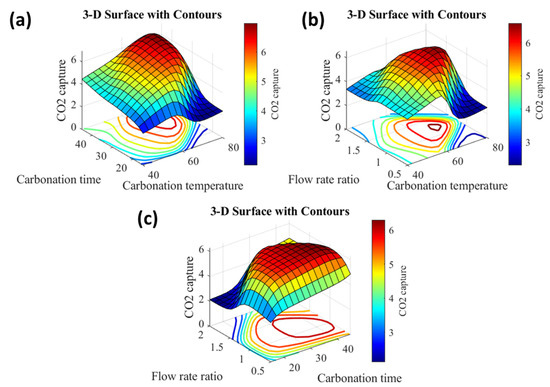
Figure 6.
3-D surfaces of the fuzzy-based model of CO2 adsorption process (a) effect of the carbonation time and temperature, (b) effect of the carbonation temperature and the H2O/CO2 ratio, and (c) effect of the carbonation time and the H2O/CO2 ratio.
Figure 6 depicts the interaction of two independent factors in the CO2 adsorption process. The figure shows an optimal operating carbonation temperature of approximately 60 °C, and the adsorption capacity increases with increasing the duration until it reaches 25 min and then remains nearly constant, indicating that there is a minimum time for the adsorption process of 25 min. While there is an optimum carbonation temperature of approximately 60 °C, lower or higher values adversely influence the CO2 adsorption process. The kinetics of the adsorption process improved with the increase of temperature. However, because of the exothermic nature of the CO2 adsorption process [52,53], the optimal adsorption temperature in this situation is approximately 60 °C. Figure 5b,c indicate that the optimal H2O/CO2 ratio is between 1 and 1.5 and that the CO2 adsorption capacity decreases beyond these levels. According to Equation (1), the positive impact of raising the H2O/CO2 ratio can be attributed to the involvement of H2O in the completion of the adsorption process. However, at higher H2O values, the catalyst can be hydrolyzed (Equation (2)), reducing the adsorption capacity.
4.2. Optimization Results
Following the verification of the reliability of the fuzzy model, the values of the governing parameters can now be estimated using one of the most modern and efficient optimizers, RUN. The three inputs of the system were regarded as the controlling variables, and CO2 capture was considered as the output. The optimization problem can be stated as follows: “Estimate the values of carbonation temperature (°C), carbonation time (min), and H2O-to-CO2 flow rate ratio to maximize the output of the CO2 capture”. The optimization problem can be mathematically expressed as follows:
where, f (X) is the output of the fuzzy model; X = [x1, x2, x3] are the three controlling inputs that vary in the ranges x1∈ (40, 80), x2∈ (0.5, 2), and x3∈ (15, 45), respectively.
max (f (X))
Consequently, the RUN optimizer was used with the five proposed solutions for 50 updating iterations. The two tuning parameters of the optimizer were set to their default values of a = 20 and b = 12. Table 3 displays the ideal set of values for the carbonation temperature, flow rate ratio, and carbonation duration that yield the highest CO2 capture using the proposed fuzzy & RUN, other experimental, and RSM approaches. The table indicates that using the fuzzy & RUN, a value of 6.99 is obtained for CO2 capture when the carbonation temperature, flow rate ratio, and carbonation time are 70.83 °C, 1.22, and 39.86 min, respectively. Referring to Figure 5 and the input ranges of (40, 80), (0.5, 2), and (15, 45), it is feasible to conclude that the optimal set of values obtained is as predicted. In other words, CO2 capture increases at high carbonation temperatures, medium flow rate ratios, and long carbonation times. Consequently, the proposed approach results match the studied 3-D surface analysis, proving that the ideal values are on the right track. Furthermore, as shown in Table 3, the combination of the fuzzy and RUN approaches yielded a maximum value of 6.99 for CO2 capture capacity, representing an increase of approximately 10.08% and 9.39% compared to the measured data and RSM, respectively. However, when utilizing the RSM approach, the increase was just 0.63% above the experimental value, yielding the highest value of 6.39. As a result, the suggested technique outperformed the RSM method and could be used to efficiently build the system model and then estimate the optimal values of the regulating parameters.

Table 3.
Optimal values of parameters using different methods.
A thorough examination of the optimization process will undoubtedly aid in trusting the generated results. From this vantage point, every dimension of the solutions is plotted during the iterative process to demonstrate their behavior (convergence) throughout the optimization phase. The output convergence curve is depicted in Figure 7a. However, Figure 7b–d illustrate the convergence curves of the respective inputs. The plots demonstrate that the solutions were widely dispersed from the beginning of the optimization process until about 80% of the way through the optimization process. Following that, as soon as a promising zone was identified, the exploitation phase started. This is evident during the last 20% period of the optimization process, as illustrated in Figure 7. The carbonation temperature, flow rate ratio, and carbonation duration curves all converge at values of 70.83 °C, 1.22, and 39.86 min, respectively, while the CO2 capture (Best Cost) curve converges at 6.99. The generated values and the precise examination of the data indicate that the proposed methodology was successful in obtaining the optimal values. To the best of the authors’ knowledge, this is the first time to use the collaboration between the FIS and the RUNge Kutta optimizer to maximize CO2 capture capacity. A comparison between the performances of the proposed methodology and the RSM tool showed that the optimal parameters resulted from the (RUN & Fuzzy) produced a CO2 capturing capacity value higher than those obtained through the RSM or experimentally. This conclusion supports the proposed methodology of adopting the collaboration between the two techniques.
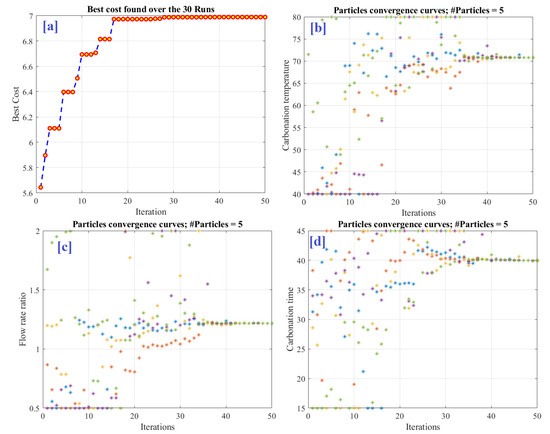
Figure 7.
Optimization results (a) best objective function variation, (b) particle convergence of carbonation temperature, (c) particle convergence of carbonation time, and (d) particle convergence of H2O-to-CO2 flow rate ratio.
5. Conclusions
This study is mainly concerned with employing an artificial intelligence (AI) tool in combination with one of the most current metaheuristic optimizers in engineering applications. This application aims to maximize CO2 capture by identifying the optimal values for three inputs, including carbonation temperature, flow rate ratio, and duration. Consequently, a two-step sequential procedure was established, including modeling and optimization. In the first stage, the fuzzy model of the 3-input single-output system was constructed using fuzzy logic. The Gaussian-shape, subtractive clustering (SC), and weighted average (Wavg) were used for the membership function shape in the fuzzification phase, fuzzy rules generator, and defuzzification phase, respectively. The robustness and effectiveness of the resultant model were assessed using the low value of root mean squared error (RMSE) and the high value of the coefficient of determination (R2) of the testing dataset, where they reached 0.3101 and 0.9873, respectively. In the second stage, the resultant reliable fuzzy model was then utilized as the core of the optimization process to estimate the optimal values of the three inputs that resulted in the highest CO2 capture. RUNge Kutta (RUN), a modern, straightforward, and effective optimizer, was used to accomplish the optimization stage. This optimizer is distinguished by its smooth transition between the exploration and exploitation stages. The optimal carbonation temperature, flow rate ratio, and carbonation time were 70.83 °C, 1.22, and 39.86 min, respectively. However, the maximal CO2 capture was determined to be 6.99. Thus, the integration of the fuzzy and RUN approaches yields a maximum value of 6.99 for the CO2 capture capacity, indicating an increase of approximately 10.08% and 9.39% compared to the observed data and RSM, respectively. Investigating the output values of the optimizer revealed that the suggested technique successfully determined the optimum values more accurately and effectively than the experimental and RSM models. In future, it is suggested that the data can be modeled using different powerful artificial intelligence tools such as ANN, LSTM, and RSVM, etc. Moreover, more studies are required on the ways of integrating CO2 capture technology with hydrogen production from renewable energy. Furthermore, optimization of post-combustion capture technology, such as the use of solvents with higher selectivity and capacity for CO2. Lastly, research on ways to optimize the operation and design of CO2 capture systems, such as by using advanced process control techniques or by incorporating process intensification strategies. It is worthy to note that the best approach for maximizing CO2 capture capacity will likely be a combination of different strategies, rather than relying on a single solution.
Author Contributions
Conceptualization, A.M.N., H.R. and M.A.A.; methodology, H.R. and M.A.A.; software, A.M.N. and H.R.; validation, A.M.N., H.R. and M.A.A.; formal analysis, A.M.N., H.R. and A.A.; investigation, A.A. and M.A.A.; writing—original draft preparation, A.M.N., H.R., A.A. and M.A.A.; writing—review and editing, A.A. and M.A.A.; visualization, A.A.; project administration, A.M.N.; funding acquisition, A.M.N. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia, for funding this research work through project number (IF2/PSAU/2022/01/22030).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zacharczuk, W.; Andruszkiewicz, A.; Tatarek, A.; Alahmer, A.; Alsaqoor, S. Effect of Ca-Based Additives on the Capture of SO2 during Combustion of Pulverized Lignite. Energy 2021, 231, 120988. [Google Scholar] [CrossRef]
- Alsaqoor, S.; Alahmer, A.; Aljabarin, N.; Gougazeh, M.; Czajczynska, D.; Krzyzynska, R. Effects of Utilization of Solid and Semi-Solid Organic Waste Using Pyrolysis Techniques. In Proceedings of the 2017 8th International Renewable Energy Congress (IREC), Amman, Jordan, 21–23 March 2017; pp. 1–5. [Google Scholar]
- Venturelli, M.; Brough, D.; Milani, M.; Montorsi, L.; Jouhara, H. Comprehensive Numerical Model for the Analysis of Potential Heat Recovery Solutions in a Ceramic Industry. Int. J. Thermofluids 2021, 10, 100080. [Google Scholar] [CrossRef]
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Doraghi, Q.; Ahmad, L.; Norman, L.; Axcell, B.; Wrobel, L.; Dai, S. Thermoelectric Generator (TEG) Technologies and Applications. Int. J. Thermofluids 2021, 9, 100063. [Google Scholar] [CrossRef]
- Olabi, A.G.; Al-Murisi, M.; Maghrabie, H.M.; Yousef, B.A.A.; Sayed, E.T.; Alami, A.H.; Abdelkareem, M.A. Potential Applications of Thermoelectric Generators (TEGs) in Various Waste Heat Recovery Systems. Int. J. Thermofluids 2022, 16, 100249. [Google Scholar] [CrossRef]
- Mansour, M.A.; Beithou, N.; Othman, A.; Qandil, A.; Khalid, M.B.; Borowski, G.; Alsaqoor, S.; Alahmer, A.; Jouhara, H. Effect of Liquid Saturated Porous Medium on Heat Transfer from Thermoelectric Generator. Int. J. Thermofluids 2022, 17, 100264. [Google Scholar] [CrossRef]
- Sayed, E.T.; Abdelkareem, M.A.; Obaideen, K.; Elsaid, K.; Wilberforce, T.; Maghrabie, H.M.; Olabi, A.G. Progress in Plant-Based Bioelectrochemical Systems and Their Connection with Sustainable Development Goals. Carbon Resour. Convers. 2021, 4, 169–183. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mohanty, K. Co-Pyrolysis of Waste Biomass and Waste Plastics (Polystyrene and Waste Nitrile Gloves) into Renewable Fuel and Value-Added Chemicals. Carbon Resour. Convers. 2020, 3, 145–155. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Elsaid, K.; Sayed, E.T.; Maghrabie, H.M.; Abdelkareem, M.A. Large Scale Application of Carbon Capture to Process Industries—A Review. J. Clean. Prod. 2022, 362, 132300. [Google Scholar] [CrossRef]
- Akpasi, S.O.; Isa, Y.M. Review of Carbon Capture and Methane Production from Carbon Dioxide. Atmosphere 2022, 13, 1958. [Google Scholar] [CrossRef]
- Gunawardene, O.H.P.; Gunathilake, C.A.; Vikrant, K.; Amaraweera, S.M. Carbon Dioxide Capture through Physical and Chemical Adsorption Using Porous Carbon Materials: A Review. Atmosphere 2022, 13, 397. [Google Scholar] [CrossRef]
- Bao, J.; Lu, W.-H.; Zhao, J.; Bi, X.T. Greenhouses for CO2 Sequestration from Atmosphere. Carbon Resour. Convers. 2018, 1, 183–190. [Google Scholar] [CrossRef]
- Alahmer, A.; Ajib, S.; Wang, X. Comprehensive Strategies for Performance Improvement of Adsorption Air Conditioning Systems: A Review. Renew. Sustain. Energy Rev. 2019, 99, 138–158. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Lootah, M.A.; Sayed, E.T.; Wilberforce, T.; Alawadhi, H.; Yousef, B.A.A.; Olabi, A.G. Fuel Cells for Carbon Capture Applications. Sci. Total Environ. 2021, 769, 144243. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Sayed, E.T.; Elsaid, K.; Abdelkareem, M.A. Progress in Carbon Capture Technologies. Sci. Total Environ. 2021, 761, 143203. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Sayed, E.T.; Shehata, N.; Alami, A.H.; Maghrabie, H.M.; Abdelkareem, M.A. Prospect of Post-Combustion Carbon Capture Technology and Its Impact on the Circular Economy. Energies 2022, 15, 8639. [Google Scholar] [CrossRef]
- Olabi, A.G.; Rezk, H.; Sayed, E.T.; Ghoniem, R.M.; Abdelkareem, M.A. Boosting Carbon Dioxide Adsorption Capacity Applying Jellyfish Optimization and ANFIS-Based Modelling. Ain Shams Eng. J. 2022, 14, 101931. [Google Scholar] [CrossRef]
- Dutcher, A.C.O. Capture Technology Development from the Beginning of 2013—A Review. ACS Appl. Mater. Interfaces 2015, 7, 2137–2148. [Google Scholar] [CrossRef]
- Liang, Z.; Fu, K.; Idem, R.; Tontiwachwuthikul, P. Review on Current Advances, Future Challenges and Consideration Issues for Post-Combustion CO2 Capture Using Amine-Based Absorbents. Chin. J. Chem. Eng. 2016, 24, 278–288. [Google Scholar] [CrossRef]
- Furukawa, H.; Ko, N.; Go, Y.B.; Aratani, N.; Choi, S.B.; Choi, E.; Yazaydin, A.Ö.; Snurr, R.Q.; O’Keeffe, M.; Kim, J. Ultrahigh Porosity in Metal-Organic Frameworks. Science 2010, 329, 424–428. [Google Scholar] [CrossRef]
- Yaumi, A.L.; Bakar, M.Z.A.; Hameed, B.H. Recent Advances in Functionalized Composite Solid Materials for Carbon Dioxide Capture. Energy 2017, 124, 461–480. [Google Scholar] [CrossRef]
- Duan, Y.; Sorescu, D.C. CO 2 Capture Properties of Alkaline Earth Metal Oxides and Hydroxides: A Combined Density Functional Theory and Lattice Phonon Dynamics Study. J. Chem. Phys. 2010, 133, 74508. [Google Scholar] [CrossRef]
- Ghanbari, T.; Abnisa, F.; Daud, W.M.A.W. A Review on Production of Metal Organic Frameworks (MOF) for CO2 Adsorption. Sci. Total Environ. 2020, 707, 135090. [Google Scholar] [CrossRef]
- Saha, D.; Kienbaum, M.J. Role of Oxygen, Nitrogen and Sulfur Functionalities on the Surface of Nanoporous Carbons in CO2 Adsorption: A Critical Review. Microporous Mesoporous Mater. 2019, 287, 29–55. [Google Scholar] [CrossRef]
- Creamer, A.E.; Gao, B. Carbon-Based Adsorbents for Postcombustion CO2 Capture: A Critical Review. Environ. Sci. Technol. 2016, 50, 7276–7289. [Google Scholar] [CrossRef] [PubMed]
- Jahangiri, S.; Mosey, N.J. Effects of Reduced Dimensionality on the Properties of Magnesium Hydroxide and Calcium Hydroxide Nanostructures. Phys. Chem. Chem. Phys. 2017, 19, 1963–1974. [Google Scholar] [CrossRef] [PubMed]
- Bararpour, S.T.; Adanez, J.; Mahinpey, N. Application of Core-Shell-Structured K2CO3-Based Sorbents in Postcombustion CO2 Capture: Statistical Analysis and Optimization Using Response Surface Methodology. Energy Fuels 2020, 34, 3429–3439. [Google Scholar] [CrossRef]
- Nassef, A.M.; Fathy, A.; Sayed, E.T.; Abdelkareem, M.A.; Rezk, H.; Tanveer, W.H.; Olabi, A.G. Maximizing SOFC Performance through Optimal Parameters Identification by Modern Optimization Algorithms. Renew. Energy 2019, 138, 458–464. [Google Scholar] [CrossRef]
- Alahmer, A.; Alsaqoor, S. Simulation and Optimization of Multi-Split Variable Refrigerant Flow Systems. Ain Shams Eng. J. 2018, 9, 1705–1715. [Google Scholar] [CrossRef]
- Rezk, H.; Nassef, A.M.; Inayat, A.; Sayed, E.T.; Shahbaz, M.; Olabi, A.G. Improving the Environmental Impact of Palm Kernel Shell through Maximizing Its Production of Hydrogen and Syngas Using Advanced Artificial Intelligence. Sci. Total Environ. 2019, 658, 1150–1160. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Monopoli, D.; Dassisti, M.; Sayed, E.T.; Abdelkareem, M.A. Design Optimization of Proton Exchange Membrane Fuel Cell Bipolar Plate. Energy Convers. Manag. 2023, 277, 116586. [Google Scholar] [CrossRef]
- Rubio, G.A.; Agila, W.E. A Fuzzy Model to Manage Water in Polymer Electrolyte Membrane Fuel Cells. Processes 2021, 9, 904. [Google Scholar] [CrossRef]
- Rezk, H.; Wilberforce, T.; Sayed, E.T.; Alahmadi, A.N.M.; Olabi, A.G. Finding Best Operational Conditions of PEM Fuel Cell Using Adaptive Neuro-Fuzzy Inference System and Metaheuristics. Energy Rep. 2022, 8, 6181–6190. [Google Scholar] [CrossRef]
- Sayed, E.T.; Rezk, H.; Abdelkareem, M.A.; Olabi, A.G. Artificial Neural Network Based Modelling and Optimization of Microalgae Microbial Fuel Cell. Int. J. Hydrogen Energy, 2023; in press. [Google Scholar] [CrossRef]
- de Ramón-Fernández, A.; Salar-García, M.J.; Ruiz-Fernández, D.; Greenman, J.; Ieropoulos, I. Modelling the Energy Harvesting from Ceramic-Based Microbial Fuel Cells by Using a Fuzzy Logic Approach. Appl. Energy 2019, 251, 113321. [Google Scholar] [CrossRef]
- Rezk, H.; Sayed, E.T.; Abdelkareem, M.A.; Olabi, A.G. Performance Improvement of Co-culture Inoculated Microbial Fuel Cell Using Fuzzy Modelling and Harris Hawks Optimization. Int. J. Energy Res. 2022, 46, 14396–14407. [Google Scholar] [CrossRef]
- Alahmer, H.; Alahmer, A.; Alkhazaleh, R.; Al-Amayreh, M.I. Modeling, Polynomial Regression, and Artificial Bee Colony Optimization of SI Engine Performance Improvement Powered by Acetone–Gasoline Fuel Blends. Energy Rep. 2023, 9, 55–64. [Google Scholar] [CrossRef]
- Salameh, T.; Kumar, P.P.; Sayed, E.T.; Abdelkareem, M.A.; Rezk, H.; Olabi, A.G. Fuzzy Modeling and Particle Swarm Optimization of Al2O3/SiO2 Nanofluid. Int. J. Thermofluids 2021, 10, 100084. [Google Scholar] [CrossRef]
- Sayed, E.T.; Rezk, H.; Olabi, A.G.; Gomaa, M.R.; Hassan, Y.B.; Rahman, S.M.A.; Shah, S.K.; Abdelkareem, M.A. Application of Artificial Intelligence to Improve the Thermal Energy and Exergy of Nanofluid-Based PV Thermal/Nano-Enhanced Phase Change Material. Energies 2022, 15, 8494. [Google Scholar] [CrossRef]
- Rezk, H.; Sayed, E.T.; Maghrabie, H.M.; Abdelkareem, M.A.; Ghoniem, R.M.; Olabi, A.G. Fuzzy Modelling and Metaheuristic to Minimize the Temperature of Lithium-Ion Battery for the Application in Electric Vehicles. J. Energy Storage 2022, 50, 104552. [Google Scholar] [CrossRef]
- Salameh, T.; Sayed, E.T.; Olabi, A.G.; Hdaib, I.I.; Allan, Y.; Alkasrawi, M.; Abdelkareem, M.A. Adaptive Network Fuzzy Inference System and Particle Swarm Optimization of Biohydrogen Production Process. Fermentation 2022, 8, 483. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.G.; Abdelkareem, M.A.; Alami, A.H.; Sayed, E.T. Optimal Parameter Determination of Membrane Bioreactor to Boost Biohydrogen Production-Based Integration of ANFIS Modeling and Honey Badger Algorithm. Sustainability 2023, 15, 1589. [Google Scholar] [CrossRef]
- Salameh, T.; Kumar, P.P.; Olabi, A.G.; Obaideen, K.; Sayed, E.T.; Maghrabie, H.M.; Abdelkareem, M.A. Best Battery Storage Technologies of Solar Photovoltaic Systems for Desalination Plant Using the Results of Multi Optimization Algorithms and Sustainable Development Goals. J. Energy Storage 2022, 55, 105312. [Google Scholar] [CrossRef]
- Alahmer, A.; Rezk, H.; Aladayleh, W.; Mostafa, A.O.; Abu-Zaid, M.; Alahmer, H.; Gomaa, M.R.; Alhussan, A.A.; Ghoniem, R.M. Modeling and Optimization of a Compression Ignition Engine Fueled with Biodiesel Blends for Performance Improvement. Mathematics 2022, 10, 420. [Google Scholar] [CrossRef]
- Reddy, S.; Panwar, L.K.; Panigrahi, B.K.; Kumar, R. Computational Intelligence for Demand Response Exchange Considering Temporal Characteristics of Load Profile via Adaptive Fuzzy Inference System. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 2, 235–245. [Google Scholar] [CrossRef]
- Alahmer, A.; Ajib, S. Solar Cooling Technologies: State of Art and Perspectives. Energy Convers. Manag. 2020, 214, 112896. [Google Scholar] [CrossRef]
- Tang, Y.M.; Zhang, L.; Bao, G.Q.; Ren, F.J.; Pedrycz, W. Symmetric Implicational Algorithm Derived from Intuitionistic Fuzzy Entropy. Iran. J. Fuzzy Syst. 2022, 19, 27–44. [Google Scholar]
- Alahmer, A.; Alahmer, H.; Handam, A.; Rezk, H. Environmental Assessment of a Diesel Engine Fueled with Various Biodiesel Blends: Polynomial Regression and Grey Wolf Optimization. Sustainability 2022, 14, 1367. [Google Scholar] [CrossRef]
- Alahmer, H.; Alahmer, A.; Alkhazaleh, R.; Alrbai, M. Exhaust Emission Reduction of a SI Engine Using Acetone–Gasoline Fuel Blends: Modeling, Prediction, and Whale Optimization Algorithm. Energy Rep. 2023, 9, 77–86. [Google Scholar] [CrossRef]
- Alahmer, H.; Alahmer, A.; Alkhazaleh, R.; Alrbai, M.; Alamayreh, M.I. Applied Intelligent Grey Wolf Optimizer (IGWO) to Improve the Performance of CI Engine Running on Emulsion Diesel Fuel Blends. Fuels 2023, 4, 35–57. [Google Scholar]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the Metaphor: An Efficient Optimization Algorithm Based on Runge Kutta Method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, Y.; Li, C.; Lu, S. Carbonation Behavior of K2CO3/AC in Low Reaction Temperature and CO2 Concentration. Chem. Eng. J. 2014, 254, 524–530. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, X.; Zhao, C. K2CO3/Al2O3 for Capturing CO2 in Flue Gas from Power Plants. Part 1: Carbonation Behaviors of K2CO3/Al2O3. Energy Fuels 2012, 26, 1401–1405. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).