Research on Air Supply Volume and Temperature Control of Subway Trains Based on Passenger Capacity

Abstract

There is currently no way for subway air-conditioning systems to adjust to changes in passenger capacity in terms of air-supply volume and air-supply temperature. In this paper, a study of the setting of the air-supply volume and controlling the temperature in subway trains was conducted. Based on the fact that the air-supply volume in a subway train needs to meet the requirements of cooling load and humidity load, as well as fresh-air volume, the minimum critical air-supply volume curve was determined on the basis of theoretical calculations under different passenger capacities. Under different passenger capacity and air-supply-volume conditions, the PMV (predicted mean vote) distribution of the subway train was simulated and calculated, and the results indicated that increasing the air-supply volume would not be sufficient to achieve PMV = 0. Therefore, in accordance with the theoretical formulation of the PMV, multiple linear regression was used to fit the temperature-control curve for various passenger capacities. A simulation calculation of the subway train was used to assess the uniformity of the flow field and the temperature field within the subway train in accordance with EN14750. It is evident from the results that under the control curve of the air-supply volume and temperature under different passenger capacities, the uniformity of the flow field and the temperature field can meet the standard requirements. By using the air-supply volume and temperature-control curve proposed in this paper, it is possible to adjust the air-supply volume in real-time, control the temperature of the air-conditioning system of the subway train, improve the passenger comfort of the train, and reduce the energy consumption of the air-conditioning system.

1. Introduction

Recent years have seen the rapid development of China’s metro system. A total of 289 urban rail lines were put into operation in 52 cities on the mainland in 2022, according to statistics provided by Journal of China Metro, adding 1004.51 kilometers of new rail transit and 616 stations. Among the main system equipment of rail transit, which includes vehicles, the traction power supply system, etc., the energy consumption of trains accounts for approximately 50–60% of the total energy consumption, and the energy consumption of the train auxiliary system accounts for approximately 30–40% of the total energy consumption, of which the energy consumption of the air-conditioning system accounts for a large amount of the auxiliary system’s energy consumption. For this reason, saving energy from the air-conditioning system is one of the most important aspects of saving energy from the operation of a vehicle. Furthermore, the heat and humidity inside the car are also of concern. According to the change in passenger capacity, the temperature of the subway air-conditioning system is controlled [1]. The frequency conversion air-conditioning system is also used in subway systems [2], which has the effect of reducing energy consumption. These control methods, however, suffer from a number of shortcomings, since they do not take into account the volume of the air supply. The paper discusses the changes in air-supply volume and temperature with passenger load in order to achieve energy savings for the fan as well as improving the thermal comfort of the human body.

Over the past few years, subway passengers have frequently complained about the internal heat and cold of the system. Currently, the subway air-conditioning system has a critical problem, which represents the rapid change in passenger capacity. As a result, the interior of the subway becomes overheated, over-cooled, unevenly distributed in temperature, and has the sensation of being blown cold [3]. In addition to causing great discomfort to passengers, this also increases the air conditioning’s energy consumption.

Evidently, there is a reason for this, as the air supply and temperature-control methods currently used in subway trains in China are largely based on the relevant standards of European or railroad coaches. The control temperature inside the train is determined by the outdoor temperature [4,5,6,7], while the air-supply volume is mostly determined by the rated air-supply volume or the wind-speed limit based on the model [7,8,9], without taking into account the influence of passenger capacity on air-supply volume and control temperature.

Accordingly, this paper considers the passenger capacity and combined it with the PMV to conduct a theoretical study of air-supply volume and temperature control in the subway compartment. The purpose of Chapter 2 is to introduce the PMV theory and the research idea of this paper. A theoretical calculation is presented in the third chapter for calculating the minimum critical air-supply curve for different passenger capacities, taking into account that cold and wet load requirements as well as fresh-air volume requirements must be met in the vehicle’s air-supply system. Through numerical simulation, the PMV distribution in the passenger compartment is simulated under different passenger capacities and air-supply conditions. It has been determined that volume control of the air supply alone cannot provide thermal comfort for the human body. Based on the PMV theoretical formula, the multiple linear regression method is used in the fourth chapter to fit the temperature-control curves under different passenger capacities. According to standard EN 14750, the uniformity of the flow and temperature fields of the passenger compartment is validated for a given air-supply volume in the fifth chapter.

2. PMV Theory and Research Ideas of the Paper

For the thermal-comfort-evaluation indicators PMV and PPD, Fanger proposed the following equations.

$$\begin{array}{c}PMV=(0.303e^{-0.036M}+0.028)\{\left(M-W\right)-3.05\times {10}^{-3}\times \left[5733-6.99\left(M-W\right)-P_a\right]\\ -0.42\times \left[\left(M-W \right)-58.15\right]-1.7\times {10}^{-5}M\left(5867-P_a\right)-0.0014M\left(34-t_a\right)\\ -3.96\times {10}^{-8}{f}_{cl}\times \left[{\left(t_{cl}+273\right)}^4-{\left({\overline{t}}_r+273\right)}^4\right]-f_{cl}{h}_c\left(t_{cl}-t_a\right)\}\end{array}$$

(1)

$$PPD=100-95\times e^{-(0.03353}{}^{\times PM{V}^4+0.2179\times PM{V}^2)}$$

(2)

where M represents the metabolic rate, W/M; W represents the mechanical work, W/m; P_a represents the water vapor partial pressure, Pa; f_cl represents the clothing thermal resistance, clo; t_a represents the air temperature, °C; t_r represents the average radiation temperature, °C; h_c represents the convective-heat-transfer coefficient, W/(m² K); and t_cl represents the clothing surface temperature, °C.

When calculating the air-supply volume for subway trains, it is necessary to consider the air-supply volume in the car. This volume must meet the requirements for cold and wet loads as well as fresh-air volume when the air-supply temperature is 19°C. A theoretical calculation as well as the air-supply volume curve that meets thermal-comfort requirements have been used to calculate the minimum air-supply volume curve for a variety of passenger capacities (PMV between ±0.5). To ensure that the air-supply volume of air conditioning meets both hot and wet loads as well as thermal comfort, it is necessary to combine the two air-supply volume curves. A temperature-control system is based on Fanger’s PMV theory, which has been discussed above. In the PMV formula, the clothing thermal resistance will be affected by the outside temperature of the vehicle and the radiation temperature will vary depending on different passenger capacities. Therefore, for different passenger capacities, the air-supply speed must be adjusted to fit the binary primary temperature-control curve relating to passenger capacity and the outside temperature by controlling PMV = 0. Finally, in order to assess the uniformity of the flow field under the air-supply curve, simulations are performed for each passenger-capacity condition under the air-supply curve and a comparison of temperature and velocity fields is conducted.

3. Air-Supply-Volume Calculation for the Passenger Compartment

3.1. Minimum Air-Supply Curve Based on the Requirement for the Cooling and Fresh-Air Volume

Taking into account the provisions of CJ/T354-2010 regarding air-conditioning units, it is recommended that the passenger-compartment temperature should be less than or equal to 27 °C when the ambient temperature is 33 °C. In addition, the relative humidity is less than or equal to 65% of the required value for solving the critical air-supply volume [4]. A wet-air enthalpy and humidity diagram is used to calculate the air-supply volume. A line is drawn parallel to the heat and humidity ratio line, using the indoor state point as a base point. This line intersects with the line of air-supply temperature of 19 °C [10], which is the point of ventilation. As a result, the air in the subway is processed to this state, which ensures the requirement of 27 °C and 65%.

Table 1. Outdoor parameters required for the calculation of the air-supply volume of air-conditioning units.

Temperature	Relative Humidity	Enthalpy	Density	Moisture Content
33 °C	70%	90.62 kJ/kg	1.138 kg/m3	22.41 g/kg

,

Table 2. Indoor parameters required for the calculation of the air-supply volume of air-conditioning units.

Temperature	Relative Humidity	Enthalpy	Moisture Content
27 °C	65%	64.32 kJ/kg	14.57 g/kg

and

Table 3. Other relevant parameters required for the calculation of the air-supply volume of air-conditioning units.

Vehicle Area	Vehicle Average Heat Transfer	Coefficient per Capita Total Heat Load [5]	Per-Capita New Air Volume [4]	Equipment Heat Dissipation [11]	Per-Capita Amount of Moisture [2]
216.52 m2	2.3 W/(m2 K)	120 W	10 m3/h	2000 W	76 g/h

provide a summary of the relevant calculation parameters.

According to

Table 4. Minimum air volume for each working condition.

Passenger Capacities N (Person)	Minimum Air-Supply Volume Q (m3/h)
60	3795
129	6441
144	7070
176	8000

, the minimum critical air-supply volume has been calculated based on the requirements for cold and wet loads as well as fresh-air volume under the given four passenger capacities.

The BC section can be fitted in Figure 1 according to the data in Table 4. In other words, when the number of people ranges from 60 to 176, the minimum critical air-supply volume curve is taken as the final air-supply volume curve in order to achieve energy efficiency. If the number of people ranges from 176 to 351, then the air-supply volume has reached the rated upper limit of 8000 m³/h when the B-vehicle’s rated air-supply volume is 8000 m³/h. The air-supply volume is taken as a fixed value of 3795 m³/h when the number of people is 0 to 60. According to Figure 1, ABCD, the air-supply volume curve, is composed of three segments based on the cold and wet loads and the fresh-air volume. In this case, N represents the capacity for passengers. Q represents the volume of air that is supplied, in m³/h.

$$0\le N<60,Q=3795$$

(3)

$$60\le N<176,Q=-0.06\times N^2+50.2\times N+988.4$$

(4)

$$176\le N\le 351,Q=8000$$

(5)

3.2. PMV Calculation for the Passenger Compartment

For the B-vehicle, CFD calculation software was used to simulate the PMV of the passenger compartment with different passenger capacities and air-supply volumes. An air duct and passenger compartment model, measuring 19 meters long, 2.6 meters wide, and 2.1 meters high, with 40 seats, was used to establish the geometric model. The air-conditioning units were equipped with four air-supply outlets and one air-return outlet. The static pressure chamber of each air duct is fed by each air-supply outlet. One carriage has a rated air-supply volume of 8000 m³/h, which is distributed equally among eight air-supply outlets. Since the internal structure of the compartment body is complex, the simulation model must ignore some of the structural details of the car body. Instead, it must focus on restoring the structural features that affect airflow and other structural factors. The geometric model of the unloaded carriage is shown in Figure 2, while the human-body model is shown in Figure 3.

3.2.1. Grid Division and Boundary Setting

On the human body and carriage wall, the grid was divided into five prismatic layers, which can better represent the fluid characteristics in the near-wall layer. Other areas were divided into cut-body grids. For the air supply and return ducts, grilles, human body intervals, etc., a polyhedral mesh was used with a global grid size of 50 mm and a minimum grid size of 2.5 mm. The number of grids reached 30 million. According to the paper, the turbulence model applied is the standard k-epsilon model. In engineering applications, this model has been verified with a number of experiments, and the accuracy of this model has been established as reliable.

• Inlet boundary: the boundary of the calculation domain simulation was set as a velocity inlet, and the velocity value was determined based on the volume of the air supply.
• Exit boundary: in the passenger compartment, the return-air outlet and exhaust-air outlet were set as the pressure export boundary, and the static pressure of the export boundary was set to 0 Pa.
• Heat boundary: the passenger surface temperature was set to 36.5 °C, and the air-supply temperature was set to 19 °C.

3.2.2. Simulation of Several Working Conditions and PMV Data

Based on the calculation of several models established for different passenger-capacity conditions under different air-supply volumes, the air-supply volume curve shown in

Table 5. Air-supply volume under different passenger-capacity conditions Q (m³/h).

PMV	60	129	160	216	302	351
−0.5	500	5000	8000	/	/	/
0	100	1000	5000	8000	/	/
0.5	50	100	3000	3800	6000	8000

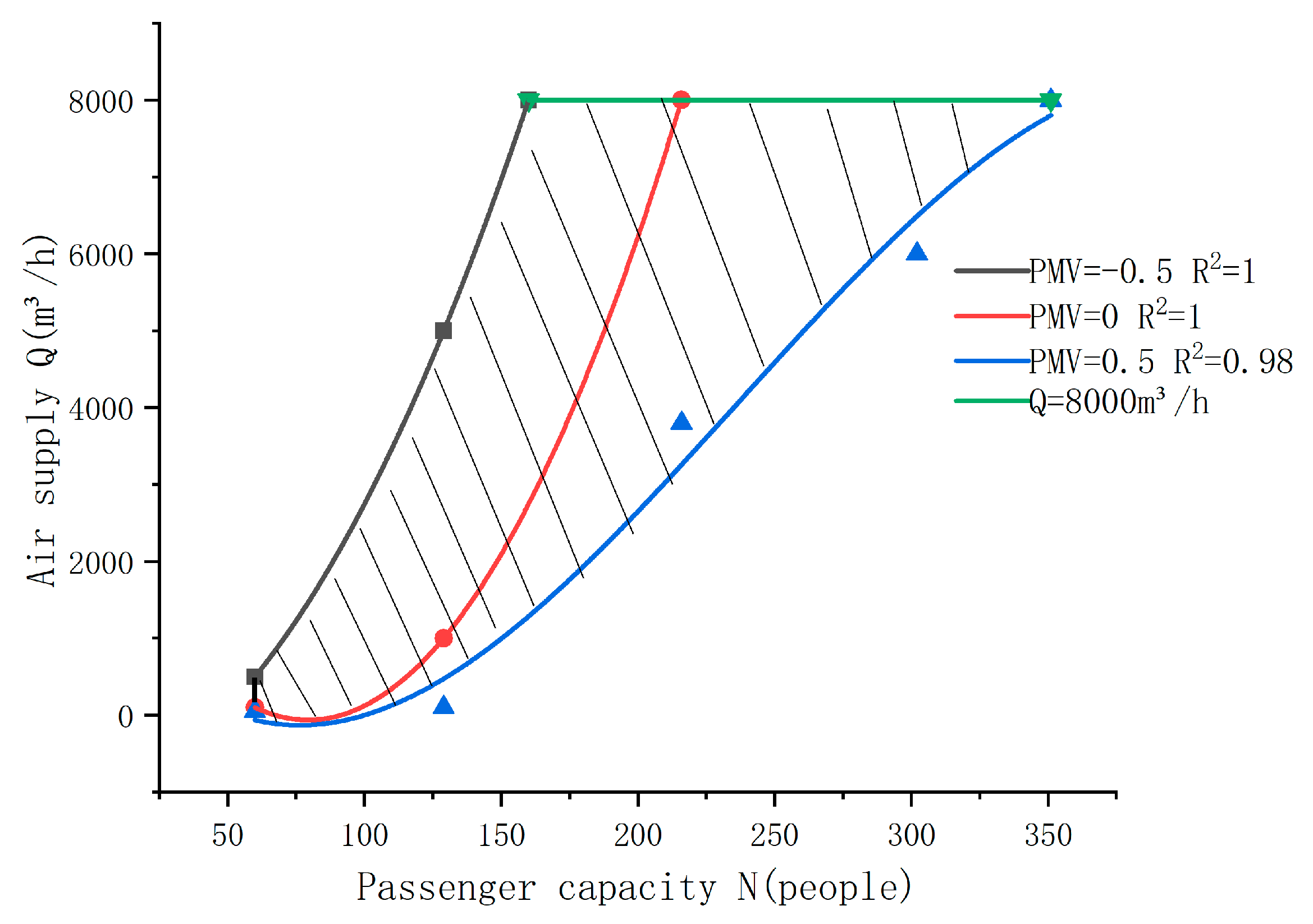
may be calculated to reach the ISO standard [12] for human-thermal-comfort index PMV (−0.5, 0.5) around people (1.1 m cross-sectional height). Specifically, the shaded area in Figure 4 represents the range of air-supply volumes that can meet the PMV between ±0.5 under different passenger capacities.

3.3. Air-Supply Curves Based on Thermal Comfort with Cooling and the Fresh-Air Volume

Figure 1 shows the air-supply-volume curve based on cooling and fresh-air volume, while Figure 4 shows the air-supply-volume variation curve based on thermal comfort. Using Figure 1 and Figure 4, we obtain Figure 5, in which only the shaded areas indicate the air-supply volume, which meets both the PMV between (−0.5, 0.5) and the cooling and fresh-air volume requirements. As a result, regulating the air-supply volume alone cannot provide a state of thermal-comfort PMV = 0 for the human body.

4. The Temperature-Control Curve

From the previous discussion, it can be seen that merely regulating the air-supply volume cannot achieve a thermal-comfort PMV = 0 for the human body at the given air-supply temperature of 19 °C. As a result, Fanger’s PMV theory was used in order to provide the regulation measures for controlling the temperature. Consequently, it is possible to meet the human body’s thermal-comfort requirements when the subway train has a variety of passenger capacities and air-supply speeds.

4.1. Analysis Methods of the Subway Train Temperature-Control Model

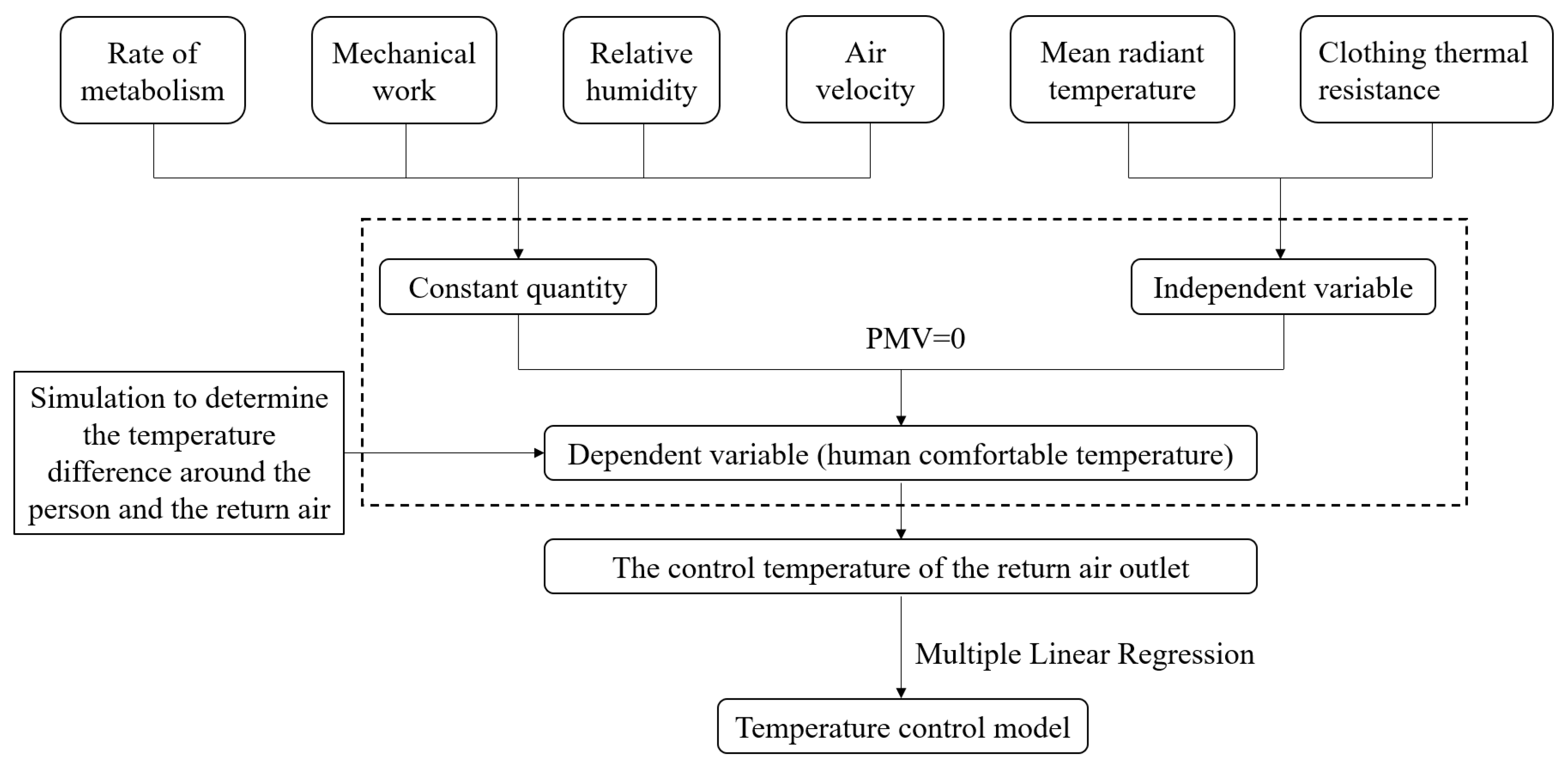
In Figure 6, the research method for the subway train temperature-control model is described. According to Fanger’s theory and the influencing factors of the PMV index, the human metabolic rate is M, the mechanical work performed by the human body is W, the average radiation temperature is t_r, the air temperature is t_a, the relative air humidity is φ, and the air-flow rate is v. The average radiation temperature inside the subway is influenced by the passenger capacity. The temperature of the wall inside the subway and the thermal resistance of clothing are influenced by the temperature outside the car. These variables are taken as independent variables in the control model. The other influencing factors are constant parameters. The temperature of the air for human thermal comfort can be obtained by controlling PMV = 0 [13]. As a result, the actual regulation is based on the deviation of the return-air temperature from the set value. In light of the simulation results, it is also necessary to correct the temperature difference between the 1.1m section and the return air. Finally, multiple linear regression was used to obtain the temperature-control curve for the return air inside the subway.

According to

Table 6. The average radiant temperature of the human body under different passenger capacities.

Passenger Capacities N (Person)	Mean Radiant Temperature (°C)
80	25.9
120	27.0
160	28.2
200	28.6
240	29.0
280	29.2
320	29.3
360	30.3

, the average radiation temperature is related to the passenger capacity. In addition, the relationship between the clothing thermal resistance f_cl and the temperature outside the vehicle t_out is $f_{cl}=-0.03\times t_{out}+1.35$.

4.2. Fitting Results of the Temperature-Control Curve

The metabolic rate of the human body inside the vehicle is 74 W/m². The mechanical work performed by the human body is 0 W/m². In the vehicle, there is a relative humidity of 65%. In accordance with the above method, for different passenger capacities and outside temperatures, the optimal control temperature is calculated at PMV = 0. Using multiple linear regression, the binary primary temperature-control curve was fitted to the passenger capacity and the outside temperature.

In cases where N is greater than 0 but less than 60 people, Q = 3795 m³/h. For field verification, the air-flow rate was set to 0.1 m/s, and an optimal control temperature was obtained by controlling PMV = 0 as shown in

Table 7. The optimal control temperature for a passenger capacity of 0 to 60 people.

Outdoor Air Temperature (°C)	Clothing Thermal Resistance (clo)	Optimal Control Temperature (°C)
		Passenger Capacity N (48 People)	Passenger Capacity N (56 People)
35	0.30	26.0	25.5
34	0.33	25.7	25.1
33	0.36	25.3	24.8
32	0.39	24.9	24.4
31	0.42	24.5	24.0
30	0.45	24.2	23.7
29	0.48	23.8	23.3
28	0.51	23.4	22.9
27	0.54	23.0	22.6
26	0.57	22.7	22.2
25	0.60	22.3	21.9
24	0.63	21.9	21.5

.

Multiple linear regression was used to fit the temperature-control curve based on the calculated data.

$$t_{in}=0.369\times t_{out}-0.06\times N+16.004$$

(6)

In cases where N is greater than or equal to 60 but less than 176.

$$Q=-0.06\times N^2+50.2\times N+988.4$$

(7)

The temperature-control curve was further fitted using the air-supply volume control curve. Due to the fact that the air-supply volume in this section varies in relation to the passenger capacity, it was also necessary to adjust the air-flow rate accordingly as passenger capacity changes. Therefore, it was necessary to calculate the optimal control temperature based on the different passenger capacities and the corresponding air-flow rate and the optimal control temperature, as shown in

Table 8. The optimal control temperature for a passenger capacity of 60 to 176 people.

Outdoor Air Temperature (°C)	Clothing Thermal Resistance (clo)	Optimal Control Temperature (°C)
		Passenger Capacity N (80 People)	Passenger Capacity N (100 People)	Passenger Capacity N (120 People)	Passenger Capacity N (140 People)
Air-flow rate v (m/s)		0.13	0.17	0.2	0.23
Air-supply volume Q (m3/h)		462	5408	6148	6840
35	0.30	25.8	25.5	25.2	24.9
34	0.33	25.7	25.1	25.0	24.8
33	0.36	25.5	24.8	24.8	24.6
32	0.39	25.3	24.4	24.7	24.4
31	0.42	25.2	24.0	24.5	24.3
30	0.45	25.0	23.7	24.4	24.1
29	0.48	24.8	23.3	24.2	23.9
28	0.51	24.7	22.9	24.0	23.8
27	0.54	24.5	22.6	23.9	23.6
26	0.57	24.4	22.2	23.7	23.5
25	0.60	24.2	21.9	23.5	23.3
24	0.63	24.0	21.5	23.4	23.1

. Based on the series of {t_in}, {t_out}, {N}, and {Q} values, we fit the temperature-control curve using multiple linear regression.

$$t_{in}=0.303\times t_{out}-0.011\times N+15.791$$

(8)

In Cases where N is greater than or equal to 176 but less than 351, Q = 8000 m³/h. According to

Table 9. The optimal control temperature considering the temperature difference between the return air and the comfort section around people.

Outdoor Air Temperature (°C)	Clothing Thermal Resistance (clo)	Optimal Control Temperature (°C)
		Passenger Capacity N (200 People)	Passenger Capacity N (240 People)	Passenger Capacity N (280 People)	Passenger Capacity N (320 People)
35	0.30	24.6	24.3	24.2	24.1
34	0.33	24.3	24.0	24.0	23.7
33	0.36	24.0	23.7	23.7	23.4
32	0.39	23.7	23.4	23.4	23.1
31	0.42	23.4	23.1	23.1	22.8
30	0.45	23.1	22.8	22.8	22.5
29	0.48	22.8	22.5	22.5	22.2
28	0.51	22.5	22.2	22.2	21.9
27	0.54	22.2	21.9	21.9	21.6
26	0.57	21.9	21.6	21.6	21.3
25	0.60	21.6	21.3	21.3	21.0
24	0.63	21.3	21.0	21.0	20.7

, the optimal control temperature was obtained by controlling PMV = 0 with a flow rate of 0.3 m/s.

Based on the calculated data, the temperature-control curve was fitted using multiple linear regression.

$$t_{in}=0.3\times t_{out}-0.004\times N+14.959$$

(9)

As shown in Figure 7, if the three control temperatures are integrated, the control temperature decreases linearly with increased passenger capacity, and increases linearly with increased outdoor temperature.

5. Passenger Compartment Flow and Temperature Field Evaluation

For the purpose of further verifying the uniformity of the flow field under the air-supply profile, a series of simulations were performed for each condition of passenger capacity under the air-supply profile. According to EN14750, the temperature and velocity fields of the passenger compartment were analyzed and evaluated [5].

5.1. The Measurement-Point Arrangement and Evaluation Method

The layout of the measurement point is shown in Figure 8. In total, three measurement points are located at 0.1 m, nine measurement points at 1.1 m, and three measurement points at 1.7 m. The measurement points L1-L2 are located at 0.1 m, where N = 1,2,3. At 1.1 meters, L2-N are arranged, where N is 1, 2, ..., 9. L3-N are located at a height of 1.7 m, where N is 1, 2, 3.

In accordance with the standard EN14750, the passenger compartment’s temperature uniformity and air-speed uniformity were evaluated. The resulting evaluation indexes are listed below.

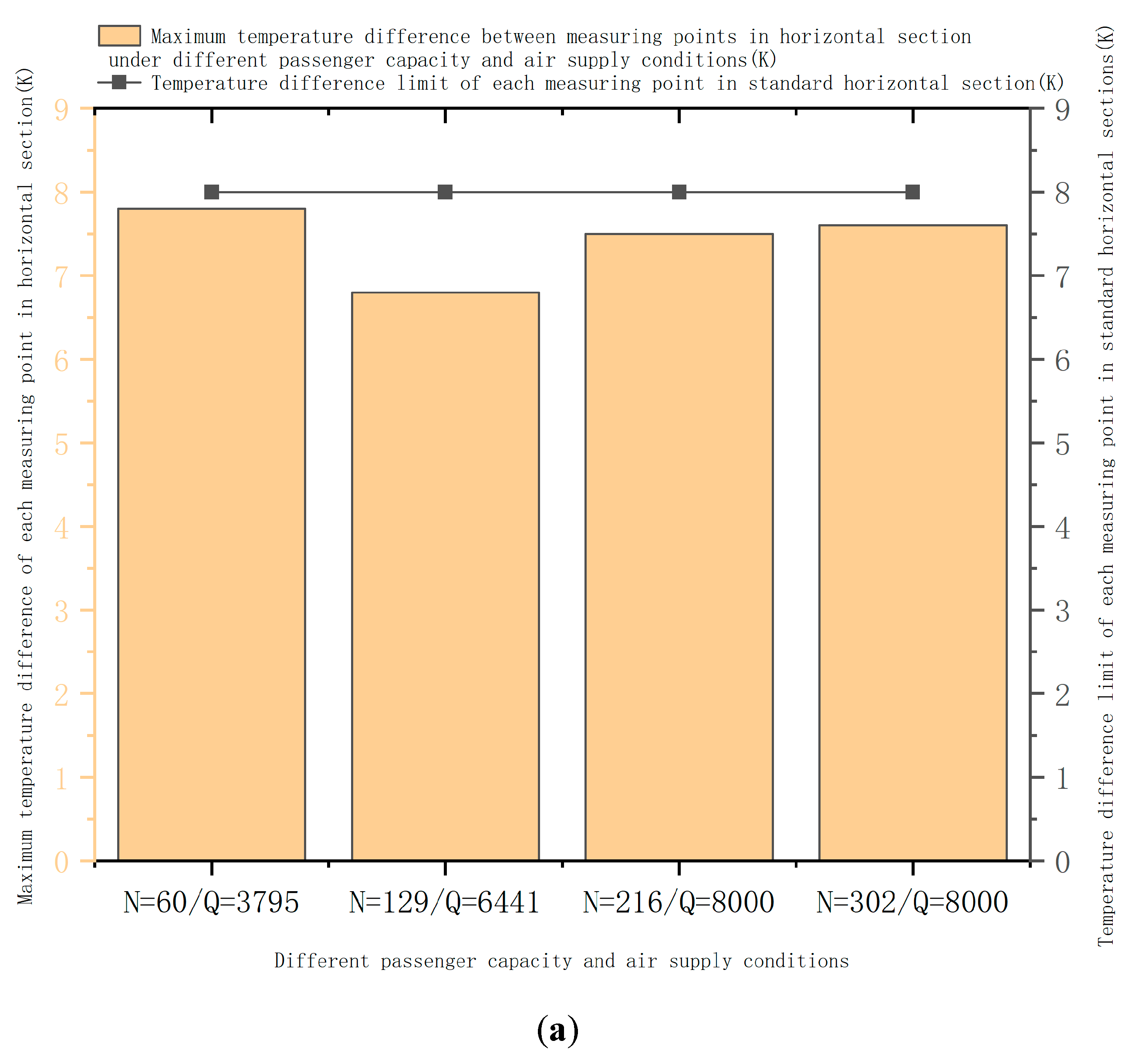
• Difference in temperature of the horizontal section: a temperature difference of less than 8K should be observed at each measurement point at 1.1 m above the ground.
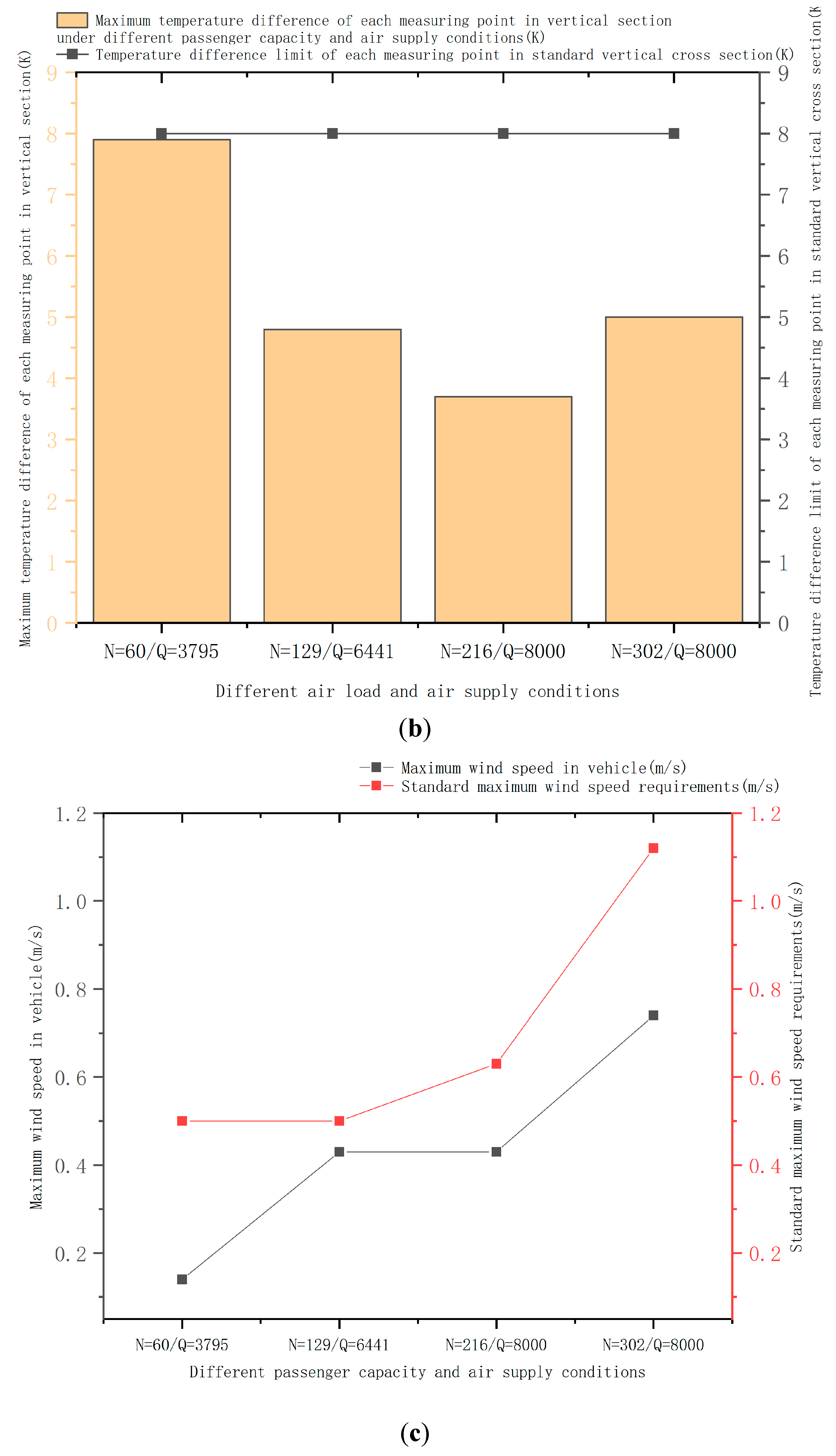
• Vertical-section temperature difference: it is necessary to maintain a maximum temperature difference of less than 8K at each measurement point in the vertical direction.
• Wind-speed requirement: The wind-speed value of each measurement point inside a compartment cannot exceed the maximum wind-speed requirements specified by Appendix B [3] of EN14750-1.

5.2. Analysis of Simulation Results for Passenger Compartments

Figure 9 illustrates the temperature field and velocity field data of the passenger compartment based on simulation calculations. According to the analysis of the data, the maximum temperature difference between horizontal and vertical sections at each measurement point is less than 8K, while the maximum wind speed inside the vehicle does not exceed the EN14750-1 maximum-wind-speed requirement. Thus, the uniformity of the flow field within the passenger compartment meets the requirements of the standard under each condition of operation of the air-supply system.

6. Conclusions

The objective of this study was to determine the air-supply volume and temperature-control curve of subway trains. First, a theoretical calculation was performed to determine the minimum critical air-supply volume curve under different passenger capacities in order to account for cold and wet load requirements, in addition to fresh-air-volume requirements. Second, the numerical simulation method was used to calculate the PMV distribution under a variety of passenger capacities and air-supply volumes. It was found that controlling the air-supply volume alone was not sufficient to produce the state of thermal comfort that corresponds to PMV = 0 in the human body. According to the PMV theory formula, multiple linear regression was used to fit the temperature-control curve under different passenger capacities. Based on the simulation calculation of the passenger compartment, the uniformity of the flow field and temperature field in the passenger compartment was evaluated in accordance with EN14750. Under all air-supply conditions, the uniformity of the flow and temperature field met the requirements of the standard, which indicates that this research method is accurate and may be used to guide the design calculations of similar practical projects in the future.

Table 10. The air-supply volume and the temperature-control curve.

Passenger Capacity N (People)	Air Output Q (m3/h)	Controlling Temperature tin (°C)
N < 60	3795	$t_{in}=0.369\times t_{out}-0.06\times N+16.004$
60 ≤ N < 176	$Q=-0.06\times N^2+50.2\times N+988.4$	$t_{in}=0.303\times t_{out}-0.011\times N+15.791$
N ≥ 176	8000	$t_{in}=0.3\times t_{out}-0.004\times N+14.959$

shows the governing equation for the volume of air supply and temperature of the air conditioners in subway trains that have a passenger capacity.

As a result of the control curve proposed in this paper for air-supply volume and temperature, it becomes possible to adjust the air-supply volume and temperature in real time in response to changes in passenger capacity, improve the human body’s thermal comfort in the vehicle, and reduce air-conditioning energy consumption. During real vehicle regulation, the air volume should be regulated first according to the number of passengers, and then the temperature should be further regulated. By reducing air-supply volume and duct resistance, excessive cooling output is avoided, and fan energy consumption is reduced. The method is currently being tested for use in subways.