SPAM: Solar Spectrum Prediction for Applications and Modeling
Abstract
1. Introduction
2. Data
2.1. F Index
2.2. TIMED Spacecraft Data
3. Solar-SPAM: Shortwave Energy Spectrum Model
4. Aero-SPAM: EUV Photon Flux Model for Aeronomic Applications
5. Discussion
6. Conclusions
- 1.
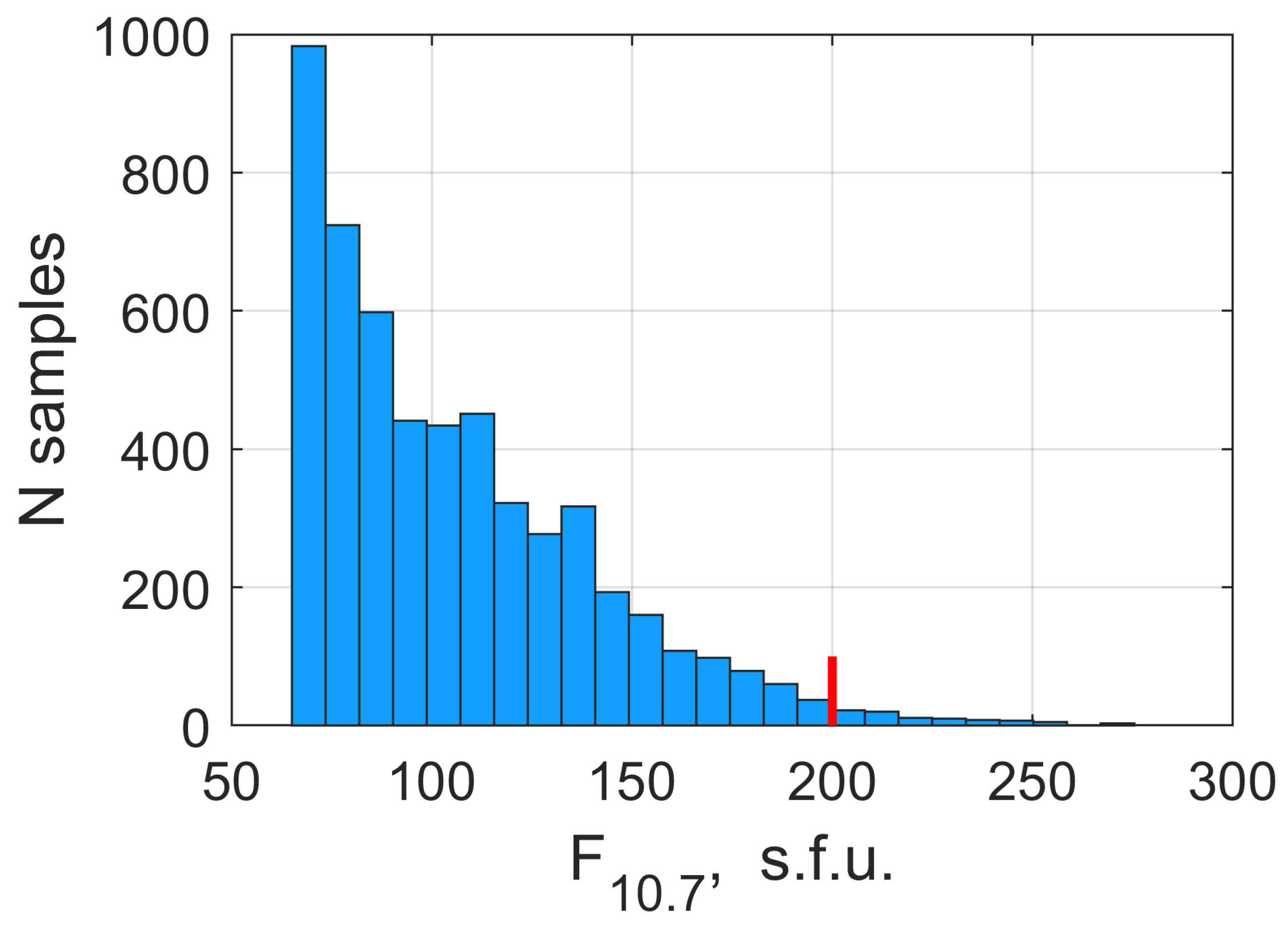
- The F index is an excellent indicator of solar activity (Tapping, 2013) and may serve as a reliable proxy for the solar spectrum variations within the limits of the SPAM model applicability 65 < F < 200 s.f.u.
- 2.
- Since the atmosphere is transparent to radiation at a wavelength of 10.7 cm, the F radio flux can be reliably measured from the Earth’s surface in any weather. The time series of the daily F has been available continuously since 1947 for seven solar cycles, so the SPAM model can be applied to large-scale retrospective studies that require solar radiation data.
- 3.
- The F index is predictable, which allows SPAM to forecast the solar spectrum for various operational tasks. There are a number of services providing the forecast of the daily averaged F index, e.g., up to 55 days ahead (http://spaceweather.izmiran.ru/eng/forecasts.html, accessed on 20 November 2022), up to 27 days ahead with open-access forecast (https://www.swpc.noaa.gov/products/27-day-outlook-107-cm-radio-flux-and-geomagnetic-indices, accessed on 20 November 2022) and up to 45 days ahead with 5-day resolution (https://www.swpc.noaa.gov/products/usaf-45-day-ap-and-f107cm-flux-forecast, accessed on 20 November 2022). In addition, there is a long-term monthly average F forecast up to 20 years, including the next solar activity cycle, that can be used for future aeronomy estimations. (https://www.swpc.noaa.gov/products/predicted-sunspot-number-and-radio-flux, accessed on 20 November 2022).
- 4.
- SPAM’s single-variable parameterization is easy to implement. Despite the model simplicity, our results are in good agreement with the measurements.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| R | RMSE | ||||
|---|---|---|---|---|---|
| 1.5 | −4.94024181 | 3.22175699 | −1.80553335 | 0.93 | 2.67305197 |
| 2.5 | −1.51234762 | 8.72873177 | −3.59300652 | 0.96 | 4.64649582 |
| 3.5 | −8.19051896 | 4.76131943 | −1.75069528 | 0.96 | 2.57208191 |
| 4.5 | −1.25299002 | 7.18966612 | −2.30913459 | 0.96 | 3.78321360 |
| 5.5 | −1.05306909 | 6.00386365 | −1.72945105 | 0.96 | 3.13381799 |
| 6.5 | −1.24449248 | 7.07626722 | −2.22302072 | 0.96 | 3.69094684 |
| 7.5 | −2.59694610 | 1.45374662 | −6.31698909 | 0.96 | 7.43469515 |
| 8.5 | −2.16866639 | 1.21455389 | −4.6505577 | 0.96 | 6.21501074 |
| 9.5 | −1.52361462 | 8.68533191 | −3.0246892 | 0.96 | 4.53196359 |
| 10.5 | −1.01521500 | 5.78430109 | −1.79161041 | 0.96 | 3.02874105 |
| 11.5 | −5.92986152 | 3.39846459 | −7.46323908 | 0.96 | 1.86757596 |
| 12.5 | −3.91620799 | 2.22633150 | −6.85281881 | 0.96 | 1.16787269 |
| 13.5 | −3.68662392 | 2.14384736 | −5.53046688 | 0.96 | 1.20433914 |
| 14.5 | −8.15473279 | 4.56904530 | −1.28641555 | 0.96 | 2.34443139 |
| 15.5 | −1.05314223 | 5.90337830 | −2.51992115 | 0.96 | 3.02143819 |
| 16.5 | −1.71833912 | 9.58528730 | −2.37694140 | 0.96 | 4.91384954 |
| 17.5 | −7.84248508 | 4.35156360 | −6.77832612 | 0.96 | 2.24071577 |
| 18.5 | −5.35989584 | 2.98171616 | −7.78638812 | 0.96 | 1.53019138 |
| 19.5 | −5.64009182 | 3.15119971 | −1.24435988 | 0.96 | 1.61351843 |
| 20.5 | −4.90601610 | 2.74377445 | −1.31174042 | 0.96 | 1.40380060 |
| 21.5 | −4.26086127 | 2.38514084 | −1.14409417 | 0.96 | 1.22091037 |
| 22.5 | −3.19159017 | 1.77982999 | −5.49342607 | 0.96 | 9.12119600 |
| 23.5 | −1.75266637 | 9.77475268 | −2.67796958 | 0.96 | 5.01372608 |
| 24.5 | −2.43810818 | 1.36192347 | −4.57043670 | 0.96 | 6.97290978 |
| 25.5 | −3.98387625 | 2.22551933 | −7.70072803 | 0.96 | 1.13958300 |
| 26.5 | −2.00773403 | 1.12849376 | −5.67602506 | 0.96 | 5.77108499 |
| 27.5 | −1.19730867 | 5.65394676 | −5.85964757 | 0.94 | 3.19981683 |
| 28.5 | −1.46295195 | 1.01404261 | −3.58365291 | 0.93 | 8.68678105 |
| 29.5 | −8.15084563 | 4.34467210 | 3.65433670 | 0.93 | 3.03848274 |
| 30.5 | −7.05077152 | 4.04741769 | 1.43586031 | 0.94 | 2.75155631 |
| 31.5 | −7.77266741 | 4.68802536 | 1.08074811 | 0.93 | 3.64885891 |
| 32.5 | −5.61602010 | 2.83431306 | −3.27491491 | 0.92 | 2.03502960 |
| 33.5 | 6.11880133 | 6.52060422 | −2.90103367 | 0.91 | 1.14428500 |
| 34.5 | −2.13887412 | 9.00810935 | −1.41575668 | 0.93 | 5.08999204 |
| 35.5 | −2.29655541 | 1.06445240 | −3.23960927 | 0.94 | 6.31089521 |
| 36.5 | −1.69356060 | 1.14642019 | −1.49427472 | 0.93 | 9.15296502 |
| 37.5 | −4.44754965 | 2.24144087 | 2.29852502 | 0.94 | 1.39955751 |
| 38.5 | −2.57264554 | 1.20451838 | 1.08315857 | 0.95 | 6.47189724 |
| 39.5 | −1.90799471 | 8.54129718 | −3.66570920 | 0.95 | 4.29404481 |
| 40.5 | −1.63110170 | 7.67917532 | 2.48479107 | 0.94 | 4.43317217 |
| 41.5 | −2.64676272 | 1.61050402 | −5.64014188 | 0.94 | 1.09306430 |
| 42.5 | −8.80727378 | 5.09406819 | 1.64104876 | 0.94 | 3.40898878 |
| 43.5 | −1.29810569 | 3.70763160 | 8.20072441 | 0.82 | 7.51972352 |
| 44.5 | −1.92736419 | 9.35286333 | 2.78944317 | 0.95 | 5.03560346 |
| 45.5 | −1.07354187 | 5.33853880 | 3.23226206 | 0.94 | 3.25167635 |
| 46.5 | 7.14925370 | 2.28505089 | 1.60620921 | 0.85 | 7.85818717 |
| 47.5 | −1.65354143 | 7.61012429 | 3.10560608 | 0.95 | 3.96736808 |
| 48.5 | −3.12973348 | 1.39150026 | 3.17305408 | 0.95 | 6.77782659 |
| 49.5 | −8.48676578 | 3.82780831 | −8.99955570 | 0.95 | 1.84750385 |
| 50.5 | −6.92148698 | 3.05273387 | −2.21022224 | 0.95 | 1.42588987 |
| 51.5 | −3.52451773 | 1.49567940 | −2.77810793 | 0.95 | 6.67205223 |
| 52.5 | −4.88285423 | 2.06597500 | −5.71616451 | 0.95 | 9.23676788 |
| 53.5 | −1.51950475 | 6.22135728 | 4.00946070 | 0.92 | 3.69972956 |
| 54.5 | −1.47270077 | 5.88009296 | 1.18884773 | 0.95 | 2.61720547 |
| 55.5 | −2.67639507 | 9.72464276 | 2.22162082 | 0.63 | 1.37799232 |
| 56.5 | −1.01960607 | 4.67610258 | 3.41494514 | 0.93 | 2.80937628 |
| 57.5 | −1.61974440 | 6.72143036 | 1.17127082 | 0.95 | 3.07827728 |
| 58.5 | −1.01763203 | 4.54759489 | 1.65241671 | 0.91 | 3.09599754 |
| 59.5 | −1.56307209 | 6.36007172 | 3.86630485 | 0.92 | 3.58530411 |
| 60.5 | −6.00806861 | 2.63372194 | 5.64617215 | 0.94 | 1.45080898 |
| 61.5 | −6.04959878 | 2.45041951 | −1.62883930 | 0.94 | 1.21428067 |
| 62.5 | −6.49554222 | 2.79301792 | 1.91126658 | 0.89 | 2.08911118 |
| 63.5 | −4.82850036 | 1.71382019 | 2.02470800 | 0.75 | 1.67842699 |
| 64.5 | −1.06653492 | 4.22914685 | 1.50553273 | 0.94 | 2.03369385 |
| 65.5 | −8.18714565 | 3.40516816 | 1.66550540 | 0.94 | 1.76539694 |
| 66.5 | −9.90389288 | 4.04518744 | 1.56394010 | 0.94 | 1.96591466 |
| 67.5 | −9.41472141 | 3.78395774 | 8.82049866 | 0.94 | 1.80481835 |
| 68.5 | −8.29145674 | 3.45290364 | 5.19960242 | 0.82 | 3.44043640 |
| 69.5 | −1.37956080 | 5.60239688 | 1.65024766 | 0.94 | 2.65869617 |
| 70.5 | −1.01440668 | 4.37751602 | 9.44754103 | 0.79 | 4.90083335 |
| 71.5 | −8.82187053 | 3.44490090 | 2.44945919 | 0.92 | 1.89763276 |
| 72.5 | −1.38052514 | 5.94292750 | 4.19292916 | 0.95 | 2.87817244 |
| 73.5 | −4.91176916 | 2.32864269 | 1.44437460 | 0.94 | 1.39806401 |
| 74.5 | −6.46953103 | 2.83325477 | 2.59377737 | 0.93 | 1.66218244 |
| 75.5 | −7.34309741 | 3.29461087 | 4.00460892 | 0.90 | 2.45820894 |
| 76.5 | −3.05657856 | 2.93068006 | 1.40723930 | 0.74 | 6.32637967 |
| 77.5 | 5.43557600 | 2.19484499 | 1.18134495 | 0.89 | 5.64382540 |
| 78.5 | −8.51779066 | 5.79401798 | 1.63692915 | 0.82 | 8.43951888 |
| 79.5 | −2.21722606 | 8.88851417 | 8.27783879 | 0.89 | 6.07167204 |
| 80.5 | −1.65576278 | 7.79627572 | 5.66367756 | 0.94 | 4.44114376 |
| 81.5 | −1.92487027 | 8.70304770 | 5.81788594 | 0.93 | 5.12896384 |
| 82.5 | −2.51845067 | 1.14456368 | 6.30086163 | 0.94 | 6.49515749 |
| 83.5 | −4.38140196 | 1.97591643 | 1.99037756 | 0.90 | 1.48395770 |
| 84.5 | −3.73488547 | 1.70436208 | 8.14608828 | 0.94 | 9.68131273 |
| 85.5 | −4.33366783 | 2.09399580 | 9.28690005 | 0.94 | 1.21724813 |
| 86.5 | −4.84412766 | 2.36665683 | 1.09788284 | 0.94 | 1.44126953 |
| 87.5 | −4.83254202 | 2.68350608 | 1.39973835 | 0.94 | 1.85920378 |
| 88.5 | −6.21282703 | 3.37561898 | 1.45738166 | 0.94 | 2.27765383 |
| 89.5 | −6.68966301 | 3.86462205 | 1.63709915 | 0.93 | 2.80715372 |
| 90.5 | −9.40447671 | 4.91524881 | 1.81668436 | 0.93 | 3.38519060 |
| 91.5 | −7.89804624 | 4.23827993 | 1.56806295 | 0.94 | 2.81369582 |
| 92.5 | −2.51717440 | 1.25207391 | 7.46452895 | 0.95 | 7.21226067 |
| 93.5 | −2.52576412 | 1.27365730 | 7.86103295 | 0.95 | 7.08295267 |
| 94.5 | −1.68630601 | 8.97996451 | 6.01452925 | 0.95 | 5.30470738 |
| 95.5 | −1.71120327 | 8.22690427 | 4.20933726 | 0.95 | 4.36420483 |
| 96.5 | −1.16976002 | 5.79214134 | 3.16068207 | 0.95 | 3.17857028 |
| 97.5 | −9.42103907 | 7.84156346 | 6.35681772 | 0.89 | 9.05302834 |
| 98.5 | −1.74979936 | 9.39505851 | 8.37957920 | 0.94 | 6.18586716 |
| 99.5 | −3.06874683 | 1.63261897 | 1.00132945 | 0.95 | 9.92576035 |
| 100.5 | −2.08354284 | 1.12300476 | 1.82943275 | 0.95 | 6.70876385 |
| 101.5 | −2.22515562 | 1.04514427 | 5.86589870 | 0.95 | 5.33557018 |
| 102.5 | −1.34390246 | 8.98461854 | 3.81054263 | 0.92 | 7.66619612 |
| 103.5 | −1.01901721 | 6.79827099 | 4.51530159 | 0.94 | 5.22679531 |
| 104.5 | −4.18859821 | 1.89817197 | 3.18890523 | 0.95 | 9.38122529 |
| 105.5 | −2.54275033 | 1.20088332 | 6.60009868 | 0.96 | 5.89125254 |
| 106.5 | −2.43809593 | 1.18160635 | 7.74794070 | 0.96 | 5.90449142 |
| 107.5 | −2.33163874 | 1.20516330 | 9.87441885 | 0.95 | 6.87291920 |
| 108.5 | −3.69477413 | 2.17542411 | 1.10904940 | 0.96 | 1.26819431 |
| 109.5 | −2.81707873 | 1.45887138 | 9.82531461 | 0.95 | 7.99552250 |
| 110.5 | −9.10934796 | 1.04423228 | 1.44644224 | 0.92 | 1.08652364 |
| 111.5 | −1.66854605 | 1.18197160 | 1.27341149 | 0.95 | 8.46551633 |
| 112.5 | −1.97256040 | 1.22023811 | 1.39870362 | 0.95 | 8.24895534 |
| 113.5 | −1.84532308 | 1.04923564 | 7.42101884 | 0.95 | 6.63927760 |
| 114.5 | −1.82255068 | 1.00964734 | 1.09676338 | 0.95 | 5.83301149 |
| 115.5 | −1.79977830 | 9.70059057 | 1.45142487 | 0.95 | 5.79507535 |
| 116.5 | −1.14063699 | 6.14789756 | 2.11095772 | 0.95 | 3.67271760 |
| 117.5 | −1.19813939 | 5.28441463 | 5.22879409 | 0.95 | 2.46827715 |
| 118.5 | −3.17606335 | 1.43250820 | 2.42879319 | 0.95 | 6.91404625 |
| 119.5 | −5.07968379 | 2.73788903 | 3.79524397 | 0.95 | 1.63559867 |
| 120.5 | −3.91694650 | 1.76667070 | 4.67276673 | 0.95 | 8.52689227 |
| 121.5 | −2.10473407 | 3.12348452 | 4.59160841 | 0.91 | 3.68717499 |
| 122.5 | −9.24069369 | 4.16785440 | 4.09787537 | 0.95 | 2.01162816 |
| 123.5 | −6.22067015 | 2.80572523 | 2.53756139 | 0.95 | 1.35419220 |
| 124.5 | −4.72854326 | 2.13272731 | 1.79398692 | 0.95 | 1.02936761 |
| 125.5 | −2.37088928 | 1.27788104 | 2.05651276 | 0.95 | 7.63398559 |
| 126.5 | −7.26808556 | 3.27814376 | 1.76920985 | 0.95 | 1.58220650 |
| 127.5 | −1.57815999 | 8.50609426 | 1.52935833 | 0.95 | 5.08149030 |
| 128.5 | −1.17377545 | 6.32650980 | 1.23296767 | 0.95 | 3.77941945 |
| 129.5 | −5.73834119 | 7.57079693 | 1.75886126 | 0.93 | 7.63296694 |
| 130.5 | −1.24053248 | 5.70638506 | 1.20965081 | 0.91 | 4.16222369 |
| 131.5 | −2.12721218 | 9.61118248 | 1.95150657 | 0.91 | 6.62435421 |
| 132.5 | −1.07001857 | 6.29334120 | 1.62571838 | 0.90 | 5.67873985 |
| 133.5 | −8.94382834 | 8.71939234 | 1.31975911 | 0.94 | 7.54203153 |
| 134.5 | −8.35494200 | 6.28665121 | 1.35754292 | 0.88 | 7.29144198 |
| 135.5 | −1.25088026 | 8.54845405 | 3.77824430 | 0.90 | 8.81264590 |
| 136.5 | −9.79967900 | 7.22954986 | 2.10731394 | 0.90 | 7.68205303 |
| 137.5 | −1.24013546 | 7.97949440 | 2.37165611 | 0.91 | 7.11357554 |
| 138.5 | −7.39876006 | 5.55570063 | 2.54832371 | 0.87 | 6.99090195 |
| 139.5 | −9.49205508 | 4.89958571 | 4.33705249 | 0.96 | 2.54613277 |
| 140.5 | − | 3.05432744 | 0.95 | 1.88073609 | |
| 141.5 | − | 1.13736869 | 0.90 | 8.95784614 | |
| 142.5 | − | 1.01825495 | 0.83 | 1.18926525 | |
| 143.5 | − | 1.15175318 | 0.88 | 1.00877166 | |
| 144.5 | − | 8.93582633 | 0.86 | 9.81989792 | |
| 145.5 | − | 1.38512452 | 0.89 | 1.19372564 | |
| 146.5 | − | 1.36559581 | 0.89 | 1.27366067 | |
| 147.5 | − | 1.39066818 | 0.89 | 1.35250470 | |
| 148.5 | − | 1.56053330 | 0.87 | 1.51332205 | |
| 149.5 | − | 1.24944106 | 0.83 | 1.51364906 | |
| 150.5 | − | 1.21205065 | 0.80 | 1.52268475 | |
| 151.5 | − | 1.16236962 | 0.80 | 1.65675848 | |
| 152.5 | − | 2.37558655 | 0.91 | 2.01495486 | |
| 153.5 | − | 1.71988954 | 0.88 | 2.21903105 | |
| 154.5 | − | 6.16487236 | 0.93 | 4.36900801 | |
| 155.5 | − | 2.92214578 | 0.92 | 3.20494890 | |
| 156.5 | − | 2.51428725 | 0.85 | 2.85808410 | |
| 157.5 | − | 1.48582781 | 0.77 | 2.79008511 | |
| 158.5 | − | 1.46877406 | 0.74 | 2.69140338 | |
| 159.5 | − | 1.10698536 | 0.73 | 2.59598688 | |
| 160.5 | − | 1.26638098 | 0.77 | 2.80522066 | |
| 161.5 | − | 1.37610016 | 0.65 | 3.39322701 | |
| 162.5 | − | 2.82618134 | 0.82 | 3.76275218 | |
| 163.5 | − | 2.30331717 | 0.83 | 4.07902394 | |
| 164.5 | − | 3.37772150 | 0.86 | 4.56771102 | |
| 165.5 | − | 2.97227900 | 0.76 | 7.93202201 | |
| 166.5 | 8.57496540 | 0.51 | 5.05815432 | ||
| 167.5 | − | 3.39319234 | 0.81 | 6.73876290 | |
| 168.5 | − | 2.79935936 | 0.66 | 6.38829474 | |
| 169.5 | 2.01744392 | 0.64 | 8.70736220 | ||
| 170.5 | − | 4.32779772 | 0.68 | 1.01094842 | |
| 171.5 | − | 4.47020613 | 0.70 | 1.06043009 | |
| 172.5 | − | 3.72615949 | 0.60 | 1.23238287 | |
| 173.5 | 2.79814116 | 0.61 | 1.18627791 | ||
| 174.5 | − | 3.92089797 | 0.61 | 1.50705494 | |
| 175.5 | − | 5.06896902 | 0.60 | 1.97468460 | |
| 176.5 | − | 6.78269058 | 0.59 | 2.01888857 | |
| 177.5 | 1.79727927 | 0.47 | |||
| 178.5 | 0.48 | ||||
| 179.5 | 0.54 | ||||
| 180.5 | − | 0.62 | |||
| 181.5 | − | 0.66 | |||
| 182.5 | 0.46 | ||||
| 183.5 | − | 0.45 | |||
| 184.5 | − | 0.47 | |||
| 185.5 | − | 0.44 | |||
| 186.5 | − | 0.44 | |||
| 187.5 | 0.35 | ||||
| 188.5 | 0.46 | ||||
| 189.5 | − | 0.51 |
| No | , nm | , nm | R | RMSE | |||
|---|---|---|---|---|---|---|---|
| 1 | 5 | 10 | − | − | 0.96 | ||
| 2 | 10 | 15 | − | − | 0.96 | ||
| 3 | 15 | 20 | − | − | 0.96 | ||
| 4 | 20 | 25 | − | − | 0.96 | ||
| 5 | 25.6 | − | − | 0.96 | |||
| 6 | 28.4 | − | − | 0.92 | |||
| 7 | 25 | 30 | − | − | 0.96 | ||
| 8 | 30.3 | − | 0.94 | ||||
| 9 | 30 | 35 | − | − | 0.93 | ||
| 10 | 36.8 | − | − | 0.93 | |||
| 11 | 35 | 40 | − | − | 0.94 | ||
| 12 | 40 | 45 | − | 0.95 | |||
| 13 | 46.5 | − | 0.84 | ||||
| 14 | 45 | 50 | − | 0.96 | |||
| 15 | 50 | 55 | − | − | 0.96 | ||
| 16 | 55.4 | − | 0.60 | ||||
| 17 | 58.4 | − | 0.91 | ||||
| 18 | 55 | 60 | − | 0.94 | |||
| 19 | 60.9 | − | 0.94 | ||||
| 20 | 62.9 | − | 0.89 | ||||
| 21 | 60 | 65 | − | 0.90 | |||
| 22 | 65 | 70 | − | 0.93 | |||
| 23 | 70.3 | − | 0.78 | ||||
| 24 | 70 | 75 | − | 0.94 | |||
| 25 | 76.5 | − | 0.72 | ||||
| 26 | 77 | − | 0.88 | ||||
| 27 | 78.9 | − | 0.81 | ||||
| 28 | 75 | 80 | − | 0.89 | |||
| 29 | 80 | 85 | − | 0.94 | |||
| 30 | 85 | 90 | − | 0.94 | |||
| 31 | 90 | 95 | − | 0.95 | |||
| 32 | 97.8 | − | 0.90 | ||||
| 33 | 95 | 100 | − | 0.95 | |||
| 34 | 102.6 | − | 0.93 | ||||
| 35 | 103.2 | − | 0.94 | ||||
| 36 | 100 | 105 | − | 0.96 | |||
| 37 | 121.6 | − | 0.92 | ||||
References
- Woodraska, D.L.; Woods, T.N.; Eparvier, F.G. In-flight calibration and performance of the Solar Extreme ultraviolet Experiment (SEE) aboard the TIMED Satellite. In Proceedings of the Instruments, Science, and Methods for Geospace and Planetary Remote Sensing, SPIE, Honolulu, HI, USA, 30 December 2004; Volume 5660, pp. 36–47. [Google Scholar] [CrossRef]
- Woods, T.N.; Rottman, G.J.; Harder, J.W.; Lawrence, G.M.; McClintock, W.E.; Kopp, G.A.; Pankratz, C. Overview of the EOS SORCE mission. In Proceedings of the Earth Observing Systems V. SPIE, San Diego, CA, USA, 15 November 2000; Volume 4135, pp. 192–203. [Google Scholar] [CrossRef]
- Lean, J.; Woods, T.; Eparvier, F.; Meier, R.; Strickland, D.; Correira, J.; Evans, J. Solar extreme ultraviolet irradiance: Present, past, and future. J. Geophys. Res. Space Phys. 2011, 116, A01102. [Google Scholar] [CrossRef]
- Vourlidas, A.; Bruinsma, S. EUV irradiance inputs to thermospheric density models: Open issues and path forward. Space Weather 2018, 16, 5–15. [Google Scholar] [CrossRef]
- Lilensten, J.; Dudok de Wit, T.; Kretzschmar, M.; Amblard, P.O.; Moussaoui, S.; Aboudarham, J.; Auchère, F. Review on the solar spectral variability in the EUV for space weather purposes. Ann. Geophys. 2008, 26, 269–279. [Google Scholar] [CrossRef]
- Rozanov, E.; Egorova, T.; Schmutz, W.; Peter, T. Simulation of the stratospheric ozone and temperature response to the solar irradiance variability during sun rotation cycle. J. Atmos. Sol. Terr. Phys. 2006, 68, 2203–2213. [Google Scholar] [CrossRef]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48, RG4001. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.; Solomon, S.; Roble, R.; Viereck, R. Impact of solar EUV, XUV, and X-ray variations on earth’s atmosphere. Geophys. Monogr. 2004, 141, 341–354. [Google Scholar] [CrossRef]
- Pacini, A.A.; Raulin, J.P. Solar X-ray flares and ionospheric sudden phase anomalies relationship: A solar cycle phase dependence. J. Geophys. Res. Space Phys. 2006, 111, 9301. [Google Scholar] [CrossRef]
- Kaufmann, P.; Paes de Barros, M. Some relationships between solar X-ray bursts and SPA’s produced on VLF propagation in the lower ionosphere. Sol. Phys. 1969, 9, 478–486. [Google Scholar] [CrossRef]
- Brasseur, G.P.; Solomon, S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere; Springer: Dordrecht, The Netherelands, 2005. [Google Scholar] [CrossRef]
- Chapman, S. The absorption and dissociative or ionizing effect of monochromatic radiation in an atmosphere on a rotating earth. Proc. Phys. Soc. 1926–1948 1931, 43, 26. [Google Scholar] [CrossRef]
- Nusinov, A.; Antonova, L.; Kazachevskaya, T.; Katyushina, V.; Svidsky, P. 11-Year solar cycle extreme ultraviolet and soft X-ray variations according to the ionospheric E-region data and results of direct measurements. Adv. Space Res. 2000, 25, 73–78. [Google Scholar] [CrossRef]
- Nikolaeva, V.; Gordeev, E.; Sergienko, T.; Makarova, L.; Kotikov, A. AIM-E: E-Region Auroral Ionosphere Model. Atmosphere 2021, 12, 748. [Google Scholar] [CrossRef]
- Cervera, M.A.; Harris, T.J.; Holdsworth, D.A.; Netherway, D.J. Ionospheric Effects on HF Radio Wave Propagation. In Ionosphere Dynamics and Applications; American Geophysical Union: Hoboken, NJ, USA, 2021; pp. 439–492. [Google Scholar] [CrossRef]
- Gao, H.; Li, G.; Li, Y.; Yang, Z.; Wu, X. Ionospheric effect of HF surface wave over-the-horizon radar. Radio Sci. 2006, 41, 1–10. [Google Scholar] [CrossRef]
- Byram, E.; Chubb, T.; Friedman, H. The solar X-ray spectrum and the density of the upper atmosphere. J. Geophys. Res. 1956, 61, 251–263. [Google Scholar] [CrossRef]
- Lean, J. Solar ultraviolet irradiance variations: A review. J. Geophys. Res. Atmos. 1987, 92, 839–868. [Google Scholar] [CrossRef]
- Vaishnav, R.; Jacobi, C.; Berdermann, J.; Schmölter, E.; Codrescu, M. Ionospheric response to solar EUV variations: Preliminary results. Adv. Radio Sci. 2018, 16, 157–165. [Google Scholar] [CrossRef]
- Ward, W.; Seppälä, A.; Yiğit, E.; Nakamura, T.; Stolle, C.; Laštovička, J.; Woods, T.N.; Tomikawa, Y.; Lübken, F.J.; Solomon, S.C.; et al. Role Of the Sun and the Middle atmosphere/thermosphere/ionosphere In Climate (ROSMIC): A retrospective and prospective view. Prog. Earth Planet. Sci. 2021, 8, 1–38. [Google Scholar] [CrossRef]
- Qian, L.; Solomon, S.C. Thermospheric density: An overview of temporal and spatial variations. Space Sci. Rev. 2012, 168, 147–173. [Google Scholar] [CrossRef]
- Svalgaard, L. Solar activity–past, present, future. J. Space Weather Space Clim. 2013, 3, A24. [Google Scholar] [CrossRef]
- Lean, J.; White, O.; Livingston, W.; Picone, J. Variability of a composite chromospheric irradiance index during the 11-year activity cycle and over longer time periods. J. Geophys. Res. Space Phys. 2001, 106, 10645–10658. [Google Scholar] [CrossRef]
- Schmidtke, G. Extreme ultraviolet spectral irradiance measurements since 1946. Hist. Geo Space Sci. 2015, 6, 3–22. [Google Scholar] [CrossRef]
- Kretzschmar, M.; Dudok de Wit, T.; Lilensten, J.; Hochedez, J.F.; Aboudarham, J.; Amblard, P.O.; Auchère, F.; Moussaoui, S. Solar EUV/FUV irradiance variations: Analysis and observational strategy. Acta Geophys. 2009, 57, 42–51. [Google Scholar] [CrossRef]
- Del Zanna, G.; Mason, H.E. Solar UV and X-ray spectral diagnostics. Living Rev. Sol. Phys. 2018, 15, 1–278. [Google Scholar] [CrossRef]
- Tobiska, W. Current status of solar EUV measurements and modeling. Adv. Space Res. 1996, 18, 3–10. [Google Scholar] [CrossRef]
- Woods, T.N. Recent advances in observations and modeling of the solar ultraviolet and X-ray spectral irradiance. Adv. Space Res. 2008, 42, 895–902. [Google Scholar] [CrossRef]
- Lean, J. A comparison of models of the Sun’s extreme ultraviolet irradiance variations. J. Geophys. Res. Space Phys. 1990, 95, 11933–11944. [Google Scholar] [CrossRef]
- Tobiska, W.K.; Eparvier, F. EUV97: Improvements to EUV irradiance modeling in the soft X-rays and FUV. Sol. Phys. 1998, 177, 147–159. [Google Scholar] [CrossRef]
- Richards, P.; Fennelly, J.; Torr, D. EUVAC: A solar EUV flux model for aeronomic calculations. J. Geophys. Res. Space Phys. 1994, 99, 8981–8992. [Google Scholar] [CrossRef]
- Nikolaeva, V.; Gordeev, E.; Rogov, D.; Nikolaev, A. Auroral ionosphere model (AIM-E) adjustment for the regular E layer. Sol.-Terr. Phys. 2021, 7, 41–46. [Google Scholar] [CrossRef]
- Nikolaeva, V.; Gordeev, E.; Rogov, D.; Novikov, S. Calibration of Empirical EUV Spectra for the Regular E-Region Modeling. Bull. Russ. Acad. Sci. Phys. 2022, 86, 329–334. [Google Scholar] [CrossRef]
- Richards, P.G.; Woods, T.N.; Peterson, W.K. HEUVAC: A new high resolution solar EUV proxy model. Adv. Space Res. 2006, 37, 315–322. [Google Scholar] [CrossRef]
- Girazian, Z.; Withers, P. An empirical model of the extreme ultraviolet solar spectrum as a function of F10. 7. J. Geophys. Res. Space Phys. 2015, 120, 6779–6794. [Google Scholar] [CrossRef]
- Chamberlin, P.C.; Woods, T.N.; Eparvier, F.G. Flare irradiance spectral model (FISM): Daily component algorithms and results. Space Weather 2007, 5, S07005. [Google Scholar] [CrossRef]
- Chamberlin, P.C.; Woods, T.N.; Eparvier, F.G. Flare irradiance spectral model (FISM): Flare component algorithms and results. Space Weather 2008, 6, S05001. [Google Scholar] [CrossRef]
- Chamberlin, P.C.; Eparvier, F.G.; Knoer, V.; Leise, H.; Pankratz, A.; Snow, M.; Templeman, B.; Thiemann, E.M.B.; Woodraska, D.L.; Woods, T.N. The flare irradiance spectral model-version 2 (FISM2). Space Weather 2020, 18, e2020SW002588. [Google Scholar] [CrossRef]
- Nusinov, A.A.; Kazachevskaya, T.V.; Katyushina, V.V. Solar extreme and far ultraviolet radiation modeling for aeronomic calculations. Remote. Sens. 2021, 13, 1454. [Google Scholar] [CrossRef]
- Tapping, K. The 10.7 cm solar radio flux (F10. 7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Gaidash, S.; Belov, A.; Abunina, M.; Abunin, A. Space weather forecasting at IZMIRAN. Geomagn. Aeron. 2017, 57, 869–876. [Google Scholar] [CrossRef]
- Huang, C.; Liu, D.D.; Wang, J.S. Forecast daily indices of solar activity, F10. 7, using support vector regression method. Res. Astron. Astrophys. 2009, 9, 694. [Google Scholar] [CrossRef]
- Lei, L.; Zhong, Q.; Wang, J.; Shi, L.; Liu, S. The Mid-Term Forecast Method of F10. 7 Based on Extreme Ultraviolet Images. Adv. Astron. 2019, 2019, 5604092. [Google Scholar] [CrossRef]
- Henney, C.; Toussaint, W.; White, S.; Arge, C. Forecasting F10. 7 with solar magnetic flux transport modeling. Space Weather 2012, 10, S02011. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, X.; Feng, X.; Liu, C.; Xiang, N.; Li, Z.; Lu, W. Predicting the Daily 10.7-cm Solar Radio Flux Using the Long Short-Term Memory Method. Universe 2022, 8, 30. [Google Scholar] [CrossRef]
- Bruevich, E.; Yakunina, G. Flux Variations in Lines of Solar EUV Radiation beyond Flares in Cycle 24. Geomagn. Aeron. 2019, 59, 155–161. [Google Scholar] [CrossRef]
- Torr, D.; Torr, M.R. Chemistry of the thermosphere and ionosphere. J. Atmos. Terr. Phys. 1979, 41, 797–839. [Google Scholar] [CrossRef]
- Banks, P.M.; Kockarts, G. Aeronomy; Elsevier: Amsterdam, The Netherlands, 2013; Available online: https://www.numilog.com/467163/Aeronomy.ebook (accessed on 20 November 2022).
- Ohshio, M.; Maeda, R.; Sakagami, H. Height distribution of local photoionization efficiency. J. Radio Res. Lab. 1966, 13, 245. [Google Scholar]
- Nikolaeva, V.; Gordeev, E.; Nikolaev, A.; Rogov, D.; Troshichev, O. Auroral Ionosphere Model with PC Index as an Input. Atmosphere 2022, 13, 402. [Google Scholar] [CrossRef]
- Smith III, F.; Smith, C. Numerical evaluation of Chapman’s grazing incidence integral ch (X, χ). J. Geophys. Res. 1972, 77, 3592–3597. [Google Scholar] [CrossRef]
- Picone, J.; Hedin, A.; Drob, D.P.; Aikin, A. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, SIA–15. [Google Scholar] [CrossRef]
- Verronen, P.; Andersson, M.; Marsh, D.; Kovács, T.; Plane, J. WACCM-D—Whole Atmosphere Community Climate Model with D-region ion chemistry. J. Adv. Model. Earth Syst. 2016, 8, 954–975. [Google Scholar] [CrossRef]
- Lanchester, B.; Rees, M.; Lummerzheim, D.; Otto, A.; Sedgemore-Schulthess, K.; Zhu, H.; McCrea, I. Ohmic heating as evidence for strong field-aligned currents in filamentary aurora. J. Geophys. Res. Space Phys. 2001, 106, 1785–1794. [Google Scholar] [CrossRef]
- Dudok de Wit, T. Detecting undocumented trends in solar irradiance observations. J. Space Weather Space Clim. 2022, 12, 10. [Google Scholar] [CrossRef]
- Mauceri, S.; Richard, E.; Pilewskie, P.; Harber, D.; Coddington, O.; Béland, S.; Chambliss, M.; Carson, S. Degradation correction of TSIS SIM. Sol. Phys. 2020, 295, 1–21. [Google Scholar] [CrossRef]
- Snow, M.; McClintock, W.; Woods, T. Solar spectral irradiance variability in the ultraviolet from SORCE and UARS SOLSTICE. Adv. Space Res. 2010, 46, 296–302. [Google Scholar] [CrossRef]
- Klimov, P.; Sigaeva, K.; Sharakin, S. Flight calibration of the photodetector in the TUS detector. Instrum. Exp. Tech. 2021, 64, 450–455. [Google Scholar] [CrossRef]
- Didkovsky, L.; Judge, D.; Wieman, S.; Woods, T.; Jones, A. EUV spectrophotometer (ESP) in extreme ultraviolet variability experiment (EVE): Algorithms and calibrations. In The Solar Dynamics Observatory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; pp. 179–205. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolaeva, V.; Gordeev, E. SPAM: Solar Spectrum Prediction for Applications and Modeling. Atmosphere 2023, 14, 226. https://doi.org/10.3390/atmos14020226
Nikolaeva V, Gordeev E. SPAM: Solar Spectrum Prediction for Applications and Modeling. Atmosphere. 2023; 14(2):226. https://doi.org/10.3390/atmos14020226
Chicago/Turabian StyleNikolaeva, Vera, and Evgeny Gordeev. 2023. "SPAM: Solar Spectrum Prediction for Applications and Modeling" Atmosphere 14, no. 2: 226. https://doi.org/10.3390/atmos14020226
APA StyleNikolaeva, V., & Gordeev, E. (2023). SPAM: Solar Spectrum Prediction for Applications and Modeling. Atmosphere, 14(2), 226. https://doi.org/10.3390/atmos14020226







