Turbulence and Pollutant Statistics around a High-Rise Building with and without Overhangs
Abstract
:1. Introduction
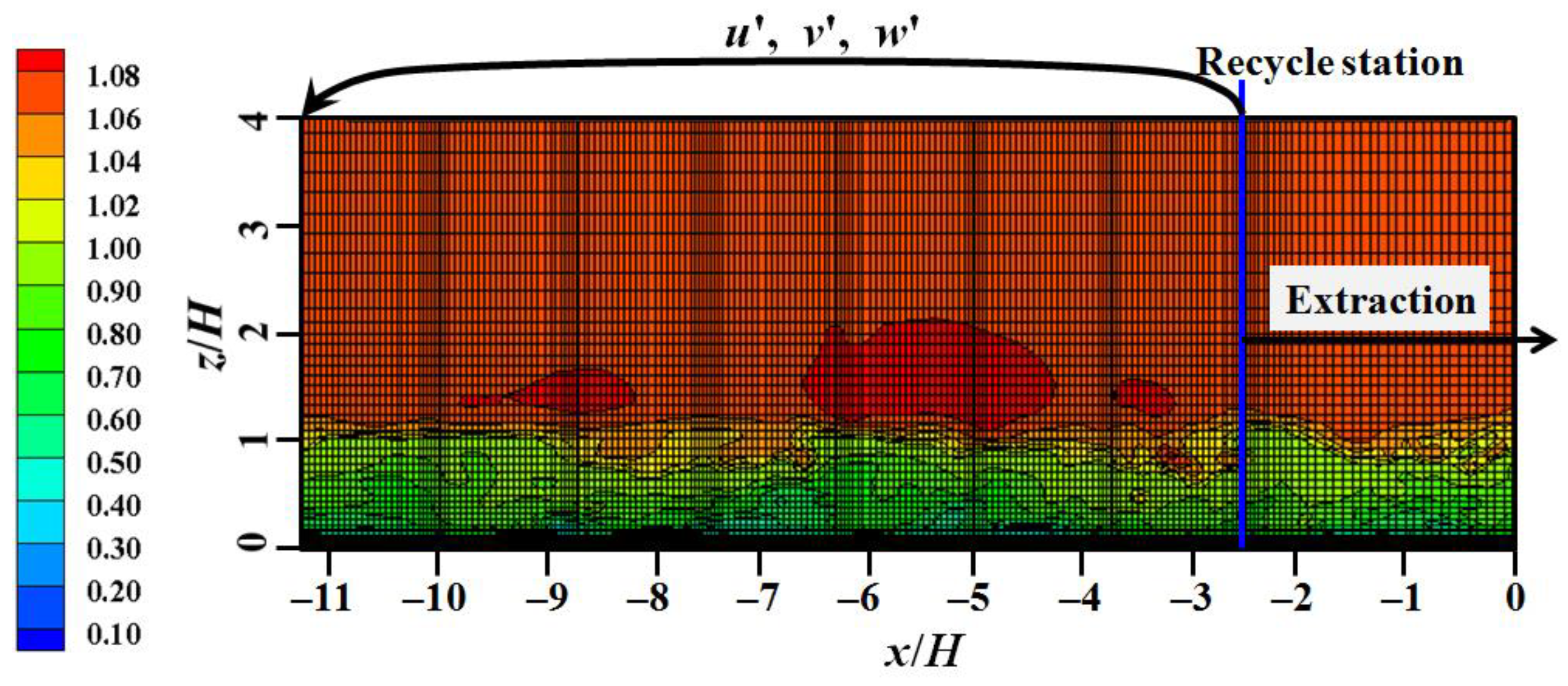
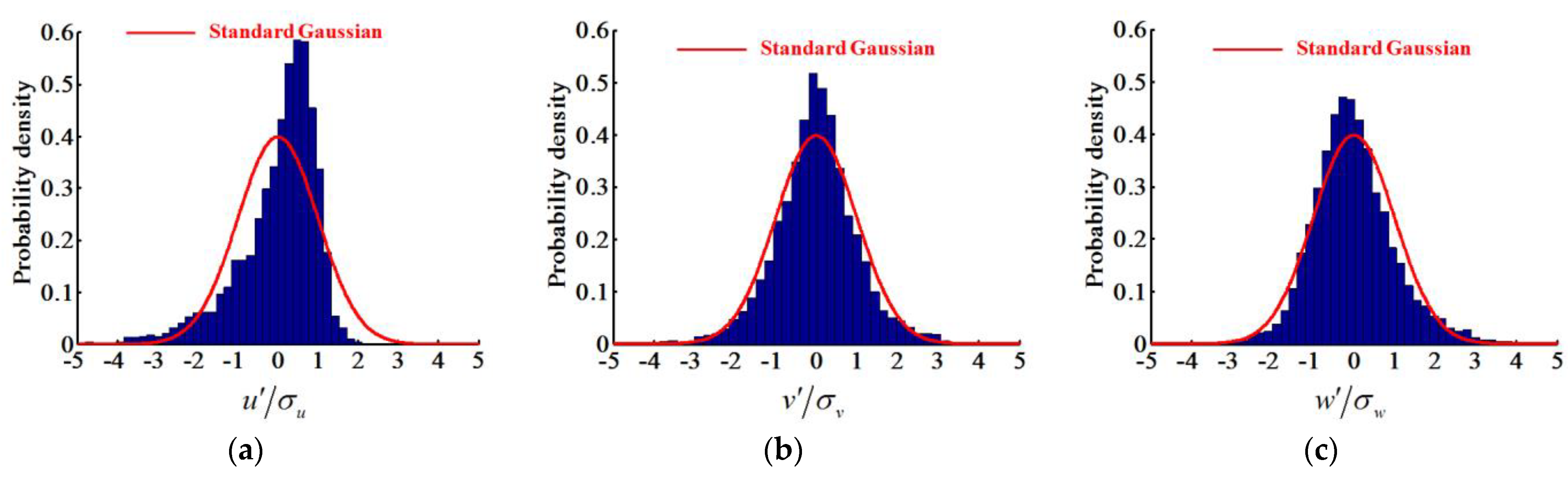
2. Generation of Inflow Fluctuations
3. Simulation Settings
3.1. Simulation Cases and Mesh Systems
3.2. Numerical Procedures and Boundary Conditions
4. Results and Discussion
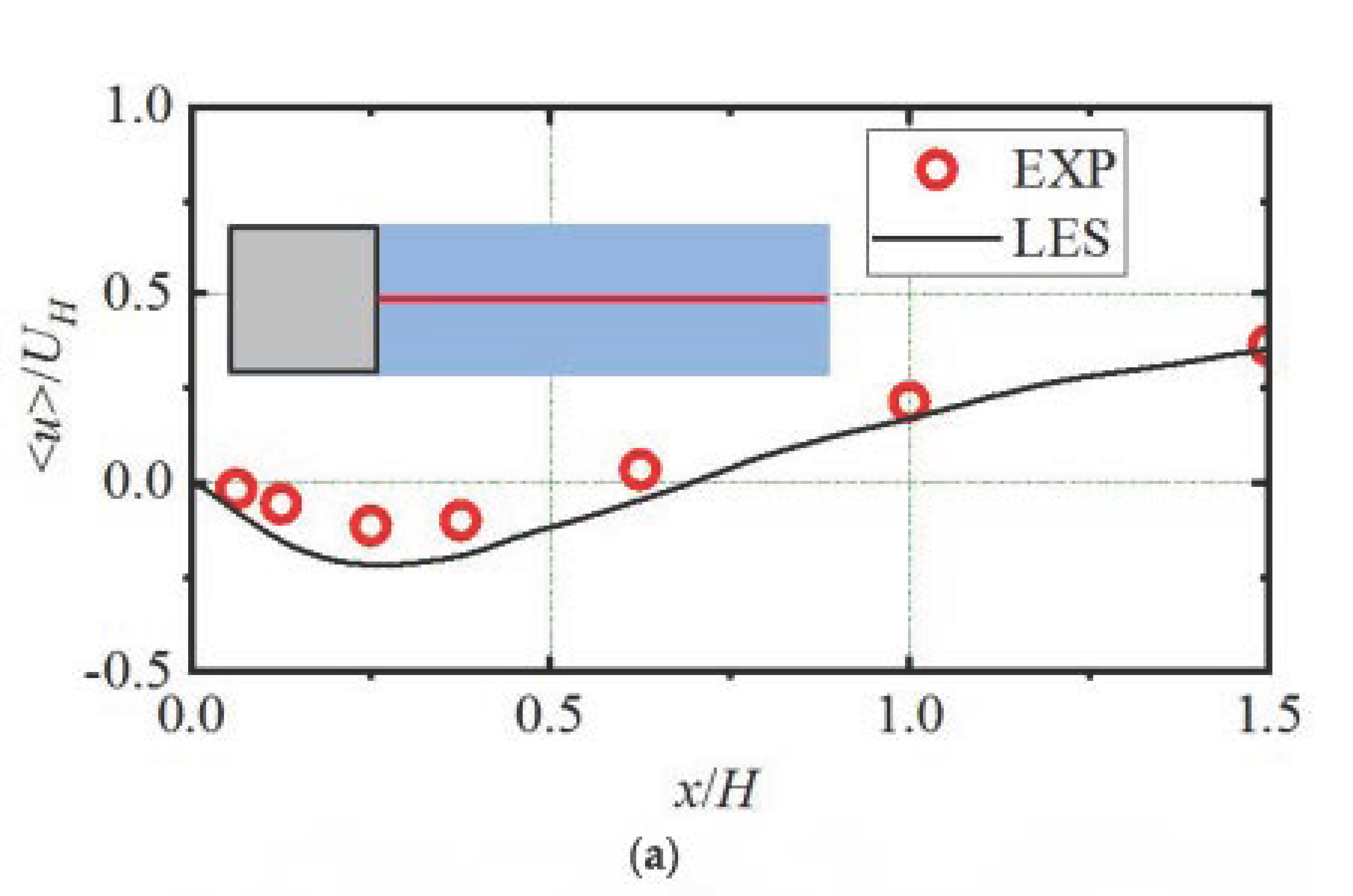
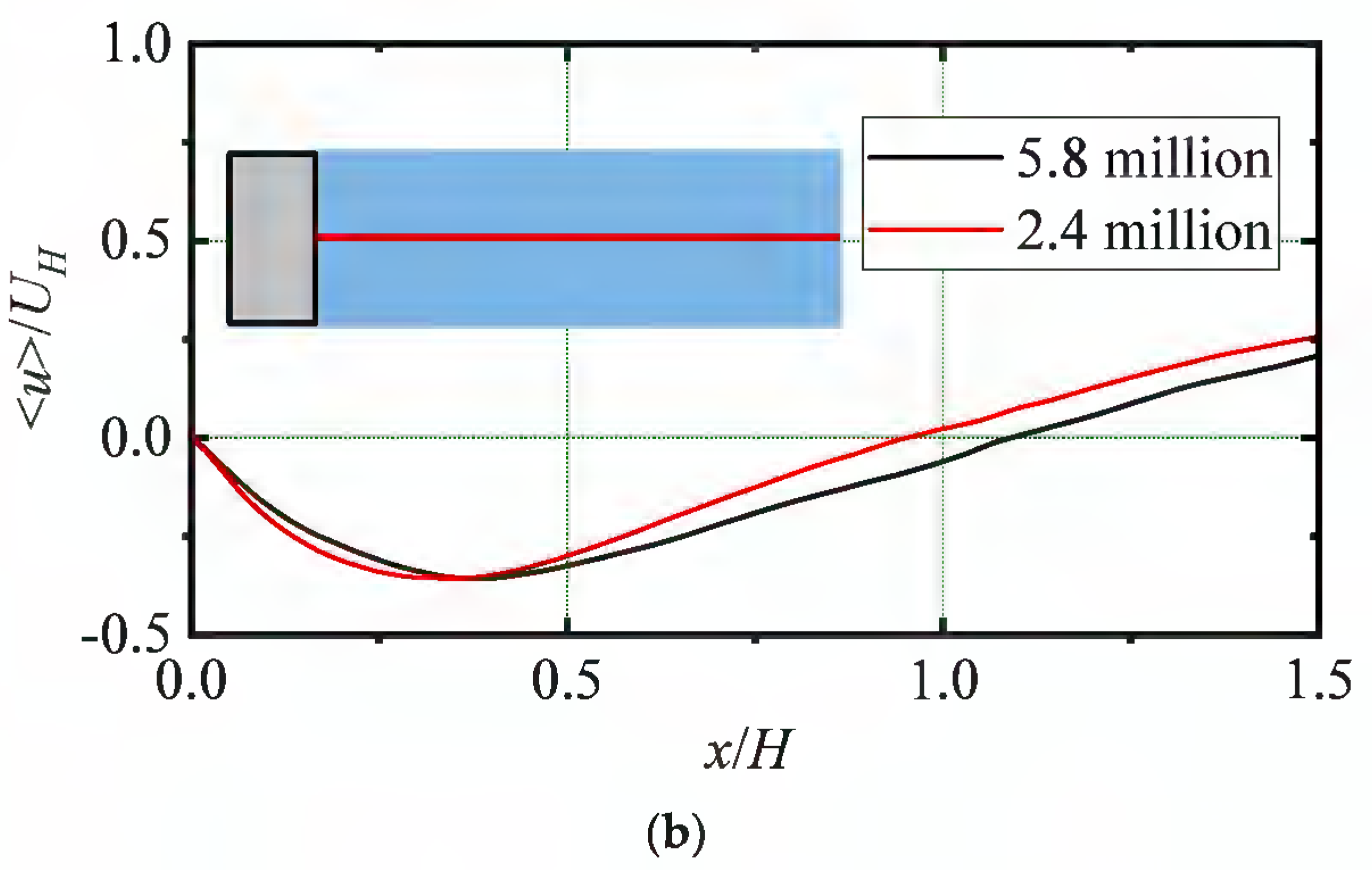
4.1. Validation of the LES Model
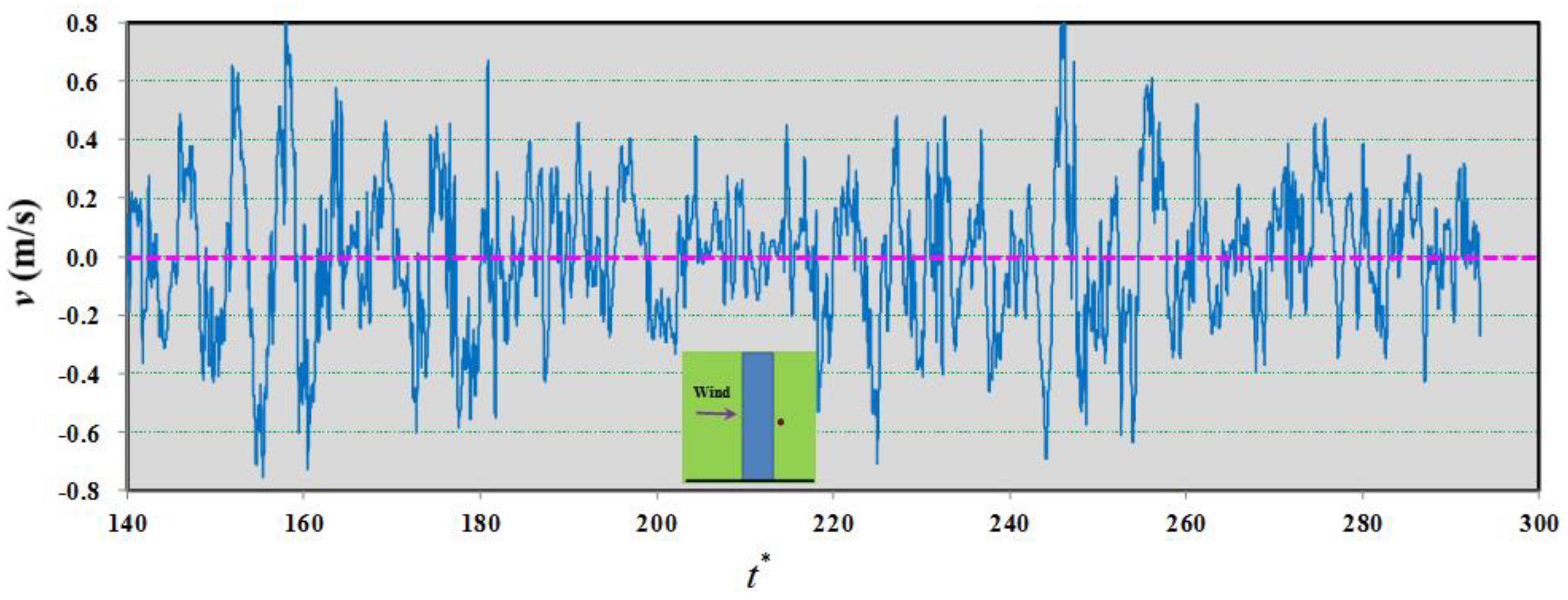
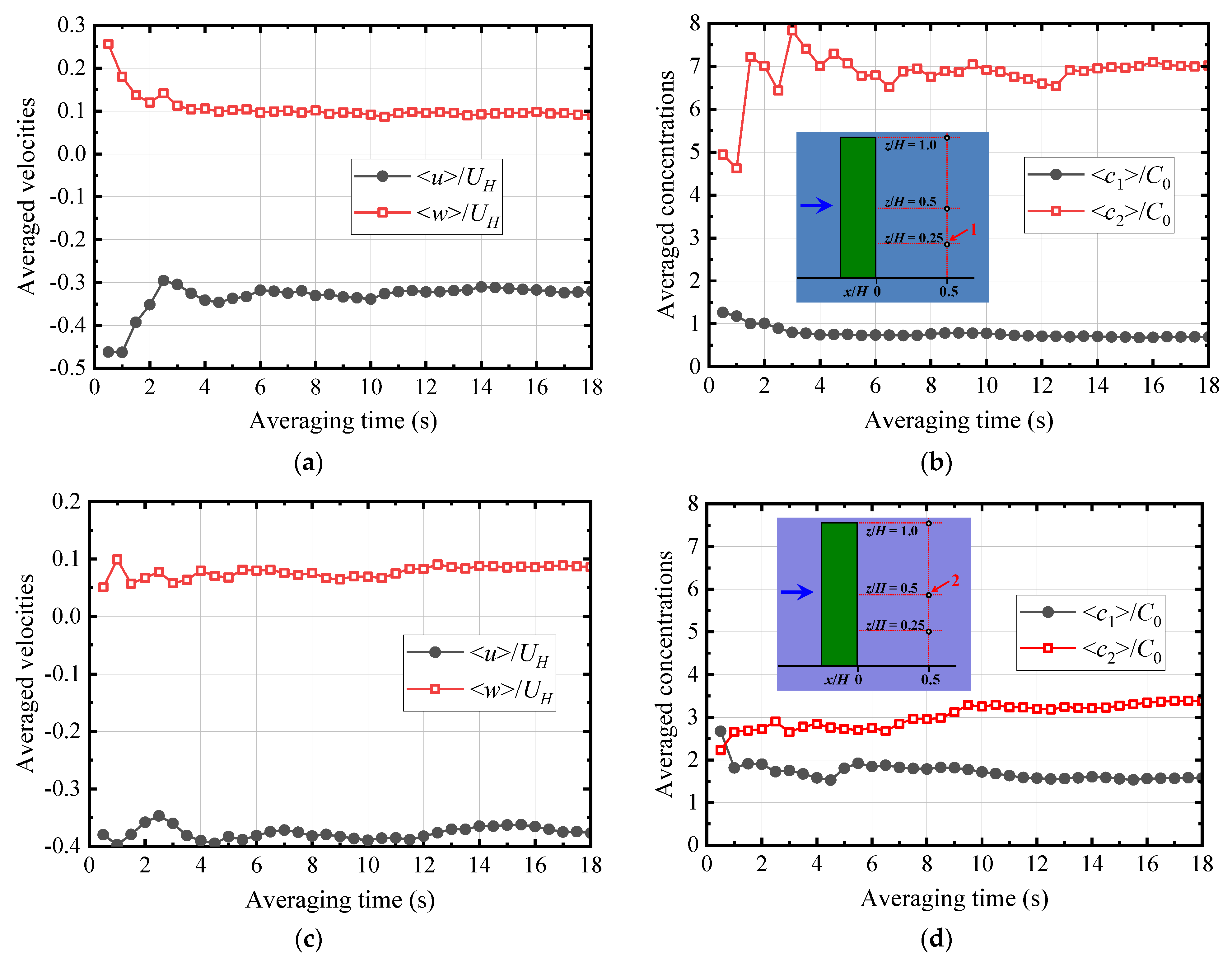
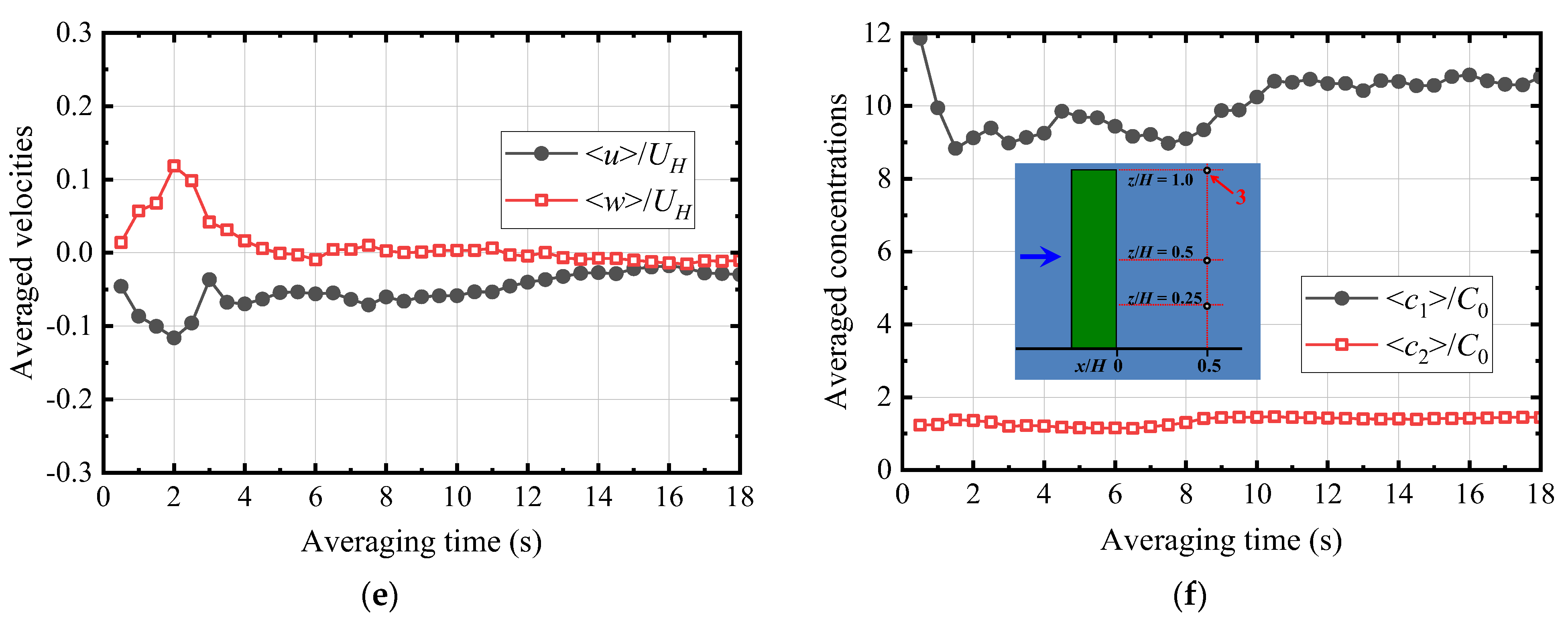
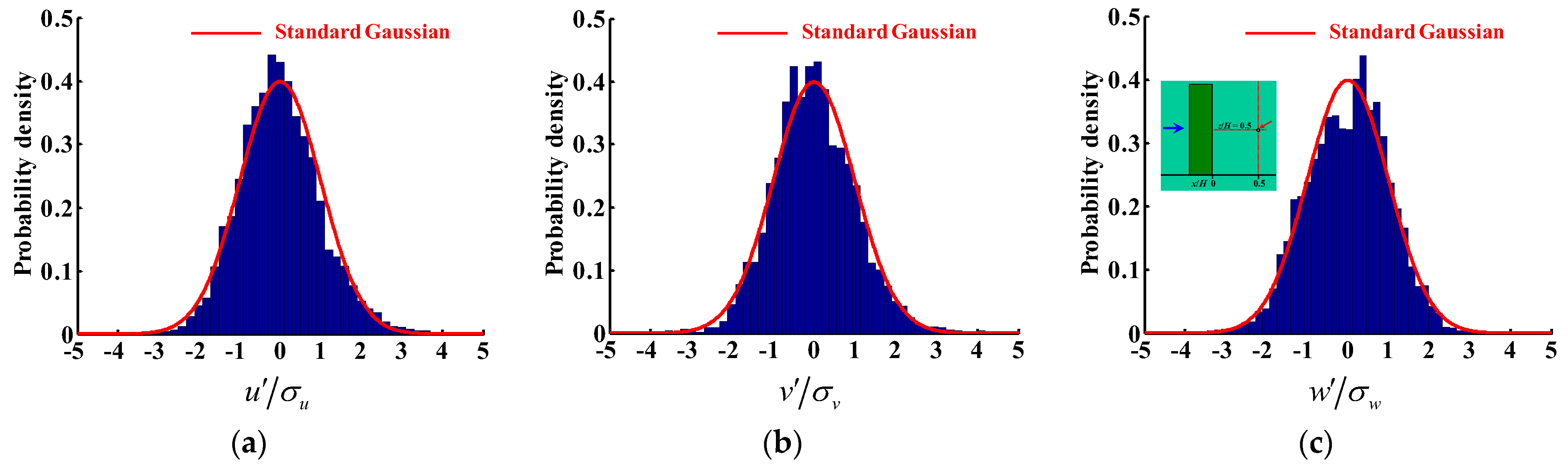
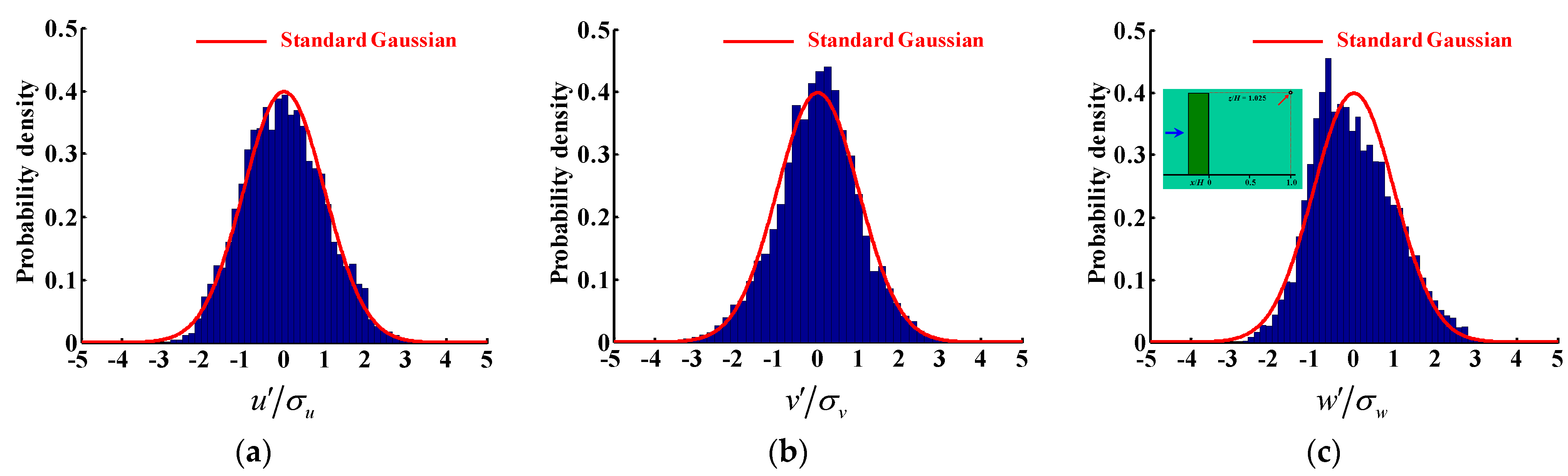
4.2. Influence of the Averaging Time
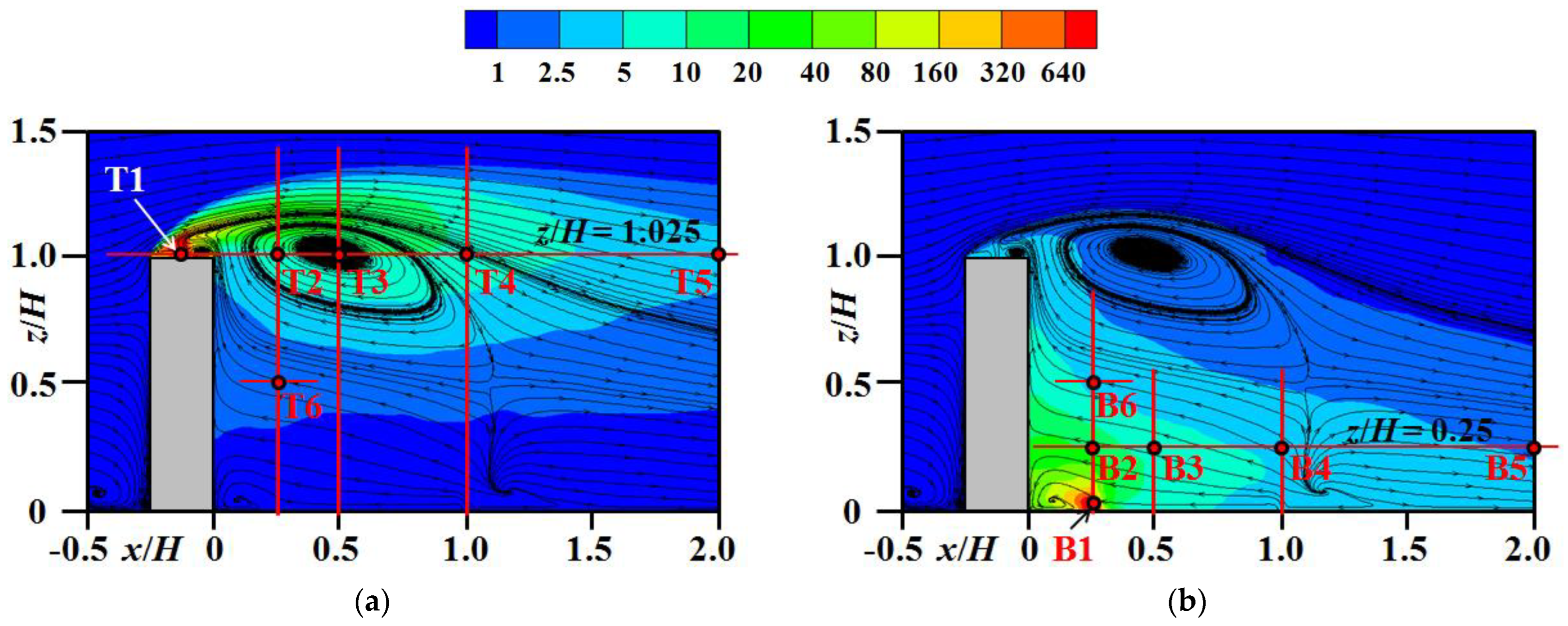
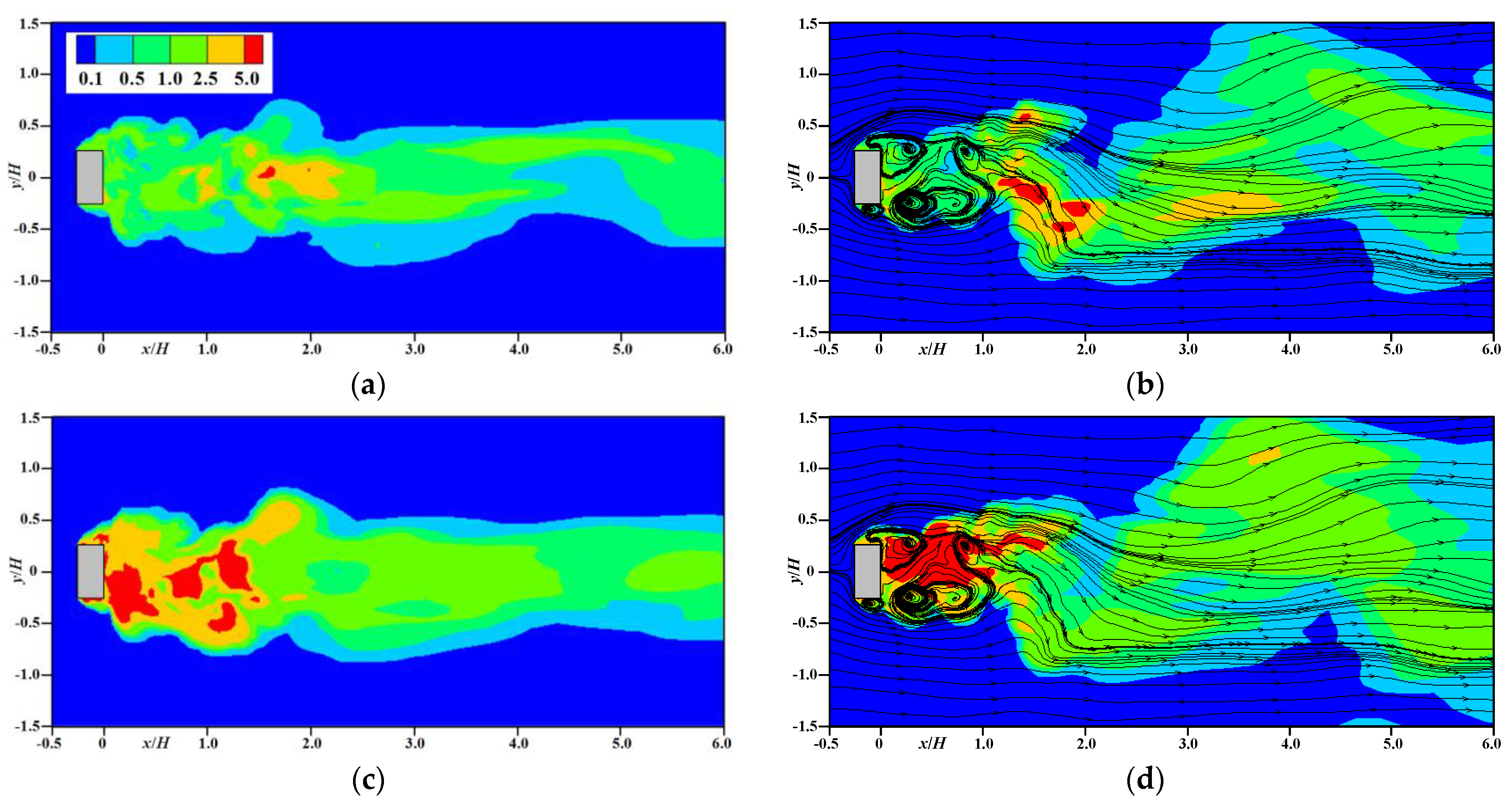
4.3. Turbulence Statistics
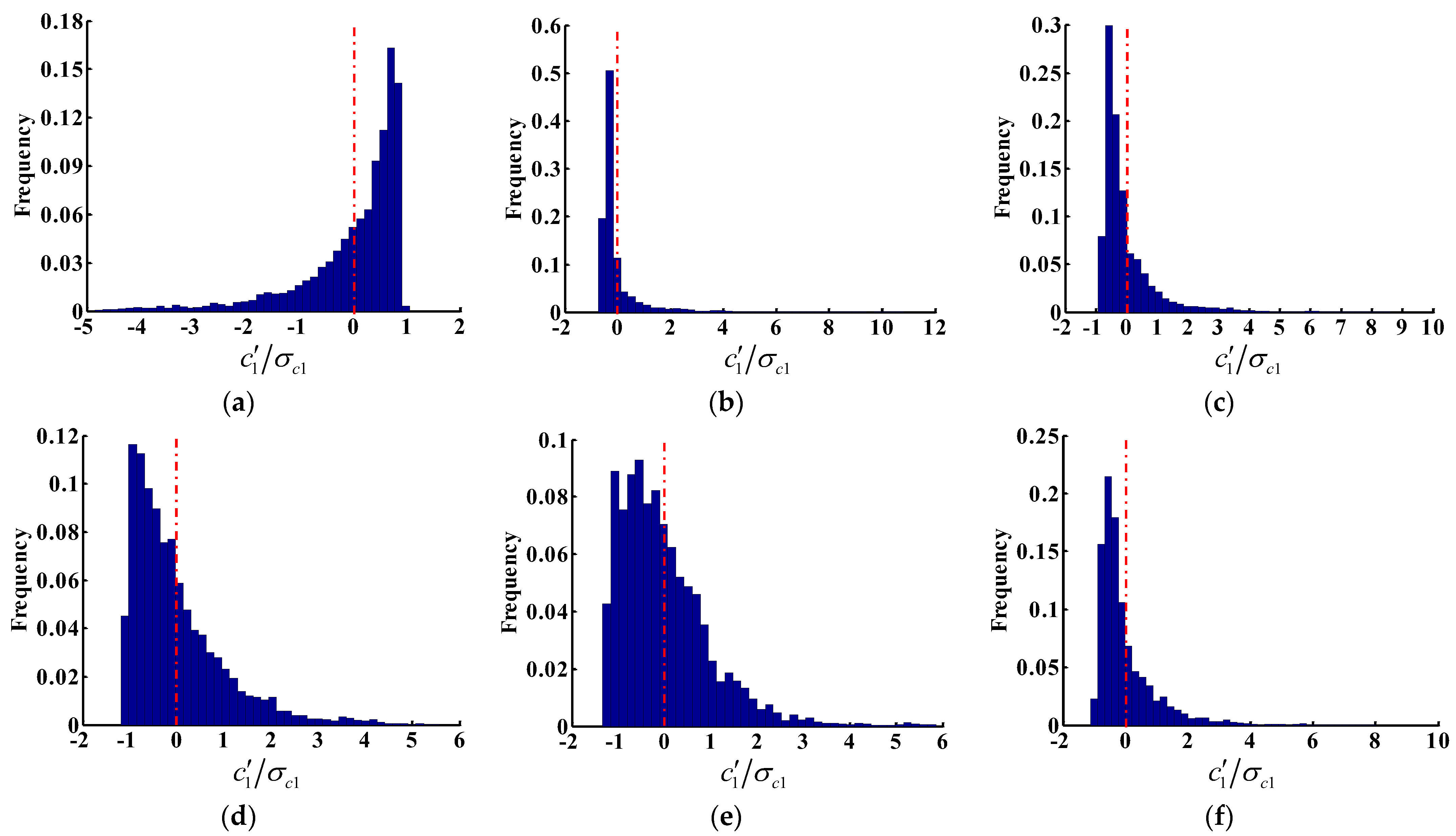
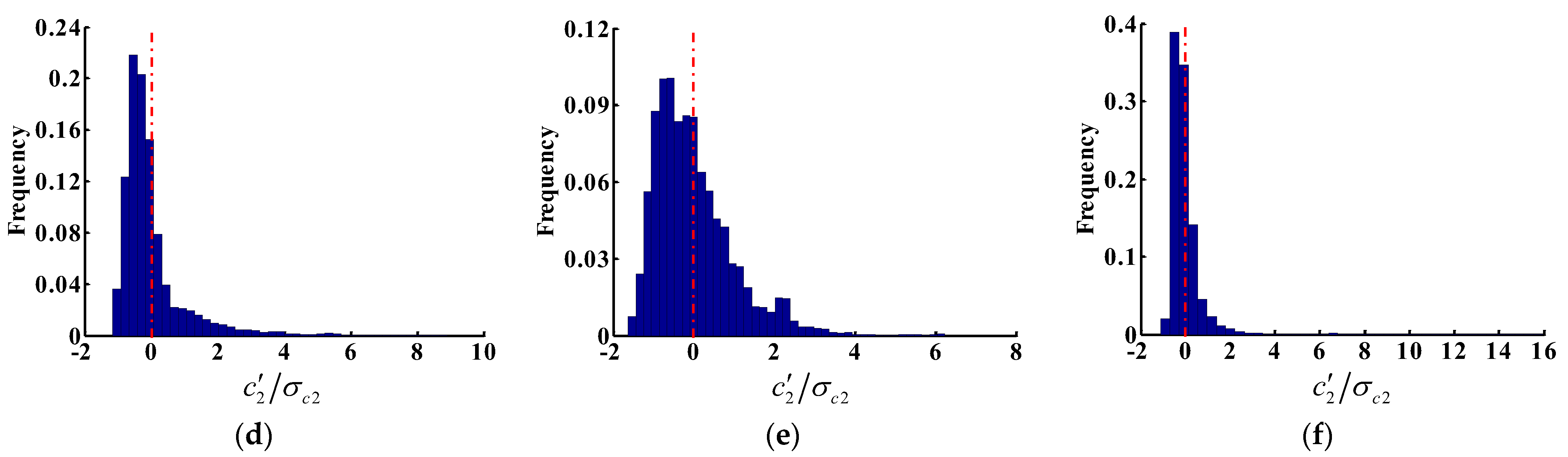
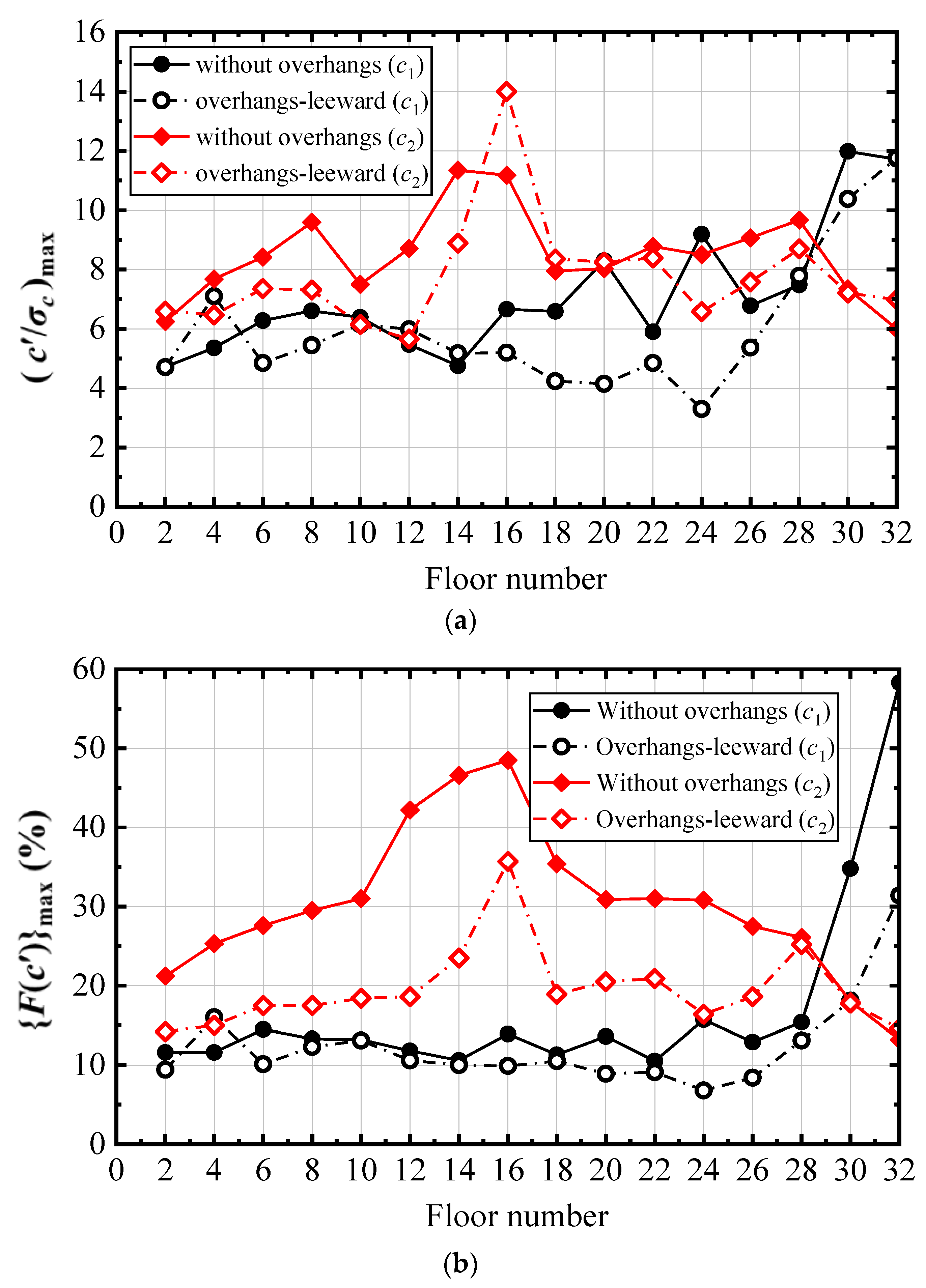
4.4. Pollutant Statistics
4.5. Effects of Overhangs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| f | instantaneous value of a quantity |
| <f> | time-averaged value |
| f′ | fluctuation from time-averaged value |
| σf | standard deviation of f |
| x, y, z | three components of space coordinates (m) |
| u, v, w | three components of velocity vector (m/s) |
| p | instantaneous pressure (Pa) |
| c | pollutant concentration (volume percentage) |
| Q | positive second invariant of the velocity gradient (s−2) |
| H | building height (160 mm) |
| B | building width (80 mm) |
| UH | inflow mean velocity at building height (1.37 m/s) |
| q | pollutant emission rate (m3/s) |
| C0 | reference concentration (=q/(UHH2)) |
| νSGS | sub-grid scale viscosity |
| σt | sub-grid scale Schmidt number |
References
- Nozawa, K.; Tamura, T. Large eddy simulation of the flow around a low-rise building immersed in a rough-wall turbulent boundary layer. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1151–1162. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Murakami, S.; Sawaki, S. Comparison of various revised k-ε models and LES applied to flow around a high-rise building model with 1:1:2 shape placed within the surface boundary layer. J. Wind Eng. Ind. Aerodyn. 2008, 96, 389–411. [Google Scholar] [CrossRef]
- Kataoka, H. Numerical simulations of a wind-induced vibrating square cylinder within turbulent boundary layer. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1985–1997. [Google Scholar] [CrossRef]
- Saeedi, M.; LePoudre, P.; Wang, B. Direct numerical simulation of turbulent wake behind a surface-mounted square cylinder. J. Fluid. Struct. 2014, 51, 20–39. [Google Scholar] [CrossRef]
- Joubert, E.C.; Harms, T.M.; Venter, G. Computational simulation of the turbulent flow around a surface mounted rectangular prism. J. Wind Eng. Ind. Aerodyn. 2015, 142, 173–187. [Google Scholar] [CrossRef]
- Okaze, T.; Kikumoto, H.; Ono, H.; Imano, M.; Ikegaya, N.; Hasama, T.; Nakao, K.; Kishida, T.; Tabata, Y.; Nakajima, K.; et al. Large-eddy simulation of flow around an isolated building: A step-by-step analysis of influencing factors on turbulent statistics. Build. Environ. 2021, 202, 108021. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Model evaluation of RANS and LES. Build. Environ. 2010, 45, 2231–2239. [Google Scholar] [CrossRef]
- Rossi, R.; Philips, D.; Iaccarino, G. A numerical study of scalar dispersion downstream of a wall-mounted cube using direct simulations and algebraic flux models. Int. J. Heat Fluid Flow 2010, 31, 805–819. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; van Heijst, G. CFD simulation of pollutant dispersion around isolated buildings: On the role of convective and turbulent mass fluxes in the prediction accuracy. J. Hazard. Mater. 2011, 194, 422–434. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; van Heijst, G. Large-Eddy Simulation of pollutant dispersion around a cubical building: Analysis of the turbulent mass transport mechanism by unsteady concentration and velocity statistics. Environ. Pollut. 2012, 167, 47–57. [Google Scholar] [CrossRef]
- Rossi, R.; Iaccarino, G. Numerical analysis and modeling of plume meandering in passive scalar dispersion downstream of a wall-mounted cube. Int. J. Heat Fluid Flow 2013, 43, 137–148. [Google Scholar] [CrossRef]
- Ai, Z.; Mak, C. Large-eddy simulation of flow and dispersion around an isolated building: Analysis of influencing factors. Comput. Fluids 2015, 118, 89–100. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Steady and unsteady RANS simulations of pollutant dispersion around isolated cubical buildings: Effect of large-scale fluctuations on the concentration field. J. Wind Eng. Ind. Aerodyn. 2017, 165, 23–33. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD simulations of near-field pollutant dispersion with different plume buoyancies. Build. Environ. 2018, 131, 128–139. [Google Scholar] [CrossRef]
- Du, Y.; Blocken, B.; Pirker, S. A novel approach to simulate pollutant dispersion in the built environment: Transport-based recurrence CFD. Build. Environ. 2020, 170, 106604. [Google Scholar] [CrossRef]
- Lin, C.; Ooka, R.; Kikumoto, H.; Sato, T.; Arai, M. Wind tunnel experiment on high-buoyancy gas dispersion around isolated cubic building. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104226. [Google Scholar] [CrossRef]
- Guo, G.; Yu, Y.; Kwok, K.; Zhang, Y. Air pollutant dispersion around high-rise buildings due to roof emissions. Build. Environ. 2022, 219, 109215. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, X.; Tominaga, Y.; Gu, M. CFD simulation of flow fields and pollutant dispersion around a cubic building considering the effect of plume buoyancies. Build. Environ. 2022, 208, 108640. [Google Scholar] [CrossRef]
- Shirasawa, T.; Yoshie, R.; Tanaka, H.; Kobayashi, T.; Mochida, A.; Endo, Y. Cross comparison of CFD results of gas diffusion in weak wind region behind a high-rise building. In Proceedings of the Fourth International Conference on Advances in Wind and Structures (AWAS08), Jeju, Republic of Korea, 29–31 May 2008. [Google Scholar]
- Yoshie, R.; Jiang, G.; Shirasawa, T.; Chung, J. CFD simulations of gas dispersion around high-rise building in non-isothermal boundary layer. J. Wind Eng. Ind. Aerodyn. 2011, 99, 279–288. [Google Scholar] [CrossRef]
- Jiang, G.; Yoshie, R. Side ratio effects on flow and pollutant dispersion around an isolated high-rise building in a turbulent boundary layer. Build. Environ. 2020, 180, 107078. [Google Scholar] [CrossRef]
- Yuan, K.; Hui, Y.; Chen, Z. Effects of facade appurtenances on the local pressure of high-rise building. J. Wind Eng. Ind. Aerodyn. 2018, 178, 26–37. [Google Scholar] [CrossRef]
- Murena, F.; Mele, B. Effect of balconies on air quality in deep street canyons. Atmos. Pollut. Res. 2016, 7, 1004–1012. [Google Scholar] [CrossRef]
- Cui, D.; Li, X.; Du, Y.; Mak, C.; Kwok, K. Effects of envelope features on wind flow and pollutant exposure in street canyons. Build. Environ. 2020, 176, 106862. [Google Scholar] [CrossRef]
- Zheng, X.; Montazeri, H.; Blocken, B. Impact of building façade geometrical details on pollutant dispersion in street canyons. Build. Environ. 2022, 212, 108746. [Google Scholar] [CrossRef]
- Zheng, X.; Montazeri, H.; Blocken, B. CFD simulations of wind flow and mean surface pressure for buildings with balconies: Comparison of RANS and LES. Build. Environ. 2020, 173, 106747. [Google Scholar] [CrossRef]
- Zheng, X.; Montazeri, H.; Blocken, B. CFD analysis of the impact of geometrical characteristics of building balconies on near-façade wind flow and surface pressure. Build. Environ. 2021, 200, 107904. [Google Scholar] [CrossRef]
- Hu, C.; Ohba, M.; Yoshie, R. CFD modelling of unsteady cross ventilation flows using LES. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1692–1706. [Google Scholar] [CrossRef]
- Jiang, G. Wind Tunnel Experiment and Large Eddy Simulation of Gas Dispersion in Non-Isothermal Boundary Layers. Ph.D. Thesis, Tokyo Polytechnic University, Atsugi, Kanagawa, Japan, 2012. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Van Driest, E. On turbulent flow near a wall. J. Aero. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- Jiang, G.; Yoshie, R. Large-eddy simulation of flow and pollutant dispersion in a 3D urban street model located in an unstable boundary layer. Build. Environ. 2018, 142, 47–57. [Google Scholar] [CrossRef]

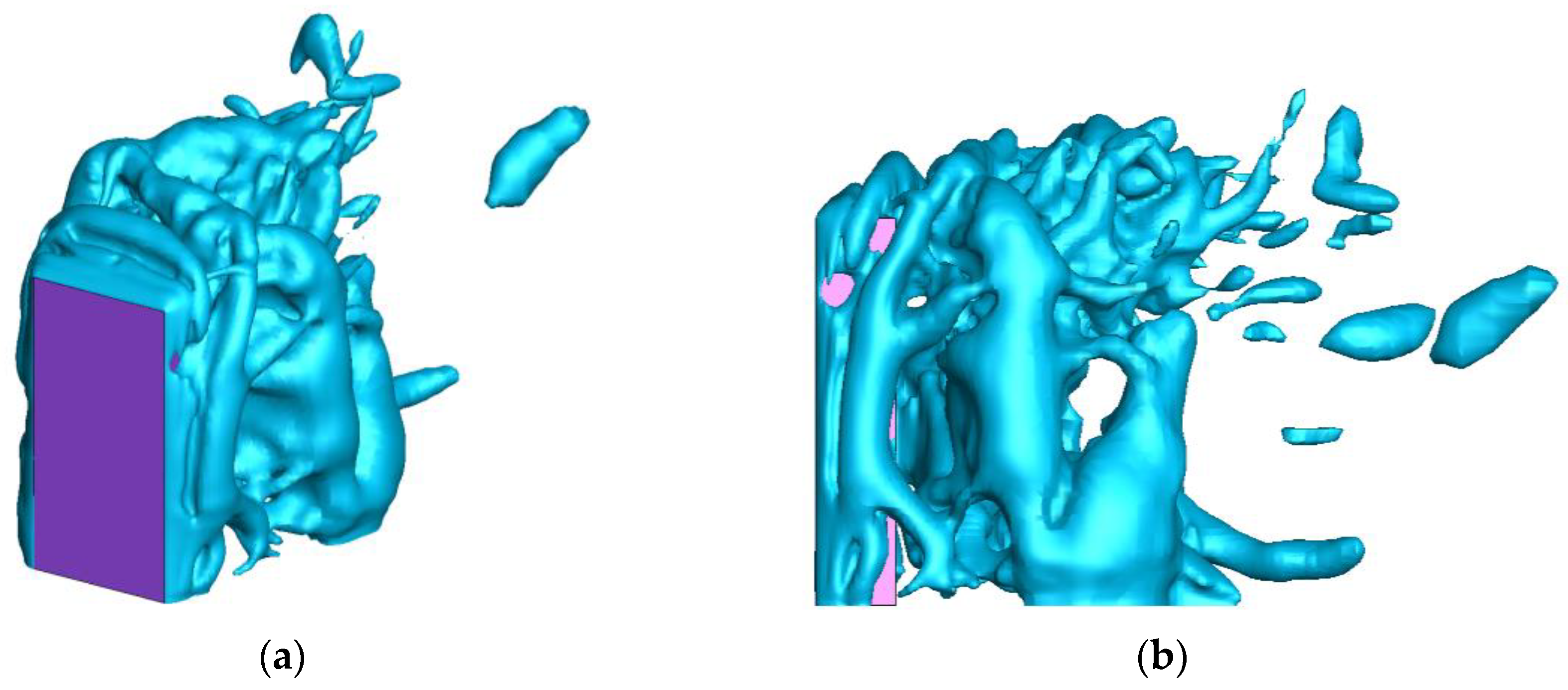






| Total Cell Numbers | Grids between Overhangs (D) | Grids along Overhangs (W) | |
|---|---|---|---|
| Base case | 5.8 million | — | — |
| Overhangs–Coarse mesh | 4.2 million | 3 | 6 |
| Overhangs–Fine mesh | 9.0 million | 5 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Wu, M.; Hu, T. Turbulence and Pollutant Statistics around a High-Rise Building with and without Overhangs. Atmosphere 2023, 14, 1771. https://doi.org/10.3390/atmos14121771
Jiang G, Wu M, Hu T. Turbulence and Pollutant Statistics around a High-Rise Building with and without Overhangs. Atmosphere. 2023; 14(12):1771. https://doi.org/10.3390/atmos14121771
Chicago/Turabian StyleJiang, Guoyi, Ming Wu, and Tingting Hu. 2023. "Turbulence and Pollutant Statistics around a High-Rise Building with and without Overhangs" Atmosphere 14, no. 12: 1771. https://doi.org/10.3390/atmos14121771
APA StyleJiang, G., Wu, M., & Hu, T. (2023). Turbulence and Pollutant Statistics around a High-Rise Building with and without Overhangs. Atmosphere, 14(12), 1771. https://doi.org/10.3390/atmos14121771







