Diagnosis of Warm-Sector Heavy Rainfall with Warm Shear in the Yangtze–Huaihe Coastal Areas from the Perspective of Moist Static Energy
Abstract
:1. Introduction
2. Materials and Methods
3. The WSWR Selection Criteria and Climatology Characteristics
- (1)
- Based on the JTWC path, precipitation within a 500 km radius of the typhoon’s center must be excluded.
- (2)
- A mesoscale rainstorm is defined as a Continuous Rainfall Area (CRA) in which the average rainfall goes beyond 5 mm/h and peaks above 20 mm/h. Additionally, the CRA’s long axis spans more than 100 km. Spatial attribute analysis is used to determine the axis length and geometric center of the CRA [39].
- (3)
- The definition of a front is based on a pronounced gradient of equivalent potential temperature at 850 hPa within the region of 20°–40° N and 110°–130° E (Fu et al., 2020; Zhang et al., 2022). If there is a low-level front within 28°–40° N and 110°–130° E, then the CRA should occur above 200 km from the front. If not, the CRA should be influenced by low-level southerlies, with no surface northerlies within 100 km of the CRA.
- (4)
- A shear line is present and the minimum distance from the shear line to CRA is between 100 and 300 km. Within the region of 28°–40° N and 110°–130° E, the shear line is characterized by the meridional shear of the zonal wind (zu/zy < 0) and the relative vorticity at 850 (ζ > 0).
4. MSE Diagnosis
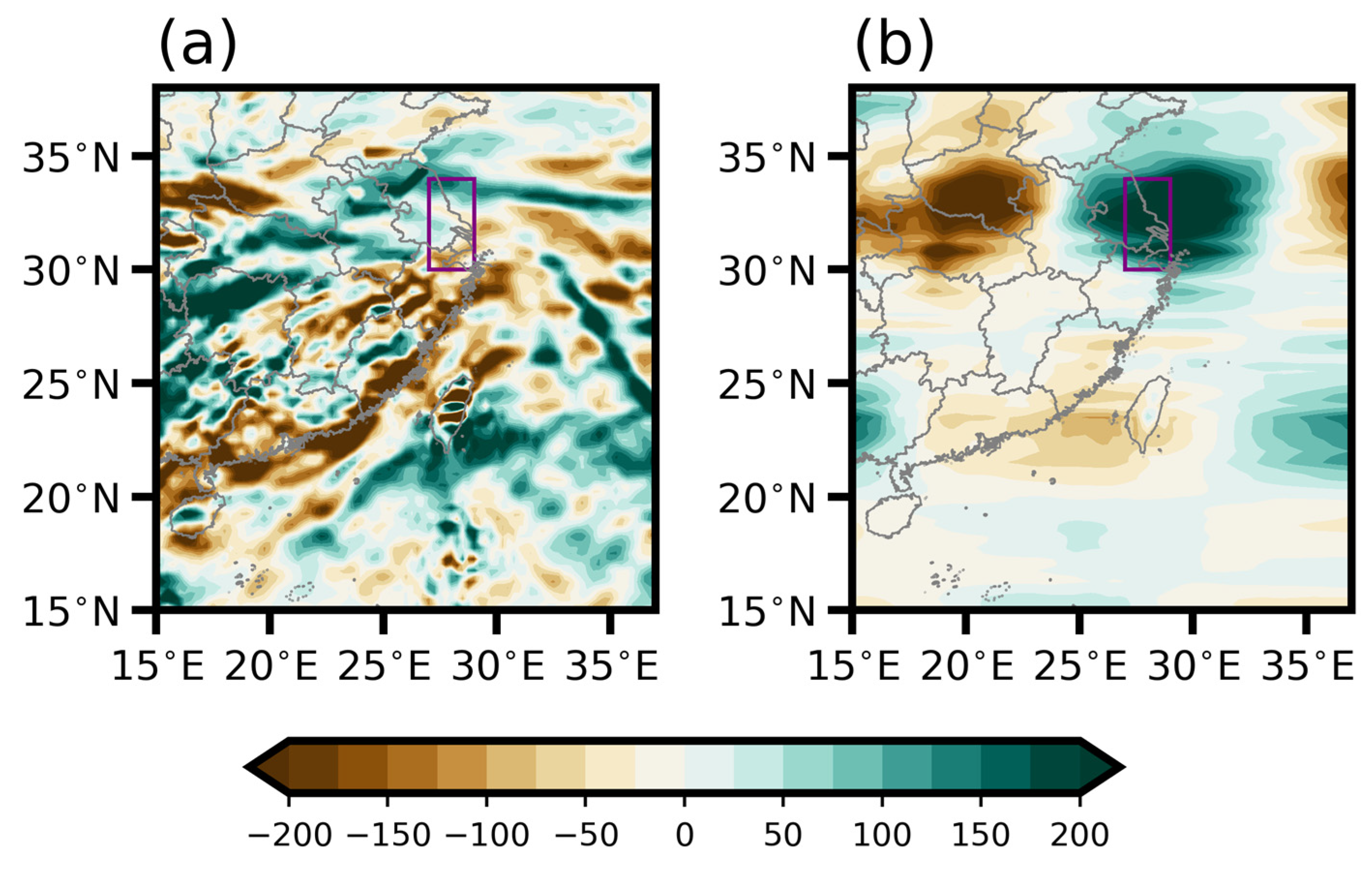
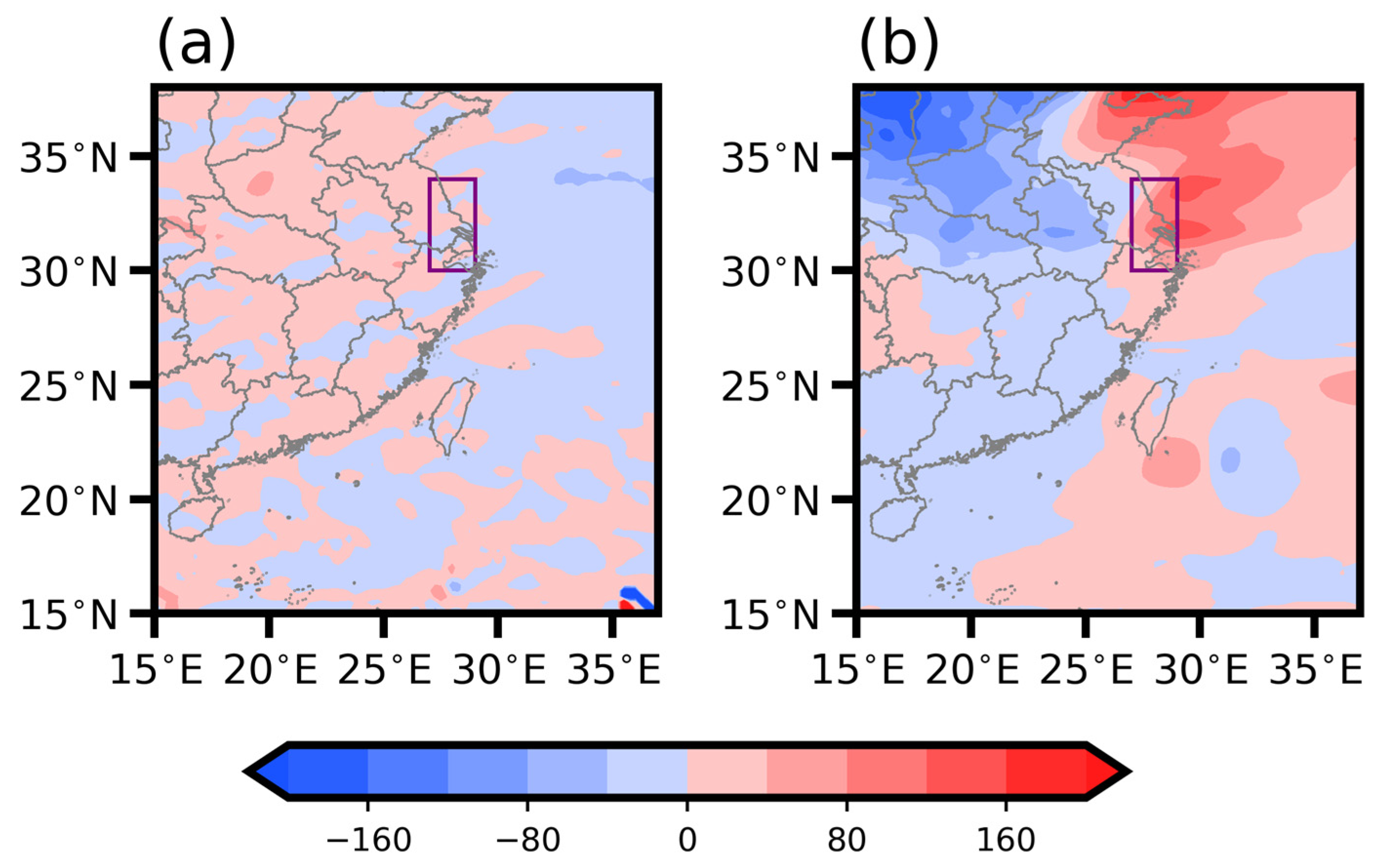
4.1. Vertical Integrated MSE Tendency Diagnosis
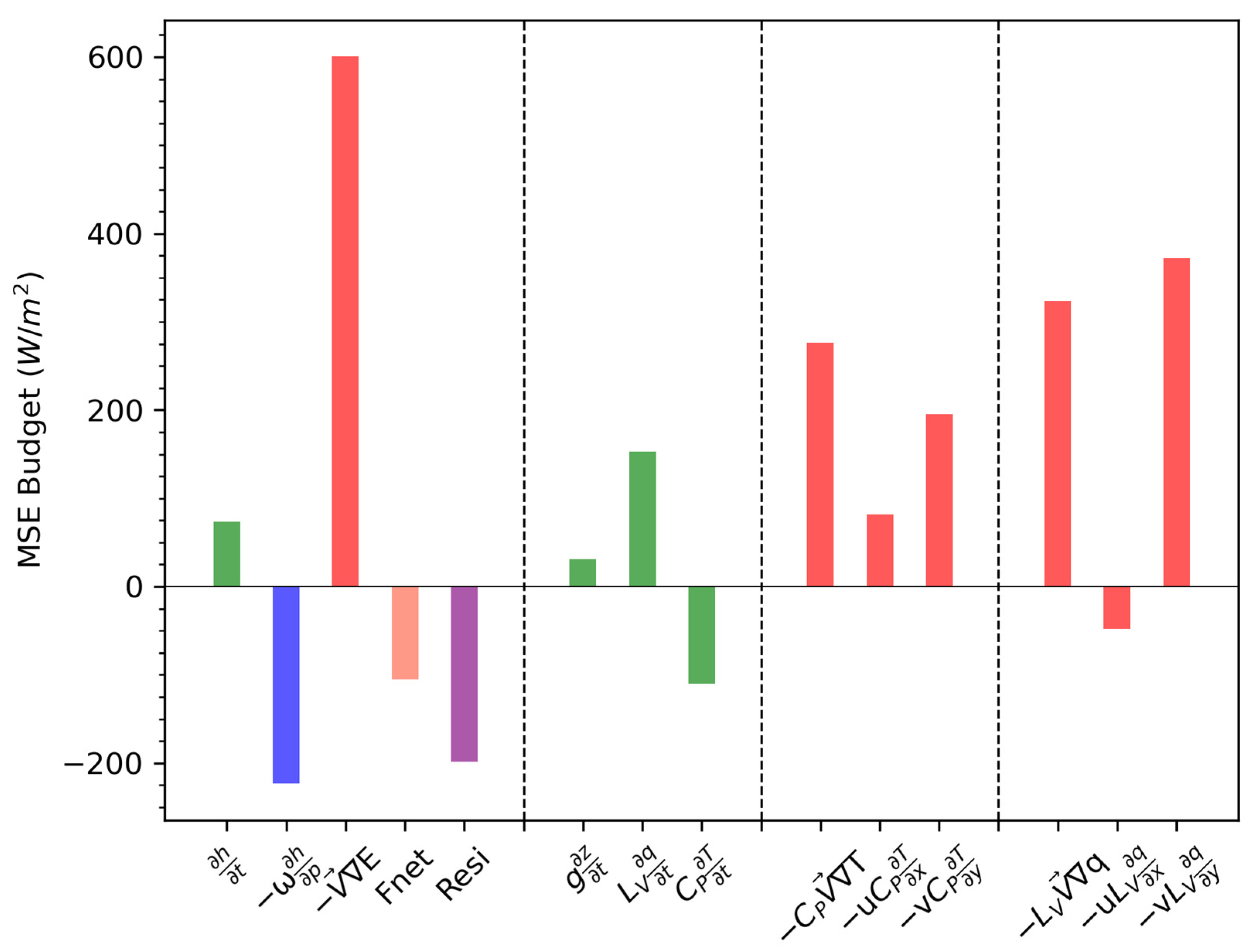
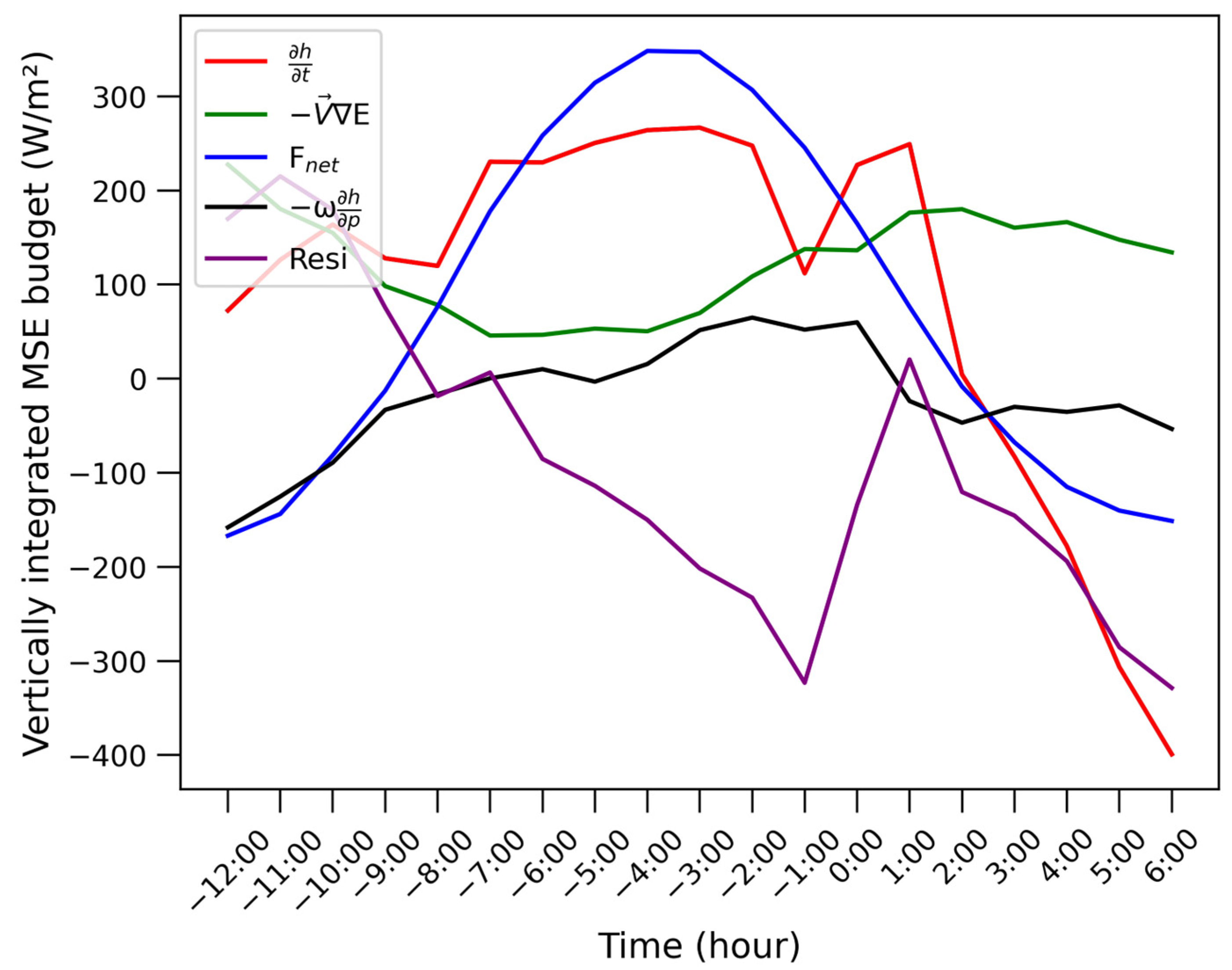
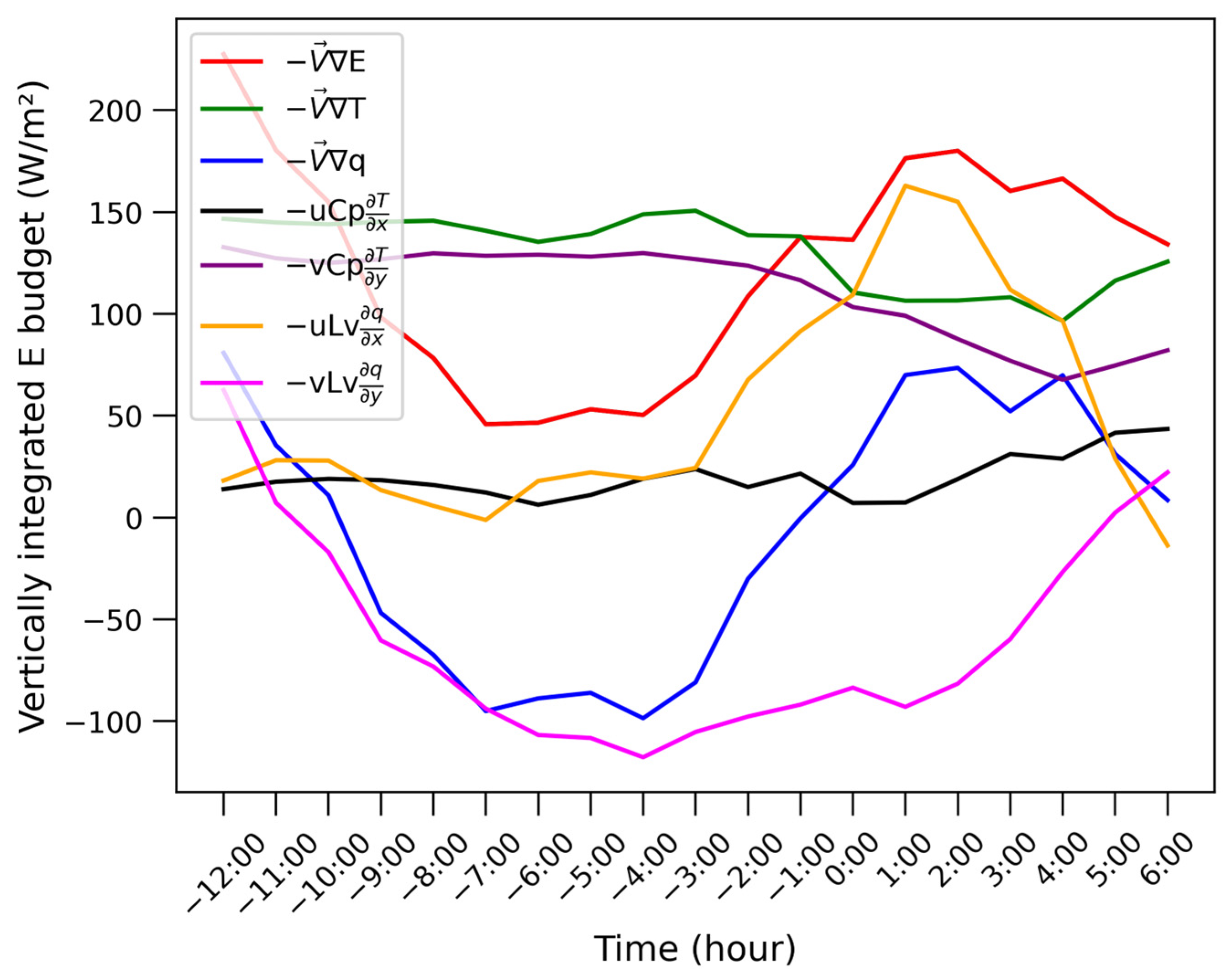
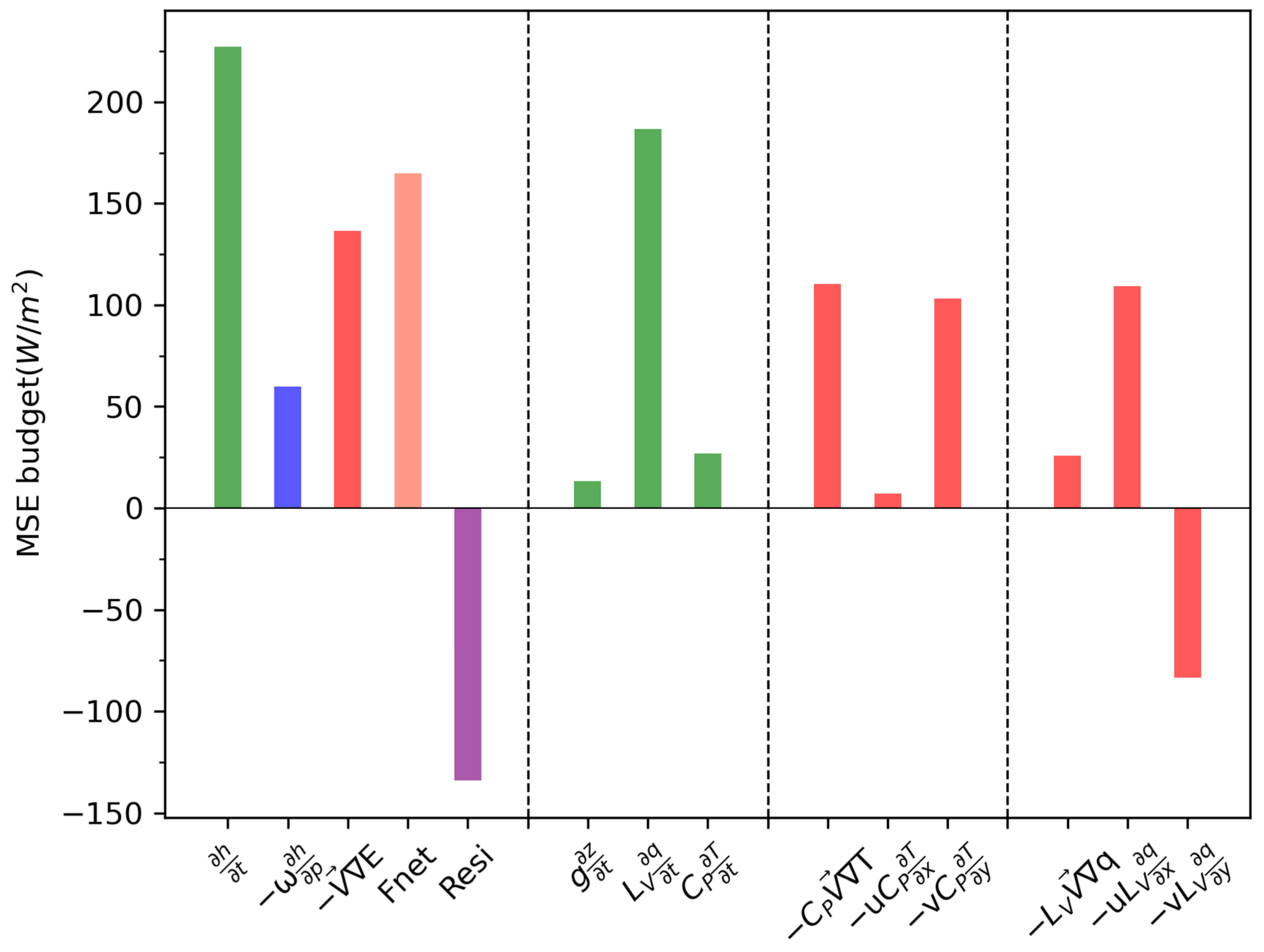
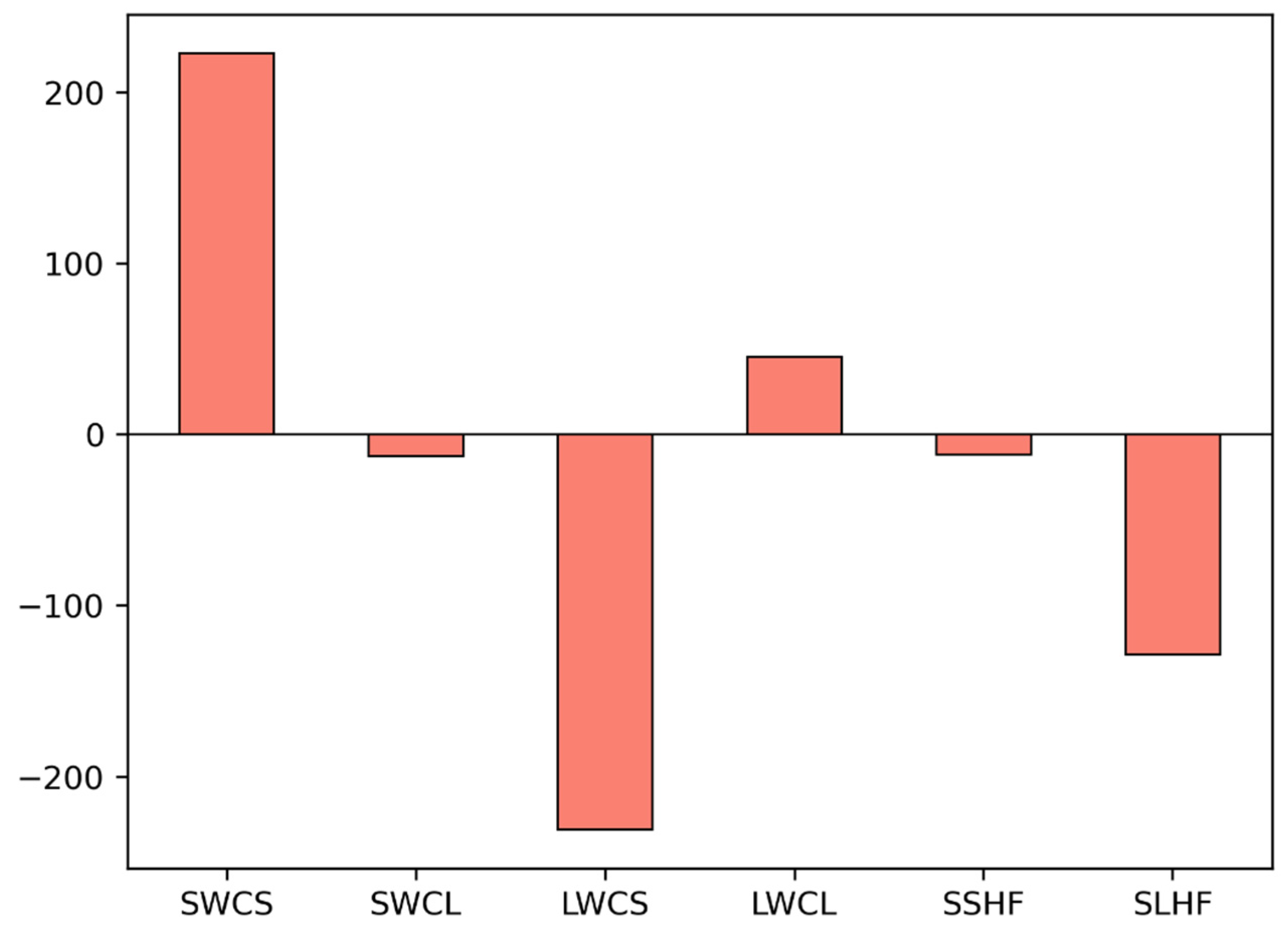
4.2. MSE Budget Diagnosis
4.2.1. Nocturnal WSWR
4.2.2. Non-Nocturnal WSWR
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, S.S. The Heavy Rain during the Pre-Summer Period Over Southern China (In Chinese); Guangdong Technology Press: Guangzhou, China, 1986. [Google Scholar]
- Zhang, L.; Ma, X.; Zhu, S.; Guo, Z.; Zhi, X.; Chen, C. Analyses and Applications of the Precursor Signals of a Kind of Warm Sector Heavy Rainfall over the Coast of Guangdong, China. Atmos. Res. 2022, 280, 106425. [Google Scholar] [CrossRef]
- Luo, Y.; Sun, J.; Li, Y.; Xia, R.; Du, Y.; Yang, S.; Zhang, Y.; Chen, J.; Dai, K.; Shen, X.; et al. Science and Prediction of Heavy Rainfall over China: Research Progress since the Reform and Opening-Up of New China. J. Meteorol. Res. 2020, 34, 427–459. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Liu, R.; Fu, S.; Tian, F. A Review of Research on Warm-Sector Heavy Rainfall in China. Adv. Atmos. Sci. 2019, 36, 1299–1307. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, Z. Warm-Sector Heavy Rainfall in Southern China and Its WRF Simulation Evaluation: A Low-Level-Jet Perspective. Mon. Weather Rev. 2019, 147, 4461–4480. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, R.; Wan, Q.; Wang, B.; Wong, W.K.; Hu, Z.; Jou, B.J.; Lin, Y.; Johnson, R.H.; Chang, C.; et al. The Southern China Monsoon Rainfall Experiment (SCMREX). Bull. Am. Meteorol. Soc. 2017, 98, 999–1013. [Google Scholar] [CrossRef]
- Xu, D.S.; Chen, H.W.; Leung, J.C.; Huang, H.; Zhang, B.L. Sensitivity of Nocturnal Warm Sector Rainfall Simulation to the Configuration of Initial and Lateral Boundary Conditions: A Case Study in Southern China Based on the Operational TRAMS Model. JGR Atmos. 2023, 128, e2022JD038452. [Google Scholar] [CrossRef]
- Pu, Y.; Hu, S.; Luo, Y.; Liu, X.; Hu, L.; Ye, L.; Li, H.; Xia, F.; Gao, L. Multiscale Perspectives on an Extreme Warm-Sector Rainfall Event over Coastal South China. Remote Sens. 2022, 14, 3110. [Google Scholar] [CrossRef]
- Du, Y.; Shen, Y.; Chen, G. Influence of Coastal Marine Boundary Layer Jets on Rainfall in South China. Adv. Atmos. Sci. 2022, 39, 782–801. [Google Scholar] [CrossRef]
- Li, S.; Meng, Z.; Wu, N. A Preliminary Study on the Organizational Modes of Mesoscale Convective Systems Associated with Warm-Sector Heavy Rainfall in South China. JGR Atmos. 2021, 126, e2021JD034587. [Google Scholar] [CrossRef]
- Han, B.; Du, Y.; Wu, C.; Liu, X. Microphysical Characteristics of the Coexisting Frontal and Warm-Sector Heavy Rainfall in South China. J. Geophys. Res. Atmos. 2021, 126, e2021JD035446. [Google Scholar] [CrossRef]
- Dong, F.; Zhi, X.; Zhang, L.; Ye, C. Diurnal Variations of Coastal Boundary Layer Jets over the Northern South China Sea and Their Impacts on Diurnal Cycle of Rainfall over Southern China during the Early-Summer Rainy Season. Mon. Weather Rev. 2021, 149, 3341–3363. [Google Scholar] [CrossRef]
- Du, Y.; Chen, G.; Han, B.; Bai, L.; Li, M. Convection Initiation and Growth at the Coast of South China. Part II: Effects of the Terrain, Coastline, and Cold Pools. Mon. Weather Rev. 2020, 148, 3871–3892. [Google Scholar] [CrossRef]
- Du, Y.; Chen, G. Heavy Rainfall Associated with Double Low-Level Jets over Southern China. Part II: Convection Initiation. Mon. Weather Rev. 2019, 147, 543–565. [Google Scholar] [CrossRef]
- Wu, N.; Ding, X.; Wen, Z.; Chen, G.; Meng, Z.; Lin, L.; Min, J. Contrasting Frontal and Warm-Sector Heavy Rainfalls over South China during the Early-Summer Rainy Season. Atmos. Res. 2020, 235, 104693. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, X.; Zhou, T. The onset and seasonal march of East Asian summer monsoon from perspective of moist static energy. Chin. Sci. Bull. 2021, 66, 3744–3756. [Google Scholar] [CrossRef]
- Zhang, Y.; Fueglistaler, S. How Tropical Convection Couples High Moist Static Energy Over Land and Ocean. Geophys. Res. Lett. 2020, 47, e2019GL086387. [Google Scholar] [CrossRef]
- Zheng, T.; Feng, T.; Xu, K.; Cheng, X. Precipitation and the Associated Moist Static Energy Budget off Western Australia in Conjunction with Ningaloo Niño. Front. Earth Sci. 2020, 8, 597915. [Google Scholar] [CrossRef]
- Wang, T.; Li, T. Diagnosing the Column-Integrated Moist Static Energy Budget Associated with the Northward-Propagating Boreal Summer Intraseasonal Oscillation. Clim. Dyn. 2020, 54, 4711–4732. [Google Scholar] [CrossRef]
- Adames, Á.F.; Ming, Y. Moisture and Moist Static Energy Budgets of South Asian Monsoon Low Pressure Systems in GFDL AM4.0. J. Atmos. Sci. 2018, 75, 2107–2123. [Google Scholar] [CrossRef]
- Inoue, K.; Back, L. Column-Integrated Moist Static Energy Budget Analysis on Various Time Scales during TOGA COARE. J. Atmos. Sci. 2015, 72, 1856–1871. [Google Scholar] [CrossRef]
- Kiranmayi, L.; Maloney, E.D. Intraseasonal Moist Static Energy Budget in Reanalysis Data: Intraseasonal Mse Budget in Ncep and Era. J. Geophys. Res. 2011, 116, D21. [Google Scholar] [CrossRef]
- Maloney, E.D. The Moist Static Energy Budget of a Composite Tropical Intraseasonal Oscillation in a Climate Model. J. Clim. 2009, 22, 711–729. [Google Scholar] [CrossRef]
- Back, L.E.; Bretherton, C.S. Geographic Variability in the Export of Moist Static Energy and Vertical Motion Profiles in the Tropical Pacific. Geophys. Res. Lett. 2006, 33, L17810. [Google Scholar] [CrossRef]
- Fontaine, B.; Philippon, N.; Camberlin, P. An Improvement of June-September Rainfall Forecasting in the Sahel Based upon Region April-May Moist Static Energy Content (1968–1997). Geophys. Res. Lett. 1999, 26, 2041–2044. [Google Scholar] [CrossRef]
- Privé, N.C.; Plumb, R.A. Monsoon Dynamics with Interactive Forcing. Part I: Axisymmetric Studies. J. Atmos. Sci. 2007, 64, 1417–1430. [Google Scholar] [CrossRef]
- Neelin, J.D.; Held, I.M. Modeling Tropical Convergence Based on the Moist Static Energy Budget. Mon. Weather Rev. 1987, 115, 3–12. [Google Scholar] [CrossRef]
- Neelin, J.D.; Chou, C.; Su, H. Tropical Drought Regions in Global Warming and El Niño Teleconnections. Geophys. Res. Lett. 2003, 30, 24. [Google Scholar] [CrossRef]
- Neelin, J.D.; Su, H. Moist Teleconnection Mechanisms for the Tropical South American and Atlantic Sector. J. Clim. 2005, 18, 3928–3950. [Google Scholar] [CrossRef]
- Chou, C.; Neelin, J.D. Mechanisms Limiting the Northward Extent of the Northern Summer Monsoons over North America, Asia, and Africa. J. Clim. 2003, 16, 406–425. [Google Scholar] [CrossRef]
- Chen, J.; Bordoni, S. Orographic Effects of the Tibetan Plateau on the East Asian Summer Monsoon: An Energetic Perspective. J. Clim. 2014, 27, 3052–3072. [Google Scholar] [CrossRef]
- Yao, J.; Zhou, T.; Guo, Z.; Chen, X.; Zou, L.; Sun, Y. Improved Performance of High-Resolution Atmospheric Models in Simulating the East Asian Summer Monsoon Rain Belt. J. Clim. 2017, 30, 8825–8840. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeor 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A High Spatiotemporal Gauge-Satellite Merged Precipitation Analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Song, L.; Zhang, L. Objective Identification and Analysis of Warm-Sector Rainstorm with Warm Shear Pattern over Yangtze-Huaihe River Region. Chin. J. Atmos. Sci. 2022, 47. [Google Scholar] [CrossRef]
- Zhang, L.; Song, L.; Zhu, S.; Guo, Z.; Wang, H.; Zhou, L.; Chen, C.; Zhi, X. Forecasts of the Warm-Sector Heavy Rainfall with a Warm Shear Pattern Over Coastal Areas of the Yangtze–Huaihe River in a Regional Business Forecast Model. Front. Earth Sci. 2022, 10, 938336. [Google Scholar] [CrossRef]
- Fu, J.; Zhang, F.; Hewson, T.D. Object-Oriented Composite Analysis of Warm-Sector Rainfall in North China. Mon. Weather Rev. 2020, 148, 2719–2735. [Google Scholar] [CrossRef]
- Ji, L.; Zhi, X.; Simmer, C.; Zhu, S.; Ji, Y. Multimodel Ensemble Forecasts of Precipitation Based on an Object-Based Diagnostic Evaluation. Mon. Weather Rev. 2020, 148, 2591–2606. [Google Scholar] [CrossRef]
- Vizy, E.K.; Cook, K.H. Mesoscale Convective Systems and Nocturnal Rainfall over the West African Sahel: Role of the Inter-Tropical Front. Clim. Dyn. 2018, 50, 587–614. [Google Scholar] [CrossRef]
- Chen, H.; Yu, R.; Li, J.; Yuan, W.; Zhou, T. Why Nocturnal Long-Duration Rainfall Presents an Eastward-Delayed Diurnal Phase of Rainfall down the Yangtze River Valley. J. Clim. 2010, 23, 905–917. [Google Scholar] [CrossRef]
- Holton, J.R. The Diurnal Boundary Layer Wind Oscillation above Sloping Terrain. Tellus 1967, 19, 200–205. [Google Scholar] [CrossRef]
- Nicolini, M.; Waldron, K.M.; Paegle, J. Diurnal Oscillations of Low-Level Jets, Vertical Motion, and Precipitation: A Model Case Study. Mon. Weather Rev. 1993, 121, 2588–2610. [Google Scholar] [CrossRef]
- Huang, L.; Luo, Y.; Bai, L. An Evaluation of Convection-Permitting Ensemble Simulations of Coastal Nocturnal Rainfall Over South China During the Early-Summer Rainy Season. J. Geophys. Res. Atmos. 2022, 127, e2021JD035656. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, M.; Zhu, K.; Zhou, B. What Is the Main Cause of Diurnal Variation and Nocturnal Peak of Summer Precipitation in Sichuan Basin, China? The Key Role of Boundary Layer Low-Level Jet Inertial Oscillations. J. Geophys. Res. Atmos. 2019, 124, 2643–2664. [Google Scholar] [CrossRef]
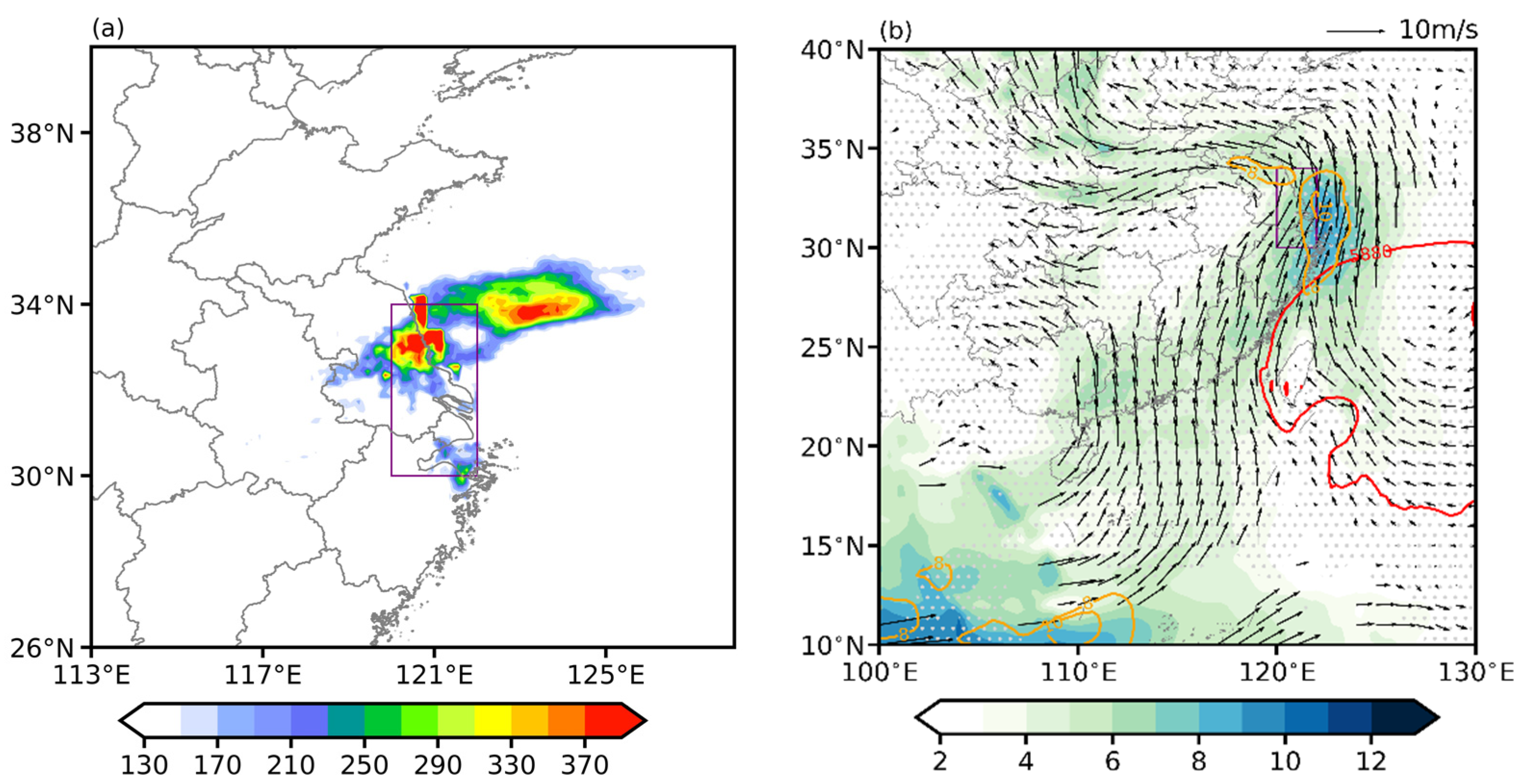
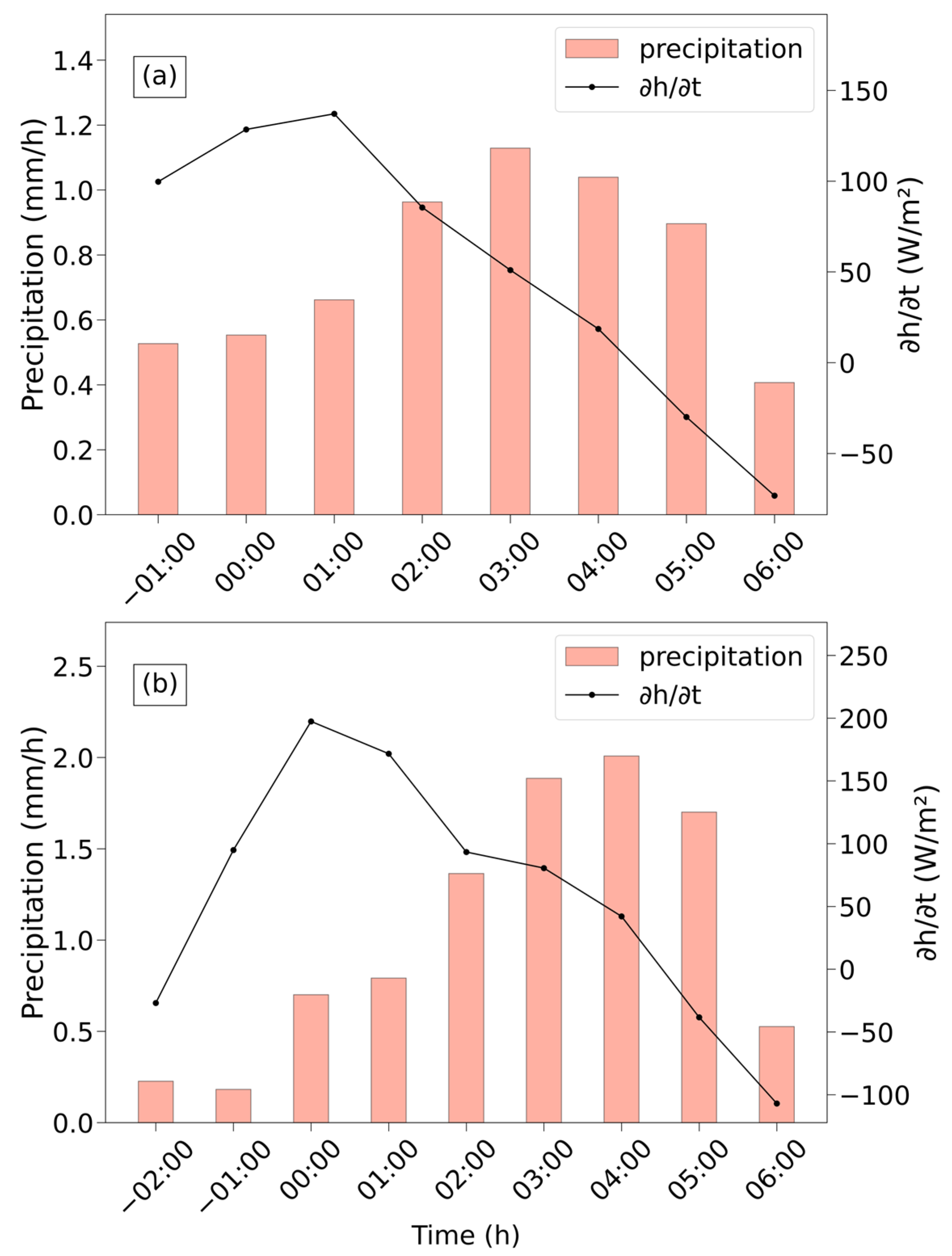
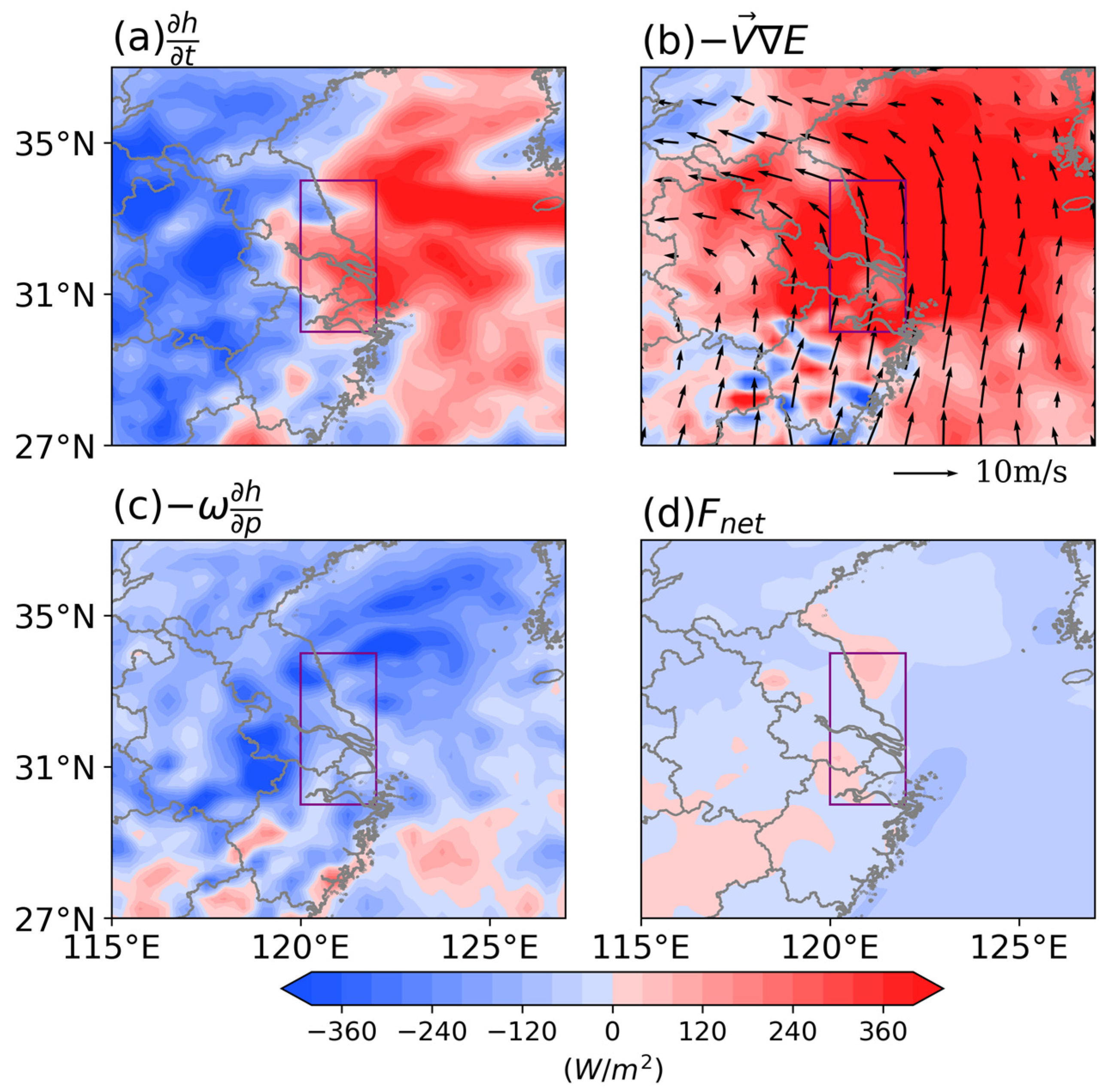

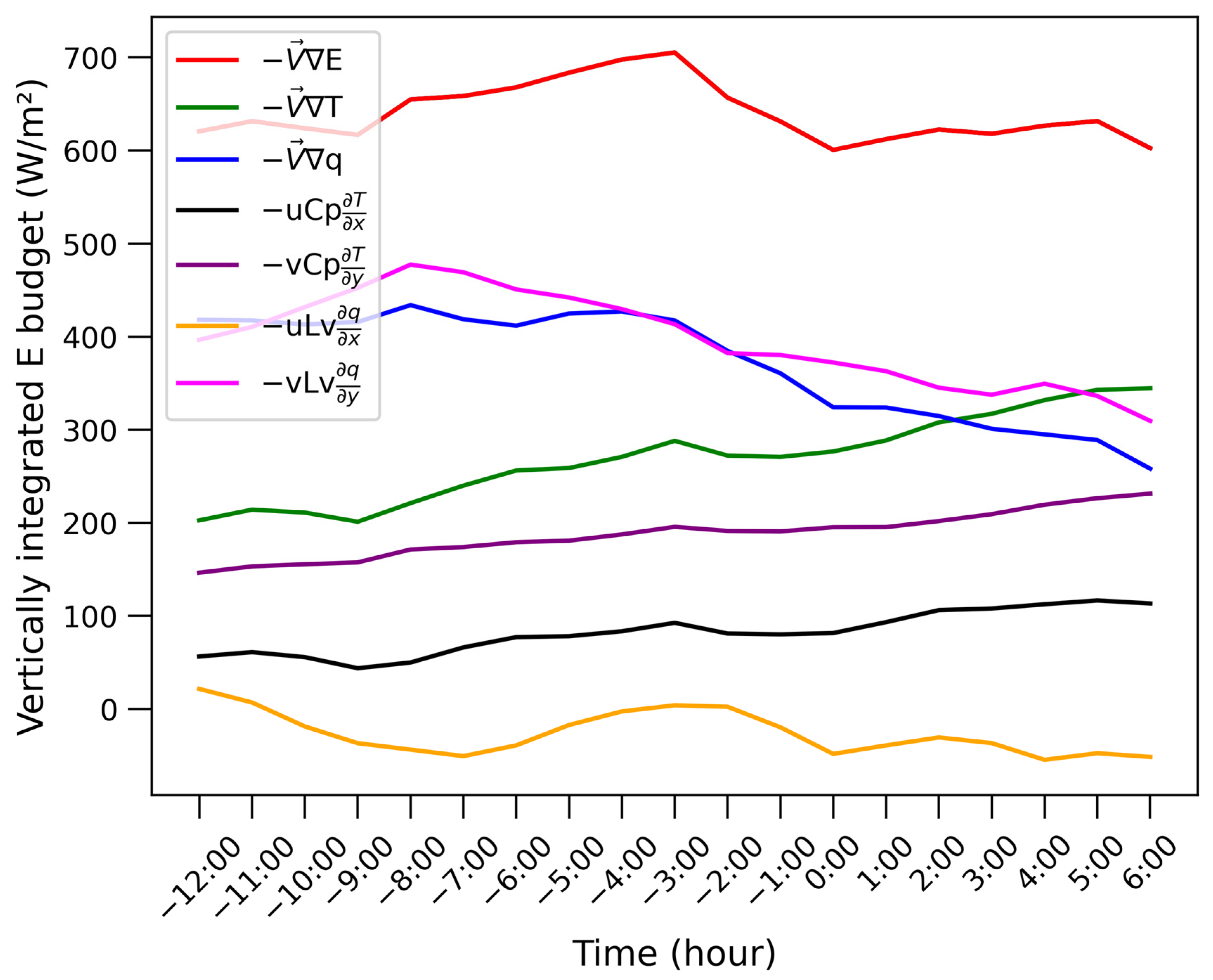
| Peak Time | Time Span | Type |
|---|---|---|
| 17 June 2011 15:00 | 17 June 2011 13:00–17 June 2011 17:00 | Nocturnal rainfall |
| 28 June 2011 17:00 | 28 June 2011 14:00–28 June 2011 20:00 | Nocturnal rainfall |
| 4 July 2014 18:00 | 4 July 2014 14:00–5 July 2014 05:00 | Nocturnal rainfall |
| 31 August 2014 23:00 | 31 August 2014 19:00–1 September 2014 02:00 | Nocturnal rainfall |
| 10 August 2015 07:00 | 10 August 2015 00:00–11 August 2015 13:00 | Nocturnal rainfall |
| 29 September 2015 16:00 | 29 September 2015 14:00–30 September 2015 03:00 | Nocturnal rainfall |
| 26 April 2016 00:00 | 25 April 2016 22:00–26 April 2016 04:00 | Nocturnal rainfall |
| 2 August 2016 16:00 | 2 August 2016 13:00–2 August 2016 21:00 | Nocturnal rainfall |
| 3 August 2016 02:00 | 2 August 2016 22:00–3 August 2016 05:00 | Nocturnal rainfall |
| 24 August 2010 15:00 | 24 August 2010 08:00–24 August 2010 18:00 | Non-nocturnal rainfall |
| 2 August 2011 13:00 | 2 August 2011 10:00–2 August 2011 15:00 | Non-nocturnal rainfall |
| 27 July 2014 10:00 | 27 July 2014 07:00–27 July 2014 15:00 | Non-nocturnal rainfall |
| 7 August 2014 17:00 | 7 August 2014 10:00–8 August 2014 06:00 | Non-nocturnal rainfall |
| 16 September 2016 12:00 | 16 September 2016 11:00–16 September 2016 16:00 | Non-nocturnal rainfall |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zhang, L. Diagnosis of Warm-Sector Heavy Rainfall with Warm Shear in the Yangtze–Huaihe Coastal Areas from the Perspective of Moist Static Energy. Atmosphere 2023, 14, 1730. https://doi.org/10.3390/atmos14121730
Yu Y, Zhang L. Diagnosis of Warm-Sector Heavy Rainfall with Warm Shear in the Yangtze–Huaihe Coastal Areas from the Perspective of Moist Static Energy. Atmosphere. 2023; 14(12):1730. https://doi.org/10.3390/atmos14121730
Chicago/Turabian StyleYu, Yiping, and Ling Zhang. 2023. "Diagnosis of Warm-Sector Heavy Rainfall with Warm Shear in the Yangtze–Huaihe Coastal Areas from the Perspective of Moist Static Energy" Atmosphere 14, no. 12: 1730. https://doi.org/10.3390/atmos14121730
APA StyleYu, Y., & Zhang, L. (2023). Diagnosis of Warm-Sector Heavy Rainfall with Warm Shear in the Yangtze–Huaihe Coastal Areas from the Perspective of Moist Static Energy. Atmosphere, 14(12), 1730. https://doi.org/10.3390/atmos14121730






