Spaceborne Algorithm for Recognizing Lightning Whistler Recorded by an Electric Field Detector Onboard the CSES Satellite
Abstract
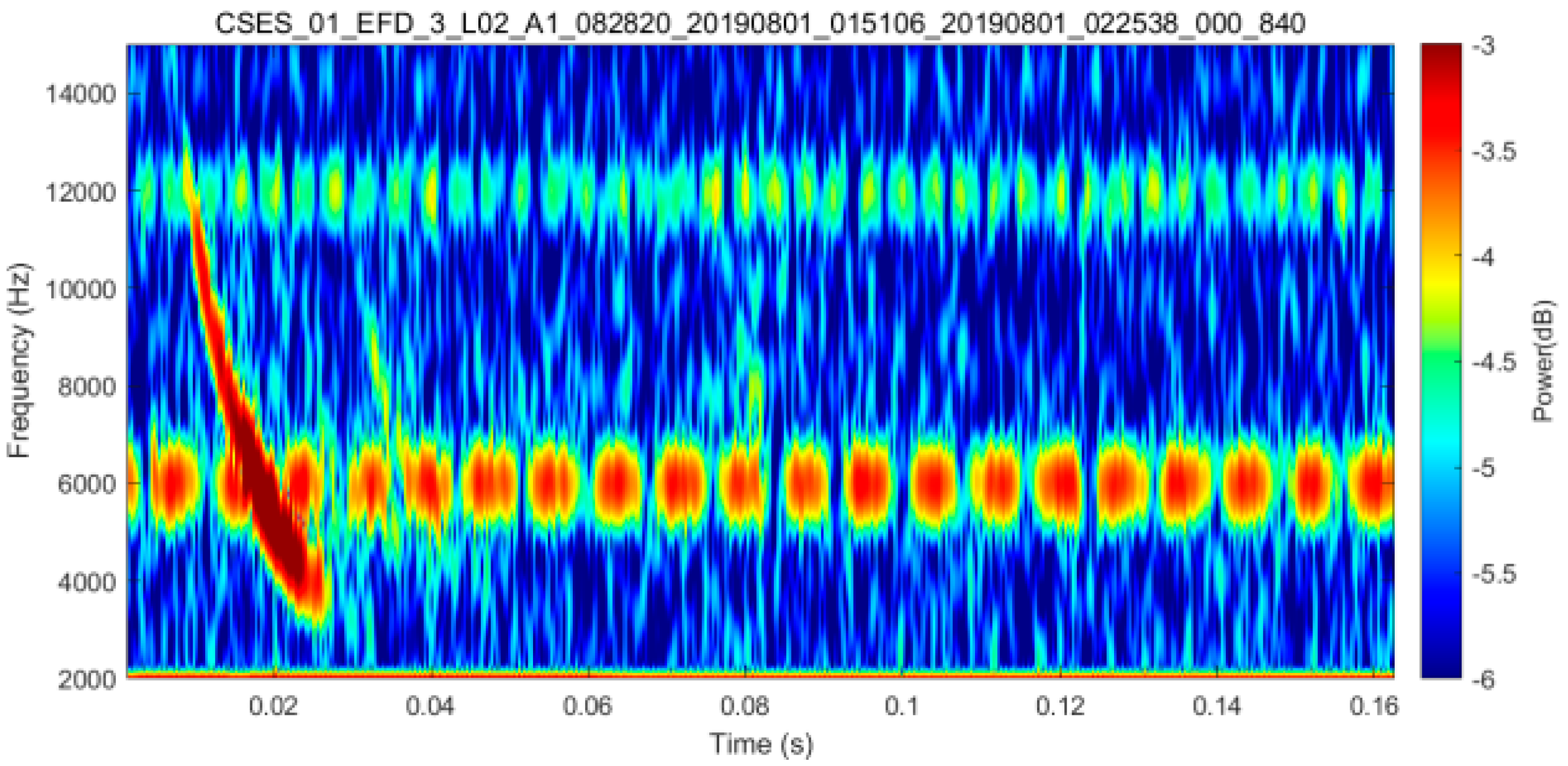
:1. Introduction
2. The Proposed Method
2.1. Data Preprocessing
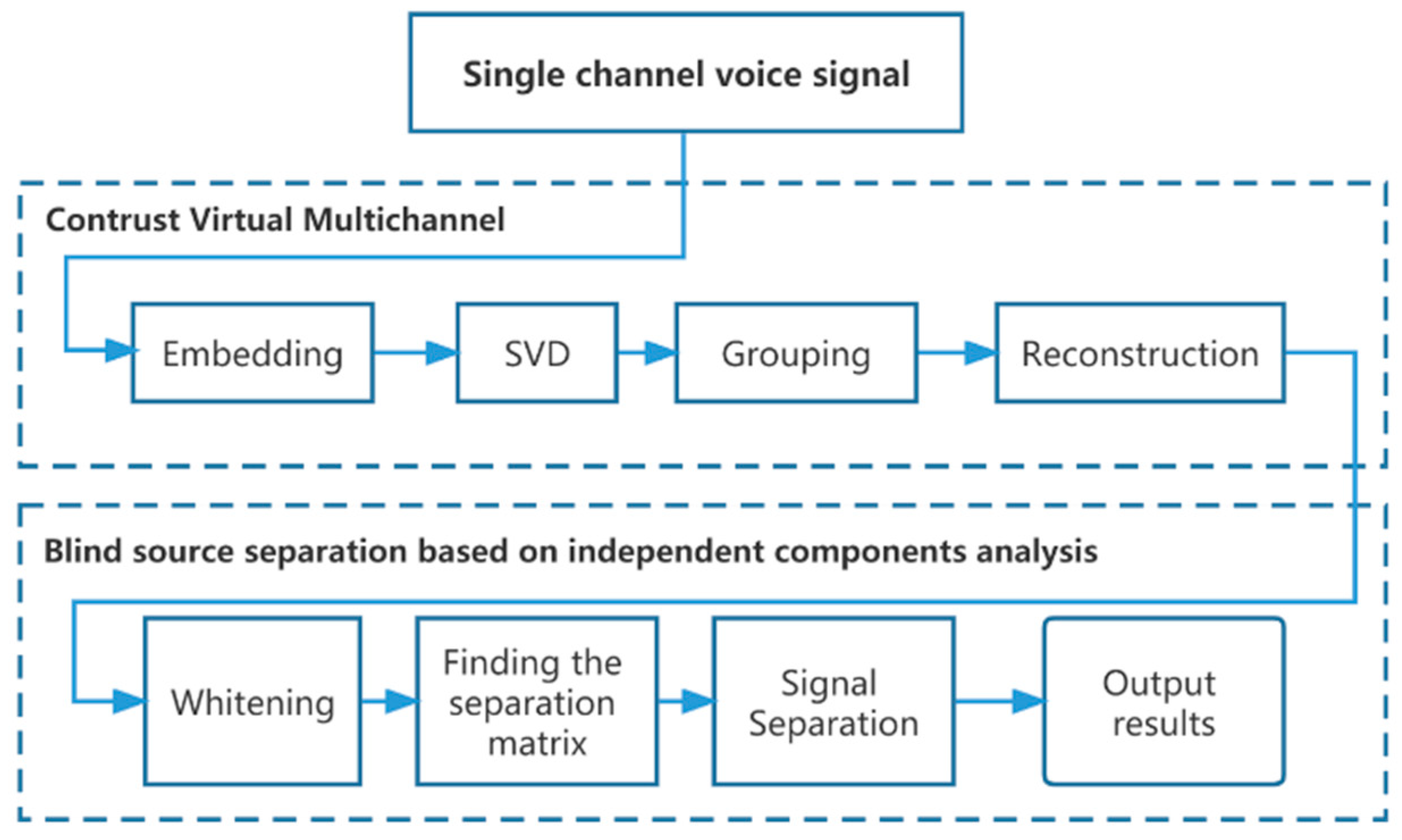
2.1.1. Construction of Virtual Multi-Channel
- A.
- Embedding
- B.
- SVD (singular value decomposition)
- C.
- Grouping
- D.
- Signal reconstruction.
2.1.2. Blind Source Separation Based on Independent Component Analysis (ICA)
- A.
- Whitening process
- B.
- Finding the separation matrix
- C.
- Signal separation
2.2. Audio Feature Extraction Stage
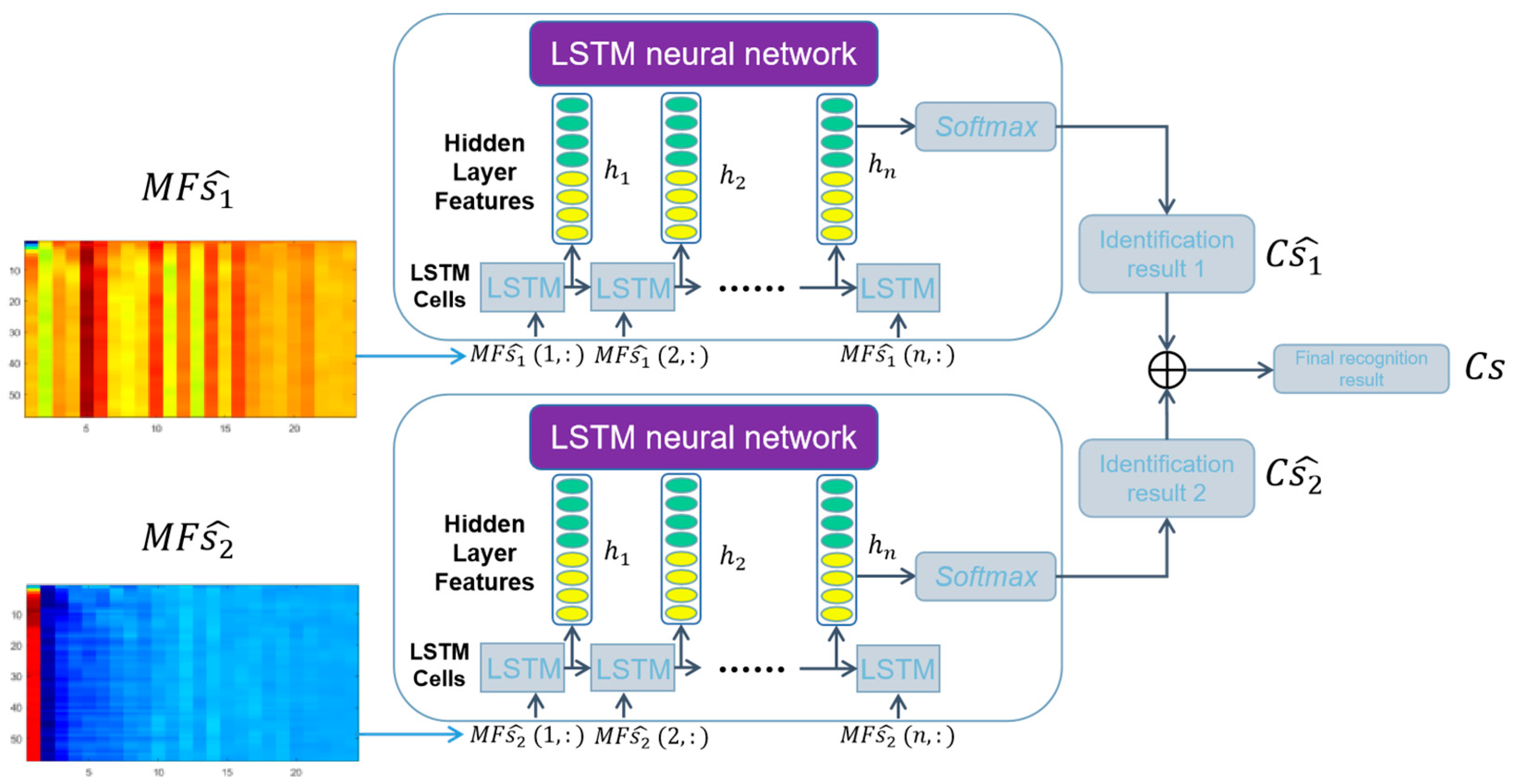
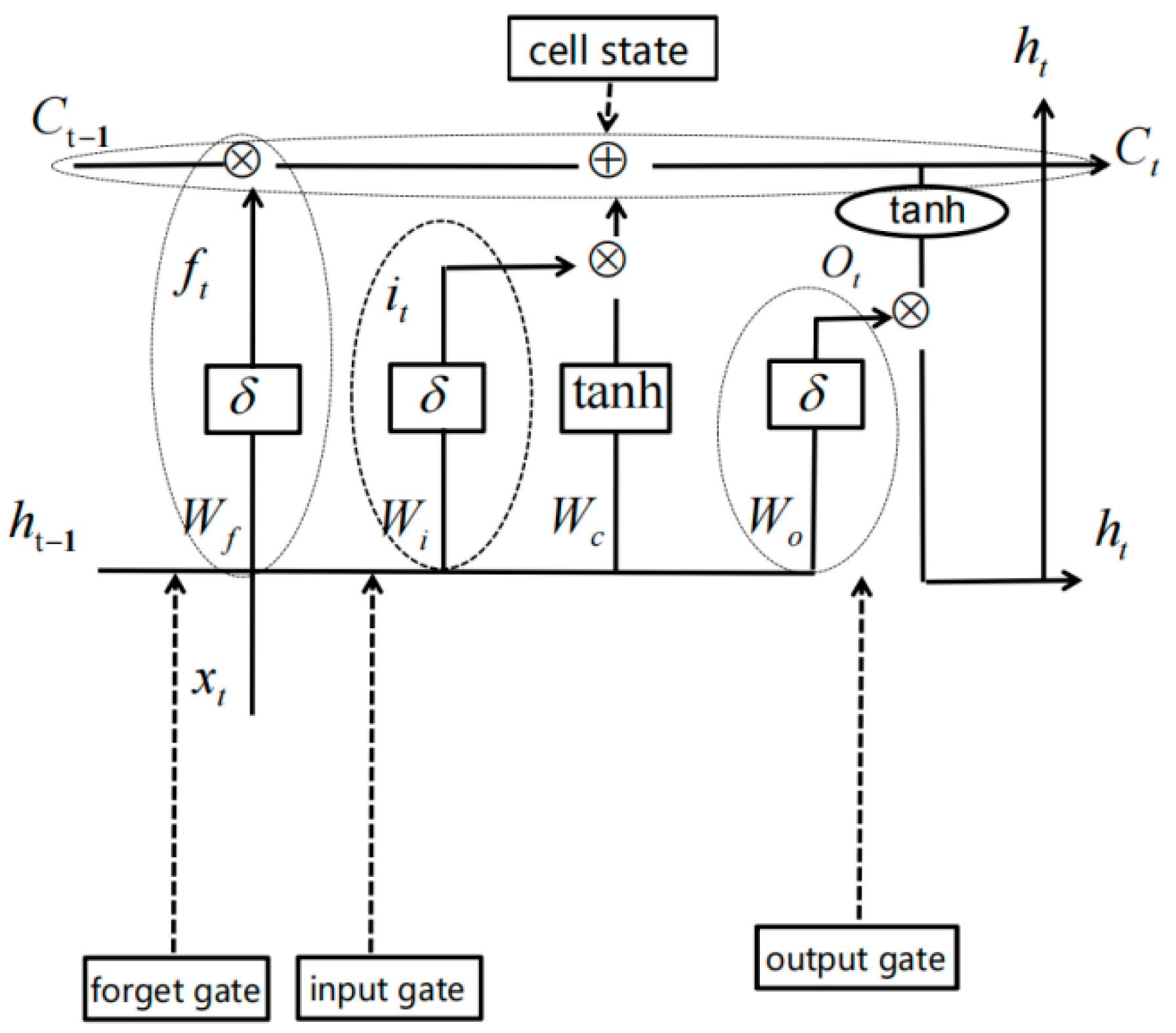
2.3. LSTM Neural Network Classification and Decision Fusion
3. Experiments and Analysis
3.1. Datasets and Evaluation Metrics
3.2. Experimental Results
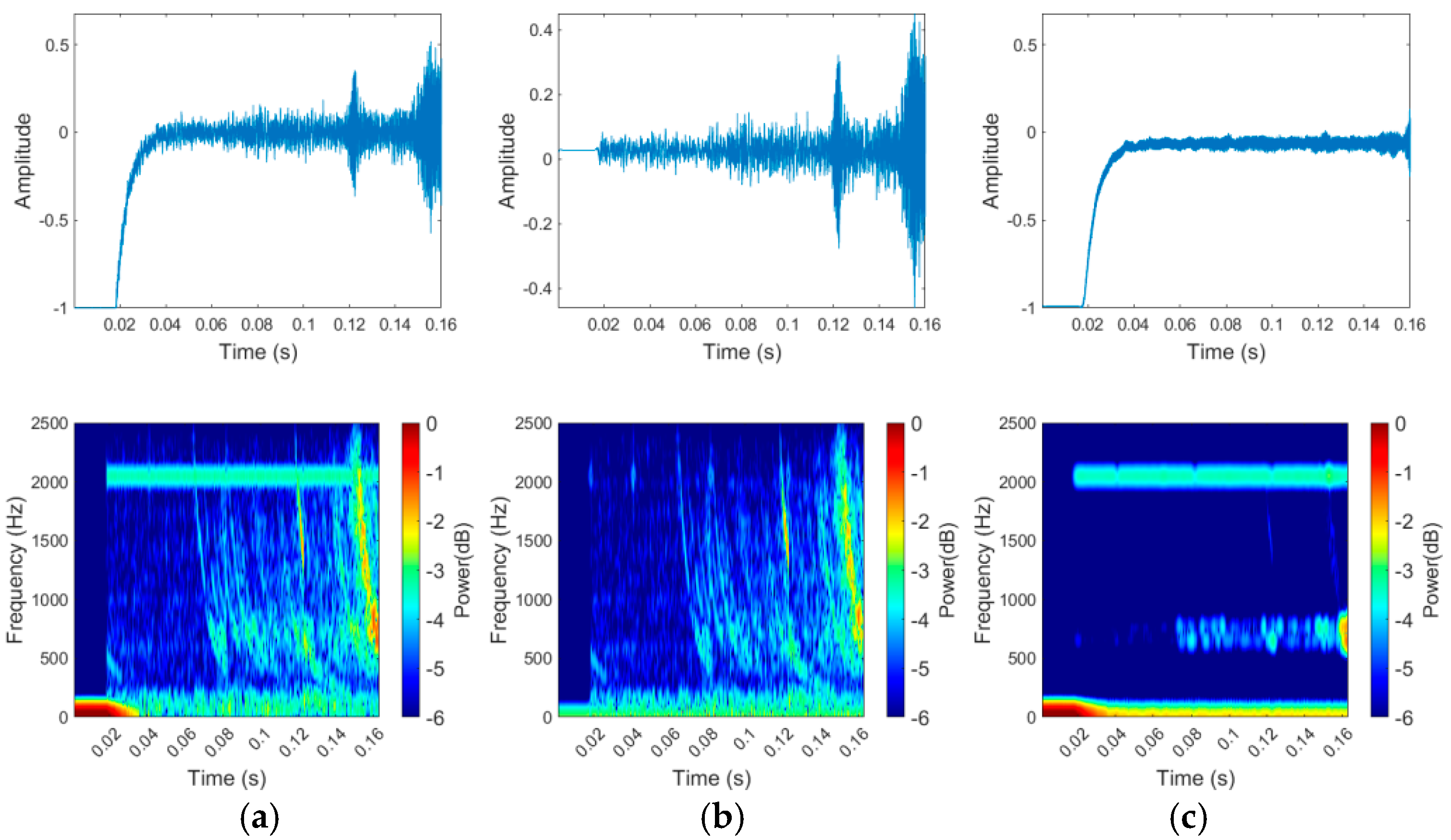
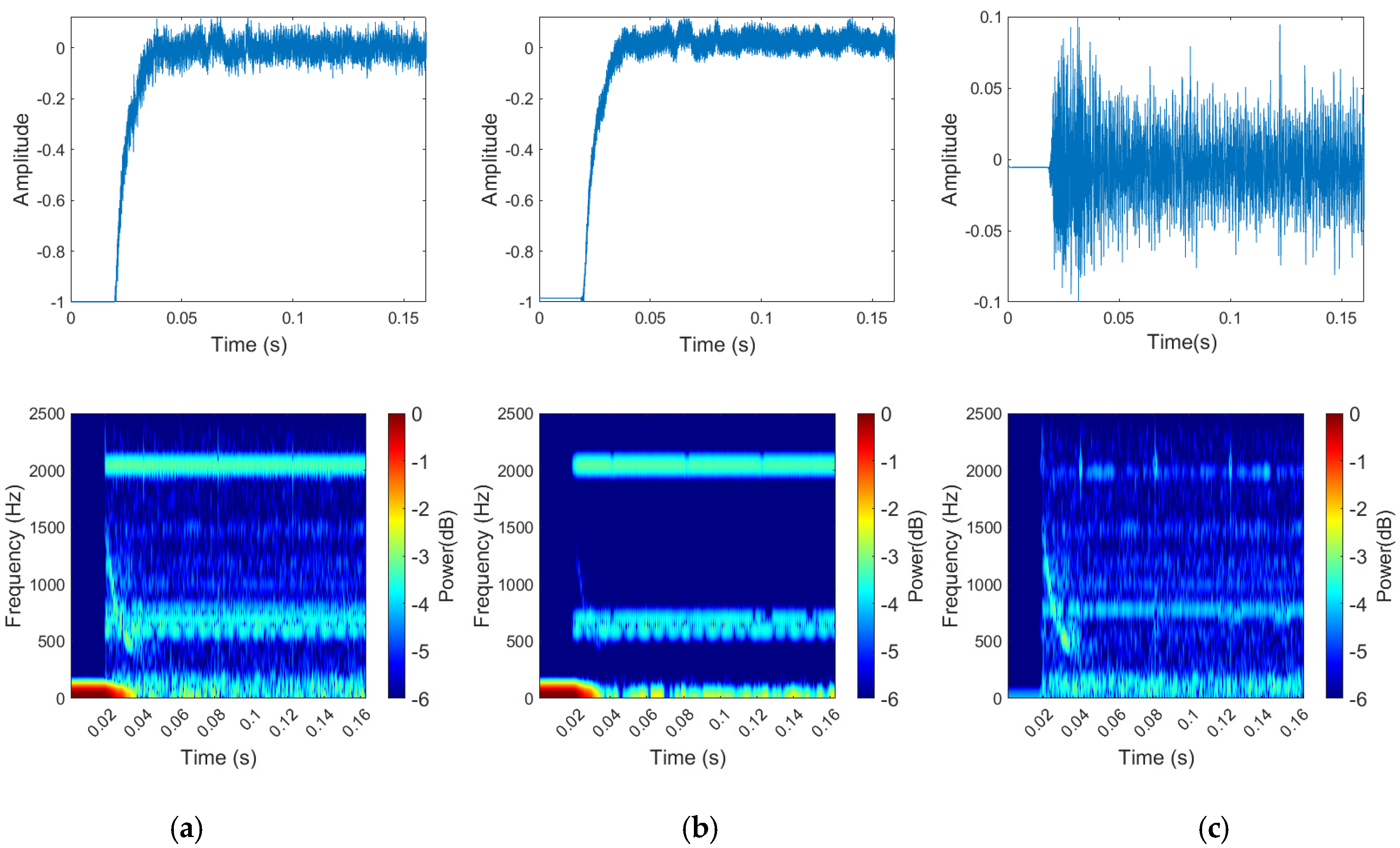
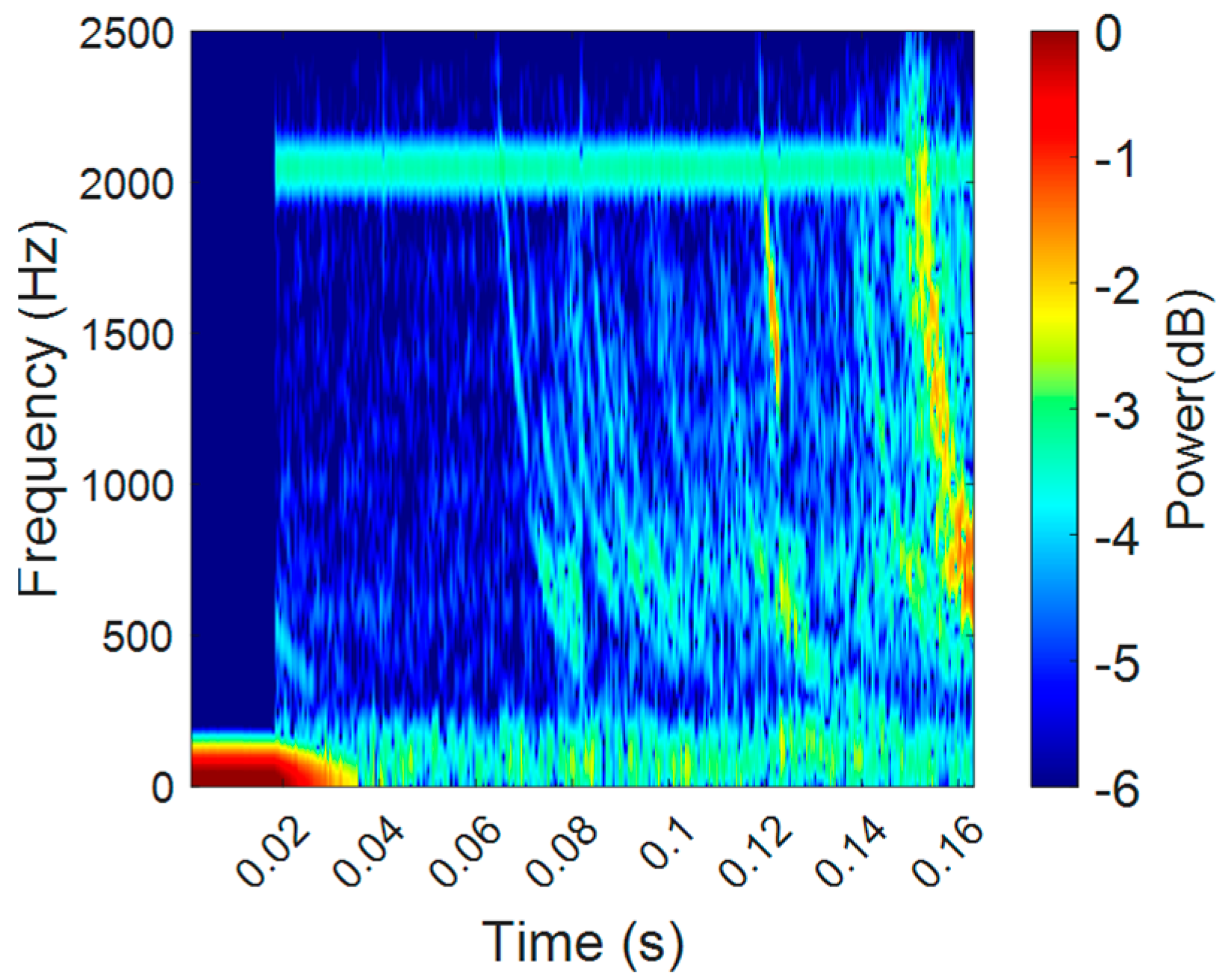
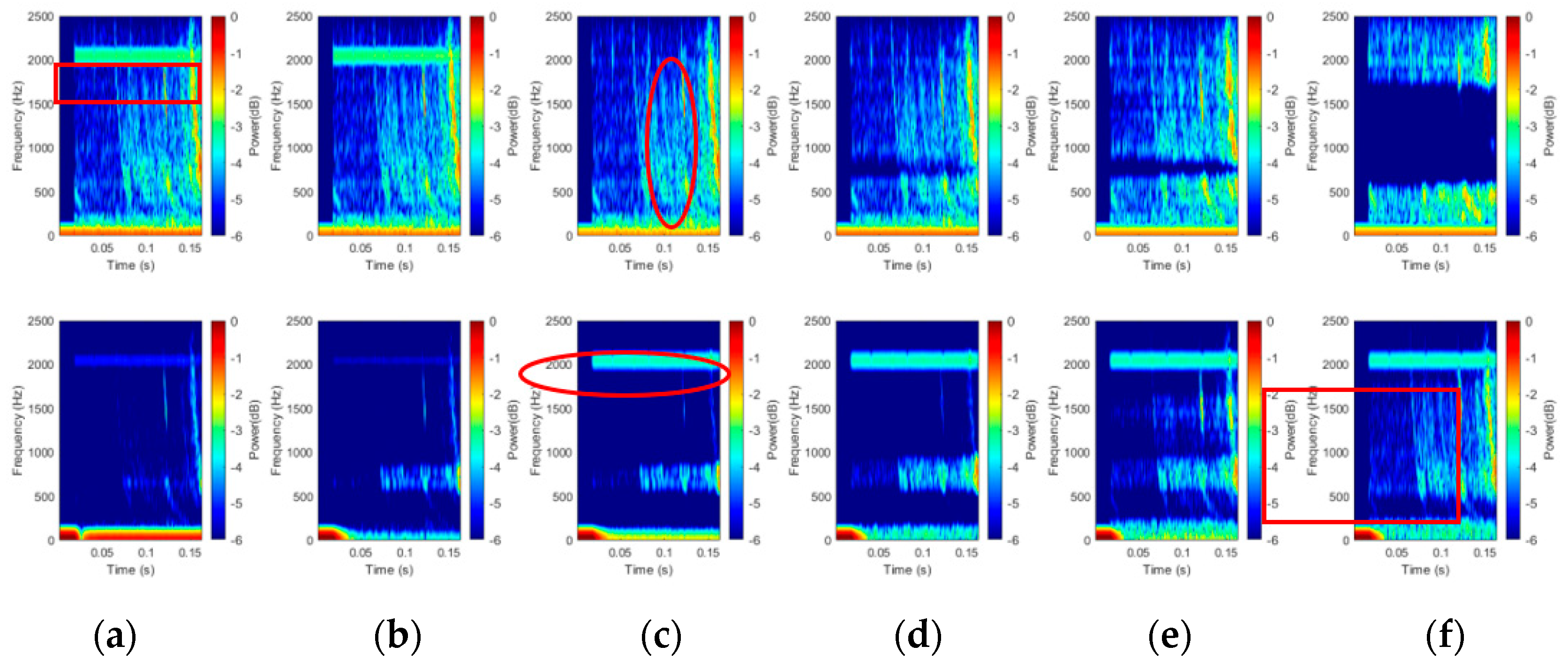
3.2.1. The Visualized Results
3.2.2. Quantitative Results
4. Discussion
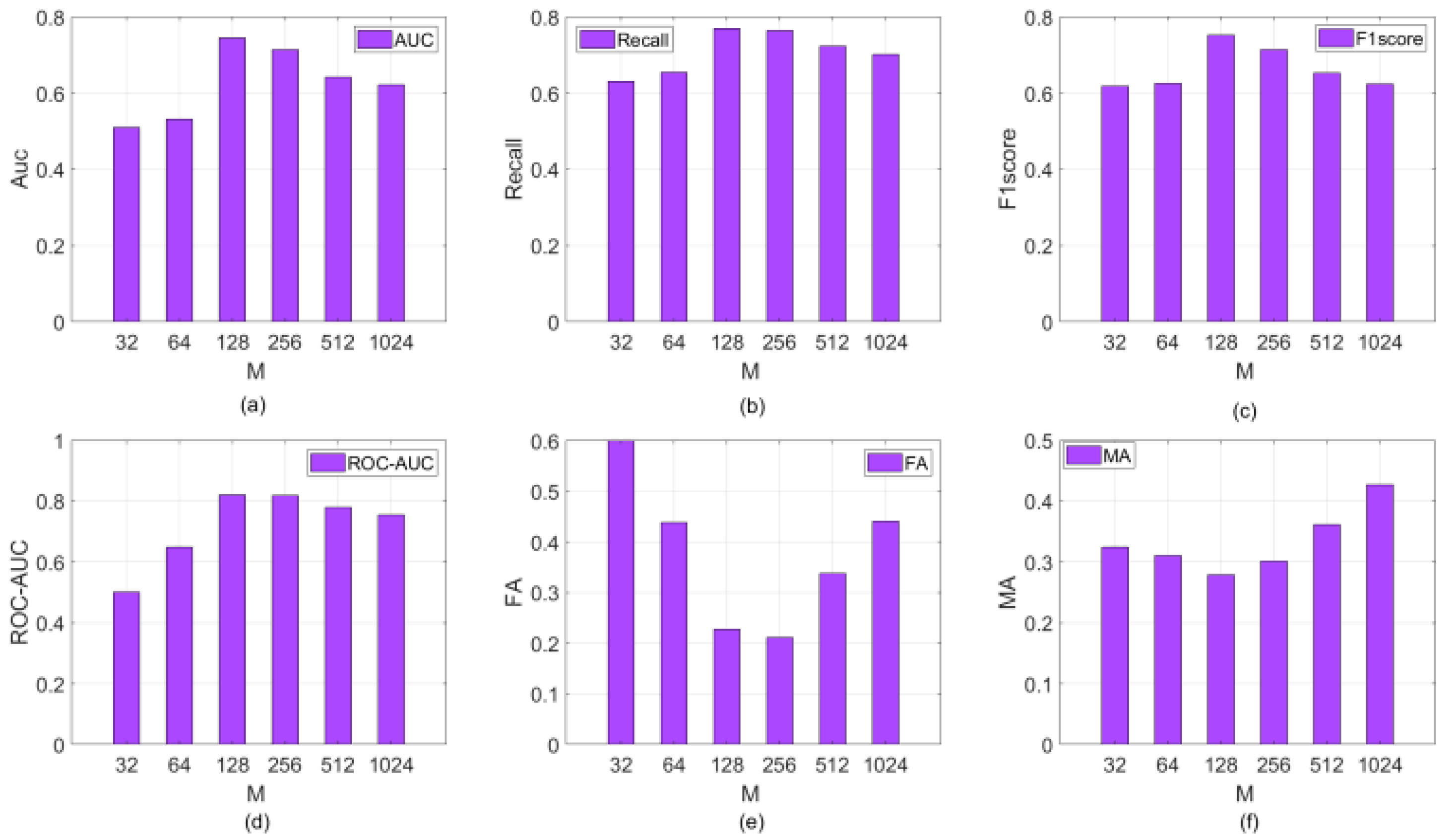
4.1. Impact of the Parameter M on the Performance of the Proposed Approach
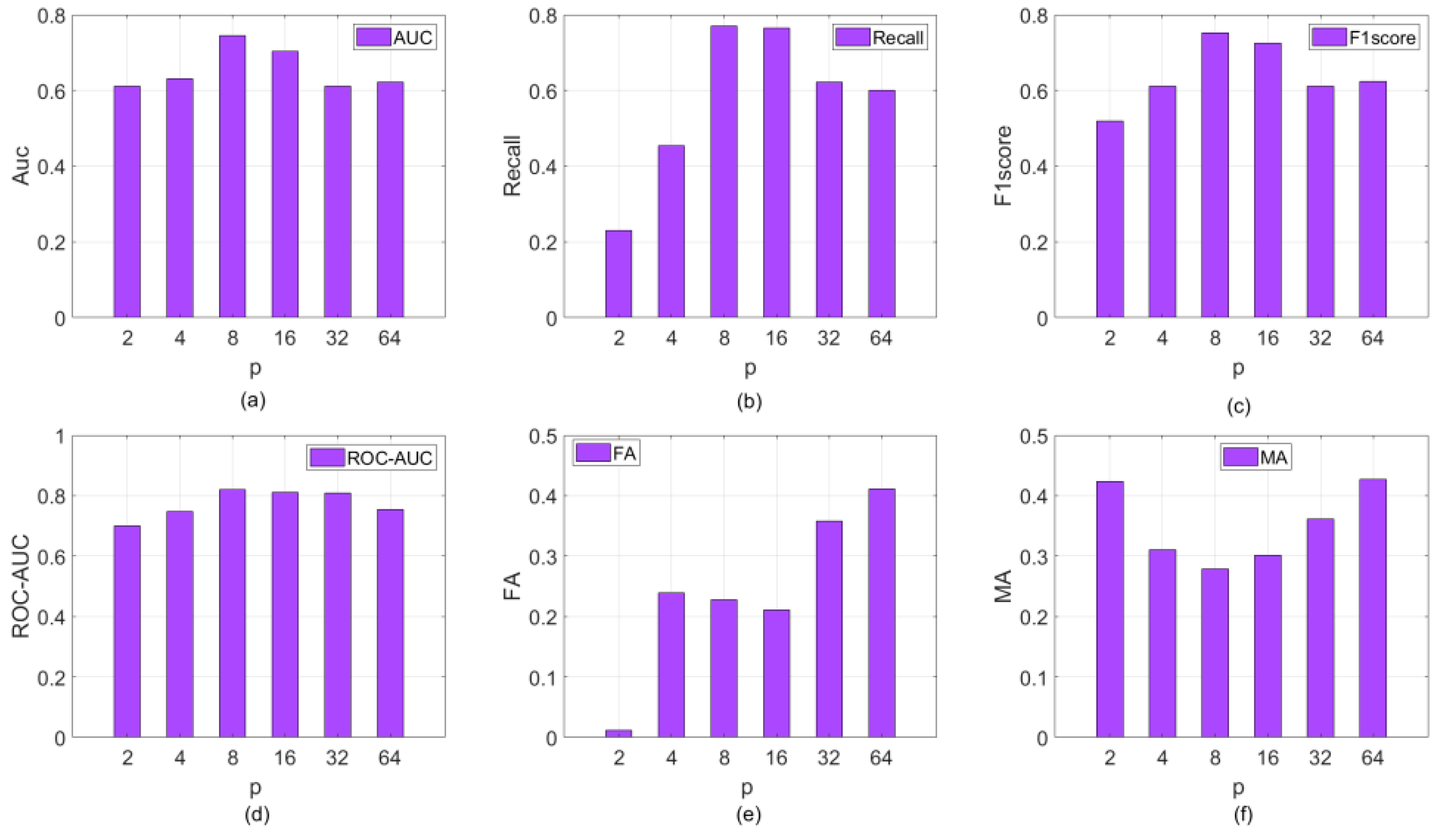
4.2. Impact of the Parameter p on the Performance of the Proposed Approach
4.3. Visualization Results of Hidden-Layer Features of LSTM Neural Network
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carpenter, D.L.; Anderson, R.R. An ISEE/Whistler model of equatorial electron density in the magnetosphere. J. Geophys. Res. Space Phys. 1992, 97, 1097–1108. [Google Scholar] [CrossRef]
- Bayupati, I.P.A.; Kasahara, Y.; Goto, Y. Study of Dispersion of Lightning Whistlers Observed by Akebono Satellite in the Earth’s Plasmasphere. IEICE Trans. Commun. 2012, E95-B, 3472–3479. [Google Scholar] [CrossRef]
- Oike, Y.; Kasahara, Y.; Goto, Y. Spatial distribution and temporal variations of occurrence frequency of lightning whistlers observed by VLF/WBA onboard Akebono. Radio Sci. 2015, 49, 753–764. [Google Scholar] [CrossRef]
- Chen, Y.; Ni, B.; Gu, X.; Zhao, Z.; Yang, G.; Zhou, C.; Zhang, Y. First observations of low latitude whistlers using WHU ELF/VLF receiver system. Sci. China (Technol. Sci.) 2017, 60, 166–174. [Google Scholar] [CrossRef]
- Kishore, A.; Deo, A.; Kumar, S. Upper atmospheric remote sensing using ELF–VLF lightning generated tweek and whistler sferics. South Pac. J. Nat. Appl. Sci. 2016, 34, 12. [Google Scholar] [CrossRef]
- Záhlava, J.; Němec, F.; Pincon, J.L.; Santolík, O.; Kolmaová, I.; Parrot, M. Whistler Influence on the Overall Very Low Frequency Wave Intensity in the Upper Ionosphere. J. Geophys. Res. Space Phys. 2018, 123, 5648–5660. [Google Scholar] [CrossRef]
- Parrot, M.; Pinçon, J.-L.; Shklyar, D. Short-Fractional Hop Whistler Rate Observed by the Low-Altitude Satellite DEMETER at the End of the Solar Cycle 23. J. Geophys. Res. Space Phys. 2019, 124, 3522–3531. [Google Scholar] [CrossRef]
- Horne, R.B.; Glauert, S.A.; Meredith, N.P.; Boscher, D.; Maget, V.; Heynderickx, D.; Pitchford, D. Space weather impacts on satellites and forecasting the Earth’s electron radiation belts with SPACECAST. Space Weather-Int. J. Res. Appl. 2013, 11, 169–186. [Google Scholar] [CrossRef]
- Lichtenberger, J.; Ferencz, C.; Bodnár, L.; Hamar, D.; Steinbach, P. Automatic Whistler Detector and Analyzer system: Automatic Whistler Detector. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- The Stanford VLF Group Automated Detection of Whistlers for the TARANIS Spacecraft Overview of the Project. 2009. Available online: https://vlfstanford.ku.edu.tr/research_topic_inlin/automated-detection-whistlers-taranis-spacecraft/ (accessed on 15 August 2023).
- Dharma, K.S.; Bayupati, I.; Buana, P.W. Automatic Lightning Whistler Detection Using Connected Component Labeling Method. J. Theor. Appl. Inf. Technol. 2014, 66, 638–645. [Google Scholar] [CrossRef]
- Fiser, J.; Chum, J.; Diendorfer, G.; Parrot, M.; Santolik, O. Whistler intensities above thunderstorms. Ann. Geophys. 2010, 28, 37–46. [Google Scholar] [CrossRef]
- Zhou, R.X.; Gu, X.D.; Yang, K.X.; Li, G.S.; Ni, B.B.; Yi, J.; Chen, L.; Zhao, F.T.; Zhao, Z.Y.; Wang, Q.; et al. A detailed investigation of low latitude tweek atmospherics observed by the WHU ELF/VLF receiver: I. Automatic detection and analysis method. Earth Planet. Phys. 2020, 4, 120–130. [Google Scholar] [CrossRef]
- Ali Ahmad, U.; Kasahara, Y.; Matsuda, S.; Ozaki, M.; Goto, Y. Automatic Detection of Lightning Whistlers Observed by the Plasma Wave Experiment Onboard the Arase Satellite Using the OpenCV Library. Remote Sens. 2019, 11, 1785. [Google Scholar] [CrossRef]
- Konan, O.J.E.Y.; Mishra, A.K.; Lotz, S. Machine Learning Techniques to Detect and Characterise Whistler Radio Waves. arXiv 2020, arXiv:2002.01244. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, Q.; Yang, D.H. Automatic recognition algorithm of lightning whistlers observed by the Search Coil Magnetometer onboard the Zhangheng-1 Satellite. Chin. J. Geophys. 2021, 64, 3905–3924. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, Z.J.; Zeren, Z.M.; Wang, Z.G.; Feng, J.L.; Shen, X.H.; WU, P.; Wang, Q.; Yang, D.H.; Wang, T.L.; et al. Automatic recognition algorithm of the lightning whistler waves by using speech processing technology. Chin. J. Geophys. 2022, 65, 882–897. [Google Scholar]
- Yilmaz, O.; Rickard, S. Blind Separation of Speech Mixtures via Time-Frequency Masking. IEEE Trans. Signal Process. 2004, 52, 1830–1847. [Google Scholar] [CrossRef]
- Li-Na, Z.; Er-Hua, Z.; Jun-Liang, J. Monaural voiced speech separation based on computational auditory scene analysis. Comput. Eng. Sci. 2019, 41, 1266–1272. [Google Scholar] [CrossRef]
- Mowlaee, P.; Saeidi, R.; Christensen, M.G.; Zheng-Hua, T.; Kinnunen, T.; Franti, P.; Jensen, S.H. A Joint Approach for Single-Channel Speaker Identification and Speech Separation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2586–2601. [Google Scholar] [CrossRef]
- Hershey, J.R.; Rennie, S.J.; Olsen, P.A.; Kristjansson, T.T. Super-human multi-talker speech recognition: A graphical modeling approach. Comput. Speech Lang. 2010, 24, 45–66. [Google Scholar] [CrossRef]
- King, B.J.; Atlas, L. Single-Channel Source Separation Using Complex Matrix Factorization. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2591–2597. [Google Scholar] [CrossRef]
- Gao, B.; Woo, W.L.; Dlay, S.S. Adaptive Sparsity Non-Negative Matrix Factorization for Single-Channel Source Separation. IEEE J. Sel. Top. Signal Process. 2011, 5, 988–1001. [Google Scholar] [CrossRef]
- Gao, B.; Woo, W.L.; Dlay, S.S. Single-Channel Source Separation Using EMD-Subband Variable Regularized Sparse Features. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 961–976. [Google Scholar] [CrossRef]
- Warner, E.S.; Proudler, I.K. Single-channel blind signal separation of filtered MPSK signals. IEE Proc.-Radar Sonar Navig. 2003, 150, 396–402. [Google Scholar] [CrossRef]
- Liao, C.; Wan, J.; Zhou, S. Single-channel blind separation performance bound of two co-frequency modulated signals. J. Tsinghua Univ. 2010, 50, 1646–1650. [Google Scholar] [CrossRef]
- Rui, G.S.; Xu, B.; Zhang, S. Amplitude estimating algorithm for single channel mixing signals. J. Commun. 2011, 32, 82–87. [Google Scholar]
- Liang, W.U.; Hua, J. Blind separation algorithm of single-channel mixed-signal. Inf. Electron. Eng. 2012, 10, 343–349. [Google Scholar] [CrossRef]
- Davies, M.E.; James, C.J. Source separation using single channel ICA. Signal Process. 2007, 87, 1819–1832. [Google Scholar] [CrossRef]
- Hong, H.; Liang, M. Separation of fault features from a single-channel mechanical signal mixture using wavelet decomposition. Mech. Syst. Signal Process. 2007, 21, 2025–2040. [Google Scholar] [CrossRef]
- Ma, H.-G.; Jiang, Q.-B.; Liu, Z.-Q.; Liu, G.; Ma, Z.-Y. A novel blind source separation method for single-channel signal. Signal Process. 2010, 90, 3232–3241. [Google Scholar] [CrossRef]
- Mijović, B.; De Vos, M.; Gligorijevic, I.; Taelman, J.; Van Huffel, S. Source Separation From Single-Channel Recordings by Combining Empirical-Mode Decomposition and Independent Component Analysis. IEEE Trans. Biomed. Eng. 2010, 57, 2188–2196. [Google Scholar] [CrossRef] [PubMed]
- Maddirala, A.K.; Shaik, R.A. Separation of Sources From Single-Channel EEG Signals Using Independent Component Analysis. IEEE Trans. Instrum. Meas. 2018, 67, 382–393. [Google Scholar] [CrossRef]
- Ji, L.; Zhuang, H.; Cheng, D.; Yi, C. Blind Source Separation of Single-Channel Background Sound Cockpit Voice Based on EEMD and FastICA. J. Technol. 2021, 21, 62–67,74. [Google Scholar] [CrossRef]
- Diego, P.; Bertello, I.; Candidi, M.; Mura, A.; Coco, I.; Vannaroni, G.; Ubertini, P.; Badoni, D. Electric field computation analysis for the Electric Field Detector (EFD) on board the China Seismic-Electromagnetic Satellite (CSES). Adv. Space Res. 2017, 60, 2206–2216. [Google Scholar] [CrossRef]




| Abbreviation | Meaning | Abbreviation | Meaning |
|---|---|---|---|
| EFD | electric field detector | LW | lightning whistler |
| SDNN | sliding deep convolutional neural network | DNN | deep convolutional neural network |
| LWRM | LW recognition model | LW-EFD | an LW event in EFD data |
| BSS | blind source separation | VLF | very low frequency |
| SCBSS | single-channel blind source separation | ROC | receiver operating characteristic |
| MFCCs | mel-frequency cepstral coefficients | MPSK | multiphase phase-shift keying |
| LSTM | long short-term memory | ICA | independent component analysis |
| SSA | singular spectrum analysis | YOLO | you only look once |
| AUC | area under the curve | SVD | singular value decomposition |
| MSK | minimum shift keying | BBS | blind source separation |
| QAM | quadrature amplitude modulated | SCM | search coil magnetometer |
| FA | false alarm rate | MA | missed alarm rate |
| Parameter Name | Learning Rate | Batch-Size | Epoch | Optimizer | BSS_p | BSS_M | |
|---|---|---|---|---|---|---|---|
|
Extraction Method | |||||||
| MFCCs–LSTM | 10 × 10−3 | 64 | 20 | Adam | - | - | |
| BSS–MFCCs–LSTM | 10 × 10−3 | 64 | 20 | Adam | 8 | 128 | |
| Recognition | Accuracy | Recall | F1-Score | ROC-AUC | FA | MA | Cost Time (s) | Cost Memory (MB) | |
|---|---|---|---|---|---|---|---|---|---|
|
Algorithm Evaluation Metrics | |||||||||
| Works by Dharma et al. [11] | 0.581 ± 0.021 | 0.236 ± 0.021 | 0.181 ± 0.021 | 0.678 ± 0.022 | 0.301 ± 0.019 | 0.78 ± 0.021 | 2.18 ± 0.117 | 68.1 ± 0.225 | |
| MFCCs–LSTM | 0.573 ± 0.031 | 0.149 ± 0.065 | 0.253 ± 0.095 | 0.778 ± 0.049 | 0.002 ± 0.003 | 0.850 ± 0.065 | 2.240 ± 0.070 | 83.026 ± 0.560 | |
| BSS–MFCCs–LSTM | 0.745 ± 0.050 | 0.771 ± 0.050 | 0.753 ± 0.028 | 0.821 ± 0.021 | 0.228 ± 0.143 | 0.279 ± 0.050 | 2.655 ± 0.050 | 128.210 ± 0.525 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yuan, J.; Cao, J.; Liu, Y.; Huang, J.; Li, B.; Wang, Q.; Zhang, Z.; Zhao, Z.; Han, Y.; et al. Spaceborne Algorithm for Recognizing Lightning Whistler Recorded by an Electric Field Detector Onboard the CSES Satellite. Atmosphere 2023, 14, 1633. https://doi.org/10.3390/atmos14111633
Li Y, Yuan J, Cao J, Liu Y, Huang J, Li B, Wang Q, Zhang Z, Zhao Z, Han Y, et al. Spaceborne Algorithm for Recognizing Lightning Whistler Recorded by an Electric Field Detector Onboard the CSES Satellite. Atmosphere. 2023; 14(11):1633. https://doi.org/10.3390/atmos14111633
Chicago/Turabian StyleLi, Yalan, Jing Yuan, Jie Cao, Yaohui Liu, Jianping Huang, Bin Li, Qiao Wang, Zhourong Zhang, Zhixing Zhao, Ying Han, and et al. 2023. "Spaceborne Algorithm for Recognizing Lightning Whistler Recorded by an Electric Field Detector Onboard the CSES Satellite" Atmosphere 14, no. 11: 1633. https://doi.org/10.3390/atmos14111633
APA StyleLi, Y., Yuan, J., Cao, J., Liu, Y., Huang, J., Li, B., Wang, Q., Zhang, Z., Zhao, Z., Han, Y., Liu, H., Han, J., Shen, X., & Wang, Y. (2023). Spaceborne Algorithm for Recognizing Lightning Whistler Recorded by an Electric Field Detector Onboard the CSES Satellite. Atmosphere, 14(11), 1633. https://doi.org/10.3390/atmos14111633






