Prediction of Gas Emission in the Working Face Based on LASSO-WOA-XGBoost

Abstract

In order to improve the prediction accuracy of gas emission in the mining face, a method combining least absolute value convergence and selection operator (LASSO), whale optimization algorithm (WOA), and extreme gradient boosting (XGBoost) was proposed, along with the LASSO-WOA-XGBoost gas emission prediction model. Aiming at the monitoring data of gas emission in Qianjiaying mine, LASSO is used to perform feature selection on 13 factors that affect gas emission, and 9 factors that have a high impact on gas emission are screened out. The three main parameters of n_estimators, learning_rate, and max_depth in XGBoost are optimized through WOA, which solves the problem of difficult parameter adjustment due to the large number of parameters in the XGBoost algorithm and improves the prediction effect of the XGBoost algorithm. "When comparing PCA-BP, PCA-SVM, LASSO-XGBoost, and PCA-WOA-XGBoost prediction models, the results indicate that utilizing LASSO for feature selection is more effective in enhancing model prediction accuracy than employing principal component analysis (PCA) for dimensionality reduction." The average absolute error of the LASSO-WOA-XGBoost model is 0.1775, and the root mean square error is 0.2697, which is the same as other models. Compared with the four prediction models, the LASSO-WOA-XGBoost prediction model reduced the mean absolute error by 7.43%, 8.81%, 4.16%, and 9.92%, respectively, and the root mean square error was reduced by 0.24%, 1.13%, 5.81%, and 8.78%. It provides a new method for predicting the gas emission from the mining face in actual mine production.

1. Introduction

Gas concentration is an important indicator to measure the degree of coal mine gas hazards. Gas concentrations exceeding the limit are closely related to malignant coal mine incidents such as gas explosions, asphyxiation of underground personnel, and coal and gas outbursts. The underground environment is complex, and the change in gas concentration is not a simple static process but has a highly complex nonlinear relationship between its influencing factors. Through the investigation and cause analysis of coal mine gas accidents, it was found that failure to accurately grasp the changing laws of gas concentration is one of the main reasons for gas accidents. Therefore, accurately and efficiently predicting gas concentration is the top priority in preventing gas accidents. China is one of the countries with the worst gas disasters in the world. With the mining and utilization of coal resources, China’s coal development is rapidly shifting to the deep at a rate of 10–25 m per year, which makes the gas problem faced by coal mining more severe [1]. Accurate prediction of gas emission in mines can provide an important basis for mine ventilation and gas disaster prevention and control measures.

Many scholars have conducted in-depth research on the prediction of gas emission. The traditional prediction methods include the source prediction method, fuzzy comprehensive evaluation method, mine statistics method [2], gas geological statistics method, gray theory method [3], etc. [4]. In recent years, machine learning methods have been widely used in gas emission prediction. In 2012, LV Fu [5] first used principal component analysis (PCA) to reduce the dimensionality of the factors affecting gas emission in the mining face and performed multi-step linear regression prediction through the dimensionality-reduced principal components. The method reduces the number of predictive influencing factors and makes the calculation of the predicting process easier, but PCA dimensionality reduction changes the feature space structure of the original data, resulting in unclear meanings for new features. From 2015 to 2019, Lu Guobin [6], Li Bing [7], and Li Xinling [8] respectively combined PCA technology with BP neural networks, support vector machines (SVM), and extreme learning machines (ELM). The gas emission is predicted, and the prediction results show that the PCA data dimensionality reduction technology can improve the prediction accuracy and speed. In 2014, Xiang [9] proposed a coal mine gas concentration prediction model that combines wavelet transform and an extreme learning machine (ELM), which can realize one-step or multi-step advance prediction. However, the above models still have limitations: for example, the BP neural network is easy to fall into the local optimal solution, and the generalization ability is poor. The number of ELM hidden layer nodes has a great influence on the prediction effect, and improper selection will affect the prediction results. The choice of parameters and kernel functions is more sensitive. In 2022, Chen Qian [10] used the LASSO regression algorithm for the first time to predict the gas emission in the mining face, which showed that the LASSO regression algorithm was significantly better than the principal component analysis regression model. In 2023, Song [11] proposed a mine working face gas concentration prediction model based on LASSO-RNN by combining the Least Absolute Shrinkage and Selection Operator (LASSO) with the Recurrent Neural Network (RNN), showing that the LASSO effectively alleviates the problems of RNN overfitting and computational overhead.

In view of this, this paper proposes a gas emission prediction model that combines the Least Absolute Shrinkage and Selection Operator (LASSO), the Whale Optimization Algorithm (WOA), and Extreme Gradient Boosting (XGBoost). LASSO technology is used to select important factors affecting gas emission. This method ensures the preservation of the original data characteristics while simplifying the sample set. It leverages WOA to optimize XGBoost parameters, leading to the construction of a LASSO-WOA-XGBoost gas emission prediction model that enhances recovery. As a result, we introduce a novel approach for gas emission prediction at the working face.

2. Research Methods and LASSO-WOA-XGBoost Prediction Model Construction

2.1. LASSO Algorithm

The Least Absolute Shrinkage and Selection Operator (LASSO) was proposed by Robert Tibshirani in 1996 [12]. The feature selection of the LASSO algorithm is to remove irrelevant or redundant features from the original feature space and select an optimal feature subset. It is now widely used in various regression prediction fields [13,14,15,16]. The objective function of the LASSO algorithm Ǫ(β) is as follows:

$$Q(\beta )={\Vert Y_n-X_n\beta \Vert }^2+\lambda \Vert \beta \Vert$$

(1)

In Equation (1), the X_n dependent variable is a matrix, Y_n is an independent variable matrix, β is a coefficient matrix, and λ is a regularization parameter.

2.2. WOA Algorithm

Whale Optimization Algorithm (WOA) is a new heuristic optimization algorithm proposed by Mirjalili and Lewis in 2016 inspired by humpback whale predation behavior [17]. Compared with the Firefly Algorithm (FA) [18], the Fruit Fly Optimization Algorithm (FOA) [19] Particle Swarm Optimization (PSO) [20] WOA is more competitive in avoiding local optima in mathematical optimization and engineering optimization problems because of its power and better search ability [21,22,23].

When humpback whales hunt their prey, they will shrink to surround or swim towards the prey in a spiral form. The probability of the two ways happening is 50%. The mathematical model is described as follows:

$$\overrightarrow{X}(t+1)=\{\begin{array}{l}{\overrightarrow{X}}^{*}(t)-\overrightarrow{A}\cdot \overrightarrow{D}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}p<0.5\\ {\overrightarrow{X}}^{*}(t)+{\overrightarrow{D}}^{\prime }\cdot e^{bl}\cdot \cos (2\pi l)\hspace{1em}p\ge 0.5\end{array}$$

(2)

When p < 0.5 and $\left|\overrightarrow{A}\right|$ < 1, the individual whale updates its position according to the contraction and encirclement method. The mathematical model is described as follows:

$$\{\begin{array}{l}\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}^{*}(t)-\overrightarrow{A}\cdot \overrightarrow{D}\hfill \\ \overrightarrow{D}=\left|\overrightarrow{C}\cdot {\overrightarrow{X}}^{*}(t)-\overrightarrow{X}(t)\right|\hfill \\ \overrightarrow{A}=2\overrightarrow{a}\cdot {\overrightarrow{r}}_1-\overrightarrow{a}\hfill \\ \overrightarrow{C}=2\cdot {\overrightarrow{r}}_2\hfill \\ \overrightarrow{a}=2-2t/t_{max}\hfill \end{array}$$

(3)

In Equation (3): $\overrightarrow{X}$(t) and $\overrightarrow{X}$*(t) are the current individual and the global optimal individual position, $\overrightarrow{A}$ and $\overrightarrow{C}$ are coefficient vectors, $\overrightarrow{D}$ is the distance between the current whale individual and the optimal individual, $\overrightarrow{a}$ is the convergence factor, $\overrightarrow{r}$₁ and $\overrightarrow{r}$₂ are random numbers in [0, 1], t and t_max are the current and maximum iteration times.

When p ≥ 0.5, the individual whale updates its position in a spiral manner, and the mathematical model is described as follows:

$$\{\begin{array}{l}\overrightarrow{X}(t+1)={\overrightarrow{X}}^{*}(t)+{\overrightarrow{D}}^{\prime }\cdot e^{bl}\cdot \cos (2\pi l)\hfill \\ \begin{array}{l}{\overrightarrow{D}}^{\prime }=\left|{\overrightarrow{X}}^{*}(t)-\overrightarrow{X}(t)\right|\hfill \end{array}\hfill \end{array}$$

(4)

In Equation (4): ${\overrightarrow{D}}^{\prime }$ is the distance between the current optimal individual and other individuals, b is the logarithmic spiral constant, and l is a random number between [–1, 1].

When p < 0.5 and $\left|\overrightarrow{A}\right|$ ≥ 1, the individual whale randomly selects a whale individual from the current whale group to approach. This random selection avoids local optima. The mathematical model is described as follows:

$$\{\begin{array}{l}\overrightarrow{X}(t+1)={\overrightarrow{X}}_{{}^{rand}}(t)-\overrightarrow{A}\cdot \overrightarrow{D}\hfill \\ \overrightarrow{D}=\left|\overrightarrow{C}\cdot {\overrightarrow{X}}_{{}^{rand}}(t)-\overrightarrow{X}(t)\right|\hfill \end{array}$$

(5)

In Equation (5): $\overrightarrow{X}$_rand(t) is the random whale individual position in the current whale population.

2.3. XGBoost Algorithm

Extreme gradient boosting (eXtreme Gradient Boosting, XGBoost) is an efficient algorithm optimized on the basis of the gradient boosting iterative decision tree (GBDT) algorithm. The objective function is optimized by continuously adding new decision trees. Each tree is trained in sequence based on the residual of the previous tree. Every time a tree is added, the value of the loss function will continue to decrease. The prediction made by the model and the real value The smaller the deviation [24]; therefore, the XGBoost algorithm is widely used in wind power forecasting [25], wildfire disaster risk forecasting [26], stock forecasting [27], and other fields [28,29].

The objective function L(ϕ) of XGBoost includes two parts: the loss function and the constraint regularization term. The loss function indicates the degree to which the model fits the data, and the constraint regularization term is a penalty mechanism to prevent the model from overfitting.

$$L(\varphi )={\displaystyle \sum _{i=1}^{n}l\left({\widehat{y}}_i,y_i\right)}+{\displaystyle \sum _{k=1}^k\mathrm{\Omega }\left(f_k\right)}$$

(6)

$$\mathrm{\Omega }\left(f_k\right)=\gamma T+\frac{1}{2}\lambda {\Vert \omega \Vert }^2$$

(7)

In Equations (6) and (7), ŷ_i is the predicted value of sample x_i, y_i is the real value, k is the number of subtrees, f_k is the output value of the kth subtree, Ω(f_k) is the regular term of the kth tree, γ, λ is the hyperparameter, T is the number of leaf nodes of the tree, ω is the leaf node value, and l(ŷ_i, y_i) is the training error of the sample x_i.

$${\widehat{y}}_i{}^{\left(t\right)}={\displaystyle \sum _{k=1}^t{f}_k}\left(x_i\right)={\widehat{y}}_i{}^{\left(t-1\right)}+f_t\left(x_i\right)$$

(8)

$${\displaystyle \sum _{k=1}^k\mathrm{\Omega }\left(f_k\right)}={\displaystyle \sum _{k=1}^{\mathrm{t}-1}\mathrm{\Omega }\left(f_k\right)}+\mathrm{\Omega }\left(f_t\right)$$

(9)

At the tth time, the objective function L^(t) is:

$$L^{\left(t\right)}={\displaystyle \sum _{i=1}^{n}l\left(y_i,{\widehat{y}}_i{}^{\left(t-1\right)}+f_t\left(x_i\right)\right)}+\mathrm{\Omega }\left(f_t\right)$$

(10)

When the structure of the optimal tree is determined, the objective function L^(t) is expanded through the second-order Taylor to obtain the optimal weight and the optimal objective function value on each leaf.

2.4. Construction of the LASSO-WOA-XGBoost Gas Emission Prediction Model

The model construction process is shown in Figure 1.

The idea of model construction is as follows:

(1) Gas emission data preprocessing. Feature selection is performed on the factors affecting gas emission through LASSO, and the data set after feature selection is divided into a training set and a test set.

(2) The optimal parameter combination of XGBoost is determined. Set the optimization range of the parameter values to be determined in XGBoost, and use WOA to adjust the parameters to determine the optimal parameter combination.

(3) XGBoost prediction model training. According to the optimal parameter combination determined in step (2), set the XGBoost parameter value and use the preprocessed training set in step (1) to train the LASSO-WOA-XGBoost prediction model.

(4) Gas emission forecast. Input the preprocessed test set in step (1) into the LASSO-WOA-XGBoost prediction model trained in step (3), and output the prediction results and regression model evaluation indicators.

The data on gas emission volume collected through the coal mine working face monitoring system was used as the research object, and predictive analysis was performed on the basis of maintaining the authenticity and integrity of the data as much as possible, achieving refined analysis of the gas emission data, which has important practical significance for strengthening the safety management of coal mine ventilation and improving the level of gas disaster prevention and control.

3. Application of the LASSO-WOA-XGBoost Gas Prediction Model

3.1. Sample Data Acquisition and Sample Data Correlation Analysis

Regarding the main natural factors and mining factors that affect the amount of gas eruption, the following principles should be followed when selecting influencing factors: (1) The value of the influencing factor is relatively stable; (2) The consistency of the influencing factor does not change with time; (3) The comprehensiveness and breadth of the influencing factors, fully covering the various factors that have a greater impact on gas emission, (4) The refinement of the influencing factors; under the premise of sufficient coverage, the number of influencing factors should be as small as possible to improve practical operability and reduce complexity; (5) Influencing factors can be quantified and analyzed. Referring to the above principles for selecting influencing factors and then referring to the theory of the separate source prediction method, this paper selected 13 factors that influence the gas emission amount of coal seams during coal mine working face mining. On the premise that the influencing factors have been selected, a prediction model for gas emission is established.

The sample data are the monitoring data of 30 groups of mining face gas emission in Qianjiaying Coal Mine [30]. X1 is the excavation depths (m), X2 is the coal seam thickness (m), X3 is the dip angle of coal seam (°), X4 is the original gas content of mining layer (m³∙t⁻¹), X5 is the coal seam spacing (m), X6 is the height mining (m), X7 is the gas content of adjacent layer (m³∙t⁻¹), X8 is the adjacent layer thickness (m), X9 is the interburden rock properties (m), X10 is the face length (m), X11 is the mining velocity (m∙d⁻¹), X12 is recovery rate (%), X13 is daily output (t∙d⁻¹), Y is gas emission (m³∙min⁻¹), where X1–X13 are 13 influencing factors of gas emission and Y is the gas emission quantity. The specific data are shown in

Table 1. Data set of gas emission and influencing factors in the working face.

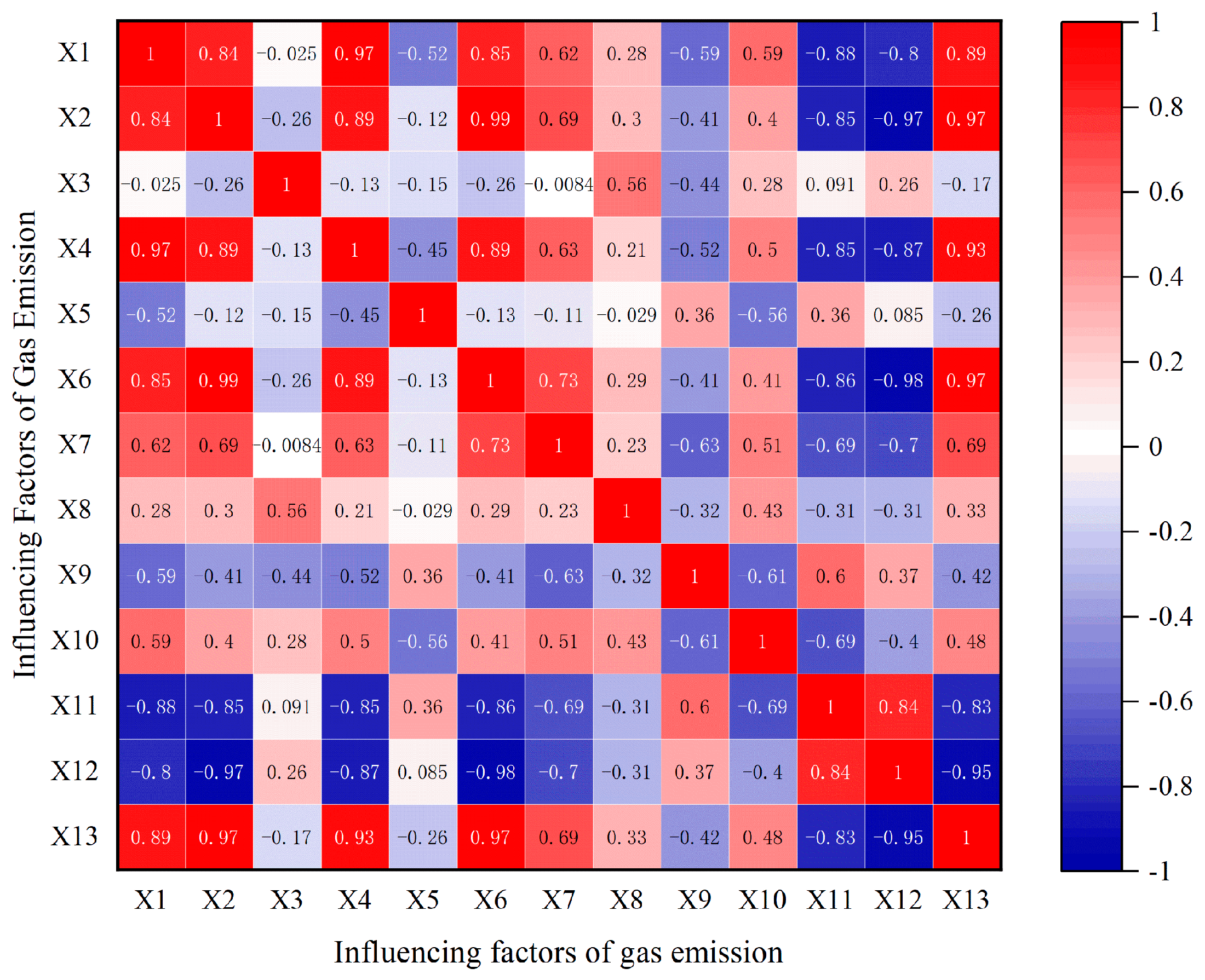
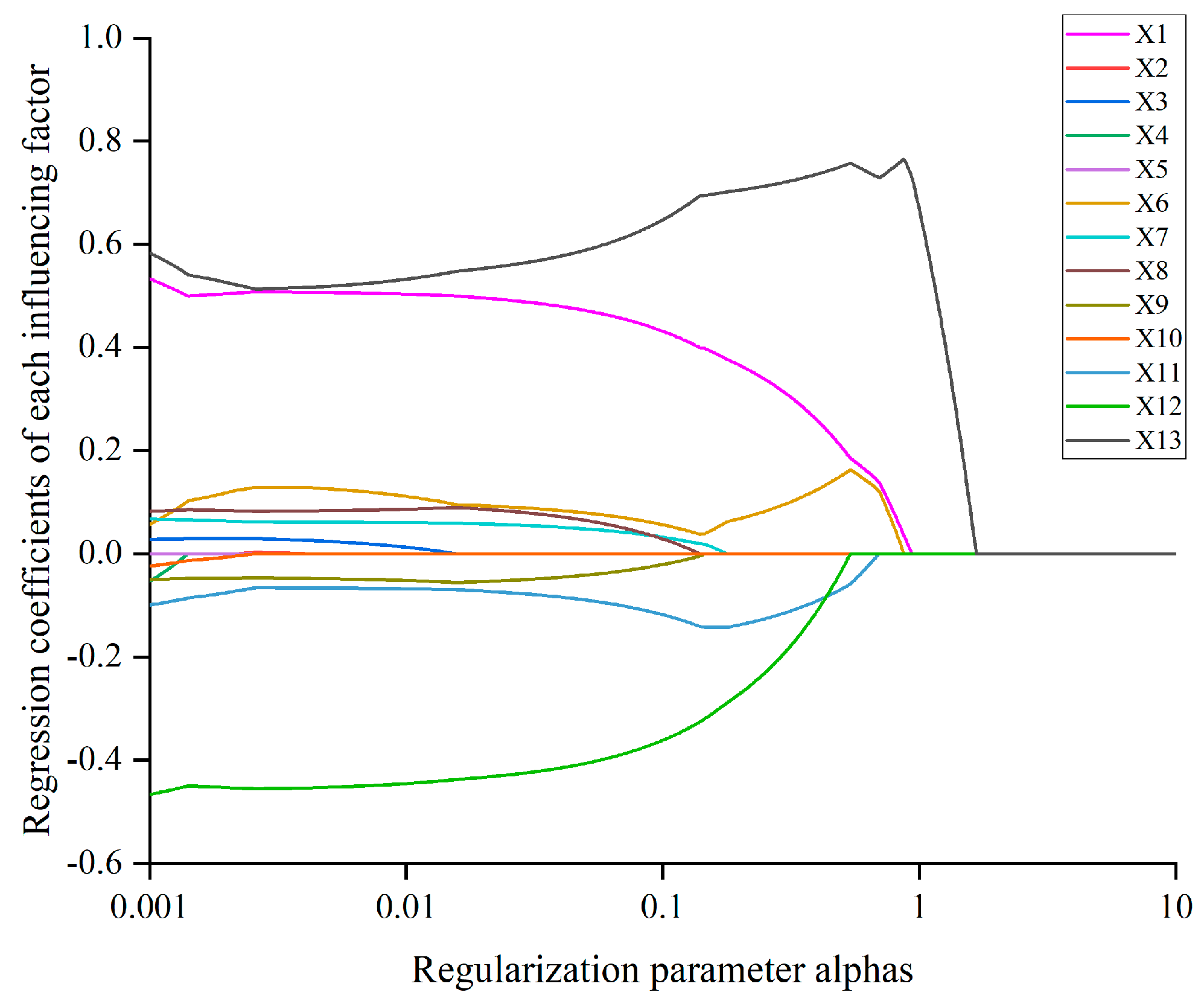
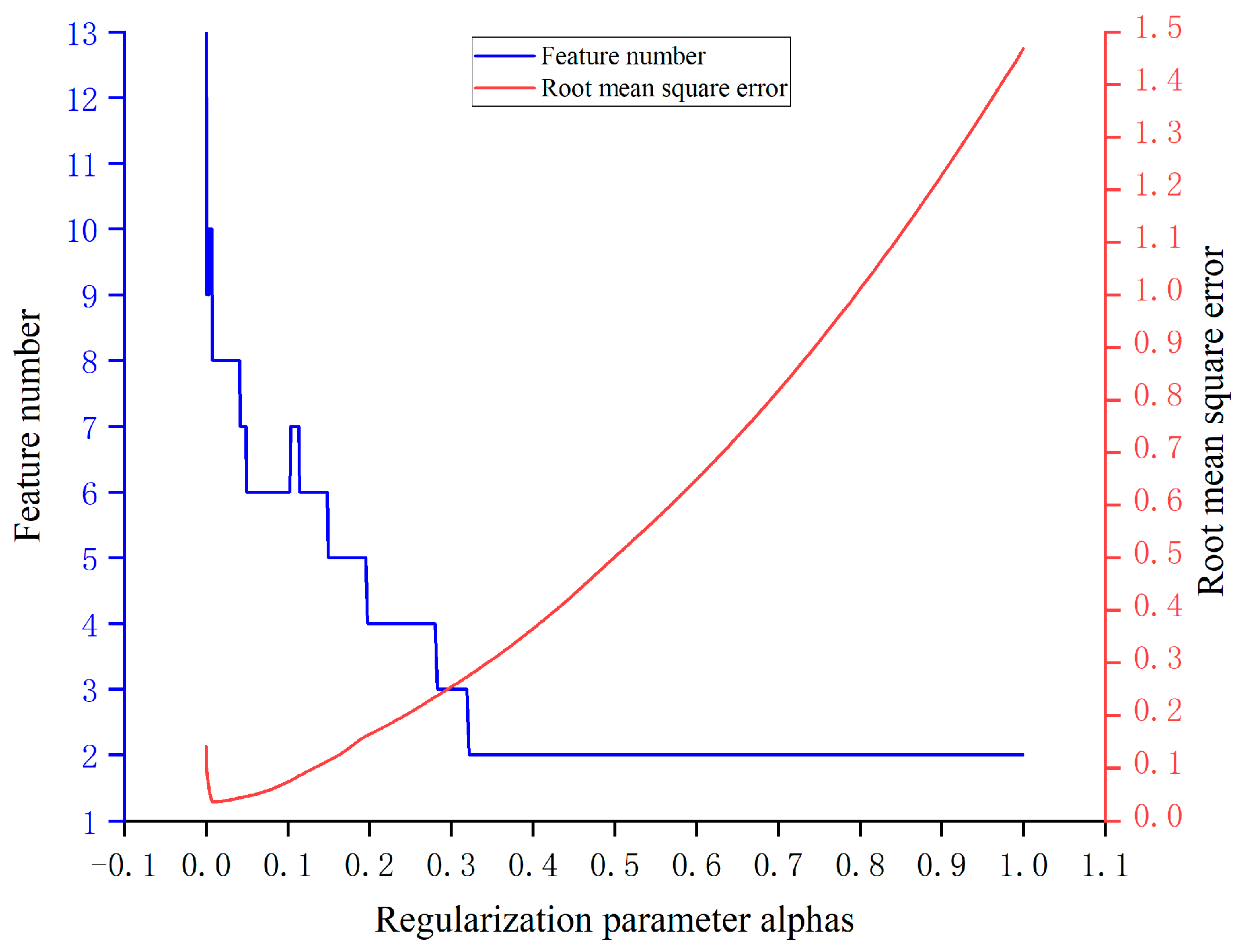
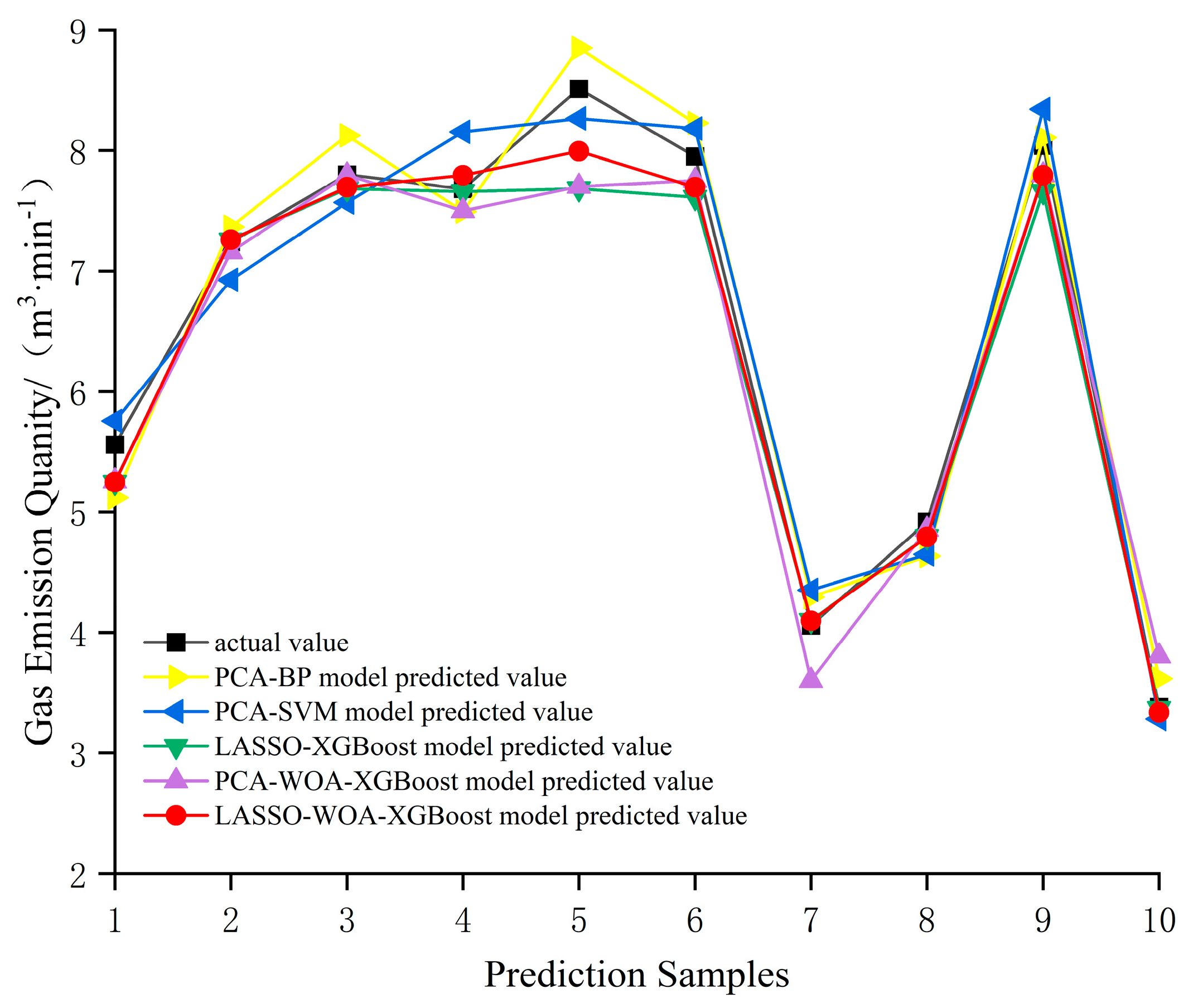
Number	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X10	X12	X13	Y
1	412	2.5	8	2.12	24	2.0	2.1	1.53	4.78	140	4.16	0.960	1 528	2.91
2	423	1.5	11	2.14	17	1.4	2.55	1.62	4.75	180	4.14	0.950	1 751	3.52
3	436	2.3	10	2.53	14	2.2	2.40	1.48	4.91	145	4.67	0.945	2 074	3.62
4	459	2.4	15	2.45	24	2.3	2.42	1.78	4.75	155	4.57	0.944	2 104	4.13
5	511	2.8	13	3.24	14	2.4	2.21	1.72	4.78	180	3.45	0.930	2 241	4.60
6	515	2.3	17	2.85	17	2.5	2.77	1.87	4.51	170	3.25	0.940	1 973	4.94
7	556	2.7	9	3.37	13	2.5	1.88	1.42	4.85	165	3.68	0.932	2 287	4.78
8	550	3.1	12	3.67	15	2.9	2.32	1.65	4.83	155	4.01	0.920	2 352	5.25
9	590	3.0	11	3.68	12	3.6	3.11	1.46	4.53	175	3.53	0.940	2 410	5.26
10	581	5.2	8	4.31	17	5.9	3.47	1.57	4.76	170	2.80	0.797	3 131	7.26
11	611	6.7	9	4.05	16	6.7	3.15	1.80	4.70	175	2.64	0.812	3 354	7.80
12	408	2.0	10	1.92	20	2.0	2.02	1.50	5.03	155	4.42	0.960	1 825	3.34
13	411	2.0	8	2.15	22	2.0	2.10	1.21	4.87	140	4.16	0.950	1 527	2.94
14	420	1.8	11	2.14	19	1.8	2.64	1.62	4.75	175	4.13	0.950	1 751	3.56
15	432	2.3	10	2.58	17	2.3	2.40	1.48	4.91	145	4.67	0.950	2 078	3.62
16	456	2.2	15	2.40	20	2.2	2.55	1.75	4.63	160	4.51	0.940	2 104	4.17
17	516	2.8	13	3.22	12	2.8	2.21	1.72	4.78	180	3.45	0.930	2 242	4.60
18	527	2.5	17	2.80	11	2.5	2.81	1.81	4.51	180	3.28	0.940	1 979	4.92
19	531	2.9	9	3.35	13	2.9	1.88	1.42	4.82	165	3.68	0.930	2 288	4.78
20	550	2.9	12	3.61	14	2.9	2.12	1.60	4.83	155	4.02	0.920	2 352	5.23
21	563	3	11	3.68	12	3.0	3.11	1.46	4.53	175	3.53	0.940	2 410	5.56
22	590	5.9	8	4.21	18	5.9	3.40	1.50	4.77	170	2.85	0.795	3 139	7.24
23	604	6.2	9	4.03	16	6.2	3.15	1.80	4.70	180	2.64	0.812	3 354	7.80
24	607	6.1	9	4.34	17	6.1	3.02	1.74	4.62	165	2.77	0.785	3 087	7.68
25	634	6.5	12	4.80	15	6.5	2.98	1.92	4.55	175	2.92	0.773	3 620	8.51
26	640	6.3	11	4.67	15	6.3	2.56	1.75	4.60	175	2.75	0.802	3 412	7.95
27	450	2.2	12	2.43	16	2.2	2.00	1.70	4.84	160	4.32	0.950	1 996	4.06
28	544	2.7	11	3.16	13	2.7	2.30	1.80	4.90	165	3.81	0.930	2 207	4.92
29	629	6.4	13	4.62	19	6.4	3.35	1.61	4.63	170	2.80	0.803	3 456	8.04
30	401	2.0	10	1.87	25	2.4	2.14	1.78	5.12	150	4.52	0.950	1 855	3.38

.

The Pearson correlation coefficient method was used to conduct correlation analysis on the 13 influencing factors of gas emission and generate a correlation heat map, as shown in Figure 2. The color of the heat map data grid represents the correlation between various influencing factors. Red indicates a positive correlation, blue indicates a negative correlation, and the darker the color, the stronger the correlation. It can be seen from Figure 2 that there is a strong correlation among multiple influencing factors, and it is suitable to use the LASSO algorithm for feature selection.

3.2. LASSO Algorithm Screening Factors

When predicting the amount of gas emission, there are many factors affecting the amount of gas emission. If all factors are directly substituted into the prediction model, the complexity of the model will be too high, which will affect the accuracy of the model [31]. Therefore, in order to reduce the complexity of the model, the LASSO algorithm is used to select the features of 13 factors that affect gas emission.

First, z-score normalization is performed on the data set (X1–X13) of factors affecting gas emission, and then LASSO is used for feature selection. The regression coefficients of the 13 feature factors vary with the regularization parameter alphas, as shown in Figure 3. It can be seen from Figure 3 that as the value of the regularization parameter alphas gradually increases, the regression coefficients of some features tend to zero, indicating that these The correlation between the feature (factors affecting gas emission) and the target variable (gas emission Y) is weak and can be eliminated.

In order to determine the optimal alpha value, the root mean square error (RMSE) and the corresponding number of features under different alpha values were calculated through ten-fold cross-validation. The results are shown in Figure 4. It can be seen in Figure 4. When the value of the regularization parameter alphas is 0.0152, the root mean square error value is the smallest. At this time, the regression coefficients of four influencing factors (X2, X4, X5, X10) converge to 0, indicating that these four feature variables do not contribute positively to model training, so these four feature variables are eliminated. Reduce the 13 influencing factors for gas emission to 9.

LASSO was used for feature selection to screen out mining depth (X1), dip angle of coal seam (X3), height mining (X6), gas content of adjacent layer (X7), adjacent layer thickness (X8), interburden rock properties (X9), mining velocity (X11), recovery rate (X12), and daily output (X13), which are nine factors that have a greater impact on the amount of gas emission. The results of the regression coefficient values for each factor are shown in

Table 2. The regression coefficient value of each feature after LASSO feature selection.

Influencing Factors	LASSO Regression Coefficient	Influencing Factors	LASSO Regression Coefficient
X1	0.5004	X8	0.0889
X2	0.0000	X9	−0.0548
X3	0.0025	X10	0.0000
X4	0.0000	X11	−0.0692
X5	0.0000	X12	−0.4392
X6	0.0984	X13	0.5444
X7	0.0595

. The first 20 groups of the data set after feature selection are used as the training set, and the last 10 groups are used as the test set. See

Table 3. Dataset of gas emission and influencing factors after LASSO feature selection (training set).

Number	X1	X3	X6	X7	X8	X9	X11	X12	X13	Y
1	412	8	2.0	2.1	1.53	4.78	4.16	0.96	1 528	2.91
2	423	11	1.4	2.55	1.62	4.75	4.14	0.95	1 751	3.52
3	436	10	2.2	2.40	1.48	4.91	4.67	0.945	2 074	3.62
4	459	15	2.3	2.42	1.78	4.75	4.57	0.944	2 104	4.13
5	511	13	2.4	2.21	1.72	4.78	3.45	0.93	2 241	4.60
6	515	17	2.5	2.77	1.87	4.51	3.25	0.94	1 973	4.94
7	556	9	2.5	1.88	1.42	4.85	3.68	0.932	2 287	4.78
8	550	12	2.9	2.32	1.65	4.83	4.01	0.92	2 352	5.25
9	590	11	3.6	3.11	1.46	4.53	3.53	0.94	2 410	5.26
10	581	8	5.9	3.47	1.57	4.76	2.80	0.797	3 131	7.26
11	611	9	6.7	3.15	1.80	4.70	2.64	0.812	3 354	7.80
12	408	10	2.0	2.02	1.50	5.03	4.42	0.96	1 825	3.34
13	411	8	2.0	2.10	1.21	4.87	4.16	0.95	1 527	2.94
14	420	11	1.8	2.64	1.62	4.75	4.13	0.95	1 751	3.56
15	432	10	2.3	2.40	1.48	4.91	4.67	0.95	2 078	3.62
16	456	15	2.2	2.55	1.75	4.63	4.51	0.94	2 104	4.17
17	516	13	2.8	2.21	1.72	4.78	3.45	0.93	2 242	4.60
18	527	17	2.5	2.81	1.81	4.51	3.28	0.94	1 979	4.92
19	531	9	2.9	1.88	1.42	4.82	3.68	0.93	2 288	4.78
20	550	12	2.9	2.12	1.60	4.83	4.02	0.92	2 352	5.23

and

Table 4. Gas emission volume and influencing factors data set after LASSO feature selection (test set).

Number	X1	X3	X6	X7	X8	X9	X11	X12	X13	Y
1	563	11	3.0	3.11	1.46	4.53	3.53	0.94	2 410	5.56
2	590	8	5.9	3.4.0	1.50	4.77	2.85	0.795	3 139	7.24
3	604	9	6.2	3.15	1.80	4.70	2.64	0.812	3 354	7.80
4	607	9	6.1	3.02	1.74	4.62	2.77	0.785	3 087	7.68
5	634	12	6.5	2.98	1.92	4.55	2.92	0.773	3 620	8.51
6	640	11	6.3	2.56	1.75	4.60	2.75	0.802	3 412	7.95
7	450	12	2.2	2.00	1.70	4.84	4.32	0.95	1 996	4.06
8	544	11	2.7	2.30	1.80	4.90	3.81	0.93	2 207	4.92
9	629	13	6.4	3.35	1.61	4.63	2.80	0.803	3 456	8.04
10	401	10	2.4	2.14	1.78	5.12	4.52	0.95	1 855	3.38

, respectively, for training and prediction of the continued model.

3.3. Optimization Settings of the Main Parameters of the XGBoost Algorithm

The XGBoost algorithm model contains a large number of parameters, and default values are usually used, but for specific data sets and problems, optimizing model parameters can improve the prediction effect of the model. This paper chooses WOA to optimize the three main parameters in the XGBoost algorithm. The specific parameter settings are shown in

Table 5. WOA-XGBoost model parameter settings.

Parameter Name	Defaults	WOA Optimized Values	Ranges	Parameter Meaning
n_estimators	100	464	[1, 500]	number of trees
learning_rate	0.1	0.2869	[0, 1]	learning rate
max_depth	6	8	[1, 10]	tree depth

.

3.4. LASSO-WOA-XGBoost Model Prediction Analysis Comparison

The PCA-BP, PCA-SVM, LASSO-XGBoost, PCA-WOA-XGBoost, and LASSO-WOA-XGBoost prediction models were respectively established. The PCA-BP model uses 3 principal components after PCA dimensionality reduction instead of the original 13. The influencing factors of gas emission are input into the BP model for prediction; the PCA-SVM model uses the 3 principal components after PCA dimensionality reduction to replace the original 13 influencing factors of gas emission, and is input into the SVM model for prediction. The LASSO-XGBoost model is input from the data set after LASSO feature selection into the XGBoost model for prediction, and XGBoost uses default parameters. The PCA-WOA-XGBoost model uses the 3 principal components after PCA dimensionality reduction to replace the original 13 gas emission factors, which are input into the XGBoost after parameter tuning by WOA for prediction. LASSO-WOA-XGBoost. The prediction model is that the data set after LASSO feature selection is input into XGBoost after parameter tuning by WOA for prediction. The prediction results of the five models are shown in Figure 5.

In order to further verify the prediction effect of the LASSO-WOA-XGBoost model on gas emission, two evaluation indexes, mean absolute error (MAE) and root mean square error (RMSE), were selected to compare the five prediction models. The lower the MAE and RMSE, the higher the accuracy of model predictions. The comparison of the evaluation index results of the five prediction models is shown in

Table 6. Comparison of the evaluation index results of the three prediction models.

Model Name	Mean Absolute Error (MAE)	Root Mean Square Error (RMSE)
PCA-BP	0.2518	0.2721
PCA-SVM	0.26555	0.2810
LASSO-XGBoost	0.2191	0.3278
PCA-WOA-XGBoost	0.2767	0.3575
LASSO-WOA-XGBoost	0.1775	0.2697

.

As can be seen from Table 6, the LASSO-WOA-XGBoost model optimized through WOA parameter adjustment has higher prediction accuracy than the LASSO-XGBoost model. Compared with PCA-WOA-XGBoost, the prediction accuracy of the LASSO-WOA-XGBoost model constructed after LASSO feature selection is higher, indicating that LASSO feature selection has more advantages than PCA dimensionality reduction in gas emission prediction. The mean absolute error of the LASSO-WOA-XGBoost prediction model is 0.1775, and the root mean square error is 0.2697. Compared with the other two prediction models, the LASSO-WOA-XGBoost model has the lowest MAE and RMSE and the best prediction effect.

4. Conclusions

(1) LASSO is used to select the factors affecting gas emission, and the optimal regularization parameters are determined by ten-fold cross-validation. It shows that when the regularization parameter alphas = 0.0152, the 13 factors affecting gas emission can be reduced to 9, which simplifies the data set and reduces the model training time.

(2) The three main parameters in XGBoost are optimized by the WOA algorithm, and the optimal parameter combination is determined. The results show that when the parameter combination values are n_estimators = 464, learning_rate = 0.2859, and max_depth = 8, the prediction accuracy of the XGBoost model is higher.

(3) Through the comparative analysis of the prediction results of the LASSO-XGBoost, PCA-WOA-XGBoost, and LASSO-WOA-XGBoost models, it can be seen that LASSO feature selection has more advantages than PCA dimensionality reduction in the gas emission prediction model. The mean absolute error of the LASSO-WOA-XGBoost prediction model is 0.1775, and the root mean square error is 0.2697, which is the same as other models. Compared with the four prediction models, the LASSO-WOA-XGBoost prediction model reduced the mean absolute error by 7.43%, 8.81%, 4.16%, and 9.92%, respectively, and the root mean square error was reduced by 0.24%, 1.13%, 5.81%, and 8.78%. Compared with the other four prediction models, this model has the lowest MAE and RMSE and the best prediction effect.