Abstract
Due to climate change, extreme temperature events are receiving increased attention. Based on the climate state deviation and threat score (TS), the ability of the Global/Regional Assimilation and Prediction System (GRAPES) ensemble model to forecast extreme temperature events was examined. The “optimal” Extreme Forecast Index (EFI) was derived for plateau forecasting, and its predictability was examined based on the receiver operating characteristic (ROC) curve method. Meanwhile, the applicability of the Shift of Tails (SOT) index to extreme temperature forecasting was analyzed using extreme temperature cases. Results showed that the GRAPES model has a warm bias for both summer extreme high temperature and winter extreme low temperature, and the warm bias decreases slightly with an increase in the forecasting lead time. The ensemble mean and median forecasts are less effective, and the maximum value is more predictable. However, for the ensemble forecast model, the extreme information in its forecast is more unstable, and the limitation of the extreme temperature forecast in the plateau region is higher. With different forecast lead times, the TS tends to increase and then decrease with an increase in the EFI threshold, which means that there is an optimal EFI. The optimal EFI thresholds for summer extreme high-temperature forecasts are all less than −0.5, while for winter extreme low-temperature forecasts, they are almost all less than 0. From the ROC curves, the EFI has a certain level of predictability for summer extreme high temperatures but poorer forecasting effects. Furthermore, the EFI has some predictability for extreme summer high temperatures, but the prediction effect is poor. For the extremely low temperatures in winter, which are poorly predicted by the model itself, post-processing of the extreme information predicted by the model with the EFI can improve the forecasting effect of the model. Through analysis of individual cases, it was found that the extreme intensity reflected by the SOT_+ (0.9) index of the model was closer to reality for the prediction of extremely high temperatures, whereas for the prediction of extremely low temperatures, the extreme intensity indicated by the SOT_− (0.1) index of the model was weaker. Therefore, the SOT index can play an important auxiliary role in the prediction of the intensity of extreme events based on the EFI.
1. Introduction
Extreme weather is defined as small-probability events in which the value of a weather variable is above (or below) a certain upper (lower) threshold within the range of values of the observed variable, and the probability of occurrence is generally less than 10% [1,2,3]. The extreme temperature thresholds in the Qinghai–Tibet plateau region are significantly affected by the terrain. Therefore, to analyze extreme temperatures in this region, the introduction of the concept of relative thresholds is particularly important. Therefore, the 10th and 90th percentiles of climate states are defined as thresholds for extremely low and extremely high temperatures. In recent decades, extreme weather events (torrential rain, heat waves, cold waves, etc.) have been occurring more frequently because of climate change. The economic losses and social impacts caused by such events are huge [4]. The Qinghai–Tibet plateau is in the transitional region between arid Northwest China, the Qinghai–Tibet alpine region, and the eastern monsoon region. It is affected by the East Asian monsoon, southwest monsoon, and plateau monsoon and is a sensitive and vulnerable area for climate change in China [5,6,7,8]. Extreme climate events and their changes in the plateau region have unique characteristics [9] and play an important role in environmental changes in Asia and even the Northern Hemisphere as a whole [10,11]. The intensity and frequency of extreme warm events on the plateau have increased in recent years [12,13,14], and the impacts on regional temperature extremes on the plateau have been associated with multiscale temperature variability [11] and climate change [15]. Clearly, the influencing factors are complex, and therefore, research about forecasting methods of extreme temperature in the plateau is urgently needed.
Many studies have been carried out regarding extreme weather, such as using “natural time” instead of “conventional clock time” in forecasting extreme weather, which not only made an excellent achievement in air pollution but also in El Nino [16,17] and also many studies regarding the extreme temperatures over the Tibetan plateau have been carried out, all of which have shown that predicting Tibetan plateau extreme weather is difficult [18,19,20]. All of them have made a great contribution to forecasting the extreme temperatures over the Tibetan plateau. However, for extreme weather events with low probability and high levels of uncertainty in terms of development, the use of numerical weather models with a single initial value to predict them is far from sufficient. Instead, it is necessary to introduce the concept of ensemble forecasting. As an important direction in the development of numerical forecasting, ensemble forecasting can take into account the uncertainty of initial values and models, and its results reflect various possible changes in future weather conditions, which can provide forecasters with probabilistic information that single deterministic forecasts cannot provide (such as the credibility of the forecast results) [21,22,23,24,25,26]. The probabilistic forecast results provided by this approach can give information on the possibility of extreme events occurring in the future and have better forecasting effects on extreme weather events. Therefore, the method has become an important tool for extreme weather forecasting. However, currently, China’s ability to forecast extreme weather is still relatively weak, and relevant research is urgently needed. With continuous improvements in the numerical prediction of each forecast variable (temperature, precipitation etc.), as well as the ensemble forecast system, forecasters hope to issue early-warning signals for extreme weather. However, it is difficult to achieve this by simply comparing the differences between observations of local meteorological variables and direct forecasts from models [27]. Accordingly, Lalaurette [28,29] used the European Center for Medium-Range Weather Forecasts (ECMWF) ensemble forecasting to develop an extreme weather forecasting method—the Extreme Forecast Index (EFI)—to measure the continuous difference between the ensemble forecast cumulative probability distribution function and the model climate state, as well as sum the difference between the climate state distribution and the forecast distribution. This index has been used by ECMWF and shown to be very useful as an early-warning indicator of extreme events [30,31].
To further improve the EFI’s forecasting skill for extreme weather, as well as the ability of its ensemble prediction system to forecast such events, ECMWF uses the same model back-calculation data to update the “model climate” of the EFI and improve its calculation formula to be more sensitive to the information at both ends of the cumulative distribution function, and designed the Shift of Tails (SOT) index as a supplement to the EFI, which is used to indicate the probability of an extreme event relative to the climatological probability [32], thus enabling the forecasting of extreme weather to be further optimized [33,34,35].
In the present study, the Global/Regional Assimilation and Prediction System (GRAPES) ensemble forecast product, independently developed by China, was used to compare and analyze the effects of adopting different EFI and SOT index thresholds on the forecasting of extreme temperatures in China—especially the plateau region, where extreme temperature changes have indicative significance for China’s climate change. This work aimed to provide forecasters with an ensemble forecasting product that can extract extreme information in their operational work, therefore enabling them to be more confident in the release of early-warning signals of extreme weather.
2. Data and Methods
2.1. Data
This study used historical real-time 2-m temperature ensemble forecast data from January 2019 to December 2020 from GRAPES starting at 12:00 UTC. The schema contained 31 collection members, and the forecast lead times were 24 h, 48 h, 72 h, 96 h, 120 h, 144 h, 168 h, 192 h, 216 h, 240 h, 264 h, 288 h, 312 h, 336 h, and 360 h, spanning a total of 15 days.
Also employed was a 0.5° × 0.5° grid-point dataset of normalized daily temperature from national surface meteorological stations in China as the actual data to compare with the model results. The source of this dataset comprised two parts: (1) China’s National Surface Meteorological Station Normalized Temperature Daily Value Data Set (V1.0) developed by the National Meteorological Information Center and (2) the 2′ × 2′ digital elevation model of China’s land produced by ETOPO5 (Earth topography five-minute grid) Global Surface Relief. In addition, we selected the study area with a terrain height of more than 3000 m (Figure 1), for which the plateau boundary was based on the ETOPO5 data [36].
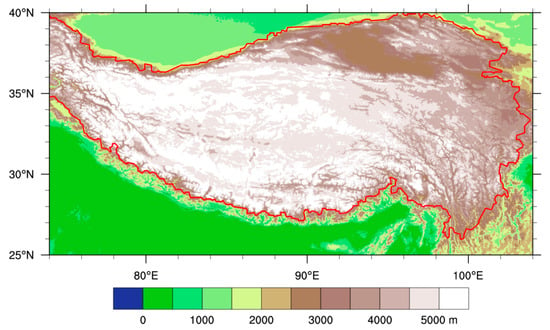
Figure 1.
Topographic map of the Qinghai–Tibet Plateau (unit: m), with the red contour marking the terrain height of 3000 m.
2.2. Methods
To calculate the observed climate percentile, historical data from 1991 to 2020 were used. The calculation date and live field with a sliding time window (7 d) of 3 days before and after the calculation was selected as the climate sequence for sorting in ascending order (the sequence length was 30 yr × 7 d grid points), with each percentile point (0.01, 0.02, …, 0.99, 1) corresponding to a threshold, i.e., the actual climate percentile distribution was a function of grid-point location and time. Due to the short duration of the schema data, there were only data for 2019–2020. However, the schema contained 31 collection members, so the climate percentile calculation of the model forecast field considered the use of multiple ensemble members to increase the number of samples (sequence length was 2 yr × 31 members × 7 d) based on the calculation of the actual field percentile, i.e., the model climate percentile distribution was a function of the grid location, the start time, and the forecast time. Among them, using the data of the model itself to calculate the climate state of the model can make the EFI/SOT index automatically eliminate the systematic deviation of the model, as well as make the extreme events represented by the EFI/SOT index highly correlated with the season. After completing the calculation of the observed and forecasted climatic states, the values corresponding to the 1–100 percentile points of each daily forecast timeliness for each grid point of the nationwide live field and model climate were output. At the beginning of the 21st century, the Intergovernmental Panel on Climate Change (IPCC) provided a clear definition of extreme weather in its third and fourth assessment reports [37,38]: extreme weather refers to weather events whose probability of occurrence is less than the 10th percentile of the observed probability density function or exceeds the 90th percentile. In this study, the variable values corresponding to the 10th/90th percentile of the defined climate series were the thresholds for extreme weather.
After continuous updating, the current EFI definition for ECMWF applications is [25]
where p is the probability and is the probability that the ensemble forecast is less than or equal to the “model climate” p-quantile. The weighting will make more sensitive to extreme values at both ends. The value of EFI is between −1 and 1, and the closer to −1 the index value, the more extreme and low the forecast event (e.g., extremely low temperature), while the closer the value to 1, the more extreme and high the forecast event (e.g., extreme high temperature or extreme heavy precipitation). When the EFI reaches 1 (−1), it means that all members of the ensemble prediction system forecast are larger (smaller) than the maximum (minimum) value of the model climate state.
Since the EFI integrates the probability of occurrence of different events, resulting in the “loss” of some information, the same EFI does not mean the same probability of an extreme event, so the SOT index is introduced, which is defined as follows:
These formulae represent the relative magnitudes of the quantiles of the ensemble forecast and the maximum and minimum values of the model climatology, representing extreme high and low situations. Among them, and are the maximum and minimum values of the model climate state, respectively, and and are the p-quantiles of the ensemble forecast and the model climate state, respectively. When the 90% quantile of the ensemble forecast () is greater (less than) the 90% quantile of the model climate state (), > −1 (or < −1); and when is greater than the maximum value of the model climate state, i.e., at least 10% of the members of the ensemble forecast are greater than the maximum value of the model climate state, . Essentially, when , it means that for 90% of quantile events of the model climate state, the ensemble forecast probability is greater than the climate probability, and there is a certain possibility of extreme events. The larger the value of , the more member forecasts of the ensemble forecast are greater than the maximum value of the model climate state, i.e., the greater the possibility of extreme events occurring. The case for is similar, indicating the possibility of extremely low-temperature events, so the steps are not repeated.
To be clear, there is a “-” in each forecast lead day in the paper. “-” indicates the meaning of the prediction of the model in advance relative to the test sample, rather than the forecast time, to distinguish between the two time variables.
3. Verification of the Model in Forecasting Extreme Temperatures over the Plateau
3.1. Comparative Analysis of Simulated and Real Climate Extreme Thresholds
It can be seen from Figure 2 that the overall temperature in the plateau area is relatively low, the monthly average temperature is between −12 °C and 11 °C, and the monthly variation in temperature presents a unimodal pattern, with high temperatures appearing in July and the lowest temperatures appearing in January. From the distribution of the frequency of extreme temperatures, the frequency of extreme high temperatures in plateau areas is significantly higher than that of extreme low temperatures. This may be due to the impact of global warming. For the plateau region, the occurrence frequency of extremely high temperatures shows an increasing trend after July until November, but it can be seen from the monthly average temperature changes that the temperature in the plateau area shows a monthly declining trend from August onwards. Therefore, June to August is selected as the research period for extremely high temperatures on the plateau. Looking at the monthly changes in the frequency of extremely low temperatures, they occur more often in two periods—namely October–February and April–May. Similarly, since the monthly average temperature in April–May is on the rise, combined with the trend of change in monthly average temperature, December–February is chosen to study extremely low temperatures.
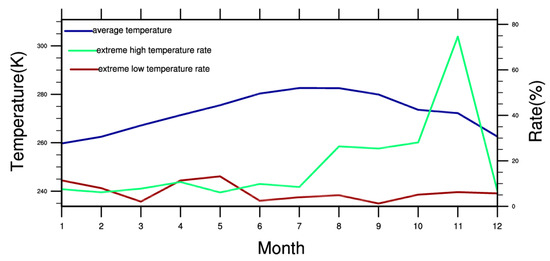
Figure 2.
Average monthly temperature and occurrence rate of extreme high/low temperatures in the plateau region.
The grid points with an altitude of more than 3000 m were selected as the geographical selection area of the plateau, and the 10th and 90th percentiles of the climate state as the thresholds of extremely low temperature and extremely high temperature to show the thresholds of extreme low temperature in December–February and extreme high temperature in June–September in the plateau area (as seen in Figure 3). The average extreme low-temperature threshold of the plateau from December to February presents a geographical distribution trend of low in the north and high in the south. The extreme low-temperature threshold of the Kunlun Mountains and Qilian Mountains in the northern part of the plateau is lower than −20 °C; that is, the topography has a more obvious impact on the average temperature in this area, and the extreme low-temperature threshold is lower, but for the high-terrain area in the southwest of the plateau, the extreme low-temperature threshold is higher than that in the north of the plateau. This is related to the data quality for high-altitude temperatures, which also shows that, for areas with high-altitude terrain, such as plateaus, there are greater challenges in terms of the performance of numerical models or the quality of data. Compared with other areas, the analysis of extreme temperatures requires the introduction of the concept of relative thresholds. Judging from the distribution of extreme high-temperature thresholds from June to September for the Tarim Basin and low-altitude areas south of the Hengduan Mountains, the extreme high-temperature thresholds are significantly higher than those in higher-altitude areas. Combined with the analysis of the distribution of extreme low-temperature thresholds, the extreme temperature thresholds in the Qinghai–Tibet plateau region are significantly affected by the terrain, and for the southern plateau region with higher altitudes, the distribution of extreme temperature thresholds is limited by the data quality. Therefore, to analyze extreme temperatures in this region, the introduction of the concept of relative thresholds is particularly important.
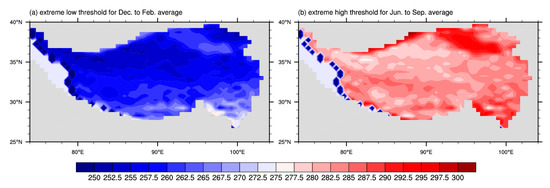
Figure 3.
Distribution of (a) extremely low-temperature thresholds from December to February and (b) extremely high-temperature thresholds from June to September in the plateau region (unit: K).
3.2. Error Analysis of the Model Climatic State
For the subsequent calculation of the extreme forecast-related indices (i.e., the EFI and SOT index), the matching degree between the model climate state and the historical climate state is crucial, which directly determines the accuracy of the EFI and SOT index. In addition, a comparative analysis of the model climate state and the historical climate state can also test the systematic deviation of the model.
To test the climate percentile of 2-m temperature in summer, we chose July as a representative for analysis. From Figure 4, we can see from the model deviation for the actual temperature below the 50th percentile that the climatological curves of each lead time are located near the actual climatological curves; that is, the forecast effect of the model on the percentile is better, but the climatological curves under each forecast period are scattered, and the forecast stability of the model is poor. Meanwhile, for temperatures above the 50th percentile, the climate percentile of the model has a certain degree of warm bias, and the climatological curves under each lead time are relatively concentrated; that is, the forecast stability of the model is relatively high. However, for the extremely high temperatures that we are more concerned about in summer, the warm bias of the model is more obvious, and the warm bias decreases slightly with the increase in lead time.
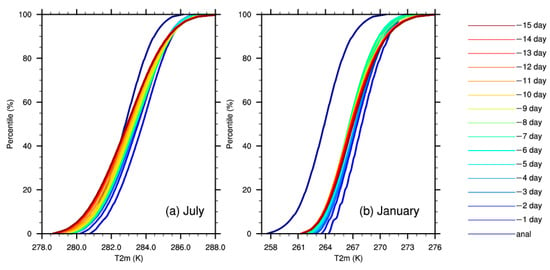
Figure 4.
Climatic percentile distribution of 2-m-average model (live) temperature in (a) July and (b) January over the plateau (anal stands for observation climatic percentile distribution).
For the equivalent test in winter, the 2-m temperature climate percentile in January is selected. The model has an obvious systematic warm bias; that is, the number of days in advance of the forecast is lower. In addition, the climatic states predicted by the model are all located on the right side of the actual situation; that is, the model climatic states are warmer than the historical climatic states. Regarding the stability of the model, judging from the scatter of the climatological curves for each lead time, the stability of the model is poor, especially for the forecasting of extremely low temperatures, which has a more serious impact. For the 2-m temperature climate state in January, with the increase in lead time, the lower end of the climate state is closer to the actual lower end; that is, as the lead time increases, the overall warm bias of the model’s extreme low-temperature forecast in January decreases, which may be due to the smoother extremes of the model’s forecast as the lead time increases.
3.3. Evaluation of Extreme Temperature Forecast on the Plateau Based on a Simple Ensemble Method
According to the above analysis, it can be seen that, for the average climatological extreme temperature in the plateau region, the threshold values of the model and the actual situation are different, and the difference is different under each lead time. To further illustrate the effect of the model on the extreme temperature forecast in the plateau region, the 90th and 10th percentiles of the climate state are selected as the thresholds of extreme high temperature and extreme low temperature; the arithmetic mean, maximum value, minimum value, and median of the ensemble model are used for deterministic forecasting; and the threat score (TS) is used to test the model forecast.
Using the ensemble mean and ensemble median for forecasting, the TSs for summer extreme high temperature and winter extreme low temperature are relatively close, and the effect of the summer extreme high-temperature forecast shows a consistent downward trend with the forecast lead time. For the forecast of extremely low temperatures in winter, the TS score in the lead time of one to three days increases with the lead time and then shows a consistent downward trend. The TSs from using the maximum and minimum values of the ensemble to forecast extremely high temperatures in summer and extremely low temperatures in winter in the plateau area are higher than those from using the ensemble mean and median. For the extreme high-temperature forecast in summer, the improvement from using the ensemble maximum is particularly obvious, and with the increase in lead time, the TS shows a monotonous increasing trend. For extremely low temperatures in winter, the TS using the ensemble minimum value at lead times of one to five days shows an increasing trend with lead time, while after six days, the TS shows a trend of less movement with lead time (Figure 5).
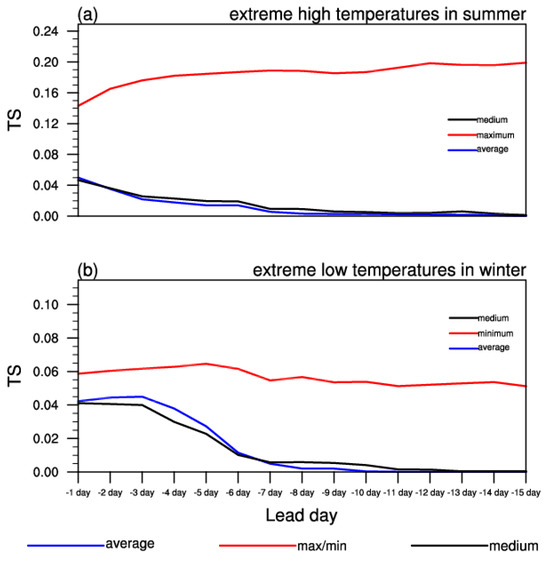
Figure 5.
Evaluation of the ensemble mean, ensemble maximum value, and ensemble median forecast of (a) extreme high temperatures in summer and (b) extreme low temperatures in winter in the plateau area.
It can be seen that, for the forecasting of extremely high temperatures in summer and extremely low temperatures in winter in the plateau region, the effect on the deterministic forecast after processing the ensemble information with the traditional ensemble average is poor. Meanwhile, the TS of forecasting with the ensemble maximum value is higher, but with an increase in lead time, the forecasted TS does not show a monotonous decreasing trend, i.e., for the ensemble forecast model, the extreme information of its forecast is relatively unstable, which also shows the limitations of the model as a whole for extreme temperature forecasting in the plateau region.
4. Analysis of the EFI and SOT Index for Forecasting Extreme Temperatures
4.1. Analysis of “Optimal” EFI Thresholds
Against the background of global warming, extreme temperatures have a more serious impact on people’s lives and economic development, and the accuracy of extreme temperature forecasting needs to be improved. In this section, we analyze the changes in TS in different regions under different EFI thresholds for extreme temperature forecasting to find the “optimal” EFI thresholds for extreme high and low-temperature forecasting in different regions on different forecast days.
To obtain the “optimal” EFI thresholds for predicting extremely low temperatures in winter and extremely high temperatures in summer under each lead time, TS scores were performed on each EFI threshold for extreme temperatures, and the highest TS score EFI threshold was obtained as the “optimal” EFI prediction threshold. As shown in Figure 6, the TSs of the forecasts with different EFI thresholds at different forecasting lead times are different for both summer extreme high temperatures and winter extreme low temperatures, and the trends are also different. As the EFI threshold increases, the TS tends to increase and then decrease. This means that when the EFI is used to forecast the plateau region, it is not the case that the larger the EFI threshold is, the better the forecast effect is; rather, the optimal EFI threshold needs to be selected through experiments under different lead times. In terms of the TS, the model is more effective in forecasting extreme summer temperatures, which is the same as the findings from the above analysis. The legend in the figure shows the lead time represented by different colored curves, and the EFI value corresponding to the highest TS for the lead time is given. The optimal EFI value varies under different lead times, regardless of whether it is for the prediction of summer extreme high temperatures or winter extreme low temperatures in the plateau region. From the comparative analysis of the model and the real climate state, the model has a certain degree of warm bias in the high-end tail part of the summer climate state, and the warm bias is more obvious with the increase in lead time. This means that the model’s positive bias in the forecasting of extremely high temperatures is more significant, and the positive bias is more obvious with the increase in lead time. Also, the EFI is more sensitive to the model, based on which the EFI is used for the forecasting of extreme high temperatures in summer and extreme low temperatures in winter. Based on this feature, when the EFI is used to forecast the extreme summer high temperatures in the plateau region, the optimal EFI thresholds are less than −0.5, which also verifies the warm bias of the model for extreme high-temperature prediction. For the winter extreme low-temperature forecast in the plateau region, it is not the case that the TS is highest when the EFI is equal to −1. Similar to the analysis of summer extreme high temperatures, the thresholds of the optimal EFI are different for each lead time, but almost all of them are less than 0. The optimal EFI thresholds are less than −0.5 when the model forecasts extremely high temperatures. However, almost all are less than 0. TS scores are used to select the “optimal” EFI threshold for the EC ensemble model of extremely low temperatures in Guangzhou [39], and the results showed that the EFI extreme low-temperature threshold for the Guangzhou site was −0.5.
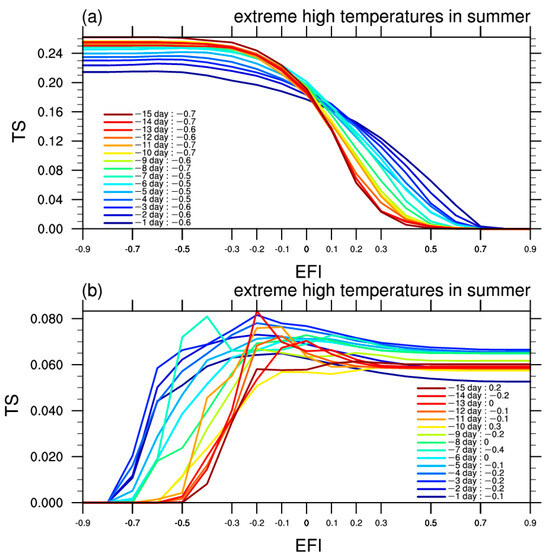
Figure 6.
TSs for forecasting (a) extreme summer high temperatures and (b) extreme winter low temperatures with different EFI thresholds under each lead time.
4.2. Probabilistic Forecast Analysis
The hit rates and false alarm rates of the EFI thresholds for summer extreme high-temperature and winter extreme low-temperature forecasts in the plateau region are shown in Figure 7, with the forecast lead time and the area under the ROC curve shown in the legend for each color curve. According to the previous analysis, the TSs of the GRAPES ensemble model for summer extreme high-temperature forecasts in the plateau region are high, and the climate state forecasts of the model have a certain degree of warm bias compared with the actual conditions, meaning the model itself is more extreme for the summer high-temperature forecasts in the plateau region. If the EFI is used for forecasting, it can be seen from Figure 7 that the ROC curve of the forecast is close to 0.5, which means there is a certain degree of predictability, but the forecast effect is poor. Compared with the summer extreme high-temperature forecast, the effect of the EFI on the winter extreme low-temperature forecast in the plateau region is better, and with the increase in lead time, the curve is closer to the upper-left corner, i.e., with the increase in lead time, the area under the curve of the forecast is the most increased, indicating that the EFI should be used by GRAPES for the forecasting of extremely low temperatures in winter in the plateau region, which has a worse prediction effect. This indicates that, for the GRAPES ensemble model, it is necessary to use the EFI to post-process the extreme information forecasted by the model to improve the forecasting effect of the model on it.
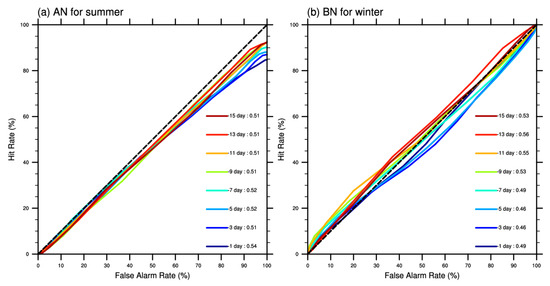
Figure 7.
ROC curves of (a) extreme summer high-temperature and (b) extreme winter low-temperature forecasts in the plateau region using the EFI at each lead time.
The EFI was analyzed in conjunction with the SOT index and the percentile of events as a percentage of observations, selected from two events with correlation coefficients of 0.65 or higher between the EFI and the percentile of events over the plateau range, to compare the relationship between the EFI and SOT index versus the percentile of time. Scatter plots from and versus actual daily mean temperature as a percentile of the historical period are shown in Figure 8. When is greater than 0.3, the average temperature percentile is mostly above 80%, while in the three-point plot of versus the live daily mean temperature percentile, is always less than 0.4. However, the live temperature is more dispersed in the distribution of the historical contemporaneous percentile but mostly distributed below the 50th percentile, which means that the extreme intensities reflected in the ensemble members of the model are more predictive of the intensity of the extremely high temperatures in the live situation. This means that the extreme intensity reflected by the model’s ensemble members is more indicative of the forecast of extremely high temperatures under real conditions, whereas for the forecast of extremely low temperatures, the extreme intensity indicated by the model’s index is less indicative, which matches the model’s bias of over-forecasting the extremes of high temperatures and underestimating the extremes of low temperatures in the above analyses. The scatter plot between the EFI and the percentile of real temperature over the historical period shows a good correspondence between them, which means that the extreme information exhibited by the model ensemble members can be reflected to some extent by the forecasts of extreme temperatures by the EFI. In addition, from the scatter plot of the EFI and SOT index, it can be seen that when the EFI is close to −0.8/0.8, there is still a big difference in the SOT index, which reflects that the SOT index can have a better auxiliary effect on the prediction of the intensity of extreme events.
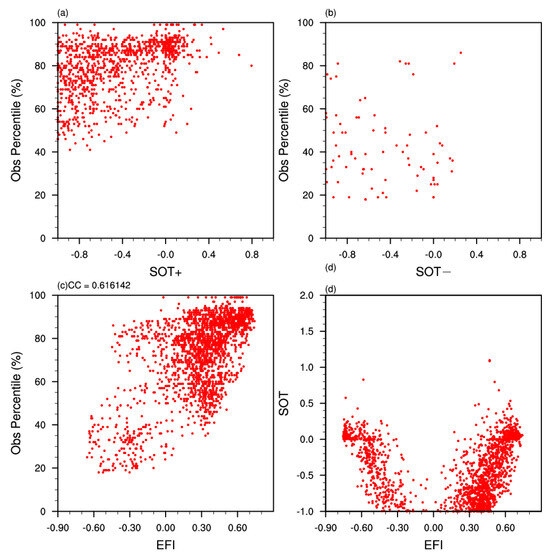
Figure 8.
Scatter plots of (a) , (b) , and (c) EFI at the three-day lead time versus the percentile of real temperature in the historical period, and (d) the EFI and SOT index scatter plots for the plateau region.
5. Conclusions
In this study, based on China’s self-developed GRAPES ensemble forecasting model, the climate states of the model forecast and the real situation were calculated, and the typical months for studying extreme temperatures were selected based on the distribution of the 90th percentile summer and 10th percentile winter thresholds for 2-m temperatures in the real climate state. The model’s ability to forecast extreme events was comprehensively examined by comparing and analyzing the climate state deviations of the model and the real state and by analyzing the computation of extreme temperature TSs using the simple ensemble average, maximum, and median. Second, the EFI and SOT index were calculated, and different forecast thresholds were used to forecast the extreme temperatures under real conditions, which were analyzed with the help of the TS to derive the optimal EFI threshold for the plateau. Meanwhile, to test the predictability of the EFI for extreme temperatures on the plateau, the ROC curve method was used. Finally, a case study was conducted to illustrate the complementarity of the SOT index to the EFI and analyze its applicability in extreme temperature forecasting. The following conclusions were obtained:
(1) For the plateau region, extremely high and extremely low temperatures were analyzed during June–September and December–February, respectively, by combining the month-to-month changes in the monthly average temperature and the frequency of extreme temperature occurrence. Extreme temperature thresholds were significantly affected by the topography, and the introduction of the concept of relative thresholds was found to be particularly important for the southern plateau region, where the distribution of extreme temperature thresholds is limited by the data quality at higher altitudes.
(2) The warm bias of the GRAPES model was more obvious for the forecasting of extremely high temperatures in summer, and the warm bias decreased slightly with the increase in lead time. For extremely low temperatures in winter, there was also a certain warm bias, but the bias decreased with lead time, which may be due to the smoothing of the extremes in the model with the increase in lead time.
(3) For the prediction of extremely high temperatures in summer and extremely low temperatures in winter in the plateau region, the effect of deterministic prediction after processing the ensemble information using the traditional ensemble mean was poor, and the TS of the ensemble maximum was higher. However, with the increase in lead time, the TS of the prediction did not show a monotonous decreasing trend; that is, for the ensemble forecast model, the extreme information of the forecast was more unstable, which also indicates that the extreme information of the model was more unstable with an increase in lead time, i.e., for the ensemble forecasting model, the extreme information of its forecast is unstable, which also indicates the limitation of the model in the forecasting of extreme temperatures in the plateau region as a whole.
(4) The TSs of forecasts with different EFI thresholds were different for different lead times. As the EFI threshold increased, the TS tended to increase and then decrease, which means that there was an optimal EFI threshold. The optimal EFI thresholds for extremely high-temperature forecasts in summer were all less than −0.5, which also verified the warm bias characteristics of the model for extreme high-temperature forecasts. The optimal EFI thresholds for extreme low-temperature forecasts in winter were almost all less than 0.
(5) For the GRAPES ensemble model, from the ROC curves, the EFI has a certain level of predictability for extreme summer high temperatures, but the prediction effect is poor. For winter extreme low temperatures, which are poorly predicted by the model itself, post-processing the extreme information predicted by the model using the EFI can improve the forecast effect of the model.
(6) From the analysis of the applicability of the SOT index in individual cases, the extreme intensity reflected by the model through the index to the ensemble members was more obvious for the forecasting of extremely high temperatures in the real situation, but for the forecasting of extremely low temperatures, the extreme intensity indicated by the index of the model was weaker. The extreme information exhibited by the model ensemble members can be somewhat reflected by the EFI for the forecasting of extreme temperatures. Also, when the absolute value of the EFI is large, there is still a large difference in the SOT index, i.e., the SOT index can be a better aid to the prediction of the intensity of extreme events.
Author Contributions
Conceptualization, H.C.; methodology, J.Z.; software, R.W.; validation, R.W. and Y.L.; formal analysis, R.W. and Y.L.; investigation, R.W.; resources, Y.L.; data curation, R.W.; writing—original draft preparation, R.W.; writing—review and editing, H.C.; visualization, R.W. and Y.L.; supervision, H.C. and J.Z.; project administration, H.C.; funding acquisition, H.C. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly funded by the National Natural Science Foundation of China (U20A2097, 42075087), the National Key Research and Development Program of China (2021YFC3000902), and the Guangzhou Meteorological Society Science and Technology Research Project (M202205).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
GRAPES Ensemble Forecast Product was obtained from the Earth System Modeling and Prediction Center with the permission of China Meteorological Administration, China’s National Surface Meteorological Station Normalized Temperature Daily Value Data Set (V1.0) can be obtained from the China Meteorological Data Service Centre at https://data.cma.cn (accessed on 26 October 2023), ETOPO5 Global Surface Relief can be downloaded from the National Centers for Environmental Information at https://www.ncei.noaa.gov/products/etopo-global-relief-model (accessed on 26 October 2023), the plateau boundary data can be obtained from the National Tibetan Plateau Data Center at https://data.tpdc.ac.cn/zh-hans/data/61701a2b-31e5-41bf-b0a3-607c2a9bd3b3 (accessed on 26 October 2023).
Acknowledgments
All figures were created using the NCAR Command Language (NCL) (2021), http://www.ncl.ucar.edu (accessed on 26 October 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yin, H.; Sun, Y. Characteristics of Extreme Temperature and Precipitation in China in 2017 Based on ETCCDI Indices. Adv. Clim. Chang. Res. 2018, 9, 218–226. [Google Scholar] [CrossRef]
- Xin, J.; Zhan, M.; Xu, B.; Li, H.; Zhan, L. Variations of Extreme Temperature Event Indices in Six Temperature Zones in China from 1961 to 2020. Sustainability 2023, 15, 11536. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, W.; He, Y. Impact of land surface forcings on mean and extreme temperature in eastern China. J. Geophys. Res. 2010, 115, D19117. [Google Scholar] [CrossRef]
- Zhai, P.; Liu, J. Extreme weather/climate events and disaster prevention and mitigation under global warming background. Eng. Sci. 2012, 14, 55–63. [Google Scholar]
- Wu, G.X.; Zhang, Y. Tibetan Plateau Forcing and the Timing of the Monsoon Onset over South Asia and the South China Sea. Mon. Weather. Rev. 1998, 126, 913–927. [Google Scholar] [CrossRef]
- Wu, G.X.; Liu, Y.M.; Hong, J.L.; Dong, B.W.; Duan, A.M.; Bao, Q.; Zhou, L.J. Revisiting Asian monsoon formation and change associated with Tibetan Plateau forcing: I. Formation. Clim. Dyn. 2012, 39, 1169–1181. [Google Scholar] [CrossRef]
- Duan, A.M.; Wu, G.X. Role of the Tibetan Plateau thermal forcing in the summer climate patterns over subtropical Asia. Clim. Dyn. 2005, 24, 793–807. [Google Scholar] [CrossRef]
- Yanai, M.; Wu, G.X. Effects of the Tibetan Plateau. In The Asian Monsoon; Wang, B., Ed.; Springer: New York, NY, USA, 2006; pp. 513–549. [Google Scholar] [CrossRef]
- Du, W.; Kang, S.; Chen, J.; Sun, W.; Qin, X.; Sun, W.; Zhang, Y. Arctic air mass triggered the extreme temperature events recorded in the Laohugou ice core from the northeastern Tibetan Plateau. Atmos. Res. 2022, 265, 105909. [Google Scholar] [CrossRef]
- Wan, B.; Gao, Z.; Chen, F.; Lu, C. Impact of Tibetan Plateau surface heating on persistent extreme precipitation events in southeastern China. Mon. Weather. Rev. 2017, 145, 3485–3505. [Google Scholar] [CrossRef]
- Song, C.; Pei, T.; Zhou, C. The role of changing multiscale temperature variability in extreme temperature events on the eastern and central Tibetan Plateau during 1960–2008. Int. J. Climatol. 2014, 34, 3683–3701. [Google Scholar] [CrossRef]
- Yin, H.; Sun, Y.; Donat, M. Changes in temperature extremes on the Tibetan Plateau and their attribution. Environ. Res. Lett. 2019, 14, 124015. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Pepin, N.; Yan, Y. Relationship between trends in temperature extremes and elevation in the eastern and central Tibetan Plateau, 1961–2005. Geophys. Res. Lett. 2008, 35, L04704. [Google Scholar] [CrossRef]
- Liu, D.; Wang, T.; Yang, T.; Yan, Z.; Liu, Y.; Zhao, Y.; Piao, S. Deciphering impacts of climate extremes on Tibetan grasslands in the last fifteen years. Sci. Bull. 2019, 64, 446–454. [Google Scholar] [CrossRef]
- Duan, J.; Ma, Z.; Yuan, N.; Li, L.; Chen, L. Extremes in the magnitude of annual temperature cycle on the Tibetan Plateau over the past three centuries. Clim. Dyn. 2018, 52, 3599–3608. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Mazei, Y.; Saldaev, D.; Efstathiou, M.; Voronova, T.; Xue, Y. Nowcasting of air pollution episodes in megacities: A case study for Athens, Greece. Atmos. Pollut. Res. 2021, 12, 101099. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C.G.; Sarlis, N.V. On the Progress of the 2015–2016 El Niño Event. Atmos. Chem. Phys. 2016, 16, 2007–2011. [Google Scholar] [CrossRef]
- Ding, J.; Cuo, L.; Zhang, Y.; Zhu, F. Monthly and annual temperature extremes and their changes on the Tibetan Plateau and its surroundings during 1963–2015. Sci. Rep. 2018, 8, 11860. [Google Scholar] [CrossRef]
- Yao, L.; Lu, J.; Zhang, W.; Qin, J.; Zhou, C.; Tran, N.N.; Pinagé, E.R. Spatiotemporal Analysis of Extreme Temperature Change on the Tibetan Plateau Based On Quantile Regression. Earth Space Sci. 2022, 9, e2022EA002571. [Google Scholar] [CrossRef]
- You, Q.; Jiang, Z.; Wang, D.; Pepin, N.; Kang, S. Simulation of temperature extremes in the Tibetan Plateau from CMIP5 models and comparison with gridded observations. Clim. Dyn. 2018, 51, 355–369. [Google Scholar] [CrossRef]
- Palmer, T.N.; Brankovic, C.; Richardson, D.S. A probability and decision-model analysis of PROVOST seasonal multi-model ensemble integrations. Q. J. R. Meteorol. Soc. 2000, 126, 2013–2034. [Google Scholar] [CrossRef]
- Richardson, D.S. Skill and relative economic value of the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 2000, 126, 649–668. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: New York, NY, USA, 2005; 627p. [Google Scholar]
- Murphy, A.H. Decision making and the value of forecasts in generalized model of the cost-loss ratio situation. Mon. Weather. Rev. 1985, 113, 362–369. [Google Scholar] [CrossRef]
- Van Den Dool, H.M.; Toth, Z. Why do forecasts for “near normal” often fail? Weather Forecast. 1991, 6, 76–85. [Google Scholar] [CrossRef]
- Ghelli, A.; Lalaurette, F. Verifying precipitation forecasts using upscaled observations. ECMWF Newsl. 2000, 87, 9–17. [Google Scholar]
- Lalaurette, F. Early detection of abnormal weather conditions using a probabilistic extreme forecast index. Q. J. R. Meteorol. Soc. 2003, 129, 3037–3057. [Google Scholar] [CrossRef]
- Lalaurette, F. Two Proposals to Enhance the EFI Response Near the Tails of the Climate Distribution[EB/OL]. American Meteor Society. 2003. Available online: https://www.ecmwf.int/products/forecasts/efi_guide.pdf (accessed on 20 June 2018).
- Lavers, D.A.; Pappenberger, F.; Richardson, D.S.; Zsoter, E. ECMWF Extreme Forecast Index for water vapor transport: A forecast tool for atmospheric rivers and extreme precipitation. Geophys. Res. Lett. 2016, 43, 11852–11858. [Google Scholar] [CrossRef]
- Dutra, E.; Diamantakis, M.; Tsonevsky, I.; Zsoter, E.; Wetterhall, F.; Stockdale, T.; Richardson, D.; Pappenberger, F. The extreme forecast index at the seasonal scale. Atmos. Sci. Lett. 2013, 14, 256–262. [Google Scholar] [CrossRef]
- Zsoter, E. Recent developments in extreme weather forecasting. ECMWF Newsl. 2006, 107, 8–17. [Google Scholar]
- Tsonevsky, I.; Richardon, D.S. Application of the new EFI products to a case of early snowfall in Central Europe. ECMWF Newsl. 2012, 133, 4–5. [Google Scholar]
- Persson, A. User guide to ECMWF forecast products. Meteorol. Bull. 2011, 3, 63–67. [Google Scholar]
- Gupta, N.; Chavan, S.R. Assessment of temporal change in the tails of probability distribution of daily precipitation over India due to climatic shift in 1970s. J. Water Clim. Chang. 2021, 12, 2753–2773. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, H.; Pan, X. Integration Dataset of Tibet Plateau Boundary; National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; Van Der Linden, P.J.; Dai, X.; Johnson, C.A. Contribution of working group 1 to the third assessment report of the intergovernmental panel on climate change. In Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Contrbution of working group 1 to the fourth assessment report of the intergovernmental panel on climate change. In Climate Change 2007: The Scientific Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Liu, X.; Li, H.; Zheng, J.; Li, H. On the Application of a Weather Forecast Index for Extremely Low Temperature in Guangzhou Using ECMWF Ensemble. Guangdong Meteorol. 2020, 42, 6–9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).