The Sensitivity of the Icosahedral Non-Hydrostatic Numerical Weather Prediction Model over Greece in Reference to Observations as a Basis towards Model Tuning
Abstract
:1. Introduction
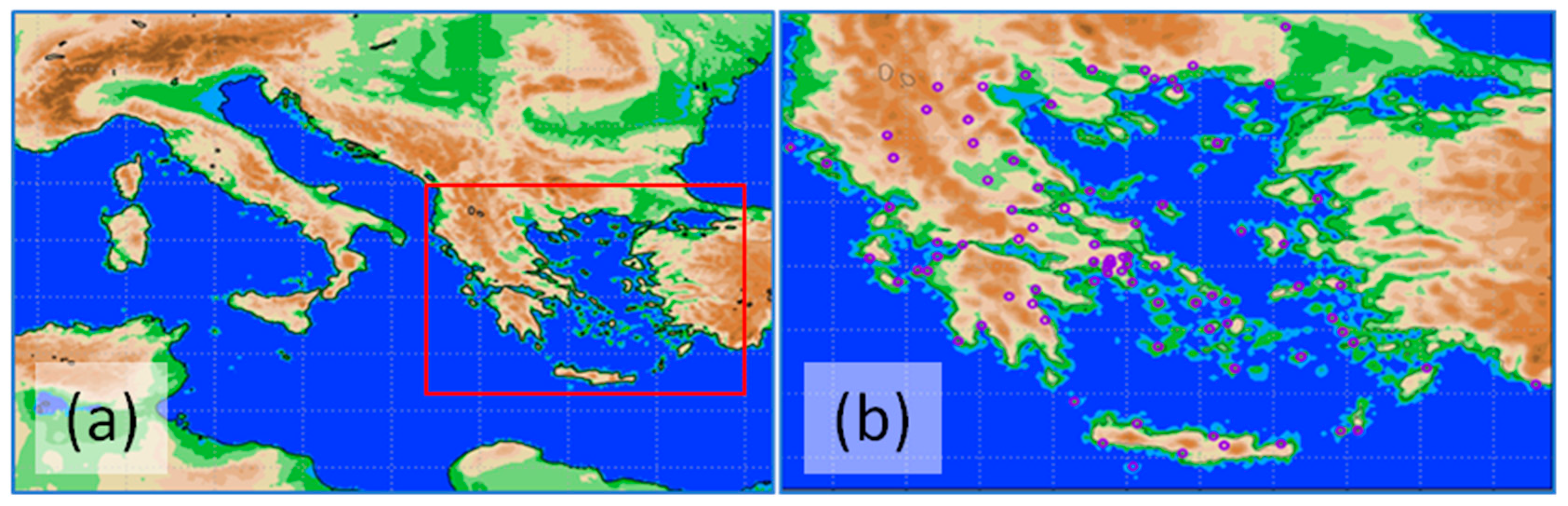
2. Materials and Methods
- Turbulence (p01, p02, p03, p04, p05, p11, p17, p20, p23);
- Land processes (p06, p08);
- Convection (p07, p09, p12, p14, p15, p16, p18, p19);
- Subscale orography tuning (p10);
- Grid-scale microphysics (p13, p24);
- Cloud cover (p21, p22).
3. Results
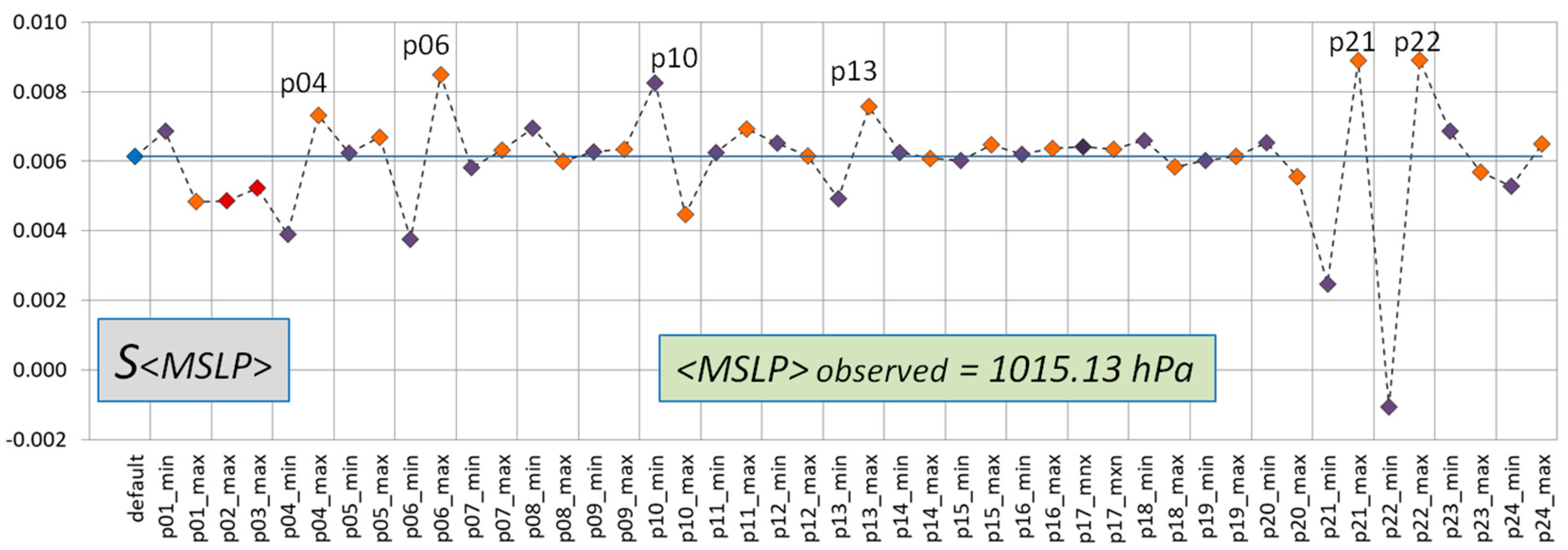
3.1. MSLP Sensitivities
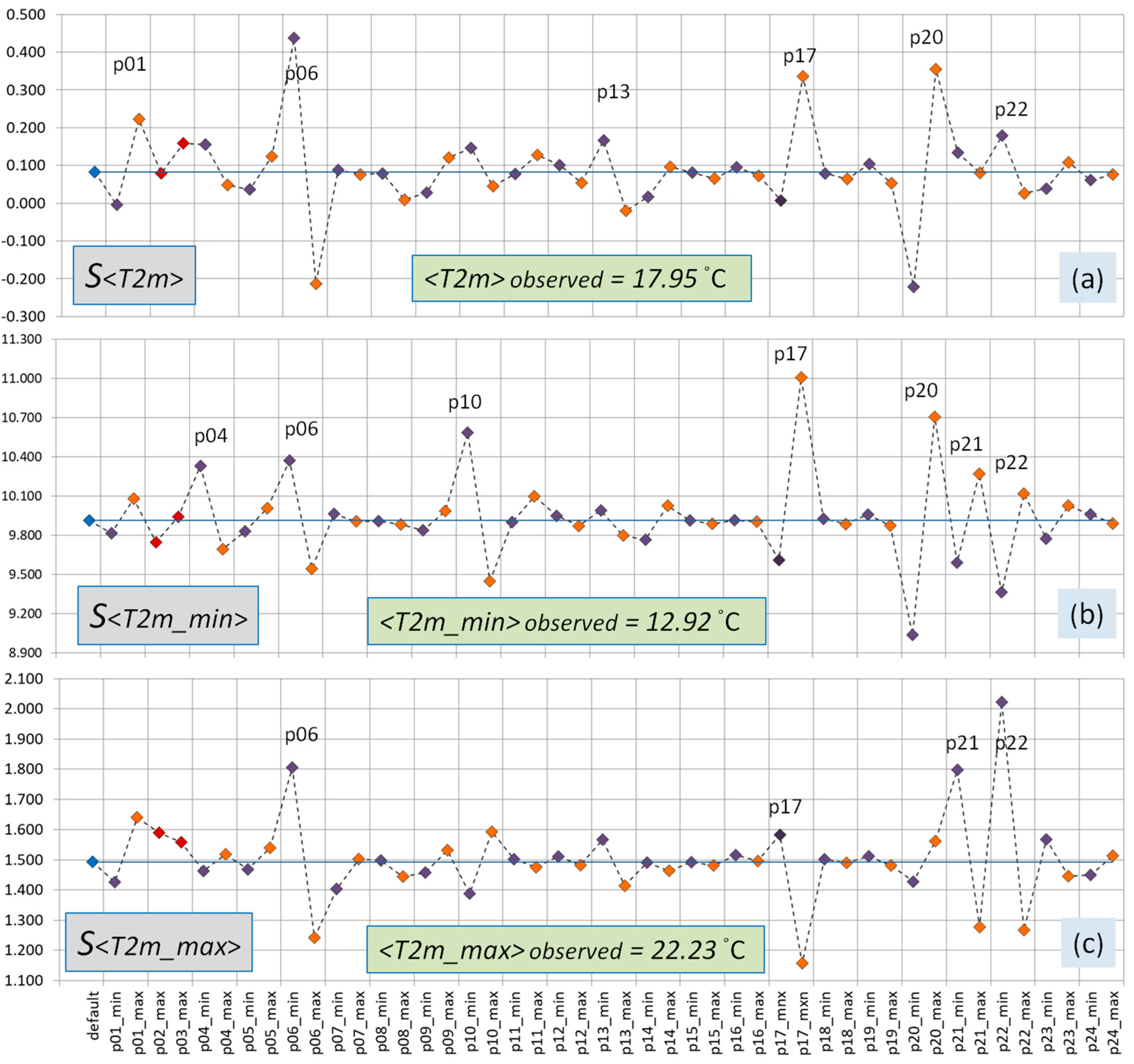
3.2. T2m, T2m_min, T2m_max and Td2m Sensitivities
3.3. TOTPREC Sensitivities
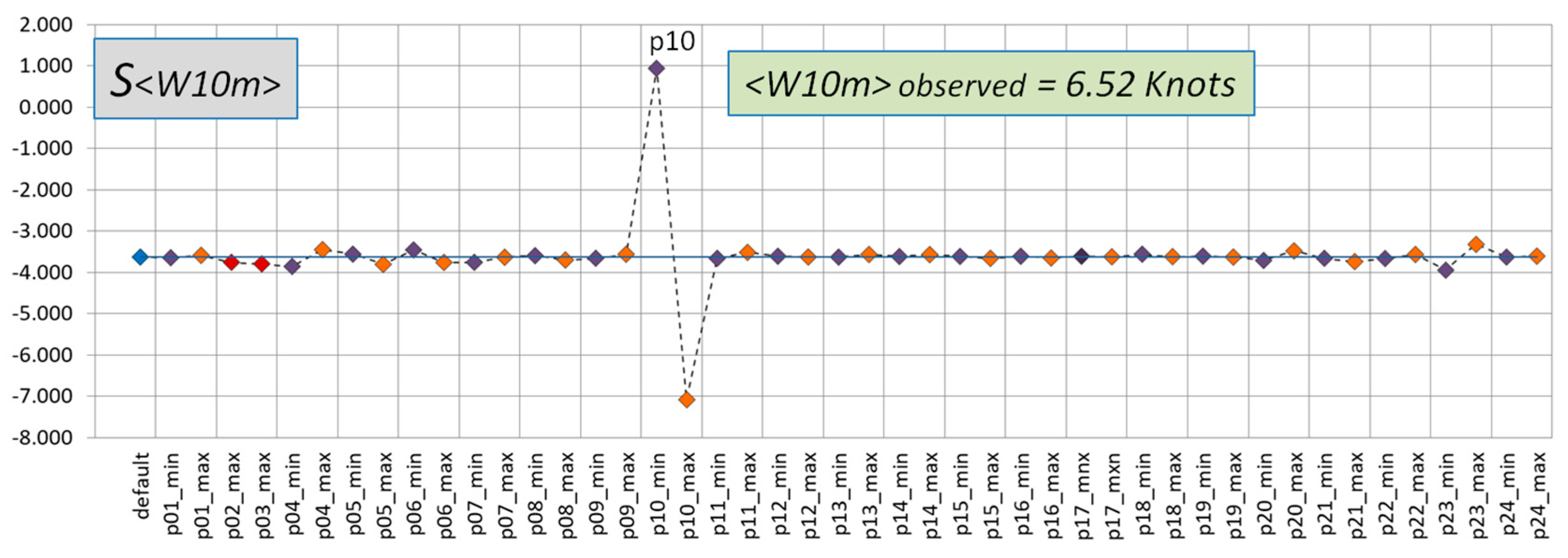
3.4. W10m Sensitivities
4. Discussion
5. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Avgoustoglou, E.; Voudouri, A.; Carmona, I.; Bucchignani, E.; Levi, Y.; Bettems, J.-M. A Methodology Towards the Hierarchy of COSMO Parameter Calibration Tests Via the Domain Sensitivity Over the Mediterranean Area. COSMO Tech. Rep. 2020, Volume 42. Available online: https://www.cosmo-model.org/content/model/cosmo/techReports/docs/techReport42.pdf (accessed on 22 October 2023).
- Baki, H.; Chinta, S.; Balaji, D.; Srinivasan, B. Determining the sensitive parameters of the Weather Research and Forecasting (WRF) Model for the simulation of tropical cyclones in the Bay of Bengal using global sensitivity analysis and machine learning. Geosci. Model Dev. 2022, 15, 2133–2155. [Google Scholar] [CrossRef]
- Campos, T.B.; Sapucci, L.F.; Lima, W.; Silva Ferreira, D. Sensitivity of Numerical Weather Prediction to the Choice of Variable for Atmospheric Moisture Analysis into the Brazilian Global Model Data Assimilation System. Atmosphere 2018, 9, 123. [Google Scholar] [CrossRef]
- Kim, S.-M.; Kim, H.M. Effect of observation error variance adjustment on numerical weather prediction using forecast sensitivity to error covariance parameters. Tellus A 2018, 70, 1492839. [Google Scholar] [CrossRef]
- Merja, H.; Tölle, M.H.; Churiulin, E. Sensitivity of Convection-Permitting Regional Climate Simulations to Changes in Land Cover Input Data: Role of Land Surface Characteristics for Temperature and Climate Extremes. Front. Earth Sci. Sec. Atmos. Sci. 2021, 9, 722244. [Google Scholar] [CrossRef]
- De Lucia, C.; Bucchignani, E.; Mastellone, A.; Adinolfi, M.; Montesarchio, M.; Cinquegrana, D.; Mercogliano, P.; Schiano, P. A Sensitivity Study on High Resolution NWP ICON—LAM Model over Italy. Atmosphere 2022, 13, 540. [Google Scholar] [CrossRef]
- Marsigli, C. Final report on priority project SREPS (Short Range Ensemble Prediction System). COSMO Tech. Rep. 2009, 13. [Google Scholar] [CrossRef]
- Avgoustoglou, E.; Shtivelman, A.; Khain, P.; Marsigli, C.; Levi, Y.; Cerenzia, I. On the Seasonal Sensitivity of ICON Model. COSMO Newsl. 2023, Volume 22. Available online: http://www.cosmo-model.org/content/model/documentation/core/default.htm (accessed on 22 October 2023).
- Zängl, G.; Reinert, D.; Rípodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) Modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Q. J. R. Meteorol. Soc. 2015, 141, 563–579. [Google Scholar] [CrossRef]
- Prill, F.; Reinert, D.; Rieger, D.; Zängl, G. ICON Tutorial: Working with the ICON Model; Deutscher Wetterdienst: Offenbach, Germany, 2020. [Google Scholar]
- Avgoustoglou, E.; Carmona, I.; Voudouri, A.; Levi, Y.; Will, A.; Bettems, J.M. Calibration of COSMO Model in the Central-Eastern Mediterranean area adjusted over the domains of Greece and Israel. Atmos. Res. 2022, 279, 106362. [Google Scholar] [CrossRef]
- Voudouri, A.; Avgoustoglou, E.; Carmona, I.; Levi, Y.; Bucchignani, E.; Kaufmann, P.; Bettems, J.M. Objective Calibration of Numerical Weather Prediction Model: Application on Fine Resolution COSMO Model over Switzerland. Atmosphere 2021, 12, 1358. [Google Scholar] [CrossRef]
- Voudouri, A.; Khain, P.; Carmona, I.; Avgoustoglou, E.; Kaufmann, P.; Grazzini, F.; Bettems, J.M. Optimization of high resolution COSMO Model performance over Switzerland and Northern Italy. Atmos. Res. 2018, 213, 70–85. [Google Scholar] [CrossRef]
- Voudouri, A.; Khain, P.; Carmona, I.; Bellprat, O.; Grazzini, F.; Avgoustoglou, E.; Bettems, J.M.; Kaufmann, P. Objective calibration of numerical weather prediction Models. Atmos. Res. 2017, 190, 128–140. [Google Scholar] [CrossRef]
- Consortium for Small-Scale Modeling. Available online: https://www.cosmo-Model.org (accessed on 22 October 2023).
- COSMO Limited-Area Ensemble Prediction System. Available online: https://www.cosmo-Model.org/content/tasks/operational/cosmo/leps/default.htm (accessed on 22 October 2023).
- Montani, A.; Cesari, D.; Marsigli, C.; Paccagnella, T. Seven years of activity in the field of mesoscale ensemble forecasting by the COSMO-LEPS system: Main achievements and open challenges. Tellus A 2011, 63, 605–624. [Google Scholar] [CrossRef]
- Tomasso, D.; Marsigli, C.; Montani, A.; Nerozzi, F.; Paccagnella, T. Calibration of Limited-Area Ensemble Precipitation Forecasts for Hydrological Predictions. Mon. Weather Rev. 2014, 142, 2176–2197. [Google Scholar] [CrossRef]
- COSMO Priority Project PROPHECY. Available online: http://www.cosmo-model.org/content/tasks/priorityProjects/prophecy/pp-prophecy.pdf (accessed on 22 October 2023).
- Crueger, T.; Giorgetta, M.A.; Brokopf, R.; Esch, M.; Fiedler, S.; Hohenegger, C.; Kornblueh, L.; Mauritsen, T.; Nam, C.; Naumann, A.K.; et al. ICON-A, The Atmosphere Component of the ICON Earth System Model: II. Model Evaluation. J. Adv. Model. Earth Syst. 2018, 10, 1638–1662. [Google Scholar] [CrossRef]
- Khain, P.; Shpund, J.; Levi, Y.; Khain, A. Warm-phase spectral-bin microphysics in ICON: Reasons of sensitivity to aerosols. Atmos. Res. 2022, 279, 106388. [Google Scholar] [CrossRef]
- Van Pham, T.; Christian Steger, C.; Rockel, B.; Keuler, K.; Kirchner, I.; Mertens, M.; Rieger, D.; Zängl, G.; Früh, B. ICON in Climate Limited-area Mode (ICON release version 2.6.1). Geosci. Model Dev. 2021, 14, 985–1005. [Google Scholar] [CrossRef]
- Khain, P.; Shtivelman, A.; Muskatel, H.; Baharad, A.; Uzan, L.; Vadislavsky, E.; Amitai, E.; Meir, N.; Meerson, V.; Levi, Y.; et al. Israel uses ECMWF supercomputer to advance regional forecasting. ECMWF Newsl. 2022, 171, 29–35. [Google Scholar]
- ICON Model Parameters Suitable for Model Tuning. Available online: https://www.cosmo-model.org/content/support/icon/tuning/icon-tuning.pdf (accessed on 22 October 2023).
- ECMWF Integrated Forecasting System. Available online: https://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-Model (accessed on 22 October 2023).
- Hawkins, M.; Isabella Weger, I. Supercomputing at ECMWF. ECMWF Newsl. 2015, 32–38. [Google Scholar]
- ECMWF’s File Storage System. Available online: https://confluence.ecmwf.int/display/UDOC/ECFS+user+documentation (accessed on 27 October 2023).
- Singh, S.; Kalthoff, N.; Gantner, L. Sensitivity of convective precipitation to model grid spacing and land-surface resolution in ICON. Q. J. R. Meteorol. Soc. 2021, 147, 2709–2728. [Google Scholar] [CrossRef]
- Puh, M.; Keil, C.; Gebhardt, C.; Marsigli, C.; Hirt, M.; Jakub, F.; Craig, G.C. Physically based stochastic perturbations improve a high-resolution forecast of convection. Q. J. R. Meteorol. Soc. 2023, 1–11. [Google Scholar] [CrossRef]
- Ju-Hye Kim, J.-H.; Jiménez, P.A.; Sengupta, M.; Dudhia, J.; Yang, J.; Alessandrini, S. The Impact of Stochastic Perturbations in Physics Variables for Predicting Surface Solar Irradiance. Atmosphere 2022, 13, 1932. [Google Scholar] [CrossRef]
- Ma, P.-L.; Harrop, B.E.; Larson, V.E.; Neale, R.B.; Gettelman, A.; Morrison, H.; Wang, H.; Zhang, K.; Klein, S.A.; Zelinka, M.D.; et al. Better calibration of cloud parameterizations and subgrid effects increases the fidelity of the E3SM Atmosphere Model version 1. Geosci. Model Dev. 2022, 15, 2881–2916. [Google Scholar] [CrossRef]
- Wang, J.; Fan, J.; Houze, R.A., Jr.; Brodzik, S.R.; Zhang, K.; Guang, J.; Zhang, G.J.; Po-Lun Ma, P.-L. Using radar observations to evaluate 3-D radar echo structure simulated by the Energy Exascale Earth System Model (E3SM) version 1. Geosci. Model Dev. 2021, 14, 719–734. [Google Scholar] [CrossRef]
- Introductory Description of the Term Big Data. Available online: https://en.wikipedia.org/wiki/Big_data (accessed on 22 October 2023).
- Düben, P. AI and machine learning at ECMWF. ECMWF Newsl. 2020, 163, 6–7. [Google Scholar]
- Salcedo-Sanz, S.; Pérez-Aracil, J.; Ascenso, G.; Javier Del Ser, J.; Casillas-Pérez, D.; Kadow, C.; Fister, D.; Barriopedro, D.; García-Herrera6, R.; Giuliani, M.; et al. Analysis, characterization, prediction, and attribution of extreme atmospheric events with machine learning and deep learning techniques: A review. Theor. Appl. Climatol. 2023. [Google Scholar] [CrossRef]
- Schultz, M.G.; Betancourt, C.; Gong, B.; Kleinert, F.; Langguth, M.; Leufen, L.H.; Mozaffari, A.; Stadtler, S. Can deep learning beat numerical weather prediction? R. Soc. A 2021, 379, 20200097. [Google Scholar] [CrossRef]


| Parameter, Encoded Name (Meaning) Relevance: High [H]/Medium [M] | MIN, DEFAULT, MAX |
| p01: a_hshr (scale for the separated horizontal shear mode) [M] | 0.1, 1.0, 2.0 |
| p02: a_stab (stability correction of turbulent length scale factor) [M] | 0.0, 0.0, 1.0 |
| p03: alpha0 (lower bound of velocity-dependent Charnock param) [H] | 0.0123, 0.0123, 0.0335 |
| p04: alpha1 (scaling for the molecular roughness of water waves) [H] | 0.1, 0.5, 0.9 |
| p05: c_diff (length scale factor for vertical diffusion of TKE) [H] | 0.1, 0.2, 0.4 |
| p06: c_soil (evaporating fraction of soil) [H] | 0.75, 1.0, 1.25 |
| p07: capdcfac_et (extratropics CAPE diurnal cycle correction) [H] | 0.0, 0.5, 1.25 |
| p08: cwimax_ml (scaling for maximum interception storage) [H] | 0.5 × 10−7, 1.0 × 10−6, 0.5 × 10−4 |
| p09: entrorg (entrainment convection scheme valid for dx = 20 km) [H] | 0.00175, 0.00195, 0.00215 |
| p10: gkwake (low-level wake drag constant for blocking) [H] | 1.0, 1.5, 2.0 |
| p11: q_crit (normalized supersaturation critical value) [H] | 1.6, 2.0, 4.0 |
| p1 p12: qexc (test parcel ascent excess grid-scale QV fraction) [M] | 0.0075, 0.0125, 0.0175 |
| p13: rain_n0_factor (raindrop size distribution change) [H] | 0.02, 0.1, 0.5 |
| p14: rdepths (maximum allowed shallow convection depth) [H] | 15000, 20000, 25000 |
| p15: rhebc_land (RH threshold for onset of evaporation below cloud base over land) [M] | 0.70, 0.75, 0.80 |
| p16: rhebc_ocean (ibid over ocean) [H] | 0.80, 0.85, 0.90 |
| p17: rlam_heat_rat_sea (scaling of laminar boundary layer for heat and latent and heat fluxes over water (constant product)) [H] | (0.25,28.0), (1.0,7.0), (4.0,1.75) |
| p18: rprcon (precipitation coefficient conversion of cloud water) [H] | 0.00125, 0.0014, 0.00165 |
| p19: texc (excess value for temperature used in test parcel ascent) [M] | 0.075, 0.125, 0.175 |
| p20: tkhmin_tkmmin (common scaling for minimum vertical diffusion for heat–moisture and momentum) [H] | 0.55, 0.75, 0.95 |
| p21: box_liq (box width for liquid cloud diagnostic) [H] | 0.03, 0.05, 0.07 |
| p22: box_liq_asy (liquid cloud diagnostic asymmetry factor) [H] | 2.0, 3.5, 4.0 |
| p23: tur_len (asymptotic maximal turbulent distance (m)) [H] | 250, 300, 350 |
| p24: zvz0i (terminal fall velocity of ice) [H] | 0.85, 1.25, 1.45 |
| Met. Variables | Obs. Avg. | Order of S (%) | Most Sensitive Parameters |
|---|---|---|---|
| MSLP | 1015.13 hPa | 10−3 | p04, p06, p10, p13, p21, p22 |
| T2m | 17.95 °C | 10−1 | p01, p06, p13, p17, p20, p22 |
| T2m_min | 12.92 °C | 10 | p01, p06, p10, p17, p20, p21, p22 |
| T2m_max | 22.23 °C | 1 | p06, p17, p21, p22 |
| Td2m | 10.68 °C | 1 | p04, p06 |
| TOTPREC | 0.98 mm | 10 | p04, p07, p09, p13, p14 |
| W10m | 6.52 Knots | 5 | p10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avgoustoglou, E.; Shtivelman, A.; Khain, P.; Marsigli, C.; Levi, Y.; Cerenzia, I. The Sensitivity of the Icosahedral Non-Hydrostatic Numerical Weather Prediction Model over Greece in Reference to Observations as a Basis towards Model Tuning. Atmosphere 2023, 14, 1616. https://doi.org/10.3390/atmos14111616
Avgoustoglou E, Shtivelman A, Khain P, Marsigli C, Levi Y, Cerenzia I. The Sensitivity of the Icosahedral Non-Hydrostatic Numerical Weather Prediction Model over Greece in Reference to Observations as a Basis towards Model Tuning. Atmosphere. 2023; 14(11):1616. https://doi.org/10.3390/atmos14111616
Chicago/Turabian StyleAvgoustoglou, Euripides, Alon Shtivelman, Pavel Khain, Chiara Marsigli, Yoav Levi, and Ines Cerenzia. 2023. "The Sensitivity of the Icosahedral Non-Hydrostatic Numerical Weather Prediction Model over Greece in Reference to Observations as a Basis towards Model Tuning" Atmosphere 14, no. 11: 1616. https://doi.org/10.3390/atmos14111616
APA StyleAvgoustoglou, E., Shtivelman, A., Khain, P., Marsigli, C., Levi, Y., & Cerenzia, I. (2023). The Sensitivity of the Icosahedral Non-Hydrostatic Numerical Weather Prediction Model over Greece in Reference to Observations as a Basis towards Model Tuning. Atmosphere, 14(11), 1616. https://doi.org/10.3390/atmos14111616






