Theoretical Calculation and Experimental Verification of Wind-Driven Rain Aerodynamic Forces on the Bridge Main Beam
Abstract
:1. Introduction
2. Summary of Raindrop Characteristics
3. Derivation of Wind-Driven Rain Aerodynamic Forces of the Main Beam
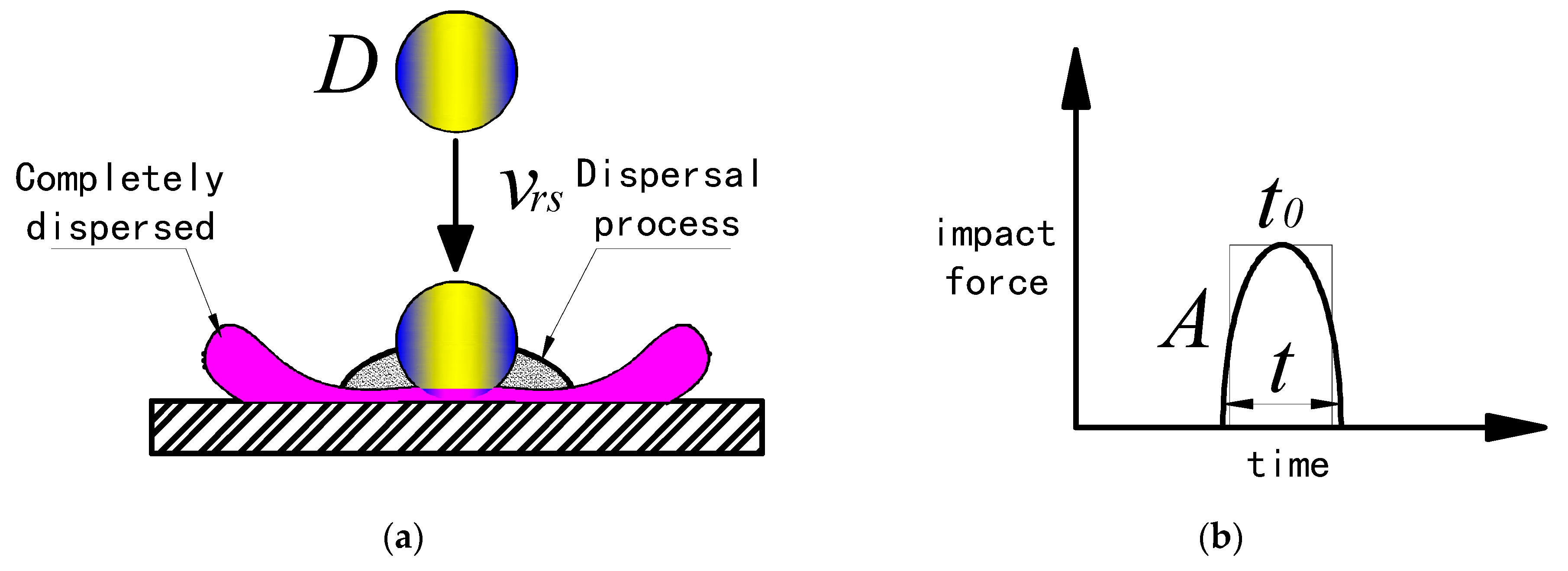
3.1. Rain Drop Impact Analysis and Simplified Calculation Model
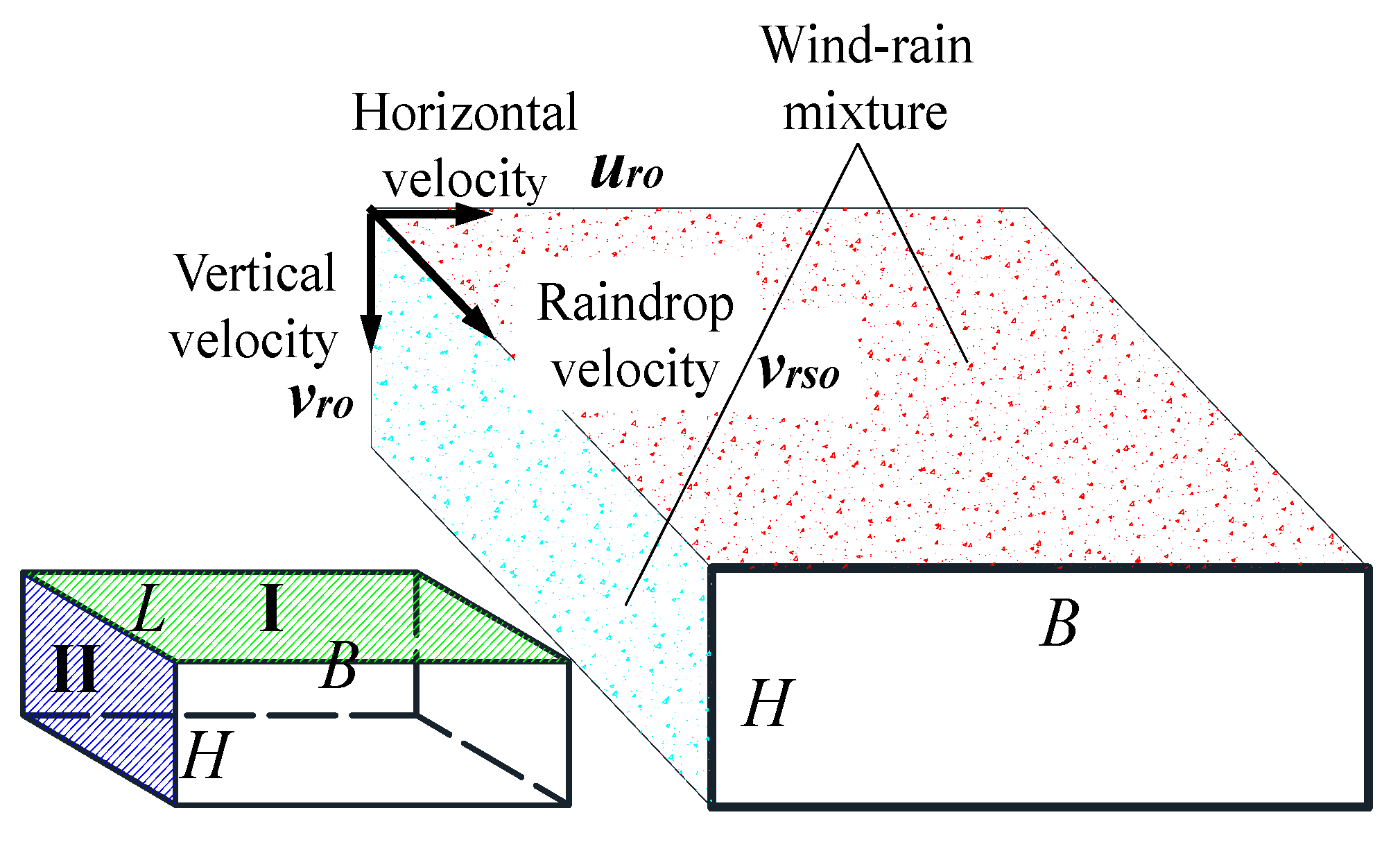
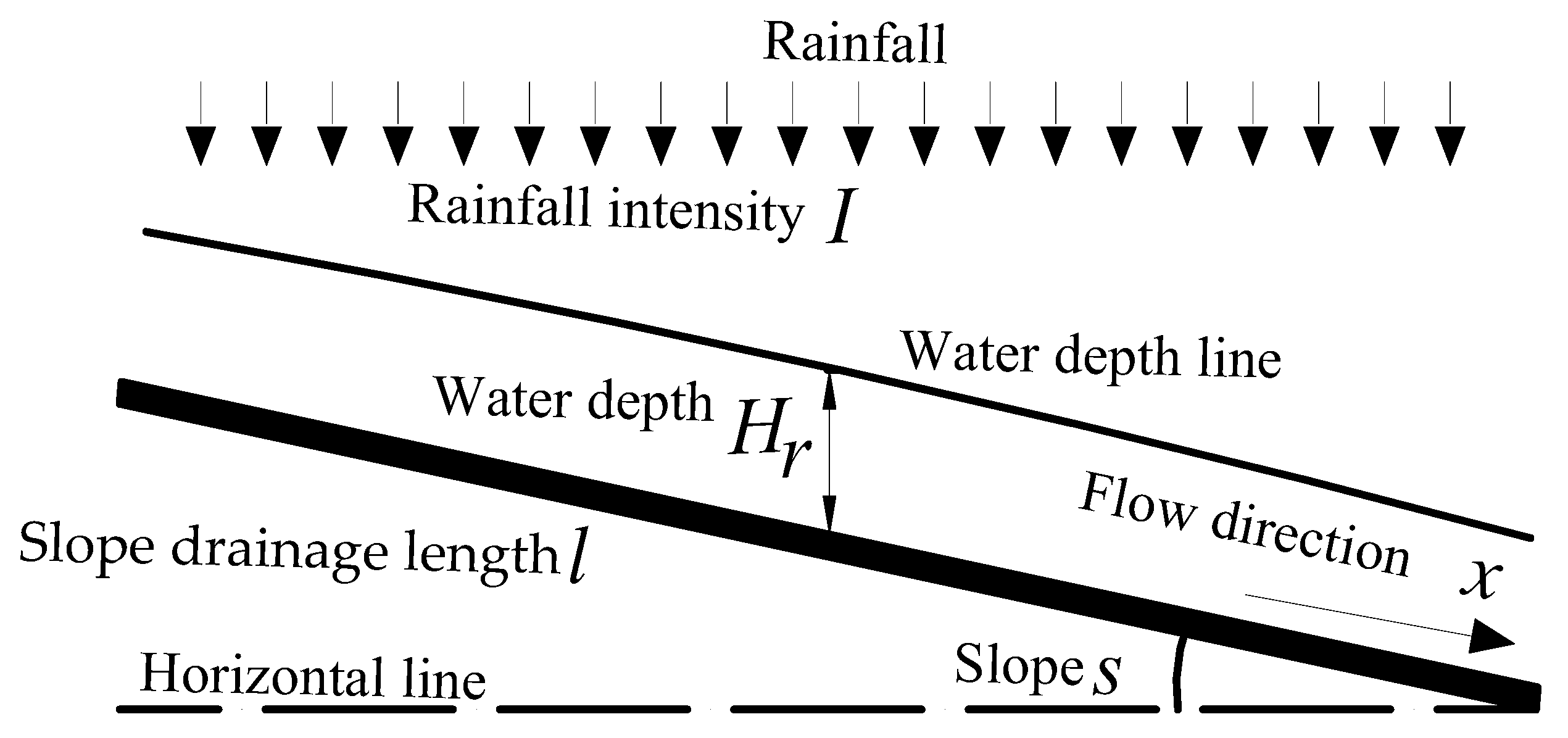
3.2. Water Accumulation Model on the Main Beam Surface
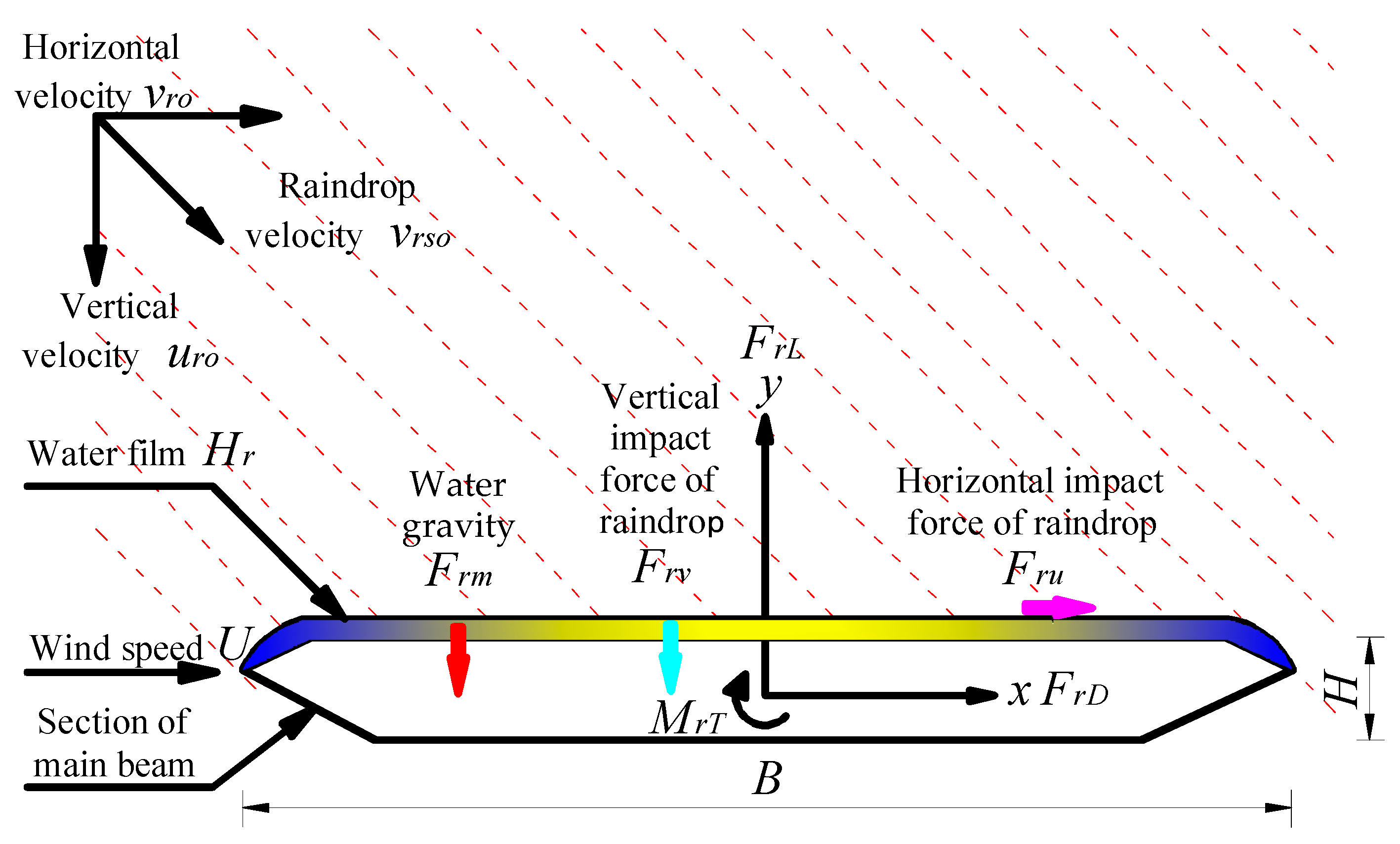
3.3. Analysis of the Wind-Driven Rain Pneumatic Three-Component Force of Main Beam
4. Wind-Driven Rain Aerodynamic Force Test of the Main Beam
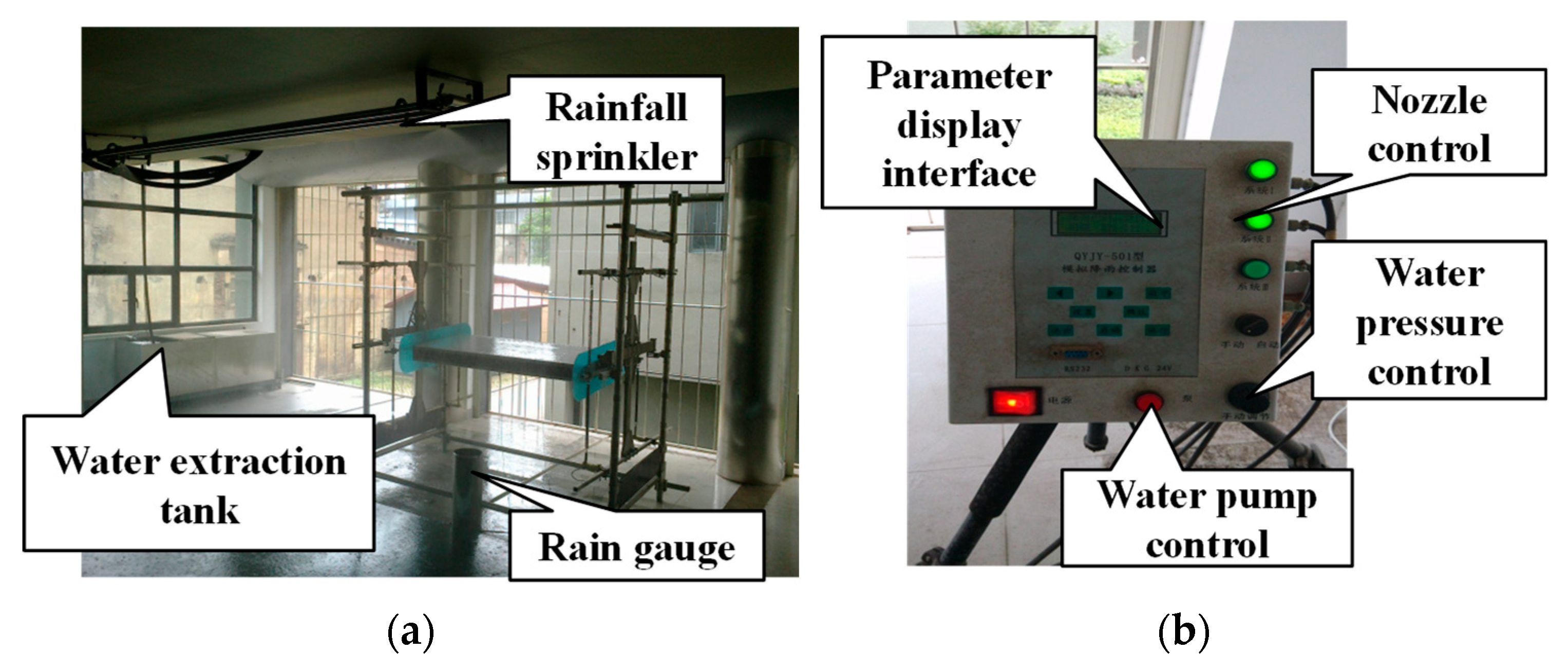
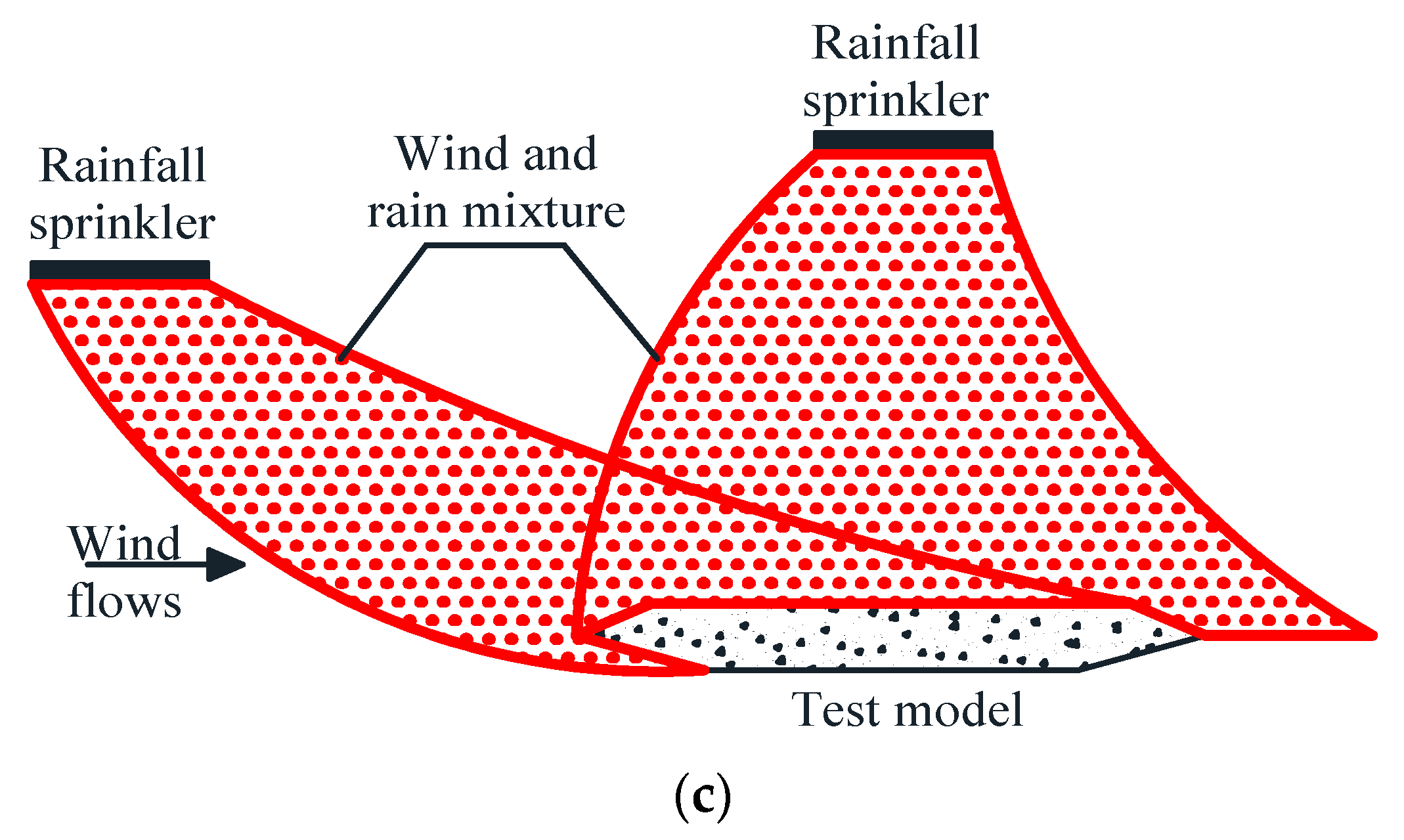
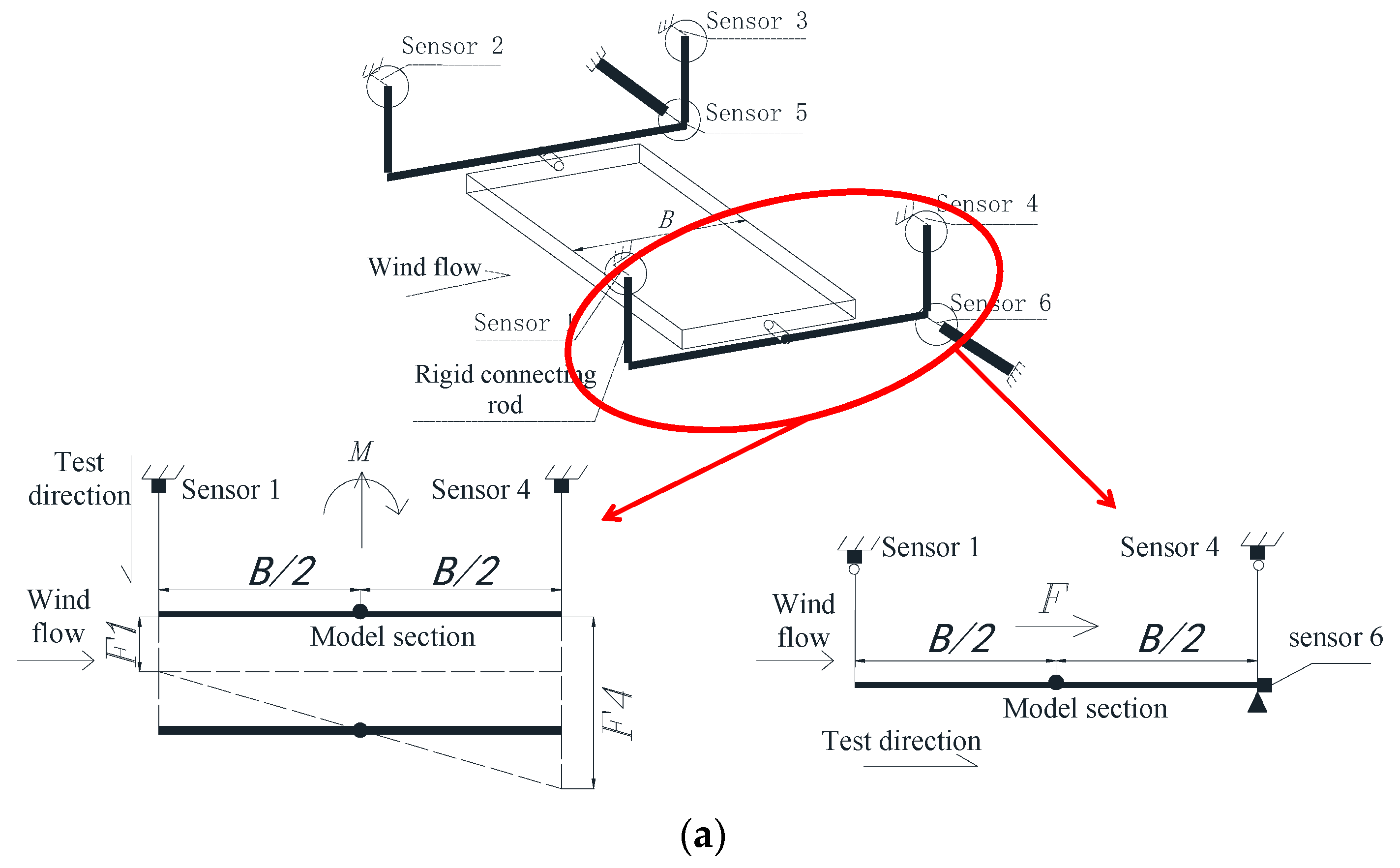
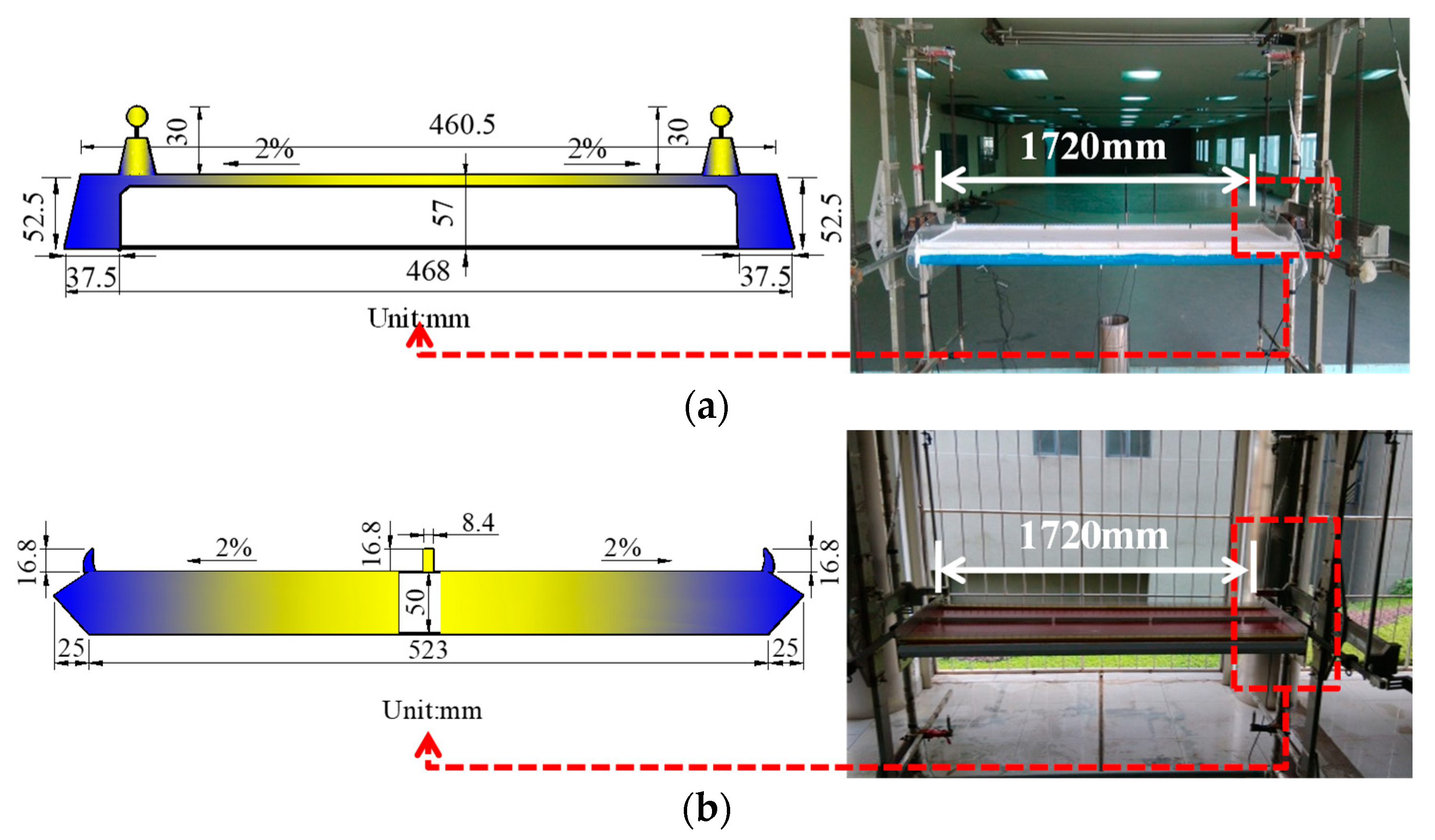
4.1. Overview of the Test
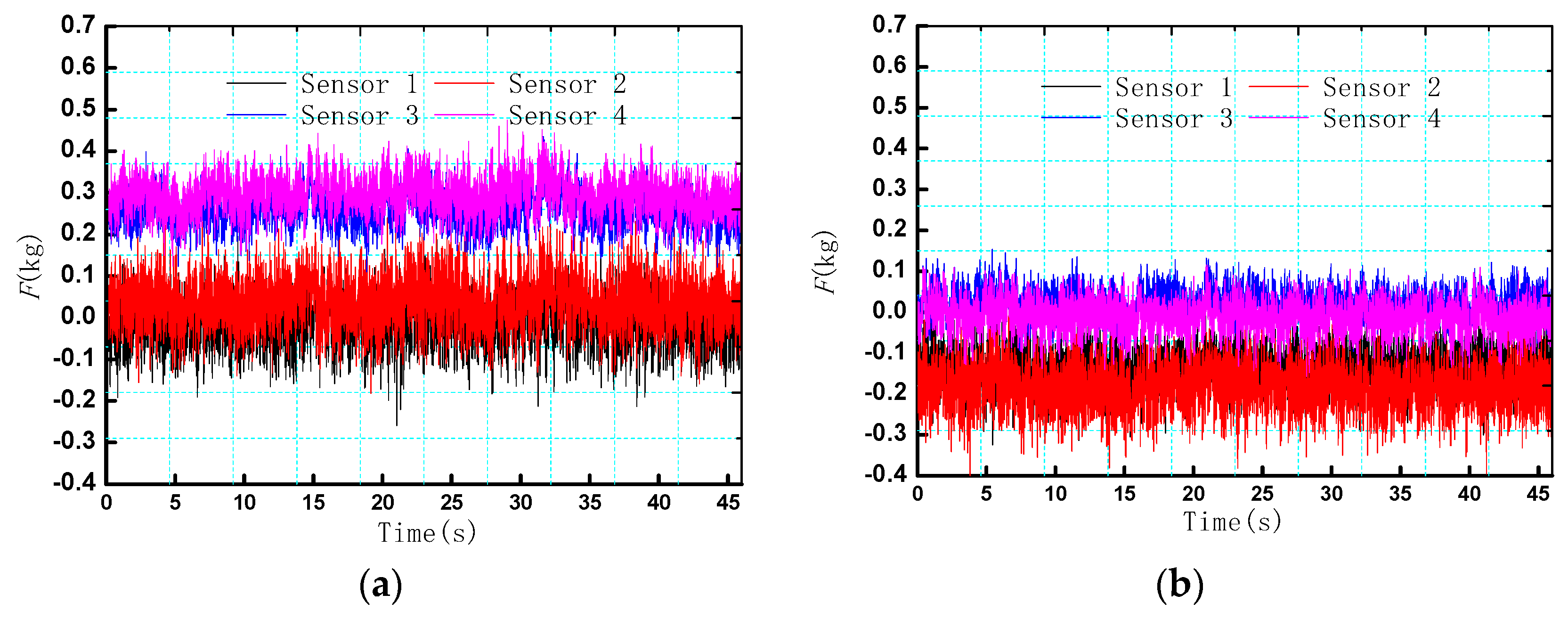
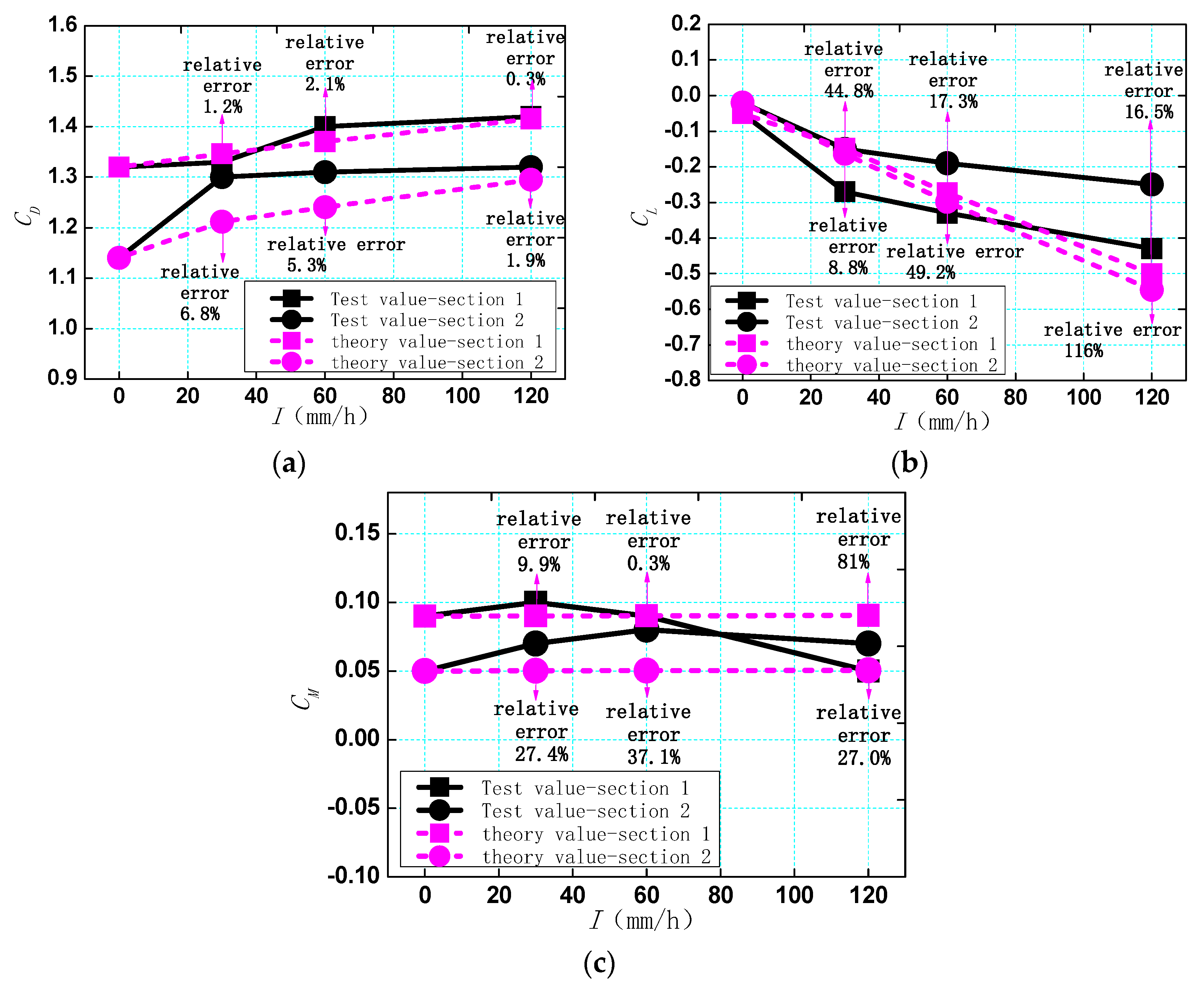
4.2. Test Results and Analysis
5. Discussion
- Firstly, the water content in a unit volume of air, the raindrop size, the raindrop spectral characteristics, and the falling velocity of experimental rainfall and natural rainfall may not be completely consistent, while theoretical calculations ideally use natural rainfall characteristic parameters, which will inevitably lead to a deviation in the results.
- Secondly, under the wind axis coordinate system used in this article, the aerodynamic drag force of the experimental model is mainly affected by the impact force of raindrops, while the aerodynamic lift and torque force, especially for the aerodynamic lift force, are more affected by the gravity of surface water accumulation. This conclusion is consistent with the literature [35,36]. Therefore, the error of surface water accumulation, especially under heavy rain, can cause significant deviation in the results of the surface runoff model. However, the surface water accumulation runoff model used in this article is an empirical model (Equation (20)), but for water accumulation on the surface of the main beam, its accuracy and applicability still need to be verified.
- Thirdly, the reasons for differences in the consistency between theoretical and experimental values of two types of cross-sections is that the side of the streamlined section is in a broken line form, and the lower edge of the side may not be fully impacted by raindrops, due to the obstruction of the upper edge. However, in theoretical calculations, the entire side is treated as a straight line, resulting in an increase in error.
- Finally, the reason the error tends to increase with the increase in rain intensity may be related to the more complex water accumulation state on the surface of the main beam under heavy rain intensity and its influence on the impact force of raindrops. This reason has been mentioned and analyzed in detail in the literature [21,23]. So, in Figure 10, the two maximum deviation values (116% and 81%) both occurred during a rain intensity of 120 mm/h, barring any problems with the rainfall equipment.
6. Conclusions
- 1.
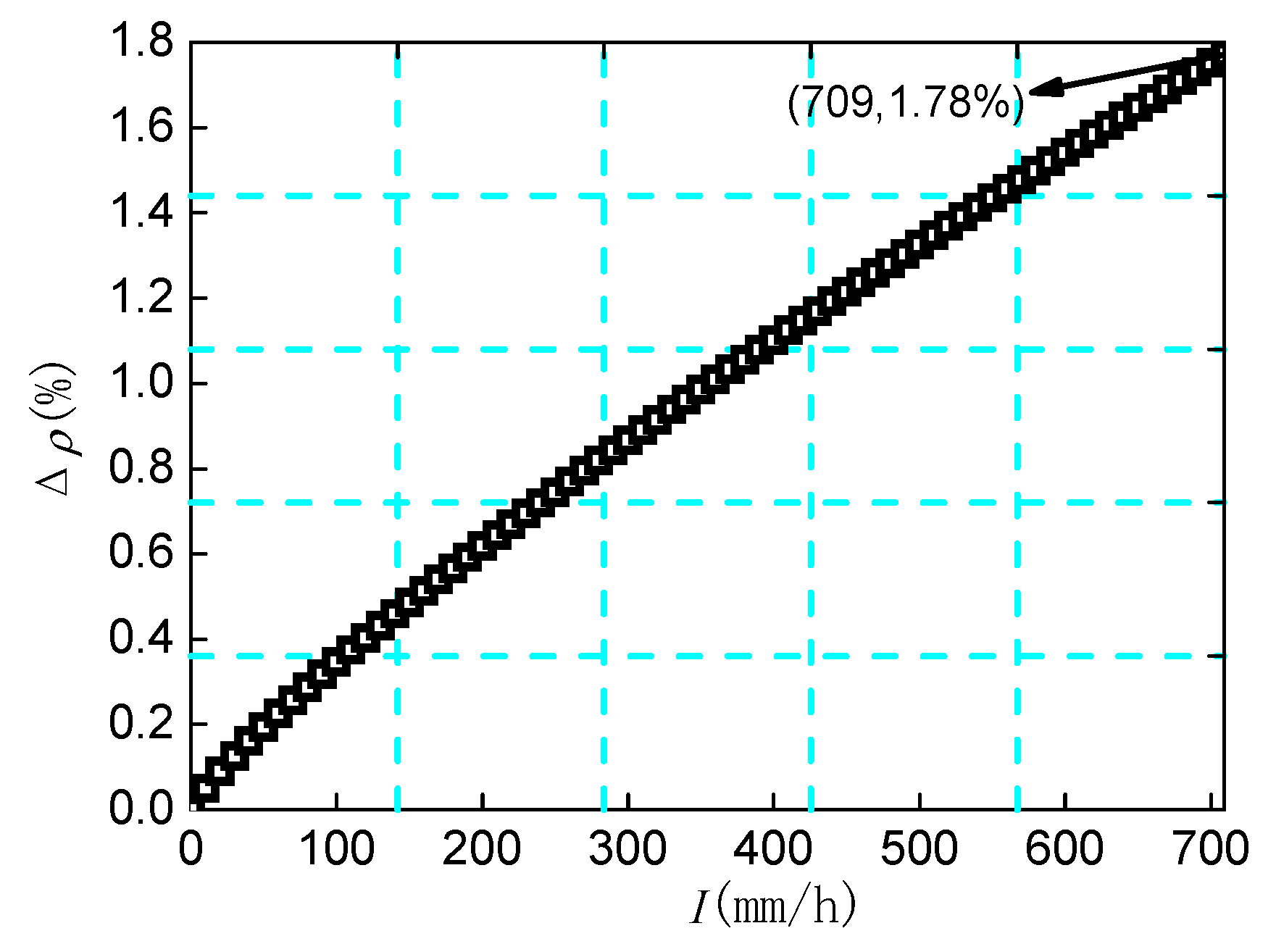
- Even when the rainfall intensity reaches 709 mm/h (extreme value in China), the increase in density of air is less than 2%, and the change in density of air caused by rainfall can be ignored.
- 2.
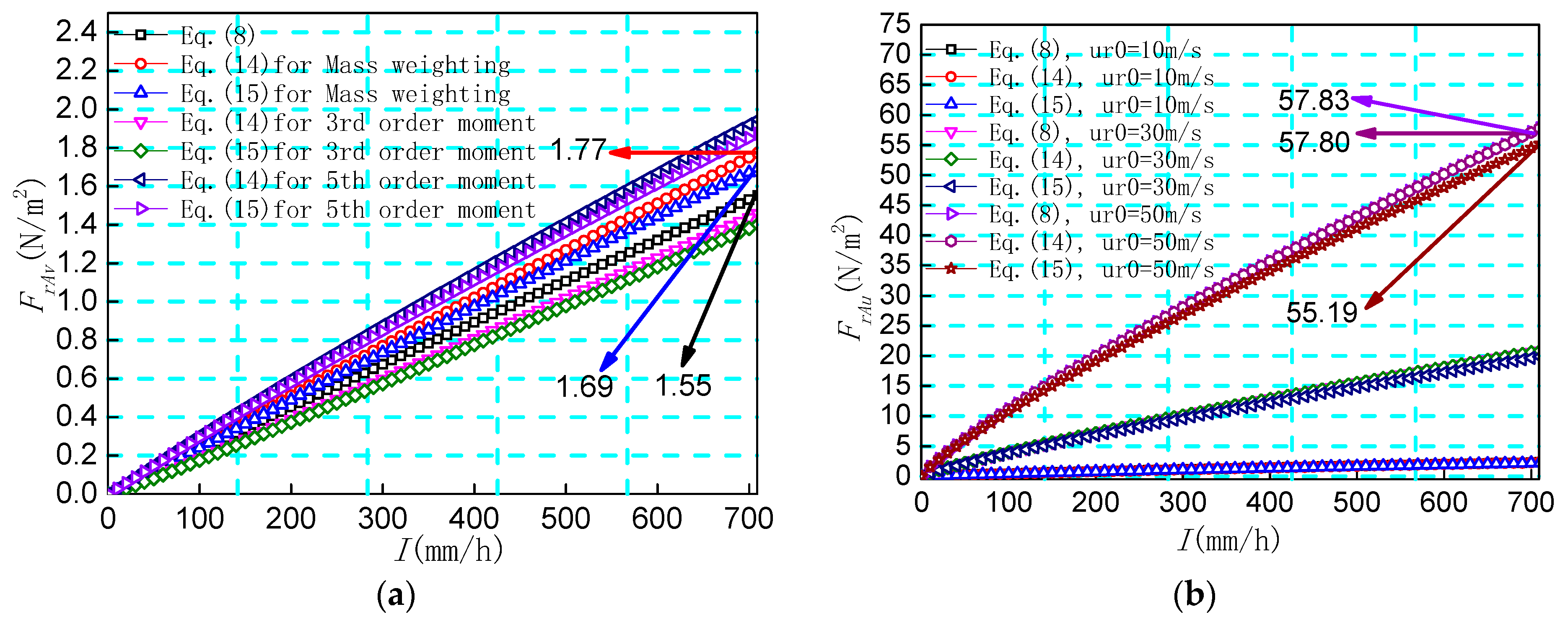
- This article proposes the mass-weighted equivalent method (MWEM) to simplify the calculation process of raindrop impact force. Compared with the theoretical method, the error of the simplified calculation method (MWEM) increases with the increase in rainfall intensity, but even if the rainstorm intensity reaches 709 mm/h, the error is only about 4%, which can meet the accuracy of engineering applications. At the same time, the accuracy of the MWEM is verified through wind-driven rain experiments of two typical bridge main beam sections. It can be used for engineering applications.
- 3.
- For the additional aerodynamic force of the main beam under the action of wind-driven rain, in the wind axis coordinate system used in this article, the drag force mainly considers the impact force of raindrops, which is different from the lift and torque force that must simultaneously consider the impact force of raindrops and the complex water accumulation on the surface of the main beam. Therefore, under the existing empirical formulas for calculating the thickness of accumulated water, there is a significant deviation between the theoretical and experimental results of lift and torque force. Furthermore, it is worth noting that as the rainfall intensity increases, there is also a trend toward an increase in the deviation between theoretical and experimental results. So, the more complex water accumulation state on the surface of the main beam under heavy rain intensity and its influence on the impact force of raindrops need to be further studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, Z. The Bridge Wind Engine Engineering; China Communication Press: Beijing, China, 2005; pp. 1–200. [Google Scholar]
- Rhode, R.V. Some Effects of Rainfall on Flight of Airplanes and on Instrument Indications; Research Report No. ADB814123; Technical Report Archive & Image Library: Washington, DC, USA, 1941. [Google Scholar]
- Haines, P.; Luers, J. Aerodynamic penalties of heavy rain on landing airplanes. J. Aircr. 1983, 20, 111–119. [Google Scholar] [CrossRef]
- Hastings, E.C.; Manuel, G.S. Scale-model tests of airfoils in simulated heavy rain. J. Aircr. 1985, 22, 536–540. [Google Scholar] [CrossRef]
- Bilanin, A.J. Scaling laws for testing airfoils under heavy rainfall. J. Aircr. 1987, 24, 31–37. [Google Scholar] [CrossRef]
- Wan, T.; Wu, S. Aerodynamic analysis under influence of heavy rain. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004. [Google Scholar]
- Douvi, E.C.; Margaris, D.P. Aerodynamic performance investigation under the influence of heavy rain of a NACA 0012 airfoil for wind turbine applications. Int. Rev. Mech. Eng. 2012, 6, 1228–1235. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Z.; Xu, Z. Effects of rainfall on aircraft aerodynamics. Prog. Aerosp. Sci. 2014, 71, 85–127. [Google Scholar] [CrossRef]
- Choi, E.C.C. Wind-driven rain and driving rain coefficient during thunderstorms and non-thunderstorms. J. Wind. Eng. Ind. Aerodyn. 2001, 89, 293–308. [Google Scholar] [CrossRef]
- Blocken, B.; Derome, D.; Cameliet, J. Rainwater runoff from building facades: A review. Build. Environ. 2013, 60, 339–361. [Google Scholar] [CrossRef]
- Huang, S.; Li, Q. Large eddy simulations of wind-driven rain on tall building facades. J. Struct. Eng. 2012, 138, 967–983. [Google Scholar] [CrossRef]
- Erkal, A.; Dayal, A.D.; Sequeir, A.L. Assessment of wind-driven rain impact, related surface erosion and surface strength reduction of historic building materials. Build. Environ. 2012, 57, 336–348. [Google Scholar] [CrossRef]
- Baher, U.T.; Chowdhury, A.G.; Bitsuamlak, G.; Masters, F.J.; Tokay, A. Simulation of wind-driven rain associated with tropical storms and hurricanes using the 12-fan wall of wind. Build. Environ. 2014, 76, 18–29. [Google Scholar] [CrossRef]
- Tian, L.; Zeng, Y. Stat-of-the-art review of structural resistance to wind rain loads. Struct. Eng. 2016, 32, 197–204. [Google Scholar] [CrossRef]
- Tian, L.; Zeng, Y.; Fu, X. Velocity ratio of wind-driven rain and its application on a transmission tower subjected to wind and rain loads. J. Perform. Constr. Facil. 2018, 32, 04018065. [Google Scholar] [CrossRef]
- Baskaran, B.A.; Brown, W.C. Dynamic evaluation of the building envelope for wind and wind-driven rain performance. J. Build. Phys. 1995, 18, 261–275. [Google Scholar] [CrossRef]
- Fu, X.; Li, H. Dynamic analysis of transmission tower-line system subjected to wind and rain load. J. Wind. Eng. Ind. Aerodyn. 2016, 157, 95–103. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.; Huang, S. Large eddy simulation of wind-driven rain effects on a large span retractable roof stadium. J. Wind. Eng. Ind. Aerodyn. 2019, 195, 104009. [Google Scholar] [CrossRef]
- Yu, W.; Ke, S. Flow field characteristics and surface aerodynassmic force of large cooling tower under coupling of wind and rain. J. Nanjing Univ. Aeronaut. Astronaut. 2020, 52, 666–674. [Google Scholar] [CrossRef]
- Yang, Q.; Ke, S.; Yu, W.; Wang, T.; Cao, S. Study of wind-driven rain distribution characteristics for MW level wind turbine under adverse stopped status. Act Energiae Solaris Sin. 2020, 41, 32–40. [Google Scholar]
- Hikami, Y.; Shiraishi, N. Rain-wind vibration of cables in cable-stayed bridges. J. Wind. Eng. Ind. Aerodyn. 1988, 29, 409–419. [Google Scholar] [CrossRef]
- Gu, M.; Du, X. Experimental investigation of rain–wind-induced vibration of cables in cable-stayed bridges and its mitigation. J. Wind. Eng. Ind. Aerodyn. 2005, 93, 79–95. [Google Scholar] [CrossRef]
- Gu, M.; Du, X.; Li, S. Experimental and theoretical simulations on wind–rain induced vibration of 3-D rigid stay cables. J. Sound Vib. 2009, 320, 184–200. [Google Scholar] [CrossRef]
- Matsumoto, M.; Yagi, T.; Sakai, S.; Ohya, J.; Okada, T. Steady wind force coefficients of inclined stay cables with water rivulet and their application to aerodynamics. Wind. Struct. 2005, 8, 107–120. [Google Scholar] [CrossRef]
- Ni, Y.; Wang, X.; Chen, Z.; Ko, J. Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 303–328. [Google Scholar] [CrossRef]
- Liu, Q.; Matsumoto, M.; Yagi, T. LES study on the mechanism of rain-wind induced vibration of cables of cable-stayed bridge. In Proceedings of the 12th International Conference on Wind Engineering, Cairns, Australia, 2–7 July 2007. [Google Scholar]
- Liu, Q.; Qiao, F.; Du, Y. Initial research of precipitation effect on aerodynamic characteristics of basic bluff. J. Shijiazhuang Railw. Inst. 2007, 20, 14–18. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Xu, F.; Li, F.; Ou, J. A numerical and experimental hybrid approach for the investigation of aerodynamic forces on stay cables suffering from rain-wind induced vibration. J. Fluids Struct. 2010, 26, 1195–1215. [Google Scholar] [CrossRef]
- Xin, D. Wind-Rain Induced Flutter Stability Analysis and Boundary Layer Control Methods of Bridges. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Xin, D.; Li, H.; Wang, L.; Ou, J. Experimental study on static characteristics of the bridge deck section under simultaneous actions of wind and rain. J. Wind. Eng. Ind. Aerodyn. 2012, 107, 17–27. [Google Scholar] [CrossRef]
- Hu, J. Study on the In-Field Measured Data, Wind Rain Action and Wind-Induced Fatigue of a Long-Span Suspension Bridge. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Zhao, L.; Ge, Y.; Wu, Z.; Xu, L. Theoretic and testing investigation of wind-rain coupling loads on bridges and structures. J. Vib. Eng. 2014, 27, 507–517. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, J.; Xue, F.; Cai, C.; Han, Y. Numerical simulation of wind-rain coupling effect on typical bridge section based on lagrangian system. J. Hunan Univ. 2017, 27, 507–517. [Google Scholar] [CrossRef]
- Liu, S.; Huang, S.; Li, Q.; Chen, F.B. 3D numerical simulation of wind-driven rain on bridge deck sections based on eulerian multiphase model. Eng. Mech. 2017, 34, 63–71. [Google Scholar] [CrossRef]
- Huang, S.; Li, Q.; Liu, M.; Chen, F.; Liu, S. Numerical simulation of wind-driven rain on a long-span bridge. Int. J. Struct. Stab. Dyn. 2019, 19, 1950149. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Atmos. Sci. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Atmos. Sci. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Ji, T. The Influence of Rainfall on the Tire and Road Adhesion Coefficient. Ph.D. Thesis, Southeast University, Nanjing, China, 2004. [Google Scholar]


| Rain Intensity Level | Light Rain | Moderate Rain | Heavy Rain | Rainstorm | Weak Heavy Rainstorm | Medium Heavy Rainstorm | Strong Rainstorm | Domestic Extreme Value |
|---|---|---|---|---|---|---|---|---|
| Precipitation (mm/h) | 2.5 | 8 | 16 | 32 | 64 | 100 | 200 | 709.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Shen, L.; Chen, Z.; Zhang, X.; Wei, C.; Han, Y. Theoretical Calculation and Experimental Verification of Wind-Driven Rain Aerodynamic Forces on the Bridge Main Beam. Atmosphere 2023, 14, 1535. https://doi.org/10.3390/atmos14101535
Lei X, Shen L, Chen Z, Zhang X, Wei C, Han Y. Theoretical Calculation and Experimental Verification of Wind-Driven Rain Aerodynamic Forces on the Bridge Main Beam. Atmosphere. 2023; 14(10):1535. https://doi.org/10.3390/atmos14101535
Chicago/Turabian StyleLei, Xu, Lian Shen, Zhengqing Chen, Xuewen Zhang, Chenglong Wei, and Yan Han. 2023. "Theoretical Calculation and Experimental Verification of Wind-Driven Rain Aerodynamic Forces on the Bridge Main Beam" Atmosphere 14, no. 10: 1535. https://doi.org/10.3390/atmos14101535
APA StyleLei, X., Shen, L., Chen, Z., Zhang, X., Wei, C., & Han, Y. (2023). Theoretical Calculation and Experimental Verification of Wind-Driven Rain Aerodynamic Forces on the Bridge Main Beam. Atmosphere, 14(10), 1535. https://doi.org/10.3390/atmos14101535





