An Ensemble Model for PM2.5 Concentration Prediction Based on Feature Selection and Two-Layer Clustering Algorithm
Abstract
:1. Introduction
1.1. Related Works
1.2. Novelty of the Study
- (a)
- We employ a multi-objective optimization algorithm for selecting features from atmospheric pollutant and meteorological factor datasets that influence PM2.5 concentration, thereby supplying valuable feature data input for subsequent modules. Specifically, we use the non-dominated sorting genetic algorithm-III (NSGA-III) to compute the weight coefficient between the multi-factor feature variables and PM2.5 concentration prediction. By comparing this with a defined threshold value, we select Pareto-optimal input feature variables.
- (b)
- The features selected using the multi-objective optimization algorithm are subsequently clustered, further mining the irregularity of the multi-factor dataset and establishing a weak learner for each class. This enables data with high similarity to be predicted under the same model. In our study, we adopt a two-layer clustering method (initially using the SOM neural network, followed by K-means clustering). This method’s primary advantage lies in noise reduction, as the prototype of SOM constitutes average data, exhibiting lower sensitivity to random changes than the original data [25].
- (c)
- In our model, we harness the reinforcement learning method in ensemble learning to curtail the bias of preceding weak learners through iterative training, dynamically adjust the weight distribution of multiple weak learners, and ultimately transform these trained weak learners into a robust learner through linear combination. Specifically, we utilize the AdaBoost algorithm for integrating the weak learner composed of multiple extreme learning machine models. The resulting integrated prediction model seeks to enhance prediction accuracy.
2. Materials and Methods
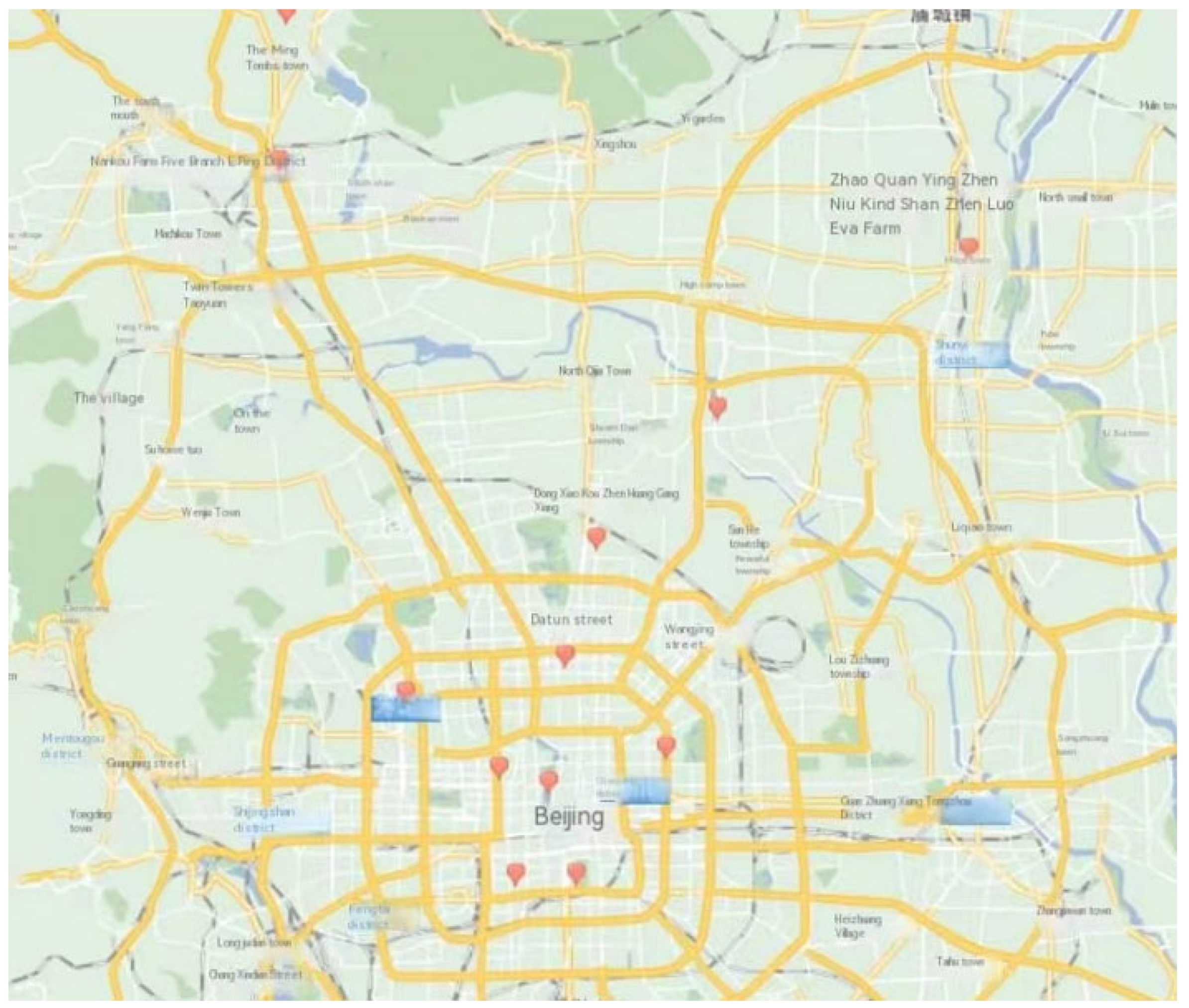
2.1. Description of Experimental Data
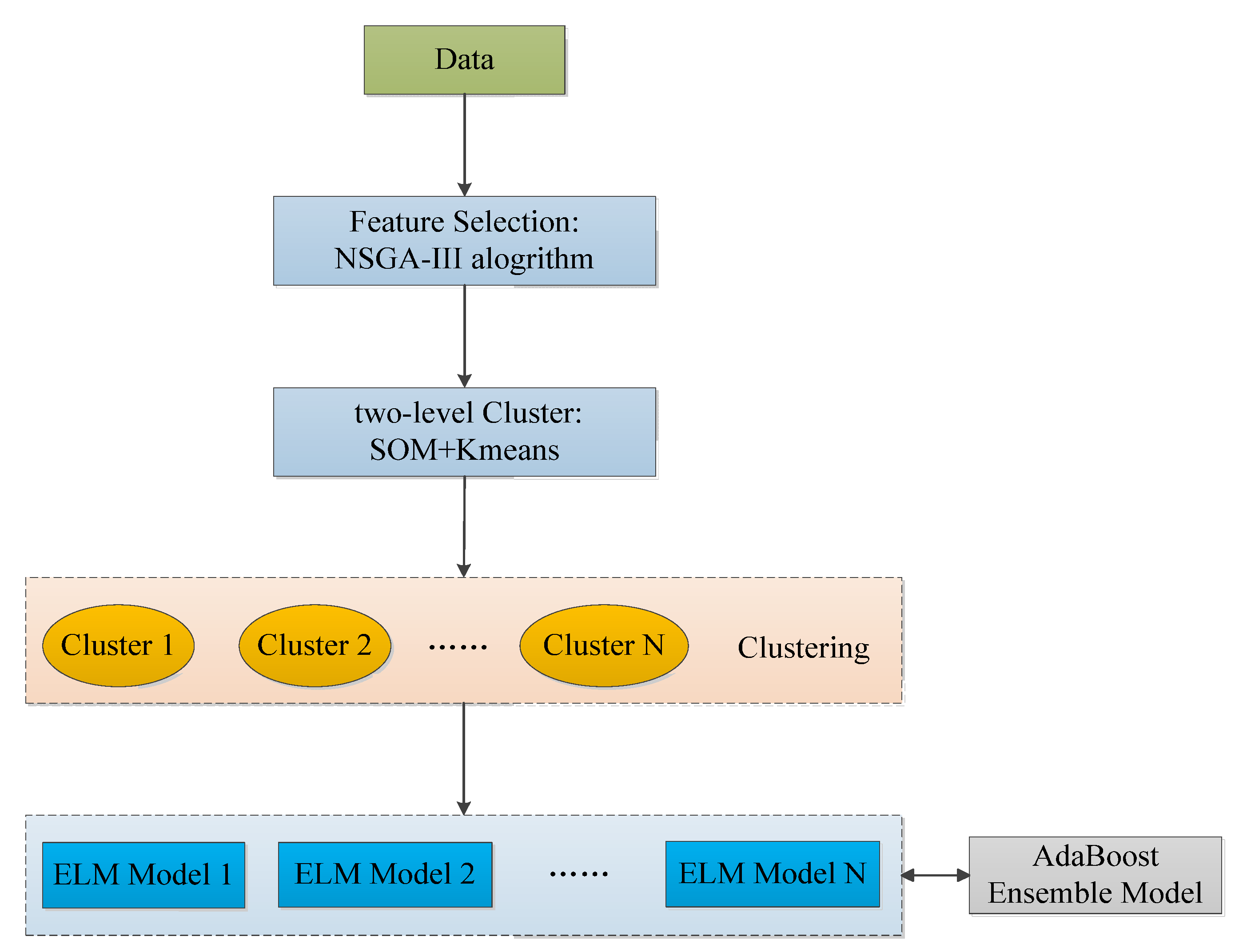
2.2. Framing
- The utilization of NSGA-III for feature selection;
- Implementation of a two-layer clustering method (SOM-Kmeans) to cluster data post feature selection;
- Use the ELM model for the clustered data resulting from each cluster;
- Lastly, integration with AdaBoost is facilitated to realize the prediction of the PM2.5 concentration.
2.3. Feature Selection: Multi-Objective Optimization: NSGA-III Algorithm
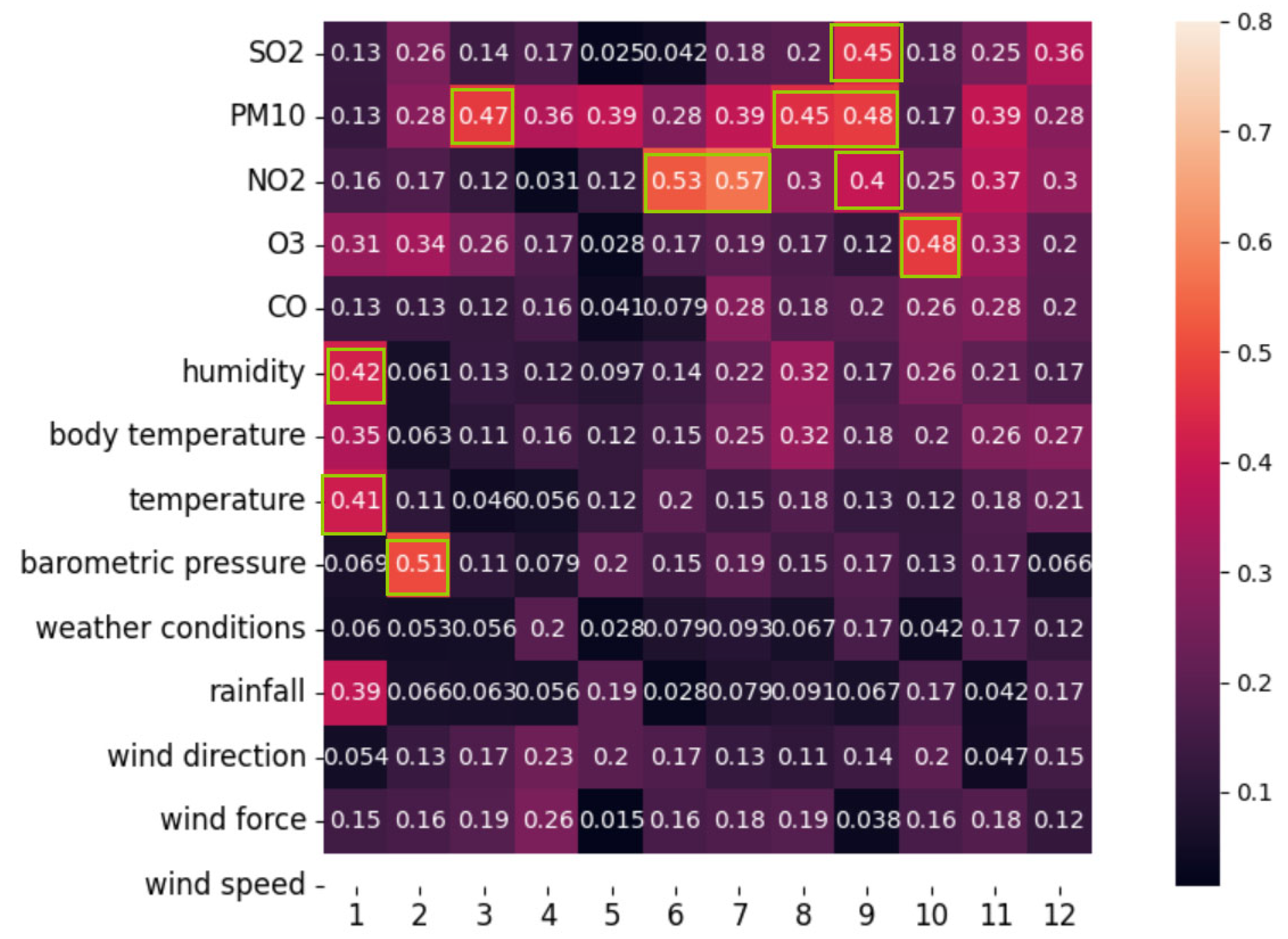
- The primary variables include PM10, CO, SO2, NOx, O3, air temperature, sensible temperature, air pressure, humidity, rainfall, wind direction, wind power, and wind speed, totaling 13 factors
- The focus for prediction is the PM2.5 concentration, identified as our target feature
- The Extreme Learning Machine (ELM) model is used individually with each feature as an input for prediction. Each feature’s predictive capability is assessed and an aggregated prediction is achieved using weighted reconstruction (Equation (1)),
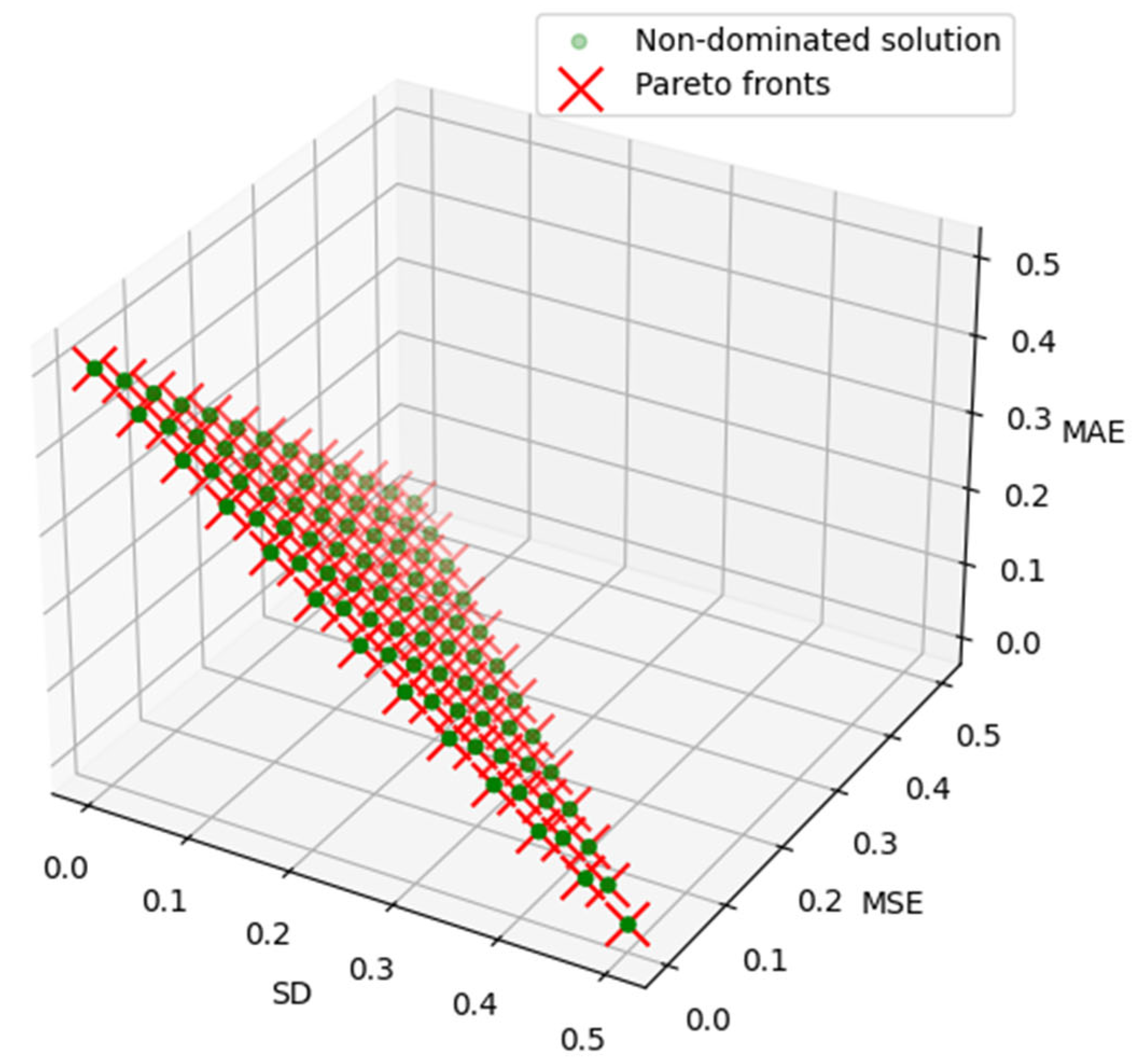
- The evaluation is objective using the NSGA-III algorithm, taking into account the mean square error (MSE), Mean Absolute Error (MAE), and standard deviation (SD). These metrics, outlined in Equation (2) through (4), are deployed to measure the divergence between the predicted results and the actual values accurately,
- To realize multi-objective optimization featuring Mean Absolute Error (MAE), Mean Square Error (MSE), and Standard Deviation (SD), we harness the capabilities of the NSGA-III algorithm. Our strategy embodies an iterative search for a weight-set that concurrently minimizes MAE, MSE, and SD. Given the defined threshold value—, only those features that comply with the condition are selected. This precision-guided approach enables us to optimize feature selection effectively.
2.4. Two-Layer Clustering
2.5. Prediction Model
- (a)
- From the collection of weak classifiers, identify the classifier with the lowest current error rate. This is designated as the -base classifier, , and calculate its value . The corresponding error and distribution of the weak classifier are enumerated in Equation (7).
- (b)
- Ascertain the weight of the weak classifier within the final classifier ensemble (Equation (8)).
- (c)
- Update the weight distribution (Equation (9)) for the training sample set.
3. Case Study
3.1. Evaluation Criteria
3.2. Experimental Design
3.2.1. The NSGA-III Based Feature Selection Method Analysis
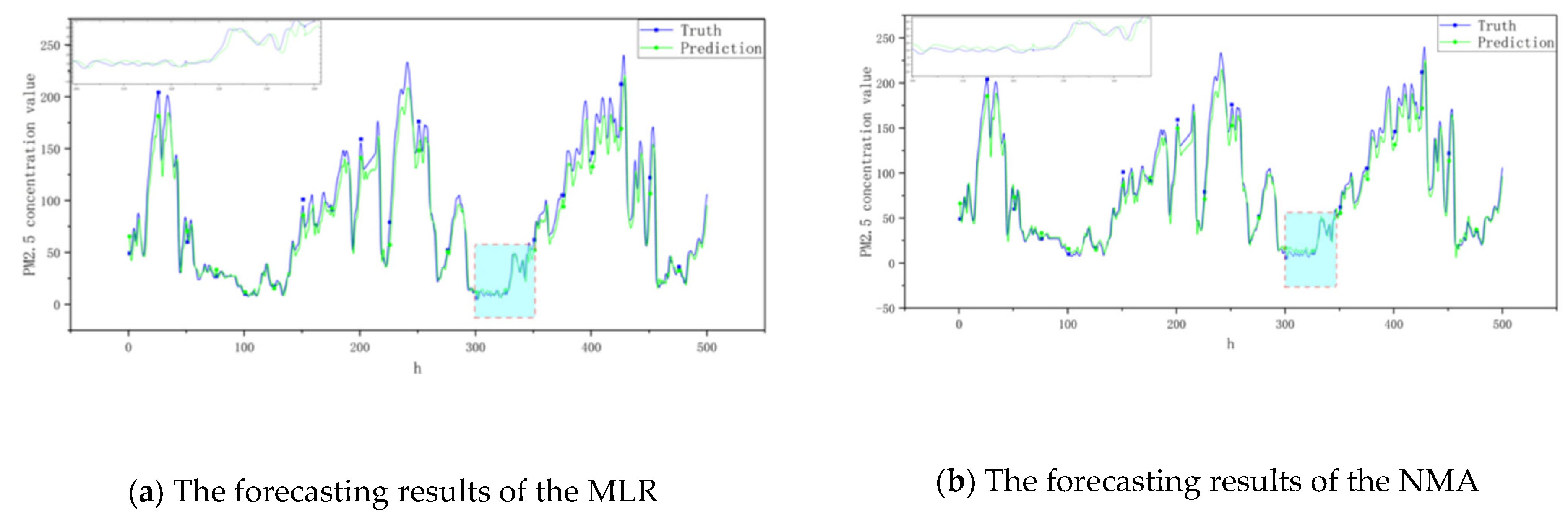
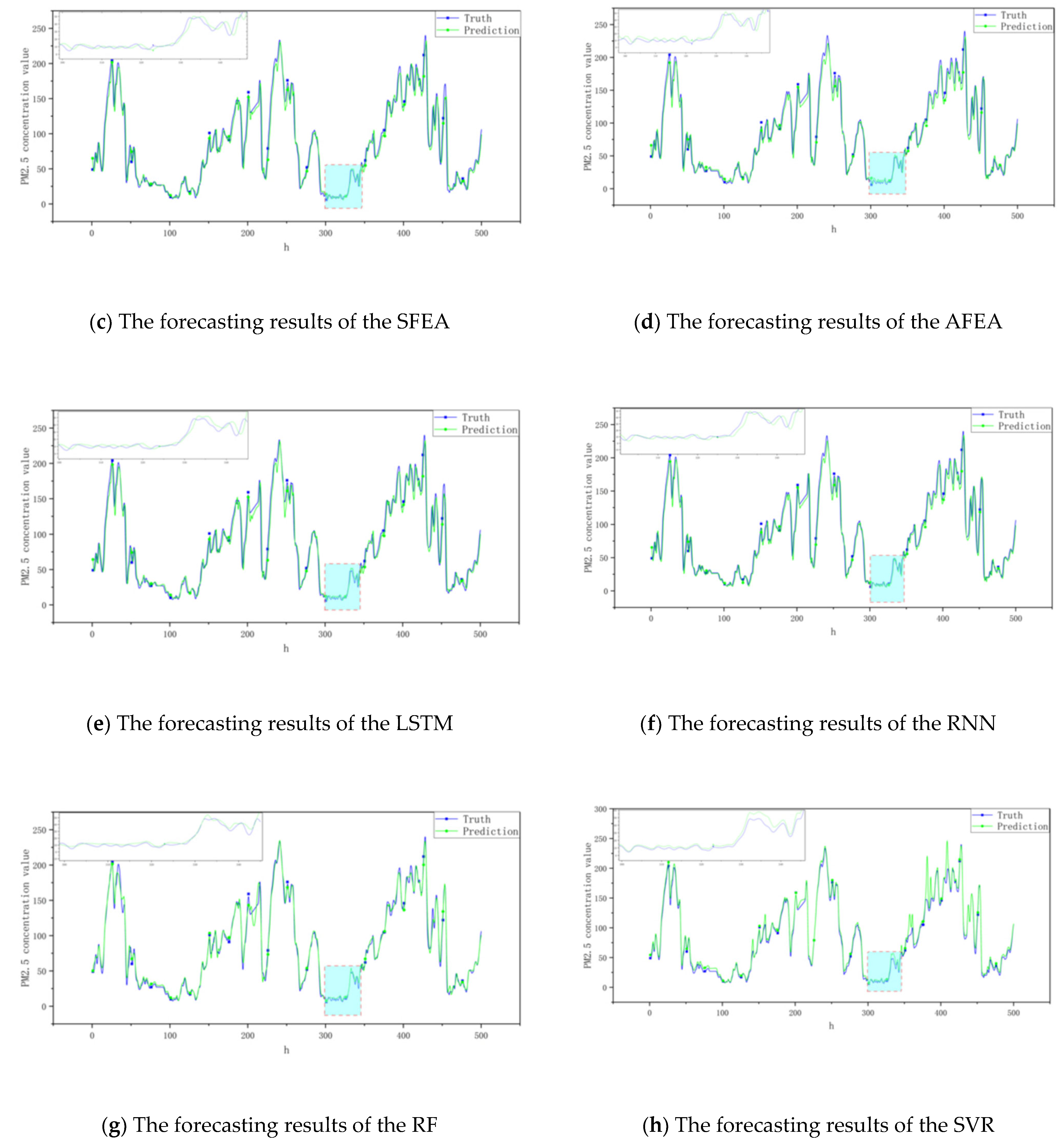
3.2.2. Ensemble Model Analysis
3.3. Discussion
4. Conclusions
- (1)
- The model outlined herein enhances PM2.5 concentration prediction accuracy. Demonstrating significant adaptability, the NSKEA model capably mines data, evident in its performance amidst PM2.5 seasonal fluctuations.
- (2)
- Implementing multi-objective optimization for multi-factor feature selection supports enhanced diversity preservation, consequential in advancing the predictive model’s precision.
- (3)
- The study employed the ELM as a weak learner without considering variations in the prediction model in light of diverse basic learners. Future research will explore this area further, focusing on identifying the optimal basic learner to enhance the robustness and accuracy of the integrated predictive model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jamei, M.; Ali, M.; Malik, A.; Karbasi, M.; Sharma, E.; Yaseen, Z.M. Air quality monitoring based on chemical and meteorological drivers: Application of a novel data filteringbased hybridized deep learning model. J. Clean. Prod. 2022, 374, 134011. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short term PM2.5 concentration forecasting. Atmos. Environ. 2016, 134, 168–180. [Google Scholar] [CrossRef]
- Yin, S.; Liu, H.; Duan, Z. Hourly PM2.5 concentration multi-step forecasting method based on extreme learning machine, boosting algorithm and error correction model. Digit. Signal Process. 2021, 118, 103221. [Google Scholar] [CrossRef]
- Ren, C.R.; Xie, G. Prediction of PM2.5 concentration level based on random forest and meteorological parameters. Comput. Eng. Appl. 2019, 55, 213–220. [Google Scholar]
- Hong, K.Y.; Pinheiro, P.O.; Weichenthal, S. Predicting global variations in outdoor PM2.5 concentrations using satellite images and deep convolutional neural networks. arXiv 2019, arXiv:1906.03975v1. [Google Scholar]
- Wu, X.X.; Zhang, C.; Zhu, J.; Zhang, X. Research on PM2.5 concentration prediction based on the CE-AGA-LSTM model. Appl. Sci. 2022, 12, 7009. [Google Scholar] [CrossRef]
- Pruthi, D.; Liu, Y. Low-cost nature-inspired deep learning system for PM2.5 forecast over Delhi, India. Environ. Int. 2022, 166, 107373. [Google Scholar] [CrossRef]
- Zaini, N.; Ean, L.W.; Ahmed, A.N.; Malek, M.A.; Chow, M.F. PM2.5 forecasting for an urban area based on deep learning and decomposition method. Sci. Rep. 2022, 12, 17565. [Google Scholar] [CrossRef]
- Li, W.L.; Jiang, X.C. Prediction of air pollutant concentrations based on TCN-BiLSTM-DMAttention with STL decomposition. Sci. Rep. 2023, 13, 4665. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Chang, F.J.; Chang, L.C.; Kao, I.F.; Wang, Y.S. Explore a deep learning multi-output neural network for regional multi-step-ahead air quality forecasts. J. Clean. Prod. 2019, 209, 134–145. [Google Scholar] [CrossRef]
- Hu, S.; Liu, P.F.; Qiao, Y.X.; Wang, Q.; Zhang, Y.; Yang, Y. PM2.5 concentration prediction based on WD-SA-LSTM-BP model: A case study of Nanjing city. Environ. Sci. Pollut. Res. 2022, 29, 70323–70339. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Zhang, F.; Du, Z.H.; Liu, R.Y.; Cao, X.P. Hourly concentration prediction of PM2.5 based on RNN-CNN ensemble deep learning model. J. Zhejiang Univ. (Sci. Ed.) 2019, 46, 370–379. [Google Scholar]
- Liu, X.L.; Tan, W.A.; Tang, S. A Bagging-GBDT ensemble learning model for city air pollutant concentration prediction. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Gothenburg, Sweden, 8–12 October 2019. [Google Scholar]
- Liu, H.; Yang, R. A spatial multi-resolution multi-objective data-driven ensemble model for multi-step air quality index forecasting based on real-time decomposition. Comput. Ind. 2021, 125, 103387. [Google Scholar] [CrossRef]
- Liu, B.; Tan, X.H.; Jin, Y.Q.; Yu, W.W.; Li, C.Y. Application of RR-XGBoost combined model in data calibration of micro air quality detector. Sci. Rep. 2021, 11, 15662. [Google Scholar] [CrossRef] [PubMed]
- Joharestani, M.; Cao, C.X.; Ni, X.L.; Bashir, B.; Joharestani, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef]
- Wei, L.X.; Zhang, L.Y.; Wang, H. Impact analysis and simulation study of air pollution and meteorological conditions in Baoding city. Environ. Dev. 2018, 30, 162–163. [Google Scholar]
- Liu, T.; Wu, M.P.; Zhang, K.D.; Liu, Y.; Zhong, J. Correlation Analysis and Control Scheme Research on PM2.5. Appl. Mech. Mater. 2014, 590, 888–894. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, M.E.; Zhang, H.X. Correlation between atmospheric PM2.5 concentration and meteorological factors during summer and autumn in Beijing, China. J. Appl. Ecol. 2014, 25, 2695–2699. [Google Scholar]
- Wei, Y.Y.; Chen, Z.Z.; Zhao, C.; Chen, X.; He, J.H.; Zhang, C.Y. A time-varying ensemble model for ship motion prediction based on feature selection and clustering methods. Ocean Eng. 2023, 270, 113659. [Google Scholar] [CrossRef]
- Redkar, S.; Mondal, S.; Joseph, A.; Hareesha, K.S. A machine learning approach for drug-target interaction prediction using wrapper feature selection and class balancing. Mol. Inform. 2020, 39, 1900062. [Google Scholar] [CrossRef]
- Wu, H.P.; Liu, H.; Duan, Z. PM2.5 concentrations forecasting using a new multi-objective feature selection and ensemble framework. Atmos. Pollut. Res. 2020, 11, 1187–1198. [Google Scholar] [CrossRef]
- Got, A.; Moussaoui, A.; Zouache, D. Hybrid filter-wrapper feature selection using whale optimization algorithm: A multi-objective approach. Expert Syst. Appl. 2021, 183, 115312. [Google Scholar] [CrossRef]
- Han, F.; Chen, W.T.; Ling, Q.H.; Han, H. Multi-objective particle swarm optimization with adaptive strategies for feature selection. Swarm Evol. Comput. 2021, 62, 100847. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Fei, P.; Li, Z.; Zhu, D.; Yu, X. Multi-objective multi-learner robot trajectory prediction method for IoT mobile robot systems. Electronics 2022, 11, 2094. [Google Scholar]
- Wang, Y.K.; Chen, X.B. A joint optimization QSAR model of fathead minnow acute toxicity based on a radial basis function neural network and its consensus modeling. RSC Adv. 2020, 10, 21292–21308. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.Y.; Chen, Z.Z.; Zhao, C.; Chen, X.; He, J.H.; Zhang, C.Y. A threestage multi-objective heterogeneous integrated model with decompositionreconstruction mechanism and adaptive segmentation error correction method for ship motion multi-step prediction. Adv. Eng. Inform. 2023, 56, 101954. [Google Scholar] [CrossRef]
- Yang, X.T.; Bao, Z.X.; Wang, G.Q.; Liu, C.S.; Jin, J.L. Trends and changes in hydrologic cycle in the Huanghuaihai river basin from 1956 to 2018. Water 2022, 14, 2148. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]


| Weather Conditions | Code | Weather Conditions | Code |
|---|---|---|---|
| Clear | 1 | Fog | 10 |
| Haze | 2 | Rain and snow | 11 |
| Cloudy | 3 | Snow | 12 |
| Yin | 4 | Moderate to heavy snow | 13 |
| Light rain | 5 | Heavy Snow | 14 |
| Moderate to heavy rain | 6 | Heavy to blizzard | 15 |
| Heavy rain | 7 | Floating dust | 16 |
| Showers | 8 | Medium Rain | 17 |
| Thundershowers | 9 | Rainstorm | 18 |
| Wind Direction | Code |
|---|---|
| North Wind | 1 |
| Northeast Wind | 2 |
| East Wind | 3 |
| Southeast Wind | 4 |
| South Wind | 5 |
| Southwest Wind | 6 |
| West Wind | 7 |
| Northwest Wind | 8 |
| Wind Power | Code |
|---|---|
| Breeze | 1 |
| Level 1 | 2 |
| Level 2 | 3 |
| Level 3 | 4 |
| Level 4 | 5 |
| Level 5 | 6 |
| Criteria | Definition |
|---|---|
| RMSE | |
| IA |
| Models | Parameters | Values |
|---|---|---|
| NSGA-III | Maximum number of iterations | 400 |
| Population size | 100 | |
| Mutation percentage | 0.5 | |
| Crossover percentage | 0.5 | |
| Mutation rate | 0.03 | |
| Cross parameter | 20 | |
| Mutation parameter | 20 | |
| ELM | Number of hidden neurons | 20 |
| Activation function | sigmoid | |
| AdaBoost | Learning rate | 1, there is a trade-off between learning rate and maximum integration number |
| Maximum integration number | 50 |
| Monitoring Point Dataset | Model | Criteria | Monitoring Point Dataset | Model | Criteria | ||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | IA | MAE | RMSE | IA | ||||
| 1 | NSKEA | 13.418 | 21.401 | 0.95 | 7 | NSKEA | 13.418 | 21.401 | 0.95 |
| NEA | 15.241 | 22.127 | 0.92 | NEA | 14.521 | 22.064 | 0.92 | ||
| SFEA | 17.727 | 25.671 | 0.87 | SFEA | 16.702 | 25.717 | 0.88 | ||
| AFEA | 16.502 | 24.518 | 0.90 | AFEA | 16.217 | 24.601 | 0.91 | ||
| RNN | 17.031 | 25.126 | 0.89 | RNN | 17.258 | 25.102 | 0.89 | ||
| LSTM | 16.557 | 24.673 | 0.82 | LSTM | 16.343 | 24.720 | 0.83 | ||
| MLR | 20.826 | 28.855 | 0.71 | MLR | 20.520 | 28.728 | 0.73 | ||
| SVR | 17.782 | 26.703 | 0.79 | SVR | 17.681 | 26.537 | 0.80 | ||
| RF | 16.364 | 26.114 | 0.81 | RF | 16.305 | 26.246 | 0.81 | ||
| 2 | NSKEA | 13.418 | 21.401 | 0.95 | 8 | NSKEA | 13.418 | 21.401 | 0.95 |
| NEA | 15.026 | 22.536 | 0.92 | NEA | 14.414 | 23.212 | 0.93 | ||
| SFEA | 17.838 | 25.603 | 0.82 | SFEA | 17.515 | 25.372 | 0.82 | ||
| AFEA | 16.882 | 24.126 | 0.87 | AFEA | 16.683 | 24.505 | 0.85 | ||
| RNN | 17.524 | 25.331 | 0.83 | RNN | 17.518 | 25.002 | 0.83 | ||
| LSTM | 16.266 | 24.791 | 0.85 | LSTM | 16.206 | 24.751 | 0.88 | ||
| MLR | 20.244 | 28.855 | 0.71 | MLR | 21.206 | 28.506 | 0.70 | ||
| SVR | 17.313 | 26.703 | 0.77 | SVR | 17.534 | 26.643 | 0.80 | ||
| RF | 16.654 | 26.114 | 0.81 | RF | 17.028 | 25.811 | 0.84 | ||
| 3 | NSKEA | 13.418 | 21.401 | 0.95 | 9 | NSKEA | 13.418 | 21.401 | 0.95 |
| NEA | 14.857 | 22.822 | 0.92 | NEA | 14.138 | 23.222 | 0.92 | ||
| SFEA | 17.685 | 26.101 | 0.81 | SFEA | 17.371 | 25.618 | 0.80 | ||
| AFEA | 15.863 | 25.237 | 0.88 | AFEA | 16.617 | 24.379 | 0.85 | ||
| RNN | 17.106 | 25.639 | 0.84 | RNN | 17.113 | 25.338 | 0.82 | ||
| LSTM | 16.313 | 24.604 | 0.86 | LSTM | 16.653 | 24.472 | 0.88 | ||
| MLR | 20.933 | 28.360 | 0.73 | MLR | 20.637 | 28.537 | 0.75 | ||
| SVR | 17.462 | 26.813 | 0.80 | SVR | 17.073 | 26.612 | 0.81 | ||
| RF | 16.578 | 25.807 | 0.81 | RF | 16.511 | 25.377 | 0.84 | ||
| 4 | NSKEA | 13.418 | 21.401 | 0.95 | 10 | NSKEA | 13.418 | 21.401 | 0.95 |
| NEA | 14.776 | 21.702 | 0.93 | NEA | 14.538 | 22.502 | 0.91 | ||
| SFEA | 17.371 | 25.419 | 0.83 | SFEA | 17.219 | 25.421 | 0.82 | ||
| AFEA | 15.013 | 24.665 | 0.87 | AFEA | 16.619 | 24.315 | 0.87 | ||
| RNN | 17.077 | 25.028 | 0.85 | RNN | 17.787 | 24.801 | 0.83 | ||
| LSTM | 16.326 | 24.552 | 0.89 | LSTM | 16.175 | 24.390 | 0.85 | ||
| MLR | 21.212 | 28.527 | 0.75 | MLR | 20.667 | 28.677 | 0.77 | ||
| SVR | 17.650 | 26.539 | 0.80 | SVR | 17.751 | 26.414 | 0.80 | ||
| RF | 16.283 | 25.367 | 0.84 | RF | 16.566 | 25.361 | 0.84 | ||
| 5 | NSKEA | 13.418 | 21.401 | 0.95 | 11 | NSKEA | 13.418 | 21.401 | 0.95 |
| NEA | 14.872 | 22.108 | 0.91 | NEA | 14.716 | 22.667 | 0.92 | ||
| SFEA | 17.983 | 25.433 | 0.78 | SFEA | 17.131 | 25.366 | 0.80 | ||
| AFEA | 16.382 | 24.712 | 0.81 | AFEA | 16.618 | 24.212 | 0.81 | ||
| RNN | 17.321 | 25.114 | 0.80 | RNN | 17.812 | 25.771 | 0.80 | ||
| LSTM | 16.505 | 24.536 | 0.83 | LSTM | 16.326 | 24.405 | 0.83 | ||
| MLR | 20.831 | 28.312 | 0.74 | MLR | 20.335 | 28.378 | 0.73 | ||
| SVR | 17.624 | 26.647 | 0.78 | SVR | 17.402 | 26.412 | 0.80 | ||
| RF | 16.414 | 25.557 | 0.83 | RF | 16.613 | 25.534 | 0.82 | ||
| 6 | NSKEA | 13.418 | 21.401 | 0.95 | 12 | NSKEA | 13.418 | 21.401 | 0.95 |
| NEA | 14.761 | 23.134 | 0.92 | NEA | 14.515 | 23.521 | 0.91 | ||
| SFEA | 17.382 | 25.662 | 0.81 | SFEA | 17.617 | 25.780 | 0.83 | ||
| AFEA | 16.287 | 24.404 | 0.86 | AFEA | 16.280 | 24.271 | 0.87 | ||
| RNN | 17.680 | 25.311 | 0.78 | RNN | 17.428 | 25.263 | 0.79 | ||
| LSTM | 16.627 | 24.573 | 0.87 | LSTM | 16.750 | 24.542 | 0.84 | ||
| MLR | 20.622 | 28.602 | 0.75 | MLR | 21.137 | 28.732 | 0.73 | ||
| SVR | 17.371 | 26.221 | 0.79 | SVR | 17.772 | 26.467 | 0.80 | ||
| RF | 16.505 | 25.516 | 0.81 | RF | 16.379 | 25.205 | 0.81 | ||
| Criteria | Definition |
|---|---|
| F-measure (FM) | |
| Accuracy (ACC) | |
| Normalized Mutual Information (NMI) |
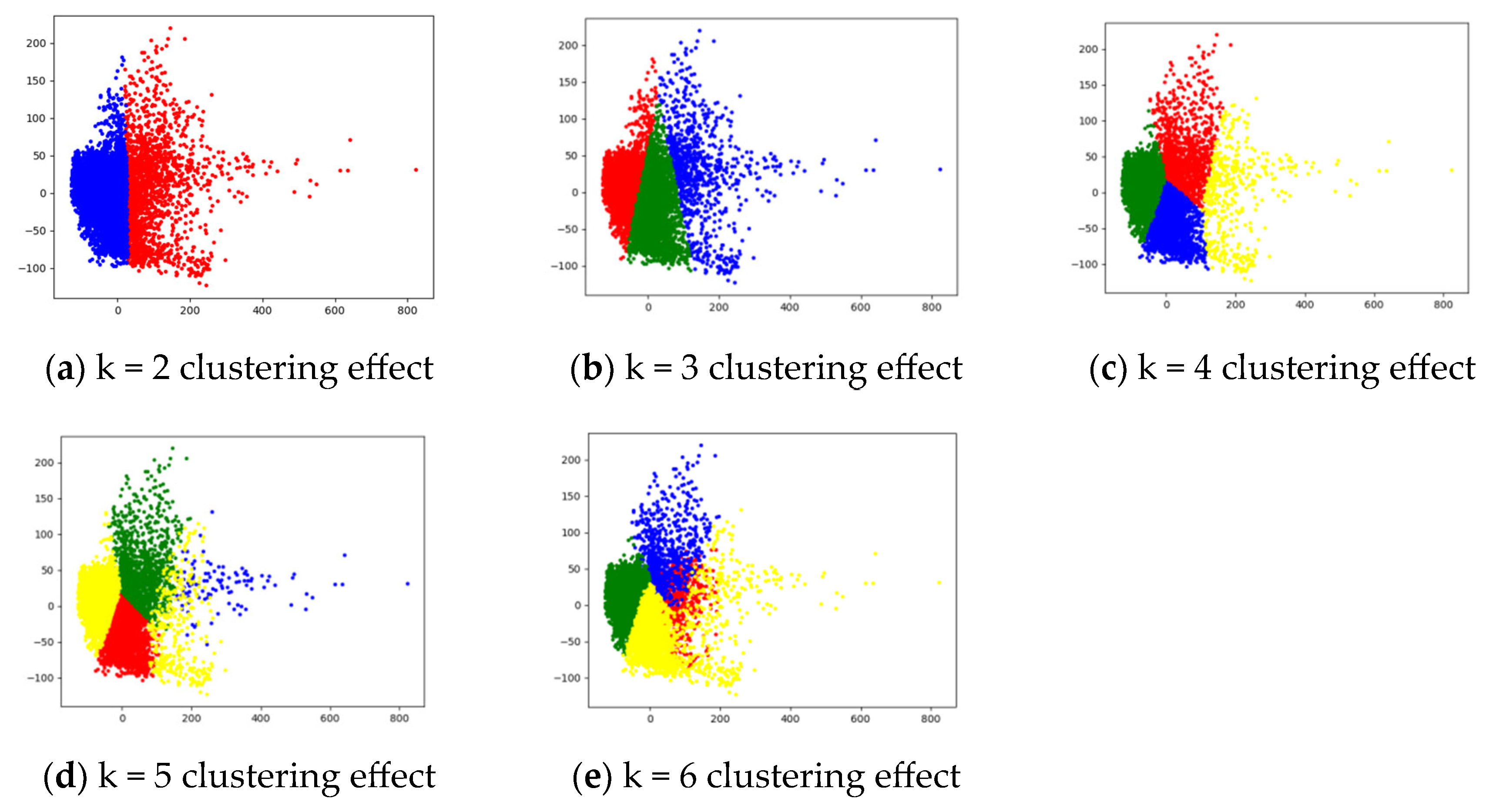
| Cluster Number | FM | ACC | NMI |
|---|---|---|---|
| 2 | 0.00289 | 0.03401 | 0.07301 |
| 3 | 0.00443 | 0.33880 | 0.15358 |
| 4 | 0.01354 | 0.63023 | 0.16661 |
| 5 | 0.00576 | 0.42640 | 0.18444 |
| 6 | 0.00583 | 0.38350 | 0.19668 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wen, Q.; Zhu, J. An Ensemble Model for PM2.5 Concentration Prediction Based on Feature Selection and Two-Layer Clustering Algorithm. Atmosphere 2023, 14, 1482. https://doi.org/10.3390/atmos14101482
Wu X, Wen Q, Zhu J. An Ensemble Model for PM2.5 Concentration Prediction Based on Feature Selection and Two-Layer Clustering Algorithm. Atmosphere. 2023; 14(10):1482. https://doi.org/10.3390/atmos14101482
Chicago/Turabian StyleWu, Xiaoxuan, Qiang Wen, and Jun Zhu. 2023. "An Ensemble Model for PM2.5 Concentration Prediction Based on Feature Selection and Two-Layer Clustering Algorithm" Atmosphere 14, no. 10: 1482. https://doi.org/10.3390/atmos14101482
APA StyleWu, X., Wen, Q., & Zhu, J. (2023). An Ensemble Model for PM2.5 Concentration Prediction Based on Feature Selection and Two-Layer Clustering Algorithm. Atmosphere, 14(10), 1482. https://doi.org/10.3390/atmos14101482







