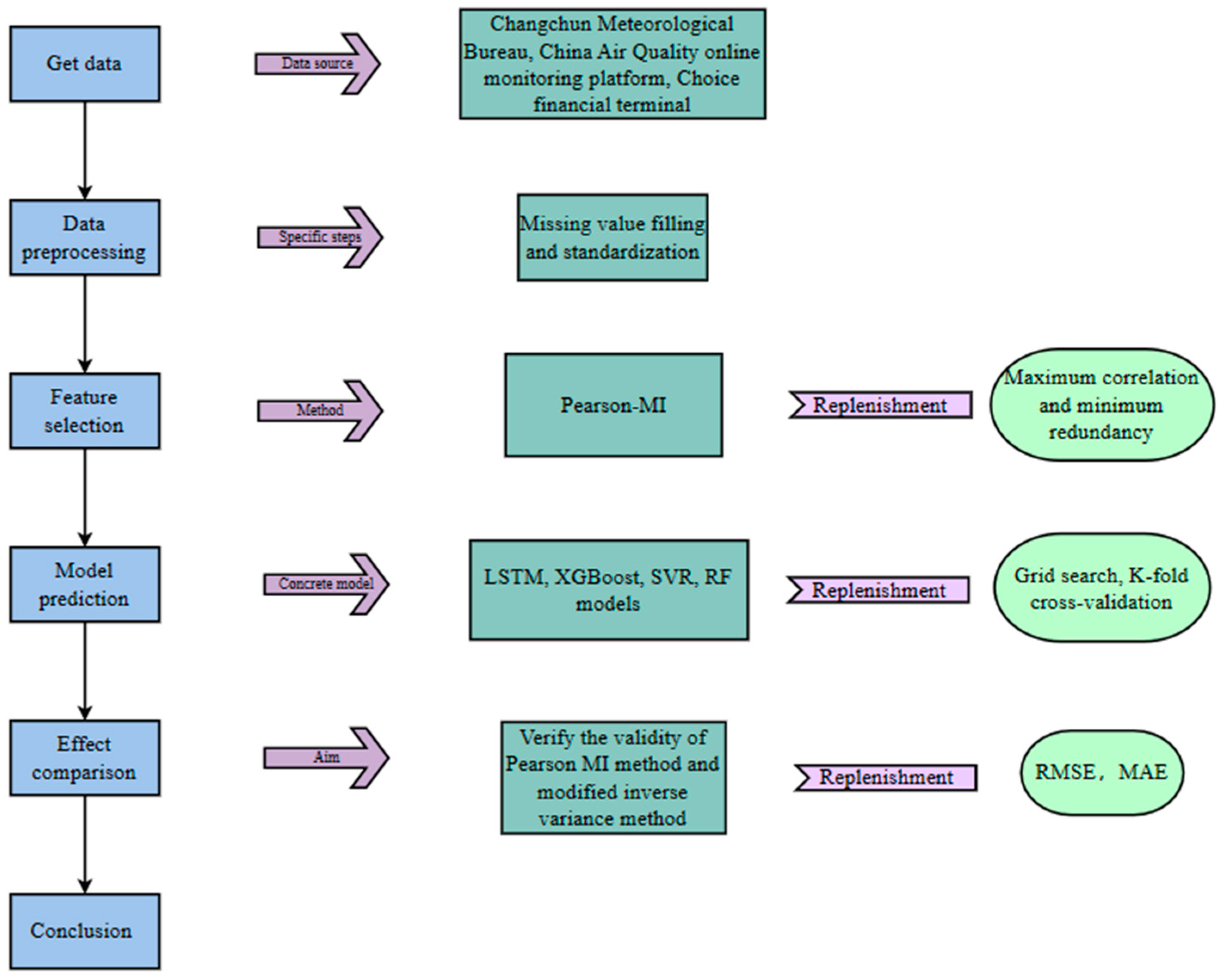
3.1. Data Introduction and Preprocessing
The data in this paper are mainly divided into various pollutant concentration data in the air, meteorological data, and energy price data, among which the concentration data of various pollutants in the air include CO concentration, NO2 concentration, PM2.5 concentration, PM10 concentration, SO2 concentration, and O3 concentration. Meteorological data include average air pressure, maximum air pressure, minimum air pressure, average air temperature, maximum air temperature, minimum air temperature, average relative humidity, minimum relative humidity, daily precipitation, maximum wind speed, and maximum wind speed. Energy price data include natural gas prices and gas prices, in addition to the air quality index and air quality index ranking.
The air quality index can be directly calculated from the concentration data of various pollutants in this article. The changes in the meteorological data can directly or indirectly affect the generation, diffusion, and removal processes of pollutants, thereby affecting the air quality. There is a certain inverse relationship between energy price data and energy usage. For example, natural gas, as a non-renewable clean energy source, releases fewer pollutants from its combustion compared to other traditional fuels such as coal and oil. Lower natural gas prices can encourage energy consumers to choose natural gas as a substitute for more polluting fuels. Therefore, the selection of various pollutant concentration data, meteorological data, and energy price data in the air for the study of the air quality index in this article has good practical significance.
The data used in this paper are the daily data from 1 January 2014 to 31 December 2022. The concentration data of various pollutants in the air derive from the China Air Quality Online Detection Platform, meteorological data are from the Changchun Meteorological Station, and energy price data derive from the Choice Financial Terminal.
Because the meteorological data are from the Changchun Meteorological Station, there are no missing data. For the pollutant concentration data and energy price data with few missing values, this paper fills them with the mean value method. Because the data of adjacent dates usually have a certain correlation, the trend and periodicity of the data can be maintained as much as possible by using the mean method to fill in, and the mean method is simple and easy to implement and does not require complex calculations or models.
where
is the missing data, and
i represents day
i. Because the dimensions of the data filled with missing values are inconsistent, this paper removes the dimensions by standardizing the data, namely:
where
is the standardized data,
represents the mean value and
represents the standard deviation.
In this paper, the dataset is divided into a training set and a test set, with a ratio of 8:2. The training set data are from 1 January 2014 to 13 March 2021, and the testing set data are from 14 March 2021 to 31 December 2022. At the same time, in order to effectively improve the learning ability of the model, this paper makes the learning model increasingly robust via K-fold cross-validation, which is K = 5 in this paper.
3.2. Feature Selection
Feature selection is carried out based on the Pearson correlation coefficient and mutual information with the principle of maximum correlation and minimum redundancy, namely the Pearson-MI method. Firstly, the Pearson correlation coefficient can be used to measure the linear correlation between independent variables and dependent variables and between independent variables. Secondly, mutual information can be used to measure the nonlinear correlation between independent variables and dependent variables and between independent variables. Finally, feature selection is carried out according to the principle of maximum correlation and minimum redundancy. The independent variables (also known as influencing factors or characteristics) in this paper are CO concentration, NO2 concentration, PM2.5 concentration, PM10 concentration, SO2 concentration, O3 concentration, average air pressure, maximum air pressure, minimum air pressure, average air temperature, maximum air temperature, minimum air temperature, average relative humidity, minimum relative humidity, daily precipitation, maximum wind speed, maximum wind speed, natural gas price, gas price, etc. For the air quality index ranking, the dependent variable is the air quality index.
Firstly, the mutual information and Pearson correlation coefficient between independent variables and dependent variables are calculated, and the correlation (linear correlation and nonlinear correlation) between independent variables and dependent variables is measured using mutual information and the Pearson correlation coefficient. The calculation results are shown in
Table 2:
It can be seen from
Table 2 that the minimum relative humidity, maximum wind speed, daily precipitation, and natural gas price have low mutual information values, and the Pearson correlation coefficients are all less than 0.3, so they are eliminated according to the principle of maximum correlation.
Secondly, mutual information values and the Pearson correlation coefficients for CO concentration, NO
2 concentration, PM2.5 concentration, PM10 concentration, SO
2 concentration, O
3 concentration, average air pressure, maximum air pressure, minimum air pressure, average air temperature, maximum air temperature, minimum air temperature, average relative humidity, maximum wind speed, gas price, and AQI ranking were calculated, and the calculation results are shown in
Table 3.
It can be seen from
Table 3 that there is a high correlation between average air pressure, maximum air pressure, minimum air pressure, average air temperature, maximum air temperature, and minimum air temperature, and the linear correlation between maximum air temperature and minimum air temperature is one. Eliminating any feature can reduce the correlation between independent variables. At the same time, in order to reduce the calculation amount, only one such feature is reserved in this paper. That is, the maximum air temperature and maximum air pressure are reserved.
The average value of mutual information in
Table 3 represents the average value of mutual information between an influencing factor and all other influencing factors; the number of linear correlations represents the number of highly linear correlations between an influencing factor and all other influencing factors; the table shows the influencing factors with linear correlations greater than 0 and the corresponding average value of mutual information and linear correlations. As can be seen from
Table 3, there is a high correlation between average air pressure, maximum air pressure, minimum air pressure, average air temperature, maximum air temperature, and minimum air temperature, and the linear correlation between maximum air temperature and minimum air temperature is one. Removing any feature can reduce the correlation between independent variables, and in order to reduce the calculation amount, only one index of the same kind is retained in this paper; that is, the maximum air temperature and maximum air pressure are retained, and the required variables are NO
2 concentration, SO
2 concentration, O
3 concentration, maximum air temperature, maximum air pressure, gas price, AQI ranking, and maximum wind speed, while the alternative variables are average relative humidity, PM10 concentration, CO concentration, and PM2.5 concentration.
To sum up, there are at least 8 and at most 12 factors influencing the AQI of Changchun. By calculating the mutual information (redundancy) of the combination of each influencing factor among the required variables and alternative variables, the factors influencing the AQI of Changchun were finally selected.
In
Table 4, when the number of influencing factors is 8, the influencing factors are selected as mandatory variables; when the number of influencing factors is 9, the influencing factors are selected as mandatory variables and any alternative variables; and when the number of influencing factors is 12, the influencing factors are selected as mandatory variables and alternative variables. Minimum redundancy means that the number of influencing factors is the same. The combination of influencing factors with minimum redundancy is selected as the combination of influencing factors under the number of influencing factors. It can be seen from
Table 4 that the minimum redundancy is obtained when the combination of influencing factors is 12. Therefore, the factors influencing the AQI ranking, CO concentration, NO
2 concentration, PM2.5 concentration, PM10 concentration, SO
2 concentration, O
3 concentration, gas price, maximum pressure, maximum temperature, average relative humidity, and maximum wind speed are selected in this paper.
3.3. Single Model Prediction
For the data of missing value filling, normalization, and feature selection, appropriate models for fitting can be selected. The models selected in this paper include the support vector regression model, extreme gradient lifting model, random forest model, and long-term and short-term memory network model. In the process of fitting, in order to obtain the best-fitting effect and avoid over-fitting, this paper uses grid search to select the best parameters, and we avoid over-fitting by using K-fold cross-validation. Because grid search requires the search range to be given in advance, this paper first sets a larger parameter range for different parameters in each model when selecting the optimal parameters through grid search, and this gradually reduces the search range according to the training results until the optimal parameters are obtained.
In order to show that the selected single model in this paper has a better prediction accuracy and to verify the effectiveness of the feature selection method used in this paper, firstly, the dataset is trained using a single model. The datasets are all datasets without feature selection and part of the datasets after feature selection, and the fitting value of the test set is compared with the true value of the Changchun air quality index to judge the fitting effect of the single model selected in this paper. Secondly, the fitting effect of the test set trained using the single model is compared with that of all datasets without feature selection and part of the datasets after feature selection. This is used to judge the effectiveness of the feature selection method used in this paper. The single models used in this paper include the support vector regression model, extreme gradient lifting model, random forest model, and long-term and short-term memory network model. The evaluation indices of the models are root mean square error and average absolute error.
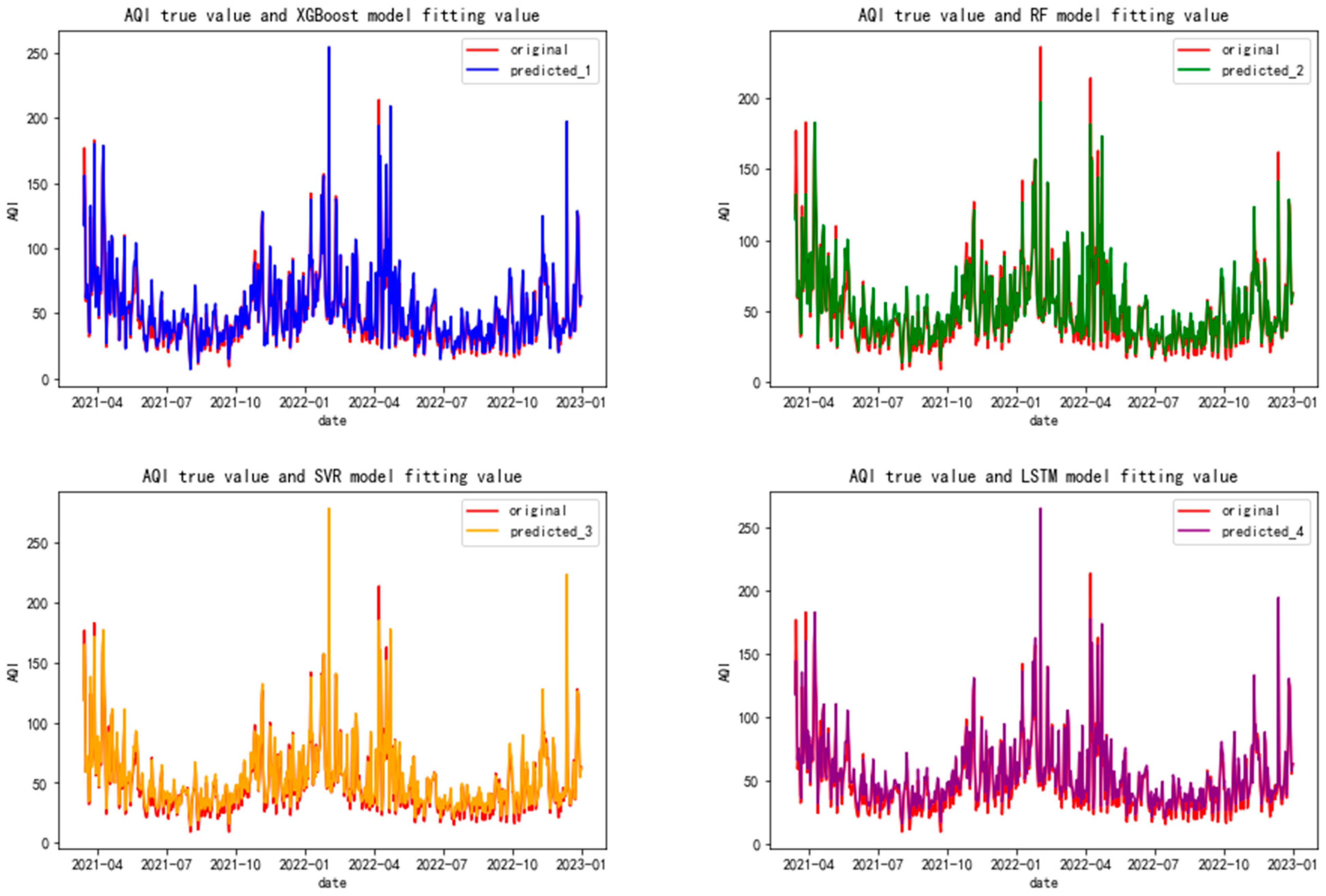
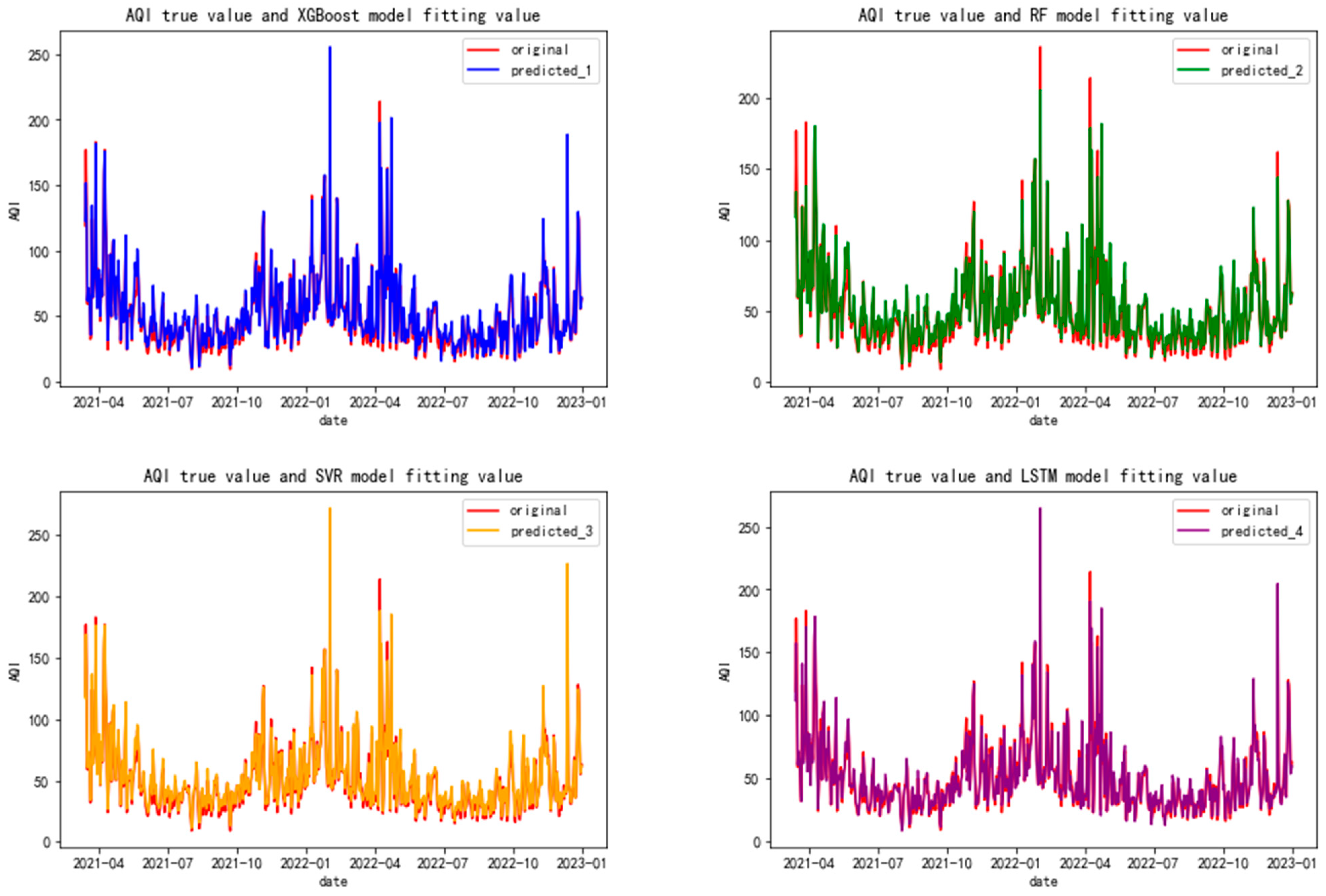
Figure 4 shows the comparison between the fitting value of the test set of the dataset without feature selection in each single model and the true value of the Changchun air quality index. In
Figure 4, the red curve represents the true value of the Changchun air quality index, the green curve represents the fitting value of the test set trained using the random forest model, the yellow curve represents the fitting value of the test set trained via the SVR model, and the purple curve represents the fitting value of the test set trained using the LSTM model. It can be seen from
Figure 4 that after the dataset without feature selection is trained using the SVR model, LSTM model, XGBoost model, and random forest model, the curve composed of the test set values basically coincides with the curve composed of the real value of the Changchun air quality index, indicating that the single model selected in this paper can better train and fit the data.
Figure 5 shows the comparison between the fitting value of the test set of the feature-selected dataset in each single model and the true value of the Changchun air quality index. In
Figure 5, the red curve represents the true value of the Changchun air quality index, the green curve represents the fitting value of the test set trained using the random forest model, the yellow curve represents the fitting value of the test set trained via the SVR model, and the purple curve represents the fitting value of the test set trained using the LSTM model. As can be seen from
Figure 5, after the dataset after feature selection is trained using the SVR model, LSTM model, XGBoost model, and random forest model, the curve composed of test set values basically coincides with the curve composed of the real value of the Changchun air quality index, which preliminarily shows that the dataset after feature selection using the Pearson-MI method has a good fitting effect after being trained by four single models.
Figure 4 and
Figure 5 show the comparison between the fitting values of the test sets in each model and the real values of the Changchun air quality index of all datasets without feature selection and some datasets after feature selection, respectively.
Table 5 shows the prediction accuracy of different datasets according to the evaluation indices.
Table 5 shows the fitting effects of the SVR model, LSTM model, XGBoost model, and random forest model on the test set. The evaluation indices include root mean square error and average absolute error to reflect the feature selection effect. It can be seen from
Table 5 that when the LSTM model and XGBoost model are used to fit the data, the fitting effect of the dataset after feature selection is obviously improved compared with the dataset without feature selection. When using the SVR model and random forest model to fit the data, we can see that the fitting effect of the dataset after feature selection is not significantly improved compared with the dataset without feature selection, but it does not make the fitting effect worse, indicating that using fewer datasets can obtain the same fitting effect as using all datasets. To sum up, the feature selection method used in this paper achieves the purpose of removing redundant features, reducing computational costs, and obtaining a higher learning accuracy.
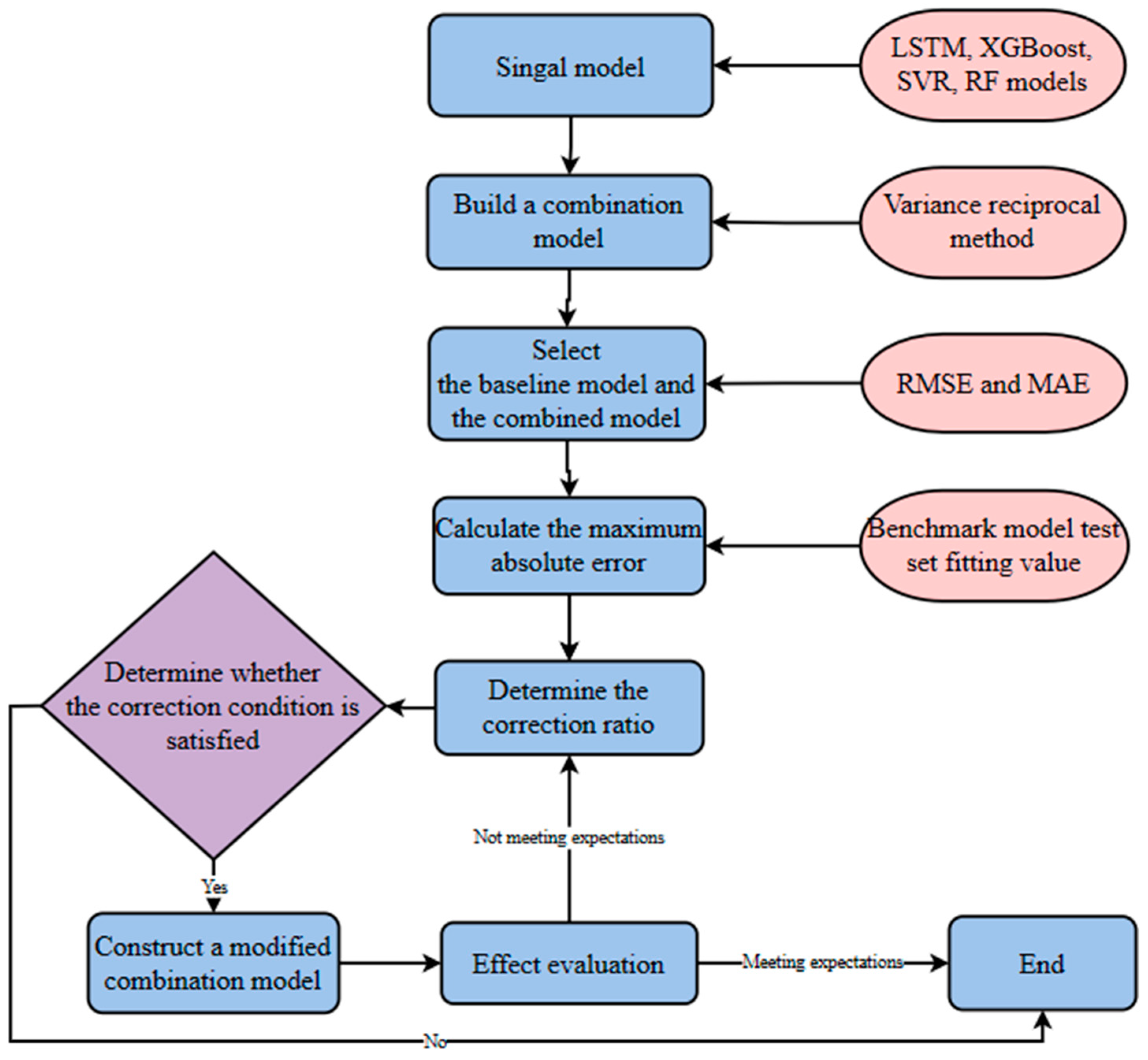
3.4. Combination Model Prediction
In order to improve the prediction accuracy of the model, this paper uses the reciprocal variance method to combine a single model to form a new combined model. Whether the combined model has a better prediction accuracy than the single model can be judged by comparing the prediction accuracy of the combined model with that of the single model. The combined model composed by the reciprocal variance method is composed by providing different weights to a single model test set, and the weights are obtained from the verification dataset, so only the predicted values composed by a single model test set through the reciprocal variance method exist in the combined model.
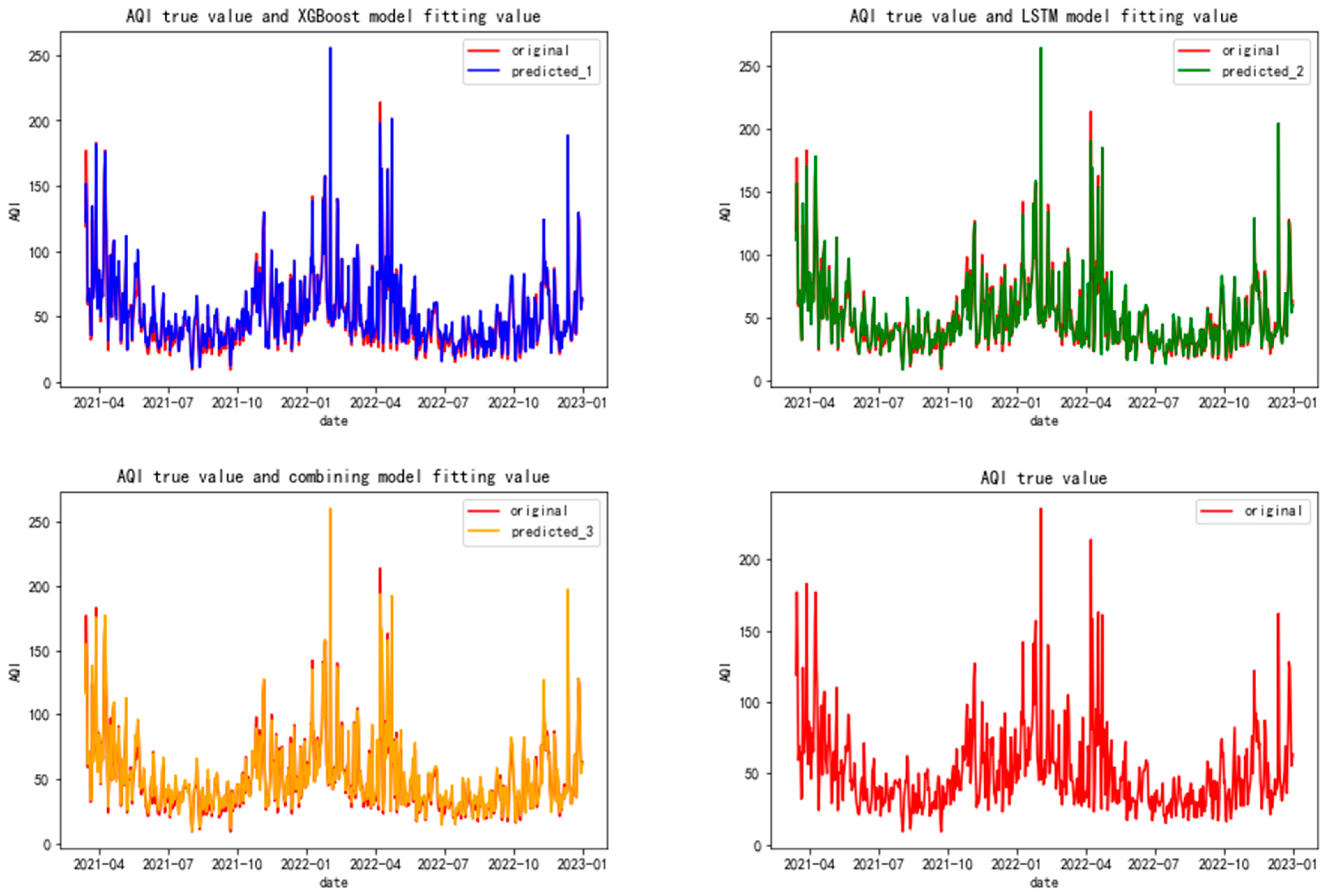
Figure 6 shows the comparison between the true value of the Changchun air quality index and the fitting value of the XGBoost model test set, the comparison between the true value of the Changchun air quality index and the fitting value of the LSTM model test set, the comparison between the true value of the Changchun air quality index and the predicted value of the combined model (composed of XGBoost model and LSTM model), and the true value of the Changchun air quality index. As can be seen from
Figure 6, the LSTM model, XGBoost model, and combined model (composed of XGBoost model and LSTM model) have a good fitting effect.
Table 6 shows the evaluation indices of the LSTM model, XGBoost model test set fitting value, and the combined model (composed of XGBoost model and LSTM model) prediction value. From
Table 6, it can be seen that the root mean square error and average absolute error of the LSTM model in a single model are smaller than the XGBoost model, indicating that the LSTM model has a better fitting effect than the XGBoost model and the combined model composed of the LSTM model and XGBoost model has a better prediction accuracy than two single models.
Table 7 shows the prediction accuracy of the predicted values obtained by combining different single models by the reciprocal variance method, and the number of single models used in the combined model includes two, three and four; that is, multiple single models form a combined model via the reciprocal variance method. It can be seen from
Table 7 that the predicted values obtained using the LSTM model and XGBoost model through the reciprocal variance method have a higher prediction accuracy than other combined models, and the predicted values obtained by the SVR model and random forest model via the reciprocal variance method have the worst prediction accuracy compared with other combined models. It can be seen from
Table 5 that the LSTM model and XGBoost model have higher fitting accuracy compared with other single models, indicating that the combined model composed of single models with a better prediction accuracy still has a higher prediction accuracy. It can also be seen from
Table 7 that the increase in the number of single models used in combined models cannot improve the prediction accuracy of combined models.
To sum up, the LSTM model and XGBoost model have good fitting effects in a single model, and the combined model composed of the LSTM model and XGBoost model via the reciprocal variance method also has a good fitting effect. Therefore, when the models are combined by the reciprocal variance method, the models with a better fitting effect should be selected for combination. Meanwhile, it should be noted that there is no absolute relationship between the increase in the number of single models used in combination and the improvement in the prediction accuracy of the models.
3.5. Modified Combination Model Prediction
In order to further improve the prediction accuracy of the model and to verify the fitting effect of the modified reciprocal variance method proposed in this paper, this paper selects two models with a better fitting effect as the baseline models in the SVR model, random forest model, XGBoost model, and LSTM model, and we take the remaining two models as modified models to construct a combined model through the modified reciprocal variance method. At the same time, comparing the prediction accuracy of the modified combined models under different correction ratios, it can be seen from
Table 8 that the LSTM model and XGBoost can be used as the baseline models, and the SVR model and random forest model are the modified models. Compared with the original reciprocal variance method, the modified reciprocal variance method further considers the influence of extreme values in the fitted values of the baseline model on the fitted results.
As can be seen from
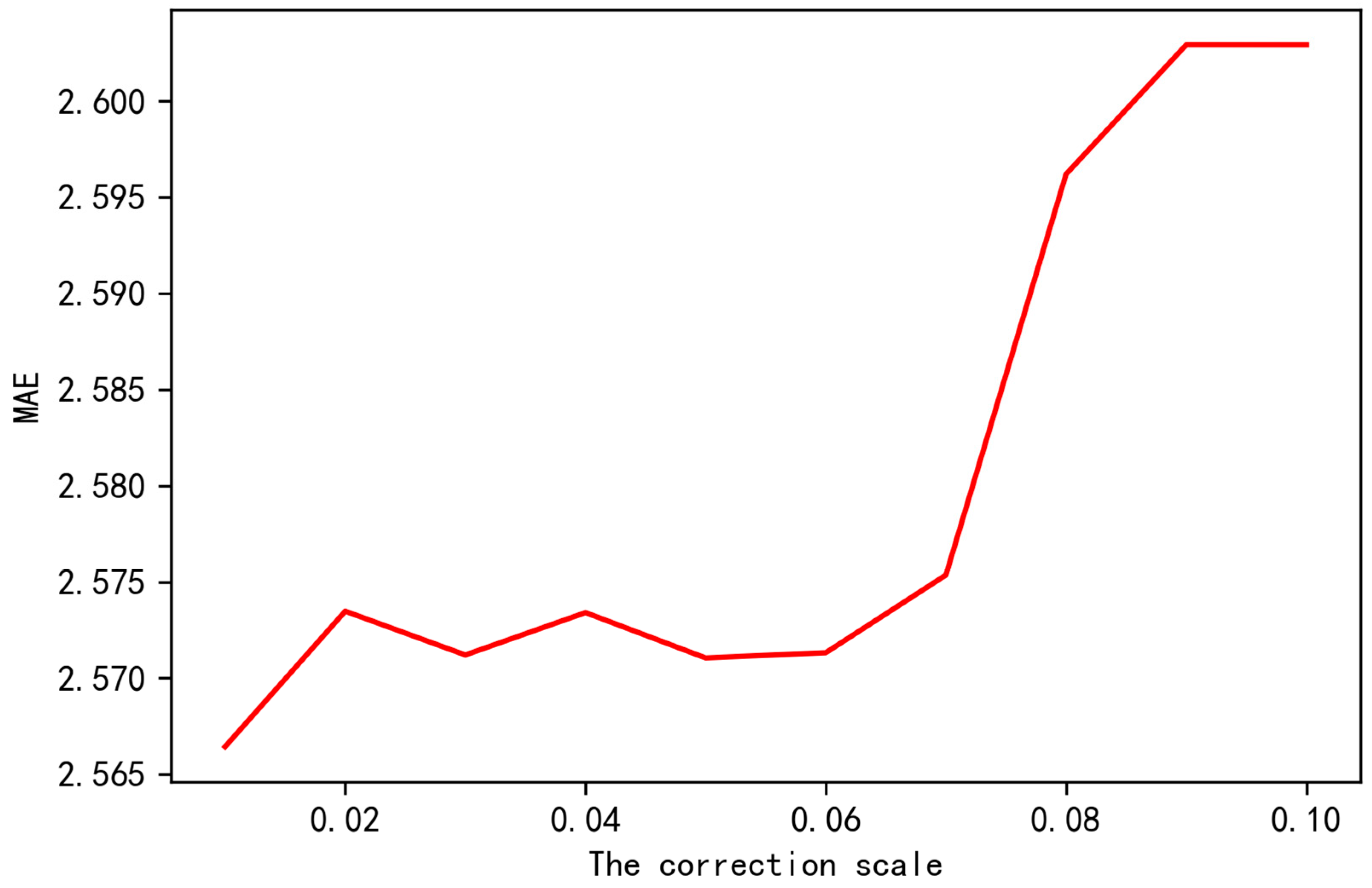
Figure 7, the root mean square error of the modified combined model of the LSTM model and XGBoost model via the modified reciprocal variance method shows an upward trend with the increase in the correction ratio. According to the modified reciprocal variance method, before modifying the combined model composed of the reference models, the absolute error between the two reference models is first calculated, and according to the absolute error, the fitting values of the test sets of the reference model are sorted according to the order from large to small, and then whether the fitting values of the reference model and the modified model test sets meet the modification rules of the modified reciprocal variance method is judged. If so, the fitting values of the Changchun air quality index can be modified according to the modified reciprocal variance method to make it have better accuracy, and with the continuous improvement in the modification ratio, the absolute error between the reference models will decrease, which means that the probability of the extreme deviation value will decrease. At this time, the probability of error when correcting the fitting value of the baseline model test set by correcting the fitting value of the model test set also increases, so the following situation, outlined in
Figure 7, appears: with the continuous increase in the correction ratio, the root mean square error also shows an upward trend.
As can be seen from
Figure 8, the average absolute error of the modified combined model composed of the LSTM model and XGBoost model via the modified reciprocal variance method shows an upward trend with the increase in the correction ratio. Similar to the conclusion in
Figure 7, with the continuous increase in the correction ratio, the absolute error between baseline models decreases, which means that the probability of an extreme deviation value decreases. At this time, the probability of error when correcting the fitting value of the baseline model test set by correcting the fitting value of the model test set also increases, so the situation outlined in
Figure 8 appears: with the continuous increase in the correction ratio, the average absolute error also shows an upward trend.
It can be seen from
Figure 7 and
Figure 8 that when the correction ratio is from 1% to 10%, the root mean square error and the average absolute error also show an upward trend with the continuous increase in the correction ratio. When the correction ratio is 1%, both the root mean square error and the average absolute error can reach the minimum.
Table 8 shows the prediction accuracy of the modified combined model composed of the LSTM model and XGBoost model as the baseline model, SVR model, and random forest model as the modified model and the modified reciprocal variance method under different modified ratios. It can be seen from
Table 8 that the root mean square error and average absolute error of the combined model composed of the LSTM model and XGBoost model via the reciprocal variance method are 4.131 and 2.581, respectively. When the correction ratio is 8%, the average absolute error of the modified combined model is 2.596, and with continuous improvement in the correction ratio, the average absolute error of the modified combined model reaches 2.603. Therefore, it can be obtained that the modified combined model composed of the LSTM model and XGBoost model via the reciprocal variance method can improve the fitting accuracy when the correction ratio is from 1% to 7% and when the correction ratio is from 8% to 10%, although the average absolute error of the modified combined model is slightly higher than that of the combined model (composed of the LSTM model and XGBoost model via the reciprocal variance method). However, the root mean square error of the modified combined model is still better than that of the combined model. To sum up, the modified reciprocal variance method can effectively improve the prediction accuracy of the model.
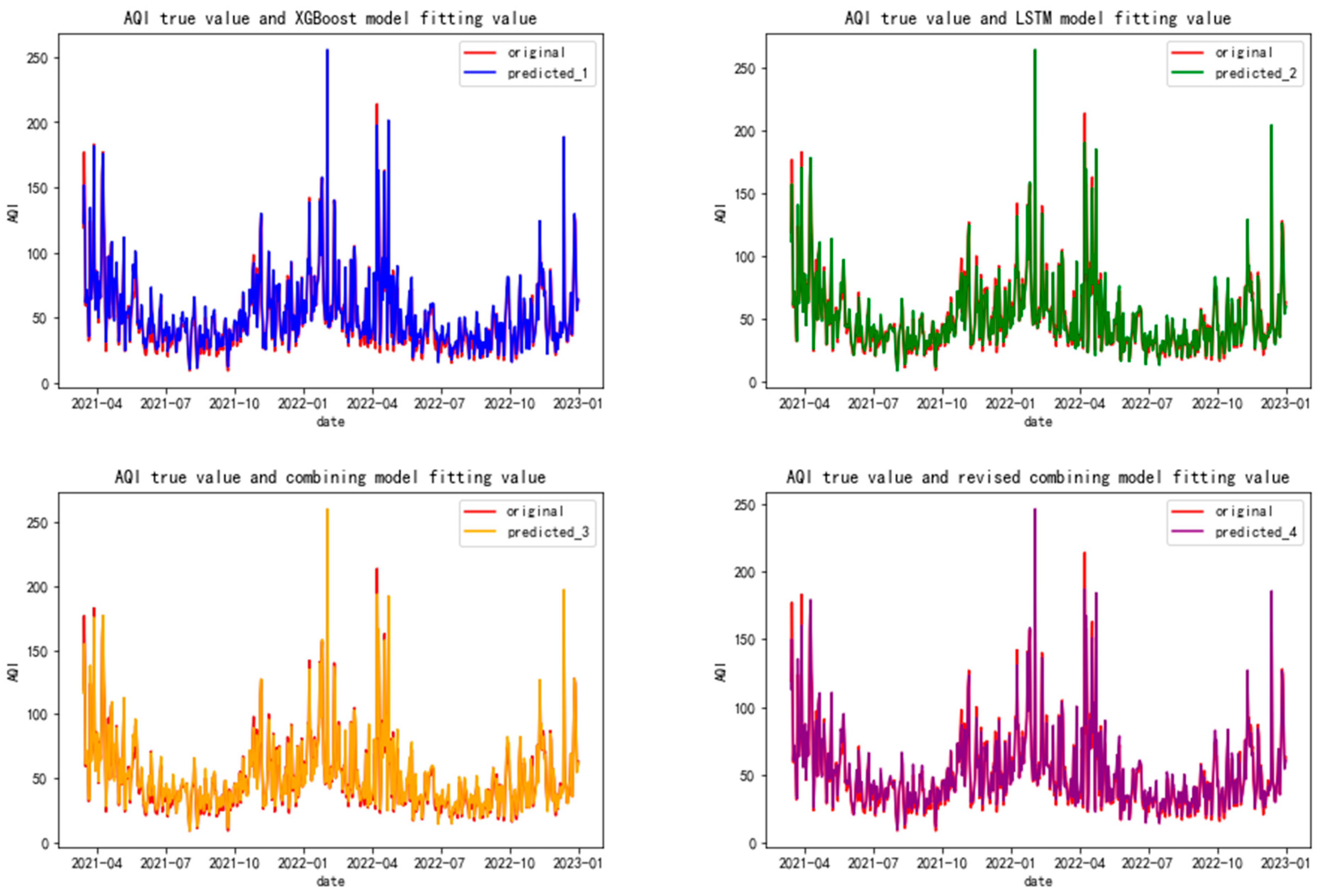
Figure 9 shows the comparison charts of the Changchun air quality index true value and XGBoost model test set, the Changchun air quality index true value and LSTM model test set, the Changchun air quality index true value and combined model (composed of XGBoost model and LSTM model) predicted value, and the Changchun air quality index true value and modified combined model (composed of XGBoost model and LSTM model) predicted value. From
Figure 9, it can be seen that the LSTM model, XGBoost model, combined model, and modified combined model all have a good fitting effect.
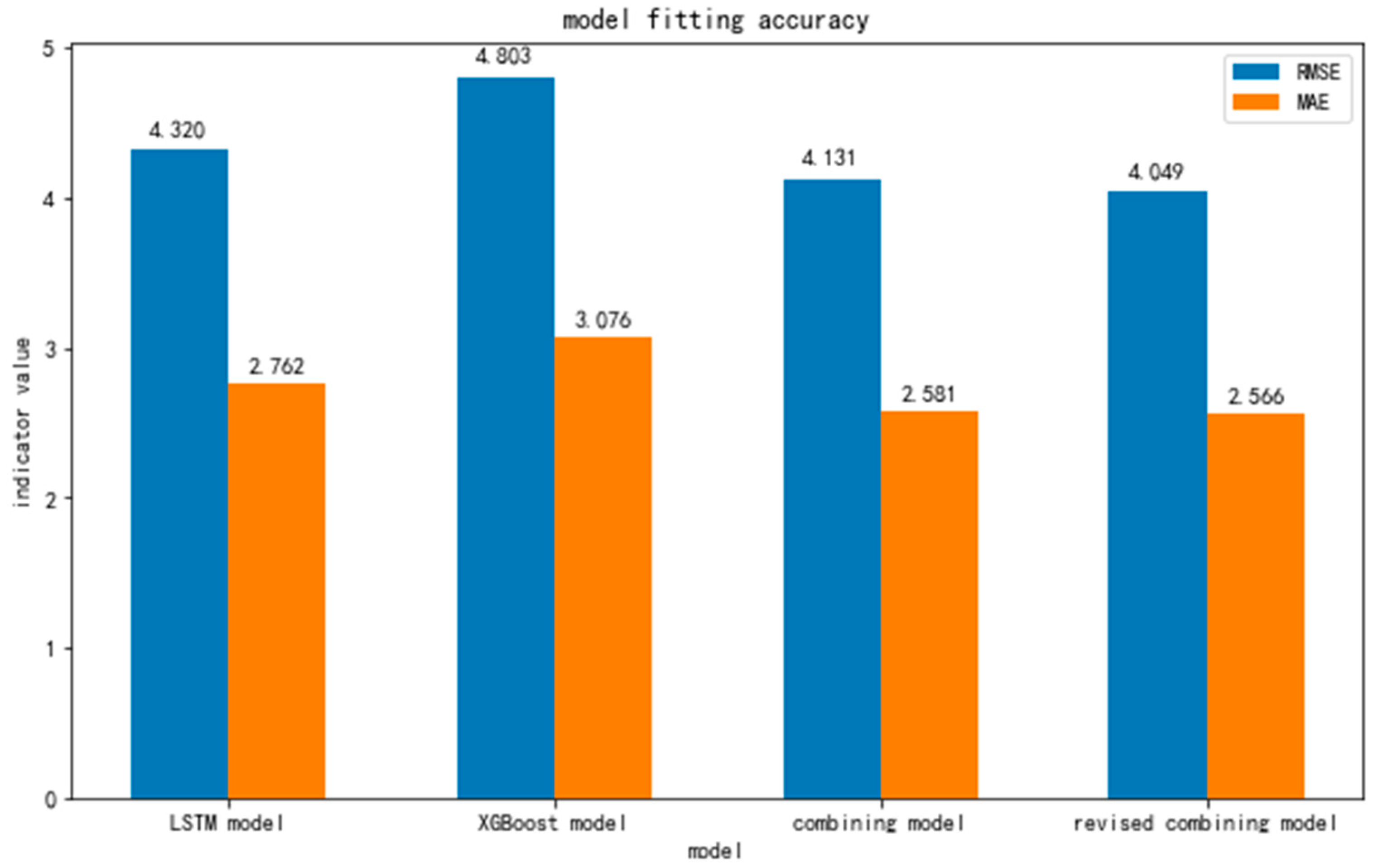
Figure 9 shows the RMSE and MAE for the different models, where the modified combined model uses a correction ratio of 1%. As can be seen from
Figure 10, the combined model composed of the reciprocal variance method of the LSTM model and XGBoost model has a better prediction accuracy than the LSTM model and XGBoost model, and the modified combined model composed of the modified reciprocal variance method has a better prediction accuracy. Therefore, it can be concluded that the modified inverse variance method can effectively improve the prediction accuracy of the model under the condition that the correction proportion is 1%. To sum up, the modified inverse variance method proposed in this paper has a good effect.