Abstract
Based on 35-year (1981–2015) ensemble (24 members) hindcasts of the IAP/LASG global seasonal prediction system named FGOALS-f2 V1.0 (FGOALS-f2), the tropical cyclone (TC) seasonal prediction skills over the South China Sea (SCS) during the TC peak season (July–November) are evaluated. Starting the prediction from June 20th, FGOALS-f2 can well capture the seasonal mean characteristics for both the genesis location and track of TCs over the SCS. For seasonal anomalous TC numbers, FGOALS-f2 underestimates the maximum and minimum of the TC number compared to the observation. The temporal correlation coefficients (TCCs) between FGOALS-f2 and the observation are 0.39 for the TC number and 0.51 for accumulated cyclone energy (ACE) over the SCS, respectively, which are both above the 95% significant level. Additionally, FGOALS-f2 has acceptable prediction skill for the seasonal mean number of TCs landing on three areas (coastal southeastern China, Indochina Peninsula, and Philippines) surrounding the SCS. The skillful prediction of SCS TCs could be ascribed to the well-predicted tropical anomaly of sea surface temperature (SSTA), TC and El Niño-Southern Oscillation (TC-ENSO) relations, and Genesis potential index (GPI).
1. Introduction
A tropical cyclone (TC) is one of the most destructive weather phenomena, affecting public safety and economic activities along the coast. The South China Sea (SCS) is the largest semi-enclosed marginal sea in the Western Pacific (WP), which is the area affected by the locally generated and remotely generated TCs [1,2]. According to the statistics, 10.3 TCs are passing through the SCS and 3.5 TCs are generated locally [3], which accounts for 40% of the TC genesis number in the whole WP. The TC in SCS can make landfall in China, Vietnam, and the Philippines, and the disasters caused by TCs, such as strong winds, extreme rainfall, and storm surges, cause a significant loss of human life and property in many Southeast Asian countries [4]. Skillful prediction of TC activity in the SCS is the most effective method for disaster prevention and mitigation.
Seasonal prediction of TC activity in the SCS can better satisfy the demands from all sectors of society in countries around the SCS. Although the weather forecasting (1–7 days) of TC genesis locations and tracks in SCS is relatively accurate, the buffer time is not enough for society and policymakers [5,6,7]. The main reason is that a locally generated TC in SCS tends to be closer to the coast, which means the lifetime of the TC from generation to landfalling is shortened. On the other hand, the lack of inputs for disaster prevention and mitigation in the developing countries around SCS will prolong the preparation time for landfalling a TC [8,9,10,11]. Although the initial condition is dominant for the TC forecasting in a synoptic time scale, the skillful prediction of a TC on a monthly to seasonal timescale needs to consider not only the initial condition but also the external forces, oceanic conditions, land surface processes, and large-scale slow varying processes [12]. The TC activity can be considered a random process under large-scale circulation. If the relationship between the TC and large-scale circulation is well managed, there is an opportunity to predict TCs on a longer time scale [13,14,15].
Statistical methods were first applied for the seasonal prediction of TCs in the SCS. Researchers [16] developed an operational–statistical prediction system to predict the TC activity in SCS based on the ENSO (El Niño-Southern Oscillation) phenomenon and the parameters related to large-scale circulation (e.g., subtropical high over the SCS, the westward extension of the 500-hPa subtropical ridge, 500-hPa height over the Tibetan Plateau). A researcher [17] established a TC landfalling model in SCS by using the Niño3.4 index. It is worth noting that these statistical methods are highly dependent on the changes in ENSO, which means that the prediction skill of TC will be reduced when the signal of ENSO is not significant. On the one hand, it is convenient to establish statistical models based on individual or multiple parameters [18,19,20,21,22]. On the other hand, the statistical prediction skill of TC is sensitive to the selection of predictors and statistical methods. In addition, TC prediction using statistical methods is essentially modeling based on historical data and the impact of future climate change is not considered [23,24,25,26].
Dynamical sub-seasonal to seasonal prediction of TC based on global climate models (GCMs) is a new research direction [27,28,29,30]. The advantage of using global models to simulate and predict TCs is that there are no lateral-boundary effects, which is a benefit for the fidelity of the interaction between large-scale circulation and TC. In addition, with the increased resolution and the improved physical process parameterization, GCMs have been able to simulate many aspects of TCs. The researcher [30] systematically evaluated the seasonal prediction skill of TCs in the global prediction system of the European Centre for Medium Range Weather Forecasts (ECMWF) and found that the dynamical prediction system showed considerable predictive skill for TCs in the generation, movement, and intensity aspects. In addition, a combination of statistical methods and dynamical models can improve the prediction skill of TCs in sub-seasonal to seasonal time scales. A researcher [15] used the statistical–dynamical seasonal prediction model of the Geophysical Fluid Dynamics Laboratory (GFDL) to predict the TC activity in the Northern Atlantic and they found a significant improvement in prediction skill in the landfalling number of TC aspects.
The accurate reproduction of the relationship between large-scale circulation and TC activity is an essential source of prediction skills in the global dynamical prediction system. A researcher [31] found that ENSO modulated the global TC genesis number, especially in the WP based on the general circulation model (GCM) in GFDL. A researcher [32] peovided a possible mechanism to explain the reason why ENSO can affect the TC genesis in the WP. In addition, the large-scale patterns, such as the western Pacific Subtropical High (WPSH; [33]), Madden–Julian Oscillation (MJO; [13,34,35]), and the steering flow [4], contribute to the TC activity in WP. A researcher [36] systematically summarized the contribution of large-scale circulation to the generation of TC. Then, they developed a genesis potential index (GPI), which used large-scale factors to represent global TC generation. GPI can well characterize the generation of TC in multiple time scales [37,38].
In this study, the seasonal prediction skill of TC in SCS is given by using the hindcast of a global dynamical seasonal prediction system named FGOALS-f2 version 1.0 [39]. The climate system model used in the seasonal prediction system, named CAS FGOALS-f2 [40,41,42,43], was developed by the State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics (IAP), and Chinese Academy of Sciences (CAS). The simulating performance of TC in CAS FGOALS-f2 with 1° (approximately 100 km) horizontal resolution was evaluated, and the relationship between the large-scale pattern and TC is reasonable, especially in the WP [41]. Therefore, it is worth evaluating the prediction skill of TC in SCS. The motivations of this study are (1) to give the seasonal prediction skill of TC activity in SCS based on the hindcasts of FGOALS-f2; (2) the possible reasons contributing to the prediction skill of TCs in SCS are given from the perspective of the large-scale pattern.
This paper is organized as follows. Section 2 introduces the configuration of the seasonal prediction system, the observational dataset, the TC detection method, the landfalling TC algorithm, the skill scores, and the genesis potential index (GPI) of predicted TCs in seasonal timescales. In Section 3, the climatology and interannual variability of the predicted TC activity in the SCS are shown. A possible linkage between TC activity and large-scale factors in the seasonal timescale is given in Section 4. Section 5 is the discussion and conclusion based on the results.
2. Model, Dataset and Method
2.1. Seasonal Prediction System FGOALS-f2 V1.0
FGOALS-f2 V1.0 is a seasonal prediction system that is developed based on the climate system model name CAS FGOALS-f2 [41,42,43]. The original goal of FGOALS-f2 V1.0 was to predict the global weather and climate from month to season. Recently, the FGOALS-f2 V1.0 prediction system was submitted to the China multi-model ensemble prediction system (CMME v1.0) of the Beijing Climate Center [44] and the National Marine Environment Forecasting Center of China for operational use.
A 36-year hindcast (1981–2016) of FGOALS-f2 V1.0 was completed with 24 ensemble members. The incremental analysis updating (IAU) process [45] was used to assimilate the Japanese 55-year Reanalysis dataset (JRA55; [46]), which includes the temperature, surface wind, surface pressure, and sea-level pressure into the atmospheric component of FGOALS-f2 V1.0. In the oceanic component of FGOALS-f2 V1.0, the initial condition was derived from the three-dimensional potential temperature in the Global Ocean Data Assimilation System (GODAS) reanalysis data [47] by using the nudging method. Although the initial conditions in the land-surface and sea-ice components of FGOALS-f2 V1.0 are not assimilated directly, the initial conditions in the atmospheric and oceanic components drive the others to coordination. Thus, 24 individual ensemble members were generated based on a time-lag perturbation method [48,49] in the hindcast. The predicted frequency was once per month, and each of the members in the hindcast was integrated for up to six months.
2.2. Observational Data and the Hindcast of FGOALS-f2 V1.0
The ERA-Interim data [50] and OISSTv2 data [51,52] for the period 1981–2015 were used to evaluate the seasonal hindcast skill of TC in FGOALS-f2 V1.0. As an observation of TCs in SCS, the International Best Track Archive for Climate Stewardship v03r10 (IBTrACS; [53]) was used. IBTrACS is global mixed data from multiple sources of TC, and the TC data source in SCS is derived from the CMA-Shanghai Typhoon Institute [54]. The time interval of the dataset is six hours. It is necessary to transform the 10 min-averaged maximum sustained wind to the 1 min-averaged maximum sustained wind to provide a suitable platform to make a comparison between IBTrACS and the hindcast of FGOALS-f2 V1.0 [30] and the coefficient was set to 0.88 [30,41,55]. In addition, A 24-ensemble hindcast dataset of FGOALS-f2 from 1981 to 2015 is used to evaluate the monthly to seasonal prediction skill of TCs in SCS. Since the seasonal prediction system is initialized from the 20th of every month, the predicted information for the first 10 days is not used. Because the effective lifetime of TC is about 7 days, the inherent TC in the initial condition will be eliminated by filtering out the first 10 days.
2.3. TC Detection Method
An objective feature-tracking approach was used to detect the model-generated TCs based on the six-hour outputs of the hindcast of FGOALS-f2 V1.0. This detection method is similar to the method used in the GFDL climate model [14,55,56]. We used this scheme to evaluate the simulated performance of TCs in a GCM and the results indicated that this method could effectively select TC events from the model output [41]. The detection algorithm consists of three parts:
- (1)
- At first, local minimum 850 hPa absolute vorticity within a 600 km × 600 km grid box is picked up as a potential TC. Then, there must be a minimum sea-level pressure and a warm core (1 °C warmer than the surroundings) within a 2° × 2° grid box centered on the 850 hPa absolute vorticity.
- (2)
- The identification of TC tracks is mainly based on the identification of potential TCs. In addition, the TC tracks must satisfy the following criteria: (1) the lifetime of TC is greater than 72 h; (2) the surface wind is greater than 15.84 m s−1. The wind-speed threshold is consistent with a recent study, which clarified the relationship between the horizontal resolution of GCMs and the TC detection algorithms [57].
- (3)
- TCs are then classified based on the Saffir–Simpson hurricane wind scale [58].
2.4. Recognition of Landfalling TC
In order to quantitatively evaluate the prediction skill of landfalling TCs, it is necessary to select the signal of landfalling TCs from the IBTrACS and the hindcast of FGOALS-f2. We define a landfalling TC as a TC propagating within a 200 km buffer zone from the coastline. When the TC propagates into the buffer zone, which we set for the first time, we regard it as a landfalling TC event. In addition, the width of the buffer zone has no significant effect on the results, when the buffer zone varies from 0 km to 500 km.
2.5. Skill Scores
The temporal correlation coefficient (TCC) and root mean square error (RMSE), which are shown in Equation (1) and Equation (2), respectively, are used as the skill scores of TC interannual variability between the IBTrACS and the hindcast of FGOALS-f2.
where n is the length of a time series, xf is the predicted value, xo is the observation, is the mean of predicted value, and is the mean of observation. Spearman’s rank correlation coefficient is used as the skill scores of TC track and the equation is defined as
where is the difference in the ranks between the predicted value and the observation. The anomaly correlation coefficient (ACC) is used to quantitatively assess the similarity of large-scale factors between the predicted value and the observation and the equation is defined as
where g is the total number of grid points.
2.6. Genesis Potential Index
The GPI used in this paper is defined as:
where vort850 is the 850-hPa absolute vorticity (s−1), RH is the 600-hPa relative humidity (%), Vm is the maximum potential intensity [59], Vshear is the magnitude of the wind shear between 850 hPa and 200 hPa (m s−1), and ω is the 500-hpa vertical velocity (Pa/s). In addition, the Vm (the maximum potential intensity) used in this paper is defined as:
where Ck is the exchange coefficient of enthalpy, Cd is the drag coefficient, TS is the SST, and T0 is the mean outflow temperature. CAPE* is the convective available potential energy (CAPE) of the air lifted from saturation at sea level, and CAPEb is the CAPE of the boundary layer air.
3. Evaluation of the Prediction Skill of TC in SCS
3.1. The Climatology of Seasonal TC Activity in SCS
Approximately more than 8 TCs were generated or transmitted to the SCS from July to November, which accounts for 70% of total TCs in the whole year. In addition, the disasters caused by landfalling TCs also occur mainly in this season [4,8]. It is essential to pay attention to the TC activity from July to November in SCS. Figure 1 shows the seasonal (from July to November) density of TC genesis location and track between the IBTrACS and the hindcast of FGOALS-f2 from 1981 to 2015. On the one hand, the predicted generated locations of TC (Figure 1b) are relatively centralized compared to the IBTrACS in SCS (Figure 1a). An underestimation of TC generation appeared in the hindcasts of FGOALS-f2 along the Indochina Peninsula on the west side of the SCS. One possible reason for this bias is that the predicted intensities of TC in FGOALS-f2 get to the tropical storm category faster than the process in the observation. On the other hand, the pattern of predicted track densities of TC (Figure 1c) is similar to the observation (Figure 1d). An underestimation of the westward TC appeared in the hindcasts of FGOALS-f2 compared to the observation, but the northeastward TCs in the hindcast of FGOALS-f2 are close to the observation.
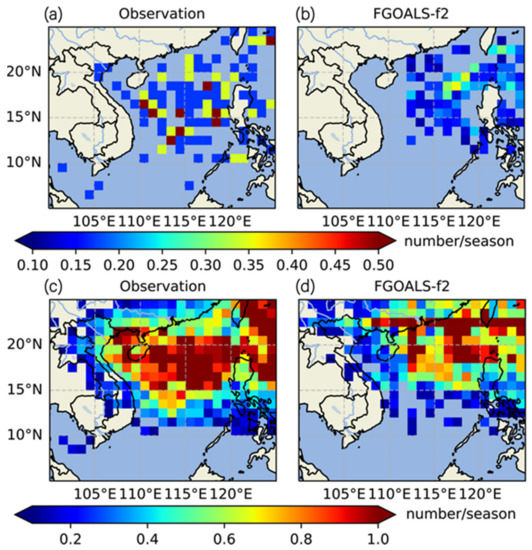
Figure 1.
The densities of genesis (a,b) location and track (c,d) of tropical cyclones (TC) in the South China sea (SCS). Both the observation and the hindcasts are analyzed in a 1° × 1° equidistance grid box with six-hour intervals.
3.2. Interannual Variability in Seasonal TC Activity in SCS
The interannual variability of seasonal TC activity is one of the main concerns in seasonal prediction [60]. A researcher [61] found that there was significant interannual variability and a trend of TCs in WP and SCS. Seasonal prediction skill in the prediction system for TC number and intensity in SCS reflects the synergetic degree between large-scale pattern and TCs [60,62,63]. Figure 2 shows the interannual variability in TC number and accumulated cyclone energy (ACE) between FGOALS-f2 and IBTrACS. ACE is a measure used by the National Oceanic and Atmospheric Administration (NOAA), which means approximate power over the lifetime of TC is calculated every 6-hour period. Thus:
where Vm is the estimated sustained wind speed of TC in knots. The results indicate that the TCC (Figure 2a) and RMSE (Figure 2b) of seasonal TC number (from 1981 to 2015) between the FGOALS-f2 and IBTrACS are 0.39 and 4.45, respectively. The amplitude of TC number change is weak in FGOALS-f2 compared with the IBTrACS. One possible reason for the underestimation is that the horizontal resolution used in FGOALS-f2 (approximately 1o) is insufficient to reproduce strong typhoon events [64]. On the other hand, the TCC and RMSE (Figure 2a) of seasonal ACE of TC (from 1981 to 2015) between the FGOALS-f2 and IBTrACS are 0.51 and 11.12, respectively. The main bias of ACE between the FGOALS-f2 and IBTrACS appears in the period from 1997 to 2010, when the FGOALS-f2 overestimates the ACE of TC. It is worth noting that the correlation coefficient of TC number and ACE decreased significantly from 2000 to 2015. One possible reason is that there are obvious biases of Central Pacific (CP) type of ENSO in model simulation and prediction [65,66], which will directly affect the simulation and prediction performance of TCs in SCS.
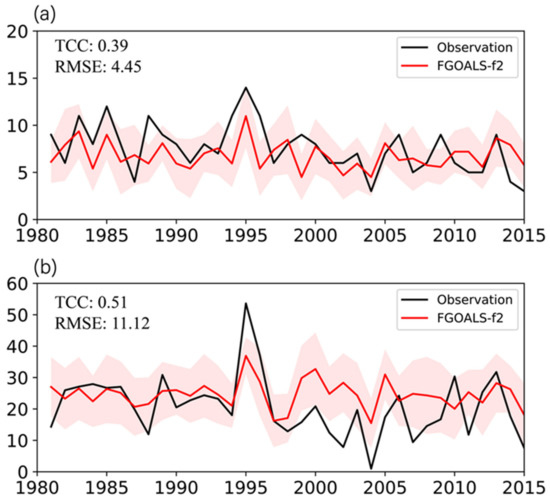
Figure 2.
The interannual variability in the number of TCs (a) and the accumulated cyclone energy (ACE) of TCs (b) in the SCS from July to November during 1981–2015. The International Best Track Archive for Climate Stewardship (IBTrACS) dataset (black line) is compared with the results predicted by the FGOALS-f2, which include the result with ensemble mean (red line) and the spread (defined by the standard deviation) based on the 24 ensembles (red area). The temporal correlation coefficient (TCC) and root mean square error (RMSE) of the interannual variability of the number and ACE of TC between the IBTrACS and FGOALS-f2 are also given.
Figure 3 shows the rank correlation between the FGOALS-f2 and IBTrACS based on the track density of TCs in SCS. The result indicates that there is a high correlation coefficient region in the TC generation and landfalling region, but there is a low correlation coefficient region in the middle area of TC movement. This phenomenon also exists in another seasonal prediction system, which can be regarded as a general issue. Previous studies have evaluated the seasonal prediction skill of TCs in the WP [67,68]. The results [15,30] indicate that the rank correlation of TC track in SCS shows relatively low skill, which does not pass the significance testing.
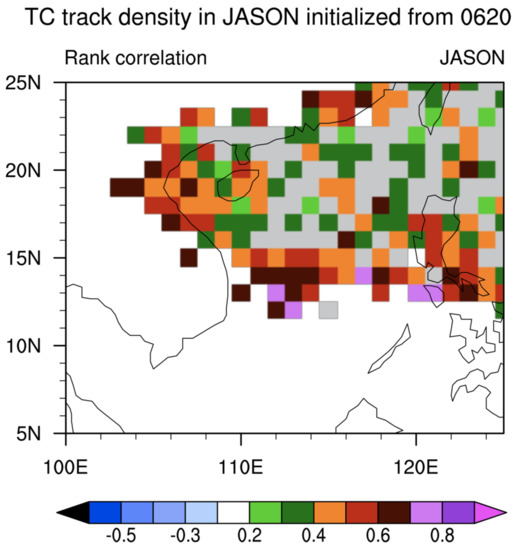
Figure 3.
The rank correlation between the IBTrACS and the hindcast of FGOALS-f2 based on the track density of TCs in the SCS. Data are analyzed in a 1° × 1° equidistance grid box with six-hour intervals. Color shading indicates the correlation coefficients that are significant at a two-sided P = 0.1 level. The grey shading indicates the regions where the observed track density is non-zero for at least 25% of the years (approximately 9 years).
To evaluate the seasonal prediction skill of landfalling TCs in SCS, we choose the landfalling TC from the FGOALS-f2 and IBTrACS. The interannual variability in the number of landfalling TCs on the southeast coast of China is shown in Figure 4a. The selected coastline includes Fujian, Guangdong, Guangxi, and Hainan, which are provinces in China. The shoreline in China is mainly affected by the northeastern movement of TCs in SCS. The results indicate that the TCC and RMSE of seasonal landfalling TC numbers on the southeast coast of China (from 1981 to 2015) between the FGOALS-f2 and IBTrACS are 0.34 and 3.65, respectively. The landfalling TC on the Indochina Peninsula is the westward movement of TC in SCS and the landfalling TC on the Philippines is mainly from the outside of SCS. The results indicate that the TCC and RMSE of seasonal landfalling TC numbers in the Indochina Peninsula are 0.30 and 4.05 (Figure 4b), respectively, and the TCC and RMSE of seasonal landfalling TC numbers in the Philippines are 0.33 and 2.73 (Figure 4c), respectively. Previous studies [15,30] analyzed the rank correlation of TC track in SCS, and the results indicated that the TC landfalling skill in the above regions is not satisfying when we use the results of dynamical prediction directly. The statistics–dynamic approaches are effective ways to improve the prediction skill for TC landfalling [69,70].
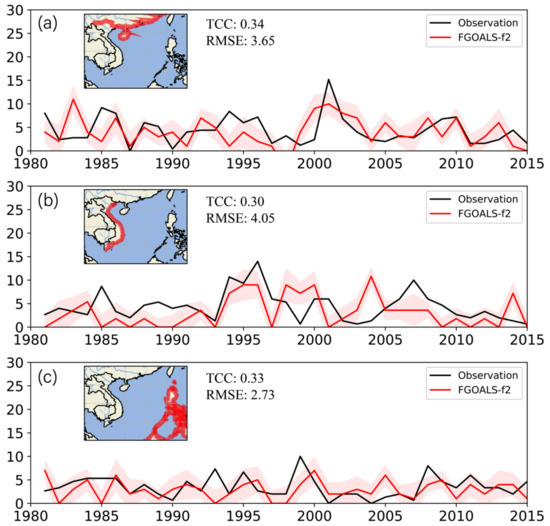
Figure 4.
The interannual variability in the number of landing TCs in the southeast coast of China (a), the Indochina Peninsula (b), and the Philippines (c) from July to November during 1981–2015. The temporal correlation coefficient (TCC) and root mean square error (RMSE) of the interannual variability in the landing number and ACE of TC between the IBTrACS and FGOALS-f2 are also given.
4. Possible Reasons Contributing to the Prediction Skill
4.1. The Relationship between the TC Activity and ENSO
As a large-scale pattern, ENSO modulates the interannual variability in TC activity in WP and SCS [3,60,71,72,73]. A researcher [32] used a GCM in GFDL to simulate the global TC activity directly and they found the GCM could reproduce the relationship between the ENSO and TC. A researcher [16] regards the ENSO as a large-scale factor in improving the seasonal prediction skill of TCs in WP. There are high TCCs of SST between the observation and the seasonal prediction (from July to November) in FGOALS-f2 appearing in WP (Figure 5a), which will provide a stable ocean condition for the seasonal prediction of TC. Furthermore, the difference in the seasonal mean (July to November) track density of TC between El Niño and La Niña years for the observation is shown in Figure 5b. The result indicates that there is a seesaw pattern between the SCS and WP, which means more TC activity in WP and less TC activity in SCS during the years of El Niño compared to the pattern of TC track densities during the La Niña year. The track densities of TC predicted by the FGOALS-f2 can reproduce this seesaw pattern of TC activity between the WP and SCS, reflecting that FGOALS-f2 can capture the relationship between the ENSO and TC in WP and SCS.
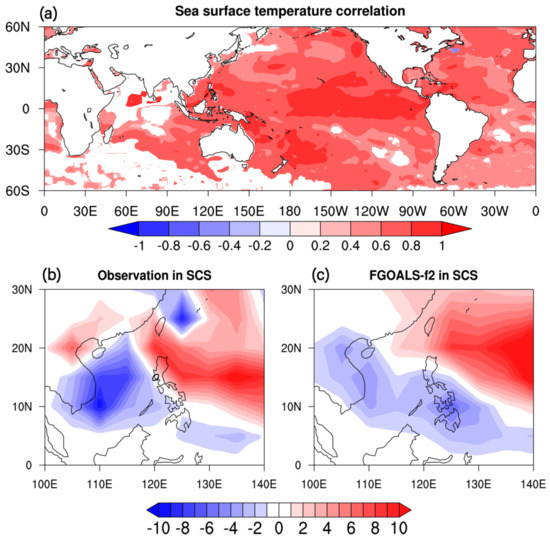
Figure 5.
The correlation coefficients of global SST between the hindcast of FGOALS-f2 and OISSTv2 from July to November during 1981 to 2015 (a) at the 95% confidence level. In addition, the seasonal mean (July to November) track density of TC between El Niño and La Niña years for OISSTv2 (b) and the hindcast of FGOALS-f2 (c) in SCS are also given. Blue (red) anomalies show a negative (positive) El Niño effect.
4.2. Genesis Potential Index
Many studies have shown that large-scale circulation is closely related to the generation, movement, and development of a TC [74,75,76,77]. As long as the relationships between the large-scale factors and TC can be found, the large-scale factors can be used to describe and predict TC activity. A researcher [16] found that the statistical model could provide a skillful seasonal prediction of TCs in WP and SCS when the ENSO and large-scale circulation are considered. A researcher [37] discussed the problem of climate control of TC activities, then developed a genesis potential index (GPI) of TCs, which considers the four large-scale variabilities. A researcher [77] found that the GPI can better represent the TC activity in WP after considering large-scale vertical motion. Furthermore, previous studies have revealed that the GPI has the ability to reproduce the observed variations in TC genesis activity over the SCS [78].
Figure 6a shows the TCC for the seasonal (July to November) GPI of TC between the ERAI and FGOALS-f2. The result indicates that a high correlation coefficient of GPI appears in the SCS, and this correlation coefficient is significant at a two-sided P = 0.05 level. The main reason for the high TCC of GPI is the accurate prediction of large-scale circulation by FGOALS-f2, especially relative humidity (Figure 6b), potential intensity (Figure 6c), vorticity (Figure 6d), vertical velocity (Figure 6e), and wind shear (Figure 6f).
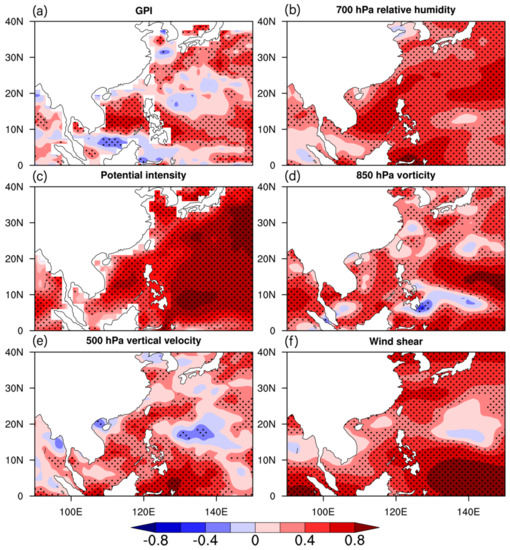
Figure 6.
The temporal correlation coefficient (TCC) for the seasonal (July to November) tropical cyclone genesis potential index (GPI; a), 700 hPa relative humidity (b), potential intensity (c), 850 hPa vorticity (d), 500 hPa vertical velocity (e), and wind shear (f) between the hindcast of FGOALS-f2 and the ERAI from 1981 to 2015. Black dot means the correlation coefficients that are significant at a two-sided P = 0.05 level.
Figure 7 shows the TCC of monthly GPI of TC between the ERA-interim and FGOALS-f2 (Figure 7a,c,e,g,i), and the ACC of GPI and each part of GPI equation between ERA-interim and the FGOALS-f2 are also given (Figure 7b,d,f,h,j). The result indicates that the monthly prediction skill of GPI is higher than the monthly prediction skill of TC, which is detected by the objective feature-tracking approach. In addition, the ACC of GPI between the ERAI and FGOALS-f2 is low in August and October, which is consistent with the results detected by the objective feature-tracking approach (Figure 7b,d). The lower ACC of GPI in August is mainly due to the predicted biases of Vm (Figure 7d), and the lower ACC of GPI in August is primarily due to the predicted biases of RH and Vshear (Figure 7h).
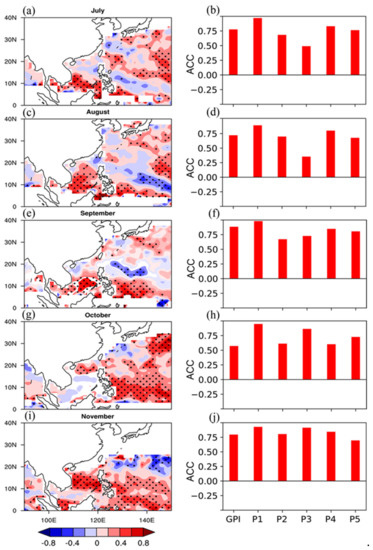
Figure 7.
The temporal correlation coefficient (TCC) for the monthly tropical cyclone genesis potential index (GPI) between the observation and FGOALS-f2. The monthly hindcast results from July to November (a,c,e,g,i) with 10-day leading are given, respectively, based on the different initial conditions. In addition, the anomaly correlation coefficient (ACC) of the monthly tropical cyclone genesis potential index (GPI) and each part of the equation between ERA-interim and the hindcast of FGOALS-f2 from July to November are also given, respectively (b,d,f,h,j). P1 to P4 means parts 1 to 4 of Equation (2). P1 represents the equation: , P2 represents the equation: , P3 represents the equation: , P4 represents the equation: , and P5 represents the equation: .
5. Discussion and Conclusions
The seasonal prediction skill of TCs in SCS is given by using the 35-year (1981–2015) hindcast datasets of FGOALS-f2 V1.0, which is a global dynamical seasonal prediction system based on the climate system model named CAS FGOALS-f2. The atmospheric component participated in the CMIP6 activities, GMMIP, and HighresMIP [79,80,81,82,83]. The simulation performance of TCs in FAMIL2, which is the atmospheric component of CAS FGOALS-f2, has been well evaluated [41], and the result indicates that the FAMIL2 can capture the TC generation, track, and variability well in the middle horizontal resolution (approximately 100 km). The sub-seasonal to seasonal prediction of TC activity in SCS is mainly based on statistical methods, but the prediction skill is not stable, especially when the predictors selected by the statistical methods are weak. The global dynamical prediction system has the potential to overcome these problems. It is necessary to evaluate the seasonal prediction skill of TCs in SCS by using the FGOALS-f2 and finally find the method to improve the prediction skill of TCs in SCS. The main findings and conclusions in this study are shown as follows:
1. According to a 35-year hindcast (1981–2015) of FGOALS-f2 V1.0, the seasonal prediction (from July to November) of TC activity in SCS has been evaluated. The FGOALS-f2 can reproduce the seasonal genesis location and track of TCs reasonably compared to the IBTrACS when the prediction was initialized on June 20th. There are considerable TCCs of seasonal TC number and ACE between the FGOALS-f2 and IBTrACS. The high-rank correlation coefficient appears in the TC generation and landfalling region, where they are significant at a two-sided P = 0.1 level. In addition, FGOALS-f2 has the prediction skill of landfalling TCs in the coastal areas of South China, the Indochina Peninsula, and the Philippines.
2. The reasonable prediction of the relationship between the large-scale pattern (SSTA, TC-ENSO relations, and GPI) and TC activity will contribute to the seasonal prediction of TC activity in the SCS. Obviously, the monthly prediction skill of large-scale patterns is higher than the prediction skill of TC, which is detected by an objective feature-tracking approach. The result indicates that there is still room for the monthly to seasonal prediction skill of TC in FGOALS-f2 by using a combination of statistical and dynamical methods, which will consider the relationship between large-scale circulations and TC activity.
Author Contributions
Methodology, J.L. and Z.S.; software, J.L.; validation, M.L., Q.T. and J.X.; formal analysis, Y.Y. and Z.Y.; investigation, L.Z.; writing, Y.Z., S.L., J.L. and Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (grant No. 42005117), the Strategic Priority Research Program of the Chinese Academy of Sciences (grant No. XDB40030205), and the Key Special Project for the Introduced Talents Team of the Southern Marine Science and Engineering Guangdong Laboratory (Guangdong) (grant No. GML2019ZD0601).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All observed and reanalysis dataset used in this study are freely available for public. The IBTrACS datasets are from https://www.ncei.noaa.gov/data/international-best-track-archive-for-climate-stewardship-ibtracs/v04r00/access/csv/; The ERA-interim datasets are from https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim, 29 November 2022; The OISSTv2 datasets are from https://psl.noaa.gov/data/gridded/data.noaa.oisst.v2.html, 29 November 2022; The FGOALS-f2 datasets are from https://apps.ecmwf.int/datasets/data/s2s-realtime-daily-averaged-anso/levtype=sfc/type=cf/, 29 November 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ling, Z.; Wang, G.; Wang, C. Out-of-phase relationship between tropical cyclones generated locally in the South China Sea and non-locally from the Northwest Pacific Ocean. Clim. Dyn. 2015, 45, 1129–1136. [Google Scholar] [CrossRef]
- Li, H.; Xu, F.; Sun, J.; Lin, Y.; Wright, J.S. Subtropical high affects interdecadal variability of tropical cyclone genesis in the South China Sea. J. Geophys. Res. Atmos. 2019, 124, 6379–6392. [Google Scholar] [CrossRef]
- Wang, G.; Su, J.; Ding, Y.; Chen, D. Tropical cyclone genesis over the South China Sea. J. Mar. Syst. 2007, 68, 318–326. [Google Scholar] [CrossRef]
- Cao, X.; Wu, R.; Bi, M. Contrasting contributions of flows on different time scales to tropical cyclone tracks over the South China Sea. Environ. Res. Lett. 2020, 15, 034003. [Google Scholar] [CrossRef]
- Robertson, A.W.; Kumar, A.; Peña, M.; Vitart, F. Improving and promoting subseasonal to seasonal prediction. Bull. Am. Meteorol. Soc. 2015, 96, ES49–ES53. [Google Scholar] [CrossRef]
- Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M. The subseasonal to seasonal (S2S) prediction project database. Bull. Am. Meteorol. Soc. 2017, 98, 163–173. [Google Scholar] [CrossRef]
- White, C.J.; Carlsen, H.; Robertson, A.W.; Klein, R.J.; Lazo, J.K.; Kumar, A.; Vitart, F.; Coughlan de Perez, E.; Ray, A.J.; Murray, V. Potential applications of subseasonal-to-seasonal (S2S) predictions. Meteorol. Appl. 2017, 24, 315–325. [Google Scholar] [CrossRef]
- Yang, L.; Du, Y.; Wang, D.; Wang, C.; Wang, X. Impact of intraseasonal oscillation on the tropical cyclone track in the South China Sea. Clim. Dyn. 2015, 44, 1505–1519. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, R. Interannual variability of the tropical cyclone landfall frequency over the southern and northern regions of East Asia in autumn. J. Clim. 2019, 32, 8677–8686. [Google Scholar] [CrossRef]
- Camp, J.; Roberts, M.J.; Comer, R.E.; Wu, P.; MacLachlan, C.; Bett, P.E.; Golding, N.; Toumi, R.; Chan, J.C. The western Pacific subtropical high and tropical cyclone landfall: Seasonal forecasts using the Met Office GloSea5 system. Q. J. R. Meteorol. Soc. 2019, 145, 105–116. [Google Scholar] [CrossRef]
- Sparks, N.; Toumi, R. On the seasonal and sub-seasonal factors influencing East China tropical cyclone landfall. Atmos. Sci. Lett. 2021, 22, e1014. [Google Scholar] [CrossRef]
- Manganello, J.V.; Hodges, K.I.; Kinter, J.L., III; Cash, B.A.; Marx, L.; Jung, T.; Achuthavarier, D.; Adams, J.M.; Altshuler, E.L.; Huang, B. Tropical cyclone climatology in a 10-km global atmospheric GCM: Toward weather-resolving climate modeling. J. Clim. 2012, 25, 3867–3893. [Google Scholar] [CrossRef]
- Zhang, C. Madden–Julian oscillation: Bridging weather and climate. Bull. Am. Meteorol. Soc. 2013, 94, 1849–1870. [Google Scholar] [CrossRef]
- Xiang, B.; Lin, S.-J.; Zhao, M.; Zhang, S.; Vecchi, G.; Li, T.; Jiang, X.; Harris, L.; Chen, J.-H. Beyond weather time-scale prediction for Hurricane Sandy and Super Typhoon Haiyan in a global climate model. Mon. Weather Rev. 2015, 143, 524–535. [Google Scholar] [CrossRef]
- Murakami, H.; Vecchi, G.A.; Villarini, G.; Delworth, T.L.; Gudgel, R.; Underwood, S.; Yang, X.; Zhang, W.; Lin, S.-J. Seasonal forecasts of major hurricanes and landfalling tropical cyclones using a high-resolution GFDL coupled climate model. J. Clim. 2016, 29, 7977–7989. [Google Scholar] [CrossRef]
- Chan, J.C.; Shi, J.-E.; Lam, C.-M. Seasonal forecasting of tropical cyclone activity over theWestern North Pacific and the South China Sea. Weather Forecast. 1998, 13, 997–1004. [Google Scholar] [CrossRef]
- Liu, K.; Chan, J.C. Climatological characteristics and seasonal forecasting of tropical cyclones making landfall along the South China coast. Mon. Weather Rev. 2003, 131, 1650–1662. [Google Scholar] [CrossRef]
- Gray, W.M.; Landsea, C.W.; Mielke, P.W.; Berry, K.J. Predicting Atlantic basin seasonal tropical cyclone activity by 1 August. Weather Forecast. 1993, 8, 73–86. [Google Scholar] [CrossRef]
- Gray, W.M.; Landsea, C.W.; Mielke, P.W., Jr.; Berry, K.J. Predicting Atlantic basin seasonal tropical cyclone activity by 1 June. Weather Forecast. 1994, 9, 103–115. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Mu, M.; Duan, W. Seasonal modulations of different impacts of two types of ENSO events on tropical cyclone activity in the western North Pacific. Clim. Dyn. 2013, 40, 2887–2902. [Google Scholar] [CrossRef]
- Choi, W.; Ho, C.-H.; Kim, J.; Kim, H.-S.; Feng, S.; Kang, K. A track pattern–based seasonal prediction of tropical cyclone activity over the North Atlantic. J. Clim. 2016, 29, 481–494. [Google Scholar] [CrossRef]
- Nath, S.; Kotal, S. Seasonal prediction of tropical cyclone activity over the North Indian Ocean using the neural network model. Atmósfera 2015, 28, 271–281. [Google Scholar] [CrossRef]
- Zhang, W.; Vecchi, G.A.; Murakami, H.; Delworth, T.; Wittenberg, A.T.; Rosati, A.; Underwood, S.; Anderson, W.; Harris, L.; Gudgel, R. Improved simulation of tropical cyclone responses to ENSO in the western North Pacific in the high-resolution GFDL HiFLOR coupled climate model. J. Clim. 2016, 29, 1391–1415. [Google Scholar] [CrossRef]
- Zhang, W.; Vecchi, G.A.; Villarini, G.; Murakami, H.; Rosati, A.; Yang, X.; Jia, L.; Zeng, F. Modulation of western North Pacific tropical cyclone activity by the Atlantic Meridional Mode. Clim. Dyn. 2017, 48, 631–647. [Google Scholar] [CrossRef]
- Zhang, W.; Villarini, G. Seasonal forecasting of western North Pacific tropical cyclone frequency using the North American multi-model ensemble. Clim. Dyn. 2019, 52, 5985–5997. [Google Scholar] [CrossRef]
- Camargo, S.J.; Emanuel, K.A.; Sobel, A.H. Use of a genesis potential index to diagnose ENSO effects on tropical cyclone genesis. J. Clim. 2007, 20, 4819–4834. [Google Scholar] [CrossRef]
- Vitart, F. Evolution of ECMWF sub-seasonal forecast skill scores. Q. J. R. Meteorol. Soc. 2014, 140, 1889–1899. [Google Scholar] [CrossRef]
- Robertson, A.W.; Vitart, F.; Camargo, S.J. Subseasonal to seasonal prediction of weather to climate with application to tropical cyclones. J. Geophys. Res. Atmos. 2020, 125, e2018JD029375. [Google Scholar] [CrossRef]
- Harris, L.; Zhou, L.; Lin, S.J.; Chen, J.H.; Chen, X.; Gao, K.; Morin, M.; Rees, S.; Sun, Y.; Tong, M. GFDL SHiELD: A unified system for weather-to-seasonal prediction. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002223. [Google Scholar] [CrossRef]
- Manganello, J.V.; Hodges, K.I.; Cash, B.A.; Kinter, J.L., III; Altshuler, E.L.; Fennessy, M.J.; Vitart, F.; Molteni, F.; Towers, P. Seasonal forecasts of tropical cyclone activity in a high-atmospheric-resolution coupled prediction system. J. Clim. 2016, 29, 1179–1200. [Google Scholar] [CrossRef]
- Wu, G.; Lau, N.-C. A GCM simulation of the relationship between tropical-storm formation and ENSO. Mon. Weather Rev. 1992, 120, 958–977. [Google Scholar] [CrossRef]
- Chan, J.C. Tropical cyclone activity over the western North Pacific associated with El Niño and La Niña events. J. Clim. 2000, 13, 2960–2972. [Google Scholar] [CrossRef]
- Wang, B.; Xiang, B.; Lee, J.-Y. Subtropical high predictability establishes a promising way for monsoon and tropical storm predictions. Proc. Natl. Acad. Sci. USA 2013, 110, 2718–2722. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43, 1–36. [Google Scholar] [CrossRef]
- Hendon, H.H.; Wheeler, M.C.; Zhang, C. Seasonal dependence of the MJO–ENSO relationship. J. Clim. 2007, 20, 531–543. [Google Scholar] [CrossRef]
- Emanuel, K.; Nolan, D.S. Tropical cyclone activity and the global climate system. In Proceedings of the 26th Conference on Hurricanes and Tropical Meteorolgy, Miami, FL, USA, 3–7 May 2004. [Google Scholar]
- Camargo, S.J.; Sobel, A.H.; Barnston, A.G.; Emanuel, K.A. Tropical cyclone genesis potential index in climate models. Tellus A 2007, 59, 428–443. [Google Scholar] [CrossRef]
- Wang, B.; Moon, J.-Y. An anomalous genesis potential index for MJO modulation of tropical cyclones. J. Clim. 2017, 30, 4021–4035. [Google Scholar] [CrossRef]
- Bao, Q.; Wu, X.; Li, J.; Wang, L.; He, B.; Wang, X.; Liu, Y.; Wu, G. Outlook for El Niño and the Indian Ocean Dipole in autumn-winter 2018–2019. Chin. Sci. Bull. 2018, 64, 73–78. [Google Scholar] [CrossRef]
- He, B.; Bao, Q.; Wang, X.; Zhou, L.; Wu, X.; Liu, Y.; Wu, G.; Chen, K.; He, S.; Hu, W. CAS FGOALS-f3-L model datasets for CMIP6 historical atmospheric model intercomparison project simulation. Adv. Atmos. Sci. 2019, 36, 771–778. [Google Scholar] [CrossRef]
- Li, J.; Bao, Q.; Liu, Y.; Wu, G.; Wang, L.; He, B.; Wang, X.; Li, J. Evaluation of FAMIL2 in simulating the climatology and seasonal-to-interannual variability of tropical cyclone characteristics. J. Adv. Model. Earth Syst. 2019, 11, 1117–1136. [Google Scholar] [CrossRef]
- Bao, Q.; Li, J. Progress in climate modeling of precipitation over the Tibetan Plateau. Natl. Sci. Rev. 2020, 7, 486–487. [Google Scholar] [CrossRef]
- Zhou, L.; Bao, Q.; Liu, Y.; Wu, G.; Wang, W.C.; Wang, X.; He, B.; Yu, H.; Li, J. Global energy and water balance: Characteristics from F inite-volume A tmospheric M odel of the IAP/LASG (FAMIL 1). J. Adv. Model. Earth Syst. 2015, 7, 1–20. [Google Scholar] [CrossRef]
- Ren, H.-L.; Wu, Y.; Bao, Q.; Ma, J.; Liu, C.; Wan, J.; Li, Q.; Wu, X.; Liu, Y.; Tian, B. The China multi-model ensemble prediction system and its application to flood-season prediction in 2018. J. Meteorol. Res. 2019, 33, 540–552. [Google Scholar] [CrossRef]
- Bloom, S.; Takacs, L.; Da Silva, A.; Ledvina, D. Data assimilation using incremental analysis updates. Mon. Weather Rev. 1996, 124, 1256–1271. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Huang, B.; Xue, Y.; Zhang, D.; Kumar, A.; McPhaden, M.J. The NCEP GODAS ocean analysis of the tropical Pacific mixed layer heat budget on seasonal to interannual time scales. J. Clim. 2010, 23, 4901–4925. [Google Scholar] [CrossRef]
- Hoffman, R.N.; Kalnay, E. Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus A Dyn. Meteorol. Oceanogr. 1983, 35, 100–118. [Google Scholar] [CrossRef]
- Kang, I.-S.; Jang, P.-H.; Almazroui, M. Examination of multi-perturbation methods for ensemble prediction of the MJO during boreal summer. Clim. Dyn. 2014, 42, 2627–2637. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, D.P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Chin, T.M.; Liu, C.; Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling and environmental studies. Earth Syst. Sci. Data 2016, 8, 165–176. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The international best track archive for climate stewardship (IBTrACS) unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Zhao, M.; Held, I.M.; Lin, S.-J.; Vecchi, G.A. Simulations of global hurricane climatology, interannual variability, and response to global warming using a 50-km resolution GCM. J. Clim. 2009, 22, 6653–6678. [Google Scholar] [CrossRef]
- Chen, J.-H.; Lin, S.-J. Seasonal predictions of tropical cyclones using a 25-km-resolution general circulation model. J. Clim. 2013, 26, 380–398. [Google Scholar] [CrossRef]
- Walsh, K.; Fiorino, M.; Landsea, C.; McInnes, K. Objectively determined resolution-dependent threshold criteria for the detection of tropical cyclones in climate models and reanalyses. J. Clim. 2007, 20, 2307–2314. [Google Scholar] [CrossRef]
- Simpson, R.H.; Saffir, H. The Hurricane Disaster—Potential Scale. Weatherwise 1974, 27, 169–186. [Google Scholar] [CrossRef]
- Emanuel, K.A. Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics. J. Atmos. Sci. 1995, 52, 3969–3976. [Google Scholar] [CrossRef]
- Zhan, R.; Wang, Y.; Lei, X. Contributions of ENSO and East Indian Ocean SSTA to the interannual variability of Northwest Pacific tropical cyclone frequency. J. Clim. 2011, 24, 509–521. [Google Scholar] [CrossRef]
- Chan, J.C.; Shi, J.E. Long-term trends and interannual variability in tropical cyclone activity over the western North Pacific. Geophys. Res. Lett. 1996, 23, 2765–2767. [Google Scholar] [CrossRef]
- Vitart, F.; Anderson, J.; Stern, W. Simulation of interannual variability of tropical storm frequency in an ensemble of GCM integrations. J. Clim. 1997, 10, 745–760. [Google Scholar] [CrossRef]
- Mei, W.; Lien, C.-C.; Lin, I.-I.; Xie, S.-P. Tropical cyclone–induced ocean response: A comparative study of the South China Sea and tropical northwest Pacific. J. Clim. 2015, 28, 5952–5968. [Google Scholar] [CrossRef]
- Strachan, J.; Vidale, P.L.; Hodges, K.; Roberts, M.; Demory, M.-E. Investigating global tropical cyclone activity with a hierarchy of AGCMs: The role of model resolution. J. Clim. 2013, 26, 133–152. [Google Scholar] [CrossRef]
- Brown, J.R.; Brierley, C.M.; An, S.-I.; Guarino, M.-V.; Stevenson, S.; Williams, C.J.; Zhang, Q.; Zhao, A.; Abe-Ouchi, A.; Braconnot, P. Comparison of past and future simulations of ENSO in CMIP5/PMIP3 and CMIP6/PMIP4 models. Clim. Past 2020, 16, 1777–1805. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, X. Prediction of eastern and central Pacific ENSO events and their impacts on East Asian climate by the NCEP Climate Forecast System. J. Clim. 2014, 27, 4451–4472. [Google Scholar] [CrossRef]
- Klotzbach, P.; Blake, E.; Camp, J.; Caron, L.-P.; Chan, J.C.; Kang, N.-Y.; Kuleshov, Y.; Lee, S.-M.; Murakami, H.; Saunders, M. Seasonal tropical cyclone forecasting. Trop. Cyclone Res. Rev. 2019, 8, 134–149. [Google Scholar] [CrossRef]
- Camp, J.; Bett, P.E.; Golding, N.; Hewitt, C.D.; Mitchell, T.D.; Scaife, A.A. Verification of the 2019 GloSea5 seasonal tropical cyclone landfall forecast for East China. J. Meteorol. Res. 2020, 34, 917–925. [Google Scholar] [CrossRef]
- Feng, X.; Hodges, K.I.; Hoang, L.; Pura, A.G.; Yang, G.Y.; Luu, H.; David, S.J.; Duran, G.A.M.; Guo, Y.P. A new approach to skillful seasonal prediction of Southeast Asia tropical cyclone occurrence. J. Geophys. Res. Atmos. 2022, 127, e2022JD036439. [Google Scholar] [CrossRef]
- Feng, X.; Klingaman, N.P.; Hodges, K.I.; Guo, Y.-P. Western North Pacific tropical cyclones in the Met office global seasonal forecast system: Performance and ENSO teleconnections. J. Clim. 2020, 33, 10489–10504. [Google Scholar] [CrossRef]
- Chen, G. How does shifting Pacific Ocean warming modulate on tropical cyclone frequency over the South China Sea? J. Clim. 2011, 24, 4695–4700. [Google Scholar] [CrossRef]
- Camargo, S.J.; Sobel, A.H. Western North Pacific tropical cyclone intensity and ENSO. J. Clim. 2005, 18, 2996–3006. [Google Scholar] [CrossRef]
- Kim, H.-M.; Webster, P.J.; Curry, J.A. Modulation of North Pacific tropical cyclone activity by three phases of ENSO. J. Clim. 2011, 24, 1839–1849. [Google Scholar] [CrossRef]
- Chu, P.-S. Large-scale circulation features associated with decadal variations of tropical cyclone activity over the central North Pacific. J. Clim. 2002, 15, 2678–2689. [Google Scholar] [CrossRef]
- Yoshida, R.; Kajikawa, Y.; Ishikawa, H. Impact of boreal summer intraseasonal oscillation on environment of tropical cyclone genesis over the western North Pacific. Sola 2014, 10, 15–18. [Google Scholar] [CrossRef]
- Walsh, K.; Lavender, S.; Scoccimarro, E.; Murakami, H. Resolution dependence of tropical cyclone formation in CMIP3 and finer resolution models. Clim. Dyn. 2013, 40, 585–599. [Google Scholar] [CrossRef]
- Camargo, S.J. Global and regional aspects of tropical cyclone activity in the CMIP5 models. J. Clim. 2013, 26, 9880–9902. [Google Scholar] [CrossRef]
- Wang, L.; Pan, X. Diagnosis of seasonal variations of tropical cyclogenesis over the South China Sea using a genesis potential index. J. Ocean Univ. China 2012, 11, 267–278. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- He, B.; Liu, Y.; Wu, G.; Bao, Q.; Zhou, T.; Wu, X.; Wang, L.; Li, J.; Wang, X.; Li, J. CAS FGOALS-f3-L model datasets for CMIP6 GMMIP Tier-1 and Tier-3 experiments. Adv. Atmos. Sci. 2020, 37, 18–28. [Google Scholar] [CrossRef]
- Zhou, T.; Turner, A.G.; Kinter, J.L.; Wang, B.; Qian, Y.; Chen, X.; Wu, B.; Liu, B.; Zou, L.; He, B. GMMIP (v1. 0) contribution to CMIP6: Global monsoons model inter-comparison project. Geosci. Model Dev. 2016, 9, 3589–3604. [Google Scholar] [CrossRef]
- Haarsma, R.J.; Roberts, M.J.; Vidale, P.L.; Senior, C.A.; Bellucci, A.; Bao, Q.; Chang, P.; Corti, S.; Fučkar, N.S.; Guemas, V. High resolution model intercomparison project (HighResMIP v1. 0) for CMIP6. Geosci. Model Dev. 2016, 9, 4185–4208. [Google Scholar] [CrossRef]
- Roberts, M.J.; Camp, J.; Seddon, J.; Vidale, P.L.; Hodges, K.; Vanniere, B.; Mecking, J.; Haarsma, R.; Bellucci, A.; Scoccimarro, E. Impact of model resolution on tropical cyclone simulation using the HighResMIP–PRIMAVERA multimodel ensemble. J. Clim. 2020, 33, 2557–2583. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).