Ionospheric Variability over the Brazilian Equatorial Region during the Minima Solar Cycles 1996 and 2009: Comparison between Observational Data and the IRI Model
Abstract
1. Introduction
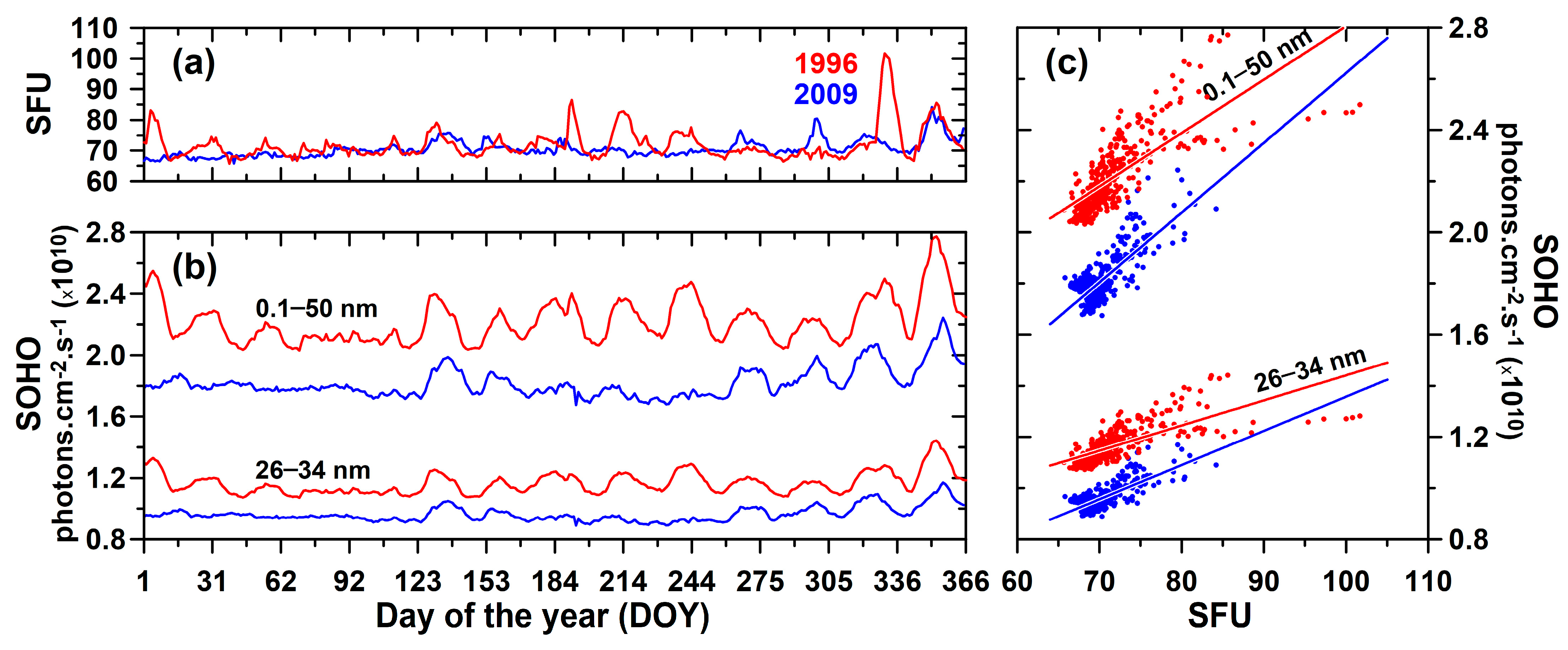
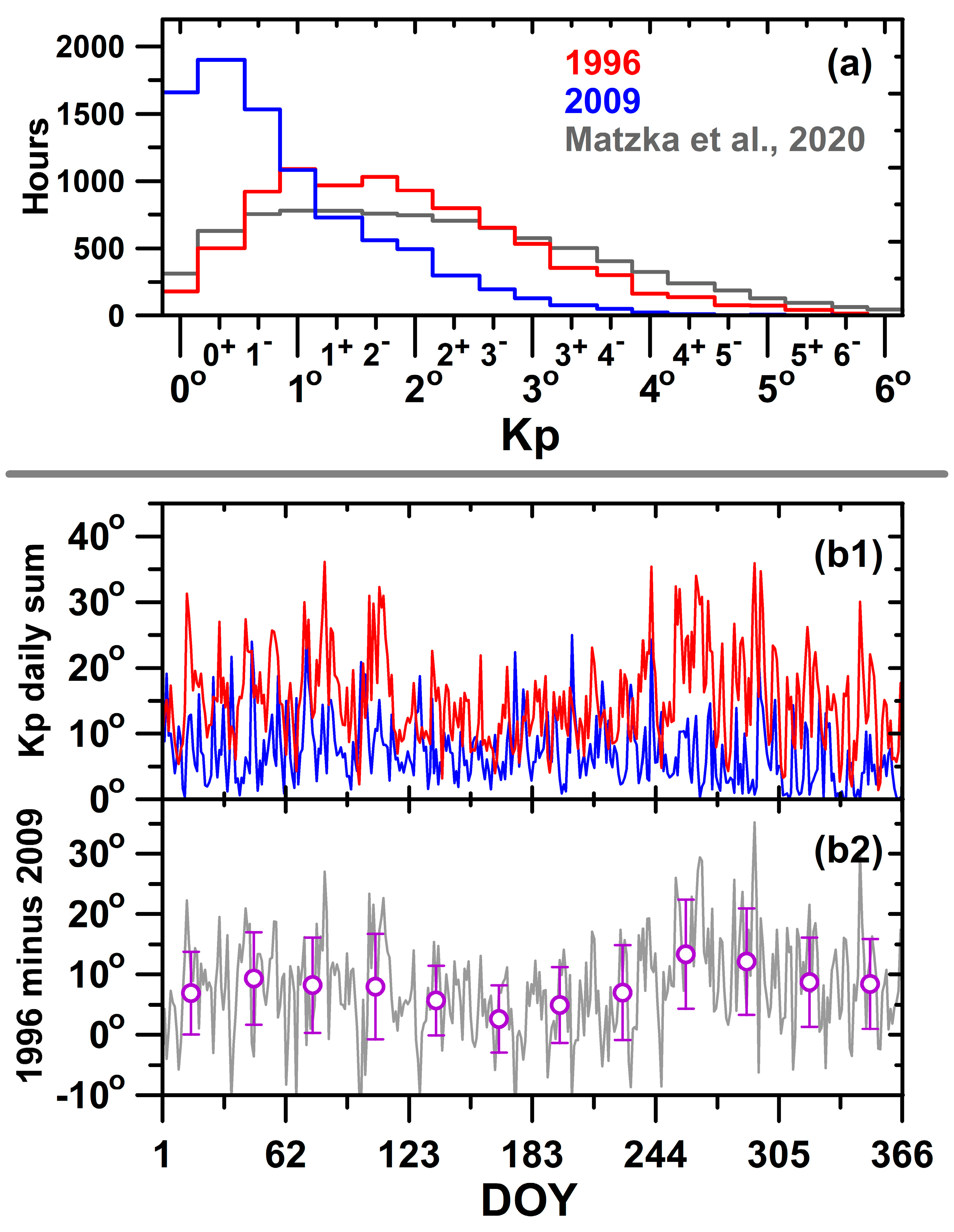
2. Instrumentation, Data Set, and Geophysical Conditions
3. Results
3.1. Dependence of the Model and the Observational F2 Peak Parameters with Respect to Time and Season
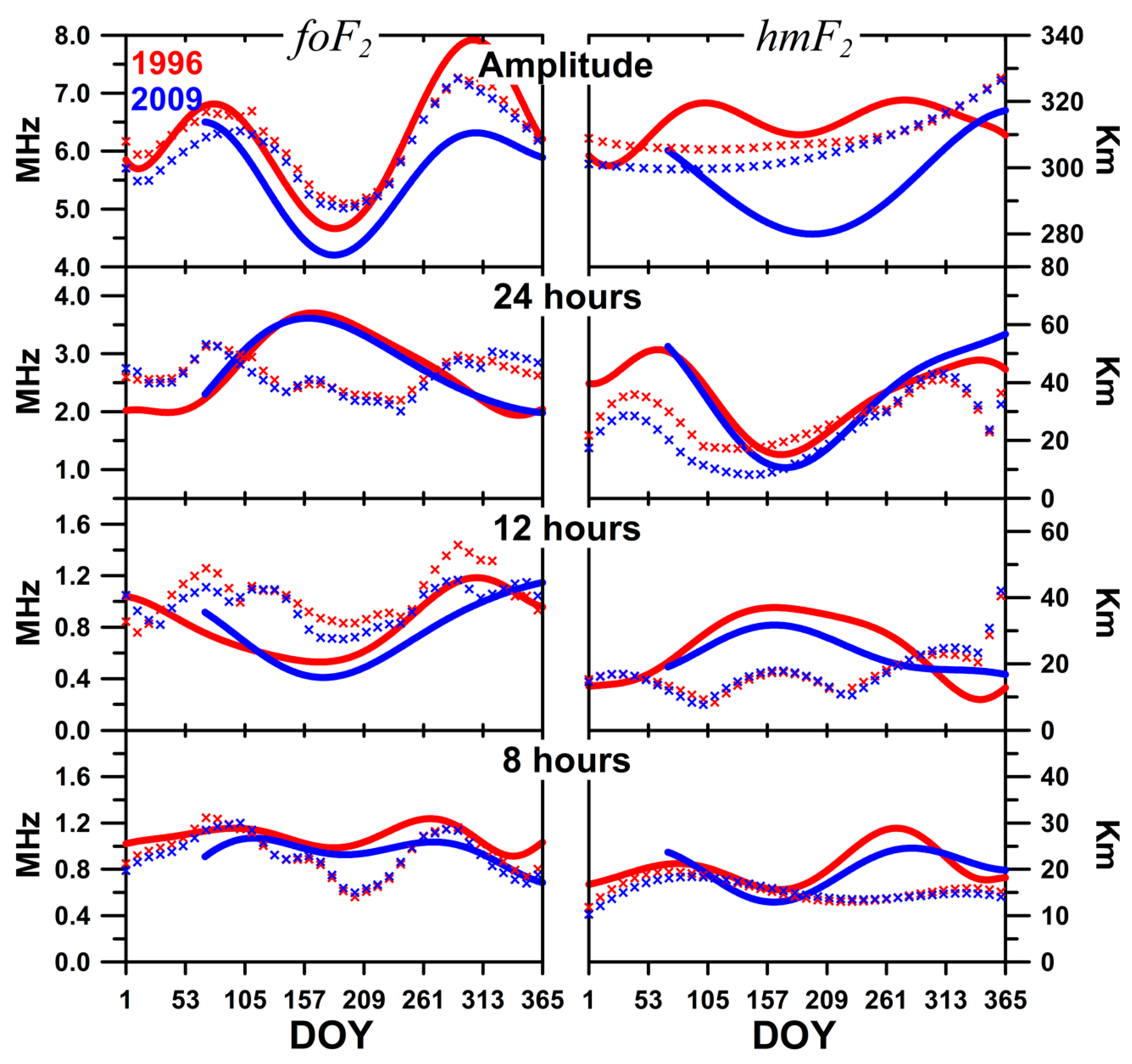
3.2. Climatology of the Tidal Modes
4. Discussion
4.1. Influence of Solar Flux in the Equatorial Ionosphere
4.2. IRI-2016 Performance during Anomalous Solar Minimum
5. Final Remarks
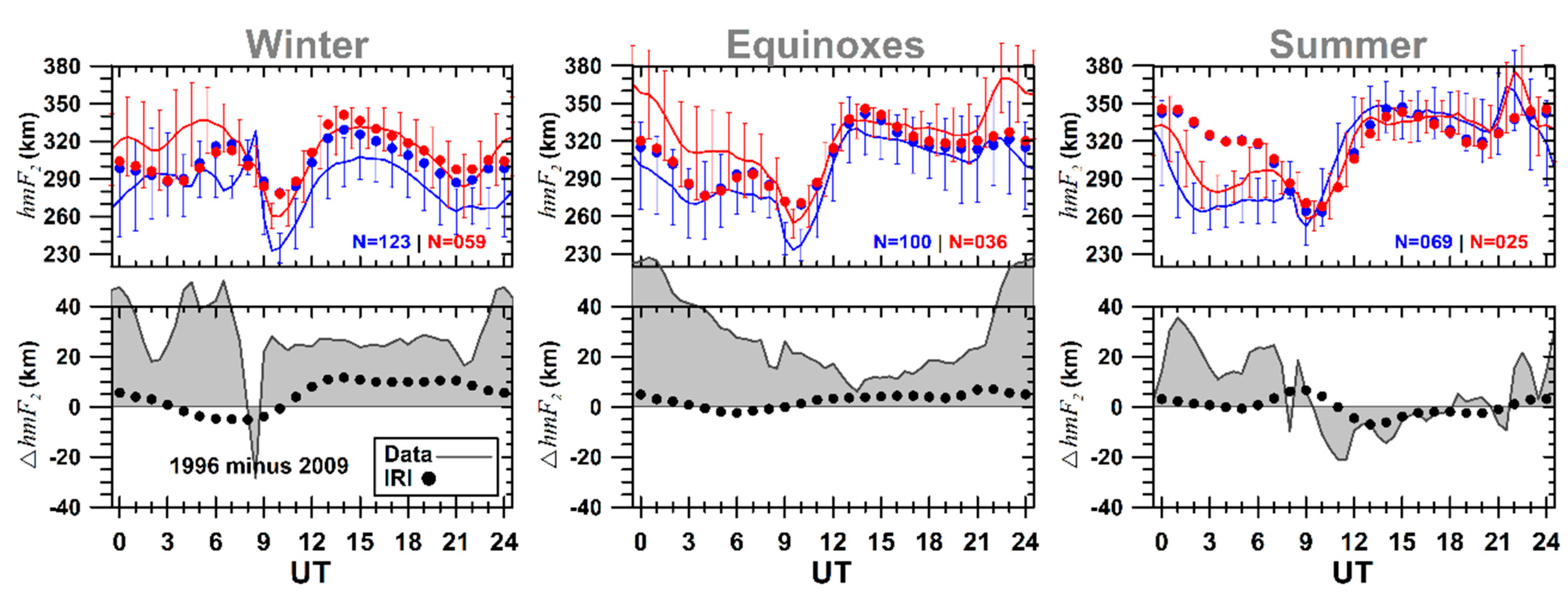
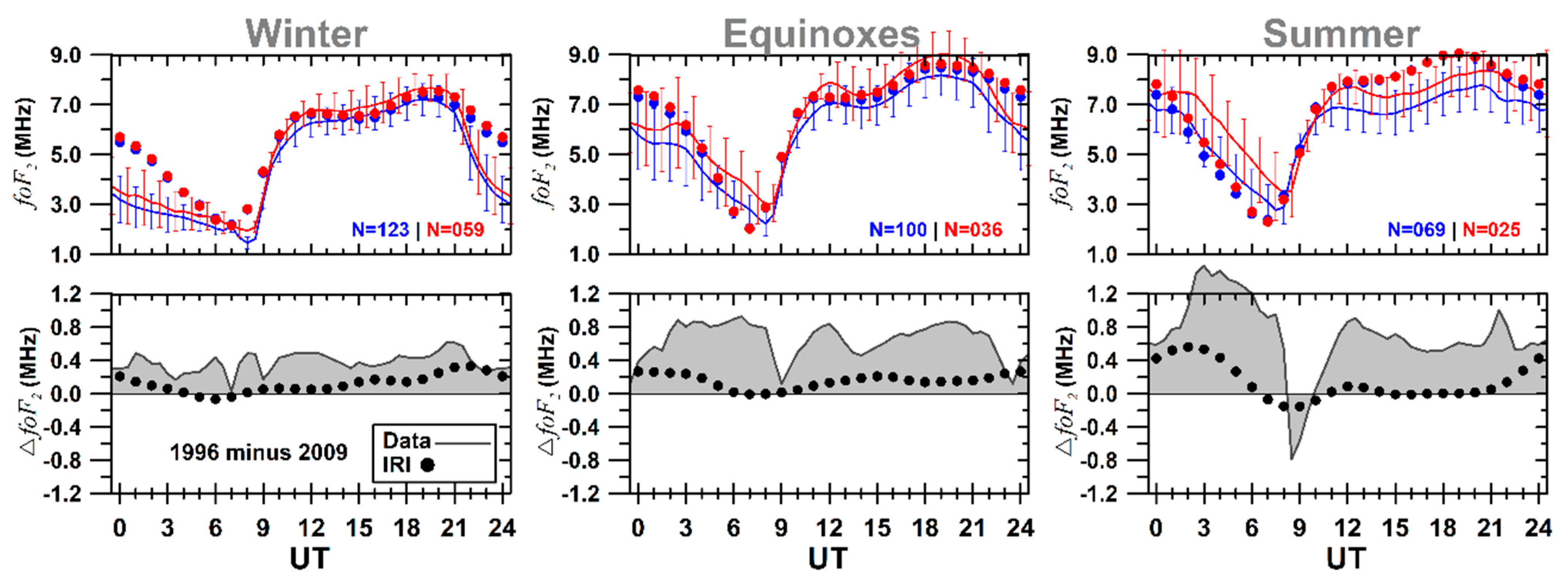
- In general, the mean values of the hmF2 and the foF2 during the deep solar minimum were lower than in 1996, except in some intervals, such as in the summer, when the hmF2 in 2009 presented slightly higher values in a specific interval of daytime when compared to 1996. Interestingly, such behavior was predicted by the IRI but with a smaller amplitude when compared with data;
- The seasonal mean values of the hmF2 and the foF2 presented significant deviations between their respective values for 2009 and 1996. The considerable discrepancy between the observation and the model was also observed during both years, except during some daytime intervals;
- During the equinoxes, the prereversal vertical drift (Vz) was slightly higher in 2009 (~4.00 m/s) than in 1996 (3.54 m/s). In the summer, a small difference in the Vz value for both periods (6.57 m/s in 2009 and 6.78 m/s in 1996) was found. Additionally, the PRE occurred in 2009 occurred some minutes earlier than in 1996, mainly during the equinoxes.
- The analysis of atmospheric tides showed some differences between the two minima for both amplitudes of hmF2 and foF2, which were higher in 1996 than in 2009 for almost all the days analyzed. Regarding the different tide components, the contribution of the diurnal component to the hmF2 variability was similar in both periods. When compared to 12 h tide, the most important contribution of the semidiurnal tide was observed from April to September for both 1996 and 2009. It is also important to mention that the terdiurnal and the semidiurnal periodicities have similar annual amplitude, about 21 km (hmF2) and 0.8 MHz (foF2). However, the hmF2 and foF2 terdiurnal and the semidiurnal tide components present opposite behavior throughout the year; the terdiurnal hmF2/foF2 component is smaller/higher than the semidiurnal component during the winter and higher/smaller for the summer period.
- The amplitude of foF2 was higher in 1996 than in 2009, mainly in the second half of the year. In general, the higher intensity of tide components was observed for 1996, except for the 24 h component, which presented similar results for both solar minimum periods. Additionally, besides the important contribution of the diurnal component in the foF2 variability, the terdiurnal component in the foF2 is also highlighted when compared with the semidiurnal component, which has been higher than the semidiurnal tide for almost the whole year, except for the southern summer.
- In the case of the foF2 amplitude, a good representation by the IRI model was observed during the first four months of 1996; however, an overestimation was observed in the mid of April to the end of July. On the other hand, an underestimation was noted in the last months of the year, with a maximum in November. In 2009, the model overestimated the observational data during almost the period analyzed. For the 24 h, 12 h, and 8 h components, the representation by the IRI model was not good for both years, except in some cases.
- In the case of the hmF2 amplitude, the prediction made by the IRI was very poor for both years. The best representation of the diurnal component was found in the second half of the year during both 1996 and 2009. In the case of the terdiurnal component, the best representation was found during the first half of the year. Finally, the importance of the terdiurnal component to hmF2 and foF2 variability was not predicted by the IRI, which is different from what was observed in the observational data.
- Finally, our results clearly showed the impacts of a decrease in the level of solar extreme ultraviolet radiation in 2009 on both the ionospheric parameters of frequency and height. However, it was also shown that such a decrease alone could not totally explain all the observed features. Additionally, similar to what has been reported by other authors, the model IRI needs some improvements to better represents the solar minimum periods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basu, S. The peculiar solar cycle 24—Where do we stand? J. Phys. Conf. Ser. 2013, 440, 012001. [Google Scholar] [CrossRef]
- Balan, N.; Chen, C.Y.; Rajesh, P.K.; Liu, J.Y.; Bailey, G.J. Modeling and observations of the low latitude ionosphere plasmasphere system at long deep solar minimum. J. Geophys. Res. 2012, 117, A08316. [Google Scholar] [CrossRef]
- Kutiev, I.; Tsagouri, I.; Perrone, L.; Pancheva, D.; Mukhtarov, P.; Mikhailov, A.; Lastovicka, J.; Jakowski, N.; Buresova, D.; Blanch, E.; et al. Solar activity impact on the Earth’s upper atmosphere. J. Space Weather Space Clim. 2013, 3, A06. [Google Scholar] [CrossRef]
- Solomon, S.C.; Woods, T.N.; Didkovsky, L.V.; Emmert, J.T.; Qian, L. Anomalously low solar extreme-ultraviolet irradiance and thermospheric density during solar minimum. Geophys. Res. Lett. 2010, 37, L16103. [Google Scholar] [CrossRef]
- Mansoori, A.A.; Khan, P.A.; Ahmad, R.; Atulkar, R.; Aslam, A.M.; Bhardwaj, S.; Malvi, B.; Purohit, P.K.; Gwal, A.K. Evaluation of long term solar activity effects on GPS derived TEC. J. Phys. Conf. Ser. 2016, 759, 012069. [Google Scholar] [CrossRef]
- Araujo-Pradere, E.A.; Fuller-Rowell, T.J.; Codrescu, M.V. Storm: An empirical storm-time ionospheric correction model—1. Model description. Radio Sci. 2002, 37, 1–12. [Google Scholar] [CrossRef]
- Moses, M.; Panda, S.K.; Dodo, J.D.; Ojigi, L.M.; Lawal, K. Assessment of long-term impact of solar activity on the ionosphere over an African equatorial GNSS station. Earth Sci. Inf. 2022, 15, 2109–2117. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Le, H.; Kurkin, V.I.; Polekh, N.M.; Lee, C.-C. The ionosphere under extremely prolonged low solar activity. J. Geophys. Res. 2011, 116, A04320. [Google Scholar] [CrossRef]
- Liu, L.; Yang, J.; Le, H.; Chen, Y.; Wan, W.; Lee, C.-C. Comparative study of the equatorial ionosphere over Jicamarca during recent two solar minima. J. Geophys. Res. 2012, 117, A01315. [Google Scholar] [CrossRef]
- Heelis, R.A.; Coley, W.R.; Burrell, A.G.; Hairston, M.R.; Earle, G.D.; Perdue, M.D.; Power, R.A.; Harmon, L.L.; Holt, B.J.; Lippincott, C.R. Behavior of the O+/H+ transition height during the extreme solar minimum of 2008. Geophys. Res. Lett. 2009, 36, L00C03. [Google Scholar] [CrossRef]
- Aponte, N.; Brum, C.G.M.; Sulzer, M.P.; González, S.A. Measurements of the O+ to H+ transition height and ion temperatures in the lower topside ionosphere over Arecibo for equinox conditions during the 2008–2009 extreme solar minimum. J. Geophys. Res. Space Phys. 2013, 118, 4465–4470. [Google Scholar] [CrossRef]
- Coley, W.R.; Heelis, R.A.; Hairston, M.R.; Earle, G.D.; Perdue, M.D.; Power, R.A.; Harmon, L.L.; Holt, B.J.; Lippincott, C.R. Ion temperature and density relationships measured by CINDI from the C/NOFS spacecraft during solar minimum. J. Geophys. Res. 2010, 115, A02313. [Google Scholar] [CrossRef]
- Brum, C.G.M.; Rodrigues, F.S.; dos Santos, P.T.; Matta, A.C.; Aponte, N.; Gonzalez, S.A.; Robles, E. A modeling study of foF2 and hmF2 parameters measured by the Arecibo incoherent scatter radar and comparison with IRI model predictions for solar cycles 21, 22, and 23. J. Geophys. Res. 2011, 116, A03324. [Google Scholar] [CrossRef]
- Klenzing, J.; Simões, F.; Ivanov, S.; Heelis, R.A.; Bilitza, D.; Pfaff, R.; Rowland, D. Topside equatorial ionospheric density and composition during and after extreme solar minimum. J. Geophys. Res. 2011, 116, A12330. [Google Scholar] [CrossRef]
- Abdu, M.A.; CBrum, G.M.; Batista, I.S.; Sobral, J.H.A.; de Paula, E.R.; Souza, J.R. Solar flux effects on equatorial ionization anomaly and total electron content over Brazil: Observational results versus IRI representations. Adv. Space Res. 2008, 42, 617–625. [Google Scholar] [CrossRef]
- Souza, J.R.; Brum, C.G.M.; Abdu, M.A.; Batista, I.S.; Asevedo, W.D.; Bailey, G.J.; Bittencourt, J.A. Parameterized Regional Ionospheric Model and a comparison of its results with experimental data and IRI representations. Adv. Space Res. 2010, 46, 1032–1038. [Google Scholar] [CrossRef]
- Batista, I.S.; Abdu, M.A. Ionospheric variability at Brazilian low and equatorial latitudes: Comparison between observations and IRI model. Adv. Space Res. 2004, 34, 1894–1900. [Google Scholar] [CrossRef]
- Rush, C.; Fox, M.; Bilitza, D.; Davies, K.; McNamara, L.; Stewart, F.; PoKempner, M. Ionospheric mapping—An update of foF2 coefficients. Telecomm. J. 1989, 56, 179–182. [Google Scholar]
- Altadill, D.; Magdaleno, S.; Torta, J.M.; Blanch, E. Global empirical models of the density peak height and of the equivalent scale height for quiet conditions. Adv. Space Res. 2013, 52, 1756–1769. [Google Scholar] [CrossRef]
- Bilitza, D. The International Reference Ionosphere—Status 2013. Adv. Space Res. 2015, 55, 1914–1927. [Google Scholar] [CrossRef]
- Bilitza, D. IRI the International Standard for the Ionosphere. Adv. Radio Sci. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Brown, S.; Bilitza, D.; Yiğit, E. Ionosonde-based indices for improved representation of solar cycle variation in the International Reference Ionosphere model. J. Atmos. Sol.-Terr. Phys. 2018, 171, 137–146. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Terra, P.; Vargas, F.; Brum, C.G.M.; Miller, E.S. Geomagnetic and solar dependency of MSTIDs occurrence rate: A climatology based on airglow observations from the Arecibo Observatory ROF. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027770. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The geomagnetic Kp index and derived indices of geomagnetic activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Araujo-Pradere, E.A.; Redmon, R.; Fedrizzi, M.; Viereck, R.; Fuller-Rowell, T.J. Some Characteristics of the Ionospheric Behavior During the Solar Cycle 23–24 Minimum. Sol. Phys. 2011, 274, 439–456. [Google Scholar] [CrossRef]
- Qian, L.; Solomon, S.C.; Roble, R.G.; Kane, T.J. Model simulations of global change in the ionosphere. Geophys. Res. Lett. 2008, 35, L07811. [Google Scholar] [CrossRef]
- Chaitanya, P.P.; Patra, A.K.; Balan, N.; Rao, S.V.B. Unusual behavior of the low-latitude ionosphere in the Indian sector during the deep solar minimum in 2009. J. Geophys. Res. Space Phys. 2016, 121, 6830–6843. [Google Scholar] [CrossRef]
- Abdu, M.A. Equatorial spread F development and quiet time variability under solar minimum conditions. Indian J. Radio Space Phys. 2012, 42, 168–183. [Google Scholar]
- Rishbeth, H.; Mendillo, M. Patterns of F2-layer variability. J. Atmos. Sol.-Terr. Phys. 2001, 63, 1661–1680. [Google Scholar] [CrossRef]
- Kilpua, E.K.J.; Luhmann, J.G.; Jian, L.K.; Russell, C.T.; Li, Y. Why have geomagnetic storms been so weak during the recent solar minimum and the rising phase of cycle 24? J. Atmos. Sol.-Terr. Phys. 2014, 107, 12–19. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Le, H.; Wan, W. Geomagnetic activity effect on the global ionosphere during the 2007–2009 deep solar minimum. J. Geophys. Res. Space Phys. 2014, 119, 3747–3754. [Google Scholar] [CrossRef]
- Liu, J.; Liu, L.; Zhao, B.; Wei, Y.; Hu, L.; Xiong, B. High-speed stream impacts on the equatorial ionization anomaly region during the deep solar minimum year 2008. J. Geophys. Res. 2012, 117, A10304. [Google Scholar] [CrossRef]
- Buresova, D.; Lastovicka, J.; Hejda, P.; Bochnicek, J. Ionospheric disturbances under low solar activity conditions. Adv. Space Res. 2014, 54, 185–196. [Google Scholar] [CrossRef]
- Santos, Â.M.; Brum, C.G.M.; Batista, I.S.; Sobral, J.H.A.; Abdu, M.A.; Souza, J.R. Responses of intermediate layers to geomagnetic activity during the 2009 deep solar minimum over the Brazilian low-latitude sector. Ann. Geophys. 2022, 40, 259–269. [Google Scholar] [CrossRef]
- Cai, X.; Burns, A.G.; Wang, W.; Qian, L.; Pedatella, N.; Coster, A.; Zhang, S.; Solomon, S.C.; Eastes, R.W.; Daniell, R.E. Variations in thermosphere composition and ionosphere total electron content under “geomagnetically quiet” conditions at solar-minimum. Geophys. Res. Lett. 2021, 48, e2021GL093300. [Google Scholar] [CrossRef]
- Dos Santos, Â.M.; Batista, I.S.; Abdu, M.A.; Sobral, J.H.A.; de Souza, J.R.; Brum, C.G.M. Climatology of intermediate descending layers (or 150 km echoes) over the equatorial and low-latitude regions of Brazil during the deep solar minimum of 2009. Ann. Geophys. 2019, 37, 1005–1024. [Google Scholar] [CrossRef]
- Santos, A.M.; Brum, C.G.M.; Batista, I.S.; Sobral, J.H.A.; Abdu, M.A.; Souza, J.R.; Chen, S.S.; Denardini, C.M.; de Jesus, R.; Venkatesh, K.; et al. Anomalous responses of the F2 layer over the Brazilian equatorial sector during a counter electrojet event: A case study. J. Geophys.Res. Space Phys. 2022, 127, e2022JA030584. [Google Scholar] [CrossRef]
- Pancheva, D.; Miyoshi, Y.; Mukhtarov, P.; Jin, H.; Shinagawa, H.; Fujiwara, H. Global response of the ionosphere to atmospheric tides forced from below: Comparison between COSMIC measurements and simulations by atmosphere-ionosphere coupled model GAIA. J. Geophys. Res. 2012, 117, A07319. [Google Scholar] [CrossRef]
- Chang, J.L.; Avery, S.K. Observations of the diurnal tide in the mesosphere and lower thermosphere over Christmas Island. J. Geophys. Res. 1997, 102, 1895–1907. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Zhang, X. The characteristics of terdiurnal tides in the ionosphere. Astrophys. Space Sci. 2020, 365, 155. [Google Scholar] [CrossRef]
- Gong, Y.; Zhou, Q. Incoherent scatter radar study of the terdiurnal tide in the E- and F-region heights at Arecibo. Geophys. Res. Lett. 2011, 38, L15101. [Google Scholar] [CrossRef]

| 1996 2009 | foF2 | hmF2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Ionosonde | IRI | Ionosonde | IRI | |||||
| 12 months | 6 months | 12 months | 6 months | 12 months | 6 months | 12 months | 6 months | |
| Amplitude | ×× | ×× | ×× | ×× | ×× | × | ×× | |
| m = 1 (24 h) | ×× | ×× | ×× | ×× | ×× | ×× | ||
| m = 2 (12 h) | ×× | ×× | ×× | ×× | ×× | ×× | ||
| m = 3 (8 h) | ×× | ×× | ×× | ×× | ×× | ×× | ×× | ×× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, Â.M.; Brum, C.G.M.; Batista, I.S.; Sobral, J.H.A.; Abdu, M.A.; Souza, J.R.; de Jesus, R.; Manoharan, P.K.; Terra, P. Ionospheric Variability over the Brazilian Equatorial Region during the Minima Solar Cycles 1996 and 2009: Comparison between Observational Data and the IRI Model. Atmosphere 2023, 14, 87. https://doi.org/10.3390/atmos14010087
Santos ÂM, Brum CGM, Batista IS, Sobral JHA, Abdu MA, Souza JR, de Jesus R, Manoharan PK, Terra P. Ionospheric Variability over the Brazilian Equatorial Region during the Minima Solar Cycles 1996 and 2009: Comparison between Observational Data and the IRI Model. Atmosphere. 2023; 14(1):87. https://doi.org/10.3390/atmos14010087
Chicago/Turabian StyleSantos, Ângela M., Christiano G. M. Brum, Inez S. Batista, José H. A. Sobral, Mangalathayil A. Abdu, Jonas R. Souza, Rodolfo de Jesus, Periasamy K. Manoharan, and Pedrina Terra. 2023. "Ionospheric Variability over the Brazilian Equatorial Region during the Minima Solar Cycles 1996 and 2009: Comparison between Observational Data and the IRI Model" Atmosphere 14, no. 1: 87. https://doi.org/10.3390/atmos14010087
APA StyleSantos, Â. M., Brum, C. G. M., Batista, I. S., Sobral, J. H. A., Abdu, M. A., Souza, J. R., de Jesus, R., Manoharan, P. K., & Terra, P. (2023). Ionospheric Variability over the Brazilian Equatorial Region during the Minima Solar Cycles 1996 and 2009: Comparison between Observational Data and the IRI Model. Atmosphere, 14(1), 87. https://doi.org/10.3390/atmos14010087







