Abstract
Hydrological extremes are common throughout the world and can be considered a globally significant phenomenon with severe environmental and social consequences. In recent decades, especially in the second half of the 20th century, Extreme Hydrological Events (EHEs) have attracted extensive attention. Physiological and anthropogenic factors have increased the frequency and severity of hydrological extremes worldwide in the last few decades. Recently, it has become a significant environmental issue in Sri Lanka. Both floods and droughts are widespread throughout the country, and the influence of floods is becoming more common every year. Currently, the frequency and severity of EHEs in the Kelani River Basin (KRB), Sri Lanka, are very common and have increased due to climate variations. Therefore, this study focused mainly on evaluating the EHEs and the impact of long-term El Niño Southern Oscillation (ENSO), Sea Surface Temperature (SST), and Indian Ocean Dipole (IOD) dynamics on extreme events. Rainfall Anomaly Index (RAI) and Extreme Precipitation Indices (EPIs) were calculated to examine the EHEs and their spatial variability. In addition, the relationships between EHEs and ENSO were investigated using several climate indices based on SST anomalies. Both observed and satellite-derived daily precipitation from 1951 to 2019 were used to assess the EHEs in the KRB. The trend of EHEs and the change points were evaluated using the Pettitt test, and teleconnection with global indices was examined using the correlation coefficient in the R application. The result of the study revealed that the pattern of EHEs varied spatially from 1951 to 2019. The strong La Niña years showed a high degree of teleconnection with EHEs in April (r = 0.622 at 0.05 significance level) and August (r = −0.732 at 0.05 significance level). NINO3.4 and the Southern Oscillation Index (SOI) have shown a significant positive impact on EHEs in the Northeast Monsoon (NEM) period. This research on KRB will be a popular scientific measure that can provide scientific results and solutions for the comprehensive decision-making process in the future. Investigating the global physical changes that influence EHEs is critical to taking the necessary steps to reduce the severity of hydrological extremes in Sri Lanka.
1. Introduction
Extreme Hydrological Events (EHEs) have severely affected human life, the economy, and the environment. In recent decades, especially in the second half of the 20th century, EHEs have attracted worldwide attention. Both the frequency and the magnitude of EHEs have increased due to the changing climate [1,2,3]. According to the World Meteorological Organization (WMO), the impact of EHEs, such as drought, extreme temperature and precipitation, storms, floods, landslides, flash floods, and related disasters on society, included 1.94 million deaths, and economic loss was estimated at USD 2400 billion from 1970 to 2012 [4]. According to the 2012 Intergovernmental Panel on Climate Change (IPCC) report, disaster losses have increased since the 1950s, with developing countries being the most affected [5]. Further, IPCC, 2014 showed an increase in global heavy rainfall events in land areas [6]. Furthermore, the average precipitation at the mid-latitudes of the northern hemisphere increased, and heavy precipitation events increased in some areas, especially after 1951 [3]. The increasing trend of extreme precipitation shows that the risk of flooding increases and causes severe losses, which has become a common concern [4].
The global climate system, the hydrological cycle of the river basin, the precipitation patterns at the global and regional levels, and the intensification of extreme precipitation events have been impacted by climate change and humans [4,6,7,8]. The seasonal variability of EHEs is related mainly to global changes, such as ENSO, Sea Surface Temperature (SST), and IOD [3,9,10]. Climate change has influenced nature and human society recently and has always been one of the most popular research fields [11]. Therefore, investigating the correlation between global climate changes and EHEs is vital for future forecasting and hydrological management of river basins. In this context, estimating and simulating the impact of climate change on hydrology has become an important research topic worldwide [11].
ENSO is one of the most significant climate phenomena, which is the cause of the variability of the global and local hydrological cycle [12,13,14,15,16]. According to the characteristics of ENSO, it can be identified as warm events (El Niño), cold events (La Niña), and neutral conditions based on the anomalies of the Pacific SST [11,12]. The SST and the Southern Oscillation Index (SOI) were used primarily to characterize the intensities of El Niño and La Niña [15,16]. ENSO is a complex ocean–atmosphere interaction in the tropical Pacific [12], and extreme global climates, such as floods [15,17,18,19] and droughts [18,19,20,21,22,23,24], are greatly influenced by ENSO events.
Precipitation is one of the main factors of spatiotemporal changes in water balance on the daily, seasonal, annual, and decade scales. Variability in precipitation influences mainly hydrological extremes. Studying the trend of short- and long-term precipitation is very important to understanding the potential impact of global climate change on the hydrology of river basins [25]. Global changes in ENSO and IOD are significant factors that influence extreme precipitation [26]. Studying the impact of global climate change on local precipitation helps to understand the hydrological changes of the river basin and future management at the local level [3].
Sri Lanka is located at the southern tip of the Indian subcontinent, with the main climatic variability closer to rainfall, especially due to the Indian Ocean monsoon system [26,27]. Sri Lanka’s climate can be described as tropical and monsoon, divided into four seasons. However, the Southwest Monsoon—SWM (May to September) and the Northeast Monsoon—NEM (December to February) are the main monsoons, heavily dependent on wind direction. Moreover, these two cycles have two inter-monsoon periods: the First Inter-Monsoon—FIM (March to April) and the Second Inter-Monsoon—SIM (October to November). In addition, the wind in the east and northeast causes monsoon showers in the northeast and affects the east and northeast of the country. During inter-monsoons, the island has showers in the afternoon or at night [26,27]. Therefore, this typical pattern of Sri Lanka’s climate can be changed due to global phenomena (ENSO, IOD, etc.), and rainfall in Sri Lanka is directly affected by the SST of the Indian Ocean and Pacific conditions [20].
Many researchers have studied the hydrological countermeasures of climate change and human activities. They believe that human-induced global climate change and anthropogenic activities have seriously affected the global and river basin hydrological cycle and have led to changes in the spatial and temporal distribution of components of water balance at global and local levels [11,28,29,30]. Various studies have been carried out on the possible impact of ENSO events on seasonal or annual precipitation changes at global and local levels [31]. As in [15,16,19,31,32], ENSO is one of the main drivers of periodic or extreme precipitation and has led to significant changes in EHEs, especially floods and droughts. Ref. [15] examined the influence of El Niño on daily rainfall and pointed out that variability in frequency and intensity of precipitation is essential to understanding the precision of the impact of ENSO. Diverse research studies have used various methods to assess the relationship between rainfall and ENSO to understand the EHEs at the local level. Ref. [16] indicated that Extreme Precipitation Indices (EPIs) are more suitable for analyzing precipitation characteristics using daily values and can be used to reveal the global climate impact. Refs. [26,31,32] also used EPIs to examine the variability of local-level precipitation. Therefore, the current study also used EPIs to examine long-term precipitation variability in the study area.
Furthermore, the Rainfall Anomaly Index (RAI) is a commonly used precipitation index to assess rainfall variability and its relationship to global climate change. Refs. [2,15,17,29] have shown the relationship between rainfall anomalies and ENSO. Pearson’s correlation coefficients have also been commonly used to assess the correlation [17,33]. In addition, many studies have identified the impact of ENSO on precipitation or streamflow worldwide, focusing on the whole country [26,27,34] and on a river basin scale [3,35,36]. According to [17,26,27,34,37], they evaluated the characteristics of ENSO and its impact on the variability of seasonal rainfall in Sri Lanka using observations from the main rain gauges. However, [35] quantified the long-term rainfall relationship in Sri Lanka with ENSO and IOD to predict rainfall in the two selected river basins using some selected rainfall stations. Furthermore, [38] examined the relationship between ENSO and stream flow using a stream flow record in a station, and seasonal streamflow changes have been discussed in a river basin. These studies focused mainly on precipitation and rainfall data on a local scale; however, the current study focused on the impact of global climate change on EHEs at the river basin level using the EPI and RAI methods on monthly, yearly, and seasonal scales. Furthermore, this study classified different types of ENSO and wet and dry periods according to changes in index values. Instead of categorizing the various events, this research attempted to observe how global change influences the water cycle of the river basin. This research will help to understand the global impact on the levels of small-scale river basins. Monitoring the global impact on EHEs will help to understand changes in water balance on a river basin scale and future management, and the study results will help decision-makers choose the best solution for EHEs and their impact. The primary objective of this study was to examine the impact of global climate change on rainfall variability to understand EHEs in the KRB, Sri Lanka. To achieve the main objective, the research has formulated three specific objectives: (1) to evaluate EHEs using EPI and RAI from 1951 to 2019 over KRB, (2) to summarize the long-term trend of extreme precipitation events in the study area, and (3) to examine the influence of global climate change on EHEs in the river basin.
2. Materials and Methods
2.1. Study Area
The KRB is the fourth longest basin in Sri Lanka [39] of 103 major river basins. It is located in the southwest of Sri Lanka [40]. The KRB originates from the western face of the central hills and flows to the west coast through the capital city of Colombo in Sri Lanka [31,32], drains approximately 2292 km2 of the land area [36], and discharges to the sea 144 km downstream of Colombo [40]. The KRB is located in the wet zone of the country [39] and is exposed mainly to the southwest monsoon.
The country’s topography plays a vital role in the rainfall pattern in the river basin. The weather pattern in Sri Lanka is characterized by a peak of rains around May to September, resulting in thunderstorms associated with convective cells and the location of the Intertropical Convergence Zone (ITCZ) in Sri Lanka [40]. The study area map is shown in Figure 1. The KRB typically experiences an average annual rainfall of 3.450 mm, and the discharge from the river varies between 600 and 1800 m3/s during the monsoon period [36]. Therefore, the basin is hit with heavy rainfall, which leads to a rapid increase in river flow and is subject to frequent flood disasters in the lower and middle areas of the KRB. Many industries and residents primarily cover the lower part of the river basin. Paddy fields are the main land use in the lower river basin. The upper and middle river basins are covered mainly with tea and rubber. Natural forest areas can also be recognized in the upper part of the KRB [36].
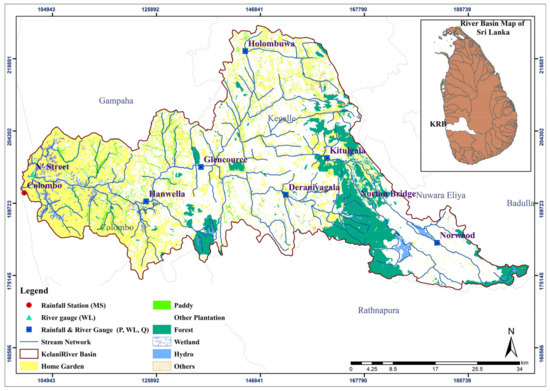
Figure 1.
The map of the study area.
2.2. Climate Data
2.2.1. Rainfall Data
The spatial–temporal variability of RAI and EPI was examined using observed and gridded satellite data for seven stations from 1951 to 2019 (69 years). Daily observed rainfall data for the study area were obtained from the Meteorological Department and the Irrigation Department in Sri Lanka. APHRODITE (Asian Precipitation—Highly Resolved Observational Data Integration toward Evaluation) satellite precipitation data were downloaded from the https://www.chikyu.ac.jp/precip/english/ (accessed on 12 December 2021) website, and data can be downloaded for a long term (1951 onward). The gridded products are available for four subdomains: Monsoon Asia, Middle East, Russia, and Japan as well as a combined domain. The time-varying data have a horizontal resolution of 0.25 × 0.25 or 0.5 × 0.5 degrees in each domain. All satellite data were used after performing the accuracy assessment for all stations. Rainfall was selected on the basis of the lower, middle, and upper parts of the KRB, and details of all stations are shown in Table 1.

Table 1.
Characteristics of the rainfall stations. Observed and satellite-based data were collected for the seven rainfall stations, and locations were selected on the basis of the upper, middle, and lower parts of the KRB.
2.2.2. Climate Indices and SST Anomalies
ENSO’s warm and cold phases are called El Niño and La Niña, respectively [16,17,26,38]. The oscillations of two climate change indices, including NINO3.4 and SOI, were used as substitutes for ENSO to examine the impact of climate change on EHEs in the KRB. These two indices have been widely used in previous studies around the world [16,17,26].
The Oceanic Niño Index (ONI) has become the basic standard used by the National Oceanic and Atmospheric Administration (NOAA) to identify El Niño (warm) and La Niña (cold) events [17,33]. In this study, monthly SST anomalies were used for the El Niño 3.4 region (i.e., 5° N–5° S, 120°–170° W). The three ENSO phases of El Niño, La Niña, and neutral were identified when the NINO3.4 was equal to or above the +0.5 °C anomaly for warm (El Niño) events and at or below the −0.5 anomaly for cold (La Niña) events. The values were further classified into weak events (with an anomaly of +0.5 to +0.9 SST), moderate (+1.0 to +1.4), and strong events (≥+1.5) [33].
The SOI was used to measure ENSO strength, defined as the normalized monthly Sea Level Pressure (SLP) anomaly between Tahiti (18° S, 150° W) and Darwin (12° S, 131° E) [17]. Both ONI and SOI data were downloaded from http://iridl.ldeo.columbia.edu/SOURCES/.Indices/ (accessed on 23 November 2021). All monthly data were obtained from 1951 to 2019. Negative (warm) SOI values indicate El Niño events, and positive (cold) values indicate La Niña events.
Furthermore, IOD was downloaded from the http://iridl.ldeo.columbia.edu/SOURCES/.NOAA/.NCDC/.ERSST/.version4/ (accesses on 23 November 2021) website from 1961 to 2015. The intensity of IOD is represented by SST gradients between the western equatorial Indian Ocean (50° E–70° E and 10° S–10° N) and the southeast equatorial Indian Ocean (90° E–110° E and 10° S–0° S). Positive index values are termed positive IOD, and negative values are termed negative IOD [26].
2.3. Methods
2.3.1. Identification of the EHEs Using Precipitation Indices
- Rainfall Anomaly Index (RAI)
The RAI was calculated to analyze the frequency and intensity of dry and rainy events in the study area. It was originally developed and used by Rooy (1965) and adapted by Freitas (2005) [41,42,43,44,45]. The monthly and annual RAI were calculated using the “Precintcon” package in the R programme using daily rainfall data from 1951 to 2019. Equations (1) and (2) were used to calculate wet and dry rainfall anomalies for seven stations covered by the study area.
where N = current monthly/seasonal/annual rainfall, in other words, of the month/season/year when RAI will be generated (mm); N = monthly/seasonal/annual average rainfall of the historical series (mm); M = average of the ten highest monthly/seasonal/annual precipitations of the historical series (mm); and X = average of the ten lowest monthly/seasonal/annual precipitations of the historical series (mm). Positive RAI have values above average, and negative RAI have values below average [41]. The RAI values have been categorized by six regimes (Table 2).
RAI (Positive Anomalies) = 3 (N − ¯N)/(¯M − ¯N)
RAI (Negative Anomalies) = -3 (N − ¯N)/(¯X − ¯N)

Table 2.
Categorized rainfall based on RAI values.
- Extreme precipitation indicators (EPIs)
Eleven precipitation indices were used as EHEs in the study area to identify extreme precipitation events [17,31,32]. The precipitation indices were obtained from the ETCCDI climate change indices; http://etccdi.pacificclimate.org/data.shtml (accessed on 17 November 2021). As of [17], the 11 EPIs are divided into three categories by thresholds, including fixed thresholds, station-related thresholds, and non-threshold EPIs. The selected EPIs for this study can be identified in Table 3. Fixed threshold EPIs represent the frequency of extreme precipitation events, such as continuous dry days (CDD) and extremely heavy precipitation days (R25mm), etc. Station-related threshold and non-threshold EPIs represent precipitation intensity, such as very wet days (R95p), 1-day monthly maximum precipitation (Rx1 days), simple daily intensity index (SDII), etc. Daily rainfall data were used to calculate EPIs, and from 1961 to 2019, the data were calculated using the Rclimdex software package from the R programme. Before using Rclimdex, the observed daily rainfall data were prepared according to the software requirements, and the accuracy of the data was verified to make the results creditable. These indices helped to obtain a complete and accurate description of precipitation variability in the study area.

Table 3.
Description of the extreme precipitation indicators (EPIs) used in this study.
2.3.2. Statistical Analyses
The Pettitt test and correlation analyses were used as statistical methods in this investigation to achieve the objectives of this study. The long-term trend of RAI and EPIs was calculated using the Pettit test. The Pettitt test (Pettitt 1979) is a rank-based nonparametric method for detecting change points in a data series and has been widely used in climate change and hydrological analyses [46]. In addition, it is an effective tool to determine the trend of hydrology and water resources [46]. Additionally, correlation coefficients were used to measure the degree of association between precipitation indices and indices of global climate change (ENSO, SST, and IOD). In this study, the Pearson correlation coefficient (PCC) was used and all analyses were performed using the R program. Pearson’s correlation coefficient is a widely used method for assessing the correlation. A correlation was significant when the null hypothesis without correlation was exceeded with a probability of 95% [27].
2.3.3. Evaluation of Gridded Precipitation Dataset
The study assessed the precision of the satellite gridded rainfall data and found the difference between the gridded data and the observed data using the analysis of variance (ANOVA) test. ANOVA is a statistical test that uses the F-test to assess differences among variables [47]. The study used a single-factor analysis due to two single variables without classifications. The two hypotheses of the variable test play a vital role. One is the null hypothesis (Ho), that is, there is no variance change in the mean of the two variables, and the other is the alternate hypothesis (H1), that is, there is a variance in all means of the two variables. Numerically, this is a generalization of the two-independent-sample t-test. The F-test provides statistical comparison of variability between groups and within groups. The statistics for the one-way ANOVA test are as follows:
where F is the variance ratio for the overall test, MST is the mean square due to treatments/groups (between groups), MSE is the mean square due to error (within groups, residual mean square), Yij is an observation, Ti is a group total, G is the total of all observations, ni is the number in group i and n is the total number of observations, and k is the total number of groups (https://www.statsdirect.com/help/analysis_of_variance/one_way.htm, accessed on 15 December 2021).
3. Results
3.1. Evaluation of Gridded Satellite Rainfall
The accuracy evaluation on the gridded satellite data was performed using the statistical ANOVA test. The F-value of the one-way ANOVA and R2 (coefficient of determination) of the scatter plots were considered to evaluate the accuracy of the dataset. As the F-value of the statistical tests, the null hypothesis (Ho) cannot be rejected for all variables, and a similar pattern can be identified between the estimated and observed rainfall data. Since the APHRODITE precipitation data set is generated by interpolating rainfall observations, the results are consistent with the rain gauge data [47].
The results of the ANOVA test revealed that the F-value is lower than the F crit for all stations, and the p-value is greater than the significance level of 0.05.77 Therefore, the null hypothesis cannot be rejected, and there is no significant change of variance between the two variables. Colombo has the lowest difference between observed and satellite data (F = 0.281, F crit = 3.843), and R2 was 0.83. When comparing other stations, Holombuwa, Gelencourse, and Norwood have obtained much closer F-values to the F crit of 3.84, and the F-values were 3.1, 3.2, and 3.5, respectively. However, these three stations have shown a high positive significant relationship, and R2 were 0.82, 0.72, and 0.76, respectively (Figure 2). Finally, it can be concluded that there is no significant difference between gridded and observed rainfall data. Therefore, the study used gridded satellite precipitation data to fill gaps and missing data during the study period for better analysis.
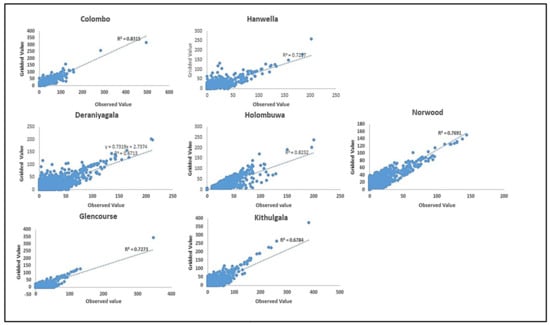
Figure 2.
Scatter plots the output and R2 for observed and gridded daily rainfall at the seven KRB stations.
3.2. Long-Term Variability of EHEs in the KRB
3.2.1. Spatiotemporal Variability of Rainfall Anomalies
The temporal variability of the monthly average rainfall anomalies from 1951 to 2019 is shown in Figure 3 (Table S1). The months of rain anomalies are not uniform for all the years. It has fluctuated throughout the year, as well as monthly and seasonally. As Figure 3 shows, there is a high temporal variability of rainfall in the study area. According to the overall RAI average of the KRB, the highest number of dry months was recorded from 1951 to 1960, and the highest number of very dry months (eleven months) can be identified in 1952 and 1956. The highest number of humid months (nine months) was recorded in 1984. As an average RAI of the study area, 1961, 1963, 1998, 2003, 2009, and 2010 were recorded as very humid years, and eight months have shown high positive rainfall anomalies for the years mentioned above. However, when considering the average RAI in the KRB from 1951 to 2019, there were no records for the extremely dry (RAI<-4) period.
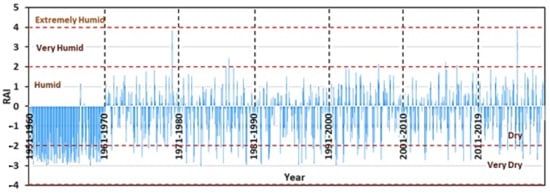
Figure 3.
Temporal variability of monthly rainfall anomalies from 1951 to 2019. The figure is shown for the RAI classification as wet and dry. Positive anomalies have appeared in the wet months and negative rainfall anomalies have appeared in the dry months during the study period.
The RAI values have also depicted spatial variability in the KRB (Table S2), and the characteristics of dry and wet incidents are not similar for the upper, middle, and lower parts of the river basin. Colombo has represented the characteristics of the rainfall of the lower river basin; the highest positive anomaly (extreme wet) was recorded in November 2010, and the value of the RAI was 4.19. Extreme dry months (RAI < −4) were not recorded in any part of the study area. Very dry incidents (RAI = −3) were normally recorded in the study area in January, February, March, and August. However, extreme wet events have appeared in all stations except Colombo, with Hanwella, Kithulgala, Glencourse, and Norwood recording their highest positive anomaly in March 1970. Colombo has recorded it as a very light, dry month (−0.2). Deraniyagala showed the highest positive RAI in May 2016, and May 2016 was an extremely wet month for all areas (lower, middle, and upper) of the study area.
This study considered mainly the seasonal variability of extreme rainfall of the KRB, and the four most prominent monsoon seasons in Sri Lanka were recognized. The extreme rainfall variability of the Southwest Monsoon—SWM (May to September), Northeast Monsoon—NEM (December to February), First Inter Monsoon—FIM (March to April), and Second Inter Monsoon—SIM (October, November) can be identified. Extreme or very dry periods are not prominent in the SWM, and an extreme dry incident was recorded only in May 1953 during the study period. It was the lowest RAI value recorded in the SWM period from 1951 to 2019 in the KRB. Humidity and extreme humidity are prevalent in this season, and according to the average RAI, the highest positive RAI was recorded as 3.92 in May 2016. Generally, July, August, and September show RAI values between −2 and −3 (dry), and May and June are mostly positive rainfall anomalies. SWM does not have significant spatial variability in the study area (Table S3(a)).
The RAI values of the NEM period have fluctuated (Table S3(b)), and extremely dry or wet events were not recorded in the study area. Very dry, dry, and humid events are prevalent in this period. Dry events are common in January and February. The lowest RAI (negative) value was 3.5 in the KRB. However, the number of dry events is higher than that of wet events. In the FIM, March 1970 was recorded as a highly wet period, and all the stations recorded high positive RAI (above 4) values (Table S3(c)). In addition, a very dry event (lower −3) was recorded in March 1959. The RAI value of the SIM also fluctuated during the period (Table S3(d)). However, as per the results of RAI, most of the monthly events were recorded (more than 70 percent) as positive anomalies (wet events) during the study period. Extreme humid events can be identified in November 2010 in the lower river basin. The most extreme wet events (extremely wet and very wet events) occurred in the lower river basin during the SIM period. The annual variability of the average RAI in the KRB for seven stations is shown in Figure 4, and the variability of the long-term wet and dry events appears there.
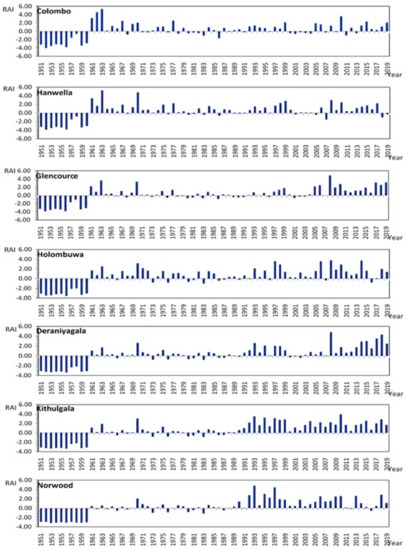
Figure 4.
Annual variability of RAI from 1951 to 2019 at the seven selected stations in the study area.
As in Figure 4, generally, the first ten years of the study period were dry and after 1961, the RAI fluctuated until 1990. The last 20-year period was prominent as a humid period. However, spatial variability can be recognized. Spatial changes in rainfall patterns in the study area began in 1990, and many changes have appeared in the lower river basin. The spatial variability of the RAI for the selected years is shown in Figure 5. The annual RAI fluctuated at the Colombo station, and the number of wet years is lower than at other stations. Hanwella, Glencourse, and Deraniyagala (middle part of the river basin) appear with a similar pattern of RAI distribution, and Holombuwa, Kithulgala, and Norwood (upper part of the river basin) appear with different temporal patterns of RAI over the KRB.
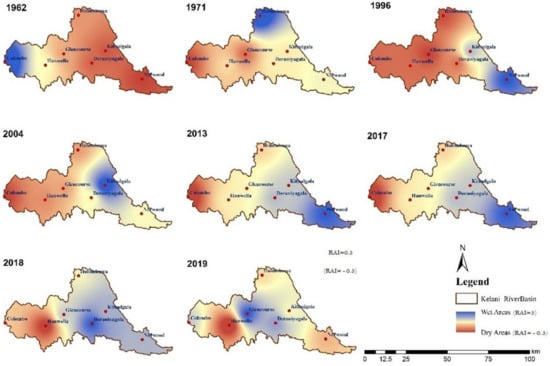
Figure 5.
Spatial variability of annual RAI for the selected years (years with the highest spatial variability of RAI were selected for mapping).
3.2.2. Spatiotemporal Variability of Fourteen EPIs
The maximum, minimum, and average PRCPTOT of the study area for all stations are shown in Table 4. PRCPTOT, Rx1days, Rx5days, and SDII can be identified as non-threshold EPIs. When considering annual total rain-day precipitation (PRCPTOT), spatiotemporal variability can be determined over the KRB. The average total annual wet-day precipitation of the river basin was approximately 3092 mm. The maximum and minimum annual average precipitation in the river basin were approximately 4095 mm and 2220 mm, respectively. Typically, KRB receives more than 1500 mm of annual precipitation. However, these average figures of total annual precipitation can be changed due to the spatial variability of the study area.

Table 4.
Maximum, minimum, and average PRCPTOT (mm), Rx1days, Rx5days, and SDII in the study area from 1961 to 2019.
In Table 4, the highest maximum annual total rainfall can be identified in Deraniyagala (6205 mm). Hanwella and Norwood also appear with more than 4000 mm of total precipitation. However, the maximum PRCPTOT in Colombo was 3921 mm and was lower than in other areas. The minimum PRCPTOT in Colombo was 1441 mm. Generally, the middle and lower parts of the study area show similar spatial and temporal precipitation patterns, but the lower river basin shows different patterns throughout the study period. The upper and middle parts of the study area had more than 2500 mm PRCPTOT from 1961 to 2019.
Additionally, a maximum of one day of precipitation (Rx1day) is essential to understand extreme events in the study area. Generally, the monthly maximum precipitation was less than 200 mm; after 1990, the Rx1day changed for all the stations. It fluctuated until 2019. The other six stations reached a maximum of up to 350 mm, except for Colombo. In Colombo (lower river basin), the maximum value of Rx1day has increased by more than 400 mm, and more notable changes in rainfall can be observed in the lower part of the study area. The maximum amount of precipitation for five days (Rx5day) has also shown high spatial and temporal variability during the study period. According to the results of Rx5day, Kithulgala and Glencourse reached more than 500 mm peaks after 1990, and Norwood reached nearly 400 mm maximums after 1990. Deraniyagala showed the highest amount of 5-day maximum peak after 2008, nearly 700 mm. Colombo also exceeded the maximum rainfall of 400 mm in five days, and in the last two decades, the frequency of more than 400 mm peaks has increased in Colombo. Except for Colombo, the Simple Daily Intensity Index (SDII) has increased in the last two decades for all stations. However, the SDII value of Colombo fluctuated throughout the study period.
As station-related thresholds, the EPIs, R95p, and R99p are also important to understand the wet and dry extremes in the study area. R95p has shown more than 1000 mm peaks throughout the study period, exceeding 2000 mm annual rainfall after 1990 in all stations. However, during the 1980 to 1990 period, the total annual recorded its lowest values. R99p has also shown a similar spatial and temporal pattern in the study area, and the maximum value of R99p has not exceeded 1000 mm.
Fixed threshold EPIs will help to define EHE in the study area. The spatial variability of consecutive dry days was very high in the study area. The statistics of the maximum number of consecutive days with RR < 1 mm for seven stations, and its maximum, minimum, and average days are shown in Table 5.

Table 5.
CDD statistics from 1961 to 2019 for seven KRB stations.
The highest number (79) of consecutive dry days was recorded in Colombo and more than 50 were recorded in Deraniyagala, Holombuwa, and Norwood in the study area. Furthermore, the statistics of the maximum number of consecutive days with RR > 1 mm (CWD) are shown in Table 6. The highest number of consecutive wet days (243) was recorded in Deraniyagala, and the lowest (27) was recorded in Colombo. It can be concluded that the lower river basin is much dryer than other parts of the study area.

Table 6.
CWD statistics from 1961 to 2019 for seven stations in the KRB.
The statistics of EIPs R25mm, R50mm, R100mm, and R150mm are shown in Table 7. Kithulgala was recorded for 77 days with more than 25 mm rainfall, and Deraniyagala, Glencourse, and Norwood were recorded for 76, 74, and 65 days, respectively. Colombo and Hanwella were recorded for 52 and 48 days, respectively. The highest number of days with more than 100 mm of rainfall and more than 150 mm of rainfall was recorded in Deraniyagala. Each station has shown at least one day with more than 150 mm of rainfall during the study period.

Table 7.
Statistics of R10mm, R20mm, and R25mm from 1961 to 2019 for seven stations in the KRB; (a) Statistics of R10mm in the study area, (b) Statistics of R20mm in the study area, and (c) Statistics of R25mm in the study area.
3.3. Long-Term Trend of EPIs over KRB
3.3.1. Long-Term Trend of RAI
The average results of the RAI revealed a significantly increased trend in wet and dry events. The temporal pattern of the annual average RAI has depicted negative anomalies (dry events) from 1951 to 1960. After 1961, the RAI fluctuated over the study area until 1990, and after 1990, mainly wet months can be identified. The trend of seasonal dry and wet months from 1951 to 2019 in the KRB is shown in Figure 6. As in Figure 6, the average seasonal RAI has also appeared as a significant positive trend over the KRB. As a temporal trend of wet and dry events in the seven stations, except for Colombo, there was a significant increasing trend of wet months over the study period, and Colombo appeared to have a decreasing trend. However, all stations have shown a significant increase trend for dry months in the 69 years in the study area.
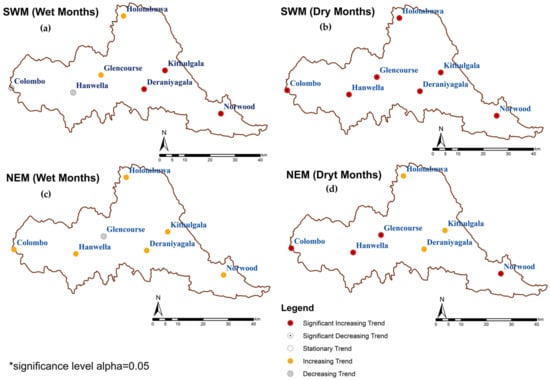
Figure 6.
Trend of seasonal dry and wet months from 1951 to 2019 in the KRB. (a) Long-term trend of SWM (wet months), (b) long-term trend of SWM (dry months), (c) long-term trend of NEM (wet months), and (d) long-term trend of NEM (dry months).
Moreover, seasonal wet and dry days trends were also identified, and two inter-monsoons have shown an increasing trend of both dry and wet days. The FIM period has recorded a Significant Increasing Trend (SIT) of dry months, and wet days have also recorded a slightly increasing trend for all stations in the FIM. Furthermore, SIM has also shown a high positive significant trend for dry months in the study period. The spatial trend of wet and dry days in SWM and NEM is shown in Figure 6. In SWM, dry days increased significantly (p-value < 0.0001) at all stations at the significance level of 0.05. The days of wetness increased significantly in Deraniyagala (p-value 0.004), Kithulgala (p-value < 0.0001), and Norwood (p-value 0.036) at the 0.05 significance level. Hanwella and Colombo appear to have a slightly decreasing trend. A similar pattern can be identified in the NEM, and although all the stations have shown a slightly increasing trend of wet days in the NEM, the Glencourse has appeared to have a decreasing trend.
3.3.2. The Trend of EPIs
When considering the trend of EPIs, the highest variation and extremes changed after 1980. More fluctuations in the EPIs distribution can be identified in the last forty-year period. The spatial and temporal variability of the trend of EPIs in the last 40 years in the study area is shown in Figure 7, Figure 8 and Figure 9. The variability of the temporal pattern of the EPIs is not similar in the study area, and different patterns can be recognized in the upper, middle, and lower parts of the study area. The upper and middle parts have recorded similar characteristics of different EPIs trends. However, the lower part of the river basin (Colombo) has appeared in a different temporal pattern. CWD decreased significantly, and the p-value has been recorded as 0.045 at a significance level of 0.05 during the study period. The trend of PRCPTOT, R10mm, R20mm, R95p, and R99p has decreased slightly during the study period. Due to the higher variability of EPIs in the last 40 years, the spatial and temporal variability of the trend of EPIs from the previous 40 years is shown in Figure 7, Figure 8 and Figure 9.
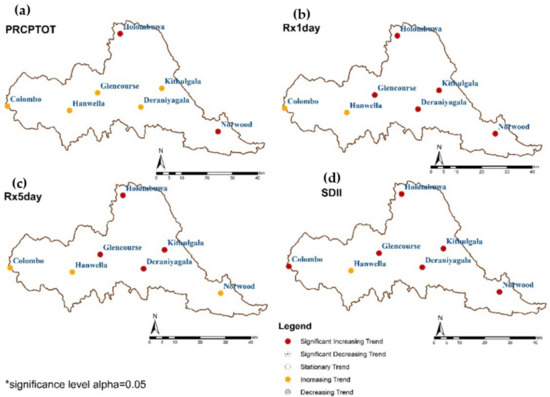
Figure 7.
The spatial and temporal variability of the trend of non-threshold EPIs in the last 40 years in the study area. (a) The spatial and temporal trend of PRCPTOT, (b) the spatial and temporal trend of Rx1day, (c) the spatial and temporal trend of Rx5day, and (d) the spatial and temporal trend of SDII.
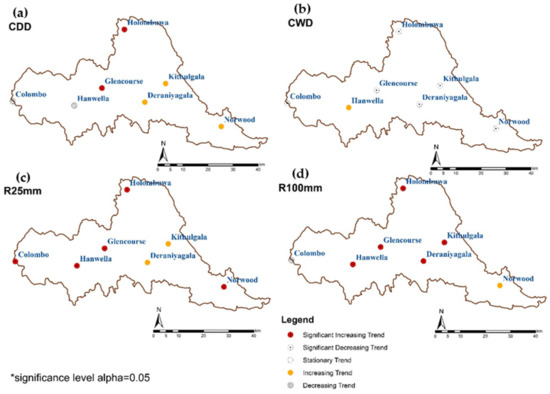
Figure 8.
The spatial and temporal variability of the trend of fixed threshold EPIs in the last 40 years period in the study area: (a) CDD, (b) CWD, (c) R25mm, and (d) R100mm.
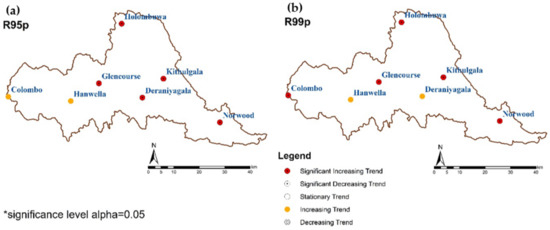
Figure 9.
The spatial and temporal variability of the trend of station-related threshold EPIs in the last 40 years period in the study area: (a) R95p and (b) R99p.
Non-threshold EPIs (PRCPTOT, Rx1day, Rx5day, and SDII) had a similar spatial distribution of trends, and all stations appeared to have an increasing trend (Figure 7). However, Glencourse and Kithulgala had a significant increasing trend for all non-threshold EPIs except PRCPTOT. PRCPTOT has shown an increasing trend, and the p-values were <0.0001 and 0.004, respectively. Except for Colombo and Hanwella, the trend value of the maximum amount of precipitation on a day has increased significantly in all other stations (p-value at a significance level of 0.05 = Deraniyagala − <0.0001, Glencourse − 0.05, Holombuwa − 0.001, Kithulgala − 0.001, and Norwood − 0.015). The trend of maximum precipitation amount for 5 days has increased significantly in Deraniyagala (0.035), Gelencourse (0.002), Holombuwa (0.040), and Kithulgala (0.044). Other stations have shown a slightly increasing trend during the study period at a significance level of 0.05. Moreover, except for Hanwella, the trend of SDII has recorded a significant increasing trend at a significance level of 0.05, and Hanwella has shown an increasing trend during the last 40-year period in the KRB.
During the last 40 years, fixed threshold EPIs (CDD, CWD, R25mm, and R100mm) have appeared to show significant spatial changes in the study area (Figure 8). CWD has decreased significantly in the middle and upper part of the study area, while the lower part shows a slightly increasing trend. A significant increase in the trend of extremely heavy precipitation has appeared in Colombo, Deraniyagala, Glencourse, Kithulgala, and Norwood. The CDD has shown a significant increasing trend in the middle part of the river basin at a significance level of 0.05, and the upper part (Deraniyagala, Kithulgala, and Norwood) of the river basin has shown an increasing trend. However, the lower part of the basin (Colombo and Hanwella) has shown a decreasing trend of dry extremes throughout the last 40 years. Furthermore, the decreasing trend can be recognized in Colombo for more than 100 mm rainfall, and except for Colombo and Norwood, all other stations have shown a significant increasing trend of receiving more than 100 mm rainfall in the study area. Moreover, except for Colombo and Hanwella, station-related threshold EPIs have shown a significantly increasing trend for very wet days (R95p) in the study area (Figure 9). However, extreme wet days have increased in Colombo. Hanwella and Deraniyagala have shown an increasing trend throughout the last 40 years.
3.4. Global Climate Change Influence on the Variability of EHEs
The ENSO indices (IOS and NINO 3.4) and the IOD indices were analyzed to understand the variability of the EHEs in the study area. As in the analysis of NINO3.4, the strong El Niño (≥+1.5) was recorded in 1958, 1965, 1972, 1973, 1982, 1983, 1987, 1991, 1992, 1997, 1998, 2002, 2004, 2010, 2015, and 2016. Strong La Niña (<−1.5) has been recorded in 1955, 1970, 1971, 1973, 1974, 1975, 1976, 1988, 1989, 2000, 2008, and 2011. The study was highly concerned with the correlation between strong ENSO years and extreme wet and dry days. According to the results of this study, the river basin appeared mostly dry in the strong El Niño years and humid in the strong La Niña years.
Moderate significant correlation at a significance level of 0.05 (r = +0.30 to +0.49) can be identified between ENSO and RAI in the NEM and SIM periods. As a monthly correlation (Supplementary D) of RAI and ENSO (SOI), a strong El Niño event was significantly correlated at a significance level of 0.05 in March (r = 0.326), July (r = 0.345), November (r = 0.439), and December (r = 0.439). In January, July, and December, it caused mostly dry events (more than 75 percent), and in November (more than 80 percent), it caused the wet events. Strong La Niña years appeared to have a high degree of correlation with RAI and SOI in February (r = 0.543), April (r = 0.622), August (r = −0.732), and October (r = −0.520) during the study period. The IOD also was highly correlated with RAI (Table S4) in August (r = 0.652) and had a moderate relationship in March (r = 0.479), June (r = −0.467), September (r = 0.398), and October (r = 0.421). The results of the correlation test show that IOD accompanies the high rainfall of SWM, and there is no high impact of ENSO on extremes of rainfall. However, the year’s NEM, FIM, and SIM have been significantly impacted by El Niño and La Niña (Table S5).
On the basis of the spatial impact of global climate changes in the study area, the same seasonal pattern can be identified, and the overall results revealed that the La Niña events had been significantly correlated with RAI in Colombo, Glencourse, and Hanwella. Other areas have also appeared to have a low degree of positive correlation. In the El Niño period, Deraniyagala, Kithulgala, Holombuwa, and Norwood recorded a significant positive correlation with RAI and Colombo, and other stations had a negative low-degree correlation at the 0.05 significance level.
The correlations of SOI, NINO3.4, IOD, and EPIs are shown in Table 8. As in Table 8, SOI and NINO3.4 appear to have a significant moderate correlation (positive at NINO3.4 and negative at SOI) with CDD, and consecutive days were recorded in the study area due to the ENSO impact. Colombo (NINO3.4: r = 0.303), Deraniyagala (NINO3.4: r = 0.349), Hanwella (NINO3.4: r = 0.349), Holombuwa (NINO3.4: r = 0.396), and Kithulgala (NINO3.4: r = 0.444) have shown this relationship, and ENSO has not influenced CDD in the upper part of the study area. However, a significantly low degree of correlation can be identified at the 0.05 significance level. IOD also appeared to have a significant positive correlation of low and moderate degrees with fixed threshold EPIs, and in Colombo, IOD had an impact on a higher degree of rainfall and extreme wet events.

Table 8.
Relationship between climate indices and EPIs over the study area (correlation coefficient values at the 0.05 significance level).
The variability of ENSO and EPIs has changed spatially, and the significant positive relationship between NINO3.4 and fixed thresholds (CDD, CWD, R25mm, and R100mm) EPIs can be identified at all stations. However, CDD appears to have a significant correlation with NINO3.4 (El Niño events), and a high positive significant correlation can be identified in Holombuwa (r = 0.862) and Glencourse (r = 0.660) at the significance level of 0.05. The La Niña events have also affected CDD in Deraniyagala (r = 0.756) and Norwood (r = 0.765). Furthermore, R20 and R10 in Colombo were not significantly correlated with La Niña. However, it has shown a moderately significant correlation with El Niño events. Except for Deraniyagala and Glencourse, CWD was significantly correlated with El Niño events at all other stations in the study area. However, it was not significantly correlated with the La Niña events. R99p and R95p showed a low/moderate degree positive correlation with NINO3.4 in Colombo, Deraniyagala, and Glencourse. Most of them were not significant at other stations. Except for Glencourse, a positive low-degree correlation was identified between NINO3.4 and PRCPTOT with El Niño in the study area.
4. Discussion
Precipitation is the key component of the water balance in the river basin water cycle and the water input of the water cycle. Therefore, understanding precipitation variability helps to examine EHEs. This study focused primarily on evaluating extreme wet and dry hydrological extremes using EPI and interpreting the impact of climate change indices on EHEs variability in the study area. Due to the rainfall pattern of Sri Lanka, the country can be divided into three parts: wet zone, intermediate zone, and dry zone. The KRB belongs to the wet zone and receives a large amount of rainfall annually. The frequency and severity of EHEs in the study area have recently increased [48]. Therefore, studying the relationship between extreme events and global climate change is essential for future planning in the study area.
According to the long-term rainfall pattern from 1951 to 2019, the first decade appeared as a dry period, and after 1961, it fluctuated, and in the last few decades, it has shown a humid pattern in the study area. The week, moderate, and strong El Niño and La Niña events were recorded throughout the first decades (1951 to 1960), and they had a great impact on the climate during that period in the study area. The EPIs in the study area have also changed spatially, and the lower river basin has appeared in a different pattern than the other study area. It receives a lower amount of precipitation than other areas, and the trend of EPIs also had differences. The country’s capital city is located in the lower part of the river basin, and many anthropogenic activities and changes in land use can be identified. The urbanization of this area is increasing daily, and floods are now the most common disaster [48]. These human-induced changes may be the main reason for the change in the rainfall pattern in the study area. This has also influenced the increase in the study area’s extreme wet and dry peaks. As the results of the study revealed, all stations had many changes during the last four decades during the study period.
The results revealed that the wet extremes (floods) are associated mainly with La Niña, and the dry extremes are highly associated with El Niño events. The ENSO highly impacts rainfall variability in the NEM and the other two inter-monsoons in the study area. However, sometimes flood events have also increased with El Niño phases. In particular, NEM has appeared to have this ENSO impact in the study area, and November was associated with extreme wet events and floods in the El Niño years. Wet events significantly influence IOD, and the impact can be identified in the onset of SWM (May). It has contributed significantly to extreme wet events and led to flood extremes in the study area. Ref. [26] overviewed a similar relationship between climate change indices and rainfall variability. However, this study has been conducted in the dry zone of Sri Lanka. Ref. [17] also noted rainfall variability and ENSO in Sri Lanka and discussed the significant impact of IOD on rainfall variability in SWM. In the southwest monsoon, the wind starts from the southwest and brings moisture from the Indian Ocean. When these winds collide with the hillsides of the central highlands, they will unleash heavy rain on the hillsides and the southwest part of the island. Southwest monsoon rainfall occurs at any time of the day or night, sometimes intermittently, mainly in the country’s southwest [17]. Ref. [37] revealed that the strong impact of ENSO is evident in NEM, and the results of this study also found this through analysis.
Furthermore, some previous literature has discussed the delayed influence of ocean indices on precipitation extremes [49,50,51,52,53]. As discussed in [53], atmospheric anomalies have a delayed impact on precipitation. However, [50] pointed out that the impact of ENSO on extreme temperatures is statistically significant, and no delayed impact on temperature variation was identified. With the result of [49], the maximal correlations were identified at lag times of 2–4 months. The correlation between times series of different climate variables is usually time-shifted and can occur over a long space distance. However, this could depend on many factors, and the lag time can vary by location [50]. Therefore, climate indices could be influenced by local and seasonal climates differently. This is consistent with previous studies showing a direct impact of climate indices on extreme precipitation [11,12,19,20,26,28,31,32,54,55]. As described by [31], seasonal and heavy precipitation is more sensitive to the alternation in ENSO of the eastern Pacific. Furthermore, as mentioned in [32], ENSO is one of the main drivers of annual or extreme precipitation variation. Ref. [55], also mentioned that the correlation coefficients between SOI and precipitation showed positive and negative associations. Reference [26] reviewed the situation in Sri Lanka and indicated the direct association with the change in seasonal rainfall in Sri Lanka. Therefore, with previous studies, it was confirmed that the influence of climate and ocean indices on precipitation varied in different areas, and the direct impact was on both temperature and precipitation. Therefore, the results of the current study showed the direct impact of climate indices on precipitation extremes in a river basin at the local level.
As discussed in [26], precipitation in Sri Lanka is directly influenced by SST in the Indian Ocean. Therefore, the current study also used similar indices. However, the teleconnection of ocean indices is a bit complex with different factors, and, as mentioned earlier, the influence of the variability of ocean indices on regional climate behavior has a delayed effect [56] as well as multi-indices. However, this study focuses on the popularity of previous studies and evidence-based results to minimize the complexity.
The study used RAI and EPIs to assess extreme rainfall at the local level, and most of the literature has focused on EPIs to assess extremes at the local level [31,32]. Trend analysis has focused on nonparametric trend analysis methods to assess the long-term pattern of extremes [26,31,32,55]. Furthermore, most studies focused their research on correlation to discover the teleconnection of ENSO and extremes [26,55]. However, it has become a discussion point and correlation mainly for pairwise analysis. However, as indicated by [18], the correlation is useful for identifying the significant relationship between rainfall and climate indices. Correlation and univariate regression methods are still the most common data-driven tools to analyze relationships in Earth system science [56]. Therefore, some scientific papers have discussed the causal inference method for assessing systematic correlation in earth science studies [57,58,59,60]. However, most papers related to the current study have used Pearson’s correlation for analysis, and this paper used the same method to assess the relationship between climate indices and rainfall extremes.
Some studies [17,26,27,34,36] have been conducted to understand the impact of ENSO on rainfall variability in Sri Lanka, focusing on agriculture, the dry zone, and the KRB. However, the data sources and methods are not similar to those in this study. This study concentrates highly on understanding the impact of ENSO on hydrological changes by discussing wet and dry extremes in the study area. This will be helpful in evaluating the impact of ENSO on streamflow variability, impact on water balance, etc., in the future. When conducting a study in a small-scale area, data collection has some limitations. This study also had to obtain long-term continuous rainfall data and many missing data were found. However, this study overcame these limitations by obtaining data using satellite data. This research structure is different from other studies due to its uniqueness.
5. Conclusions
This study highlighted the prominent relationship between climate indices and extreme rainfall indices in the KRB. The RAI and 14 EPIs were calculated to assess the extreme hydrological event for seven rainfall stations in the study area from 1951 to 2019. SOI, SST, and IOD indices were used to understand climate change, and the relationship between these two types of indices was assessed using Pearson’s correlation coefficient. The results of the study can be concluded as follows;
- The spatiotemporal variability of rainfall extremes was identified on a monthly, annual, and seasonal scale. The results revealed that the extremes are not uniform throughout the year, and they have fluctuated in a timely and spatial manner. A higher number of dry months were recorded from 1951 to 1960 in the KRB. The highest number of dry months can be identified in 1952 and 1956. In addition, the highest number of humid months was recorded in 1984. Colombo represented the characteristics of the rainfall of the lower river basin; the highest positive anomaly (extreme wet) was recorded in November 2010, and the value of the RAI was 4.19. Extreme dry months (RAI > 4) were not recorded in any part of the study area. Humidity and extreme humidity events are common in the SWM period. According to the mean RAI, the highest positive RAI was recorded as 3.92 in May 2016. Dry anomalies have been recorded in July, August, and September annually, and wet anomalies have been recorded in May and June. Rainfall anomalies fluctuated in the NEM. Normally, the number of dry events is higher than the number of wet events in the study area. Extreme humid events can be recognized in November 2010 in the lower river basin, and extreme wet events in the middle or upper part of the basin cannot be observed during this period. The most extreme and very wet events have appeared only in the lower river basin in the SWM period. Furthermore, the average annual precipitation in the river basin was approximately 3092 mm on wet days. The maximum and minimum average precipitation were approximately 4095 and 2220 mm, respectively. The highest annual maximum average rainfall can be identified in Deraniyagala. The lowest average was recorded in Colombo (2405 mm). In addition, the amount of precipitation per day is very essential in identifying the extremes of rainfall, and the maximum monthly precipitation was reached at maximum up to 350 mm for all stations except Colombo. Colombo has increased more than 400 mm. Extreme and very wet events (R95p and R99p) also fluctuated throughout the study period. R95p has shown more than 1000 mm peaks and R99p has not exceeded 1000 mm in the study area. The spatial variability of consecutive dry days was very high in the study area. The highest number of 79 consecutive dry days was recorded in Colombo, and the highest number of consecutive wet days of 243 was recorded in Deraniyagala. Furthermore, the highest number of extreme rainfall days (more than 100 mm and 150 mm) was recorded in Deraniyagala.
- Further, the study indicated that negative anomalies (dry events) were identified between 1951 and 1960. After 1961, the RAI fluctuated over the study area until 1990, and after 1990, mainly wet months were identified. Except in Colombo, there was a significant increasing trend of wet months over KRB. SIM also showed a high positive significant trend for dry months in the study period. In SWM, dry days increased significantly (p-value < 0.0001) at all stations at a significance level of 0.05. In addition, more fluctuations in the EPIs distribution have been identified in the last 40 years. The variability of the temporal pattern of the EPIs was not similar in the study area, and different patterns were recognized in the upper, middle, and lower parts of the study area. The trend of PRCPTOT, R10mm, R20mm, R95p, and R99p has slightly decreased during the study period; the non-threshold EPIs also had a similar spatial distribution of trends, and all stations appeared to have an increasing trend. During the last 40 years, fixed threshold EPIs have appeared to show significant spatial changes in the study area. CWD decreased significantly in the middle and upper part of the study area, while the lower part shows a slightly increasing trend. Moreover, except for Colombo and Hanwella, station-related threshold EPIs have increased significantly in the study area.
- Finally, strong La Niña years appeared to have a high degree correlation with RAI and SOI in February (r = 0.543), April (r = 0.622), August (r = −0.732), and October (r = −0.520) during the study period. IOD was also highly correlated with RAI in August (r = 0.652) and moderately in March (r = 0.479), June (r = −0.467), September (r = 0.398), and October (r = 0.421). The results of the correlation test showed that IOD accompanies high rainfall in SWM, and there was no high impact of ENSO on the extremes of rainfall in SWM. The variability of ENSO and EPIs has changed spatially, and the significant positive relationship between NINO3.4 and the fixed threshold EPIs was identified at all stations.
This study will be helpful for the management of water resources and disaster preparedness and management, and it will aid decision-makers in the relevant fields to make decisions in the study area. In addition, this research will open up many new research ideas for researchers in this field. Such research and projects on KRB will also be popular scientific measures that can provide scientific results and solutions for the comprehensive decision-making process in the future.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos14010079/s1, Table S1: Temporal Changes of RAI from 1951 to 2019 in the KRB; Table S2: Temporal Changes of RAI in Seven Stations from 1951 to 2019; Table S3(a): Temporal variability of RAI in the Southwest Monsoon; Table S3(b): Temporal variability of RAI in the Southwest Monsoon; Table S3(c): Temporal variability of RAI in the Southwest Monsoon; Table S3(d): Temporal variability of RAI in the Southwest Monsoon; Table S4. Correlation between ENSO, IOD and RAI; Table S5: Correlation between ENSO, NINO34, IOD and RAI.
Author Contributions
Conceptualization, V.P.I.S.W.; methodology, V.P.I.S.W.; software, V.P.I.S.W.; validation, V.P.I.S.W. and M.S.M.; formal analysis, V.P.I.S.W. and M.S.M.; investigation, V.P.I.S.W. and G.L.; resources, G.L.; data curation V.P.I.S.W.; writing—original draft preparation, V.P.I.S.W.; writing—review and editing, V.P.I.S.W., G.L., and A.A.; visualization, V.P.I.S.W. and A.A.; supervision, G.L.; project administration, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data and tools/models used for this work are publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Min, S.K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human Contribution to More-Intense Precipitation Extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Ramírez, I.J. Exploring Tropical Variability and Extremes Impacts on Population Vulnerability in Piura, Peru: The Case of the 1997–98 El Niño; Elsevier Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780128092484. [Google Scholar]
- Jiang, R.; Wang, Y.; Xie, J.; Zhao, Y.; Li, F.; Wang, X. Assessment of Extreme Precipitation Events and Their Teleconnections to El Niño Southern Oscillation, a Case Study in the Wei River Basin of China. Atmos. Res. 2019, 218, 372–384. [Google Scholar] [CrossRef]
- WMO State of Climate in 2021: Extreme Events and Major Impacts | World Meteorological Organization. In Proceedings of the State of Climate in 2021: Extreme Events and Major Impacts 2021, Geneve, Switzerland, 29–31 October 2021.
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Synthesis Report: Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014.
- Kim, J.; Habimana, J.D.D.; Kim, S. Assessment of Climate Change Impacts on the Hydroclimatic Response in Burundi Based on CMIP6 ESMs. Sustainability 2021, 13, 12037. [Google Scholar] [CrossRef]
- Abbas, A.; Ullah, S.; Ullah, W.; Waseem, M.; Dou, X.; Zhao, C.; Karim, A.; Zhu, J.; Hagan, D.F.T.; Bhatti, A.S.; et al. Evaluation and Projection of Precipitation in Pakistan Using the Coupled Model Intercomparison Project Phase 6 Model Simulations. Int. J. Climatol. 2022, 42, 6665–6684. [Google Scholar] [CrossRef]
- Yoon, S.K.; Kim, J.S.; Lee, J.H.; Moon, Y.I. Hydrometeorological Variability in the Korean Han River Basin and Its Sub-Watersheds during Different El Niño Phases. Stoch. Environ. Res. Risk Assess. 2013, 27, 1465–1477. [Google Scholar] [CrossRef]
- Kim, J.S.; Jain, S. Precipitation Trends over the Korean Peninsula: Typhoon-Induced Changes and a Typology for Characterizing Climate-Related Risk. Environ. Res. Lett. 2011, 6, 034033. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Z.; Wang, D.; Liu, T.; Yang, J. Impact of Climate Change on Hydrologic Extremes in the Upper Basin of the Yellow River Basin of China. Adv. Meteorol. 2016, 2016, 1404290. [Google Scholar] [CrossRef]
- Chowdhury, M.R. The El Niño-Southern Oscillation (ENSO) and Seasonal Flooding—Bangladesh. Theor. Appl. Clim. 2003, 76, 105–124. [Google Scholar] [CrossRef]
- Yeh, S.W.; Kug, J.S.; An, S. il Recent Progress on Two Types of El Niño: Observations, Dynamics, and Future Changes. Asia Pac. J. Atmos. Sci. 2014, 50, 69–81. [Google Scholar] [CrossRef]
- Guimarães Nobre, G.; Muis, S.; Veldkamp, T.I.E.; Ward, P.J. Achieving the Reduction of Disaster Risk by Better Predicting Impacts of El Niño and La Niña. Prog. Disaster Sci. 2019, 2, 100022. [Google Scholar] [CrossRef]
- Lv, A.; Qu, B.; Jia, S.; Zhu, W. Influence of Three Phases of El Niño—Southern Oscillation on Daily Precipitation Regimes in China. Hydrol. Earth Syst. Sci. 2019, 23, 883–896. [Google Scholar] [CrossRef]
- Li, J.; Garshick, E.; Huang, S.; Koutrakis, P. Impacts of El Niño-Southern Oscillation on Surface Dust Levels across the World during 1982–2019. Sci. Total Environ. 2021, 769, 144566. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.S.U.; Jayawardena, I.M.S.P. Modulation of Seasonal Rainfall in Sri Lanka by ENSO Extremes. Dec. Sri Lanka J. Meteorol. 2015, 1, 3–11. [Google Scholar]
- Ma, F.; Ye, A.; You, J.; Duan, Q. 2015–16 Floods and Droughts in China, and Its Response to the Strong El Niño. Sci. Total Environ. 2018, 627, 1473–1484. [Google Scholar] [CrossRef]
- Moura, M.M.; dos Santos, A.R.; Pezzopane, J.E.M.; Alexandre, R.S.; da Silva, S.F.; Pimentel, S.M.; de Andrade, M.S.S.; Silva, F.G.R.; Branco, E.R.F.; Moreira, T.R.; et al. Relation of El Niño and La Niña Phenomena to Precipitation, Evapotranspiration and Temperature in the Amazon Basin. Sci. Total Environ. 2019, 651, 1639–1651. [Google Scholar] [CrossRef]
- Zambrano Mera, Y.E.; Rivadeneira Vera, J.F.; Pérez-Martín, M.Á. Linking El Niño Southern Oscillation for Early Drought Detection in Tropical Climates: The Ecuadorian Coast. Sci. Total Environ. 2018, 643, 193–207. [Google Scholar] [CrossRef]
- Singh, R.M.; Shukla, P. Drought Characterization Using Drought Indices and El Niño Effects. Natl. Acad. Sci. Lett. 2020, 43, 339–342. [Google Scholar] [CrossRef]
- Waseem, M.; Khurshid, T.; Abbas, A.; Ahmad, I.; Javed, Z. Impact of Meteorological Drought on Agriculture Production at Different Scales in Punjab, Pakistan. J. Water Clim. Chang. 2022, 13, 113–124. [Google Scholar] [CrossRef]
- Abbas, A.; Waseem, M.; Ullah, W.; Zhao, C.; Zhu, J. Spatiotemporal Analysis of Meteorological and Hydrological Droughts and Their Propagations. Water 2021, 13, 2237. [Google Scholar] [CrossRef]
- Waseem, M.; Jaffry, A.H.; Azam, M.; Ahmad, I.; Abbas, A.; Lee, J.E. Spatiotemporal Analysis of Drought and Agriculture Standardized Residual Yield Series Nexuses across Punjab, Pakistan. Water 2022, 14, 496. [Google Scholar] [CrossRef]
- Xu, Z.; Pan, B.; Han, M.; Zhu, J.; Tian, L. Spatial–Temporal Distribution of Rainfall Erosivity, Erosivity Density and Correlation with El Niño–Southern Oscillation in the Huaihe River Basin, China. Ecol. Inf. 2019, 52, 14–25. [Google Scholar] [CrossRef]
- Burt, T.P.; Weerasinghe, K.D.N. Rainfall Distributions in Sri Lanka in Time and Space: An Analysis Based on Daily Rainfall Data. Climate 2014, 2, 242–263. [Google Scholar] [CrossRef]
- Yahiya, Z.; Chandimala, J.; Siriwardhana, M.; Zubair, L. Sri Lankan Rainfall Climate and Its Modulation by El Nino and La Nina Episodes. Eng. J. Inst. Eng. Sri Lanka 2009, 42, 11. [Google Scholar] [CrossRef]
- Shimizu, M.H.; Ambrizzi, T.; Liebmann, B. Extreme Precipitation Events and Their Relationship with ENSO and MJO Phases over Northern South America. Int. J. Climatol. 2017, 37, 2977–2989. [Google Scholar] [CrossRef]
- Horrevoets, A.C.; Savenije, H.H.G.; Schuurman, J.N.; Graas, S. The Influence of River Discharge on Tidal Damping in Alluvial Estuaries. J. Hydrol. 2004, 294, 213–228. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Wang, G.; Wang, J.; Ju, Q.; Yang, C.; Fan, C. Impact of Climate Change on Hydrological Extremes in the Yangtze River Basin, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 693–707. [Google Scholar] [CrossRef]
- Heng, C.; Lee, T.; Kim, J.S.; Xiong, L. Influence Analysis of Central and Eastern Pacific El Niños to Seasonal Rainfall Patterns over China Using the Intentional Statistical Simulations. Atmos. Res. 2020, 233, 104706. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Zhan, H.; Jin, M.; Liang, X. Influence of Solar Activity and EI Niño-Southern Oscillation on Precipitation Extremes, Streamflow Variability and Flooding Events in an Arid-Semiarid Region of China. J. Hydrol. 2021, 601, 126630. [Google Scholar] [CrossRef]
- Rojas, O.; Li, Y.; Cumani, R. Uerstanding the Drought Impact of El Niño on the Global Agricultural Areas; Food and Agriculture Organization of the United Nations: Rome, Italy, 2014; ISBN 9789251086711. [Google Scholar]
- Jayawardene, H.K.W.I.; Jayewardene, D.R.; Sonnadara, D.U.J. Interannual Variability of Precipitation in Sri Lanka. Res. Artical 2015, 43, 75–82. [Google Scholar] [CrossRef]
- De Silva, T.M.; Hornberger, G.M. Identifying El Niño-Southern Oscillation Influences on Rainfall with Classification Models: Implications for Water Resource Management of Sri Lanka. Hydrol. Earth Syst. Sci. 2019, 23, 1905–1929. [Google Scholar] [CrossRef]
- Dissanayaka, K.D.C.R.; Rajapakse, R.L.H.L. Long-Term Precipitation Trends and Climate Extremes in the Kelani River Basin, Sri Lanka, and Their Impact on Streamflow Variability under Climate Change. Paddy Water Environ. 2019, 17, 281–289. [Google Scholar] [CrossRef]
- Jayakody, P.M. The Influence of La Nina on Sri Lanka Rainfall. Sri Lanka J. Meterol. 2015, 1, 6. [Google Scholar]
- Chandimala, J.; Zubair, L. Predictability of Stream Flow and Rainfall Based on ENSO for Water Resources Management in Sri Lanka. J. Hydrol. 2007, 335, 303–312. [Google Scholar] [CrossRef]
- Wijeratne, V.P.I.S.; Senavirathne, H.A.C.D.; Manawadu, L. To Assess the Impact of Urbanization-Associated Land Use Changes on Actual Evapotranspiration and Water Balance in the Kelani River Basin, Sri Lanka. Int. J. Adv. Remote Sens. Gis 2019, 8, 3145–3155. [Google Scholar] [CrossRef]
- Vuillaume, J.F.; Dorji, S.; Komolafe, A.; Herath, S. Sub-Seasonal Extreme Rainfall Prediction in the Kelani River Basin of Sri Lanka by Using Self-Organizing Map Classification. Nat. Hazards 2018, 94, 385–404. [Google Scholar] [CrossRef]
- Costa, J.A.; Rodrigues, G.P. Space-Time Distribution of Rainfall Anomaly Index (Rai) for the Salgado Basin, Ceará State—Brazil. Ciênc. Nat. 2017, 39, 627. [Google Scholar] [CrossRef]
- Aryal, A.; Maharjan, M.; Talchabhadel, R. Characterizing Meteorological Droughts in Nepal: A Comparative Analysis of Standardized Precipitation Index and Rainfall Anomaly Index. Earth 2022, 3, 409–432. [Google Scholar] [CrossRef]
- Kemela, B.; Phoebe, A. Assessment of Climate Variability in the Niger Delta Region of Nigeria. Int. J. Chem. Chem. Eng. Syst. 2021, 6, 17–28. [Google Scholar]
- Martorano, L.G.; Vitorino, M.I.; Paula, B.; Caxias, P.; Reinaldo, J.; de Moraes, C.; Lisboa, L.S.; Sotta, E.D.; Reichardt, K. Climate Conditions in the Eastern Amazon: Rainfall Variability in Belem and Indicative of Soil Water Deficit. Afr. J. Agric. Res. 2017, 12, 1801–1810. [Google Scholar] [CrossRef]
- Waghmare, P.T.; Panhalkar, S.S.; Pawar, S.D. Drought Assessment of Eastern Satara District of Maharashtra Using Rainfall Anomaly Index. Res. Sq. 2020. [Google Scholar] [CrossRef]
- Conte, L.C.; Bayer, D.M.; Bayer, F.M. Bootstrap Pettitt Test for Detecting Change Points in Hydroclimatological Data: Case Study of Itaipu Hydroelectric Plant, Brazil. Hydrol. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
- Zhao, C.; Yao, S.; Zhang, S.; Han, H.; Zhao, Q.; Yi, S. Validation of the Accuracy of Different Precipitation Datasets over Tianshan Mountainous Area. Adv. Meteorol. 2015, 2015, 617382. [Google Scholar] [CrossRef]
- Manawadu, L.; Wijeratne, V.P.I.S. Anthropogenic Drivers and Impacts of Urban Flooding- A Case Study in Lower Kelani River Basin, Colombo Sri Lanka. Int. J. Disaster Risk Reduct. 2021, 57, 102076. [Google Scholar] [CrossRef]
- Bejranonda, W.; Koch, M. The Role of Ocean State Indices in Seasonal and Inter-Annual Climate Variability of Thailand. J. West. Rajabhat Univ. Nakhon PathomThail. 2010, 5, 5–23. [Google Scholar]
- Quagliolo, C.; Pezzoli, A.; Ignaccolo, R.; Davila, J.L.S. Time-Lagged Inverse-Distance Weighting for Air Temperature Analysis in an Equatorial Urban Area (Guayaquil, Ecuador). Meteorol. Appl. 2020, 27, e1938. [Google Scholar] [CrossRef]
- Rieger, N.; Corral, Á.; Olmedo, E.; Turiel, A. Lagged Teleconnections of Climate Variables Identified via Complex Rotated Maximum Covariance Analysis. J. Clim. 2021, 34, 9861–9878. [Google Scholar] [CrossRef]
- Sánchez-Sesma, J. The Earth’s Climate Lagged, Recurrent and Non-Linear Solar and Lunar Multi-Millennial Scale Responses: An Oceanic Hypothesis, Evidence, Verifications and Forecasts [Preprint]. Earth Syst. Dyn. Discuss. 2021, 1–26. [Google Scholar]
- Tabari, H.; Willems, P. Lagged Influence of Atlantic and Pacific Climate Patterns on European Extreme Precipitation. Sci. Rep. 2018, 8, 5748. [Google Scholar] [CrossRef]
- Saunders, K.; Stephenson, A.G.; Taylor, P.G.; Karoly, D. The Spatial Distribution of Rainfall Extremes and the Influence of El Niño Southern Oscillation. Weather Clim. Extrem. 2017, 18, 17–28. [Google Scholar] [CrossRef]
- Xu, Z.X.; Li, J.Y.; Takeuchi, K.; Ishidaira, H. Long-Term Trend of Precipitation in China and Ist Association with El Nino-Southern Oscillation. Hydrol. Process 2007, 21, 61–71. [Google Scholar] [CrossRef]
- Yang, R.; Xing, B. Teleconnections of Large-Scale Climate Patterns to Regional. Atmosphere 2022, 13, 230. [Google Scholar] [CrossRef]
- Runge, J.; Bathiany, S.; Bollt, E.; Camps-Valls, G.; Coumou, D.; Deyle, E.; Glymour, C.; Kretschmer, M.; Mahecha, M.D.; Muñoz-Marí, J.; et al. Inferring Causation from Time Series in Earth System Sciences. Nat. Commun. 2019, 10, 2553. [Google Scholar] [CrossRef]
- Delforge, D.; de Viron, O.; Vanclooster, M.; van Camp, M.; Watlet, A. Detecting Hydrological Connectivity Using CausalInference from Time Series: Synthetic and Real Karstic Case Studies. Hydrol. Earth Syst. Sci. 2022, 26, 2181–2199. [Google Scholar] [CrossRef]
- Gentine, P.; Runge, J. Causal Inference for Process Understanding in Earth Sciences. arXiv 2021, arXiv:2105.00912. [Google Scholar]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).