Abstract
The crop leaf color is tightly connected with its meteorological environment. Color gradation skewness-distribution (CGSD) parameters can describe the information of leaf color more accurately, systematically, and comprehensively from five dimensions. We took photographs of pepper growing in the greenhouse at a fixed time every day and observed the meteorological factors. The results showed that the CGSD parameters were significantly correlated with meteorological factors, especially with the accumulated temperature, which showed the strongest correlation. Since the relationship between canopy leaf color and accumulated temperature is nonlinear, the piecewise inversion models were constructed by taking the stationary point of the high-order response model of Gskewness to accumulated temperature as the point of demarcation. The rate of outliers had decreased by 57.72%; moreover, the overall inversion accuracy had increased by 3.31% compared with the linear model directly constructed by the stepwise regression. It was observed that the pepper in the greenhouse had a different response to the same meteorological environmental stimulus before and after the stationary point. This study will provide a new method for constructing crop growth models in future research.
1. Introduction
Meteorological conditions are crucial factors that determine crop growth and leaf development [1,2]. Agrometeorologists are very concerned about the impact of meteorological environment on the growth of crops [3,4] and try to build various evaluation indexes to monitor the growth of crops [5], evaluate the agrometeorological conditions, and even predict the yield of crops [6,7]. Recently, more and more qualitative and quantitative descriptions of plant phenotype based on digital imaging technology have been studied [8]; the deepening research on the phenotype of crop for building intelligent agriculture, in particular, is growing vigorously. The progress that builds quantitative analysis of genotype-by-environment interactions by obtaining high-quality and massive visual feature data is an important aspect of plant phenotype research [9].
Crop leaf is a vital vegetative organ, while leaf color is a typical phenotypic characteristic of crop that is affected by meteorological conditions and can help to understand crop growth status [10,11,12]. This can assist in monitoring the growth of crops and evaluating the agrometeorological conditions, and eventually in conducting corresponding management for crops. Therefore, understanding the influence of meteorological conditions on leaf color and simulation of plant leaf color is very important for the crop production.
The RGB model is the most commonly used color representation for digital images [13]. It is widely used to determine the chlorophyll content of potato, rice, wheat, cauliflower, cabbage, barley, tomato, quinoa, and amaranth [14,15,16,17,18]. Since the nutritional status of plants can also be reflected in their leaf color [19], the RGB model is also used to assess whether plants lack certain nutrients [20]. This is simpler and more efficient than laboratory leaf analyses or even chlorophyll meter (SPAD) and nitrogen prediction [10]. In addition, the RGB model of digital color images has also been used to determine plant adaptability and degree of damage under biological or abiotic stresses [21]. Particularly when plant leaves display obvious senescence and color change after a long period of severe adversity and climate change, the RGB model is used to analyze the color depth of leaves and area size of different colors, as well as their proportion [22].
Plants cannot move freely like animals to avoid the coercion of severe environments, so they have evolved a complete set of self-regulation and adaptive mechanisms for alternatives in the environment [23]. Changes in the environment around plants tend to be cyclical and relatively moderate, without causing stress to the plants, such as changes in meteorological factors of temperature, humidity, and atmospheric pressure, from morning to night in the greenhouse. These factors cause a series of physiological and biochemical reactions within the plant [24,25], such as the leaf adjustment of stomatal movement [26], changes in chloroplast arrangement [27], and regulation of photosynthetic intensity [28,29], which can cause changes in plant color under visible light [30].
However, there is not enough research on the leaf color caused by these environmental changes especially in the stable microclimate environment of a greenhouse in visible light imaging. One reason is that these moderate changes do not significantly change the content of chlorophyll. Another important reason is that the traditional RGB model has few image parameters, so it can only describe the color depth of leaves [31] but not describe the small changes in leaf color more accurately. In our previous study, we found that the distribution of leaf color gradation follows a skewed distribution and extended the RGB model parameters from 4 to 20, and we established a method to describe the distribution of leaf color [32]. These color gradation skewness-distribution (CGSD) parameters can describe leaf color information more accurately and comprehensively [32,33]. This made it possible to study the relationship between the stable environment of a greenhouse and moderate changes in leaf color, which will fill the research gap on the leaf color caused by external meteorological changes.
In order to study whether the multi-dimensional characteristics of skewed parameters are also suitable for the studies of externally complex meteorological factors, we found images of peppers in the greenhouse and correspondent meteorological data from the microclimate observation database constructed by the Jiangsu Provincial Meteorological Bureau. We analyzed the relationship between color changes in images of pepper canopy and meteorological factors in the environment. Also, we used skewed parameters and meteorological factors such as temperature, humidity, and air pressure to construct the leaf color response model and the meteorological factor inversion model. Our study provides new ideas and methods for building the correlation model between meteorological factors and the internal physiological state of plants via leaf color as a bridge. If there is a quantitative mathematical relationship between CGSD parameters of leaves and the external environmental factors, even crop modeling will be improved.
2. Materials and Methods
2.1. Plant Material and Growth Conditions
The pepper was planted in the greenhouse located at the institute of vegetable crops, Jiangsu academy of agricultural sciences, Nanjing City, Jiangsu Province, China (25°5′ N, 116°58′ E) in 2021. The pepper was planted with a total nutrient matrix which was in the proportion of N: P2O5: K2O in a 100 g matrix at 20:10:20; trace elements included Cu, Fe, Zn, Mn, B, Mo ≥1%, and pH 5.85. Moreover, the matrix contained an active accelerator and sustained release agent of poly-fertilizer. Four plots were set up for repeated treatment (Figure 1).

Figure 1.
Image grouping scheme and image separation effect of pepper in the greenhouse.
2.2. Meteorological Data Acquisition
Meteorological data were obtained from the agricultural meteorological observation station (DZZ4, Jiangsu Provincial Radio Science Research Institute Co., LTD., Wuxi, China) in the facility. The observed meteorological elements included daily meteorological elements, such as the daily mean temperature (Tm), daily maximum temperature (Tmax), daily minimum temperature (Tmin), daily air pressure (Pm), daily maximum air pressure (Pmax), daily minimum air pressure (Pmin), daily mean relative humidity (RHm), daily minimum relative humidity (RHmin), daily mean dew point temperature (TDm), daily mean water pressure (em), daily mean carbon dioxide concentration (Cm), daily maximum carbon dioxide concentration (Cmax), and daily minimum carbon dioxide concentration (Cmin). The accumulated temperature (AT) was calculated from Tm.
2.3. Pepper Image Collection in the Greenhouse
The monitoring camera used for image acquisition (model: DH-SD-65F630U-HN-Q; manufacturer: Zhejiang Dahua Technology Co., Ltd., Hangzhou, China) had an image resolution of 1920 × 1080, and the surveillance camera was installed 360 cm high. Additionally, the study used fixed focal length shooting and automatic white balance. Each camera took a photo once at each interval from 7:00 to 18:00, and the resulting digital photo size was 2560 × 2592. The digital images of pepper canopy at 18:00 were collected for analysis.
2.4. Extraction of Canopy Leaf Color Gradation Skewed-Distribution (CGSD) Characteristics of Pepper Image
We refer to Chen’s method for processing and collecting information of the image [32]. After cutting, denoising, and collecting information of the image, a color gradation cumulative histogram of the image was constructed. Then, the mean, median, mode, skewness, and kurtosis functions were used to analyze the canopy leaf color gradation skewed-distribution characteristics, respectively. Twenty CGSD parameters were then obtained, including RMean, RMedian, RMode, RSkewness, RKurtosis, GMean, GMedian, GMode, GSkewness, GKurtosis, BMean, BMedian, BMode, BSkewness, BKurtosis, YMean, YMedian, YMode, YSkewness, and YKurtosis. Finally, the CGSD parameters tables of color gradation distribution of RGB images were formed.
2.5. Data Analysis
2.5.1. Correlation Analysis of 20 CGSD Parameters to Meteorological Factors
A correlation analysis with SPSS was used to analyze the relationship between 20 CGSD parameters of leaf RGB images collected each day, and the corresponding meteorological factors with double tail inspection were collected for examination of significance.
2.5.2. Construction of Response and Inversion Liner Models
By using SPSS, the linear response models of 20 CGSD parameters of leaf RGB images were established by a regression approach based on the least-square method, with daily meteorological factors as the independent variables. Correspondingly, the linear inversion models of meteorological factors based on 20 CGSD parameters were also established by a stepwise regression on the least-square method.
2.5.3. Construction of Curve Models and Determination of Stationary Point of Models
The main canopy leaf color factors of the inversion models built in Section 2.5.2 were selected to construct the conic and cubic model of canopy leaf color to accumulated temperature by using the curve estimation method in SPSS.
The first derivatives of the conic and cubic models were obtained by using the calculus method. According to the monotonicity theorem of the function, the corresponding × value (accumulated temperature value) when the first derivative of the two model equations is 0 was obtained, which is the stationary point of the function.
2.5.4. Construction of Piecewise Models
Taking the stationary point of the accumulated temperature obtained in Section 2.5.3 as the bound, the samples in the modeling group which were less than or equal to the stationary point were taken as the piecewise model modeling group I, and the samples greater than the boundary value were taken as group II. Then, the inversion models of canopy leaf color to accumulated temperature of these two groups were constructed, respectively, by using the method in Section 2.5.2.
2.5.5. Accuracy Analysis of Models
The piecewise inversion model was used to fit with the modeling samples and three groups of testing samples, and the fitting accuracy of each group of samples was calculated using the equation as shown in (2):
IA is the inversion accuracy, %; ATP is the fitted value of the accumulated temperature, °C·d; AT is the measured value of the accumulated temperature, °C·d. Samples with inversion accuracy outside the interval range of [0.100%] were marked as outliers. The outliers were not counted in the calculation of the average simulation of inversion accuracy.
3. Results
3.1. Skew Analysis of the Distribution of Canopy Leaf Color Gradation of the RGB Images
In previous studies, we had found the relationship between meteorological factors with CSGD parameters in Begonia fimnristipula grown in a greenhouse [34]. In this study, we found that the cumulative distribution of color gradation of pepper leaves during different growth periods in a glass greenhouse also conformed to the skew distribution and that the distribution also exhibited different distribution characteristics (Figure 2).
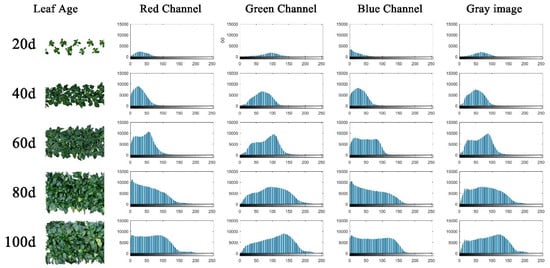
Figure 2.
RGB model color gradation distribution of population canopy images of pepper on five different dates. The cumulative frequency histogram of red, green, and blue channels, as well as gray-level images, were drawn using the imhist function of MATLAB. The X-axis is the color gradation value, and the Y-axis is the cumulative frequency.
3.2. Correlation Analysis, Multiple Linear Relationships of Microclimate Factors in a Glasshouse, and Population Canopy CGSD Parameters
The correlation analysis with SPSS shows that among 14 meteorological factors, the daily average water pressure was significantly or extremely significantly correlated with 18 CSCD parameters, respectively. Meanwhile, the accumulated temperature, maximum value of daily CO2 concentration, as well as the daily minimum temperature, were significantly or extremely significantly correlated with 17 CGSD parameters, respectively. However, the daily maximum temperature was not correlated with any CGSD parameter (Figure 3).
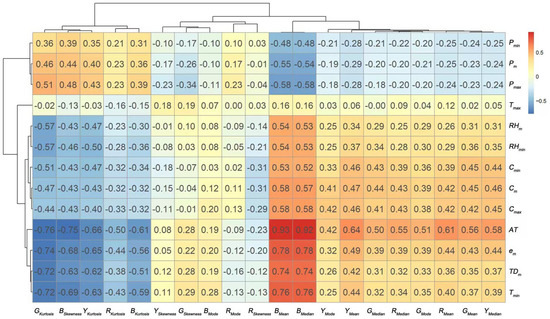
Figure 3.
Spearman correlation coefficient of population canopy CGSD parameters of pepper and microclimate factors. A Spearman correlation analysis of SPSS software was used on 20 CGSD parameters (RMean, RMedian, RMode, RSkewness, RKurtosis, GMean, GMedian, GMode, GSkewness, GKurtosis, BMean, BMedian, BMode, BSkewness, BKurtosis, YMean, YMedian, YMode, YSkewness, and YKurtosis), the microclimate factors, including daily meteorological factors (Tm, Tmax, Tmin, Pm, Pmax, Pmin, RHm, RHmin, TDm, em, Cm, Cmax, Cmin), and accumulation factors (AT) (n = 101). The correlation coefficient obtained by related analysis was drawn to CGSD parameters–daily meteorological factors heat map. The positive correlation coefficient is shown in red, and the negative correlation coefficient is shown in blue.
RMean, RMedian, RKurtosis, GMean, GMode, GKurtosis, BMean, BMedian, BSkewness, BKurtosis, YMean, YMedian, and YKurtosis were significantly and extremely significantly correlated with 13 meteorological factors, and GMedian and YMoed were significantly and extremely significantly correlated with 12 and 10 meteorological factors. RSkewness, GSkewness, and BMode were related to less than half of the meteorological factors, while RMode and YSkewness were only correlated with the daily maximum temperature.
3.3. Construction of the Canopy Leaf Color Response Regression Model
Table 1 showed that 20 models of canopy color to meteorological factors could be constructed, even the significance was extremely significant. In these models, the primary determinant of 14 CGSD response models, such as the mean, median, and kurtosis of R, G, B channels and gray image, as well as Gmode and Bskewness, was accumulated temperature. R2 of the 14 models were also generally close or more than 0.5. This indicated that accumulated temperature plays a decisive role in the canopy leaf color state formation.

Table 1.
Canopy leaf color response regression models of pepper and their goodness of fit.
3.4. Construction Inversion Models of Accumulated Temperature Based on CSCD Parameters and Analysis of Inversion Accuracy of the Models
Based on the results of 3.2 and 3.3, we used CGSD parameters as the independent variable to build an inversion model of accumulated temperature, which is the decisive factor of the canopy leaf color state formation. The model was as follows:
AT: Y21 = 48.020 BMean + 374.594 GSkewness − 15.344 RMedian − 3.303 BMode − 91.688
Furthermore, by verifying the inversion accuracy of the model, it was found that Y21 had a high inversion accuracy of 87.87% for the samples of group 2 from same planting row, while under the same environment, Y21 had a decreased accuracy, even at the lowest level reaching 76.78% for the samples (group 3 and group 4) from different planting rows (Table 2). Meanwhile, the inversion model had a large number of outliers, especially the proportion of outlier points for group 4, which out of the modeling samples had reached more than 10%, indicating that the inversion model was inappropriate.

Table 2.
Analytical results of inversion accuracy of the inversion model of Y21 for the samples of four groups.
Further research revealed that the appearance of outliers related to the plant age, which all appeared in the samples from the first 25 days of growth (Figure 4). This indicated the inversion method was not suitable for the accumulated temperature of the whole growth cycle of pepper, especially in the early growth period.
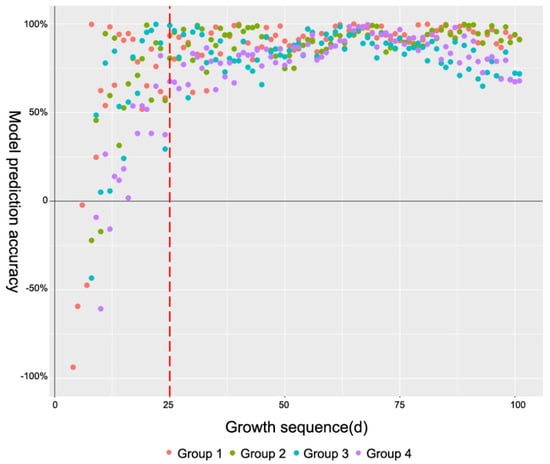
Figure 4.
Scatter plot of inversion accuracy of the inversion models for the samples of four groups. The figure shows only the inversion accuracy values in the interval [−1, 1].
3.5. Outlier Analysis
In order to find the cause of the outliers, we took the modeling group (group 1) as samples to draw a scatter plot (Figure 5, Figure 6 and Figure 7). The accumulated temperature had a stable growth with the increase of leaf age, even without fluctuations. The CGSD parameters of pepper canopy showed an obviously monotonic change between the leaf age of 20 to 40. A monotonic decrease of BMeans was observed in the first half of the leaf age, and a monotonic increase was observed in the last half. Meanwhile, the GSkewness showed a reverse monotonical change.
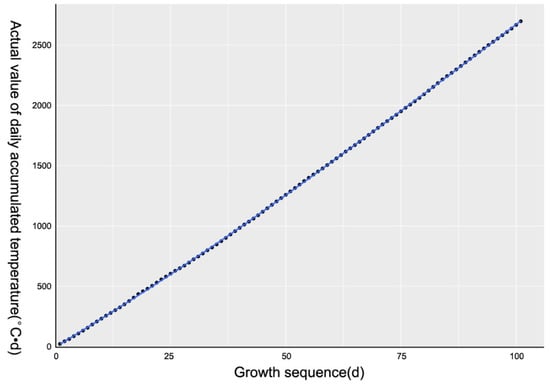
Figure 5.
Scatter plot of daily accumulated temperature during the whole growth period of pepper. GSkewness was fitted by the local polynomial regression-fitting algorithm, which was implemented by the geom_smooth function of R. X axis was the sequence of daily leaf age, and Y axis was the value of the daily accumulated temperature.
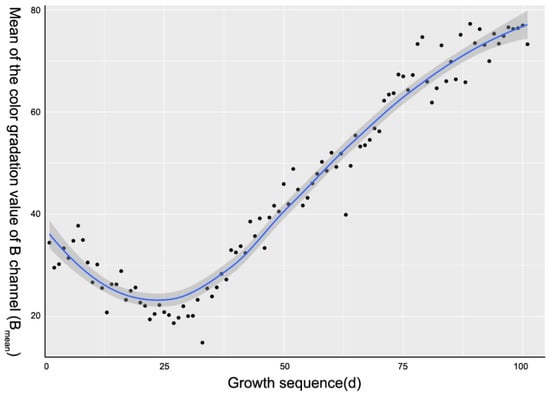
Figure 6.
Scatter plot of BMeans during the whole growth period of pepper. BMean was fitted by the local polynomial regression-fitting algorithm, which was implemented by the geom_smooth function of R. X axis was the sequence of daily leaf age, and Y axis was the daily value of BMean.
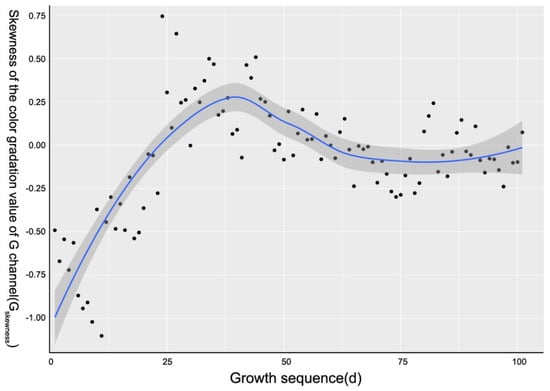
Figure 7.
Scatter plot of GSkewness during the whole growth period of pepper. GSkewness was fitted by the local polynomial regression-fitting algorithm, which was implemented by the geom_smooth function of R. X axis was the sequence of daily leaf age, and Y axis was the daily value of GSkewness.
Because CGSD parameters did not simply vary linearly, it was inappropriate to use a single linear model to build the inversion mode of canopy leaf color to accumulated temperature. The segmented linear model, with the stagnation point as the boundary, should be used to build the inversion model.
3.6. Determination of Point of Demarcation of Piecewise Function Model
The turning point (i.e., stationary point), which was between the different trends in the change process of canopy leaf color with accumulated temperature, would be taken as the point of demarcation of the piecewise function model. In order to identify the turning point, we respectively fitted the BMean and GSkewness, which had the highest correlation coefficient with accumulated temperature to the response model, by using the univariate quadratic and cubic equations (Table 3). It was shown that the cubic curve model could better characterize the relationship between BMean, GSkewness, and accumulated temperature. Therefore, the first derivatives of the two ternary equations (Y23 and Y25) were calculated, and the corresponding values of accumulated temperature were the stationary points (Table 4). Combined with the scatter plots, we defined that the points of demarcation of two piecewise function models of BMean and GSkewness to accumulated temperature were 537 and 995, respectively.

Table 3.
The univariate quadratic and cubic equation models of Bmean and Gskewness to accumulated temperature.

Table 4.
The first derivative equation models of Bmean and Gskewness to accumulated temperature.
3.7. Determination and Prediction of Piecewise Function Model
Based on the points of demarcation, we constructed the piecewise inversion model of accumulated temperature to canopy color, respectively (Table 5), and then calculated the fitting accuracy of these piecewise functions (Table 6, Figure 8 and Figure 9).

Table 5.
The piecewise inversion model of accumulated temperature to canopy color based on the points of demarcation.

Table 6.
Comparison of inversion effects of the piecewise inversion models of Y26 and Y27 to Y21.
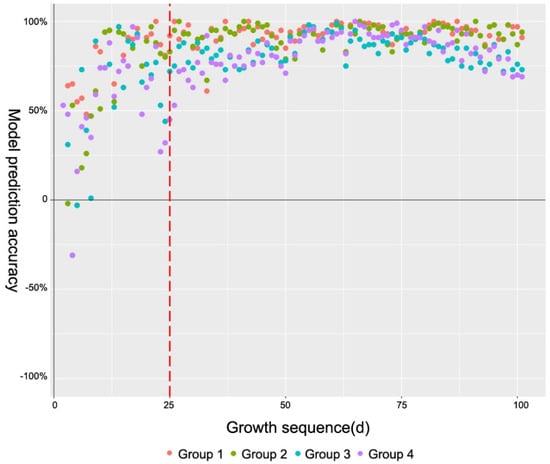
Figure 8.
Scatter plot of inversion accuracy of Y26 for the samples of four groups. The figure shows only the inversion accuracy values in the interval [−1, 1]. The red dotted line in the figure caption is the auxiliary observation line at the 25th day of growth sequence.
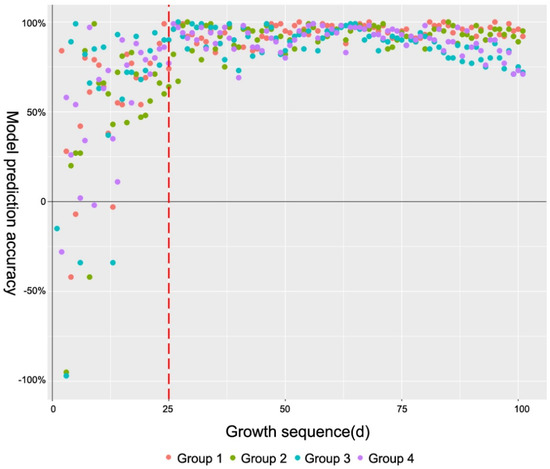
Figure 9.
Scatter plot of inversion accuracy of Y27 for the samples of four groups. The figure shows only the inversion accuracy values in the interval [−1, 1]. The red dotted line in the figure caption is the auxiliary observation line at the 25th day of growth sequence.
By using the piecewise inversion model, the rate of the outliers decreased by more than 50%. In the piecewise inversion model Y26, as the point of demarcation was calculated from the cubic curve model of BMean to accumulated temperature, the number of outliers decreased by 23; in fact, the rate of the outliers decreased by 65.70% compared with Y21. Furthermore, in the piecewise inversion model Y27, as the point of demarcation was calculated from the cubic curve model of GSkewness to accumulated temperature, the number of outliers decreased by 19, and the rate of outliers had decreased by 57.72% compared with Y21. The above results showed that the model Y26 was dominant in reducing the outliers. In addition, by using these piecewise inversion models, the overall fitting accuracy of Y26 and Y27 also increased by 1.21% and 3.31% compared with Y21, respectively. Y26 performed best in the modeling group (group 1) and group 2, while Y27 increased by 8.53% compared with Y21 in group 3 and group 4 of different planting rows. In conclusion, Y27, which used the point of demarcation calculated from the cubic curve model of GSkewness to accumulated temperature, had the best comprehensive effect.
4. Discussion
The research on the coupling effect between the environmental meteorological factors and crop growth is the basis of building collaborative environmental regulation models for a greenhouse. This has great significance to realize the precise regulation of a greenhouse environment and to promote the high-quality, high-quantity, and efficient production of greenhouse crops and even to reduce the costs.
Digital color images can reflect the growing state of plants [12], which provides a new method for research on crop growth. Based on our previous research, the traditional method, which used normal distribution and the corresponding parameter system for estimating canopy leaf color, was corrected. In fact, the color gradation of leaves follows skew distribution, and 20 CGSD parameters were established in our study [32,33,34]. CGSD parameters can describe the information of leaf color more accurately, systematically, and comprehensively from five dimensions, in which the mean value represents the mean color gradation of each pixel, the median value represents the median value of the percentile distribution of color gradation of pixels, and the mode value represents the color gradation with the largest proportion of the same color frequency of pixels. In addition, based on matrix and high-order statistics, skewness and kurtosis could quantitatively descript the bias and concentration of color gradation distribution.
The crop leaf color is tightly connected with its meteorological environment [35,36,37]. Our work indicated that the CGSD parameters of canopy leaf color are correlated with meteorological factors significantly, especially with the accumulated temperature, which shows the strongest correlation. Therefore, not only can environmental factors be used to simulate canopy leaf color changes (response model of canopy leaf color), but conversely, canopy leaf color can also be used to characterize the changes in meteorological factors (inversion model of canopy leaf color). Furthermore, parametric models could be established to characterize this relationship quantitatively. The stepwise regression is widely used because of its simple principle and convenience. However, the stepwise regression only could express the linear relationship between independent variables and dependent variables, that is, the monotonic function. If the relationship between independent variables and dependent variables is nonlinear, a large number of outliers will appear when using the monotonic function, which would affect the usability and accuracy of the model.
In this study, there were a lot of outliers in the response model of canopy leaf color to accumulated temperature, mainly due to the two main factors, BMean and GSkewness, showing the nonlinear characteristics. That is to say, the relationship between canopy leaf color and accumulated temperature is nonlinear. In the previous study of Begonia fimnristipula, even though we had built the inverse model to the accumulated temperature by using spatial high-order and the prediction accuracy had been improved [34], there were still too many outliers. Therefore, a piecewise function was used to express the relationship between canopy leaf color and accumulated temperature more accurately. Taking the stationary point of the high-order response model of the two main factors as the bound, the piecewise inversion models of canopy leaf color to accumulated temperature were constructed by using the stepwise regression method in sequence.
By comparing the inversion accuracy of these models based on the stationary point of different parameters, we found that the piecewise models constructed by taking the stationary point of the cubic curve model of GSkewness to accumulated temperature as the point of demarcation had the best effects, and the rate of outliers had decreased by 57.72%; moreover, the overall inversion accuracy had increased by 3.31% compared with the linear model constructed directly by the stepwise regression. It was shown that the pepper in greenhouse had a different response to the same meteorological environmental stimulus before and after the stationary point. That should be due to the accumulation of small meteorological environment changes leading to the qualitative changes of plants. We expect to further explore whether the stationary point can be used as a dividing marker of plant growth and a development cut-off point in subsequent studies.
5. Conclusions
The CGSD parameters of canopy leaf color of pepper were significantly correlated with meteorological factors in a greenhouse, especially with the accumulated temperature. Since the relationship between canopy leaf color and accumulated temperature is nonlinear, the piecewise inversion models, which had higher inversion accuracy and less outliers, were constructed by taking the stationary point of the high-order response model of GSkewness to accumulated temperature as the point of demarcation.
In conclusion, exploring and building the relationship between CGSD parameters of leaves and the internal development of plants, as well as the external environmental factors, makes it possible that canopy leaf color information could be taken as a bridge to the associated models of the internal physiological state of plants and the external environment, especially for quickly but moderately environmental changing. It will provide a new method for constructing crop growth models in future studies.
Author Contributions
Conceptualization H.W. and P.Z.; methodology, P.Z.; software, J.Z.; validation, Y.R. and X.X.; formal analysis, Z.Y.; investigation, F.W. and M.Z.; resources, H.W.; writing—original draft preparation, P.Z. and R.W.; writing—review and editing, H.W. and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
“333 project” research project for the high-level talent of Jiangsu Province (BRA2019348); National Natural Science Foundation of China (51309132).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, H.L.; Zhou, G.S.; He, Q.J.; Zhou, L.; Ji, Y.H.; Zhou, M.Z. Environmental explanation of maize specific leaf area under varying water stress regimes. Environ. Exp. Bot. 2020, 171, 103932. [Google Scholar] [CrossRef]
- Nawaz, R.; Abbasi, N.A.; Hafiz, I.A.; Khalid, A. Impact of climate variables on growth and development of Kinnow fruit (Citrus nobilis Lour × Citrus deliciosa Tenora) grown at different ecological zones under climate change scenario. Sci. Hortic. 2020, 260, 108868. [Google Scholar] [CrossRef]
- Hu, W.; Snider, J.L.; Wang, H.M.; Zhou, Z.G.; Chastain, D.R.; Whitaker, J.; Perry, C.D.; Bourland, F.M. Water-induced variation in yield and quality can be explained by altered yield component contributions in field-grown cotton. Field Crops Res. 2018, 224, 139–147. [Google Scholar] [CrossRef]
- Ayele, A.G.; Dever, J.K.; Kelly, C.M.; Sheehan, M.; Morgan, V.; Payton, P. Responses of upland cotton (Gossypium hirsutum L.) lines to irrigated and rainfed conditions of texas high plains. Plants 2020, 9, 1598. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Mu, Q.Z.; Huang, J.X. Assessing the remotely sensed drought severity index for agricultural drought monitoring and impact analysis in North China. Ecol. Indic. 2016, 63, 296–309. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Impacts, Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2007.
- Poorter, H.; Fiorani, F.; Pieruschka, R.; Wojciechowski, T.; Van der Putten, W.H.; Kleyer, M.; Schurr, U.; Postma, J.A. Pampered inside, pestered outside? Differences and similarities between plants growing in controlled conditions and in the field. New Phytol. 2016, 212, 838–855. [Google Scholar] [CrossRef]
- Chen, D.J.; Neumann, K.; Friedel, S.; Kilian, B.; Chen, M.; Altmann, T.; Klukas, C. Dissecting the phenotypic components of crop plant growth and drought responses based on high-throughput image analysis. Plant Cell 2014, 26, 4636–4655. [Google Scholar] [CrossRef]
- Tester, M.; Langridge, P. Breeding technologies to increase crop production in a changing world. Science 2010, 327, 818–822. [Google Scholar] [CrossRef]
- Grosskinsky, D.K.; Syaifullah, S.J.; Roitsch, T. Integration of multi-omics techniques and physiological phenotyping within a holistic phenomics approach to study senescence in model and crop plants. J. Exp. Bot. 2018, 69, 825–844. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Hu, H.B.; Yu, H.; Yang, X.; Yang, H.L.; Ruan, C.X.; Wang, Y.; Tang, J.W. Relationship between leaf physiological traits and canopy color indices during the spring leaf-expansion period in an oak forest. Ecosphere 2015, 259, 1–9. [Google Scholar]
- Vasseur, F.; Bresson, J.; Wang, G.; Schwab, R.; Weigel, D. Image-based methods for phenotyping growth dynamics and fitness components in Arabidopsis thaliana. Plant Methods 2018, 14, 63. [Google Scholar] [CrossRef]
- Barker, J.; Zhang, N.Q.; Sharon, J.; Steeves, R.; Wang, X.; Wei, Y.; Poland, J. Development of a field-based high-throughput mobile phenotyping platform. Comput. Electron. Agric. 2016, 122, 74–85. [Google Scholar] [CrossRef]
- Yadav, S.P.; Ibaraki, Y.; Gupta, S.D. Estimation of the chlorophyll content of micropropagated potato plants using RGB based image analysis. Plant Cell Tiss. Org. 2010, 100, 183–188. [Google Scholar] [CrossRef]
- Adamsen, F.J.; Pinter, P.J.; Barnes, E.M.; LaMorte, R.L.; Wall, G.W.; Leavitt, S.W.; Kimball, B.A. Measuring wheat senescence with a digital camera. Crop Sci. 1999, 39, 719–724. [Google Scholar] [CrossRef]
- Cai, H.C.; Cui, H.X.; Song, W.T.; Gao, L.H. Preliminary study on photosynthetic pigment content and colour feature of cucumber initial blooms. Trans. CSAE 2006, 22, 34–38. [Google Scholar]
- Ali, M.M.; Al-Ani, A.; Eamus, D.; Tan, D.K.Y.A. New image processing based technique to determine chlorophyll in plants. Am.-Eurasian J. Agric. Environ. Sci. 2012, 12, 1323–1328. [Google Scholar]
- Han, W.T.; Sun, Y.; Xu, T.F.; Chen, X.W.; Su, K.O. Detecting maize leaf water status by using digital RGB images. Int. J. Agric. Biol. Eng. 2014, 7, 45–53. [Google Scholar]
- Barbedo, J.G.A. Detection of nutrition deficiencies in plants using proximal images and machine learning: A review. Comput. Electron. Agric. 2019, 162, 482–492. [Google Scholar] [CrossRef]
- Vibhute, A.; Bodhe, S.K.; More, B.M. Wavelength based nitrogen estimation of grapes using RGB color images. World Res. J. Eng. Techol. 2014, 3, 38–40. [Google Scholar]
- Chaerle, L.; Hagenbeek, D.; Vanrobaeys, X.; Van Der Straeten, D. Early detection of nutrient and biotic stress in Phaseolus vulgaris. Int. J. Remote Sens. 2007, 28, 3479–3492. [Google Scholar] [CrossRef]
- Bresson, J.; Bieker, S.; Riester, L.; Doll, J.; Zentgraf, U. A guideline for leaf senescence analyses: From quantification to physiological and molecular investigations. J. Exp. Bot. 2018, 69, 769–786. [Google Scholar] [CrossRef] [PubMed]
- Clauw, P.; Coppens, F.; Korte, A.; Herman, D.; Slabbinck, B.; Dhondt, S.; Van Daele, T.; De Milde, L.; Vermeersch, M.; Maleux, K.; et al. Leaf growth response to mild drought: Natural variation in Arabidopsis sheds light on trait architecture. Plant Cell 2016, 28, 2417–2434. [Google Scholar] [CrossRef] [PubMed]
- Leiv, M.M. Effects of air humidity on growth, flowering, keeping quality and water relations of four short-day greenhouse species. Sci. Hortic. 2000, 86, 299–310. [Google Scholar]
- Reich, P.B.; Oleksyn, J. Global patterns of plant leaf N and P in relation to temperature and latitude. Proc. Natl. Acad. Sci. USA 2004, 101, 11001–11006. [Google Scholar] [CrossRef] [PubMed]
- James, A.B. Responses of stomatal conductance to light, humidity and temperature in winter wheat and barley grown at three concentrations of carbon dioxide in the field. Glob. Chang. Biol. 2000, 6, 371–382. [Google Scholar]
- Jeon, M.-W.; Ali, M.B.; Hahn, E.-J.; Paek, K.-Y. Photosynthetic pigments, morphology and leaf gas exchange during ex vitro acclimatization of micropropagated CAM Doritaenopsis plantlets under relative humidity and air temperature. Environ. Exp. Bot. 2006, 55, 183–194. [Google Scholar] [CrossRef]
- Urban, J.; Ingwers, M.W.; Mcguire, M.A.; Teskey, R.O. Increase in leaf temperature opens stomata and decouples net photosynthesis from stomatal conductance in Pinus taeda and Populus deltoides × nigra. J. Exp. Bot. 2017, 68, 1757–1767. [Google Scholar] [CrossRef]
- Wang, B.; Cai, W.W.; Li, J.L.; Wan, Y.F.; Li, Y.; Guo, C.; Wilkes, A.; You, S.C.; Qin, X.B.; Gao, Q.Z.; et al. Leaf photosynthesis and stomatal conductance acclimate to elevated [CO2] and temperature thus increasing dry matter productivity in a double rice cropping system. Field Crops Res 2020, 248, 107735. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Huang, D.F. A review of imaging techniques for plant phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef]
- Chen, Z.M.; Wang, F.Z.; Zhang, P.; Ke, D.C.; Zhu, Y.; Cao, W.X.; Jiang, H.D. Skewed distribution of leaf color RGB model and application of skewed parameters in leaf color description model. Plant Methods 2020, 16, 23. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, Z.M.; Ma, S.D.; Yin, D.; Jiang, H.D. Prediction of soybean yield by using RGB model with skew distribution pattern of canopy leaf color. Trans. CSAE 2021, 37, 120–126. [Google Scholar]
- Zhang, P.; Chen, Z.M.; Wang, F.Z.; Wang, R.; Bao, T.T.; Xie, X.P.; An, Z.Y.; Jian, X.X.; Liu, C.W. Response of Population Canopy Color Gradation Skewed Distribution Parameters of the RGB Model to Micrometeorology Environment in Begonia Fimbristipula Hance. Atmosphere 2022, 13, 890. [Google Scholar] [CrossRef]
- Gous, P.W.; Meder, R.; Fox, G.P. Near Infrared Spectral Assessment of Stay-Green Barley Genotypes under Heat Stress. J. Near Infrared Spectrosc. 2015, 23, 145–153. [Google Scholar] [CrossRef]
- Cai, J.; Okamoto, M.; Atieno, J.; Sutton, T.; Li, Y.; Miklavcic, S.J. Quantifying the Onset and Progression of Plant Senescence by Color Image Analysis for High Throughput Applications. PLoS ONE 2016, 11, e0157102. [Google Scholar] [CrossRef]
- Schmalko, M.E.; Scipioni, P.G.; Ferreyra, D. Effect of Water Activity and Temperature in Color and Chlorophylls Changes in Yerba Mate Leaves. Int. J. Food Prop. 2005, 8, 313–322. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).