1. Introduction
Quantified visibility estimation is of great significance in applications such as air safety [
1], ground transport control [
2], as well as air quality assessment [
3]. Recognizing the current visibility state has been an urgent need for many areas [
4,
5] and plays a key role in machine learning [
6].
Typical visibility estimation methods rely largely on the professional meteorological stations with expensive sensors and human observations. However, limited by the manufacturing costs, these stations are often distributed in a non-uniform way, which in turn, restricts the capability of accurate visibility estimation. Recently, with the widespread use of mobile cameras, thousands of images have been collected under different weather conditions, which might provide an alternative solution for quantified visibility estimation.
In fact, many researchers have tried to explore the possibility of estimating visibility from single images in the past decades [
7,
8,
9,
10,
11,
12]. Hautiére et al. [
7] propose a probabilistic model-based approach, which takes into account the distribution of contrasts in the scene. Thus, the proposed model is more robust to illumination variations. Though helpful, this method is still limited in ability to deal with cameras captured in daylight. In order to improve the performance during night, Varjo et al. [
8] propose a method based on feature vectors that are projections of the scene images with lighting normalization. Li et al. [
9] estimate the extinction coefficient in a clear atmosphere by assuming it to be approximately a constant. Combined with the dark channel prior [
13], the ratio of two extinction coefficients in the current and clear atmosphere can be calculated, and the quantified visibility can then be obtained. It is further improved by employing an edge collapse-based transmission refinement [
10].
With the rapid development of visibility estimating methods, one notable issue is that the precise visibility label is difficult to obtain, and the not necessarily accurate visibility label has agreement on image-based visibility estimation. On one hand, Song et al. [
11] solve this by associating a label distribution with each image. The label distribution contains all of the possible visibilites with corresponding probabilities. After that, typical machine learning-based methods can be employed. On the other hand, Xun et al. [
12] use the extra ordinal information and relative relation of images for visibility estimation. They pre-train a model using classified outdoor foggy images and then fine-tune the model via indoor synthetic continuous annotation.
Though effective, most of the former mentioned methods confront the following problems. Under the influence of camera angle, previous methods need large efforts on parameter calibration, which (a) restricts the model generalization and increases the model costs. Moreover, (b) the image scale is also sensitive. For instance, some cameras focus on local road details (small scale), while others concentrate on global information (large scale). Apart from that, the precedent visibility estimation approaches exploit (c) either data-driven or physical-constrained techniques. We believe the physical constraint plays a key role in visibility estimation and the data-driven strategy is also important in future work.
Consequently, to solve these issues and achieve quantified visibility estimation from images, this paper proposes a new network architecture, named Deep Quantified Visibility Estimation Network (abbreviated DQVENet), especially for traffic images. The contributions of this paper are summarized as follows.
By integrating physical constraint with deep learning network, a novel framework named DQVENet is proposed for single image visibility estimation.
Within this framework, a Transmission Estimation Module (TEM), a Depth Estimation Module (DEM), and an Extinction Coefficient Estimation Module (E3M) is unified as a whole according to meteorological theory.
A new benchmark dataset, which is especially designed for traffic image-based quantified visibility estimation, is constructed.
2. Related Work
From the perspective of machine learning, image-based quantified visibility estimation is equal to learning a regression model. This paper focuses on deep learning-based visibility estimation. As a result, this section first presents a short investigation of deep learning methods followed by discussing single image visibility estimation. Considering the great similarity between visibility estimation and weather recognition, we give a brief introduction to it. Furthermore, taking the fact that visibility can be estimated via dehazing techniques into consideration, single image-based haze removal is also discussed.
2.1. Deep Learning
Since the emergence of AlexNet [
14] in computer vision, deep learning has attracted attention among areas such as speech recognition [
15], natural language processing [
16], video understanding [
17], etc. Recently, it also shows great potential in atmospheric science. For example, by a thorough combination of materials such as satellite, radar, and ground station, Sønderby et al. [
18] propose MetNet for precipitation forecasting. Results show that it is superior to pure numerical weather prediction. For getting precise and accurate prediction, Yu et al. [
19] proposes an auxiliary guided spatial distortion network. However, few existing methods take both a deep learning architecture design and meteorological theory into account, which might be a possible avenue for future research. To achieve that, Kuang et al. [
20] introduce three branches corresponding to the temperature variation equation in deep learning and propose a new method for temperature forecasting.
2.2. Image-Based Visibility Estimation
Visibility-related studies have been a hot research topic for decades. Basically, both the parameter settings of the camera and the environmental conditions highly affect image quality, which influences estimation accuracy. To solve this issue, Li et al. [
21] employ a pre-trained convolutional neural netwok to extract the visibility features automatically instead of manual extraction. Giyenko et al. [
22] also implement a simple but useful three-layer network for visibility estimation and trained it on a dataset collected in South Korea. Palvanov et al. [
23] propose a new approach based on deep integrated convolutional neural networks for the estimation of visibility distances from camera imagery. This network uses three paralleled streams of deep integrated convolutional neural networks.
2.3. Weather Recognition from Images
Apart from quantified visibility estimation, recognizing the weather conditions from images is also of great significance. Under the framework of pattern recognition, a possible solution is treating weather recognition as image classification [
6]. Casting on this mechanism, there are methods concentrating on extracting discriminative features such as global histogram [
24] as input for classification methods such as support vector machine [
25]. With the overwhelming successes of deep learning, many brilliant methods have also been proposed [
24,
26,
27].
2.4. Single Image Haze Removal
There is a deterministic correlation between the fog image and clear image, and the visibility can be mathematically calculated through an investigation of these two images. Consequently, there are also methods estimating image visibility via dehazing techniques. Specifically, Zhou et al. [
28] propose a visibility estimation method based on dark channel prior and image entropy. The dark channel prior is used to estimate atmospheric transmittance and optimized via guided filter. The road region is extracted based on a region growing algorithm. After that, the depth map is calculated using lane information and the haze visibility is obtained based on the minimum image entropy of road images. Bae et al. [
29] propose a visibility distance estimation method using dark channel prior-based single image haze removal. Hence, the dark channel for an input sea-fog image is first calculated. The binary transmission image is obtained by applying a threshold to the estimated transmission from the dark channel. Then, the sum of the distance values of pixels, corresponding to the sea-fog boundary, is averaged, in order to derive the visibility distance. Furthermore, image dehazing is a highly ill-posed problem [
30] and various methods have been developed to tackle this problem. Specifically, the key ingredient for haze removal is the estimation of the transmission map. Except for dark priors [
13], Cai et al. [
31] introduce an end-to-end network for estimating it with a novel activation unit. Ren et al. [
32] and Li et al. [
33] also provide effective frameworks for transmission map estimation.
3. Materials
3.1. Motivation
Quantified visibility estimation is quite important to traffic control. Nevertheless, there is few datasets focusing on this, which limits the developing of estimation methods. To illustrate this key issue and demonstrate the effectiveness of the proposed method, this paper provides a new dataset named QVEData (abbreviation for Quantified Visibility Estimation Dataset).
3.2. Dataset Construction
Images are first obtained via real high-speed road cameras and 24,031 traffic images are collected during this stage. The corresponding quantified visibility observation are acquired using the nearest meteorological station. Basically, five cameras (denoted as C1, C2, C3, C4, and C5) are employed and the distances between the camera and the nearest visibility station are listed as following
Table 1.
Unfortunately, most of these images have high similarity and the corresponding visibility observations tend to be consistent. After similarity eliminating and manual quality control, 3236 images are finally preserved for constructing the final dataset. We denote this dataset Quantified Visibility Estimation Dataset (abbreviated as QVEData). Considering the fact that this paper is devoted to visibility estimation of traffic images, the selected cameras are along a high-speed road. Therefore, the road is the main content of the image. Nevertheless, due to the variation of traffic cameras, camera angles, weather conditions, illuminations, moving vehicles, etc., the finally preserved 3326 images are quite different, which increases the difficulty of visibility estimation.
Figure 1 presents the visibility distribution of QVEData. Specifically, most of the corresponding visibility lies in the interval of 0–20 km, with a focus on 0–10 km.
3.3. Comparison with Other Datasets
Generally, there are many significant fog-related datasets.
Table 2 gives an intuitive comparison among these datasets and the proposed QVEData. Specifically, we divide these datasets into three categories according the corresponding tasks, i.e., image dehazing, weather recognition, and visibility estimation.
4. Methods
4.1. Preliminary
For a given hazy image
I, it is degraded due to the presence of haze, which can be mathematically formulated as
where
J is the groundtruth image (without haze),
t is the transmission map,
A is the global atmospheric light, and
x is the pixel position. Specifically, the transmission map
t can be expressed as
where
represents the atmospheric extinction coefficient and
d is the scene depth.
According to Koschmieder’s law, the visibility can be expressed as a function of the atmospheric extinction coefficient, i.e.,
where
C is a threshold contrast and
V is the visibility in metres. In other words, the visibility can be quantified as
Typically, the threshold
C is set to be 0.05. Consequently, Equation (
4) can be approximately formulated as
For Equation (
2), we can rewrite it as
Consequently, for a given position, the corresponding visibility can be roughly estimated as
by integrating Equation (
6) to Equation (
5).
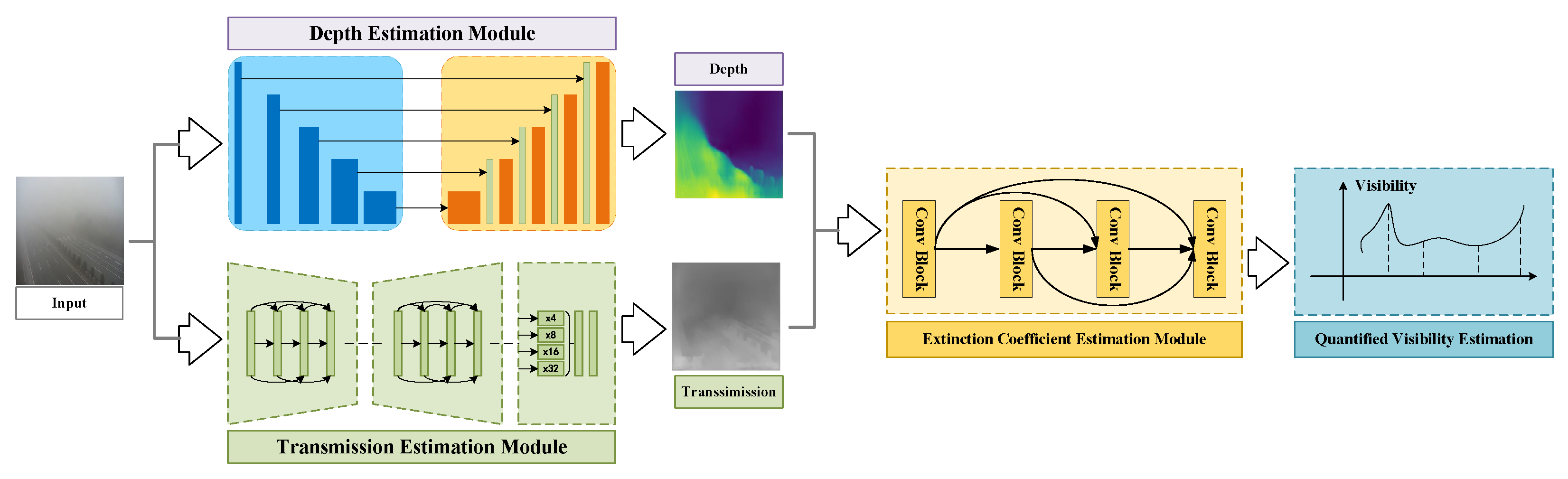
4.2. Overall Architecture
From Equation (
7), the visibility
V is highly correlated with transmission map
t and scene depth
d. This motivates us to design a network that is physically constrained by Equation (
7). As a result, this paper proposes Deep Quantified Visibility Estimation network (abbreviated as DQVENet), an elaborately designed convolutional architecture, especially for single image-based quantified visibility estimation. The overall architecture can be found in
Figure 2.
Following the working mechanism of Equation (
5), DQVENet mainly consists of three basic modules, i.e., the Transmission Estimation Module (TEM), the Depth Estimation Module (DEM), and the Extinction coEfficient Estimation Module (E3M). We then present the details of each module.
4.3. Transmission Estimation Module
To estimate the transmission map from a single image, previous methods [
30,
32,
47] often use the multi-level features. DQVENet employs the densely connected pyramid network [
30] as the Transmission Estimation Module (TEM). Specifically, TEM adopts a densely connected UNet [
30,
48] structure for feature encoder-decoder.
Denote the input image as
, where
w,
h, and
c represent the width, height, and the number of channels of
X. It is first processed by a
convolution with stride 2, followed by batch normalization, ReLU activation, and Max-pooling, which can be mathematically formulated as
Here,
is the pre-processed feature for the following cascaded encoder-decoder. Without loss of generality and for simplicity, we still use
X to represent the input feature in the following.
The encoder comprises of both a dense block and a transition block. For dense block, it contains two sequential batch normalization—ReLU activation—convolution layers. Mathematically, it can be defined as
For the transition block, it contains an additional Max-pooling layer for enlarging receptive fields compared with the dense block, i.e.,
Similar to the encoder, the decoder also involves a dense block and a transition block as
We should note that the stride of the transpose convolution is set to 1, and the up-sampling operation is indeed achieved by the nearest interpolation. Moreover, the encoder feature at different levels are also fed to the corresponding decoder layer for precise feature extraction.
For getting global structural information at different scales, the multi-level pyramid pooling block is employed. Specifically, four Max-pooling operations with size
,
,
, and
are used, i.e.,
and they are concatenated for estimating the final transmission map
using Tanh activation as
4.4. Depth Estimation Module
Depth estimation from a single image has been explored through various approaches such as non-parametric scene sampling [
49], supervised end-to-end learning [
50], semi-supervised estimation [
51], and generative adversarial prediction [
52].
Taking the fact that obtaining ground-truth scene depth from unconstrained images is relatively hard into consideration, DQVENet focuses on seeking the approximated scene depth in an unsupervised or self-supervised manner. Specifically, the pre-trained self-supervised scene estimation method proposed by Godard et al. [
53] is employed as the Depth Estimation Module (DEM).
Basically, the DEM consists of several ResNet [
54]-based encoder-decoder blocks, i.e., Res-UNet [
55]. Compared with vanilla UNet [
48] or other backbones, taking Res-UNet as our quantified visibility-oriented depth estimation, i.e., DEM, has the following advantages.
It contains more layers with more parameters. Consequently, it can describe the more abstract high-level features accurately.
The structure is more sophisticated. In application, the images can be obtained at any place, any time, and any view, which increases the difficulty of image recognition. This architecture promotes the corresponding generalization.
Benefiting from the residual connection, training such a network is supposed to be more easy with less risk of gradient vanishing.
4.5. Joint Atmospheric Extinction Coefficient and Quantified Visibility Estimation
Denoting the estimated transmission map and the depth map as
and
, respectively, the atmospheric extinction coefficient can be obtained according to Equation (
6) and the quantified visibility estimation can be further achieved via Equation (
5).
However, imposing
and
to Equation (
6) directly confronts the following two main inconveniences.
Due to the lack of labeled transmission and depth maps, we cannot fine-tune the TEM and DEM on our own data or other weather images. Consequently, we only use the pre-trained model and the pre-obtained transmission map and depth map are relatively coarse, which will restrict the performance of quantified visibility estimation.
The two modules, i.e., TEM and DEM, work separately. Limited by this strategy, the obtained transmission map and depth map are relatively independent. Nevertheless, for a given image, these items should be highly correlated. Moreover, bringing
and
into Equation (
6) makes the network not end-to-end, which in turns constraints the efficiency.
To overcome the former illustrated problems, this paper attempts to integrate the TEM and DEM together for joint atmospheric extinction coefficient and quantified visibility estimation. As a result, the DenseNet [
56]-based Extinction coEfficient Estimation Module (E3M) with joint quantified visibility estimation is introduced.
For E3M, the estimated transmission map and depth map are first concatenated as the input, and then processed via a pre-trained 121-layer DenseNet by replacing the last classification layer with a regression layer. The number of channel inputs for the first convolutional layer is also set to 4 instead of the original 3. This makes the whole network end-to-end trainable, and we denote this architecture DQVENet.
4.6. Iterative Training
For getting better performance, this paper employs an iterative training strategy. To be specific, both TEM and DEM are first pre-trained using the corresponding dehaze dataset [
30] and depth estimation dataset [
53]. After that, these two modules are frozen and combined to the DQVENet for training E3M. Finally, the whole DQVENet is fine-tuned with a relatively small learning rate.
DQVENet is implemented using Pytorch (
https://pytorch.org/, accessed on 28 November 2022). During pre-training of TEM and DEM, we use the same setting as the original paper. For E3M, the stochastic gradient descent optimizer with learning rate
is employed. The learning rate drops by 0.1 during epoch 150 and 225. The early stopping strategy is also implemented, i.e., training stops after 300 epochs or the validation loss does not decrease within 10 epochs. As for fine-tuning DQVENet, a small learning rate
is employed.
5. Results
To validate the performance of the proposed DQVENet, this section conducts experiments on QVEData. Specifically, there are a total of 3236 images for QVEData. We split these images randomly into training, validation, and testing with ratio 60%, 10%, and 30%, respectively. Casting on this, these experiments can be mainly divided into two categories, i.e., qualitative results and quantitative results.
5.1. Qualitative Results
Figure 3 first presents an intuitive illustration of the learned depth map and transmission map with their corresponding original image. For depth map, the green area represents short depth and the blue area denotes long depth. While for transmission map, the dark area indicates low transmissivity and the light area stands for high transmissivity.
From this figure, both the estimated depth map of DEM and the estimated transmission map of TEM can describe the scene depth and transmission map to some extent. This is mainly due to the reason that these two modules are pre-trained using the corresponding dataset.
5.2. Quantitative Results
Figure 4 then shows the quantified visibility estimation of DQVENet and the ground truth visibility observation. To be specific, the first two rows present examples that DQVENet is underestimated. The third row gives results of DQVENet being overestimated; the last row shows the instances that DQVENet fits groundtruth observations well.
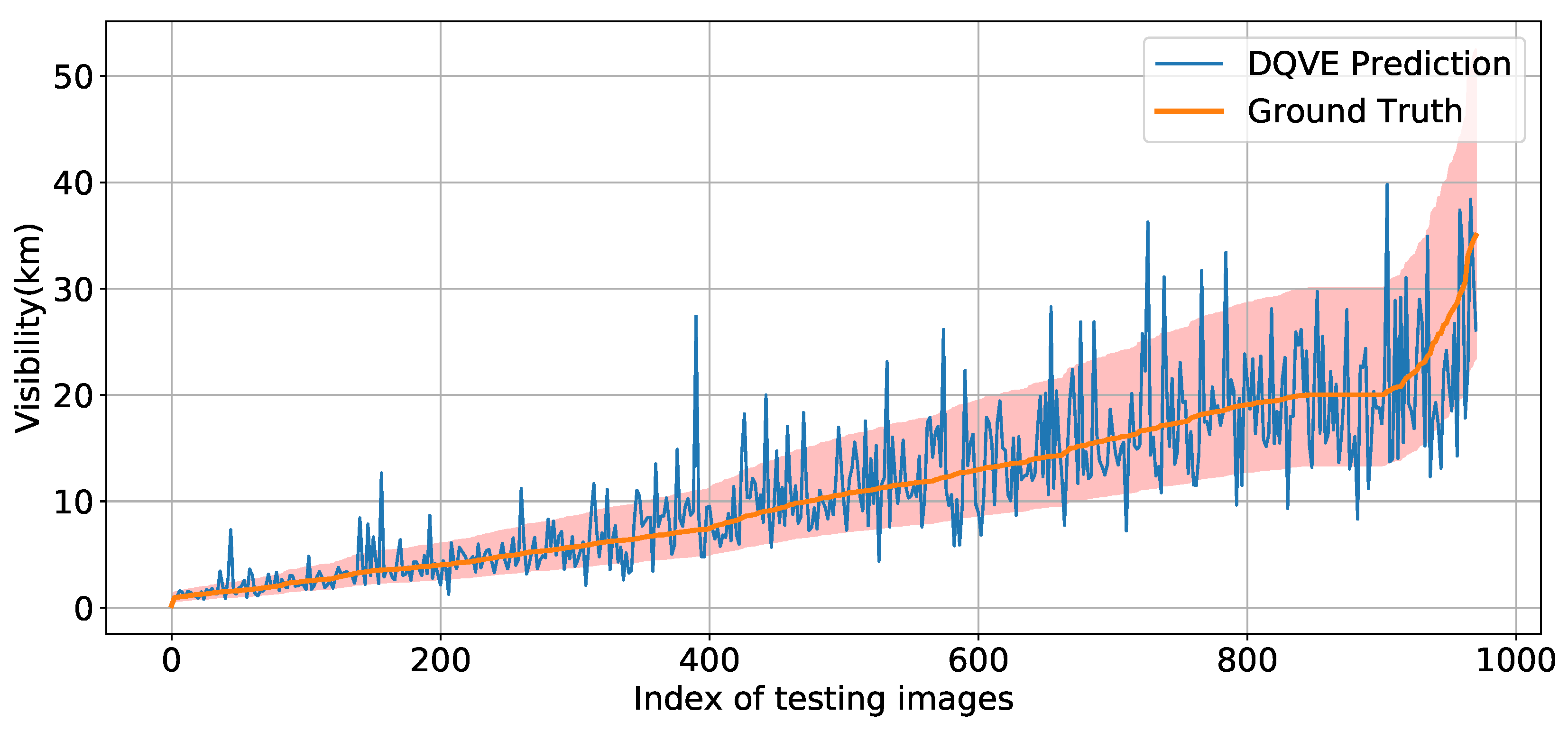
Figure 5 presents the DQVENet results and the groundtruth visibility observation on the testing set of QVEData. Specifically, the 971 testing images are first sorted from small to large according to their groundtruth visibility, i.e., the orange line. Then, the corresponding predictions are plotted along with the groundtruth, i.e., the blue line. Finally, we also present the soft gap, i.e., the red area, for better demonstrating the effectiveness of DQVENet. Except for some overestimated cases, DQVENet can fit the visibility well in general.
Furthermore,
Figure 6 shows the correlation analysis of DQVENet. Within this scatter figure, the DQVENet Prediction is treated as the x-axis, and the groundtruth observation is the y-axis. The more dots converge at the middle red line, the better the performance of the method is. Nevertheless, we cannot restrict the scatters to lie in a fixed gap shown in the following
Figure 6a. Instead, a proportional gap, as in the following
Figure 6b, might be more feasible. From this figure, the DQVENet is capable of describing the tendency of visibility estimations.
Generally, for meteorological forecasting or machine learning-based regression, the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), Bias Error, and Correlation are supposed to be significant indicators. Nevertheless, for quantified visibility estimation, the former three criterions, i.e., MAE, RMSE, and Bias, are not suitable. MAE, RMSE, or Bias for different visibility groundtruths are not comparable. In other words, if the groundtruth is 20,000 m, the estimated results within (19,000 m, 21,000 m) are acceptable for a traffic manager. However, if the groundtruth is 1000 m, the desired results should be in the range (900 m, 1100 m). As a result, we put these criterions aside and apply Correlation as a basic criterion due to the fact that correlations are overall statistical results instead of point-to-point comparisons. Suppose the predicted visibility is
and the groundtruth visibility is
Y, then it is defined as
The larger the correlation coefficient, the better the model performance. The correlation coefficient of DQVENet is 0.7237, demonstrating that DQVENet is competent to quantify visibility estimation.
6. Discussion
For further illustrating the effectiveness of DQVENet, this section compares DQVENet with several state-of-the-art methods, including the ResNet family [
54] and the EfficientNet family [
57]. The classification accuracy is discussed.
To demonstrate the performance of the estimation method, we define the classification accuracy as
Here,
and
Y denote the predicted and groundtruth visibility, respectively.
denotes the absolute value,
represents the number.
is a threshold that can be defined arbitrarily, and
is the accuracy according to
t.
In other words, the classification accuracy under threshold
t is the ratio between the number of samples that lie in the interval
and the total number of samples. We denote this accuracy as a
soft gap. This soft gap differs from the hard gap, which splits visibilities hardly into intervals such as [0–100 m], [100–500 m], etc., due to the fact that this paper focuses on quantified visibility estimation instead of classification. More specifically, if the groundtruth visibility is 200 m, the estimated 100 m will be regarded as better than 200.1 m for the hard gap. Nevertheless, within this soft partition, 200.1 m will be treated as a preferred estimation than 100 m. Detailed results can be found in the following
Figure 7.
From this figure, the classification accuracy of all compared methods increases with the threshold being larger. In general, DQVENet outperforms the ResNet family (including ResNet-50, ResNet-101, and ResNet-152) and the EfficientNet family (including EfficientNet-B0, EfficientNet-B1, EfficientNet-B2, and EfficientNet-B4), illustrating that DQVENet is a feasible method for quantified visibility estimation.
7. Conclusions
In this paper, we propose a framework (DQVENet) for quantified visibility estimation based on deep learning. Specifically, the physical constraint is employed as the guideline of network design. Under this framework, a transmission estimation module, a depth estimation module, and an extinction coefficient estimation module are introduced. Furthermore, a new dataset named QVEData, that is especially collected for traffic image-based quantified visibility estimation, is proposed. Experimental results on this dataset demonstrate the effectiveness of DQVENet. This framework is flexible so that the three modules can be replaced by any other backbones. We should also note that DQVENet tries to integrate meteorological priors into deep learning network design, which might be a promising avenue for future research. Our future work will focus on digging deeper into interdisciplinary theories between them.
Author Contributions
Conceptualization, F.Z. and T.Y.; methodology, T.Y. and F.Z.; software, K.W.; validation, T.Y.; formal analysis, Y.H.; investigation, Z.L.; resources, Q.K.; data curation, Y.C.; writing—original draft preparation, T.Y.; visualization, F.Z.; supervision, T.Y.; project administration, T.Y.; funding acquisition, T.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Natural Science Foundation of China under grant number 62106270 and in part by the Application of FY-4B for Highway Traffic Meteorological Service under grant number FY-APP-2021.0111.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DQVENet | Deep Quantified Visibility Estimation Network |
| QVEData | Quantified Visibility Estimation Dataset |
| TEM | Transmission Estimation Module |
| DEM | Depth Estimation Module |
| E3M | Extinction coEfficient Estimation Module |
| ResNet | Residual Network |
References
- Ding, J.; Zhang, G.; Wang, S.; Xue, B.; Yang, J.; Gao, J.; Wang, K.; Jiang, R.; Zhu, X. Forecast of Hourly Airport Visibility Based on Artificial Intelligence Methods. Atmosphere 2022, 13, 75. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Zhu, Y.; Yang, L.; Ge, L.; Luo, C. Visibility Prediction Based on Machine Learning Algorithms. Atmosphere 2022, 13, 1125. [Google Scholar] [CrossRef]
- Gueymard, C.A. Visibility estimates from atmospheric and radiometric variables using artificial neural networks. Air Pollut. XXV 2017, 211, 129. [Google Scholar]
- Long, Q.; Wu, B.; Mi, X.; Liu, S.; Fei, X.; Ju, T. Review on Parameterization Schemes of Visibility in Fog and Brief Discussion of Applications Performance. Atmosphere 2021, 12, 1666. [Google Scholar] [CrossRef]
- Cordeiro, F.M.; França, G.B.; de Albuquerque Neto, F.L.; Gultepe, I. Visibility and Ceiling Nowcasting Using Artificial Intelligence Techniques for Aviation Applications. Atmosphere 2021, 12, 1657. [Google Scholar] [CrossRef]
- Yu, T.; Kuang, Q.; Hu, J.; Zheng, J.; Li, X. Global-similarity local-salience network for traffic weather recognition. IEEE Access 2020, 9, 4607–4615. [Google Scholar] [CrossRef]
- Hautiére, N.; Babari, R.; Dumont, É.; Brémond, R.; Paparoditis, N. Estimating meteorological visibility using cameras: A probabilistic model-driven approach. In Proceedings of the Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; pp. 243–254. [Google Scholar]
- Varjo, S.; Hannuksela, J. Image based visibility estimation during day and night. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; pp. 277–289. [Google Scholar]
- Li, Q.; Xie, B. Visibility estimation using a single image. In Proceedings of the CCF Chinese Conference on Computer Vision, Tianjin, China, 11–14 October 2017; pp. 343–355. [Google Scholar]
- Li, Q.; Li, Y.; Xie, B. Single image-based scene visibility estimation. IEEE Access 2019, 7, 24430–24439. [Google Scholar] [CrossRef]
- Song, M.; Xu, H.; Liu, X.F.; Li, Q. Visibility Estimation via Deep Label Distribution Learning. J. Cloud Comput. 2021, 10, 46. [Google Scholar] [CrossRef]
- Xun, L.; Zhang, H.; Yan, Q.; Wu, Q.; Zhang, J. VISOR-NET: Visibility Estimation Based on Deep Ordinal Relative Learning under Discrete-Level Labels. Sensors 2022, 22, 6227. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Abdel-Hamid, O.; Mohamed, A.r.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional neural networks for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Yu, T.; Wang, L.; Guo, C.; Gu, H.; Xiang, S.; Pan, C. Pseudo low rank video representation. Pattern Recognit. 2019, 85, 50–59. [Google Scholar] [CrossRef]
- Sønderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. Metnet: A neural weather model for precipitation forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar]
- Yu, T.; Kuang, Q.; Zheng, J.; Hu, J. Deep precipitation downscaling. IEEE Geosci. Remote. Sens. Lett. 2021, 19, 1001405. [Google Scholar] [CrossRef]
- Kuang, Q.; Yu, T. MetPGNet: Meteorological Prior Guided Network for Temperature Forecasting. IEEE Geosci. Remote. Sens. Lett. 2021, 19, 1004305. [Google Scholar] [CrossRef]
- Li, S.; Fu, H.; Lo, W.L. Meteorological visibility evaluation on webcam weather image using deep learning features. Int. J. Comput. Theory Eng. 2017, 9, 455–461. [Google Scholar] [CrossRef]
- Giyenko, A.; Palvanov, A.; Cho, Y. Application of convolutional neural networks for visibility estimation of CCTV images. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 875–879. [Google Scholar]
- Palvanov, A.; Cho, Y.I. Visnet: Deep convolutional neural networks for forecasting atmospheric visibility. Sensors 2019, 19, 1343. [Google Scholar] [CrossRef]
- Yan, X.; Luo, Y.; Zheng, X. Weather recognition based on images captured by vision system in vehicle. In Proceedings of the International Symposium on Neural Networks, Wuhan, China, 26–29 May 2009; pp. 390–398. [Google Scholar]
- Lu, C.; Lin, D.; Jia, J.; Tang, C.K. Two-class weather classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3718–3725. [Google Scholar]
- An, J.; Chen, Y.; Shin, H. Weather classification using convolutional neural networks. In Proceedings of the 2018 International SoC Design Conference (ISOCC), Daegu, Korea, 12–15 November 2018; pp. 245–246. [Google Scholar]
- Guerra, J.C.V.; Khanam, Z.; Ehsan, S.; Stolkin, R.; McDonald-Maier, K. Weather Classification: A new multi-class dataset, data augmentation approach and comprehensive evaluations of Convolutional Neural Networks. In Proceedings of the 2018 NASA/ESA Conference on Adaptive Hardware and Systems (AHS), Edinburgh, UK, 6–9 August 2018; pp. 305–310. [Google Scholar]
- Zhou, K.; Cheng, X.; Tan, M.; Li, H. Visibility estimation based on dark channel prior and image entropy. J. Nanjing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2016, 36, 90–95. [Google Scholar]
- Bae, T.W.; Han, J.H.; Kim, K.J.; Kim, Y.T. Coastal Visibility Distance Estimation Using Dark Channel Prior and Distance Map Under Sea-Fog: Korean Peninsula Case. Sensors 2019, 19, 4432. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Patel, V.M. Densely connected pyramid dehazing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3194–3203. [Google Scholar]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. Dehazenet: An end-to-end system for single image haze removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Liu, S.; Zhang, H.; Pan, J.; Cao, X.; Yang, M.H. Single image dehazing via multi-scale convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 154–169. [Google Scholar]
- Li, B.; Peng, X.; Wang, Z.; Xu, J.; Feng, D. An all-in-one network for dehazing and beyond. arXiv 2017, arXiv:1707.06543. [Google Scholar]
- Ancuti, C.; Ancuti, C.O.; De Vleeschouwer, C. D-hazy: A dataset to evaluate quantitatively dehazing algorithms. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2226–2230. [Google Scholar]
- Ancuti, C.; Ancuti, C.O.; Timofte, R.; Vleeschouwer, C.D. I-HAZE: A dehazing benchmark with real hazy and haze-free indoor images. In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems, Poitiers, France, 24–27 September 2018; pp. 620–631. [Google Scholar]
- Ancuti, C.O.; Ancuti, C.; Timofte, R.; De Vleeschouwer, C. O-haze: A dehazing benchmark with real hazy and haze-free outdoor images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 754–762. [Google Scholar]
- Li, B.; Ren, W.; Fu, D.; Tao, D.; Feng, D.; Zeng, W.; Wang, Z. Benchmarking single-image dehazing and beyond. IEEE Trans. Image Process. 2018, 28, 492–505. [Google Scholar] [CrossRef]
- Ancuti, C.O.; Ancuti, C.; Sbert, M.; Timofte, R. Dense-haze: A benchmark for image dehazing with dense-haze and haze-free images. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1014–1018. [Google Scholar]
- Liu, Y.; Zhu, L.; Pei, S.; Fu, H.; Qin, J.; Zhang, Q.; Wan, L.; Feng, W. From synthetic to real: Image dehazing collaborating with unlabeled real data. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event. 20–24 October 2021; pp. 50–58. [Google Scholar]
- Ancuti, C.O.; Ancuti, C.; Timofte, R. NH-HAZE: An image dehazing benchmark with non-homogeneous hazy and haze-free images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 444–445. [Google Scholar]
- Zhang, X.; Dong, H.; Pan, J.; Zhu, C.; Tai, Y.; Wang, C.; Li, J.; Huang, F.; Wang, F. Learning to restore hazy video: A new real-world dataset and a new method. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 9239–9248. [Google Scholar]
- Zhang, Z.; Ma, H. Multi-class weather classification on single images. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4396–4400. [Google Scholar]
- Chu, W.T.; Zheng, X.Y.; Ding, D.S. Camera as weather sensor: Estimating weather information from single images. J. Vis. Commun. Image Represent. 2017, 46, 233–249. [Google Scholar] [CrossRef]
- Lin, D.; Lu, C.; Huang, H.; Jia, J. RSCM: Region selection and concurrency model for multi-class weather recognition. IEEE Trans. Image Process. 2017, 26, 4154–4167. [Google Scholar] [CrossRef]
- Zhao, B.; Hua, L.; Li, X.; Lu, X.; Wang, Z. Weather recognition via classification labels and weather-cue maps. Pattern Recognit. 2019, 95, 272–284. [Google Scholar] [CrossRef]
- Narasimhan, S.G.; Wang, C.; Nayar, S.K. All the images of an outdoor scene. In Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 148–162. [Google Scholar]
- Ancuti, C.O.; Ancuti, C. Single image dehazing by multi-scale fusion. IEEE Trans. Image Process. 2013, 22, 3271–3282. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Karsch, K.; Liu, C.; Kang, S.B. Depth transfer: Depth extraction from video using non-parametric sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2144–2158. [Google Scholar] [CrossRef]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2002–2011. [Google Scholar]
- Kuznietsov, Y.; Stuckler, J.; Leibe, B. Semi-supervised deep learning for monocular depth map prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6647–6655. [Google Scholar]
- Pilzer, A.; Xu, D.; Puscas, M.; Ricci, E.; Sebe, N. Unsupervised adversarial depth estimation using cycled generative networks. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 587–595. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3828–3838. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhang, Z.; Liu, Q.; Wang, Y. Road extraction by deep residual u-net. IEEE Geosci. Remote. Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).