Abstract
Air pollution caused by particulate matter (PM) is a current problem in many cities. With the introduction of strict emission limits and electric cars, lower particle production is expected in the future. However, there are sources of particles that cannot be easily influenced. These include resuspension, where particles deposited on surfaces re-enter the air, causing pollution multiple times. Resuspension can account for up to 18% of the total emissions in some cases. The present paper focuses on the use of the computational fluid dynamics (CFD) tools to describe the flow in a street canyon where resuspension by wind occurs. Based on the calculated flow, a resuspension model is applied to see where resuspension occurs and how far the particles can travel. The shear stresses on the surfaces and the character of the flow field in the boundary layer are evaluated. Different building configurations and flow parameters are tested using a simple 2D model. The model makes it possible to see in which parts of the street canyon resuspension can occur. It shows that the particles leave the street canyon only from the surfaces where the conditions are suitable for resuspension. These particles then enter the mainstream. However, most of the particles stay in the canyon, which can cause resuspension to pollute the air repeatedly. This effect can have a severe impact on human health. The total dispersion of particles in the urban environment is evaluated. The results may be useful for cities that clean the streets, as it is clear which areas will benefit most from the cleaning.
Keywords:
resuspension; particles; PM; pollution; modelling; boundary layer; street canyon; urban environment; CFD; turbulence 1. Introduction
Many populated areas are still facing problems related to the particulate matter (PM or particle) pollution. Traffic and intense human activity are the main sources [1]. The World Health Organization has classified air pollution by particles with a diameter of less than 10 μm (PM10) as the biggest health risk of the 21st century [2]. Domestic fire burning and traffic are responsible for 45% of particle emission in cities [3]. These particles are exhaust related. However, in the future city environment, where motorized cars are replaced with electric cars, and burning of solid fuels is replaced with green technology, a higher proportion of non-exhaust particle sources is expected. The focus should be shifted to these sources producing larger particles [4]. Some sources of non-exhaust particles can be affected by mitigation measures, but the resuspension of particles is not one of them. In this process, strong winds lift previously deposited particles into the atmosphere multiple times [5]. The production of particles in cities, in combination with suitable surfaces, creates ideal conditions for this process. From roads, paved surfaces, and roofs, particles are lifted more easily than in the case of bare soil or green surface [6]. The contribution of wind-induced resuspension to the total pollution is difficult to determine. According to [3], it can reach up to 18% of the total air pollution. In the future, its contribution will only increase.
Wind-induced resuspension was previously studied in a city environment by [6,7,8]. By evaluating long-term data series, these studies can determine when this process starts. The strength of this source can also be determined. There are two components of PM10 concentration in the urban air. The first decreases with an increasing wind speed. The other increases, with its source being the particle resuspension [9]. The threshold wind speed causing resuspension was 1.58 m/s at a 2 m height [6].
The results of these studies are interesting. However, they only give us information about the consequence of resuspension. That is, the increase in the concentration of PM in the air. It is not known from where exactly the particles originate. This information may be important with regard to street cleaning, which many cities are introducing [10,11]. A few details need to be known before regions where the particles are detached are studied. The first detail is the nature of the flow in an urban area. This problem can be solved using detailed computational fluid dynamics (CFD) modelling. The second detail is of the properties of the particles being resuspended. The third point is the nature of the resuspension itself from a microworld perspective.
1.1. Road Dust Characteristics
In cities, various sources produce particles that are later deposited on surfaces. A significant portion of urban surfaces are composed of roads. Particles are, therefore, deposited on roads and adjacent surfaces. The accumulation of particles found on the surface is often referred to as road dust. Based on [12], road dust consists of particles smaller than 10 μm, with significant variabilities in their shape and chemical composition. However, particles in the size range of 10–1000 μm may be found on roads [13], and even < 1 μm [14]. Particles larger than 10 μm are assumed not to contribute to air pollution through the resuspension process [10]. Sources of road dust are: mineral particles—generated by construction activity; exhaust particles—originating from combustion or industrial processes; brake and tyre wear particles—generated by traffic itself [12]. These particles are subject to wind resuspension when the conditions are suitable. The properties of road dust vary considerably depending on the location where the dust is collected. Study [15] determines the density of this dust to be 1.3–1.7 g/cm3; [13] reports the value of <1.9 g/cm3; [16] reports a range of 1.7–1.9 g/cm3. Due to the varying ranges of particle sizes forming road dust, particle density decreases with a decreasing particle size [16]. Thus, for particles in the PM10 class, a density of 1.3 g/cm3 is the most likely. These particles are exposed to the flow and can potentially be resuspended.
1.2. Microworld of Particles
1.2.1. Determining the Threshold Friction Velocity
The removal of particles from surfaces takes place in the particle microworld. There are two approaches to defining this process. The first is an experiment; the other is an analytical model. Resuspension models describe the behavior of particles as they are separated from surfaces. The removal process has two phases. The first is a phase where the forces acting on the particle overcome the binding forces; the other phase is the subsequent motion of the particle near the ground [17]. There is a consensus that the most common form of breaking the bond is rolling. After breakage, the particle can be lifted from the surface, roll over the surface, or slide over it [18]. The input to the model is a description of the flow over the surface. The flow is reflected on the wall in the form of shear stresses, variable in space and time [19]. The shear stresses on the wall create drag and lift forces on the particle. Usually, wall shear stresses are used in a parameter called the friction velocity . There is a threshold value of friction velocity , when the particles leave the surface. The friction velocity is defined as [20]:
where [kg/m3] is fluid density and [Pa] is wall shear stress, which is proportional to the velocity gradient normal to the wall multiplied by a viscosity [Pa∙s], following [20]:
The result of these models is a mathematical dependence showing the amount of particles separated at a certain flow velocity [21]. However, these models have their limitations, and are therefore difficult to apply to urban dispersion models. As stated in [22], the description of surface roughness is the biggest limitation of the application of these models. Surface roughness is the most important parameter affecting resuspension [23].
Particle resuspension is also well described by experiments. The result of the experiments is the actual emission of particles from surfaces [24]. This approach contains factors that the analytical models of resuspension simplify. These may include surface roughness or the presence of turbulent flow [25]. As with analytical models, experiments are used to determine the threshold friction velocity. In the case of wind tunnels or urban flow, can be determined from the following relationship at the moment when resuspension begins to occur [26]:
where [m/s] is the flow velocity at a certain height above the surface. [-] is the Karman constant. [m] is the height above the surface, [m] is the height of the surrounding obstacles, and [m] is the surface roughness height.
Several studies have investigated resuspension in wind tunnels. Ref. [27] investigated a concrete surface with PM10 particles and reports the value of = 0.1 m/s. Ref. [28] used grassy surfaces and found the value of = 0.3 m/s. Ref. [29] reports a value of = 0.8 m/s for bare soil. Ref. [24] gives a range of values for volcanic ash, = 0.13–0.38 m/s. Ref. [30] derived an analytical relationship for for different particle sizes. For PM10, the value is m/s. This relationship was derived from measurements on volcanic ash. Ref. [31] made use of the relation derived from [32], which can be defined as follows:
where [kg/m3] is particle density, [m/s2] is acceleration due to gravity, [m] is particle diameter, [kg/m3] is fluid density, and [kg/s2] is the cohesion parameter between 1.65 × 10−4 and 5 × 10−4 kg/s2. Sand dune dust was studied by [33], which gives a value of 0.318–0.483 m/s depending on the surface humidity. Thus, it is evident that several studies have been devoted to the determination of in the past.
There is another group of studies addressing the resuspension of particles directly in the city. Based on the evaluation of particle concentration measurements, it is possible to evaluate . Ref. [6] reports a value of m/s (specifically 0.11, 0.21, 0.16, 0.13 m/s). Similar values were also derived by [7,9]. These studies are highly valuable as they focus on the PM10 fraction and urban environments with the presence of different surfaces and flow turbulence.
1.2.2. Emission Factor of Resuspension
The value of is a variable in the flow field. After exceeding , the particles begin to detach from the surface. As increases, the amount of particles separated also increases, as long as enough particles are available [19]. The determination of the resuspension emission factor can be based on analytical models. However, these models do not give a specific amount of the particles separated [19,21]. Only a percentage value of particles that have overcome the adhesion forces is given. Overcoming the adhesion forces does not mean that the particle will lift off the surface [33]. For this reason, it is better to rely on experiments performed in wind tunnels. These give a direct correlation with and the amount of particles separated. These particles have left the surface. Ref. [26] derived an empirical relationship expressing the quantity of the resuspension rate Λ [1/s] based on several wind tunnel studies. This represents the rate of resuspension from the surface, divided by the initial surface concentration variable in time. Therefore, it is only time dependent. The relationship is as follows [26]:
The initial surface concentration (called slit load or sL) can be set on the basis of US-AP-42 at sL = 0.1 g/m2 on a road with 5000 vehicles passing per day. Li et al. [34] report the value of sL = 0.6–7.6 g/m2 in the size range of less than 75 μm. In the 10 μm fraction, the sL value is smaller. Alves et al. [35] report the value of sL= 0.19–1.2 g/m2 for road and paved surfaces. A value of sL = 0.8–8.8 g/m2 for urban surfaces was defined by Padoan et al. [36]. The final emission from the surface depends on the size of the surface and the time period.
1.3. Modelling of the Pollution Dispersion in a City Environment
The urban street canyon is a well-known and well-studied case in CFD. It is mostly used to study pollutant dispersion in cities. A street canyon consists of at least two buildings with the height H [m], separated by the width W [m], with the length B [m], as depicted in Figure 1. Different H/W configurations are used across the studies [37,38,39]. Different flow regimes were described inside the street canyon for different H/W [40].
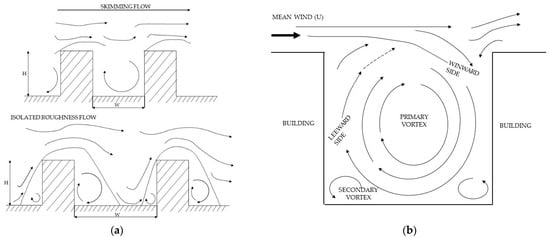
Figure 1.
(a) Different flow regimes for various H/W configurations, according to [39]. (b) Detailed description of the canyon vortex, according to [40]. Lines are representing flow streamlines.
The flow inside the street canyon is three-dimensional. Based on [37], the 3D effects of air flow in a street canyon can be neglected if B/W is larger than 20 for H/W = 1 and 50 for H/W = 2. Many studies state that by replacing 3D simulations with 2D, a lot of information related to turbulence is lost [40,41]. The standard geometry used for CFD street canyon studies are H/W = 1 [37,42], H/W = 2 [38] and other, site specific types [43,44]. Different configurations result in various flow regimes, as depicted in Figure 1. Different numbers of street canyons are used in the studies. To achieve a steady state, a higher number of street canyons is recommended. This is due to the fact that the influence of the upstream building cannot be ignored [45]. Air flow in the canyons, following the fourth canyon, can be considered to be unchanged and stable [46].
Both Reynolds-averaged Navier–Stokes (RANS) and large eddy simulation (LES) approaches are used in CFD for street canyon studies [47]. Among the RANS approaches, the k-ε turbulence model gives good results when compared to the experiments [48]. Wind speeds up to 5 m/s are used at the height H at the inlet [49]. This can be relatively low compared to the studies dealing with resuspension in cities. To start the resuspension, higher wind speeds are necessary [7]. Dominantly, traffic related emissions were studied as the source of particles [42,50].
Resuspension had never been studied as the source of particles in a street canyon. The question is, under what flow conditions does resuspension occur? How do the inlet wind speed and different H/W configurations affect the surface from which particles are separated? Across the studies dealing with resuspension, it is still unknown where particles travel after separation. This will be the subject of this study.
2. Materials and Methods
2.1. Description of CFD Model
2.1.1. Computational Domain and Grid
A simplified 2D model was created to simulate the flow in an urban environment. The street canyon is assumed to be long enough to neglect the 3D edge effects [37]. The studies available use a wide range of geometric models, i.e., the H/W ratios. The resuspension and subsequent dispersion of particles can be different for different geometrical configurations. Four configurations, H/W = 2, H/W = 1, H/W = 0.5, and H/W = 0.25, were developed. To maintain the dimensional ratio between the particles and the real environment, all the models were modelled with H = 10 m. The height of the domain was 10 × H, the upstream distance was 5 × H, and the downstream distance was 10 × H. This is in correspondence with [42,43]. The influence of the upstream building cannot be ignored [45]. Following the fourth canyon, the flow can be considered to be unchanged and stable [46]. For the cases with H/W = 2, H/W = 1, H/W = 0.5, nine street canyons were modelled. For the case H/W = 0.25, only seven street canyons were modelled. This is due to the 500 m domain size limit in the STAR CCM+ software, version 1st January 2022 (17.02.008-R8).
The resuspension process is dominant in the wall-adjacent region. Additionally, at high wind speeds, flow separation on roof edges is expected. Inside the street canyon, flow is expected to be affected by turbulence within the boundary layer [51]. Turbulence within the boundary layer significantly affects resuspension [52]. An unstructured mesh consisting of polygonal elements was created. A fine mesh was created at the bottom of the street canyon, where resuspension occurs, following [19]. From the bottom surface, the cell size gradually grows in the computational domain. The creation of prism layers was most important. The minimal cell surface size, the thickness of the prism layer near the wall, the number of prism layers, their stretching, and the total thickness of the prism layers were specified in the mesh design tool. The process of mesh creation was iterative. It involves computing the simulation and mesh refinement several times to obtain the final value of y+. The mesh was designed to reach y+ < 5 in the regions of interest. The first cell of the mesh is located in the viscous sublayer of the boundary layer, as stated in [53]. The created mesh has the following parameters. The first cell of the boundary layer had a height of 8 × 10−4 m. A total of 8 prismatic layers were used with a total thickness of 0.024 m. The target surface size was 0.008 m; the minimum surface size was 0.004 m. Beyond the boundary layer, the cell growth rate was 1.05. This provided sufficient refinement of the mesh within the street canyon and around the roofs. Further refinement was not necessary. The mesh parameters were constant across all the cases. The total number of cells ranges from approximately 1.3 million to 2 million across the cases.
2.1.2. Boundary Conditions
The bottom of the domain was treated as a no-slip wall. In this CFD study, the walls are treated as smooth walls with no characterization of surface roughness. The surface roughness effect on particle resuspension is reflected in the value of . In the RANS simulations, automated wall treatment is applied to the wall surfaces. Due to the varying value of y+, all y+ wall treatment was applied. This approach chooses the most accurate wall function based on the y+ value. The values of y+ in the region of interest are below 5, so the wall functions are only approximating the velocity profile in the viscous sublayer.
The outlet of the domain is treated as a zero-gradient outlet. The top of the region is defined as a symmetrical plane. The inlet boundary is defined as a velocity inlet. There is no consensus on how the velocity profile should be defined. Uniform profiles, power law profiles, or logarithmic law profiles are widely used. For this study, a power law profile following [54,55] was chosen, defined as:
where [m/s] is the velocity at the reference height [m], z [m] is the vertical coordinate, and n [-] is the power law parameter in which the surface roughness is included. The value of n can reach 0.2–0.26 [37,54]. The value chosen was 0.21. This profile fits the experimental data by [47]. The value of with also varies across the studies. It can range from 3.8 to 4.32 m/s [56]. Wind-induced resuspension is expected to happen in severe wind conditions. Therefore, four cases were considered, with for each geometry. The turbulence intensity was set to 1.8% according to [20] for open atmospheric flows.
2.1.3. Solver
The commercial software Star CCM+ (version 1 January 2022 17.02.008-R8) was employed. To simulate particle resuspension, multiple additional user-defined field functions were used. The 2D steady RANS equations were solved with a chosen turbulence model. A two-equation eddy-viscosity model was applied. Namely, the shear stress transport (SST) k-ω model [57]. Ref. [42] found that the k-ε model is more accurate than the SST k-ω model when comparing the experimental data. In [51], it was stated that only the LES turbulence model can match the experimental data. Those studies were conducted at much lower wind speeds compared to this study. When the inlet wind speed reaches 5, 7.5, 10, and 12.5 m/s, flow separation and re-entrainment is expected in the street canyon [51]. It is well-known that the standard k-ε model under-predicts the separation and reattachment zones [58]. In those cases, the SST k-ω model can resolve these zones more accurately, which is crucial for wall shear stress prediction [59,60,61,62]. Therefore, the SST k-ω model of turbulence was applied to all the cases. The SIMPLE algorithm was used for pressure-velocity coupling, following [42,51,60], and the author’s experience with the case. Second order interpolations and discretization schemes were used. The solution was considered to be converged when all of the residuals reached its minimum value. The minimum values of residuals vary, 10−10 for Sdr, 10−9 for Tke and continuity, 10−7 for X and Y momentum, 10−4 for intermittency (20,000 iterations were made). The values of residuals were almost identical across the cases. The value of y+ varies in the computational domain. In the region of interest, the bottom of the street canyon, the y+ values were below 5. The mesh was specifically designed to obtain this value. This means that the first layer of the mesh is in the viscous sublayer. This setting is necessary for the resuspension, and for particle transport to be resolved sufficiently [19]. In the region outside the street canyon, y+ reached higher values, still lower than 100 (mean y+ < 10 for roofs, mean y+ < 120 for the region before the array of street canyons, mean y+ < 240 for the region after the array of street canyons). Therefore, all y+ wall treatment was applied so the solver could choose the most accurate wall function.
2.2. Particle Resuspension Model
It is clear from Section 1.2.1 that the analytical resuspension models are not suitable for application to the dispersion models. This is mainly due to the fact that they require an overly detailed description of the surface roughness [33]. The results obtained in the experiments can be applied. To apply the resuspension model to CFD, two things need to be known. The first is the threshold friction velocity, and the other is the resuspension emission factor.
Various studies refer to threshold friction velocities, giving different values. This is due to the variety of the phenomena studied. Studies such as [24,31,33] cannot be used for resuspension in the urban environment. Multilayer particle deposits were studied here. The adhesion force in multilayer deposits is different from smaller particle clusters [62]. To determine the value of the threshold friction velocity, studies such as [6,27] can be used. The average threshold friction velocity is then = 0.142 m/s. Particles will be introduced on surfaces where the value of is exceeded.
The resuspension emission factor is determined from Equation (5). The value of sL is a highly variable value [63]. Based on studies [34,35,36] and US-AP-42, the value can be estimated as sL = 2.423 g/m2. Since a 2D simulation was created, the area where resuspension occurs does not have a second dimension. It is, therefore, a line source. To make the particle source real, it is necessary to estimate the second dimension. The particle source is in the boundary layer, and the surface cell is very small. The second dimension can be estimated at the same value as the dimension of the surface cell. Then, the surface area of one cell is S = 6.4 × 10−5 m2. The resulting emission from one surface cell is then equal to:
2.3. Descritpion of Multiphase Flow
To track the motion of particles or determine their dispersion characteristics, a Lagrangian approach is used. The Lagrangian approach gives information about the motion (trajectory, velocity) of each single particle. It is preferable if the location from which the particles are separated and the motion they make afterwards are examined. The phase (particles) is modelled as particle-like elements, known as parcels, dispersed in the fluid continuum. The particles, thus, do not represent a continuous phase. The use of parcels improves the efficiency of the solution. A smaller number of parcels represents the total population of dispersed phases. Each parcel represents a localized group (cluster) of dispersed phases having the same properties. Therefore, parcels with different mass contain a different number of the same particles.
Particles are released from the surface, where is exceeded with a magnitude corresponding to Equation (7). After overcoming the bounding forces, the particle velocity is small. It can be assumed to be zero [64], while the initial position of the particles is one diameter above the ground. This value is so small that the CFD simulation could not fully resolve this size range. However, the experimental data are used to model resuspension. In those experiments, particles are lifted from the ground and measured in a wind tunnel or real environment. That means that the particles leave the surface and enter the free stream. Therefore, the particle motion near the wall, after overcoming the bounding forces does not need to be included. This process is complex and yet, not fully applicable to CFD models [65]. The initial particle position is still considered to be as low as possible. A source of particles was considered to be the centroid of the first cell, 0.0004 m above the surface, where was exceeded. This ensures that the flow inside the street canyon can carry the particles away.
Separate models were used within CFD to describe the behavior of the particles. They were treated as material particles with properties corresponding to road dust (spherical particles with constant density, size 10 μm). Drag force [66] and lift force [67] were chosen as the forces acting on the particles. Boundary sampling and track file have been added because of the multiphase simulation evaluation. Position, velocity, mass, and other additional variables are captured. Two-way coupling was not added to the solution. The flow is not expected to be influenced by the particles. Interaction between the particles and the walls is modelled in two different ways. With surfaces where the value of is exceeded, particles can rebound from the wall. This is consistent with [33]. For these surfaces, forces acting on the particles are high enough, so the particles will not stick to the ground. For all other surfaces, interaction is modelled as “escape”. This means that if the particle touches the wall, it is removed from the simulation with its position captured.
A turbulent dispersion model was used to solve the particle interaction with turbulent eddies, which are not modelled by the RANS approach. A particle in a turbulent flow experiences a randomly varying velocity field to which it responds according to its inertia [68]. This field can be described as [68]:
where u [m/s] is an instantaneous velocity, [m/s] is the mean velocity computed by the RANS approach, and [m/s] is eddy velocity fluctuation. Here, an eddy is a local disturbance to the Reynolds-averaged velocity field. The particle remains in the eddy until either the eddy time-scale [s] is exceeded, or the separation between the particle and the eddy exceeds the eddy transit time [s]. The velocity fluctuation is a normal deviate with zero mean value and a standard deviation that comes from the eddy velocity scale [68]:
The turbulence model provides the length and timescales of the turbulence, [m] and [s] based on the model used. Their ratio is proportional to (k is turbulent kinetic energy [J/kg]), which is a variable calculated in a k-ω turbulence model. This model was widely used when predicting pollutant dispersion in a city environment [42,69,70].
Due to the use of a steady state simulation, it is not possible to directly track the particles over time. The particles are injected into the simulation in a single substep. In this step, their trajectory is calculated based on the computed flow field. The calculation of the particle motion is iterative. The maximum residence time of the particles in the domain is set to 100,000 s. This value is selected because of the certain amount of time required for the particles to disperse, since their initial position and velocity are very low. It is also selected because of the circulation zones in which the particles are located (street canyon vortex). The maximum residence time is expected to be much lower. The maximum number of steps to calculate the particle position is set to 100,000. The 2nd-order tracking integration method was used.
2.4. Evaluation of the Model
When the solution reaches its steady state and the residuals reach the minimum value, the model is evaluated. First, the wall shear stresses on the ground of the street canyon are evaluated. The results are compared with to determine the surface where resuspension takes place. After this, a specific single street canyon is selected to be the source of resuspended particles. The decision is made based on the fact that the influence of the upstream building cannot be ignored [45]. In a certain street canyon, the street canyon vortex can be considered to be stable [46]. When the street canyon is selected, particles are introduced to the solution. It is tracked where the particles travel after separation. It is evaluated how many particles remained in the selected street canyon, how many entered the following canyons, and how many left the whole domain. After this, the model is validated against available studies dealing with resuspension in a city environment.
3. Results
3.1. Flow Field Evaluation
Four different geometry configurations with four different flow regimes were tested in this study. In all the cases, after 20,000 iterations, the solution was stable and converged. The minimal values of the residuals vary. They are 10−10 for Sdr, 10−9 for Tke and continuity, 10−7 for X and Y momentum, and 10−4 for intermittency. The residual values were almost identical across the cases. In the region of interest, the bottom and the sides of the street canyon, the y+ values were below five. This means that the first layer of the mesh is in the viscous sublayer of the boundary layer. In the region outside the street canyon, y+ reached higher values, still lower than 100 (y+ < 10 for roofs, y+ < 120 for the region before the array of the street canyons, mean y+ < 240 for the region after the array of the street canyons). The values of y+ vary only for different flow regimes. This is further specified in the next table.
In all the cases, a single street canyon vortex was formed. There is no evidence of different flow regimes shown in Figure 1a. In each case, the flow looked like in Figure 1b with the main street canyon vortex and two smaller edge vortexes. Across an array of nine street canyons, the flow has different characteristics. In the first three canyons, the influence of the upstream building and unstructured flow was evident. In the remaining cases, the flow was steady and corresponded to the flow regime described by [39].
To quantify the resuspension process, the value of the wall shear stress of friction velocity is required. Based on Section 2.2, the threshold friction velocity is = 0.142 m/s. Inside the street canyon, the wall shear stresses are governed by the street canyon vortex. This vortex produces the vertical velocity gradient near the wall, which results in wall shear stress production. The highest values of WSS are expected in the center of the street canyon. The following figure displays the friction velocity values on the surface of the street canyon.
It is evident from Figure 2 that some configurations are missing. The geometrical configuration with H/W = 2 is not displayed here. This is because in no flow regime, even with = 12.5 m/s, did the value of exceed . The values were not even close to the threshold friction velocity. The shape of the friction velocity profile in the street canyon for H/W = 2 was similar to the other cases. What is also missing are the flow regimes with = 5 m/s. In those cases, the value of did not exceed . For all the configurations, starts exceeding the for = 7.5 m/s, however, not in all the canyons. In the cases where was not exceeded, the evaluation of resuspension was not possible. These cases are not further evaluated.
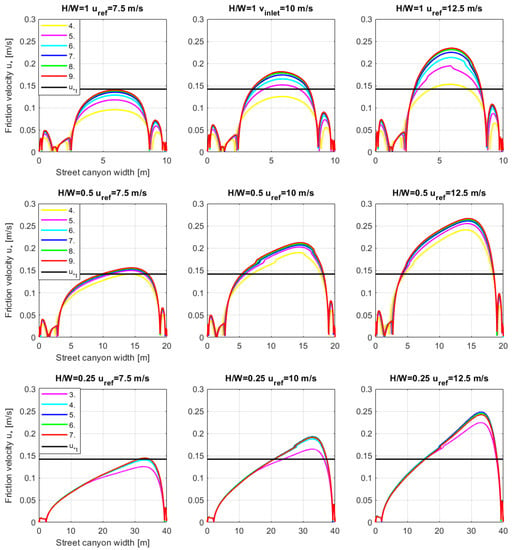
Figure 2.
Friction velocity profile in a particular street canyon (indicated by a sequence number) in the street canyon array. Different geometry and flow configurations are displayed. The threshold friction velocity is also displayed.
The friction velocity profile inside the street canyon indicates that there are a few vortexes. The main street canyon vortex covers most of the street canyon width. Then, there are two smaller vortexes formed on each of the leeward and windward sides of the canyon for H/W = 1 and H/W = 0.5. For H/W = 0.25, only one smaller vortex is formed on both sides of the canyon. Those vortexes were evident across all the flow regimes, confirmed by [71]. The peaks of the friction velocity are not located directly under the center of the vortexes, as displayed in Figure 3. There are two vortexes on the leeward side of the canyon (left), but there are three significant peaks of . The peak of produced by the main street canyon vortex is positioned slightly to the windward side (right). The higher the inlet wind speed, the higher the offset of the peak. Only the main street canyon vortex can generate friction velocity high enough to induce the resuspension process.
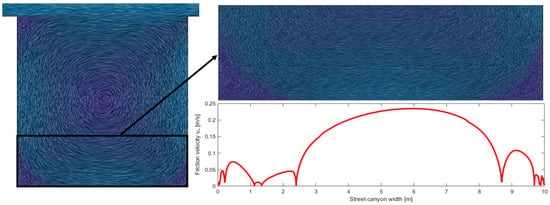
Figure 3.
Detailed view of the bottom of the street canyon (H/W = 1, = 12.5 m/s, 6th canyon), where the vortexes and the corresponding friction velocity are visible.
To evaluate the resuspension, needs to be exceeded [17]. For H/W = 2 and all the flow regimes, this requirement was not met. For the flow regime , was barely exceeded. Therefore, only the configurations H/W = 1, 0.5, 0.25, and the flow regimes were evaluated for resuspension. A representative single street canyon needs to be selected to be the source of the resuspended particles. Only one canyon is the source of the particles. Otherwise, the results would be diverse as the dispersion and deposition of particles would mix. It can be seen in Figure 2 that the friction velocity profiles in the canyons vary. They increase with each additional canyon. For H/W = 1, 0.5, the friction velocity profiles are not very different from the seventh canyon. For H/W = 0.25, this trend is visible from the fourth canyon. For comparison purposes, the seventh canyon was selected for H/W = 1, 0.5, and the fifth canyon for H/W = 0.25. This leaves two street canyons, three buildings, and the outer region for particle dispersion.
3.2. Particle Dispersion after Resuspension
With an increasing wind speed, the friction velocities at the bottom of the canyons rise. Therefore, both the source strength and the source dimension rise too. Part of the street canyon bottom surface, where was exceeded, serves as the particle source. Its magnitude corresponds to the friction velocity, as identified in Section 2.2. When the particles (parcels) are released into the flow field, they are carried away as described in Section 2.3. The contact between the particles and the wall is modelled in two ways. Where is exceeded, the particles are reflected from the wall. Otherwise, they are trapped on the wall. The position where the particles impact the wall is captured. Because of the Lagrangean approach, concentrations cannot be directly computed. Evaluation of the concentration field is not the subject of the study. The aim is to define the locations where particles are resuspended and where they are carried after resuspension.
In a steady state simulation, information about the incident mass on the surfaces is the result. No time-dependent variables are calculated, as particles are released in one substep. The results then represent a steady state going on for a long time. The total mass of the particles hitting the walls then has the dimension of [kg/s]. Resuspension is a process with strong time dependence [72], which is reflected in Equation (7). The time dependence of the resuspended mass would be visible in an unsteady simulation. Because of this, only the percentage value of the total particle mass dispersed and deposited is evaluated. The percentage is determined by the total amount of particles injected into the simulation. The results show that the particles released from the point with a higher friction velocity behave differently than the other particles.
Particle motion is defined by the computed RANS flow field and the turbulent dispersion model. Due to the turbulent dispersion model, the particles cross flow streamlines. Particle dispersion in the street canyon is displayed in Figure 4. The particles mostly follow the general shape of the street canyon vortex. Most of the particles stay very close to the ground. They are deposited even when they are positioned in the location where was exceeded. This is partly due to turbulence, which directs their initial motion towards the ground. Afterwards, the particles have very low velocity, not being able to continue in their motion. Figure 4 shows that the particles which originated in locations with low (marked as blue, which means that a parcel contains only a small number of particles) are subjected to early deposition. The opposite is true for the particles which originated in a location with high (marked as red). Those particles are dispersed and deposited in the rest of the domain. A significant surface, where the particles are deposited immediately, is the leeward side of the canyon. The rest of the particles stay in the canyon or leave the canyon. The particles can be present inside the canyon for a considerable amount of time. Across the cases, the maximum residence time inside the canyon was roughly between one and two minutes. It is worth noticing that the particles that leave the street canyon stay in the domain for a shorter period.
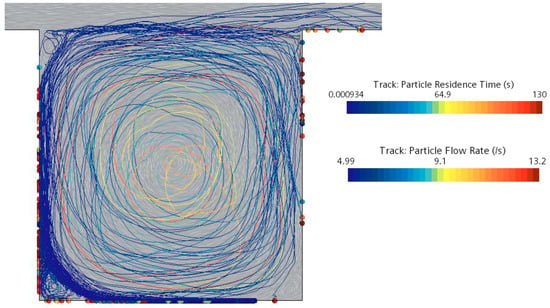
Figure 4.
Particle dispersion and deposition inside the street canyon (H/W = 1, ). The points on the street canyon surfaces represent the deposited parcels (particles) with a different mass (or number of particles). The lines represent particle tracks. On these lines, the particle residence time is displayed.
Within the first street canyon, the particles are dispersed to other parts of the domain, with those being the roofs of the consequent buildings, street canyons two and three, and the outlet. The number of particles released from the first street canyon is significantly low. The total dispersion is displayed in Figure 5.

Figure 5.
Particle dispersion and deposition in the computational domain (H/W = 0.5, ). The points on the surface represent the deposited particles and the lines represent the particle tracks.
The deposition of particles in the domain is slightly different for each configuration. The percentage of particles deposited in different parts of the domain is evaluated in Figure 6.
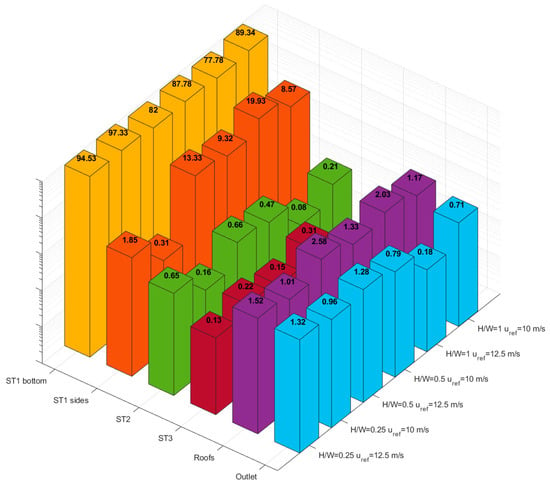
Figure 6.
Percentage of the particles (expressed as mass) deposited in different locations in the domain for all the geometrical and flow configurations. The abbreviation ST stands for street canyon. Note the logarithmic Z scale. This is due to large differences in the percentage of particle dispersion in the domain. For H/W = 1, no particles were deposited in ST3.
It is evident that most of the particles are deposited on the ground of the first street canyon. The particles released from the parts where has a lower value are also showing the minimal residence time. The second highest value of the deposited particles is on the sides of the street canyon. A significant amount of particles are also deposited on the roofs and the outer region. Fewer particles made it to the second and third street canyon. With an increasing wind speed, more particles are dispersed outside the surface. Additionally, more particles are deposited on the sides, the second street canyon, roofs, and the outer region. An exception is the configuration H/W = 1, where with an increasing wind speed, the amount of particles in the second canyon and the outer region decreases. This shows that, in almost every case, a higher wind speed causes better ventilation of the canyon. Ventilation can be expressed as the amount of particles (here, originated in resuspension) leaving the first street canyon. This was also confirmed by [38]. More interesting are the results of the geometric configurations. A more open street canyon should be better ventilated. In connection with resuspension, the opposite is true. The H/W = 0.25 configuration has the highest number of particles deposited on the street canyon ground. It also has the lowest number of particles deposited to the sides of the canyon. Overall, H/W = 1 has the worst ventilation. On the other hand, the H/W = 0.5 configuration is ventilated the most. In terms of the total particle concentration, the worst case is where the largest amount of particles is released. This case is the H/W = 0.25 configuration, where the surface available to resuspension is the greatest. The particles which originated in the resuspension remain dominant in the first street canyon. The ventilation rate of the first street canyon ranges from 2.09–4.67%.
3.3. Model Validation
Validation of the flow is problematic. No experimental data are available for the wind speeds and geometrical configurations in this study. In addition, a different turbulence model was chosen compared to other simulation studies [48]. The only factor that can be validated is the threshold friction velocity. The experimental results give information about the flow velocity within the urban environment during resuspension, especially at the beginning. Ref. [6] reports a value of 1.58 m/s at a 2 m height. Refs. [7,9] report 1.5 m/s at a 3.3 m height. These velocities can be extracted from the simulation and used for validation, as depicted in Figure 7.
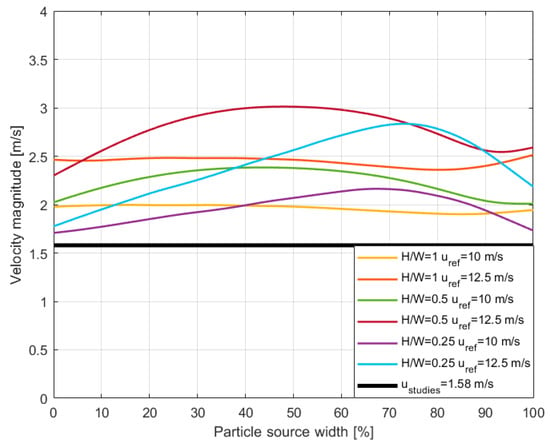
Figure 7.
Velocity magnitude at a height of 2 m in all the simulated cases, above the surface where was exceeded. For the purpose of comparison, the source width is expressed as a percentage.
The velocity at a 2 m height in the simulations was higher than the velocity reported by studies [6,7,9]. Therefore, the particle source is set correctly. The velocities inside the street canyon were in the velocity interval where resuspension should be evident. The strength of the source can be validated too. With an increasing wind speed, the amount of particles should increase exponentially. However, for each case, only two flow regimes were computed. More flow regimes would be needed to validate the source strength. Additionally, a 3D simulation would need to be performed. Particle tracking would be very difficult to validate in real environments. There are many sources of particles, in addition to resuspension. This is further discussed in the following chapter.
4. Discussion
Constructing a suitable mesh was crucial for the simulation. The mesh needed to be fine enough to resolve the boundary layer. The flow structures in this region greatly affect the resuspension process [53]. The mesh of the domain was designed to meet the y+ < 5 criterion. This value means that the first cell is located in the viscous sublayer of the boundary layer [54]. The influence of turbulence will extend into the boundary layer for the simulated cases [51]. Based on the values of y+ summarized in Table 1, it is visible that this criterion was met. A higher value of y+ (still less than 10) was reported on the roofs. In this simulation, the roofs are not sources of particles. Therefore, the mesh in these regions does not need to be fine.

Table 1.
Mean values for y+ for the bottom, the side walls, and the roof surfaces in the street canyons. Note that the y+ value was evaluated for the fourth and the following street canyons because the influence of the upstream building in the first three canyons was evident, and they are not subjected to the evaluation.
In all the cases, the street canyon vortex, as depicted in Figure 1b, was visible. As [39] suggested, for wider street canyons, different flow regimes should be present. However, in previous studies, lower wind velocities were used. At higher speeds, the street canyon vortex is evident, as suggested by [71]. The flow regime inside the street canyon then produces wall shear stresses on the surface. The results show that for all the geometrical configurations and = 5 m/s, was not exceeded. The same is true for = 7.5 m/s, where the friction velocity barely reaches the threshold. Resuspension of particles was evident for = 10, 12.5 m/s. This is in correspondence with studies [6,7,9], which revealed that higher wind speeds are needed to start the resuspension process. The areas where was exceeded are located near the center of the street canyon. This shows that roads, not sidewalks, are subjected to the wind-induced resuspension process. Surprisingly, the highest values of were evident for the H/W = 0.5 configuration. This configuration is therefore considered to be ideal for forming a street canyon vortex [39]. The influence of the upstream building is evident in the first three canyons. After the fourth canyon, neither the flow nor the WSS changed very much, which is in correspondence with [45,46].
Particle dispersion has its own patterns. Particles that are released in the parts where has a lower value are subjected to early deposition. This can be due to the turbulent characteristics of the flow near the wall [33]. In this region, the flow does not have the power to carry the particles off the ground. These regions are located at the lower side edges of the street canon vortex. In the locations where has a higher value, the particles are carried off the ground. This region is located just under the street canyon vortex. We can then say that the particles released just under the street canyon vortex are dispersed in the flow, while the particles released from the lower side edges of the vortex are subjected to creeping motion. During the creeping motion, the particles rebound from the surface and travel to the side of the street canyon. This leads to the accumulation of particles on the sides of the street canyon. In addition, the particles also collide with the walls of the canyon. These can then fall to the bottom, adding to the particle accumulation. Particle accumulation on the sides of the street canyon was confirmed experimentally [73] and numerically [74]. In general, particle accumulation on the sides of the canyon occurs for each particle source. Traffic contributes significantly to this [42,50]. Wind-induced resuspension is, therefore, of a similar nature.
The particles which travel outside the street canyon are subjected to long-range transport. Most of these particles collide with the roofs. These particles can be easily resuspended again [6]. A considerable amount of particles leaves the array of street canyons. These results confirm the claims stated in [3] that resuspension is a considerable source of particles in cities. In the future environment, its contribution to the total concentration will only increase [1]. It was also confirmed that higher wind speeds lead to better ventilation of the street canyon [38]. A general assumption of better ventilation with a more open street canyon was not confirmed. The case with H/W = 0.5 showed the highest amount of particles leaving the street canyon. This case also has the most developed street canyon vortex. This claim is consistent with [39]. Here, it is stated that there is a combination of geometry and wind speed at which the street canyon vortex has ideal conditions for formation. The formation of a vortex then leads to better ventilation. This information is only valid for percentage values of particle dispersion. The total concentration is higher for cases where there is a larger source of particles, i.e., a wider street canyon.
Validation of the presented results is problematic. The first problem is validation of the flow. For the wind speeds at which resuspension occurs, data from experiments performed in wind tunnels are not available. Additionally, a different turbulence model was chosen than that usually used in studies [48]. The model is validated only against the wind speeds at which resuspension in the street canyon was evident. This confirms that the value was determined correctly. Another validation option would be to determine the strength of the particle source. As the wind speed increases, the amount of particles should increase exponentially [7]. Due to the use of 2D simulation and the few cases where resuspension occurred, this cannot be used. Particle tracking in real situations is very difficult, almost impossible to measure. Therefore, it would be difficult to prove the results of the study experimentally. The study confirms that, due to the wind-induced resuspension, the particles are transported to the sides of the street canyon [74]. It was further confirmed that the particles which originated in resuspension dominantly remain inside the street canyon, while some particles are subjected to long-range transport [9]. Through detailed modelling, the general conclusions of experimental studies dealing with resuspension were confirmed.
5. Conclusions
In this study, wind-induced resuspension was modelled using CFD. This model included urban geometry, a fluid flow model, and a particle resuspension model. The inputs to the model were determined based on a combination of available studies. The results showed that higher wind speeds are needed to start the resuspension process. With a 5 m/s inlet wind speed, resuspension did not start for any geometrical configuration. The inlet wind speed of 7.5 m/s can be considered to be the starting wind speed for resuspension. It was the inlet wind speeds of 10 and 12.5 m/s at which resuspension was clearly evident for all the cases. It was proven that most of the particles, after being resuspended, stay on the street canyon ground. The configuration with H/W = 0.25 had the highest proportion of particles deposited on the ground. Only 2.09–4.67% of the resuspended particles leave the first canyon across all the cases. The most open canyon did not have the best ventilation. The largest number of particles left the canyon with H/W = 0.5. This configuration also had the maximum values of friction velocity on the ground. This means that the canyon where the street canyon vortex has ideal conditions for its formation is better ventilated. It was also proven that resuspension also contributes to long-range transport of the particles. However, since the resuspended particles mostly stay in the canyon, resuspension can cause pollution repeatedly. Therefore, it is a considerable source of particles, severely affecting the human health.
Author Contributions
Conceptualization, J.L. and J.P.; methodology, J.L. and J.P.; formal analysis, K.K., investigation, J.L.; resources, J.L. and K.K; data curation, J.L. and K.K.; writing—original draft preparation, J.L. and J.P.; writing—review and editing, K.K.; visualization, K.K.; supervision, J.P.; project administration, J.L. and K.K; funding acquisition, J.P. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by projects of Brno University of Technology: FAST/FSI-J-22-7905, FSI-S-20-6280.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moreno-Ríos, A.L.; Tejeda-Benítez, L.P.; Bustillo-Lecompte, C.F. Sources, Characteristics, Toxicity, and Control of Ultrafine Particles: An Overview. Geosci. Front. 2022, 13, 101147. [Google Scholar] [CrossRef]
- World Health Organization. Ambient Air Pollution: A Global Assessment of Exposure and Burden of Disease. Clean Air J. 2016, 26, 121. [Google Scholar] [CrossRef]
- Karagulian, F.; Belis, C.A.; Dora, C.F.C.; Prüss-Ustün, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to Cities’ Ambient Particulate Matter (PM): A Systematic Review of Local Source Contributions at Global Level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Alves, C.A.; Vicente, A.M.P.; Calvo, A.I.; Baumgardner, D.; Amato, F.; Querol, X.; Pio, C.; Gustafsson, M. Physical and Chemical Properties of Non-Exhaust Particles Generated from Wear between Pavements and Tyres. Atmos. Environ. 2020, 224, 117252. [Google Scholar] [CrossRef]
- Zheng, G.; Li, P. Resuspension of Settled Atmospheric Particulate Matter on Plant Leaves Determined by Wind and Leaf Surface Characteristics. Environ. Sci. Pollut. Res. 2019, 26, 19606–19614. [Google Scholar] [CrossRef] [PubMed]
- Linda, J.; Pospíšil, J.; Köbölová, K.; Ličbinský, R.; Huzlík, J.; Karel, J. Conditions Affecting Wind-Induced PM10 Resuspension as a Persistent Source of Pollution for the Future City Environment. Sustainability 2022, 14, 9186. [Google Scholar] [CrossRef]
- Kassomenos, P.; Vardoulakis, S.; Chaloulakou, A.; Grivas, G.; Borge, R.; Lumbreras, J. Levels, Sources and Seasonality of Coarse Particles (PM10–PM2.5) in Three European Capitals-Implications for Particulate Pollution Control. Atmos. Environ. 2012, 54, 337–347. [Google Scholar] [CrossRef]
- Grundström, M.; Hak, C.; Chen, D.; Hallquist, M.; Pleijel, H. Variation and Co-Variation of PM10, Particle Number Concentration, NOx and NO2 in the Urban Air-Relationships with Wind Speed, Vertical Temperature Gradient and Weather Type. Atmos. Environ. 2015, 120, 317–327. [Google Scholar] [CrossRef]
- Harrison, R.M.; Yin, J.; Mark, D.; Stedman, J.; Appleby, R.S.; Booker, J.; Moorcroft, S. Studies of the Coarse Particle (2.5–10μm) Component in UK Urban Atmospheres. Atmos. Environ. 2001, 35, 3667–3679. [Google Scholar] [CrossRef]
- Casotti Rienda, I.; Alves, C.A. Road Dust Resuspension: A Review. Atmos. Res. 2021, 261, 105740. [Google Scholar] [CrossRef]
- Bogacki, M.; Oleniacz, R.; Rzeszutek, M.; Szulecka, A.; Mazur, M. The Impact of Street Cleaning on Particulate Matter Air Concentrations: A Case Study of a Street Canyon in Krakow (Poland). In Proceedings of the E3S Web of Conferences, Krakow, Poland, 30 July 2018; EDP Sciences: Les Ulis, France, 2018; Volume 45. [Google Scholar]
- Amato, F.; Pandolfi, M.; Moreno, T.; Furger, M.; Pey, J.; Alastuey, A.; Bukowiecki, N.; Prevot, A.S.H.; Baltensperger, U.; Querol, X. Sources and Variability of Inhalable Road Dust Particles in Three European Cities. Atmos. Environ. 2011, 45, 6777–6787. [Google Scholar] [CrossRef]
- Klöckner, P.; Reemtsma, T.; Eisentraut, P.; Braun, U.; Ruhl, A.S.; Wagner, S. Tire and Road Wear Particles in Road Environment–Quantification and Assessment of Particle Dynamics by Zn Determination after Density Separation. Chemosphere 2019, 222, 714–721. [Google Scholar] [CrossRef] [PubMed]
- Kasimov, N.S.; Vlasov, D.V.; Kosheleva, N.E. Enrichment of Road Dust Particles and Adjacent Environments with Metals and Metalloids in Eastern Moscow. Urban Clim. 2020, 32, 100638. [Google Scholar] [CrossRef]
- Klöckner, P.; Seiwert, B.; Weyrauch, S.; Escher, B.I.; Reemtsma, T.; Wagner, S. Comprehensive Characterization of Tire and Road Wear Particles in Highway Tunnel Road Dust by Use of Size and Density Fractionation. Chemosphere 2021, 279, 130530. [Google Scholar] [CrossRef]
- Zhao, H.; Yin, C.; Chen, M.; Wang, W. Risk Assessment of Heavy Metals in Street Dust Particles to a Stream Network. Soil Sediment Contam. 2009, 18, 173–183. [Google Scholar] [CrossRef]
- Henry, C.; Minier, J.P. Colloidal Particle Resuspension: On the Need for Refined Characterisation of Surface Roughness. J. Aerosol Sci. 2018, 118, 1–13. [Google Scholar] [CrossRef]
- Zhang, F. The Modelling of Particle Resuspension in a Turbulent Boundary Layer. Ph.D. Dissertation, School of Mechanical and System Engineering Newcastle University, Newcastle upon Tyne, UK, 2011. [Google Scholar]
- Habchi, C.; Ghali, K.; Ghaddar, N. Coupling CFD and Analytical Modeling for Investigation of Monolayer Particle Resuspension by Transient Flows. Build. Environ. 2016, 105, 1–2. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Reeks, M.W.; Hall, D. Kinetic Models for Particle Resuspension in Turbulent Flows: Theory and Measurement. J. Aerosol Sci. 2001, 32, 1–31. [Google Scholar] [CrossRef]
- Henry, C. Particle Resuspension from Complex Surfaces: Current Knowledge and Limitations. arXiv 2018, arXiv:1802.06448. [Google Scholar]
- Li, Y.; Zhang, X.; Li, M.; Yin, S.; Zhang, Z.; Zhang, T.; Meng, H.; Gong, J.; Zhang, W. Particle Resuspension from Leaf Surfaces: Effect of Species, Leaf Traits and Wind Speed. Urban For. Urban Green. 2022, 77, 127740. [Google Scholar] [CrossRef]
- Del Bello, E.; Taddeucci, J.; Merrison, J.P.; Rasmussen, K.R.; Andronico, D.; Ricci, T.; Scarlato, P.; Iversen, J.J. Field-Based Measurements of Volcanic Ash Resuspension by Wind. Earth Planet. Sci. Lett. 2021, 554, 116684. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y.; Nepf, H. Impact of Stem Size on Turbulence and Sediment Resuspension Under Unidirectional Flow. Water Resour. Res. 2021, 57, e2020WR028620. [Google Scholar] [CrossRef]
- Loosmore, G.A. Evaluation and Development of Models for Resuspension of Aerosols at Short Times after Deposition. Atmos. Environ. 2003, 37, 639–647. [Google Scholar] [CrossRef]
- Nicholson, K.W. Wind Tunnel Experiments on the Resuspension of Particulate Material. Atmos. Environ. Part A Gen. Top. 1993, 27, 181–188. [Google Scholar] [CrossRef]
- Giess, P.; Goddard, A.J.H.; Shaw, G. Factors Affecting Particle Resuspension from Grass Swards. J. Aerosol Sci. 1997, 28, 1331–1349. [Google Scholar] [CrossRef]
- Garland, J.A. Some Recent Studies of the Resuspension of Deposited Material from Soil and Grass; Elsevier Science Publishing Co, Inc.: Berkeley, CA, USA, 1983. [Google Scholar]
- Del Bello, E.; Taddeucci, J.; Merrison, J.P.; Alois, S.; Iversen, J.J.; Scarlato, P. Experimental Simulations of Volcanic Ash Resuspension by Wind under the Effects of Atmospheric Humidity. Sci. Rep. 2018, 8, 14509. [Google Scholar] [CrossRef]
- Etyemezian, V.; Gillies, J.A.; Mastin, L.G.; Crawford, A.; Hasson, R.; Van Eaton, A.R.; Nikolich, G. Laboratory Experiments of Volcanic Ash Resuspension by Wind. J. Geophys. Res. Atmos. 2019, 124, 9534–9560. [Google Scholar] [CrossRef]
- Shao, Y.; Lu, H. A Simple Expression for Wind Erosion Threshold Friction Velocity. J. Geophys. Res. Atmos. 2000, 105, 22437–22443. [Google Scholar] [CrossRef]
- Cornelis, W.M.; Gabriels, D. The Effect of Surface Moisture on the Entrainment of Dune Sand by Wind: An Evaluation of Selected Models. Sedimentology 2003, 50, 771–790. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.; Zhang, Y.; Gao, Z.; Ying, N.; Gao, J.; Zhang, K.; Zhu, S. Dust Emissions from Urban Roads Using the AP-42 and TRAKER Methods: A Case Study. Atmos. Pollut. Res. 2021, 12, 101051. [Google Scholar] [CrossRef]
- Alves, C.A.; Evtyugina, M.; Vicente, A.M.P.; Vicente, E.D.; Nunes, T.V.; Silva, P.M.A.; Duarte, M.A.C.; Pio, C.A.; Amato, F.; Querol, X. Chemical Profiling of PM10 from Urban Road Dust. Sci. Total Environ. 2018, 634, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Padoan, E.; Ajmone-Marsan, F.; Querol, X.; Amato, F. An Empirical Model to Predict Road Dust Emissions Based on Pavement and Traffic Characteristics. Environ. Pollut. 2018, 237, 713–720. [Google Scholar] [CrossRef]
- Mei, S.J.; Luo, Z.; Zhao, F.Y.; Wang, H.Q. Street Canyon Ventilation and Airborne Pollutant Dispersion: 2-D versus 3-D CFD Simulations. Sustain. Cities Soc. 2019, 50, 101700. [Google Scholar] [CrossRef]
- Yazid, A.W.M.; Sidik, N.A.C.; Salim, S.M.; Saqr, K.M. A Review on the Flow Structure and Pollutant Dispersion in Urban Street Canyons for Urban Planning Strategies. Simulation 2014, 90, 892–916. [Google Scholar] [CrossRef]
- Oke, T.R. Street Design and Urban Canopy Layer Climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Xue, F.; Li, X. The Impact of Roadside Trees on Traffic Released PM10 in Urban Street Canyon: Aerodynamic and Deposition Effects. Sustain. Cities Soc. 2017, 30, 195–204. [Google Scholar] [CrossRef]
- Nosek, Š.; Kukačka, L.; Jurčáková, K.; Kellnerová, R.; Jaňour, Z. Impact of Roof Height Non-Uniformity on Pollutant Transport between a Street Canyon and Intersections. Environ. Pollut. 2017, 227, 125–138. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, J. CFD Simulations of Wind Flow and Pollutant Dispersion in a Street Canyon with Traffic Flow: Comparison between RANS and LES. Sustain. Cities Soc. 2021, 75, 103307. [Google Scholar] [CrossRef]
- Jiang, G.; Hu, T.; Yang, H. Effects of Ground Heating on Ventilation and Pollutant Transport in Three-Dimensional Urban Street Canyons with Unit Aspect Ratio. Atmosphere 2019, 10, 286. [Google Scholar] [CrossRef]
- Šimić, I.; Lovrić, M.; Godec, R.; Kröll, M.; Bešlić, I. Applying Machine Learning Methods to Better Understand, Model and Estimate Mass Concentrations of Traffic-Related Pollutants at a Typical Street Canyon. Environ. Pollut. 2020, 263, 114587. [Google Scholar] [CrossRef]
- Perret, L.; Blackman, K.; Fernandes, R.; Savory, E. Relating Street Canyon Vertical Mass-Exchange to Upstream Flow Regime and Canyon Geometry. Sustain. Cities Soc. 2017, 30, 49–57. [Google Scholar] [CrossRef]
- Mei, S.J.; Hu, J.T.; Liu, D.; Zhao, F.Y.; Li, Y.; Wang, Y.; Wang, H.Q. Wind Driven Natural Ventilation in the Idealized Building Block Arrays with Multiple Urban Morphologies and Unique Package Building Density. Energy Build. 2017, 155, 324–338. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD Modeling of Pollution Dispersion in a Street Canyon: Comparison between LES and RANS. J. Wind Eng. Ind. Aerodyn. 2011, 99, 340–348. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD Simulation of Near-Field Pollutant Dispersion in the Urban Environment: A Review of Current Modeling Techniques. Atmos. Environ. 2013, 79, 716–730. [Google Scholar] [CrossRef]
- Buccolieri, R.; Carlo, O.S.; Rivas, E.; Santiago, J.L. Urban Obstacles Influence on Street Canyon Ventilation: A Brief Review. Environ. Sci. Proc. 2021, 8, 11. [Google Scholar]
- Voordeckers, D.; Lauriks, T.; Denys, S.; Billen, P.; Tytgat, T.; Van Acker, M. Guidelines for Passive Control of Traffic-Related Air Pollution in Street Canyons: An Overview for Urban Planning. Landsc. Urban Plan. 2021, 207, 103980. [Google Scholar] [CrossRef]
- Chew, L.W.; Glicksman, L.R.; Norford, L.K. Buoyant Flows in Street Canyons: Comparison of RANS and LES at Reduced and Full Scales. Build. Environ. 2018, 146, 77–87. [Google Scholar] [CrossRef]
- Ziskind, G.; Fichman, M.; Gutfinger, C. Effects of Shear on Particle Motion near a Surface-Application to Resuspension. J. Aerosol Sci. 1998, 29, 323–338. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B.; Grawe, D.; Goricsán, I.; Jaňour, Z.; Karppinen, A. Best Practice Guideline for the Cfd Simulation of Flows in the Urban Environment. In 11th Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Cambridge, UK, July 2007; Cambridge Environmental Research Consultants: Cambridge, UK, 2007. [Google Scholar]
- Madalozzo, D.M.S.; Braun, A.L.; Awruch, A.M.; Morsch, I.B. Numerical Simulation of Pollutant Dispersion in Street Canyons: Geometric and Thermal Effects. Appl. Math. Model. 2014, 38, 5883–5909. [Google Scholar] [CrossRef]
- Kim, J.J.; Baik, J.J. Urban Street-Canyon Flows with Bottom Heating. Atmos. Environ. 2001, 35, 3395–3404. [Google Scholar] [CrossRef]
- Park, S.J.; Kim, J.J.; Choi, W.; Kim, E.R.; Song, C.K.; Pardyjak, E.R. Flow Characteristics Around Step-Up Street Canyons with Various Building Aspect Ratios. Boundary-Layer Meteorol. 2020, 174, 411–431. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Thangam, S.; Speziale, C.G. Turbulent Flow Past a Backward-Facing Step: A Critical Evaluation of Two-Equation Models. AIAA J. 1992, 30, 1314–1320. [Google Scholar] [CrossRef]
- Ricci, A.; Kalkman, I.; Blocken, B.; Burlando, M.; Repetto, M.P. Impact of Turbulence Models and Roughness Height in 3D Steady RANS Simulations of Wind Flow in an Urban Environment. Build. Environ. 2020, 171, 106617. [Google Scholar] [CrossRef]
- Xu, W.; Li, G.; Zheng, X.; Li, Y.; Li, S.; Zhang, C.; Wang, F. High-Resolution Numerical Simulation of the Performance of Vertical Axis Wind Turbines in Urban Area: Part I, Wind Turbines on the Side of Single Building. Renew. Energy 2021, 177, 461–474. [Google Scholar] [CrossRef]
- Valger, S.A.; Fedorova, N.N. CFD Methods in Architecture and City Planning. In Proceedings of the Journal of Physics: Conference Series, Moscow, Russian, 13–15 November 2019; IOP Publishing: Bristol, UK, 2020; Volume 1425. [Google Scholar]
- Brambilla, S.; Speckart, S.; Brown, M.J. Adhesion and Aerodynamic Forces for the Resuspension of Non-Spherical Particles in Outdoor Environments. J. Aerosol Sci. 2017, 112, 52–67. [Google Scholar] [CrossRef]
- Amato, F.; Cassee, F.R.; Denier van der Gon, H.A.C.; Gehrig, R.; Gustafsson, M.; Hafner, W.; Harrison, R.M.; Jozwicka, M.; Kelly, F.J.; Moreno, T.; et al. Urban Air Quality: The Challenge of Traffic Non-Exhaust Emissions. J. Hazard. Mater. 2014, 275, 31–36. [Google Scholar] [CrossRef]
- Ziskind, G. Particle Resuspension from Surfaces: Revisited and Re-Evaluated. Rev. Chem. Eng. 2006, 22, 1–123. [Google Scholar] [CrossRef]
- Henry, C.; Minier, J.P. Progress in Particle Resuspension from Rough Surfaces by Turbulent Flows. Prog. Energy Combust. Sci. 2014, 45, 1–53. [Google Scholar] [CrossRef]
- Schiller, L. Uber Die Grundlegenden Berechnungen Bei Der Schwerkraftaufbereitung. Z. Ver. Dtsch. Inge 1933, 77, 318–321. [Google Scholar]
- Saffman, P.G. The Lift on a Small Sphere in a Slow Shear Flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Wang, A.; Hoque, M.M.; Evans, G.; Mitra, S. Effect of Turbulence Dispersion on Bubble-Particle Collision Efficiency. Miner. Eng. 2022, 177, 107374. [Google Scholar] [CrossRef]
- Lauriks, T.; Longo, R.; Baetens, D.; Derudi, M.; Parente, A.; Bellemans, A.; van Beeck, J.; Denys, S. Application of Improved CFD Modeling for Prediction and Mitigation of Traffic-Related Air Pollution Hotspots in a Realistic Urban Street. Atmos. Environ. 2021, 246, 118127. [Google Scholar] [CrossRef]
- Pantusheva, M.; Mitkov, R.; Hristov, P.O.; Petrova-Antonova, D. Air Pollution Dispersion Modelling in Urban Environment Using CFD: A Systematic Review. Atmosphere 2022, 13, 1640. [Google Scholar] [CrossRef]
- Ahmad, K.; Khare, M.; Chaudhry, K.K. Wind Tunnel Simulation Studies on Dispersion at Urban Street Canyons and Intersections—A Review. J. Wind Eng. Ind. Aerodyn. 2005, 93, 697–717. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Yao, J. Large Eddy Simulation of Particle Deposition and Resuspension in Turbulent Duct Flows. Adv. Powder Technol. 2019, 30, 656–671. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Gu, Z.L.; Lee, S.C.; Fu, T.M.; Ho, K.F. Numerical Simulation and in Situ Investigation of Fine Particle Dispersion in an Actual Deep Street Canyon in Hong Kong. Indoor Built Environ. 2011, 20, 206–216. [Google Scholar] [CrossRef]
- Lu, K.-F.; Peng, Z.-R. Impacts of Viaduct and Geometry Configurations on the Distribution of Traffic-Related Particulate Matter in Urban Street Canyon. Sci. Total Environ. 2023, 858, 159902. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).