A Multi Criteria Decision Analysis Approach for Regional Climate Model Selection and Future Climate Assessment in the Mono River Basin, Benin and Togo
Abstract
:1. Introduction
2. Materials and Methods
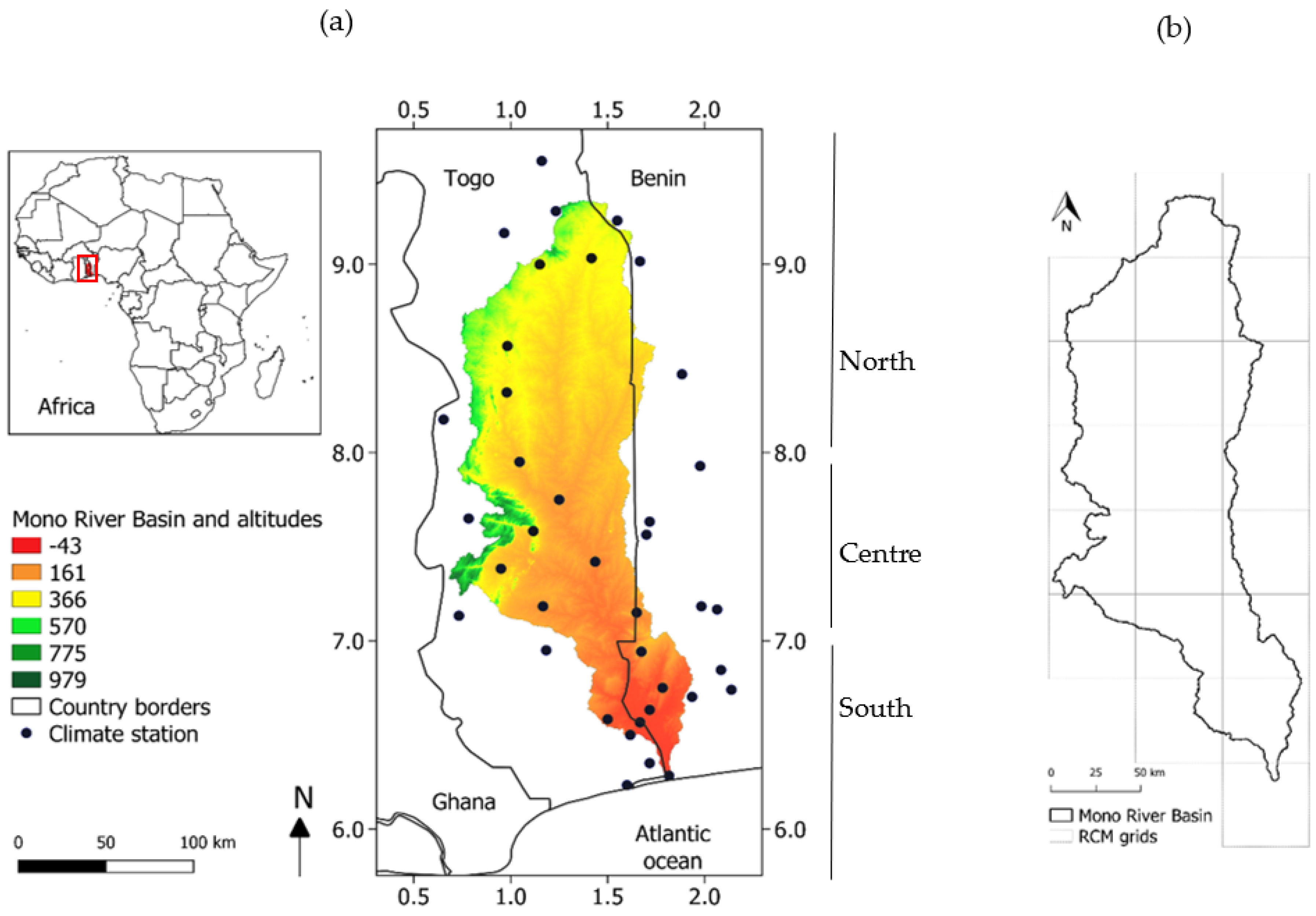
2.1. Study Area
2.2. Data
2.3. Ranking and Selection of RCMs
- Normalization of performance ratings.
- Calculation of weighted normalized ratings, :
- Derivation of positive ideal solution (PIS) and negative ideal solution (NIS).
- Estimation of separation from the PIS and the NIS.
- Derivation of similarities to the PIS.
- Ordering of alternatives according to the similarities to PIS in a decreasing order.
2.4. Bias Correction
2.5. Future Climate Trend Assessment
3. Results
3.1. Ranking and Selection of RCMs
3.1.1. TOPSIS Results: Best RCM per Location
3.1.2. RCMs Selection
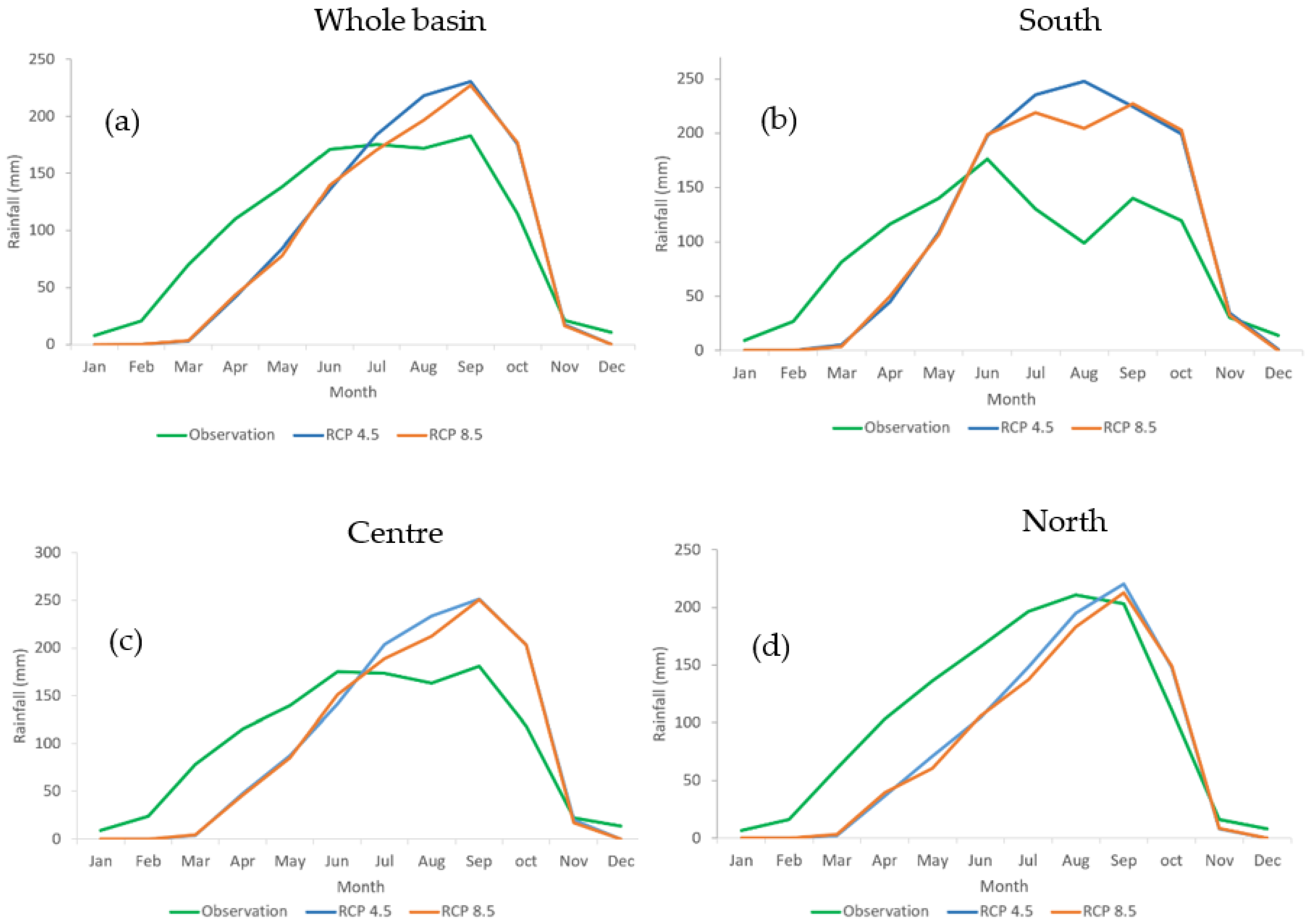
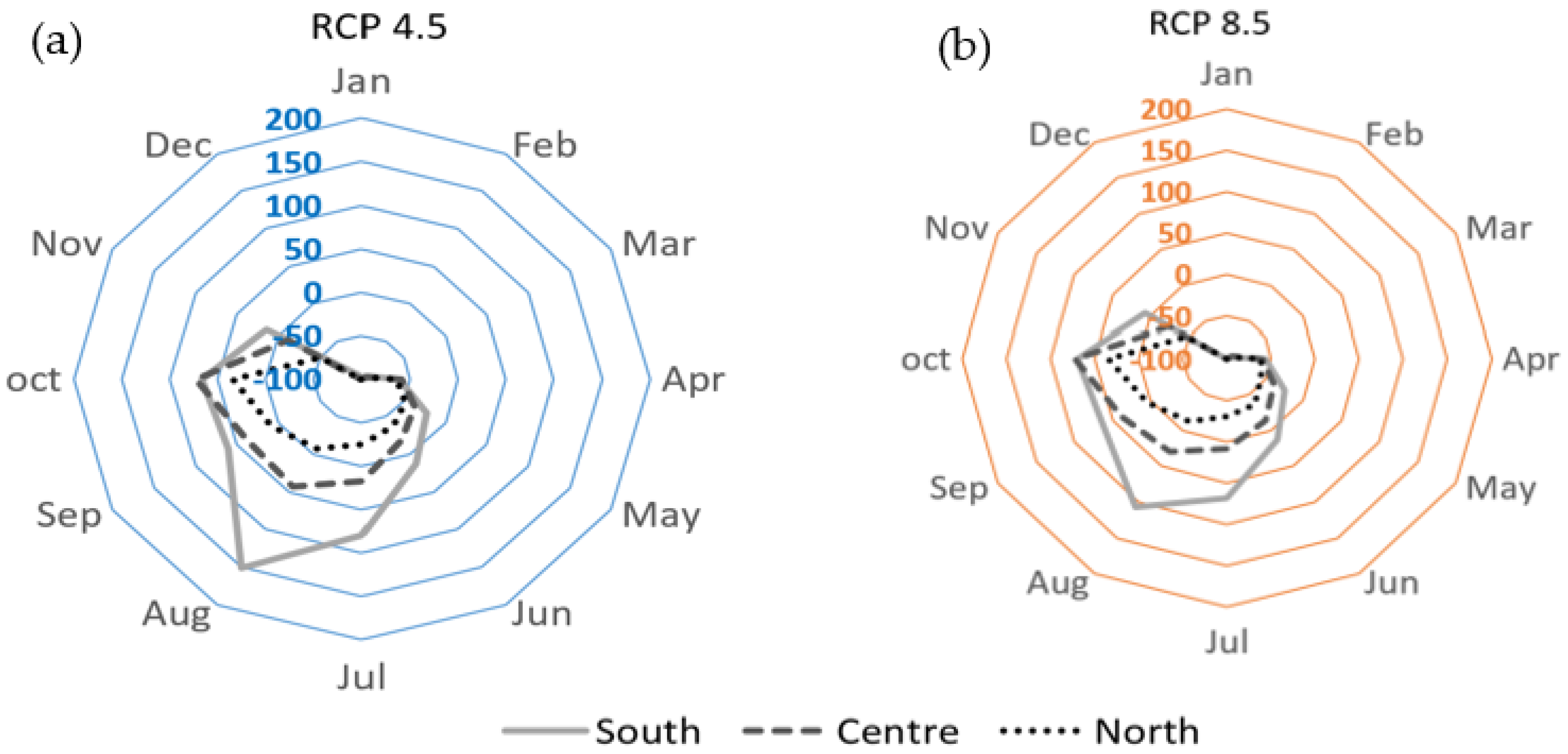
3.2. Assessment of Future Climate
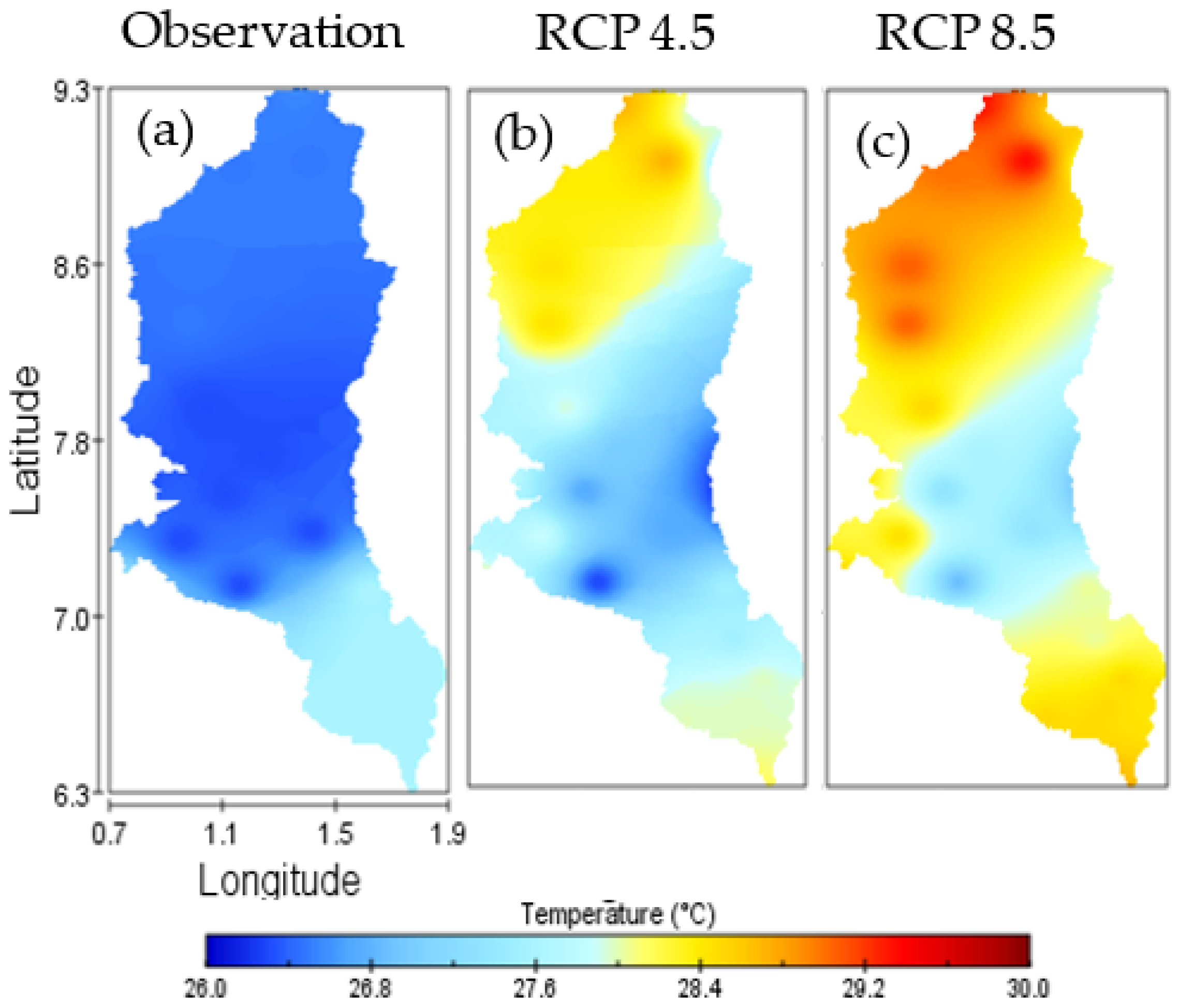
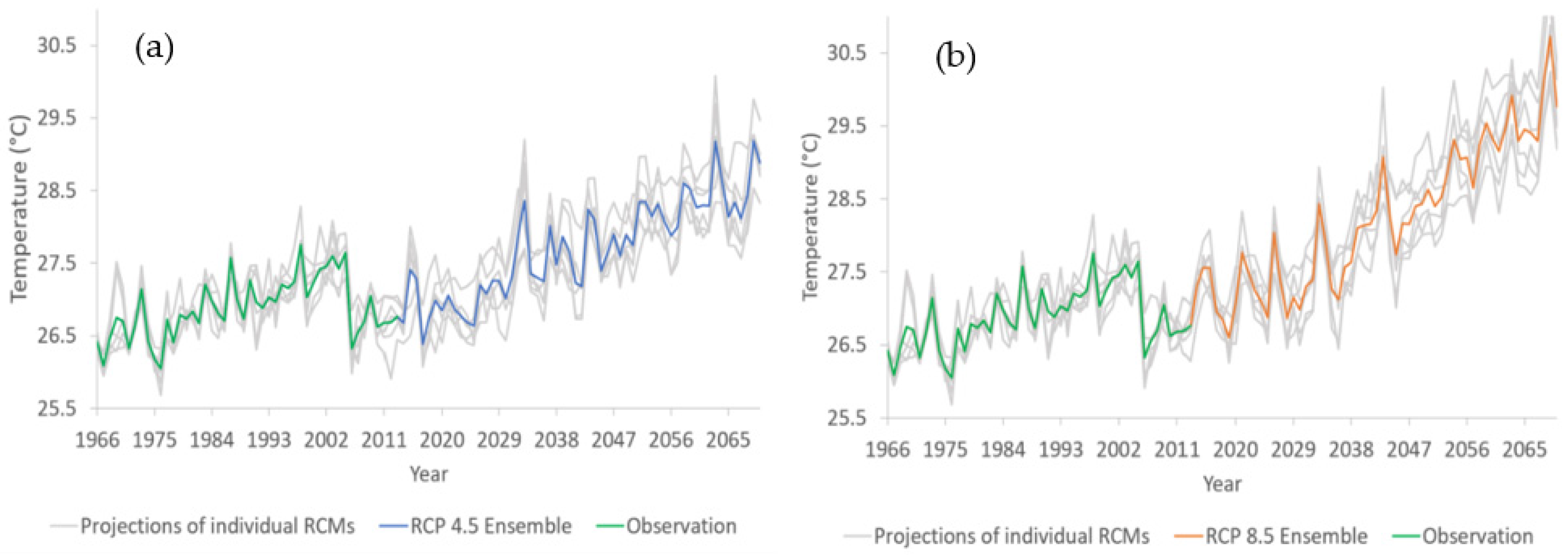
3.2.1. Temperature
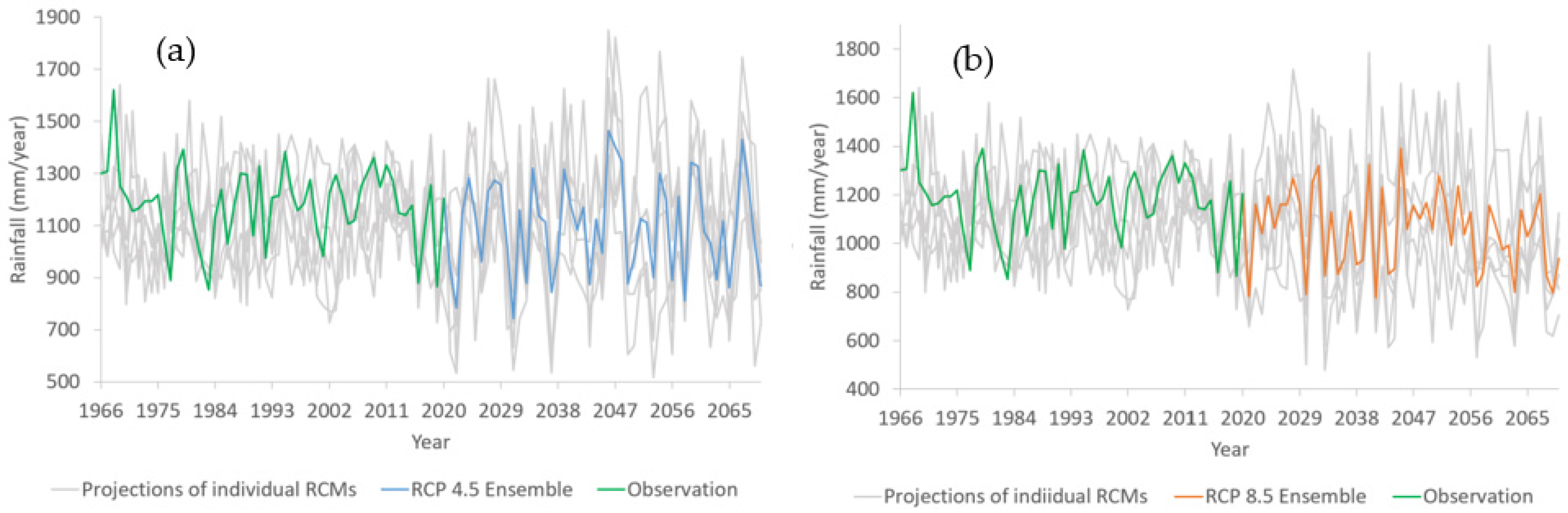
3.2.2. Rainfall
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Station | CNRM- CCLM4 | ICHEC- CCLM4 | MOHC- CCLM4 | MPI- CCLM4 | ICHEC-RACMO22T | MOHC- RACMO22T | CCCma- RCA4 | CNRM- RCA4 | CSIRO- RCA4 | IPSL- RCA4 | MIROC- RCA4 | MOHC- RCA4 | MPI-RCA4 | ICHEC-REMO | MPI-REMO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abomey | 0.03 | 0.84 | 0.83 | 0.87 | 0.87 | 0.13 | 0.10 | 0.76 | 0.25 | 0.16 | 0.88 | 0.94 | 0.94 | 0.84 | 0.27 |
| Adeta | 0.12 | 0.87 | 0.84 | 0.84 | 0.83 | 0.11 | 0.10 | 0.11 | 0.22 | 0.08 | 0.25 | 0.28 | 0.89 | 0.87 | 0.22 |
| Afagnan | 0.01 | 0.10 | 0.11 | 0.11 | 0.11 | 0.08 | 0.06 | 0.06 | 0.11 | 0.07 | 0.14 | 0.16 | 0.17 | 0.11 | 0.90 |
| Agouna | 0.03 | 0.51 | 0.52 | 0.93 | 0.92 | 0.49 | 0.06 | 0.11 | 0.16 | 0.09 | 0.52 | 0.21 | 0.53 | 0.88 | 0.18 |
| Akaba | 0.36 | 0.87 | 0.61 | 0.62 | 0.62 | 0.08 | 0.32 | 0.13 | 0.20 | 0.11 | 0.39 | 0.21 | 0.64 | 0.64 | 0.34 |
| Aklakou | 0.10 | 0.16 | 0.18 | 0.18 | 0.17 | 0.16 | 0.16 | 0.16 | 0.21 | 0.18 | 0.24 | 0.26 | 0.27 | 0.18 | 0.81 |
| Amou-Oblo | 0.18 | 0.49 | 0.74 | 0.76 | 0.53 | 0.49 | 0.12 | 0.18 | 0.22 | 0.16 | 0.26 | 0.55 | 0.48 | 0.55 | 0.47 |
| Aneho-Glidji | 0.11 | 0.20 | 0.19 | 0.23 | 0.77 | 0.23 | 0.21 | 0.18 | 0.27 | 0.25 | 0.29 | 0.34 | 0.35 | 0.66 | 0.96 |
| Anie-Mono | 0.26 | 0.91 | 0.60 | 0.93 | 0.30 | 0.45 | 0.46 | 0.53 | 0.33 | 0.19 | 0.59 | 0.59 | 0.94 | 0.35 | 0.52 |
| Aplahoue | 0.02 | 0.80 | 0.83 | 0.85 | 0.89 | 0.12 | 0.10 | 0.14 | 0.22 | 0.15 | 0.87 | 0.96 | 0.94 | 0.82 | 0.25 |
| Atakpame | 0.10 | 0.91 | 0.53 | 0.53 | 0.90 | 0.49 | 0.10 | 0.13 | 0.19 | 0.49 | 0.53 | 0.53 | 0.54 | 0.90 | 0.23 |
| Athieme | 0.03 | 0.14 | 0.14 | 0.87 | 0.91 | 0.13 | 0.13 | 0.79 | 0.18 | 0.14 | 0.20 | 0.25 | 0.25 | 0.83 | 0.18 |
| Bante | 0.47 | 0.85 | 0.92 | 0.91 | 0.53 | 0.49 | 0.46 | 0.17 | 0.23 | 0.09 | 0.54 | 0.53 | 0.93 | 0.53 | 0.53 |
| Bassila | 0.34 | 0.84 | 0.91 | 0.90 | 0.90 | 0.33 | 0.33 | 0.12 | 0.21 | 0.09 | 0.39 | 0.41 | 0.94 | 0.86 | 0.40 |
| Blitta | 0.37 | 0.89 | 0.81 | 0.83 | 0.67 | 0.61 | 0.33 | 0.34 | 0.19 | 0.07 | 0.37 | 0.41 | 0.87 | 0.94 | 0.34 |
| Bohicon | 0.02 | 0.52 | 0.51 | 0.52 | 0.84 | 0.10 | 0.09 | 0.49 | 0.18 | 0.11 | 0.52 | 0.54 | 0.54 | 0.84 | 0.21 |
| Bopa | 0.02 | 0.16 | 0.17 | 0.18 | 0.89 | 0.12 | 0.11 | 0.10 | 0.19 | 0.14 | 0.91 | 0.25 | 0.25 | 0.83 | 0.20 |
| Dogbo | 0.03 | 0.11 | 0.10 | 0.11 | 0.11 | 0.08 | 0.07 | 0.06 | 0.12 | 0.07 | 0.95 | 0.16 | 0.16 | 0.12 | 0.12 |
| Grand-Popo | 0.05 | 0.09 | 0.10 | 0.12 | 0.17 | 0.16 | 0.14 | 0.11 | 0.17 | 0.15 | 0.18 | 0.22 | 0.22 | 0.10 | 0.91 |
| Kara | 0.38 | 0.89 | 0.89 | 0.90 | 0.41 | 0.29 | 0.30 | 0.38 | 0.32 | 0.30 | 0.46 | 0.40 | 0.92 | 0.46 | 0.65 |
| Kougnohou | 0.19 | 0.82 | 0.63 | 0.65 | 0.53 | 0.31 | 0.30 | 0.31 | 0.24 | 0.18 | 0.33 | 0.38 | 0.67 | 0.77 | 0.27 |
| Kpewa-Aledjo | 0.31 | 0.90 | 0.75 | 0.91 | 0.66 | 0.29 | 0.28 | 0.30 | 0.23 | 0.29 | 0.36 | 0.35 | 0.92 | 0.78 | 0.54 |
| Lokossa | 0.02 | 0.17 | 0.89 | 0.86 | 0.82 | 0.79 | 0.17 | 0.12 | 0.23 | 0.17 | 0.22 | 0.27 | 0.30 | 0.80 | 0.25 |
| Lonkly | 0.03 | 0.84 | 0.87 | 0.87 | 0.86 | 0.11 | 0.08 | 0.14 | 0.19 | 0.10 | 0.24 | 0.26 | 0.95 | 0.21 | 0.21 |
| Malfacassa | 0.35 | 0.66 | 0.68 | 0.91 | 0.68 | 0.34 | 0.33 | 0.34 | 0.20 | 0.34 | 0.40 | 0.22 | 0.94 | 0.67 | 0.38 |
| Nangbeto | 0.05 | 0.86 | 0.93 | 0.90 | 0.79 | 0.15 | 0.11 | 0.06 | 0.26 | 0.07 | 0.80 | 0.89 | 0.31 | 0.84 | 0.29 |
| Niaouli | 0.03 | 0.12 | 0.12 | 0.13 | 0.94 | 0.10 | 0.09 | 0.07 | 0.15 | 0.11 | 0.16 | 0.20 | 0.20 | 0.87 | 0.15 |
| Notse | 0.08 | 0.88 | 0.18 | 0.92 | 0.15 | 0.09 | 0.07 | 0.10 | 0.16 | 0.07 | 0.19 | 0.22 | 0.98 | 0.16 | 0.18 |
| Penesoulou | 0.27 | 0.90 | 0.76 | 0.76 | 0.53 | 0.27 | 0.26 | 0.28 | 0.17 | 0.25 | 0.31 | 0.30 | 0.53 | 0.52 | 0.32 |
| Savalou | 0.07 | 0.87 | 0.52 | 0.92 | 0.52 | 0.49 | 0.09 | 0.09 | 0.17 | 0.08 | 0.50 | 0.52 | 0.53 | 0.88 | 0.18 |
| Sokode | 0.28 | 0.91 | 0.53 | 0.93 | 0.92 | 0.28 | 0.28 | 0.28 | 0.19 | 0.10 | 0.32 | 0.33 | 0.75 | 0.75 | 0.33 |
| Sotouboua | 0.13 | 0.93 | 0.59 | 0.59 | 0.43 | 0.22 | 0.22 | 0.22 | 0.16 | 0.06 | 0.25 | 0.28 | 0.78 | 0.62 | 0.23 |
| Tabligbo | 0.01 | 0.17 | 0.18 | 0.89 | 0.83 | 0.12 | 0.12 | 0.10 | 0.19 | 0.14 | 0.19 | 0.24 | 0.25 | 0.81 | 0.23 |
| Tchamba | 0.29 | 0.91 | 0.74 | 0.90 | 0.32 | 0.27 | 0.26 | 0.26 | 0.30 | 0.07 | 0.33 | 0.32 | 0.75 | 0.53 | 0.50 |
| Tchetti | 0.04 | 0.84 | 0.88 | 0.90 | 0.85 | 0.79 | 0.08 | 0.14 | 0.19 | 0.10 | 0.86 | 0.24 | 0.93 | 0.83 | 0.22 |
| Toffo | 0.04 | 0.17 | 0.13 | 0.16 | 0.90 | 0.08 | 0.06 | 0.10 | 0.15 | 0.11 | 0.19 | 0.22 | 0.21 | 0.88 | 0.89 |
| Wahala | 0.11 | 0.87 | 0.24 | 0.91 | 0.89 | 0.11 | 0.09 | 0.13 | 0.21 | 0.11 | 0.23 | 0.27 | 0.97 | 0.88 | 0.24 |
| Yegue | 0.34 | 0.66 | 0.68 | 0.91 | 0.40 | 0.63 | 0.33 | 0.35 | 0.19 | 0.10 | 0.40 | 0.40 | 0.93 | 0.67 | 0.40 |
Appendix B
| Station | CNRM- CCLM4 | ICHEC- CCLM4 | MOHC- CCLM4 | MPI- CCLM4 | ICHEC- RACMO22T | MOHC- RACMO22T | CCCma- RCA4 | CNRM- RCA4 | CSIRO- RCA4 | IPSL- RCA4 | MIROC- RCA4 | MOHC- RCA4 | MPI- RCA4 | ICHEC- REMO | MPI- REMO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abomey | 0.34 | 0.53 | 0.80 | 0.83 | 0.75 | 0.37 | 0.43 | 0.39 | 0.53 | 0.46 | 0.08 | 0.21 | 0.76 | 0.62 | 0.76 |
| Adeta | 0.23 | 0.75 | 0.67 | 0.63 | 0.56 | 0.31 | 0.46 | 0.26 | 0.43 | 0.31 | 0.00 | 0.18 | 0.89 | 0.46 | 0.64 |
| Afagnan | 0.38 | 0.49 | 0.75 | 0.84 | 0.75 | 0.35 | 0.41 | 0.42 | 0.56 | 0.48 | 0.00 | 0.22 | 0.67 | 0.67 | 0.82 |
| Agouna | 0.29 | 0.24 | 0.89 | 0.74 | 0.76 | 0.47 | 0.38 | 0.38 | 0.62 | 0.47 | 0.20 | 0.33 | 0.47 | 0.57 | 1.00 |
| Akaba | 0.52 | 0.22 | 0.58 | 0.31 | 0.30 | 0.21 | 0.24 | 0.66 | 0.83 | 0.72 | 0.48 | 0.56 | 0.27 | 0.18 | 0.74 |
| Aklakou | 0.44 | 0.31 | 0.67 | 0.72 | 0.50 | 0.50 | 0.53 | 0.51 | 0.65 | 0.56 | 0.03 | 0.29 | 0.42 | 0.53 | 0.94 |
| AmouOblo | 0.46 | 0.34 | 0.68 | 0.41 | 0.39 | 0.09 | 0.18 | 0.59 | 0.79 | 0.67 | 0.37 | 0.48 | 0.41 | 0.23 | 0.86 |
| AnehoGlidji | 0.44 | 0.31 | 0.67 | 0.72 | 0.50 | 0.50 | 0.53 | 0.51 | 0.65 | 0.56 | 0.03 | 0.29 | 0.42 | 0.53 | 0.94 |
| AnieMono | 0.41 | 0.14 | 0.69 | 0.49 | 0.50 | 0.38 | 0.30 | 0.55 | 0.70 | 0.60 | 0.38 | 0.45 | 0.27 | 0.38 | 0.86 |
| Aplahoue | 0.34 | 0.58 | 0.77 | 0.83 | 0.75 | 0.37 | 0.44 | 0.40 | 0.54 | 0.46 | 0.08 | 0.21 | 0.82 | 0.63 | 0.76 |
| Atakpame | 0.31 | 0.21 | 0.75 | 0.64 | 0.63 | 0.39 | 0.31 | 0.43 | 0.62 | 0.50 | 0.21 | 0.33 | 0.41 | 0.49 | 0.89 |
| Athieme | 0.38 | 0.49 | 0.75 | 0.84 | 0.75 | 0.35 | 0.41 | 0.42 | 0.56 | 0.48 | 0.00 | 0.22 | 0.67 | 0.67 | 0.82 |
| Bante | 0.40 | 0.29 | 0.56 | 0.65 | 0.53 | 0.41 | 0.40 | 0.46 | 0.67 | 0.52 | 0.12 | 0.42 | 0.45 | 0.51 | 0.51 |
| Bassila | 0.45 | 0.28 | 0.55 | 0.63 | 0.48 | 0.32 | 0.33 | 0.51 | 0.68 | 0.56 | 0.23 | 0.53 | 0.43 | 0.49 | 0.49 |
| Blitta | 0.52 | 0.34 | 0.45 | 0.43 | 0.34 | 0.31 | 0.37 | 0.58 | 0.76 | 0.67 | 0.25 | 0.56 | 0.39 | 0.28 | 0.38 |
| Bohicon | 0.34 | 0.53 | 0.80 | 0.83 | 0.75 | 0.37 | 0.43 | 0.39 | 0.53 | 0.46 | 0.08 | 0.21 | 0.76 | 0.62 | 0.76 |
| Bopa | 0.38 | 0.49 | 0.75 | 0.84 | 0.75 | 0.35 | 0.41 | 0.42 | 0.56 | 0.48 | 0.00 | 0.22 | 0.67 | 0.67 | 0.82 |
| DogboTota | 0.38 | 0.49 | 0.75 | 0.84 | 0.75 | 0.35 | 0.41 | 0.42 | 0.56 | 0.48 | 0.00 | 0.22 | 0.67 | 0.67 | 0.82 |
| GrandPopo | 0.59 | 0.53 | 0.65 | 0.62 | 0.43 | 0.12 | 0.17 | 0.62 | 0.68 | 0.68 | 0.37 | 0.62 | 0.56 | 0.47 | 0.46 |
| Kara | 0.59 | 0.53 | 0.65 | 0.62 | 0.43 | 0.12 | 0.17 | 0.62 | 0.68 | 0.68 | 0.37 | 0.62 | 0.56 | 0.47 | 0.46 |
| Kougnohou | 0.46 | 0.34 | 0.68 | 0.41 | 0.39 | 0.09 | 0.18 | 0.59 | 0.79 | 0.67 | 0.37 | 0.48 | 0.41 | 0.23 | 0.86 |
| KpewaAledjo | 0.50 | 0.33 | 0.54 | 0.58 | 0.39 | 0.11 | 0.16 | 0.60 | 0.64 | 0.64 | 0.36 | 0.68 | 0.45 | 0.39 | 0.42 |
| Lokossa | 0.38 | 0.49 | 0.75 | 0.84 | 0.75 | 0.35 | 0.41 | 0.42 | 0.56 | 0.48 | 0.00 | 0.22 | 0.67 | 0.67 | 0.82 |
| Lonkly | 0.34 | 0.58 | 0.77 | 0.83 | 0.75 | 0.37 | 0.44 | 0.40 | 0.54 | 0.46 | 0.08 | 0.21 | 0.82 | 0.63 | 0.76 |
| Malfacassa | 0.40 | 0.23 | 0.54 | 0.60 | 0.44 | 0.25 | 0.25 | 0.52 | 0.57 | 0.55 | 0.24 | 0.60 | 0.43 | 0.42 | 0.44 |
| Nangbeto | 0.31 | 0.21 | 0.75 | 0.64 | 0.63 | 0.39 | 0.31 | 0.43 | 0.62 | 0.50 | 0.21 | 0.33 | 0.41 | 0.49 | 0.89 |
| Niaouli | 0.38 | 0.49 | 0.78 | 0.85 | 0.75 | 0.32 | 0.39 | 0.42 | 0.57 | 0.48 | 0.00 | 0.22 | 0.69 | 0.67 | 0.82 |
| Notse | 0.24 | 0.66 | 0.80 | 0.89 | 0.80 | 0.44 | 0.54 | 0.28 | 0.45 | 0.33 | 0.00 | 0.18 | 0.94 | 0.68 | 0.80 |
| Penesoulou | 0.50 | 0.29 | 0.57 | 0.61 | 0.45 | 0.21 | 0.24 | 0.57 | 0.66 | 0.62 | 0.32 | 0.59 | 0.44 | 0.47 | 0.48 |
| Savalou | 0.31 | 0.17 | 0.82 | 0.60 | 0.63 | 0.39 | 0.33 | 0.45 | 0.65 | 0.51 | 0.26 | 0.34 | 0.34 | 0.49 | 0.97 |
| Sokode | 0.49 | 0.27 | 0.50 | 0.55 | 0.39 | 0.27 | 0.29 | 0.55 | 0.66 | 0.61 | 0.25 | 0.57 | 0.40 | 0.39 | 0.42 |
| Sotouboua | 0.52 | 0.34 | 0.45 | 0.43 | 0.34 | 0.31 | 0.37 | 0.58 | 0.76 | 0.67 | 0.25 | 0.56 | 0.39 | 0.28 | 0.38 |
| Tabligbo | 0.38 | 0.51 | 0.75 | 0.85 | 0.75 | 0.35 | 0.43 | 0.42 | 0.57 | 0.49 | 0.00 | 0.22 | 0.73 | 0.68 | 0.77 |
| Tchamba | 0.50 | 0.33 | 0.54 | 0.58 | 0.39 | 0.11 | 0.16 | 0.60 | 0.64 | 0.64 | 0.36 | 0.68 | 0.45 | 0.39 | 0.42 |
| Tchetti | 0.29 | 0.24 | 0.89 | 0.74 | 0.76 | 0.47 | 0.38 | 0.38 | 0.62 | 0.47 | 0.20 | 0.33 | 0.47 | 0.57 | 1.00 |
| Toffo | 0.34 | 0.53 | 0.80 | 0.83 | 0.75 | 0.37 | 0.43 | 0.39 | 0.53 | 0.46 | 0.08 | 0.21 | 0.76 | 0.62 | 0.76 |
| Wahala | 0.24 | 0.33 | 0.89 | 0.88 | 0.86 | 0.47 | 0.33 | 0.30 | 0.60 | 0.38 | 0.18 | 0.39 | 0.57 | 0.70 | 1.00 |
| Yegue | 0.44 | 0.25 | 0.50 | 0.68 | 0.53 | 0.41 | 0.38 | 0.51 | 0.68 | 0.59 | 0.16 | 0.48 | 0.44 | 0.48 | 0.43 |
References
- Rosenzweig, C.; Casassa, G.; Karoly, D.J.; Imeson, A.; Liu, C.; Menzel, A.; Rawlins, S.; Root, T.L.; Seguin, B.; Tryjanowski, P. Assessment of observed changes and responses in natural and managed systems. In Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 79–131. ISBN 9780521880107. [Google Scholar]
- IPCC Summary for Policymakers. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; p. 42. [Google Scholar]
- Wang, L.; Ranasinghe, R.; Maskey, S.; van Gelder, P.H.A.J.M.; Vrijling, J.K. Comparison of empirical statistical methods for downscaling daily climate projections from CMIP5 GCMs: A case study of the Huai River Basin, China. Int. J. Climatol. 2015, 36, 145–164. [Google Scholar] [CrossRef]
- Yip, S.; Ferro, C.A.T.; Stephenson, D.B.; Hawkins, E. A Simple, coherent framework for partitioning uncertainty in climate predictions. J. Clim. 2011, 24, 4634–4643. [Google Scholar] [CrossRef]
- Mishra, V.; Kumar, D.; Ganguly, A.R.; Sanjay, J.; Mujumdar, M.; Krishnan, R.; Shah, R.D. Reliability of regional and global climate models to simulate precipitation extremes over India. J. Geophys. Res. Atmos. 2014, 119, 2966–2989. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, 1–34. [Google Scholar] [CrossRef]
- Chen, J.; Arsenault, R.; Brissette, F.P.; Zhang, S. Climate Change Impact Studies: Should We Bias Correct Climate Model Outputs or Post-Process Impact Model Outputs? Water Resour. Res. 2021, 57, 1–22. [Google Scholar] [CrossRef]
- Sarr, M.A.; Seidou, O.; Tramblay, Y.; El Adlouni, S. Comparison of downscaling methods for mean and extreme precipitation in Senegal. J. Hydrol. Reg. Stud. 2015, 4, 369–385. [Google Scholar] [CrossRef]
- Beyer, R.; Krapp, M.; Manica, A. An empirical evaluation of bias correction methods for palaeoclimate simulations. Clim. Past 2020, 16, 1493–1508. [Google Scholar] [CrossRef]
- CCAFS GCM Downscaled Data Portal. Available online: http://www.ccafs-climate.org/statistical_downscaling_delta/ (accessed on 10 June 2022).
- Gunavathi, S.; Selvasidhu, R. Assessment of various bias correction methods and future projection of minimum and maximum temperatures using regional climate model over Thanjavur district. Arab. J. Geosci. 2022, 15, 1–18. [Google Scholar] [CrossRef]
- Luo, M.; Liu, T.; Meng, F.; Duan, Y.; Frankl, A.; Bao, A.; De Maeyer, P. Comparing bias correction methods used in downscaling precipitation and temperature from regional climate models: A case study from the Kaidu River Basin in Western China. Water 2018, 10, 1046. [Google Scholar] [CrossRef]
- Crochemore, L.; Ramos, M.H.; Pappenberger, F. Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2016, 20, 3601–3618. [Google Scholar] [CrossRef] [Green Version]
- Akinsanola, A.A.; Ogunjobi, K.O.; Gbode, I.E.; Ajayi, V.O. Assessing the Capabilities of Three Regional Climate Models over CORDEX Africa in Simulating West African Summer Monsoon Precipitation. Adv. Meteorol. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Gbobaniyi, E.; Sarr, A.; Sylla, M.B.; Diallo, I.; Lennard, C.; Dosio, A.; Dhiédiou, A.; Kamga, A.; Klutse, N.A.B.; Hewitson, B.; et al. Climatology, annual cycle and interannual variability of precipitation and temperature in CORDEX simulations over West Africa. Int. J. Climatol. 2014, 34, 2241–2257. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O. Evaluation of present-day rainfall simulations over West Africa in CORDEX regional climate models. Environ. Earth Sci. 2017, 76, 366. [Google Scholar] [CrossRef]
- Batablinle, L.; Lawin, E.; Agnide, S.; Celestin, M. Africa-Cordex simulations projection of future temperature, precipitation, frequency and intensity indices over Mono Basin in West Africa. J. Earth Sci. Clim. Chang. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Djan’na Koubodana, H.; Adounkpe, J.; Tall, M.; Amoussou, E.; Atchonouglo, K.; Mumtaz, M. Trend Analysis of Hydro-climatic Historical Data and Future Scenarios of Climate Extreme Indices over Mono River Basin in West Africa. Am. J. Rural Dev. 2020, 8, 37–52. [Google Scholar] [CrossRef]
- Lamboni, B.; Emmanuel, L.A.; Manirakiza, C.; Djibib, Z.M. Variability of Future Rainfall over the Mono River Basin of West-Africa. Am. J. Clim. Chang. 2019, 8, 137–155. [Google Scholar] [CrossRef]
- Lawin, A.E.; Hounguè, N.R.; Biaou, C.A.; Badou, D.F. Statistical analysis of recent and future rainfall and temperature variability in the Mono River watershed (Benin, Togo). Climate 2019, 7, 8. [Google Scholar] [CrossRef]
- Amoussou, E.; Awoye, H.; Vodounon, H.S.T.; Obahoundje, S.; Camberlin, P.; Diedhiou, A.; Kouadio, K.; Mahé, G.; Houndénou, C.; Boko, M. Climate and extreme rainfall events in the mono river basin (West Africa): Investigating future changes with regional climate models. Water 2020, 12, 833. [Google Scholar] [CrossRef]
- Emmanuel, L.A.; Batablinlè, L.; Célestin, M.; Hodabalo, K. Future Extremes Temperature: Trends and Changes Assessment over the Mono River Basin, Togo (West Africa). J. Water Resour. Prot. 2019, 11, 82–98. [Google Scholar] [CrossRef]
- Houngue, N.R. Assessment of Mid-Century Climate Change Impacts on Mono River’s Downstream Inflows. Master’s Thesis, Université de Lomé, Lomé, Togo, 2018. [Google Scholar]
- Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting representative climate models for climate change impact studies: An advanced envelope-based selection approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef] [Green Version]
- Refaey, M.A.; Hassan, M.; Mostafa, H.; Aboelkhear, M. Multi Criterion Decision Making Techniques for Ranking Regional climate models over Wadi El-Natrun Catchment. Aust. J. Basic Appl. Sci. 2019, 13, 85–96. [Google Scholar] [CrossRef]
- Homsi, R.; Shiru, M.S.; Shahid, S.; Ismail, T.; Harun, S.B.; Al-Ansari, N.; Chau, K.W.; Yaseen, Z.M. Precipitation projection using a CMIP5 GCM ensemble model: A regional investigation of Syria. Eng. Appl. Comput. Fluid Mech. 2020, 14, 90–106. [Google Scholar] [CrossRef]
- Shiru, M.S.; Shahid, S.; Chung, E.S.; Alias, N.; Scherer, L. A MCDM-based framework for selection of general circulation models and projection of spatio-temporal rainfall changes: A case study of Nigeria. Atmos. Res. 2019, 225, 1–16. [Google Scholar] [CrossRef]
- Raju, K.S.; Kumar, D.N. Ranking general circulation models for India using TOPSIS. J. Water Clim. Chang. 2015, 6, 288–299. [Google Scholar] [CrossRef]
- Amoussou, E. Variabilité Pluviométrique et Dynamique Hydro-Sédimentaire du Bassin Versant du Complexe Lagunaire Mono-Ahémé-Couffo (Afrique de l’Ouest). Ph.D. Thesis, Université de Bourgogne, Dijon, France, 2010. [Google Scholar]
- Hounguè, N.R.; Ogbu, K.N.; Almoradie, A.D.S.; Evers, M. Evaluation of the performance of remotely sensed rainfall datasets for flood simulation in the transboundary Mono River catchment, Togo and Benin. J. Hydrol. Reg. Stud. 2021, 36, 100875. [Google Scholar] [CrossRef]
- Thiam, S.; Salas, E.A.L.; Houngue, N.R.; Almoradie, D.A.S.; Verleysdonk, S.; Adounkpe, J.G.; Komi, K. Modelling Land Use and Land Cover in the Transboundary Mono River Catchment of Togo and Benin Using Markov Chain and Stakeholder’s Perspectives. Sustainability 2022, 14, 4160. [Google Scholar] [CrossRef]
- Yilmaz, B.; Harmancioglu, N.B. Multi-criteria decision making for water resource management: A case study of the Gediz River Basin, Turkey. Water SA 2010, 36, 563–576. [Google Scholar] [CrossRef]
- Zeyaeyan, S.; Fattahi, E.; Ranjbar, A.; Vazifedoust, M. Classification of rainfall warnings based on the TOPSIS method. Climate 2017, 5, 33. [Google Scholar] [CrossRef]
- Evers, M.; Almoradie, A.D.S.; de Brito, M.M. Enhancing flood resilience through collaborative modelling and multi-criteria decision analysis (MCDA). In Urban Disaster Resilience and Security; Fekete, A., Fiedrich, F., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 221–236. ISBN 9783319686066. [Google Scholar]
- Almoradie, A.; Cortes, V.J.; Jonoski, A. Web-based stakeholder collaboration in flood risk management. J. Flood Risk Manag. 2015, 8, 19–38. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Pérez-Sánchez, J.; Carrillo-García, J.; Soto, J. Using SWAT and fuzzy TOPSIS to assess the impact of climate change in the headwaters of the Segura River Basin (SE Spain). Water 2017, 9, 149. [Google Scholar] [CrossRef] [Green Version]
- Sofiati, I.; Nurlatifah, A. The prediction of rainfall events using WRF (weather research and forecasting) model with ensemble technique. Int. Conf. Ser. Earth Environ. Sci. 2019, 374, 12036. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N.; Son, M. Performance assessment of general circulation model in simulating daily precipitation and temperature using multiple gridded datasets. Water 2018, 10, 1793. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin climate for hydro-meteorological studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Das, P.; Zhang, Z.; Ren, H. Evaluation of four bias correction methods and random forest model for climate change projection in the Mara River Basin, East Africa. J. Water Clim. Chang. 2022, 13, 1900–1919. [Google Scholar] [CrossRef]
- Putra, I.D.G.A.; Rosid, M.S.; Sopaheluwakan, A.; Sianturi, Y.C.U. The CMIP5 projection of extreme climate indices in Indonesia using simple quantile mapping method. In AIP Conference Proceedings; Wardana, A.N.I., Purwono, S., Liem, P.H., Eds.; AIP Publishing: Yogyakarta, Indonesia, 2020; Volume 2223. [Google Scholar]
- Pierce, D.W.; Cayan, D.R.; Maurer, E.P.; Abatzoglou, J.T.; Hegewisch, K.C. Improved bias correction techniques for hydrological simulations of climate change. J. Hydrometeorol. 2015, 16, 2421–2442. [Google Scholar] [CrossRef]
- Mendez, M.; Maathuis, B.; Hein-Griggs, D.; Alvarado-Gamboa, L.F. Performance evaluation of bias correction methods for climate change monthly precipitation projections over Costa Rica. Water 2020, 12, 482. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Soriano, E.; Mediero, L.; Garijo, C. Selection of bias correction methods to assess the impact of climate change on flood frequency curves. Water 2019, 11, 2266. [Google Scholar] [CrossRef]
- Kwawuvi, D.; Mama, D.; Agodzo, S.K.; Hartmann, A.; Larbi, I.; Bessah, E.; Limantol, A.M.; Dotse, S.-Q.; Yangouliba, G.I. Spatiotemporal variability and change in rainfall in the Oti River Basin, West Africa. J. Water Clim. Chang. 2022, 13, 1151–1169. [Google Scholar] [CrossRef]
- Lawin, A.E.; Hounguè, R.; M’Po, Y.N.T.; Hounguè, N.R.; Attogouinon, A.; Afouda, A.A. Mid-century climate change impacts on Ouémé River discharge at Bonou Outlet (Benin). Hydrology 2019, 6, 72. [Google Scholar] [CrossRef]
- N’Tcha M’Po, Y.; Lawin, A.E.; Oyerinde, G.T.; Yao, B.K.; Afouda, A.A. Comparison of Daily Precipitation Bias Correction Methods Based on Four Regional Climate Model Outputs in Ouémé Basin, Benin. Hydrology 2016, 4, 58–71. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Deepthi, B.; Sunil, A.; Nair, S.C.; Mirajkar, A.B.; Adarsh, S. Ranking of Cmip5-Based General Circulation Models Using Compromise Programming and Topsis for Precipitation: A Case Study of Upper Godavari Basin, India. Int. J. Big Data Min. Glob. Warm. 2020, 2, 2050007. [Google Scholar] [CrossRef]
- Badou, D.F.; Diekkrüger, B.; Kapangaziwiri, E.; Mbaye, M.L.; Yira, Y.; Lawin, E.A.; Oyerinde, G.T.; Afouda, A. Modelling blue and green water availability under climate change in the Beninese Basin of the Niger River Basin, West Africa. Hydrol. Process. 2018, 32, 2526–2542. [Google Scholar] [CrossRef]
- Gbode, I.E.; Ogunjobi, K.O.; Dudhia, J.; Ajayi, V.O.; Liu, C. Impacts of global warming on West African monsoon rainfall. In African Handbook of Climate Change Adaptation; Oguge, N., Ayal, D., Adeleke, L., da Silva, I., Eds.; Springer: Cham, Switzerland, 2021; pp. 2469–2483. ISBN 9783030451066. [Google Scholar]
- Macadam, I.; Rowell, D.P.; Steptoe, H. Refining projections of future temperature change in West Africa. Clim. Res. 2020, 82, 1–14. [Google Scholar] [CrossRef]
- Bokhari, S.A.A.; Ahmad, B.; Ali, J.; Ahmad, S.; Mushtaq, H.; Rasul, G. Future Climate Change Projections of the Kabul River Basin Using a Multi-model Ensemble of High-Resolution Statistically Downscaled Data. Earth Syst. Environ. 2018, 2, 477–497. [Google Scholar] [CrossRef]
- Niang, I.; Ruppel, O.C.; Abdrabo, M.A.; Essel, A.; Lennard, C.; Padgham, J.; Urquhart, P. Africa. Part B: Regional Aspects: Working Group II Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014: Impacts, Adaptation and Vulnerability; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1199–1266. ISBN 9781107415386. [Google Scholar]
- IPCC Summary for Policymakers. An IPCC Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change. In Global Warming of 1.5 °C; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2018. [Google Scholar]
- Lee, S.; Kim, S.W.; Hwang, S.O.; Choi, J.N.; Ahn, K.B.; Kim, J. Comparative analysis of the cloud behavior over inland and coastal regions within single climate characteristics. Atmosphere 2020, 11, 1316. [Google Scholar] [CrossRef]
- Lischeid, G.; Dannowski, R.; Kaiser, K.; Nützmann, G.; Steidl, J.; Stüve, P. Inconsistent hydrological trends do not necessarily imply spatially heterogeneous drivers. J. Hydrol. 2021, 596, 126096. [Google Scholar] [CrossRef]
- IPCC. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2007: The Physical Science Basis; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; ISBN 9780521880091. [Google Scholar]
- FAO. Global Information and Early Warning System on Food and Agriculture (GIEWS): Country Brief Togo; Food and Agriculture Organization of the United Nations: Rome, Italy, 2020. [Google Scholar]
- Ntajal, J.; Lamptey, B.L.; Mianikpo, J.; Kpotivi, W.K. Rainfall trends and flood frequency analyses in the lower Mono River basin in Togo, West Africa. Int. J. Adv. Res. 2016, 4, 2320–9186. [Google Scholar]



| GCM | RCM | GCM-RCM Designation | ||
|---|---|---|---|---|
| Name | Developed by | Name | Institute | |
| CNRM-CERFACS-CNRM-CM5 | Centre National de Recherches Météorologiques, Centre, France (CNRM) | CCLM4-8-17 | Climate Limited-area Modelling Community (CLMcom) | CNRM-CCLM4 |
| ICHEC-EC-EARTH | Irish Centre for High-End Computing (ICHEC) | ICHEC-CCLM4 | ||
| MOHC-HadGEM2-ES | Met Office Hadley Centre, UK (MOHC) | MOHC-CCLM4 | ||
| MPI-M-MPI-ESM-LR | Max Planck Institute for Meteorology, Germany (MPI) | MPI-CCLM4 | ||
| ICHEC-EC-EARTH | ICHEC | RACMO22T | Royal Netherlands Meteorological Institute (KNMI) | ICHEC-RACMO22T |
| MOHC-HadGEM2-ES | MOHC | MOHC-RACMO22T | ||
| CCCma-CanESM2 | Canadian Centre for Climate Modelling and Analysis | RCA4 | Swedish Meteorological and Hydrological Institute (SMHI) | CCCma-RCA4 |
| CNRM-CERFACS-CNRM-CM5 | CNRM | CNRM-RCA4 | ||
| CSIRO-QCCCE-CSIRO-Mk3-6-0 | Commonwealth Scientific and Industrial Research Organization, Australia (CSIRO) | CSIRO-RCA4 | ||
| IPSL-IPSL-CM5A-MR | Institut Pierre Simon Laplace, France (IPSL) | IPSL-RCA4 | ||
| MIROC-MIROC5 | The University of Tokyo, National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | MIROC-RCA4 | ||
| MOHC-HadGEM2-ES | MOHC | MOHC-RCA4 | ||
| MPI-M-MPI-ESM-LR | MPI | MPI-RCA4 | ||
| ICHEC-EC-EARTH | ICHEC | REMO2009 | Helmholtz-Zentrum Geesthacht, Climate Service Center, Max Planck Institute for Meteorology (MPI-CSC) | ICHEC-REMO |
| MPI-M-MPI-ESM-LR | MPI | MPI-REMO | ||
| Rank | Rainfall | Temperature | ||
|---|---|---|---|---|
| Model | Score | Model | Score | |
| 1 | MPI-RCA4 | 20.23 | MPI-CCLM4 | 19.99 |
| 2 | MPI-CCLM4 | 15.59 | MPI-REMO | 18.21 |
| 3 | ICHEC-CCLM4 | 12.40 | CSIRO-RCA4 | 16.03 |
| 4 | ICHEC-RACMO22T | 11.39 | MOHC-CCLM4 | 12.6 |
| 5 | ICHEC-REMO | 11 | IPSL-RCA4 | 8.68 |
| 6 | MOHC-CCLM4 | 9.67 | MPI-RCA4 | 8.06 |
| 7 | MOHC-RCA4 | 9.02 | MOHC-RCA4 | 7.18 |
| 8 | MPI-REMO | 8.73 | ICHEC-RACMO22T | 6.95 |
| 9 | MIROC-RCA4 | 7.89 | CNRM-RCA4 | 5.79 |
| 10 | CSIRO-RCA4 | 3.96 | ICHEC-REMO | 5.09 |
| 11 | MOHC-RACMO22T | 3.77 | ICHEC-CCLM4 | 4.05 |
| 12 | CNRM-RCA4 | 3.41 | CNRM-CCLM4 | 3.94 |
| 13 | IPSL-RCA4 | 3.08 | CCCma-RCA4 | 3.54 |
| 14 | CCCma-RCA4 | 2.97 | MOHC-RACMO22T | 3.20 |
| 15 | CNRM-CCLM4 | 2.94 | MIROC-RCA4 | 2.76 |
| Scenario | Z Statistics | p-Value | Sens’ Slope |
|---|---|---|---|
| RCP 4.5 | 6.67 | 0.00 | 0.04 |
| RCP 8.5 | 7.81 | 0.00 | 0.06 |
| Scenario | Z Statistics | p-Value | Sens’ Slope |
|---|---|---|---|
| RCP 4.5 | 0.03 | 0.97 | 0.1 |
| RCP 8.5 | −1.54 | 0.12 | −2.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hounguè, N.R.; Almoradie, A.D.S.; Evers, M. A Multi Criteria Decision Analysis Approach for Regional Climate Model Selection and Future Climate Assessment in the Mono River Basin, Benin and Togo. Atmosphere 2022, 13, 1471. https://doi.org/10.3390/atmos13091471
Hounguè NR, Almoradie ADS, Evers M. A Multi Criteria Decision Analysis Approach for Regional Climate Model Selection and Future Climate Assessment in the Mono River Basin, Benin and Togo. Atmosphere. 2022; 13(9):1471. https://doi.org/10.3390/atmos13091471
Chicago/Turabian StyleHounguè, Nina Rholan, Adrian Delos Santos Almoradie, and Mariele Evers. 2022. "A Multi Criteria Decision Analysis Approach for Regional Climate Model Selection and Future Climate Assessment in the Mono River Basin, Benin and Togo" Atmosphere 13, no. 9: 1471. https://doi.org/10.3390/atmos13091471
APA StyleHounguè, N. R., Almoradie, A. D. S., & Evers, M. (2022). A Multi Criteria Decision Analysis Approach for Regional Climate Model Selection and Future Climate Assessment in the Mono River Basin, Benin and Togo. Atmosphere, 13(9), 1471. https://doi.org/10.3390/atmos13091471







