Sensitivity of the 4–10-Day Planetary Wave Structures in the Middle Atmosphere to the Solar Activity Effects in the Thermosphere
Abstract
1. Introduction
2. Methodology
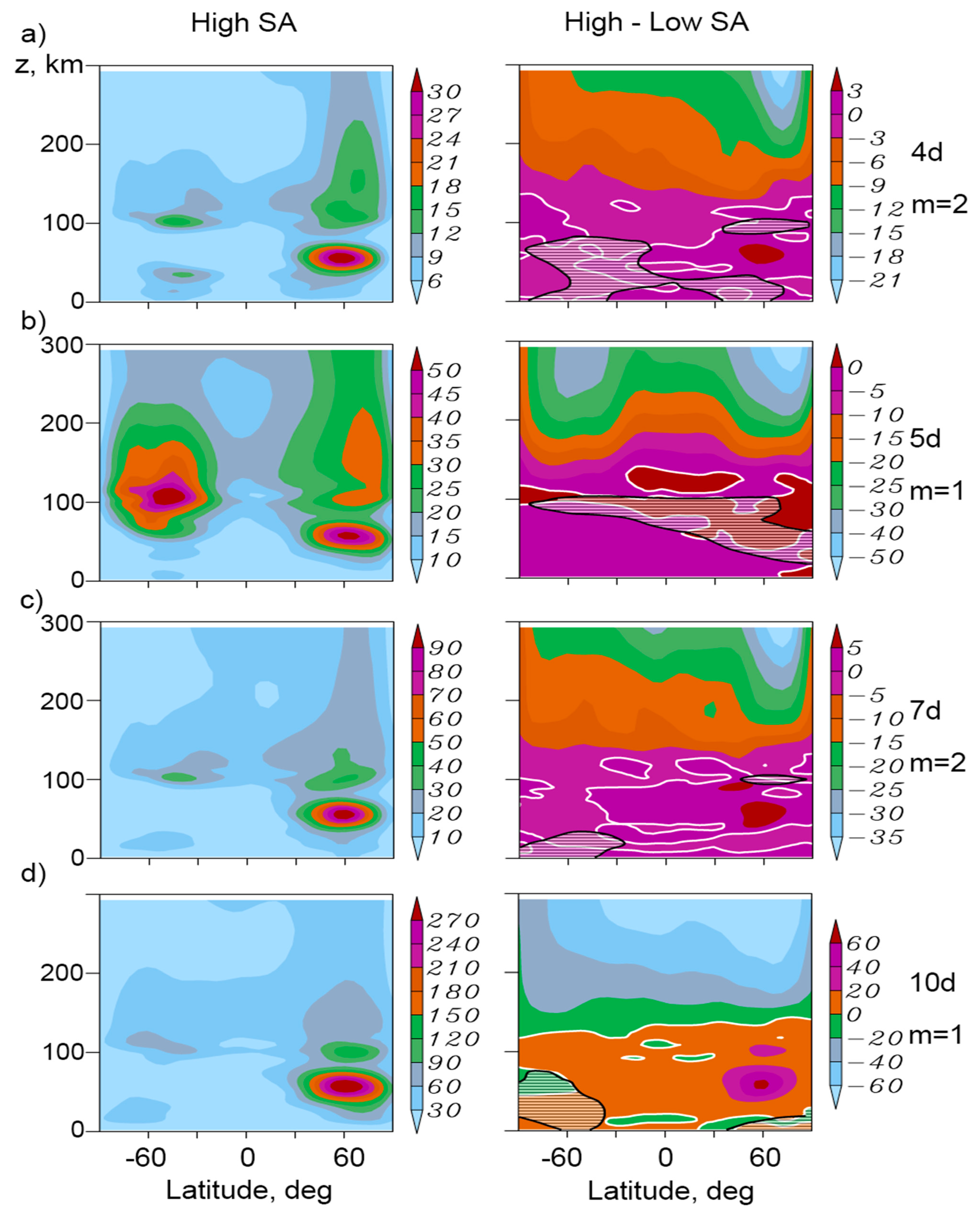
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, L.C.; Liu, J.Y.; Palo, S.E. Propagating planetary wave coupling in SABER MLT temperatures and GPS TEC during the 2005/2006 austral summer. J. Geophys. Res. 2011, 116, A10324. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P. Planetary wave coupling of the atmosphere–ionosphere system during the Northern winter of 2008/2009. Adv. Space Res. 2012, 50, 1189–1203. [Google Scholar] [CrossRef]
- Borries, C.; Hoffmann, P. Characteristics of F2-layer planetary wave-type oscillations in northern middle and high latitudes during 2002 to 2008. J. Geophys. Res. Space Phys. 2010, 115, A00G10. [Google Scholar] [CrossRef]
- Laštovicka, J. Forcing of the ionosphere by waves from below. J. Atmos. Sol. Terr. Phys. 2006, 68, 479–497. [Google Scholar] [CrossRef]
- Meyer, C.K. Gravity wave interactions with mesospheric planetary waves: A mechanism for penetration into the thermosphere-ionosphere system. J. Geophys. Res. 1999, 104, 28181–28196. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Richmond, A.D. A theory of ionospheric response to upward-propagating tides: Electrodynamic effects and tidal mixing effects. J. Geophys. Res. Space Phys. 2013, 118, 5891–5905. [Google Scholar] [CrossRef]
- Liu, H.L.; Richmond, A.D. Attribution of ionospheric vertical plasma drift perturbations to large-scale waves and the difference on solar activity. J. Geophys. Res. Space Phys. 2013, 108, 2452–2465. [Google Scholar] [CrossRef]
- Hathaway, D.H. The Solar Cycle. Living Rev. Sol. Phys. 2010, 7, 15. [Google Scholar] [CrossRef]
- Koval, A.V.; Gavrilov, N.M.; Pogoreltsev, A.I.; Shevchuk, N.O. Reactions of the middle atmosphere circulation and stationary planetary waves on the solar activity effects in the thermosphere. J. Geophys. Res. Space Phys. 2019, 124, 10645–10658. [Google Scholar] [CrossRef]
- Lu, H.; Scaife, A.A.; Marshall, G.J.; Turner, J.; Gray, L.J. Downward wave reflection as a mechanism for the stratosphere-troposphere response to the 11-year solar cycle. J. Clim. 2017, 30, 2395–2414. [Google Scholar] [CrossRef]
- Koval, A.V.; Gavrilov, N.M.; Pogoreltsev, A.I.; Shevchuk, N.O. Influence of solar activity on penetration of traveling planetary-scale waves from the troposphere into the thermosphere. J. Geophys. Res. Space Phys. 2018, 123, 6888–6903. [Google Scholar] [CrossRef]
- Pogoreltsev, A.I.; Vlasov, A.A.; Fröhlich, K.; Jacobi, C. Planetary waves in coupling the lower and upper atmosphere. J. Atmos. Sol. Terr. Phys. 2007, 69, 2083–2101. [Google Scholar] [CrossRef]
- Pogoreltsev, A.I. Generation of normal atmospheric modes by stratospheric vacillations. Izv. Atmos. Ocean. Phys. 2007, 43, 423–435. [Google Scholar] [CrossRef]
- Ebel, A.; Berger, U.; Krueger, B.C. Numerical simulations with COMMA, a global model of the middle atmosphere. SIMPO Newsl. 1995, 12, 22–32. [Google Scholar]
- Tapping, K.F. Recent solar radio astronomy at centimeter wavelength: The temporal variability of the 10.7 cm flux. J. Geophys. Res. 1987, 92, 829–838. [Google Scholar] [CrossRef]
- Royal Observatory of Belgium (ROB). 2013. Available online: http://sidc.be/silso/datafiles (accessed on 18 November 2017).
- Gulyaeva, T.L.; Huang, X.; Reinisch, B.W. Ionosphere-plasmasphere model software for ISO. Acta Geod. Geophys. Hung. 2002, 37, 143–152. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Shevchuk, N.O.; Ortikov, M.Y.; Pogoreltsev, A.I. Modeling of atmospheric tides with account of diurnal variations of ionospheric conductivity. Russ. J. Phys. Chem. B 2018, 12, 576–589. [Google Scholar] [CrossRef]
- Pogoreltsev, A.I.; Savenkova, E.N.; Pertsev, N.N. Sudden stratopheric warmings: The role of normal atmospheric modes. Geomagn. Aeron. 2014, 54, 357–372. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, H. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Swarztrauber, P.N.; Kasahara, A. The vector harmonic analysis of Laplace’s tidal equations. SIAM J. Sci. Stat. Comp. 1985, 6, 464–491. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The eigenfunctions of Laplace’s tidal equation over a sphere. Philos. Trans. R. Soc. Lond. 1968, 262, 511–607. [Google Scholar] [CrossRef]
- Pogoreltsev, A.I.; Kanukhina, A.Y.; Suvorova, E.V.; Savenkova, E.N. Variability of Planetary Waves as a Signature of Possible Climatic Changes. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1529–1539. [Google Scholar] [CrossRef]
- Gan, Q.; Wang, W.; Yue, J.; Liu, H.; Chang, L.C.; Zhang, S.; Burns, A.; Du, J. Numerical simulation of the 6 day wave effects on the ionosphere: Dynamo modulation. J. Geophys. Res. Space Phys. 2016, 121, 10–103. [Google Scholar] [CrossRef]
- Holton, J.R.; Mass, C. Stratospheric vacillation cycles. J. Atmos. Sci. 1976, 33, 2218–2225. [Google Scholar] [CrossRef]
- Koval, A.V. Statistically significant estimates of influence of solar activity on planetary waves in the middle atmosphere of the Northern Hemisphere as derived from MUAM model data. Sol. Terr. Phys. 2019, 5, 53–59. [Google Scholar] [CrossRef][Green Version]
- Reinisch, B.W.; Paznukhov, V.V.; Galkin, I.A.; Altadill, D.; McElroy, J. Advancing Digisonde Technology: The DPS-4D. Radio Sounding and Plasma Physics. American Institute of Physics. AIP Conf. Proc. 2008, 974, 127–143. [Google Scholar]
- Gavrilov, N.M.; Koval, A.V. Spectra of tides and planetary waves from the data of ionosonde measurements near Saint Petersburg. In Proceedings of the 27th International Symposium on Atmospheric and Ocean Optics, Atmospheric Physics, Moscow, Russia, 5–9 July 2021; Volume 119167, pp. 1645–1649. [Google Scholar] [CrossRef]
- Lomb, N. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263 Pt 1, 835–853. [Google Scholar] [CrossRef]
- Charney, J.G.; Drazin, P.G. Propagation of planetary-scale disturbances from the lower into the upper atmosphere. J. Geophys. Res. 1961, 66, 83–109. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Andonov, B.; Forbes, J.M. Global distribution and climatological features of the 5-6-day planetary waves seen in the SABER/TIMED temperatures (2002–2007). J. Atmos. Sol.-Terr. Phys. 2010, 72, 26–37. [Google Scholar] [CrossRef]
- Riggin, D.M.; Liu, H.-L.; Lieberman, R.S.; Roble, R.G.; Russell, J.M., III; Mertens, C.J.; Mlynczak, M.G.; Pancheva, D.; Franke, S.J.; Murayama, Y.; et al. Observations of the 5-day wave in the mesosphere and lower thermosphere. J. Atmos. Sol.-Terr. Phys. 2013, 68, 323–339. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X. Quasi-10-day wave in the atmosphere. J. Geophys. Res. 2015, 120, 11079–11089. [Google Scholar] [CrossRef]
- Borries, C.; Jakowski, N.; Jacobi, C.; Hoffmann, P.; Pogoreltsev, A.I. Spectral analysis of planetary waves seen in ionospheric total electron content (TEC): First results using GPS differential TEC and stratospheric reanalyses. J. Atmos. Sol.-Terr. Phys 2007, 69, 2442–2451. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Forbes, J.M. Modulation of the equatorial F-region by the quasi-16-day planetary wave. Geophys. Res. Lett. 2009, 36, L09105. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Andrews, D.G.; Holton, J.R.; Leovy, C.B. Middle Atmosphere Dynamics; Academic Press: New York, NY, USA, 1987; p. 489. [Google Scholar]
- Geller, M.A.; Alpert, J.C. Planetary wave coupling between the troposphere and the middle atmosphere as a possible Sun-weather mechanism. J. Atmos. Sci. 1980, 37, 1197–1215. [Google Scholar] [CrossRef]
- Arnold, N.F.; Robinson, T.R. Solar cycle changes to planetary wave propagation and their influence on the middle atmosphere circulation. Ann. Geophys. 1998, 16, 69–76. [Google Scholar] [CrossRef]
- Pancheva, D.; Alberca, L.F.; Morena, B.A. Simultaneous observations of quasi-two-day variations in the lower and upper ionosphere over Europe. J. Atmos. Sol.-Terr. Phys. 1994, 56, 43–50. [Google Scholar] [CrossRef]
- Stray, N.H.; Espy, P.J. Planetary wave-like oscillations in the ionosphere retrieved with a longitudinal chain of ionosondes at high northern latitudes. J. Atmos. Sol.-Terr. Phys. 2018, 171, 225–233. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koval, A.V.; Gavrilov, N.M.; Didenko, K.A.; Ermakova, T.S.; Savenkova, E.N. Sensitivity of the 4–10-Day Planetary Wave Structures in the Middle Atmosphere to the Solar Activity Effects in the Thermosphere. Atmosphere 2022, 13, 1325. https://doi.org/10.3390/atmos13081325
Koval AV, Gavrilov NM, Didenko KA, Ermakova TS, Savenkova EN. Sensitivity of the 4–10-Day Planetary Wave Structures in the Middle Atmosphere to the Solar Activity Effects in the Thermosphere. Atmosphere. 2022; 13(8):1325. https://doi.org/10.3390/atmos13081325
Chicago/Turabian StyleKoval, Andrey V., Nikolai M. Gavrilov, Ksenia A. Didenko, Tatiana S. Ermakova, and Elena N. Savenkova. 2022. "Sensitivity of the 4–10-Day Planetary Wave Structures in the Middle Atmosphere to the Solar Activity Effects in the Thermosphere" Atmosphere 13, no. 8: 1325. https://doi.org/10.3390/atmos13081325
APA StyleKoval, A. V., Gavrilov, N. M., Didenko, K. A., Ermakova, T. S., & Savenkova, E. N. (2022). Sensitivity of the 4–10-Day Planetary Wave Structures in the Middle Atmosphere to the Solar Activity Effects in the Thermosphere. Atmosphere, 13(8), 1325. https://doi.org/10.3390/atmos13081325






