Branching Morphology of Negative Leaders with Different Propagation Directions in Natural Lightning
Abstract
:1. Introduction
2. Observation System
3. Results and Analysis
3.1. General Features
3.2. Branching Morphology of Negative Leaders
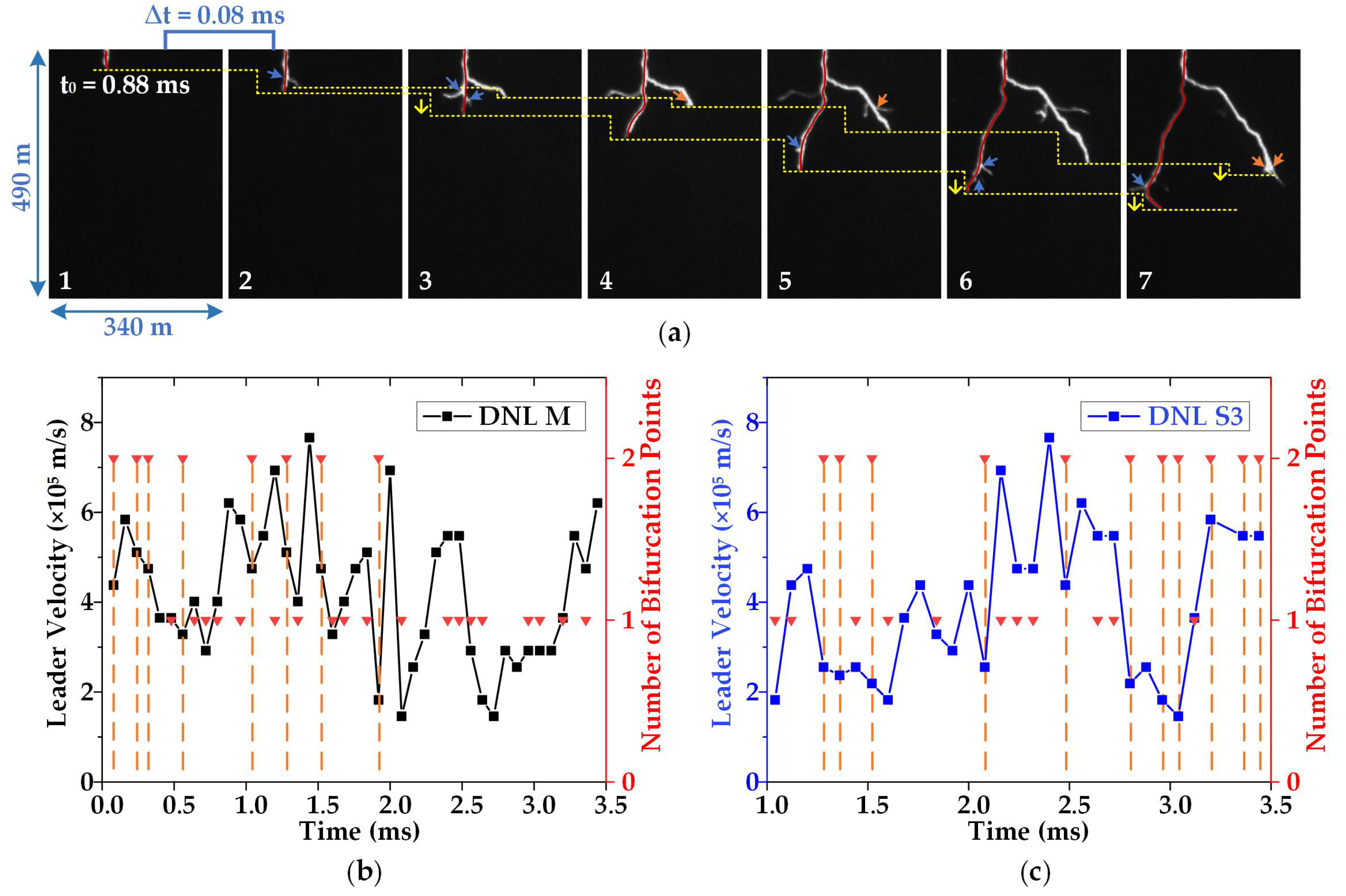
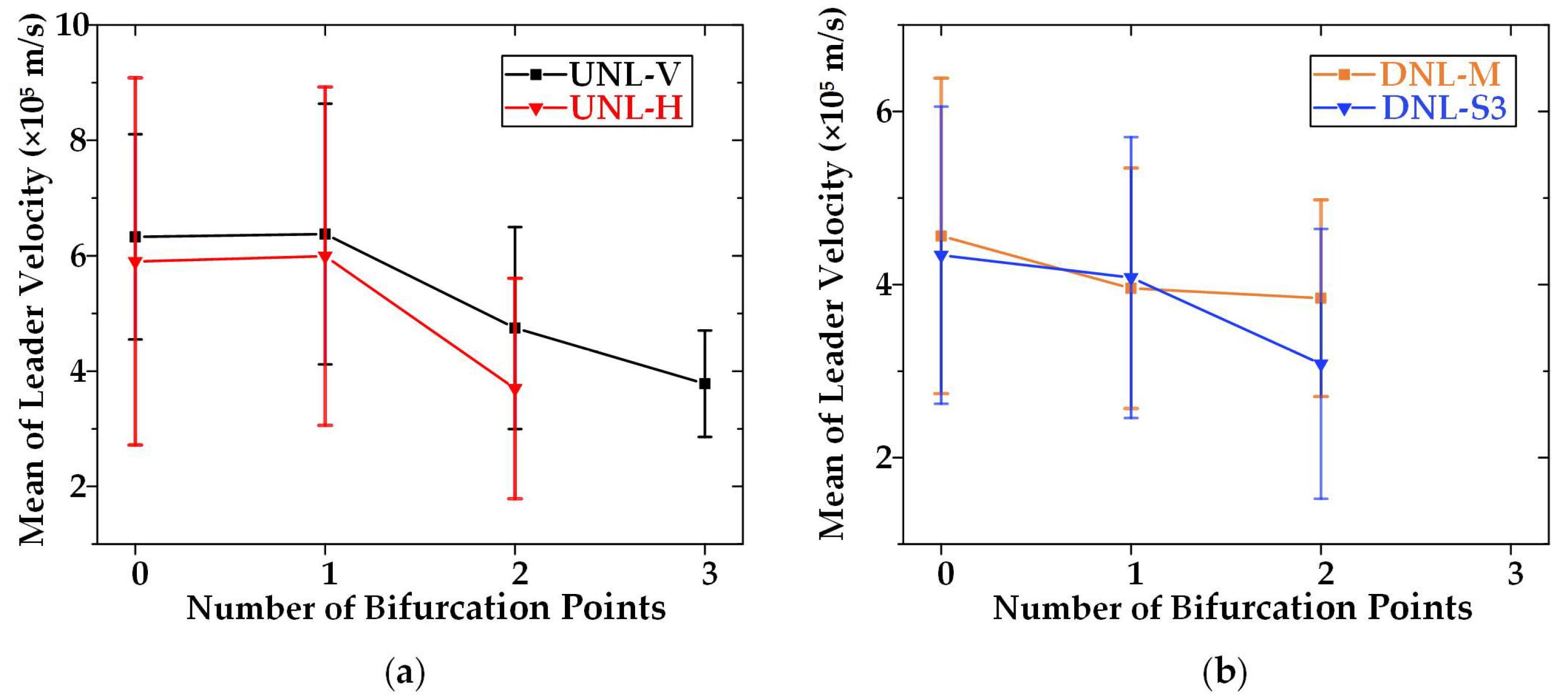
3.3. Effect of Branching on Leader Velocity
4. Discussion
5. Conclusions
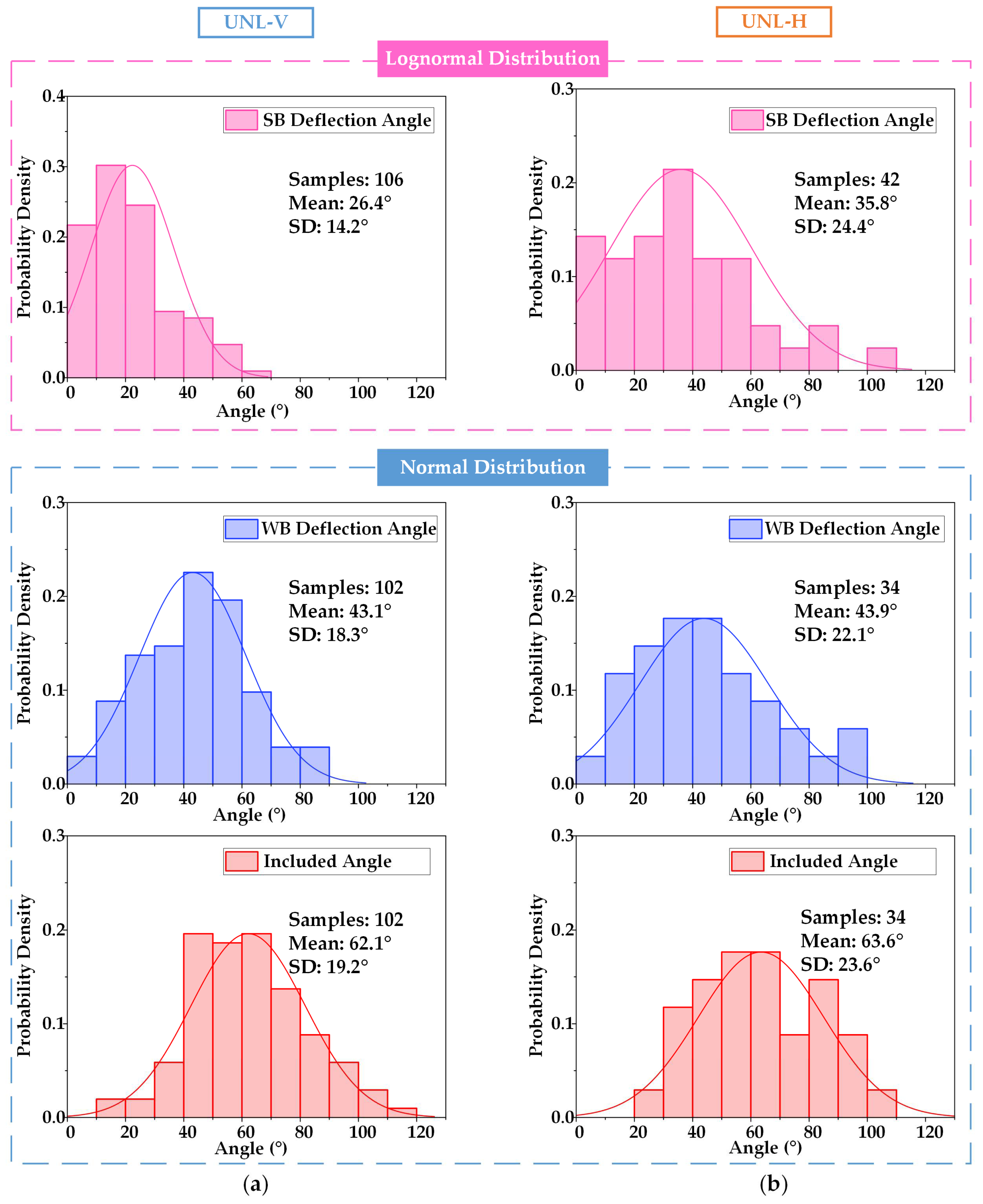
- The distribution of SB deflection angle approximately conforms to the lognormal distribution. WB deflection and included angles are in line with normal distribution. SBs tend to propagate along the previous direction of leader development with a lower deflection angle than WBs by over 10°.
- Similarities of branching morphology have been found in UNL-H, UNL-V, and DNL-S, with the mean values of near 30°, 45°, and 60°, for SB deflection angle, WB deflection angle, and included angle, respectively. In contrast, the branches of DNL-M tend to have less dispersion of angle distributions and propagations along the previous leader’s direction.
- The velocity of the four categories of negative leaders with different propagation directions could be affected by branching behaviors. When two or more branching behaviors occur, there is a downtrend in the leader velocity, and the branching behaviors of DNL-M have minimal impact on its velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berger, K. Novel observations on lightning discharges: Results of research on Mount San Salvatore. J. Frankl. Inst. 1967, 283, 478–525. [Google Scholar] [CrossRef]
- Orville, R.E.; Idone, V.P. Lightning leader characteristics in the thunderstorm research international program (TRIP). J. Geophys. Res. Ocean. 1982, 87, 11177–11192. [Google Scholar] [CrossRef]
- Rakov, V.A.; Uman, M.A. Lightning: Physics and Effects; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Hare, B.M.; Scholten, O.; Dwyer, J.; Ebert, U.; Nijdam, S.; Bonardi, A.; Buitink, S.; Corstanje, A.; Falcke, H.; Huege, T.; et al. Radio emission reveals inner meter-scale structure of negative lightning leader steps. Phys. Rev. Lett. 2020, 124, 105101. [Google Scholar] [CrossRef]
- Shindo, T. Lightning striking characteristics to tall structures. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 938–947. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Su, R.; Wang, J.; Wang, F.; Cai, L.; Zhao, Y.; Huang, Y. Observation of five types of leaders contained in a negative triggered lightning. Sci. Rep. 2022, 12, 6299. [Google Scholar] [CrossRef]
- Hill, J.; Uman, M.; Jordan, D. High-speed video observations of a lightning stepped leader. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Petersen, D.A.; Beasley, W.H. High-speed video observations of a natural negative stepped leader and subsequent dart-stepped leader. J. Geophys. Res. Atmos. 2013, 118, 12,110–112,119. [Google Scholar] [CrossRef]
- Biagi, C.; Uman, M.; Hill, J.; Jordan, D. Negative leader step mechanisms observed in altitude triggered lightning. J. Geophys. Res. Atmos. 2014, 119, 8160–8168. [Google Scholar] [CrossRef]
- Qi, Q.; Lu, W.; Ma, Y.; Chen, L.; Zhang, Y.; Rakov, V.A. High-speed video observations of the fine structure of a natural negative stepped leader at close distance. Atmos. Res. 2016, 178, 260–267. [Google Scholar] [CrossRef]
- Khounate, H.; Nag, A.; Plaisir, M.N.; Imam, A.Y.; Biagi, C.J.; Rassoul, H.K. Insights on Space-Leader Characteristics and Evolution in Natural Negative Cloud-to-Ground Lightning. Geophys. Res. Lett. 2021, 48, e2021GL093614. [Google Scholar] [CrossRef]
- Krider, E.P.; Weidman, C.D.; Noggle, R.C. The electric fields produced by lightning stepped leaders. J. Geophys. Res. 1977, 82, 951–960. [Google Scholar] [CrossRef]
- Chen, M.; Takagi, N.; Watanabe, T.; Wang, D.; Kawasaki, Z.I.; Liu, X. Spatial and temporal properties of optical radiation produced by stepped leaders. J. Geophys. Res. Atmos. 1999, 104, 27573–27584. [Google Scholar] [CrossRef]
- Lu, W.; Wang, D.; Takagi, N.; Rakov, V.; Uman, M.; Miki, M. Characteristics of the optical pulses associated with a downward branched stepped leader. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Bazelyan, E.M.; Raizer, Y.P. Lightning Physics and Lightning Protection; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Jiang, R.; Qie, X.; Zhang, H.; Liu, M.; Sun, Z.; Lu, G.; Wang, Z.; Wang, Y. Channel branching and zigzagging in negative cloud-to-ground lightning. Sci. Rep. 2017, 7, 3457. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Jiang, R.; Qie, X.; Sun, Z.; Wang, D.; Srivastava, A. Development of side bidirectional leader and its effect on channel branching of the progressing positive leader of lightning. Geophys. Res. Lett. 2019, 46, 1746–1753. [Google Scholar] [CrossRef]
- Syssoev, A.; Iudin, D.; Bulatov, A.; Rakov, V. Numerical simulation of stepping and branching processes in negative lightning leaders. J. Geophys. Res. Atmos. 2020, 125, e2019JD031360. [Google Scholar] [CrossRef]
- Qie, X.; Zhang, Y. A review of atmospheric electricity research in China from 2011 to 2018. Adv. Atmos. Sci. 2019, 36, 994–1014. [Google Scholar] [CrossRef]
- Beasley, W.; Uman, M.A.; Rustan, P., Jr. Electric fields preceding cloud-to-ground lightning flashes. J. Geophys. Res. Ocean. 1982, 87, 4883–4902. [Google Scholar] [CrossRef]
- Wang, C.; Sun, Z.; Jiang, R.; Tian, Y.; Qie, X. Characteristics of downward leaders in a cloud-to-ground lightning strike on a lightning rod. Atmos. Res. 2018, 203, 246–253. [Google Scholar] [CrossRef]
- Cooray, V.; Arevalo, L. Modeling the stepping process of negative lightning stepped leaders. Atmosphere 2017, 8, 245. [Google Scholar] [CrossRef] [Green Version]
- Schonland, B. The lightning discharge. Handb. Phys. 1956, 22, 576–628. [Google Scholar]
- Tran, M.; Rakov, V.; Mallick, S. A negative cloud-to-ground flash showing a number of new and rarely observed features. Geophys. Res. Lett. 2014, 41, 6523–6529. [Google Scholar] [CrossRef]
- Ding, Z.; Rakov, V.A.; Zhu, Y.; Tran, M.D. On a Possible Mechanism of Reactivation of Decayed Branches of Negative Stepped Leaders. J. Geophys. Res. Atmos. 2020, 125, e2020JD033305. [Google Scholar] [CrossRef]
- Ding, Z.; Rakov, V.; Zhu, Y.; Tran, M.; Kostinskiy, A.; Kereszy, I. Evidence and inferred mechanism of collisions of downward stepped-leader branches in negative lightning. Geophys. Res. Lett. 2021, 48, e2021GL093295. [Google Scholar] [CrossRef]
- Zhou, H.; Diendorfer, G.; Thottappillil, R.; Pichler, H.; Mair, M. Measured current and close electric field changes associated with the initiation of upward lightning from a tall tower. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Saba, M.M.; Schumann, C.; Warner, T.A.; Helsdon, J.H.; Orville, R.E. High-speed video and electric field observation of a negative upward leader connecting a downward positive leader in a positive cloud-to-ground flash. Electr. Power Syst. Res. 2015, 118, 89–92. [Google Scholar] [CrossRef]
- Visacro, S.; Guimaraes, M.; Murta Vale, M.H. Features of upward positive leaders initiated from towers in natural cloud-to-ground lightning based on simultaneous high-speed videos, measured currents, and electric fields. J. Geophys. Res. Atmos. 2017, 122, 12,786–712,800. [Google Scholar] [CrossRef]
- Nag, A.; Rakov, V.A. Positive lightning: An overview, new observations, and inferences. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Pu, Y.; Jiang, R.; Qie, X.; Liu, M.; Zhang, H.; Fan, Y.; Wu, X. Upward negative leaders in positive triggered lightning: Stepping and branching in the initial stage. Geophys. Res. Lett. 2017, 44, 7029–7035. [Google Scholar] [CrossRef]
- Huang, H.; Wang, D.; Wu, T.; Takagi, N. Formation Features of Steps and Branches of an Upward Negative Leader. J. Geophys. Res. Atmos. 2018, 123, 12,597–12,605. [Google Scholar] [CrossRef]
- Wu, T.; Wang, D.; Takagi, N. Upward negative leaders in positive upward lightning in winter: Propagation velocities, electric field change waveforms, and triggering mechanism. J. Geophys. Res. Atmos. 2020, 125, e2020JD032851. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, X.; Hao, Y.; Cai, H.; Liu, G.; Liao, M.; Qu, L. High-speed video observations of branching behaviors in downward stepped leaders and upward connecting leaders in negative natural lightning. J. Atmos. Sol.-Terr. Phys. 2019, 183, 61–66. [Google Scholar] [CrossRef]
- Mansell, E.R.; MacGorman, D.R.; Ziegler, C.L.; Straka, J.M. Simulated three-dimensional branched lightning in a numerical thunderstorm model. J. Geophys. Res. Atmos. 2002, 107, ACL 2-1–ACL 2-12. [Google Scholar] [CrossRef]
- Qie, X.; Yuan, S.; Zhang, H.; Jiang, R.; Wu, Z.; Liu, M.; Sun, Z.; Pu, Y.; Li, J.; Srivastava, A.; et al. Propagation of positive, negative, and recoil leaders in upward lightning flashes. Earth Planet. Phys. 2019, 3, 102–110. [Google Scholar] [CrossRef]
- Scholten, O.; Hare, B.; Dwyer, J.; Liu, N.; Sterpka, C.; Kolmašová, I.; Santolík, O.; Lán, R.; Uhlíř, L.; Buitink, S. A distinct negative leader propagation mode. Sci. Rep. 2021, 11, 16256. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; D’Alessandro, F.; Zhao, X. A three-dimensional downward leader model incorporating geometric and physical characteristics. Electr. Power Syst. Res. 2018, 163, 10–17. [Google Scholar] [CrossRef]
- Adekitan, A.I.; Rock, M. The impact of space point definition on dynamic electro-geometrical model of lightning strike probability. Electr. Power Syst. Res. 2020, 184, 106336. [Google Scholar] [CrossRef]
- Williams, E.R. The tripole structure of thunderstorms. J. Geophys. Res. Atmos. 1989, 94, 13151–13167. [Google Scholar] [CrossRef]
- Kawasaki, Z.; Matsuura, K. Does a lightning channel show a fractal? Appl. Energy 2000, 67, 147–158. [Google Scholar] [CrossRef]
- Rahiminejad, A.; Vahidi, B.; He, J. A fractal-based stepped downward leader model including branched channel charge distribution and branch fading. Electr. Power Syst. Res. 2019, 176, 105940. [Google Scholar] [CrossRef]
- Shi, W.; Li, Q.; Zhang, L. A stepped leader model for lightning including charge distribution in branched channels. J. Appl. Phys. 2014, 116, 103303. [Google Scholar] [CrossRef]
- Nguyen, D.; Deegan, G.; D’Alessandro, F. Fractal nature of probabilistic model of lightning discharge. In Proceedings of the IEEE Region 10 International Conference on Electrical and Electronic Technology, Singapore, 19–22 August 2001; pp. 814–818. [Google Scholar]
- Li, J.; Yang, Q.; Sima, W.; Sun, C.; Yuan, T.; Zahn, M. A new estimation model of the lightning shielding performance of transmission lines using a fractal approach. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1712–1723. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, X.; Wang, B.; Hao, X.; Zheng, S.; Xie, Y.Z. A three-dimensional direct lightning strike model for lightning protection of the substation. IET Gener. Transm. Distrib. 2021, 15, 2760–2772. [Google Scholar] [CrossRef]
- Ioannidis, A.I.; Tsovilis, T.E. Shielding Failure of High-Voltage Substations: A Fractal-Based Approach for Negative and Positive Lightning. IEEE Trans. Ind. Appl. 2021, 57, 2317–2325. [Google Scholar] [CrossRef]
- Grigor’Ev, A.; Shiryaeva, S. The possible physical mechanism of initiation and growth of lightning. Phys. Scr. 1996, 54, 660. [Google Scholar] [CrossRef]
- Beroual, A.; Rakotonandrasana, J.; Fofana, I. Predictive dynamic model of the negative lightning discharge based on similarity with long laboratory sparks. Part 1: Physical process and modeling. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1551–1561. [Google Scholar] [CrossRef] [Green Version]





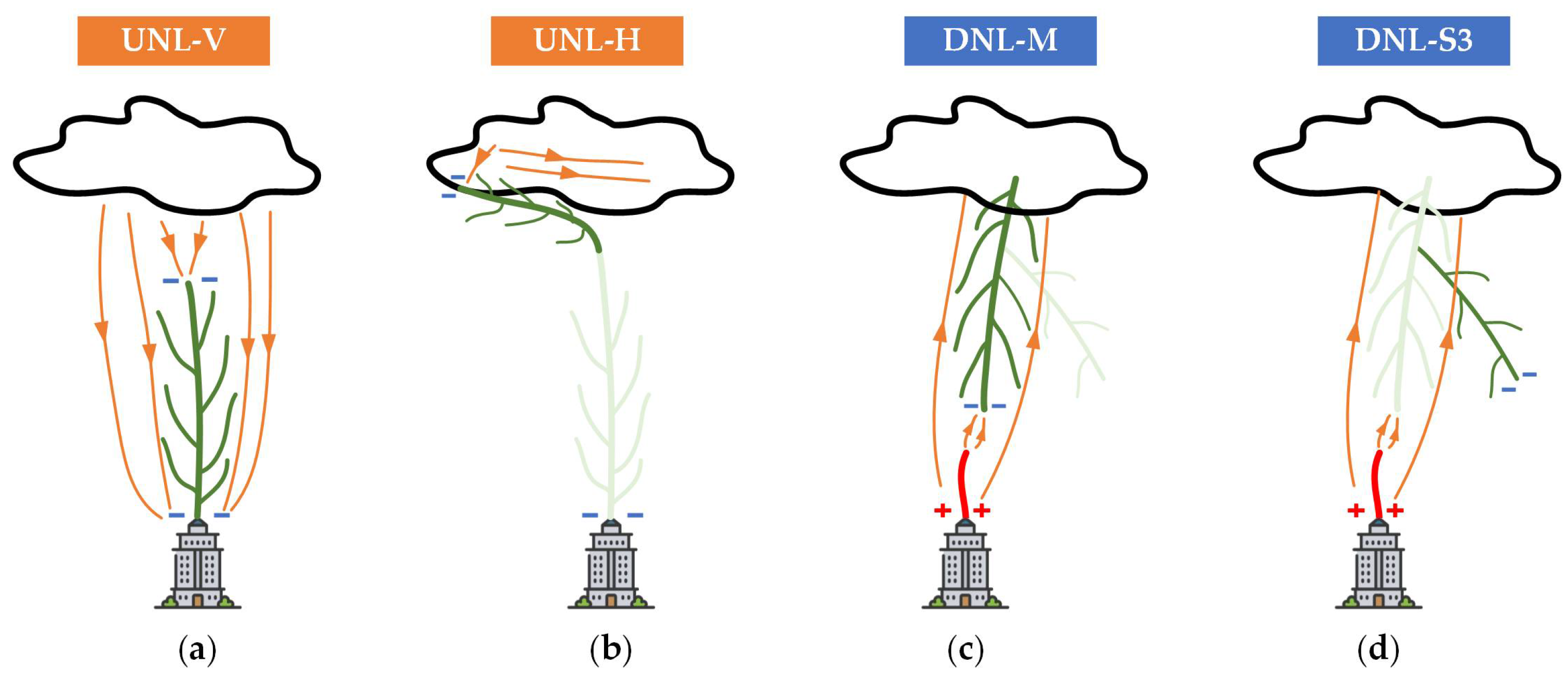
| Type of Negative Leaders | Origination Location | Polarity of Lightning | Direction of Propagation | Probability of Occurrence |
|---|---|---|---|---|
| DNL | Inside the Thundercloud | Negative | Downward | 70–90% |
| UNL | Grounded Buildings | Positive | Upward | 10% |
| Case ID | Local Time | Temporal Resolution | Spatial Resolution | Recording Duration | FOV |
|---|---|---|---|---|---|
| DNL-20180702 | 13:22:42 on 2 July 2018 | 80 μs | 2.92 m | 3.5 ms | 2990 m × 2990 m |
| UNL-20190427 | 16:20:18 on 27 April 2019 | 74.07 μs | 2.78 m | 15 ms | 2780 m × 2847 m |
| Case ID | Leader Type | Number of Branches | Average Velocity (×105 m/s) |
|---|---|---|---|
| DNL-20180702 | DNL-M | 35 | 4.23 |
| DNL-S3 | 31 | 3.82 | |
| UNL-20190427 | UNL-V | 102 | 5.63 |
| UNL-H | 34 | 5.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, X.; Liu, X.; Liu, L.; Liu, G.; Liao, M.; Qu, L.; Luo, B.; Cai, H.; He, J.; et al. Branching Morphology of Negative Leaders with Different Propagation Directions in Natural Lightning. Atmosphere 2022, 13, 1217. https://doi.org/10.3390/atmos13081217
Liu Y, Wang X, Liu X, Liu L, Liu G, Liao M, Qu L, Luo B, Cai H, He J, et al. Branching Morphology of Negative Leaders with Different Propagation Directions in Natural Lightning. Atmosphere. 2022; 13(8):1217. https://doi.org/10.3390/atmos13081217
Chicago/Turabian StyleLiu, Yang, Xiankang Wang, Xiaopeng Liu, Lei Liu, Gang Liu, Mingchuan Liao, Lu Qu, Bing Luo, Hansheng Cai, Junjia He, and et al. 2022. "Branching Morphology of Negative Leaders with Different Propagation Directions in Natural Lightning" Atmosphere 13, no. 8: 1217. https://doi.org/10.3390/atmos13081217
APA StyleLiu, Y., Wang, X., Liu, X., Liu, L., Liu, G., Liao, M., Qu, L., Luo, B., Cai, H., He, J., & Chen, L. (2022). Branching Morphology of Negative Leaders with Different Propagation Directions in Natural Lightning. Atmosphere, 13(8), 1217. https://doi.org/10.3390/atmos13081217






