Non-Stationarity of Aerosol Extinction Coefficient per Unit of Mass in Autumn and Winter in Chengdu, China

Abstract

Based on hourly observation data from the aethalometer and GRIMM180 environment particle monitor as well as the simultaneous data of visibility (V), relative humidity (RH) and nitrogen dioxide (NO₂) from October to December in 2017 in Chengdu, the corresponding time series of aerosol extinction coefficient per unit of mass is retrieved. The generalized additive models (GAMs) are adopted to analyze the non-stationarity of the time series of aerosol extinction coefficient per unit of mass and to explore the responses of the aerosol extinction coefficient per unit of mass to the aerosol component structure factors (ρ_BC/ρ_PM10, ρ_PM1/ρ_PM2.5, ρ_PM1~2.5/ρ_PM2.5 and ρ_PM2.5/ρ_PM10; ρ represents particle mass concentration) and RH. The results show that through the comparative analysis of stationary and non-stationary models, the time series of aerosol extinction coefficient per unit of mass in autumn and winter in Chengdu is non-stationary. In addition, the RH and aerosol component structure factors are all significant nonlinear covariates that affect the non-stationarity of the aerosol extinction coefficient per unit of mass. According to the influence of covariates, the sequence is as follows: RH > ρ_BC/ρ_PM10 > ρ_PM2.5/ρ_PM10 > ρ_PM1/ρ_PM2.5. At PM_2.5 pollution concentration (ρ_PM2.5 > 75 μg m⁻³), according to the influence of covariates, the sequence is as follows: RH > ρ_PM1~2.5/ρ_PM2.5 > ρ_BC/ρ_PM10 > ρ_PM2.5/ρ_PM10. Moreover, the interaction between RH and aerosol component structure factors significantly affects the aerosol extinction coefficient per unit of mass. The condition of high RH, high ρ_PM2.5/ρ_PM10, high ρ_PM1/ρ_PM2.5 and low ρ_BC/ρ_PM10 has a synergistic amplification effect on the increase of the aerosol extinction coefficient per unit of mass. At PM_2.5 pollution concentration, the synergistic effect of high RH, high ρ_PM2.5/ρ_PM10, high ρ_PM1~2.5/ρ_PM2.5 and low ρ_BC/ρ_PM10 is beneficial to the increase of the aerosol extinction coefficient per unit of mass.

1. Introduction

The atmospheric extinction coefficient is a physical quantity commonly used to measure the absorption or scattering of the solar radiation of gas molecules and particles in the atmosphere, and it is a decisive factor in the evolution of visibility [1,2,3]. Atmospheric extinction is composed of atmospheric molecular extinction and aerosol extinction, of which the latter typically accounts for more than 90%. Therefore, aerosol extinction makes up the main part of atmospheric extinction [4,5]. Aerosol extinction is not only an important indicator of the environmental air quality in autumn and winter, but also has a substantial impact on human health and traffic safety. This issue has always been a hot topic in the studies of environmental meteorology [6,7].

As early as 1982, Sun et al. [8] theoretically proposed the relationship between the extinction coefficient and the mass concentration of particulate matter. On this basis, many scholars [9,10] have used the measured particle spectrum distribution, visibility (V), relative humidity (RH) and aerosol mass concentration to complete further verifications and analyses. As a result, consensus has been reached that there is a good correlation between the aerosol extinction coefficient and the mass concentration of particulate matter, especially the concentration of fine particulate matter [11,12,13,14]. Yao et al. [15] showed that the extinction coefficient is not entirely dependent on the mass concentration of particulate matter, but is also affected by the RH, particulate matter compositions and particle size. After excluding the influence of mass concentration of particulate matter, Sun et al. [16] pointed out that the time series of aerosol extinction coefficient per unit of mass is still stochastic, and its evolution shows a complicated dynamic mechanism.

The complex evolution of the aerosol extinction coefficient per unit of mass is affected by many factors, among which the RH plays an important role. The particle-size spectrum, refractive index and other parameters of aerosols can be characterized by the functions of RH [17]. As the RH changes, the statistical characteristics of the aerosol extinction coefficient per unit of mass also exhibit systematic changes. Aerosols can deliquesce and weather with the changes of RH. After reaching the deliquescent point, the particle size of aerosols increases rapidly, leading to an increase in the scattering and absorption cross-sections and enhanced extinction ability [18,19]. Cui et al. [20] studied changes in the atmospheric extinction coefficient per unit of mass with the RH in Chengdu and found that the RH corresponding to the deliquescent point of particulate matter is 40%. Above this value, the aerosol can experience an obvious hygroscopic growth. Besides, the hygroscopic growth not only changes the particle-size distribution of aerosols, but also affects the chemical components of aerosols [21,22,23]. The RH influences the secondary formation of inorganic aerosols by affecting the heterogeneous liquid-phase reaction on the aerosol surface. Higher RH promotes the accumulation of secondary inorganic components (sulfate, nitrate and ammonium salt) on the aerosol surface, leading to an increase in the PM_2.5 concentration [24,25]. Liu et al. [26] analyzed the influence of RH on the concentration of particulate matter in winter in Chengdu and pointed out that with the increase of RH, ρ_PM2.5/ρ_PM10 increases significantly, and higher RH will worsen the pollution of fine particulate matter. The aerosol hygroscopic properties have both physical and chemical effects on the evolution of the aerosol extinction coefficient. However, systematic analysis of the dynamic process of the combined effect of the two remains rather limited in China.

Now, although there are some theoretical and application studies on the aerosol extinction coefficient per unit of mass, the analysis of the non-stationarity of aerosol extinction coefficient per unit of mass is still rare. Stationarity is one of the most important characteristics of time series [27]. It describes the property that the statistical characteristics of random processes do not change with time. If the statistical characteristics of the data change with time, the time series is non-stationary. The nonstationarity of the aerosol extinction coefficient per unit of mass is an important part of its randomness study and is the basis of building a visibility prediction model. Relevant research is of great significance to clarify the evolution mechanism of haze. Therefore, based on the stationarity analysis of the extinction coefficient series of unit mass aerosol, this study discusses the important factors and mechanisms for its evolution. The remainder of this paper is organized as follows. The data and methodology are described in Section 2. The nonstationarity of the aerosol extinction coefficient per unit of mass and its attribution are displayed in Section 3. The summary and discussion are presented in Section 4.

2. Materials and Methods

2.1. Study Area

The Sichuan Basin is bordered by the Qinghai–Tibet Plateau and the Hengduan Mountains in the west, the Qinba Mountains in the north, the mountains in Hunan, Hubei and Shaanxi in the east, and the Yungui Plateau in the south. The special geographical location and topography have created a calm and stable climate background in autumn and winter in this area, and it is one of the five areas with the most frequent haze in China [28,29]. Located at the bottom of the Sichuan Basin, Chengdu is the socio-economic and cultural center of Sichuan Province. Figure 1 shows distributions of topography, relative humidity and wind in Chengdu.The climate characteristics of Chengdu in autumn and winter are dominated by calm winds and high humidity [30,31]. The annual average wind speed in Chengdu is 1.4 m s⁻¹, and the proportion of wind speeds less than 1.5 m s⁻¹ in autumn and winter is as high as 67%. The annual average relative humidity is 81.5%, which is the highest in the Chengdu Plain urban agglomeration. The average relative humidity in autumn and winter is 83.5%. In addition, the frequent occurrence of temperature inversion in the Sichuan Basin forces the local secondary circulation to be confined within the atmospheric boundary layer, which is not conducive to the diffusion and transfer of pollutants [28,32]. Therefore, Chengdu is also a large-value center of particulate matter concentration in autumn and winter. The study of the stationarity of the time series of the aerosol extinction coefficient per unit of mass in autumn and winter in Chengdu provides a reference for understanding the characteristics of the aerosol extinction coefficient per unit of mass and the driving force for its evolution.

2.2. Data

The data used in this study include the hourly observational data from the aethalometer and GRIMM180 environment particle monitor, as well as the simultaneous data of V, RH and nitrogen dioxide (NO₂) from October to December in 2017 in Chengdu. The available quantities of particulate matter concentration and meteorological factor data are ρ_BC: 2178, ρ_PM1: 2142, ρ_PM2.5: 2144, ρ_PM10: 2144, ρ_NO2: 2105, RH: 2183, and V:2144. The related instruments are introduced as follows.

(1)

The AE-31 black carbon (BC) detector (MAGEESCIENTIFIC Company, Berkeley, CA, USA) observes the mass concentration of BC, and the data collection frequency is 5 min/time. The BC meter uses a total suspended particulate cutting head, and a silicone tube is added between the sampling head and the instrument to reduce the influence of moisture on the BC measurement.

(2)

The GRIMM180 environmental particulate monitor (GRIMM, Ainring, Germany) can measure the mass concentration of PM₁₀, PM_2.5 and PM₁ in the atmosphere with a data frequency of 5 min/time.

(3)

Atmospheric visibility was monitored by SWS-200 visibility instrument (Biral company, Bristol, UK), relative humidity was monitored by WS600 integrated weather station (LUFFT Company, Fellbach, Germany), and the concentration of gaseous pollutants (NO₂) was monitored by chemiluminescence NO and NO₂-NO_X analyzer (ThermoFisher Scientific, MA, USA).

The observation site is located on the roof of the comprehensive building of the Chengdu Academy of Environmental Sciences (30°39′ N, 104°02′ E), 21 m above the ground. There are no tall buildings within 2 km, and the visual field is wide. The observation site is within the First Ring Road of Chengdu. There are concentrated residential areas around, and there are no obvious industrial air pollution sources within 5 km. Appendix A provides detailed information on relevant instruments. The monitoring data mentioned above were uniformly processed into hourly average data. First, all data with the weather conditions of precipitation, dust, and strong winds were eliminated. Then, continuous, unchanged data and missing data were eliminated. Finally, 1466 matching samples were obtained.

2.3. Calculation of the Aerosol Extinction Coefficient per Unit of Mass

The atmospheric extinction coefficient is the attenuation of light per unit of distance caused by the absorption and scattering of solar radiation by atmospheric pollutants. The atmospheric extinction coefficient can be derived from the Koschmieder relationship, which has been widely used in the field of atmospheric research [33,34,35]. From the research of Valentini et al. [36], it can be seen that the correlation coefficient between the theoretical atmospheric visibility and the measured visibility derived from the atmospheric extinction coefficient based on the Koschmieder relationship is 0.72, presenting a close correlation. When the contrast threshold μ is 0.05, the relationship between the atmospheric extinction coefficient b_ext (km⁻¹) and the atmospheric visibility V (km) at the wavelength of 550 nm is as follows [37].

$$b_{\mathrm{ext}}=\ln (1/\mathsf{\mu })/V$$

(1)

Atmospheric extinction is composed of molecular extinction and aerosol extinction, so the atmospheric extinction coefficient is decomposed as this equation:

$$b_{\mathrm{ext}}=b_{\mathrm{sg}}+b_{\mathrm{ag}}+b_{\mathrm{aer}}$$

(2)

b_sg is the scattering coefficient of dry and clean atmosphere, generally referring to Penndorf [38] for a value of 13 × 10⁻³ km⁻¹. b_ag is the absorption coefficient of gaseous pollutants. NO₂ is the main absorber of visible light in the atmospheric gaseous pollutants in the planetary boundary layer, so generally only the absorption of NO₂ is considered, and the absorption coefficient of NO₂ is used to represent the absorption coefficient of gaseous pollutants [36,39]. The mass concentration of NO₂ can be converted into the absorption coefficient of gaseous pollutants at 550 nm (km⁻¹) through calculation. The expression is as follows [39].

$$b_{\mathrm{ag}}=0.33{\rho }_{\mathrm{NO}2}$$

(3)

where ρ_NO2 is the mass concentration of NO₂ (μg m⁻³). b_aer is the aerosol extinction coefficient. According to Equation (2), the calculation formula of the aerosol extinction coefficient b_aer at the wavelength of 550 nm is as follows,

$$b_{\mathrm{aer}}=b_{\mathrm{ext}}-b_{\mathrm{sg}}-b_{\mathrm{ag}}$$

(4)

To eliminate the influence of the mass concentration on particulate matter, Equation (5) is used to obtain the aerosol extinction coefficient per unit of mass series (E).

$$E=b_{\mathrm{aer}}/{\rho }_{{\mathrm{PM}}_{10}}$$

(5)

where ρ_PM10 (μg m⁻³) is the particle mass concentration corresponding to b_aer (km⁻¹).

Aerosol scattering hygroscopic growth factor (f) is calculated according to Equation (6),

$$f=b_{\mathrm{sg},550\mathrm{nm}}(RH)/b_{\mathrm{sg},550\mathrm{nm}}(\mathrm{dry})$$

(6)

where b_sg,550nm(dry) is dry aerosol scattering extinction coefficient (km⁻¹) at 550 nm, which is calculated according to the literature [14]. b_sg,550nm (RH) is the aerosol scattering extinction coefficient (km⁻¹) at 550 nm under environmental conditions, which is calculated by an indirect method [40].

2.4. Generalized Additive Models

The package of “mgcv” in R Studio was used to fit the GAMs, which generalized multivariate regression by relaxing the assumptions of linearity and normality, replacing regression lines with a smooth line [41]. The model is very flexible, not established in advance, but driven by the research data. The expression is as follows.

$$g(\mu )=f_1(x_1)+f_2(x_2)+\dots +f_i(x_i)+X_j\theta +\alpha$$

(7)

where μ is the expected value of the aerosol extinction coefficient per unit of mass; g(μ) is the connection function; x₁, x₂, …, x_i are explanatory variables; f₁(), f₂(), …, f_i() are various smoothing functions of the complex nonlinear relationship between the response variable and the explanatory variables; X_jθ represents the components of the full-parameter model; and α represents the residual.

The significance of the influence of different explanatory variables on the change of the aerosol extinction coefficient per unit of mass and the fitting goodness of the model are determined by the F statistic value, p value, R² and explained variance given by GAMs [42,43]. The greater the F statistic value is, the greater the relative importance is. The p value is a parameter used to judge the result of the hypothesis test. The smaller the p value is, the more significant the result is. The R² is the ratio of the regression square sum to the deviation square sum and its value is between 0 and 1. The closer to 1 the R² is, the better the fitting effect of the model is. The higher the explained variance is, the better the fitting effect is. In addition, when the estimated degree of freedom (Edf) of the explanatory variable is 1, it indicates that the explanatory variable has a linear relationship with the response variable; when the Edf is greater than 1, the relationship is non-linear. At the same time, the Akaike’s information criterion (AIC) [44] is used as the evaluation index of the GAMs. The lower the AIC value is, the better the model performs.

2.5. Candidate Explanatory Variables

For urban aerosols, when the emission source is relatively fixed, the mass concentration of particulate matter, physical and chemical structure and other factors will all change significantly due to the influence of meteorological conditions [45]. Since this study is about the aerosol extinction coefficient per unit of mass, the influence of the mass concentration of particulate matter has been excluded. Therefore, this study mainly considers the change characteristics of the aerosol extinction coefficient per unit of mass from three aspects of time (T), RH and aerosol components. The past studies [46] have shown that the ratio of particle mass concentration can characterize the information of aerosol components to a certain extent, so in this study T, RH, ρ_BC/ρ_PM1, ρ_BC/ρ_PM10, ρ_BC/ρ_PM2.5, ρ_PM1/ρ_PM2.5, ρ_PM1/ρ_PM10 and ρ_PM2.5/ρ_PM10 are used as the initial explanatory variables for the extinction coefficient of aerosol per unit of mass. Note that except for the variable T, the other variables are collectively referred to as environmental meteorological factors. Except for the variables T and RH, the other variables are collectively referred to as aerosol component structure factors.

Figure 2 shows the frequency histogram and kernel density curve of the aerosol extinction coefficient per unit of mass and the environmental meteorological factors. Seen from Figure 2a, the aerosol extinction coefficient per unit of mass shows a right-skewed characteristic, so it is preliminarily set that the change of the extinction coefficient per unit of mass conforms to the Gamma distribution. In Figure 2a, the red curve is the density distribution curve fitted by Gamma, which is consistent with the kernel density curve. Therefore, in this study the Gamma function is selected as the distribution function of GAMs. At the same time, from the frequency histogram and kernel density curve of environmental meteorological factors, it can be observed that all factors are similar to the distribution of the aerosol extinction coefficient per unit of mass, which basically conforms to the Gamma distribution pattern. Therefore, in this study the identity link function is used as the link function and the explanatory variables are connected to the response variables that obey the Gamma distribution through a linear combination. Figure 3 presents the framework of non-stationarity analysis of the aerosol extinction coefficient per unit of mass.

3. Results

3.1. Identification of Non-Stationarity

The statistical test provides a preliminary analysis of the non-stationarity of the time series of aerosol extinction coefficient per unit of mass. Firstly, the Mann–Kendall trend test [47] was used to identify the trend of the aerosol extinction coefficient per unit of mass in autumn and winter in Chengdu. The results show that the time series of the aerosol extinction coefficient per unit of mass indicates Z = −14.43, which exceeds the critical value of Z = 1.96 (with the significance level of α = 0.05) and presents a significant descending trend. Therefore, the time series of aerosol extinction coefficient per unit of mass can be regarded as a non-stationary series. To further identify its non-stationary characteristics, the stationary model and time-varying non-stationary model are established, respectively: (1) stationary model M_0, with the parameters being constant; (2) linear time-varying model M_T, with the parameters changing as a linear function of time; and (3) non-linear time-varying model M_s(T), in which the parameters change as a non-linear function of time. The model-fitting results are shown in Figure 4 and

Table 1. Summary of the fitting parameters for the stationary and time-varying models.

Model	μ	p	R2	Deviance Explained	AIC
M_0	5.28	<2 × 10−16	0	0	5806.682
M_T	6.42–0.002T	<2×10−16	0.10	12.90%	5601.626
M_s(T)	5.28 + s(T)	<2×10−16	0.13	17.30%	5539.449

. Among the three models, the AIC value of M_s(T) is the smallest, indicating that the parameters for the time series of the aerosol extinction coefficient per unit of mass are time dependent. The non-stationary model performs better than the stationary model, and the time series of aerosol extinction coefficient per unit of mass has nonstationarity. At the same time, it can be seen from the curves that the nonlinear time-varying model can better capture the variation trend of the data than the linear time-varying model, and the variation of model parameters shows a nonlinear relationship with time.

3.2. Attribution Analysis of Non-Stationarity

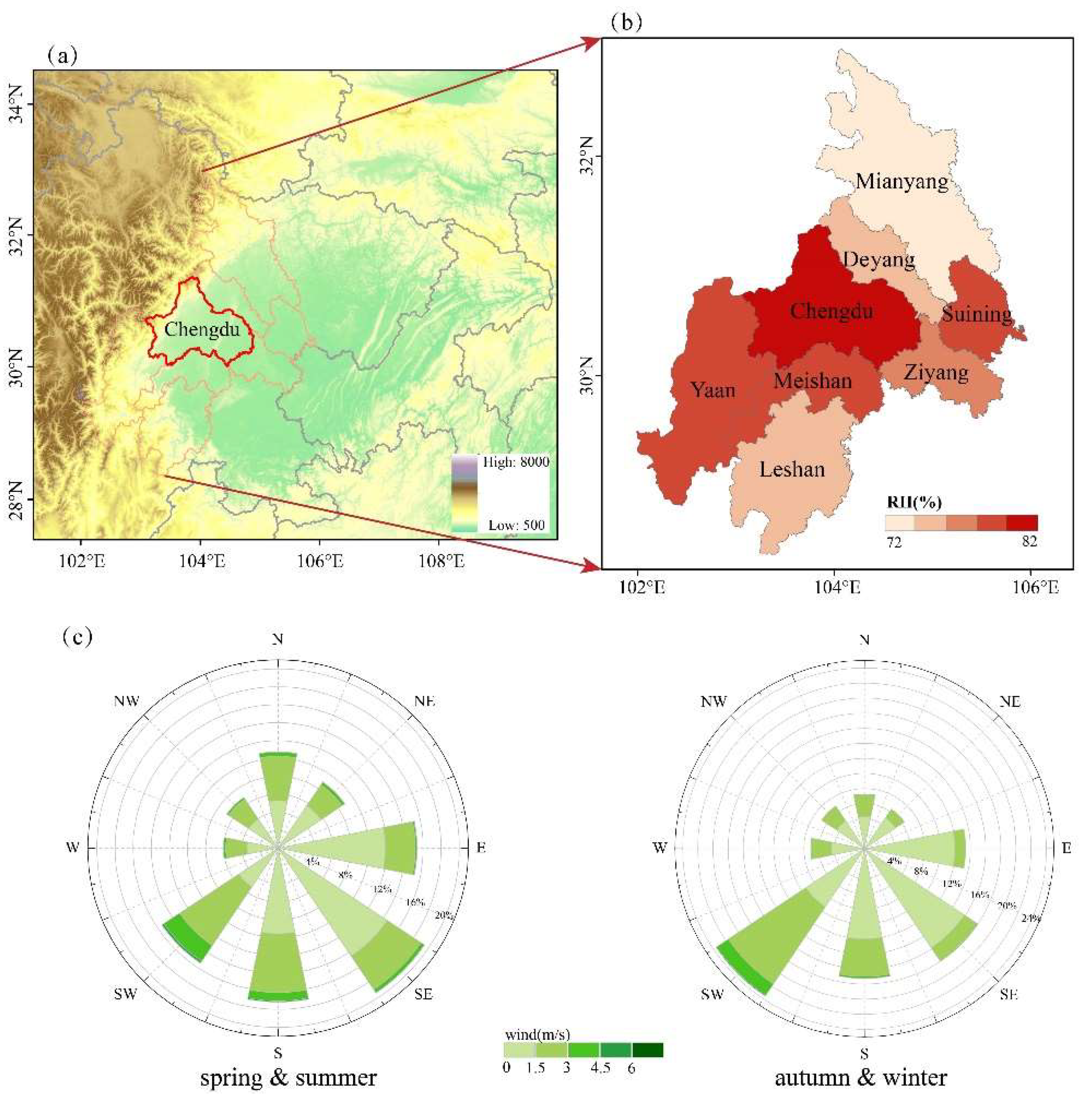
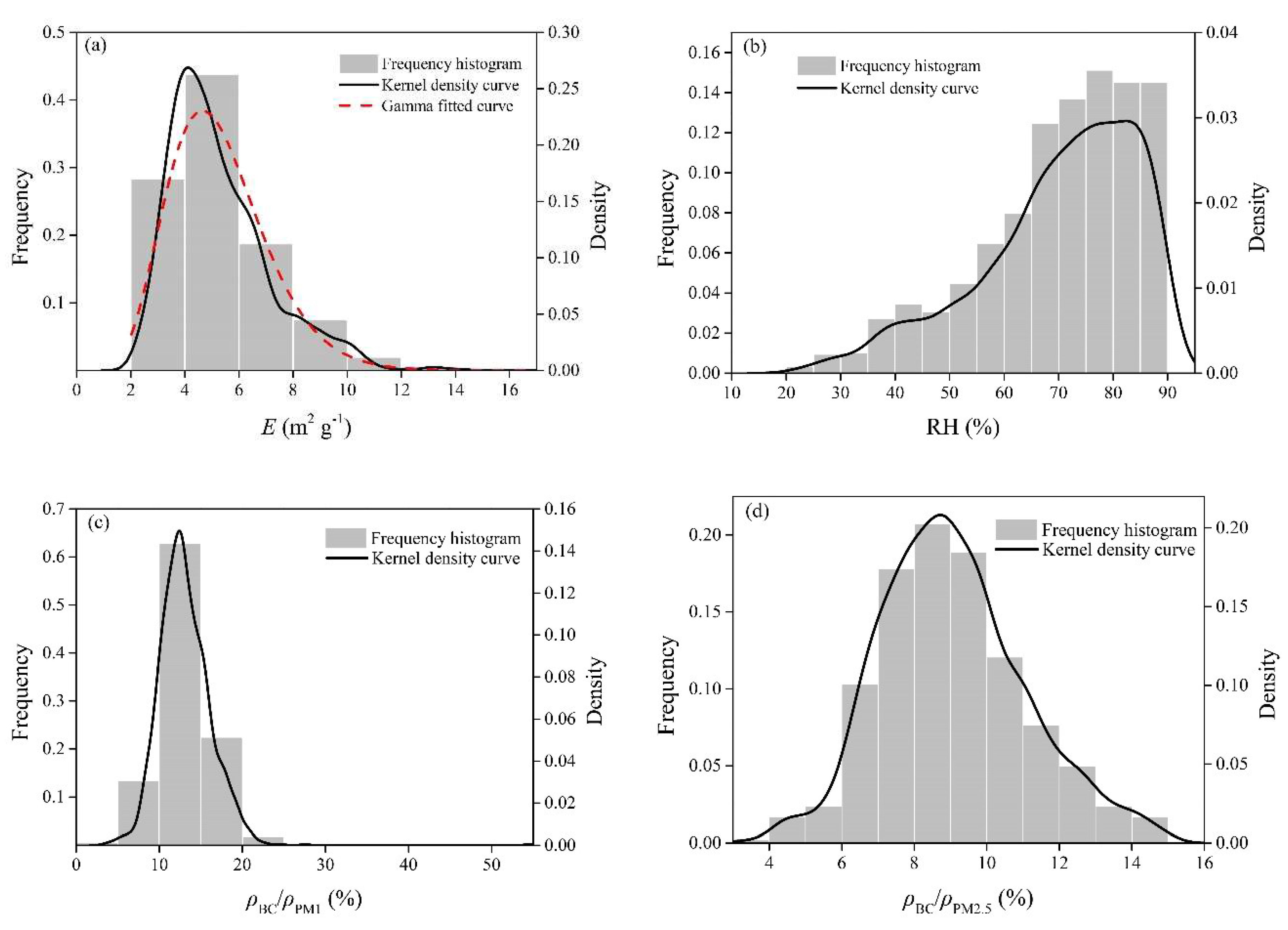
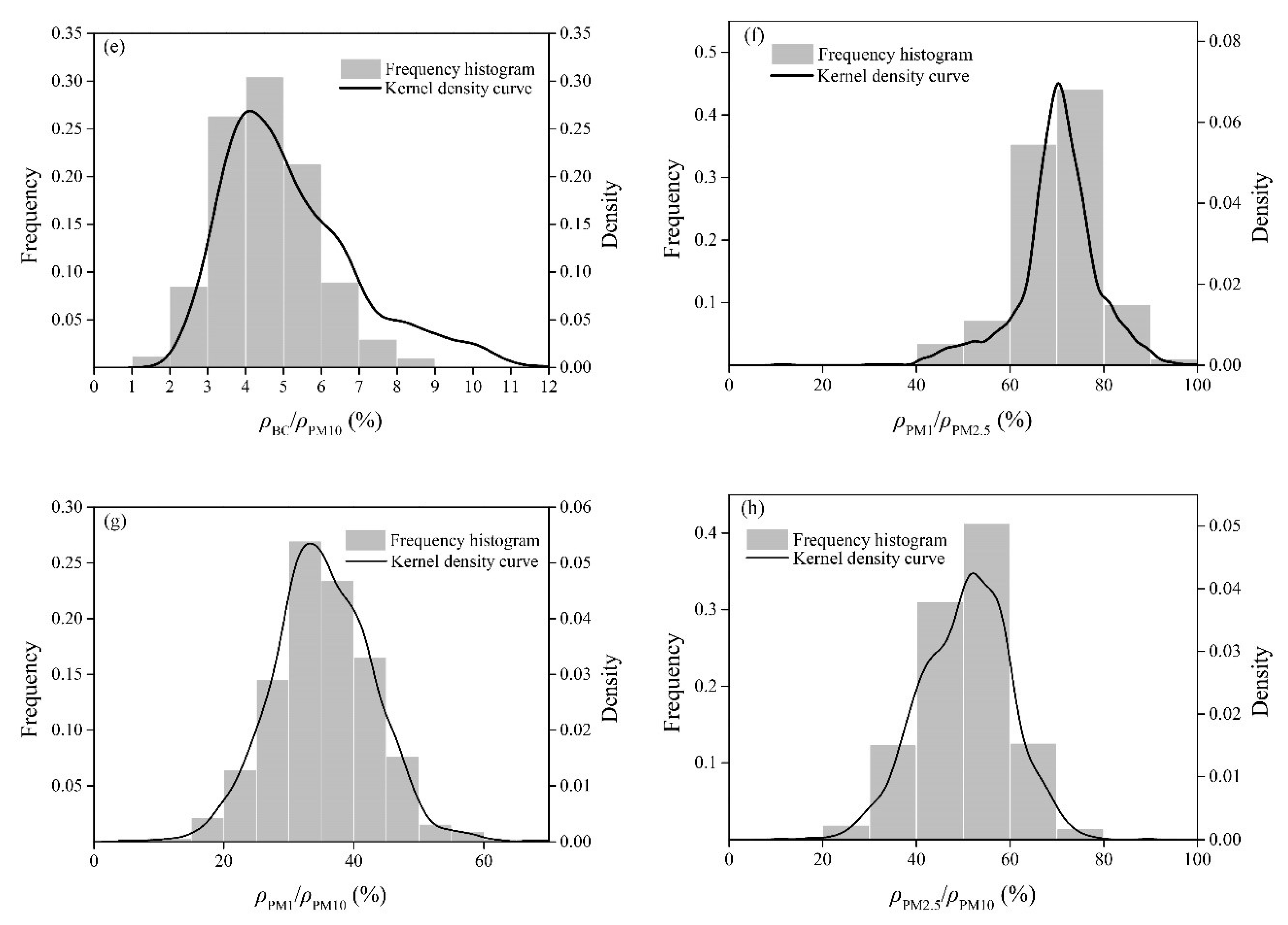
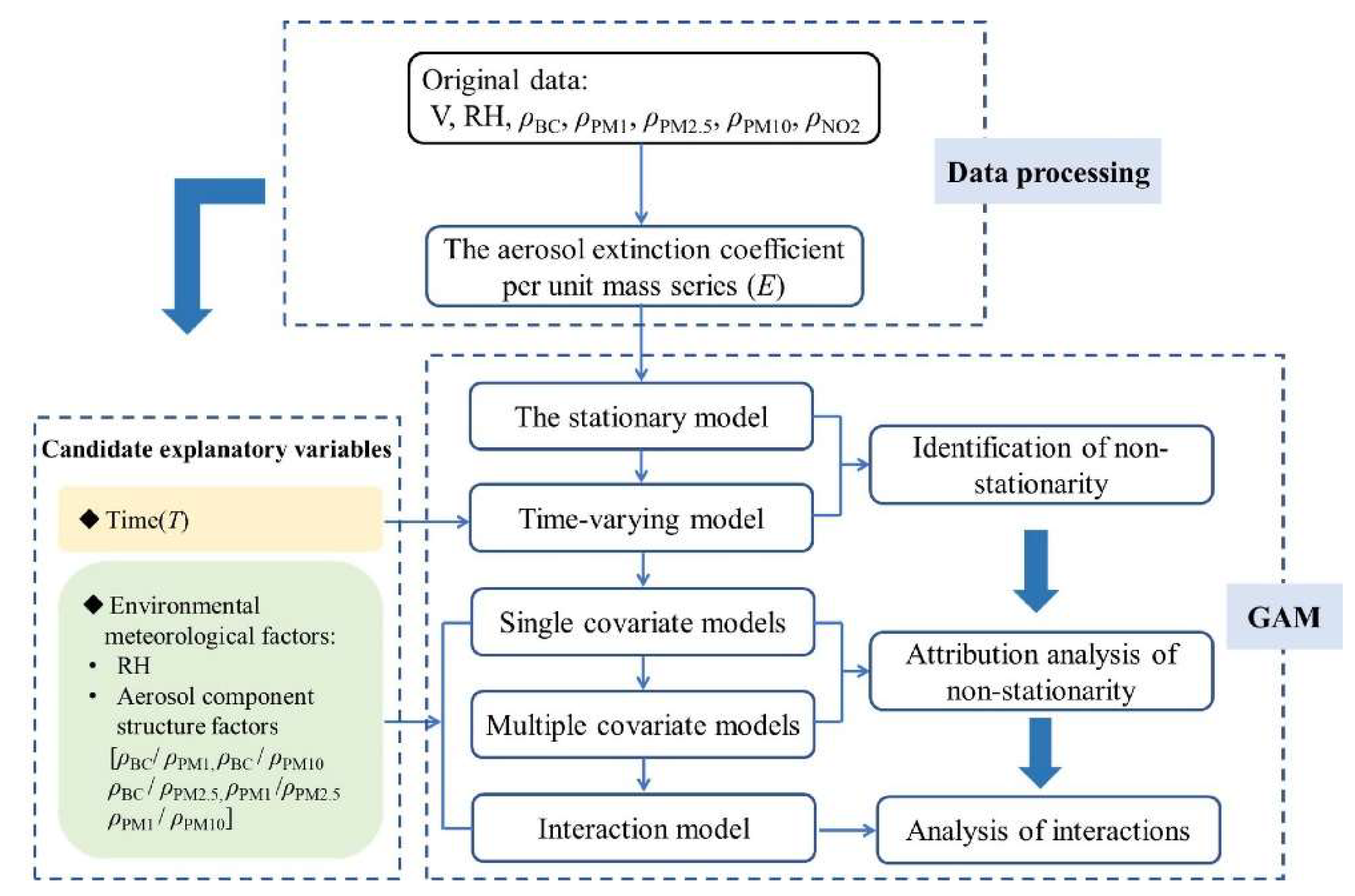
3.2.1. Single Covariate Models

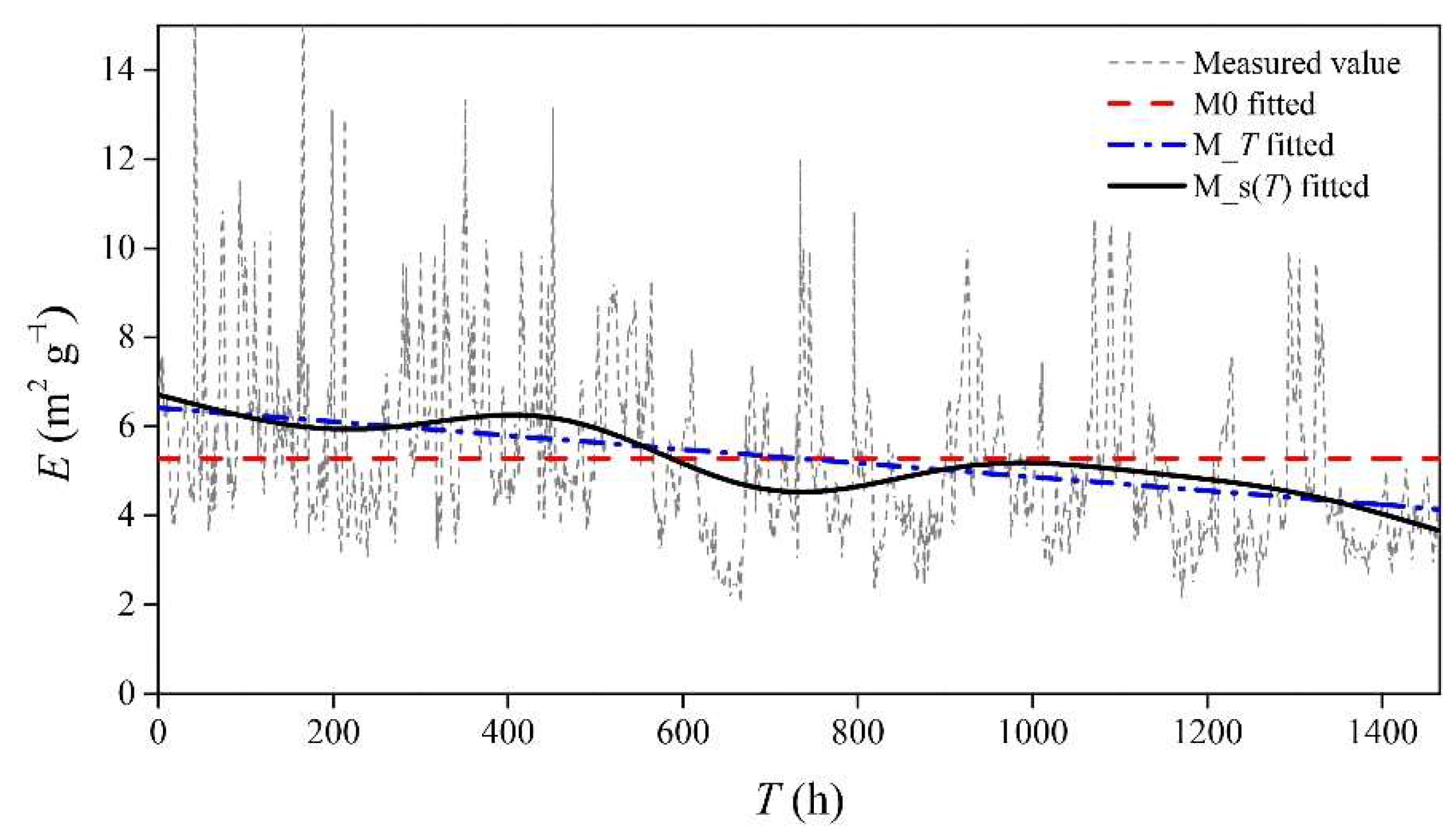
From the fitting results of the nonlinear time-varying model in Section 3.1, it can be seen that the R² and explained variance of the model are only 0.13 and 17.3%, respectively, indicating that the variable T does not have the best explanatory effect on the non-stationary change of the aerosol extinction coefficient per unit of mass. Therefore, this study introduces environmental meteorological factors RH, ρ_BC/ρ_PM1, ρ_BC/ρ_PM2.5, ρ_BC/ρ_PM10, ρ_PM1/ρ_PM2.5, ρ_PM1/ρ_PM10 and ρ_PM2.5/ρ_PM10 as initial explanatory variables to discuss the causes for the nonstationarity of the aerosol extinction coefficient per unit of mass. Due to the selection of many initial explanatory variables, there may be a problem of collinearity among the variables. This study uses the variance expansion factor (VIF) to analyze the multicollinearity of the variables and eliminates the explanatory variables with multicollinearity [48]. When the value of VIF is closer to 1, the multicollinearity is lighter, and vice versa. Therefore, the VIF of the final selection factor in this study does not exceed 3. Studies have shown [49] that ρ_BC/ρ_PM10, ρ_PM1/ρ_PM2.5 and ρ_PM2.5/ρ_PM10 have a certain correlation with the equivalent complex refractive index of aerosols, so the environmental meteorological factors of ρ_BC/ρ_PM10, ρ_PM1/ρ_PM2.5 and ρ_PM2.5/ρ_PM10 are retained. According to the diagnosis results of VIF (

Table 2. VIF values of explanatory variables.

	RH	ρPM2.5/ρPM10	ρPM1/ρPM10	ρPM1/ρPM2.5	ρBC/ρPM10	ρBC/ρPM2.5	ρBC/ρPM1
Initial variables	1.26	76.72	93.08	38.14	41.75	37.99	10.15
Final variables	1.11	1.59	\	1.05	1.73	\	\

), the collinearity among the explanatory variables is reduced, and four factors of RH, ρ_BC/ρ_PM10, ρ_PM1/ρ_PM2.5 and ρ_PM2.5/ρ_PM10 are selected as the explanatory variables of the aerosol extinction coefficient per unit of mass. Among these factors, the maximum VIF is 1.73.

The aerosol extinction coefficient per unit of mass is used as the response variable, and one of the above four environmental meteorological factors is selected as an explanatory variable each time to establish a GAMs. The individual influence of each environmental meteorological factor is analyzed in

Table 3. Simulation results by the GAMs with single influencing factor.

Models	Variables	Edf	F	p	R2	Deviance Explained
M_RH	RH	8.87	313.10	<2 × 10−16	0.63	73.3%
M_ρBC/ρPM10	ρBC/ρPM10	6.80	12.41	<2 × 10−16	0.04	6.97%
M_ρPM1/ρPM2.5	ρPM1/ρPM2.5	8.38	7.88	<2 × 10−16	0.05	6.76%
M_ρPM2.5/ρPM10	ρPM2.5/ρPM10	4.01	11.57	<2 × 10−16	0.03	4.13%

. As can be seen, each explanatory variable has a significant impact on the aerosol extinction coefficient per unit of mass (passing the significance test of α = 0.01), The Edf of each variable is greater than 1, indicating a significant non-linear relationship between the aerosol extinction coefficient per unit of mass and these four environmental meteorological factors. Seen from Table 3, RH has the greatest influence on the change of aerosol extinction coefficient per unit of mass, and the influence of the aerosol component structure factors is relatively small.

3.2.2. Multiple Covariate Models

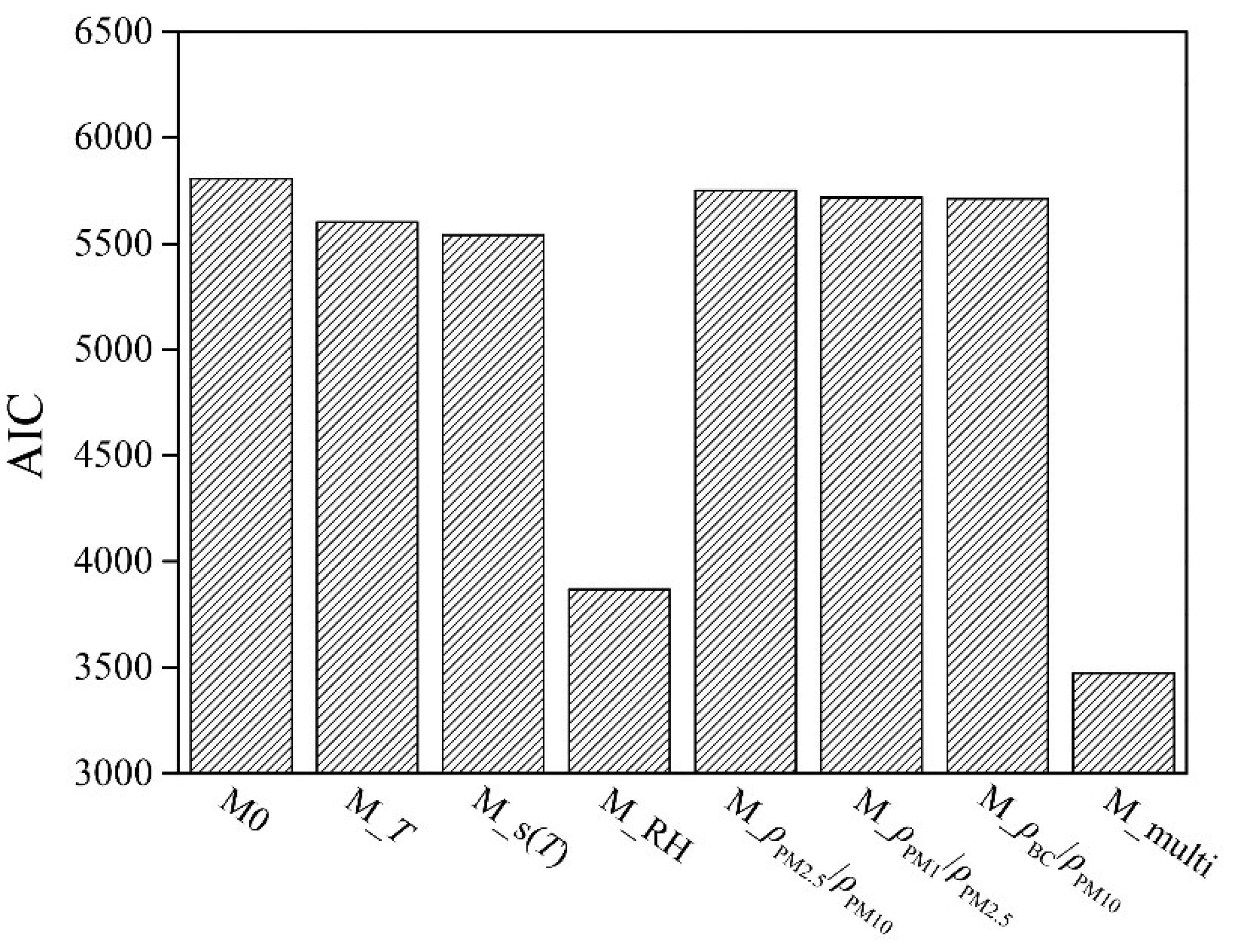
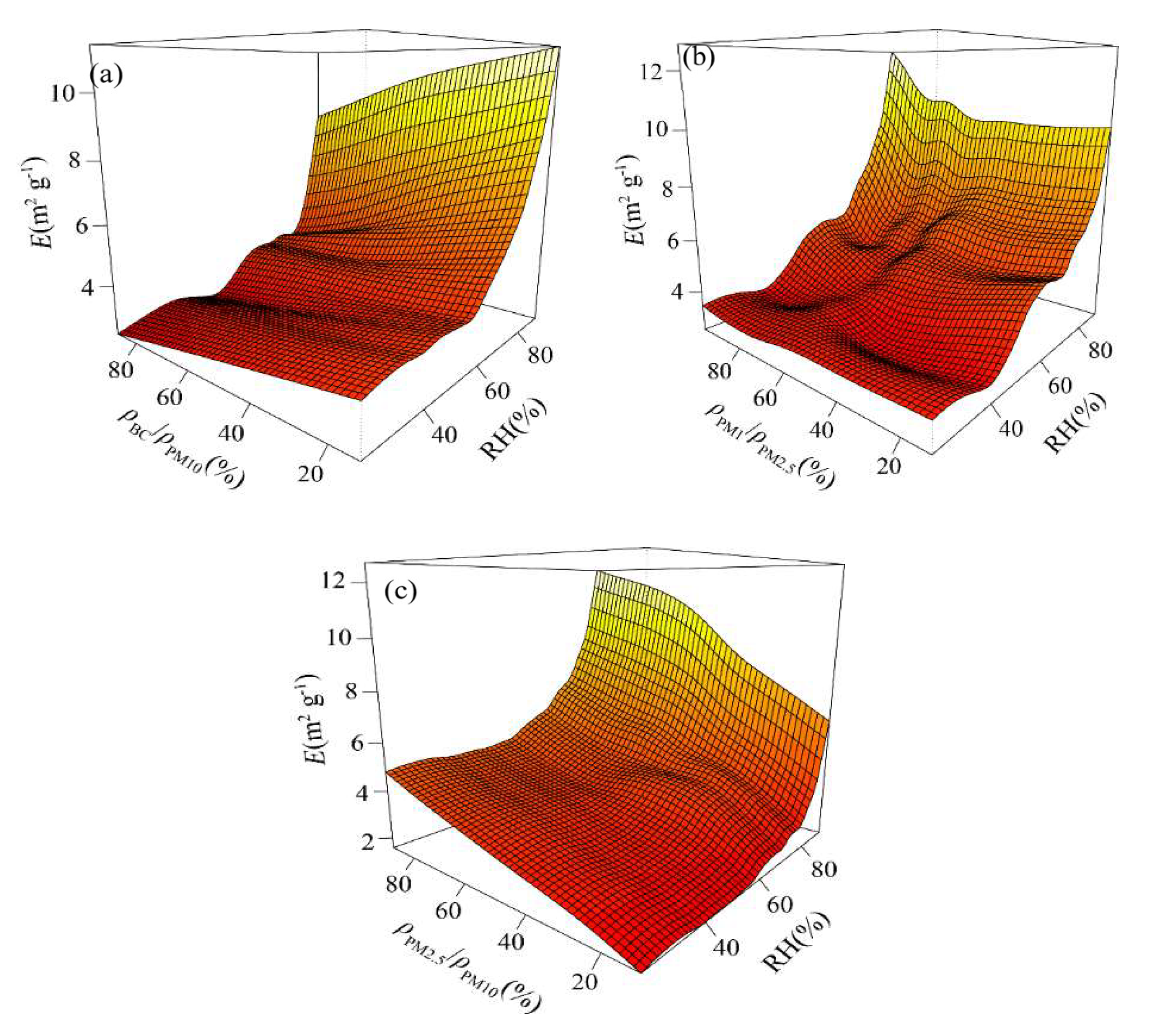
Furthermore, a multiple covariate non-stationary model is established based on the environmental meteorological factors. The AIC values of the stationary model, the time-varying non-stationary model and the non-stationary model based on the environmental meteorological factors are shown in Figure 5. The AIC value of the non-stationary model with the explanatory variable of RH is small and has a better-fitting effect. After adding the aerosol component structure factors, the AIC value of the multiple covariate model (M_multi) is reduced to the lowest. This shows that the RH plays an important role in the change of the aerosol extinction coefficient per unit of mass, but the role of the aerosol component structure factors cannot be ignored.

Table 4. Simulation results by the GAMs with multi-influencing factors.

Variables	RH	ρPM2.5/ρPM10	ρPM1/ρPM2.5	ρBC/ρPM10
Edf	8.86	7.36	6.82	4.70
F	313.36	18.07	2.37	5.81
p	<2 × 10−16	<2 × 10−16	0.0179	<2 × 10−16

shows the fitting results of the multiple covariate model, and the four environmental meteorological factors all pass the significance test of α = 0.05. As the Edf of each variable is greater than 1, there is a nonlinear relationship between the aerosol extinction coefficient per unit of mass and the four environmental meteorological factors. By comparing the statistical values of each variable F, it can be concluded that the sequence of the influence of each covariate on the aerosol extinction coefficient per unit of mass is as follows: RH > ρ_BC/ρ_PM10 > ρ_PM2.5/ρ_PM10 > ρ_PM1/ρ_PM2.5. The R² and explained variance of the model are 0.67 and 77.90%, respectively, both of which are much larger than those of the time-varying non-stationary model. This shows that the environmental meteorological factors can better characterize the non-stationary changes of the aerosol extinction coefficient per unit of mass than the time variable.

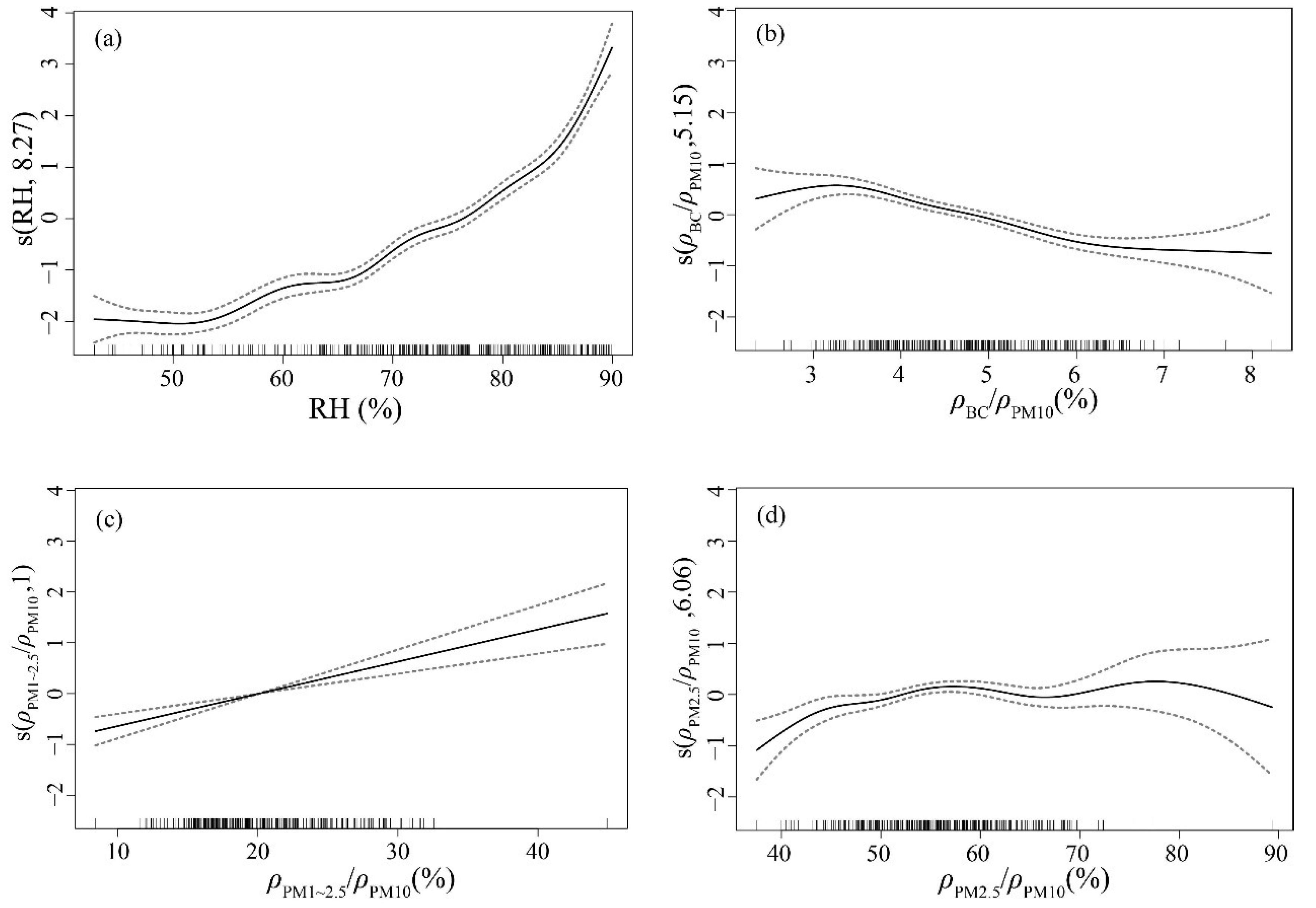
Through the established multiple covariate model, the response graph for the influence of each covariate on the aerosol extinction coefficient per unit of mass is obtained and visually displayed in Figure 6. As can be seen in Figure 6, the dotted line represents the upper and lower limits of the confidence level; the solid line represents the smooth curve of the aerosol extinction coefficient per unit of mass based on the explanatory variable; the x-axis represents the measured value of the explanatory variable; the y-axis represents the smooth-simulated value of the aerosol extinction coefficient per unit of mass, and the value in parenthesis on the y-axis represents the estimated degree of freedom. In Figure 6a it indicates that the aerosol extinction coefficient per unit of mass has a non-linear positive correlation with the RH. When the RH > 80%, the aerosol extinction coefficient per unit of mass increases rapidly with the RH. This is consistent with the research results of Liu et al. and Chen et al. [50]. Figure 6b indicates the nonlinear relationship that the aerosol extinction coefficient per unit of mass increases with ρ_PM2.5/ρ_PM10. The proportion of organic carbon, sulfate and nitrate in PM_2.5 in the Chengdu area is relatively large. The increase in the proportion of fine particles in coarse particles leads to the increase of aerosol hygroscopicity, so the aerosol extinction coefficient per unit of mass increases [51]. In Figure 6c, the aerosol extinction coefficient per unit of mass changes more slowly with the increase of ρ_PM1/ρ_PM2.5. In Figure 6d, the aerosol extinction coefficient per unit of mass decreases with the increase of ρ_BC/ρ_PM10. This may be related to the non-hygroscopicity of BC and the mixed state of BC [52]. Due to the absorbability of BC, it can adsorb a large amount of sulfate, nitrate, etc., thereby increasing the size of aerosol particles. According to the condensation growth formula, the larger the particle is, the slower the growth process of particle size [53]. Therefore, it affects the hygroscopic growth of aerosol particles.

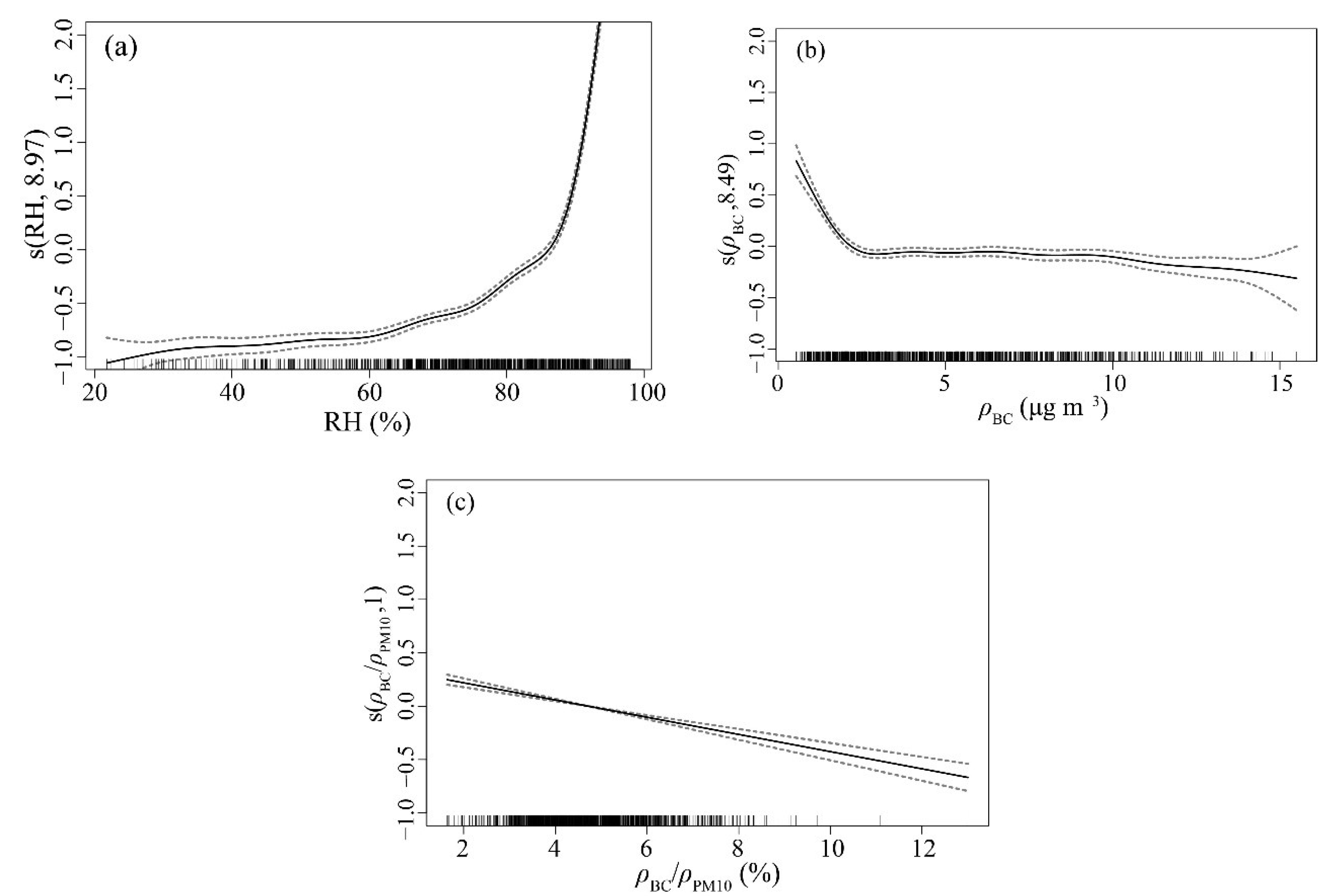
To further clarify the effect of BC on the hygroscopic growth of aerosol particles, aerosol scattering hygroscopic growth factor (f) was selected as the response variable, RH, ρ_BC and ρ_BC/ρ_PM10 were used as explanatory variables, and a GAMs model was established. It can be seen from the model results (

Table 5. GAM simulation results of aerosol scattering hygroscopic growth factors.

Variables	RH	ρBC	ρBC/ρPM10
Edf	8.97	8.49	1.00
F	334.08	20.85	109.97
p	<2 × 10−16	<2 × 10−16	<2 × 10−16

) that RH, ρ_BC and ρ_BC/ρ_PM10 all passed the significance test of α = 0.001. These three factors can well represent the growth factor of aerosol scattering hygroscopicity, of which RH has the greatest effect, followed by ρ_BC/ρ_PM10, and the smallest effect is from ρ_BC. The R² and explained variance of the model are 0.72 and 89.5%, respectively, and the fitting effect of the model is good. The response graph for the influence of each covariate on f is obtained and visually displayed in Figure 7. In Figure 7a, f has a nonlinear positive correlation with RH. When RH > 80%, f increases rapidly with the increase of RH. While in Figure 7b,c, f shows a decreasing trend with the increase of ρ_BC and ρ_BC/ρ_PM10, which illustrates that the hygroscopic growth effect of aerosol particles is weakened, which is consistent with the research results of Zhang et al. [54]. Aerosol hygroscopic growth caused by RH changes has the greatest influence on the aerosol extinction coefficient per unit of mass. When ρ_BC/ρ_PM10 increases, f decreases. In addition, due to the non-hygroscopicity of BC [53], the hygroscopic growth effect of aerosol particles is weakened, so the extinction coefficient per unit of mass of aerosol tends to decrease.

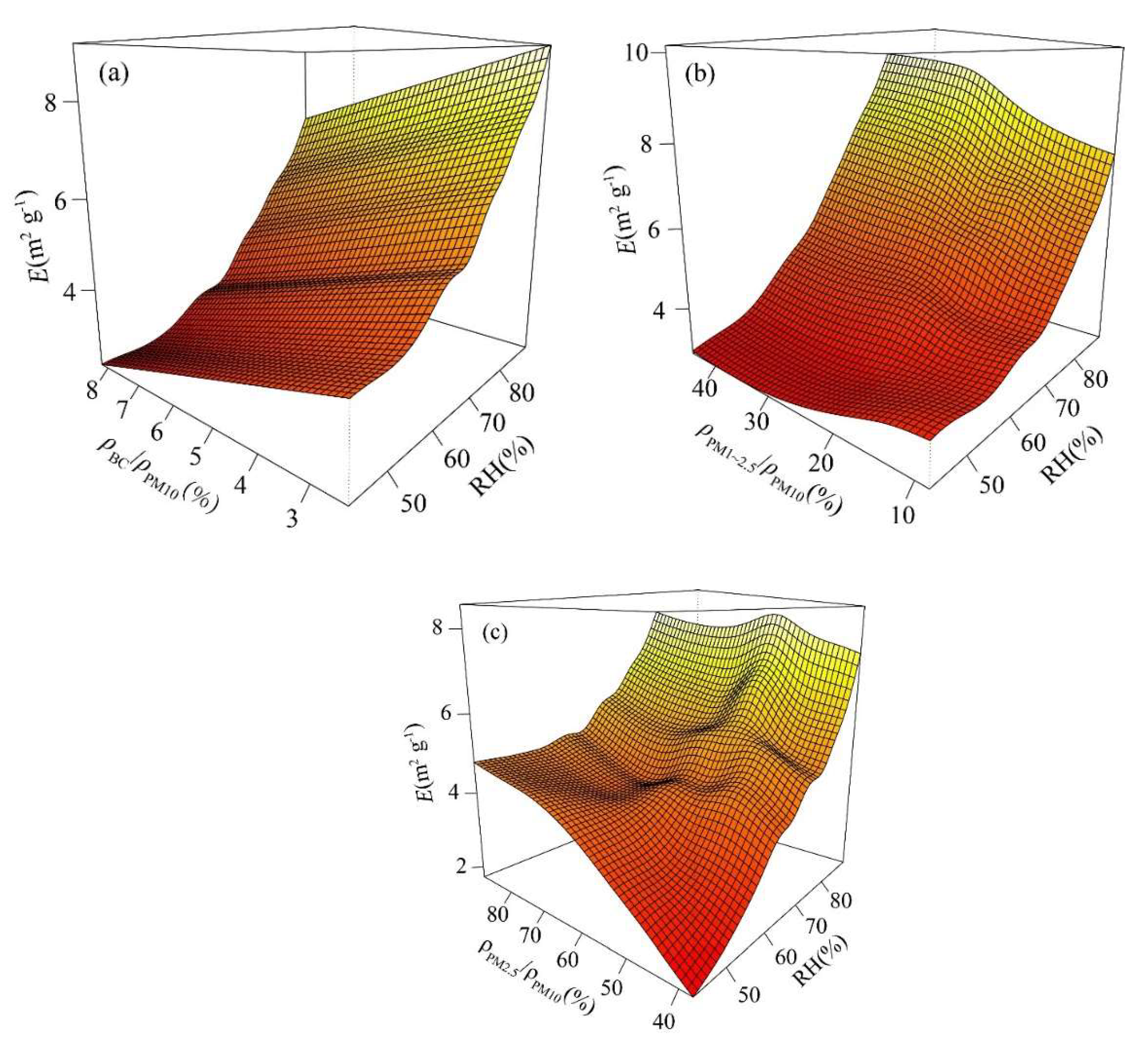
The occurrence of haze is closely related to high ρ_PM2.5. According to the Environmental Air Quality Standard (GB3095-2012), ρ_PM2.5 greater than 75 μg m⁻³ is defined as PM_2.5 pollution concentration. Furthermore, the influence of environmental meteorological factors on the aerosol extinction coefficient per unit of mass under PM_2.5 pollution concentration is analyzed. According to Liu et al. [55], ρ_PM1~2.5/ρ_PM10 increased significantly during haze episodes, while ρ_PM1/ρ_PM2.5 did not change obviously. Therefore, RH, ρ_BC/ρ_PM10, ρ_PM1~2.5/ρ_PM10 and ρ_PM2.5/ρ_PM10 are used to establish a multiple covariate model. The model results are shown in

Table 6. Simulation results by the GAMs with multi-influencing factors at PM_2.5 pollution concentration.

Variables	RH	ρPM2.5/ρPM10	ρPM1~2.5/ρPM2.5	ρBC/ρPM10
Edf	8.27	5.15	1	6.06
F	103.31	3.40	28.04	14.51
p	<2 × 10−16	0.001	4.37 × 10−7	<2 × 10−16

. The four environmental meteorological factors have all passed the significance test of α = 0.01. The R² and explained variance of the model are 0.86 and 86.30%, respectively. At PM_2.5 pollution concentration, the sequence of the influence of covariates is as follows: RH > ρ_PM1~2.5/ρ_PM2.5 > ρ_BC/ρ_PM10 > ρ_PM2.5/ρ_PM10.

At PM_2.5 pollution concentration, the response graph for the influence of each covariate on the aerosol extinction coefficient per unit of mass is obtained and visually displayed in Figure 8. The variation trend of the aerosol extinction coefficient per unit of mass with RH, ρ_BC/ρ_PM10 and ρ_PM2.5/ρ_PM10 is similar to that of the whole autumn and winter. The aerosol extinction coefficient per unit of mass increases with ρ_PM1~2.5/ρ_PM2.5, which is consistent with the results of Liu et al. [55].

3.3. Influence of Interactions between RH and Aerosol Component Structure

The change of the aerosol extinction coefficient per unit of mass is affected by the RH and aerosol component structure factors. As the physical and chemical properties of different aerosol component structure factors will change differently under different conditions of RH, this will lead to complexity in the evolution of the aerosol extinction coefficient per unit of mass [55]. The influence of RH and aerosol component structure factors on the change of the aerosol extinction coefficient per unit of mass does not exist in isolation, and there may be an interaction. Therefore, this study constructs a non-stationary model through the interaction of explanatory variables. It is beneficial to comprehensively and deeply understand the influence of the interaction between the RH and aerosol component structure factors on the aerosol extinction coefficient per unit of mass and the characteristics of their interaction. The results are shown in

Table 7. Simulation results of the GAMs with the interaction effect.

Variables	RH-ρBC/ρPM10	RH-ρPM1/ρPM2.5	RH-ρPM2.5/ρPM10
Edf	22.37	22.92	17.72
F	6.44	3.35	13.13
P	<2 × 10−16	2.17 × 10−7	<2 × 10−16

. The cross-terms, including RH-ρ_BC/ρ_PM10, RH-ρ_PM1/ρ_PM2.5 and RH-ρ_PM2.5/ρ_PM10, all have a nonlinear relationship with the aerosol extinction coefficient per unit of mass, and have all passed the significance test of α = 0.001. The R² and explained variance of the model with the interaction effect are both higher than those of the multiple-covariate model, being 0.70 and 80.8%, respectively. This indicates that it is necessary to consider the interaction between the RH and aerosol component structure factors.

Based on the fitting results of the non-stationary model with the interaction effect, the cross-term effect of RH and the aerosol component structure factors on the change in the aerosol extinction coefficient per unit of mass is given in Figure 9. In Figure 9a, when the RH is larger and ρ_BC/ρ_PM10 is smaller, the aerosol extinction coefficient per unit of mass tends to increase. As can be seen in Figure 9b, when ρ_PM1/ρ_PM2.5 remains unchanged, the aerosol extinction coefficient per unit of mass increases with the RH. When the RH is larger and ρ_PM1/ρ_PM2.5 is greater than 80%, the aerosol extinction coefficient per unit of mass has a significant ascending trend. When ρ_PM2.5/ρ_PM10 and the RH are both at maximum, the corresponding aerosol extinction coefficient per unit of mass is the largest, indicating that the high RH and high ρ_PM2.5/ρ_PM10 have a significant synergistic effect on the change in aerosol extinction coefficient per unit of mass. In summary, the synergistic effect of high RH, high ρ_PM2.5/ρ_PM10, high ρ_PM1/ρ_PM2.5 and low ρ_BC/ρ_PM10 is conducive to the increase of the aerosol extinction coefficient per unit of mass, which shows the non-stationary evolution of the aerosol extinction coefficient per unit of mass due to the different properties of aerosol component structure factors under different RH conditions

At PM_2.5 pollution concentration, the interaction results between aerosol structural factors and RH are shown in

Table 8. At PM_2.5 pollution concentration, simulation results of the GAMs with the interaction effect.

Variables	RH-ρBC/ρPM10	RH-ρPM1~2.5/ρPM2.5	RH-ρPM2.5/ρPM10
Edf	6.08	16.26	21.80
F	17.15	2.50	3.12
P	< 2 × 10−16	0.001	6.63 × 10−6

. The cross-terms (RH-ρ_BC/ρ_PM10, RH-ρ_PM1~2.5/ρ_PM2.5 and RH-ρ_PM2.5/ρ_PM10) all have a nonlinear relationship with the aerosol extinction coefficient per unit of mass and have all passed the significance test of α = 0.01. The R² and explained variance of the model are 0.87 and 89.0%, respectively.

Figure 10 shows the effects of the cross term of RH and aerosol component structure on the aerosol extinction coefficient per unit of mass at PM_2.5 pollution concentration. When ρ_PM1~2.5/ρ_PM2.5 and RH are both at the maximum, the aerosol extinction coefficient per unit of mass reaches the maximum. The relationship of the aerosol extinction coefficient per unit of mass with RH-ρ_BC/ρ_PM10 and RH-ρ_PM2.5/ρ_PM10 is similar to that of the whole autumn and winter. In summary, the synergistic effect of high RH, high ρ_PM2.5/ρ_PM10, high ρ_PM1~2.5/ρ_PM2.5 and low ρ_BC/ρ_PM10 is conducive to an increase of the aerosol extinction coefficient per unit of mass at PM_2.5 pollution concentration.

4. Discussion

The evolution of the aerosol extinction coefficient is very complicated due to the mass concentration, hygroscopicity and chemical composition of particles. Based on the randomness of the time series of the aerosol extinction coefficient per unit of mass, a stationary model and time-varying non-stationary model are established in this study. We found that the time series of the aerosol extinction coefficient per unit of mass is a non-stationary series and obtained a deeper understanding of its series characteristics.

Both relative humidity and aerosol composition have important effects on the aerosol extinction coefficient per unit of mass. Relative humidity influences the evolution of the aerosol extinction coefficient through the hygroscopic effect of aerosol. The effect of different aerosol components on the aerosol extinction coefficient is also different. In this study, the non-stationary contribution of relative humidity and aerosol component structure to the time series of the aerosol extinction coefficient per unit of mass is analyzed. Relative humidity has a greater effect on the nonstationarity, followed by the proportion of BC in the mass concentration of particulate matter. It is pointed out that BC plays an important role in the evolution of the aerosol extinction coefficient per unit of mass.

BC has a strong absorption capacity for visible light, but with an increase of relative humidity, BC has a significant effect on the hygroscopicity of aerosol. The multi-variable influence of the aerosol hygroscopic growth factor is analyzed in this study. It is found that the relationship between BC and the aerosol hygroscopic growth factor is non-linear. When the proportion of BC is larger, the hygroscopic effect of the aerosol extinction coefficient decreases so that the aerosol extinction coefficient per unit of mass decreases. Furthermore, by analyzing the interaction between RH and aerosol component structure factors, the influence of different aerosol component structures on aerosol extinction ability under different humidity conditions is revealed.

This study attempts to further understand the influence of various environmental meteorological factors on the nonstationarity of the time series of the aerosol extinction coefficient per unit of mass. We hope this study can deepen the cognition of the complex evolution mechanism of the aerosol extinction coefficient. However, the specific aerosol components are not analyzed in this study, and the influence of different aerosol components on the nonstationarity of the aerosol extinction coefficient per unit of mass is still unclear. In the future, more observational analysis and theoretical research will be carried out based on the findings in this study to better reveal the evolution mechanism of the aerosol extinction coefficient.

5. Conclusions

Non-stationary models with the time or environmental meteorological factors as the explanatory variables are established to analyze the nonstationarity of the time series of the aerosol extinction coefficient per unit of mass in autumn and winter in Chengdu. The research results show that the time series of the aerosol extinction coefficient per unit of mass in autumn and winter is nonstationary, and the environmental meteorological factors can better characterize this nonstationarity than the variable T. RH and aerosol component structure factors are all significant covariates that affect this non-stationarity. The sequence of the influence of covariates is as follows: RH > ρ_BC/ρ_PM10 > ρ_PM2.5/ρ_PM10 > ρ_PM1/ρ_PM2.5. At PM_2.5 pollution concentration, the sequence of the influence of covariates is as follows: RH > ρ_PM1~2.5/ρ_PM2.5 > ρ_BC/ρ_PM10 > ρ_PM2.5/ρ_PM10.

Considering the interaction between the RH and aerosol component structure factors, a nonstationary model with the interaction effect was established to analyze the changing characteristics of the aerosol extinction coefficient per unit of mass under the influence of different explanatory variables. The interaction between RH and aerosol component structure factors significantly affects the aerosol extinction coefficient per unit of mass. Combined with the three-dimensional graphs for the effect of the interaction between the RH and aerosol component structure factors, the synergistic effect of high RH, high ρ_PM2.5/ρ_PM10, high ρ_PM1/ρ_PM2.5 and low ρ_BC/ρ_PM10 is beneficial to the rapid increase of the aerosol extinction coefficient per unit of mass. At PM_2.5 pollution concentration, the synergistic effect of high RH, high ρ_PM2.5/ρ_PM10, high ρ_PM1~2.5/ρ_PM2.5 and low ρ_BC/ρ_PM10 is conducive to the increase of the aerosol extinction coefficient per unit of mass.