Abstract
On 4 June 2021, short-duration extreme precipitation occurred in Taipei. Within 2 h, over 200 mm of rainfall accumulated in the Xinyi district. In this study, advanced data assimilation technology (e.g., hybrid data and 3D variations) was incorporated to develop a high-resolution, small-scale (e.g., northern Taiwan) data assimilation forecast system, namely the weather research and forecast-grid statistical interpolation (WRF-GSI) model. The 3D wind field data recorded by the Doppler wind lidar system of Taipei Songshan Airport were assimilated for effective simulation of the extreme precipitation. The results revealed that the extreme rainfall was caused by the interaction between the northeast wind incurred by a front to the north of Taiwan, a humid southerly wind generated by Typhoon Choi-wan, and the regional sea–land breeze circulation. For the Xinyi district, the WRF-GSI_lidar model reported accumulated rainfall 30 mm higher than that in the non-assimilated experiment (WRF-GSI_noDA), indicating that the WRF-GSI model with lidar observation was improved 15% more than the nonassimilated run.
1. Introduction
Extreme weather refers to the weather events caused by abnormal, severe deviations from typical climatic values or their historical averages in a region, such as extreme precipitation, droughts, heatwaves, and intense cyclones. Their probability of occurrence is low, but they impact society drastically, threatening human health and safety, the environment, and the economy [1,2,3,4,5,6,7]. In the face of increasingly frequent and extreme hydroclimatic events in recent decades, research on rain, floods, and droughts has become crucial [8,9,10,11,12,13]. According to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, anthropogenic greenhouse gas emissions have heightened the frequency and severity of extreme climatic events worldwide; for each 1 °C increase in temperature, precipitation increases by 7% [14].
Numerous factors cause extreme precipitation, and its frequency and severity vary with regions and seasons [15,16,17,18,19,20]. Studies have been conducted on rainfall patterns and their driving mechanisms [21,22,23,24] to clarify the trends and changes in extreme precipitation events. Rainfall patterns have been closely associated with the state of large-scale circulation, surface temperature, total column water vapor, and advected water vapor flux.
Anthropogenic climate change has interacted with the natural atmosphere in complex ways, rendering the research and evaluation of climate change difficult [25]. Nevertheless, understanding changes in the patterns of extreme precipitation events is crucial to mitigate their damage to society and the environment [26]. Numerical weather prediction (NWP) provides information on future weather; predicting correct severe weather phenomena can mitigate their impacts on human lives and resources [27]. Further understanding of the physical mechanisms of convective events from an initial state to maturity, in which convection cells develop into organized mesoscale convective systems, is required [28], including improvements in NWP [29,30].
The prediction of small-scale heavy rainfall (10–50 km) through NWP has been limited in effectiveness because of the insufficient resolution and limitations in the parameterization of cumulus convection and data assimilation systems. The predictability of convective systems is further limited by the uncertainty and randomness of strong convection [31]. Studies have reported the necessity of conducting high-resolution simulations using explicit cloud microphysics to predict small-scale heavy rainfall [31,32,33]. Similarly, Zhang et al. [31] proposed using improved parameterizing physical processes to enhance the accuracy of weather prediction models. The models’ accuracy can also be enhanced by upgrading data assimilation technology and by increasing observational data to enhance the initial data analysis [31]. Hristova-Veleva proposed improving 3D wind fields and precipitation models through weather prediction models and the assimilation of observational data to enhance weather prediction accuracy [34]. In particular, wind field data from radar observations [35,36] and Doppler wind light detection and ranging (lidar) [37,38,39,40] can both be effectively assimilated into models.
Although radar networks are powerful tools for researching convective systems, they are only effective when water particles are present. Doppler wind lidar provides 3D wind fields with high spatial and temporal resolution [41]. It can be applied to detect wind shear near airports [42,43,44], improving the safety of airport environments during takeoff and landing [45]. Doppler wind lidar has been widely recognized for detecting wind shear and issuing corresponding safety alerts [37,40,42,43,44,45].
The wind field and wind shear data captured using Doppler wind lidar can be assimilated into the NWP model. Studies have indicated that assimilating 3D wind field data into the NWP model is conducive to identifying weather systems’ locations, intensity, and phenomena (e.g., rainfall) [37,38,39,40]. Assimilating Doppler wind lidar data is conducive to accurately predicting the ambient field of a mesoscale convective system and to the starting location and time of convection [38,39,46], thereby improving the accuracy of quantitative rainfall predictions. Similarly, Hristova-Veleva [34] maintained that the high-resolution and highly precise wind field profiles captured using Doppler wind lidar should be assimilated into the NWP model to improve ambient field analysis, thereby allowing the identification of the conditions conducive to the development of a convective system.
Studies have indicated that assimilating 3D wind field data enables the accurate prediction of severe convective rainfall events. Therefore, this study employed the weather research and forecast-grid statistical interpolation (WRF-GSI) model to assimilate the Doppler wind lidar data at Taipei Songshan Airport to simulate the extreme precipitation in Taipei. The goals were to clarify whether 3D wind field data assimilation improves the accuracy of convection and rainfall prediction, which environmental factors are corrected through data assimilation, and the effect of the correction on rainfall prediction. In this paper, Section 2 introduces the extreme precipitation event in Taipei, Section 3 presents the research materials and data assimilation method, Section 4 describes the data assimilation experiment results, Section 5 discusses the results, and Section 6 concludes the study.
2. Overview of the Heavy Rainfall Event
To explore the extreme precipitation event in Taipei on 4 June 2021, the general atmospheric environment and observational data recorded were examined.
2.1. Synoptic Environments
Figure 1 presents the surface weather map recorded at 00:00 coordinated universal time (UTC, LST = UTC + 8:00) on 4 June. A Pacific subtropical high was detected in East Asia at 140° east and 20° north. Continental highs were seen on the east of the Tibetan Plateau and Mongolia; between the two highs was an area of low atmospheric pressure spanning from the north to the south. A notable low-pressure circulation was identified in Siberia, and a subpolar low-pressure system was detected north of Japan. This system formed a notable front system with southeasterly air from the high-pressure area in the south. The front system extended from northeast to southwest across the northern waters of Taiwan, forming a stationary front from Fujian to Hainan, China.
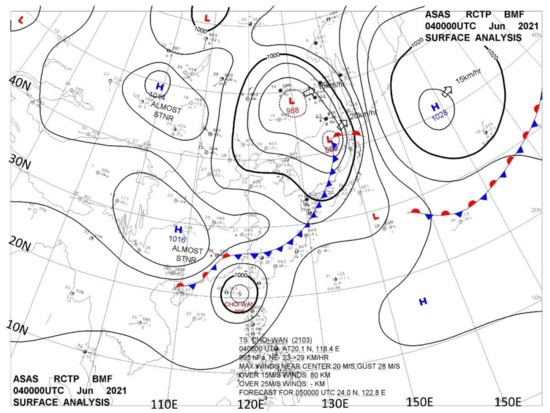
Figure 1.
Surface weather map on 4 June 2021 (source: Central Weather Bureau, Taiwan, downloaded from DBAR [https://dbar.pccu.edu.tw] accessed on 6 June 2022).
Typhoon Choi-wan was detected southwest of Taiwan. Because of the front system and the typhoon, the low-level ambient wind field near Taiwan was dominated by a south wind. As illustrated in Figure 2, water vapor was transported in the troposphere at 850 hPa, mainly from Typhoon Choi-wan. The circulation of the typhoon transported the water vapor to the north. At 2:00 UTC, the ground temperature rose rapidly to 32–33 °C. Furthermore, convectional rainfall in northern Taiwan was high because the junction between the typhoon’s circulation and the front system was in the north of Taiwan.
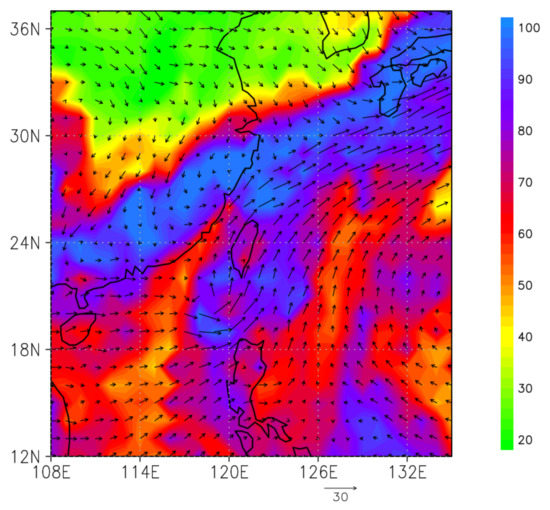
Figure 2.
Relative humidity (%) at 850 hPa, recorded using the Global Forecast System (GFS).
2.2. Observations
2.2.1. Satellite and Radar Images
Figure 3 displays satellite images from 04:10 to 06:10 UTC. At 04:10 UTC, a mesoscale system was detected in Fujian, and a band cloud pattern was identified above Taiwan. At 05:10 UTC, convection cells formed in northern Taiwan and off the northeast coast; they developed rapidly until 07:10 UTC (not shown). Figure 4 illustrates the synthetic radar echo observations. At 04:00 UTC, a convection cell was formed in northern Taiwan; as the cell continued to develop one hour later, another convection cell formed over the mountains in central Taiwan.
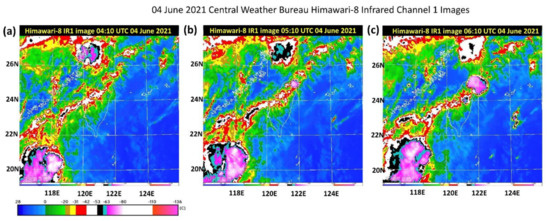
Figure 3.
Tone satellite maps on 4 June 2021: (a) 04:10, (b) 05:10, (c) 06:10 UTC (source: Taiwan Central Weather Bureau (CWB)).
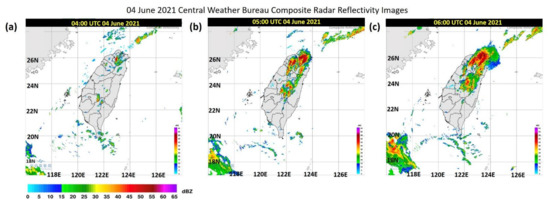
Figure 4.
Synthetic radar echoes on 4 June 2021 (dBz): (a) 04:00; (b) 05:00; (c) 06:00 UTC (source: Taiwan CWB).
With the continuing influence of the southwest wind and the southward movement of the front system, the convection cell in the north encompassed the entire Taipei metropolitan area. From 05:00 to 07:00 UTC, 200 mm of rainfall occurred in Taipei, causing floods in several districts. The short-duration extreme rainfall incurred tremendous damage to Taipei because it was not accurately predicted and forewarned.
2.2.2. Wind Profiles
Figure 5 presents the wind profiles observed from 2 to 4 June 2021. The time–height cross-section represents the 3-D flow condition of the Songshan Airport (longitude = 121.55, latitude = 25.07). On June 2 and 4, increases in wind speed were noted at 600–800 m. The wind profiles on June 2 and 3 differed primarily in the wind speed at the heights of <400 m at night. However, data on the afternoon of June 3 were incomplete because of rain. At 00:00 UTC, a sea breeze circulation as high as 600 m was observed. The lidar wind profiles before the extreme precipitation event on June 4 were assimilated into an hourly cycle using a gridpoint statistical interpolation (GSI) three-dimensional variational (3DVAR) system.
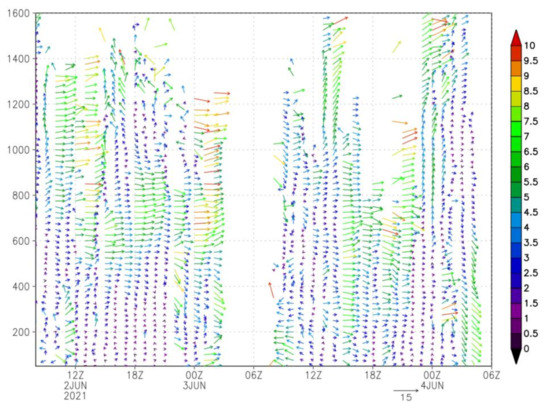
Figure 5.
Wind profiles were observed from 2 June to 4 June 2021, with the colors indicating wind speed (m/s).
2.2.3. Accumulated Rainfall
Figure 6 illustrates the accumulated rainfall observed by the Taiwan Central Weather Bureau (CWB) on 4 June. Extreme precipitation was detected in Taichung, Changhua, and Nantou counties, and the accumulated rainfall in Taipei and the northern and northeast mountainous areas exceeded 130 mm. The floods in several districts of Taipei were caused by >200 mm of rain within 1–2 h.
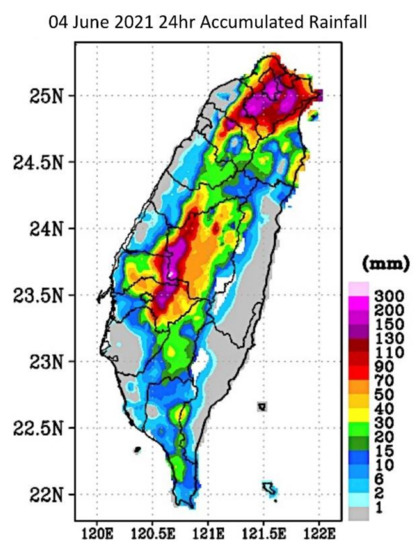
Figure 6.
The 24 h accumulated rainfall on 4 June 2021.
3. Materials and Methods
The Weather Research and Forecasting (WRF) v3.6.1 model from the United States National Center for Atmospheric Research [47] and the GSI v3.6 data assimilation system from the US National Centers for Environmental Prediction (NCEP) [48] was employed for the extreme precipitation prediction experiment.
3.1. Materials
In addition to the initial field data for model simulation, Doppler wind lidar data for assimilation were required.
3.1.1. Global Forecast System Data
The Global Forecast System (GFS) is used by the NCEP for numerical forecasting in all operations and provides a deterministic forecast over durations as long as 16 days. The GFS provides initial and boundary conditions for the regional weather, ocean weather, and wave forecasting models of the NCEP. GFS employs the global data assimilation system (GDAS), which generates initial conditions for global weather forecasts using the most available satellites and observational data from global sources.
From 1980 to 2019, the NCEP employed the global spectral model (GSM) [49,50]. In 2017, the finite-volume cubed-sphere dynamical core (FV3), developed by the National Oceanic and Atmospheric Administration, was selected as the atmospheric model for a new Unified Forecast System. The NCEP replaced the GSM with the FV3 and developed an advanced physical physics and data assimilation technology to surpass the forecast efficiency of the GFS, which is based on a spectral model. Now, the GFS publishes 16 days of forecasting data four times per day, at 00:00, 6:00, 12:00, and 18:00 UTC. Deterministic forecasts are performed using the FV3GFS model, which features a horizontal resolution of 13 km and 127 vertical layers. The model outputs hourly forecast data for the next 120 h and forecast data every three hours from days 5–16 [51]. In this study, FV3GFS data were employed as the GFS data.
3.1.2. GEFS
The NCEP has used the Global Ensemble Forecast System (GEFS) since December 1992. In its initial version, the GSM was implemented with a horizontal resolution of T62L18 (a horizontal resolution of 200 km and 18 vertical Σ layers). For the initial perturbation, breeding vectors were employed [52] to generate two pairs of perturbation members and one control member. After a major upgrade in December 2015, GEFS performed initial perturbation on 80 members selected using the GDAS. The ensemble Kalman filter [53] was applied for 6 h forecasting, tropical cyclone relocation, and the recentering of initial perturbance [54,55]. The GEFS data employed in this study were updated after 2020; the model FV3GFS was employed, the horizontal resolution was increased to C384 (25 km), and the number of ensemble members was increased by 30 + 1 group.
3.1.3. GDAS Observation
On 1 May 2007, a new GSI 3DVAR analysis system was implemented in the GDAS system of the NCEP. The GSI 3DVAR system replaced the spectral statistical interpolation 3DVAR system, used since 1991 to establish a uniform, stable, and rapid data analysis method. The new GDAS featured various upgrades in GFS, including new vertical coordinates and changes in the assimilation of observation selection, quality control, minimization algorithms, dynamic equilibrium constraints, and new types of observations [49]. The observational data employed in this study were primarily sourced from the NCEP GDAS and featured a binary format defined by the World Meteorological Organization. These data included Global Telecommunication System, satellite, ozone observation, and global positioning satellite radio occultation data. All the data were assimilated into the WRF model through GSI.
3.1.4. Doppler Wind Lidar
The 3D wind field data were sourced from the Doppler wind lidar system (Windcube 100S from Leoshpere France) in Taipei Songshan Airport. It measures the wind fields in the atmosphere by applying lasers to detect the Doppler shifts in the particles in the atmosphere (e.g., sand, water droplets, and aerosols), following the lidar principle. Reference [43] provides the scanning strategy, hardware specifications, and performance summary of the Windcube 100S. The lidar data during 2–4 June 2021 were employed in this study. However, wind lidar only operated, as the rainfall did not occur over the airport (Figure 5). The sounding data (46692, Banchao sounding, 14 km away from the airport) were compared with the wind lidar under 1.6 km (Figure 7). The one-month-long data validation of sounding and lidar was compared in July 2019, and the total number of valid data points was 351. The results showed that the mean wind speed bias was about −0.18 m/s, and the root mean square error (RMSE) was approximately 4.4 m/s. However, the primary concern is the Banchao-sounding data we obtained from DBAR (https://dbar.pccu.edu.tw/ accessed on 6 June 2022), which is too sparse below 1.6 km. The performance of wind lidar data assimilation is discussed in Section 4.
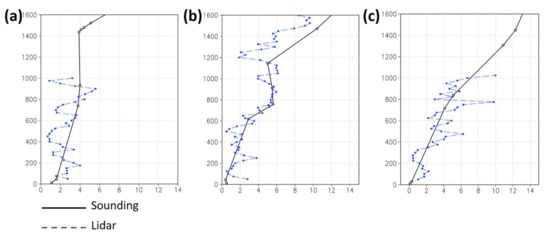
Figure 7.
The wind speed profile compares Banchao sounding(black) and Songshan lidar(blue). (a) 03 June 1200UTC, (b) 04 June 0000UTC, (c) 05 June 0000UTC.
3.2. Methods
3.2.1. Model Setting and Assimilation System
Figure 8 illustrates the research area, which was analyzed at three levels of grid resolution: 15 and 3 km for the D01 and D02 configurations, respectively. D01 was operated solitarily to establish the initial and boundary conditions for raising the grid resolution [56], whereas D02 was performed as nested grids for predicting the weather conditions in northern Taiwan. The grid points of each domain are 210 × 210 (D01) and 71 × 71 (D02).
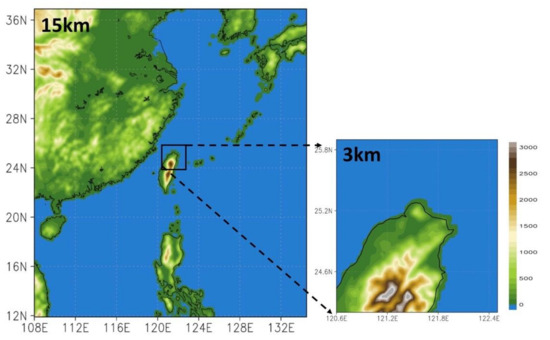
Figure 8.
Weather Research and Forecasting gridpoint statistical interpolation (WRF-GSI) forecast areas (D01: 15 km; D02: 3 km).
The top height of the model was set as 50 hPa, and 32 vertical layers were established. To reduce the impact of the spatial scale on the forecast model, D01 was parameterized through the following methods: (1) cloud microphysics—Goddard [57,58], (2) long- and short-wave radiation—rapid radiative transfer model for the general circulation model [59], (3) boundary layer parameterization—Mellor–Yamada–Nakanishi–Niino model [60,61], (4) ground parameterization—Pleim–Xiu land surface model [62,63], and (5) cumulus parameterization—new simplified Arakawa–Schubert model [64]. For D02, the atmospheric boundary layers were parameterized through the asymmetric convective model version 2 [65], which displays more detailed wind profiles than the Mellor–Yamada–Nakanishi–Niino model [66]. Cumulus parameterization was not performed because the grid spacing was <4 km. All the other physical settings were the same as those of D01. Test results for the physical configuration of the model can be found in [67].
3.2.2. Experimental Design
The data assimilation system was set up and optimized before the lidar data were assimilated into the WRF model. The radius of the influence of the observational data on the model grids was also considered. In GSI, the radius was determined according to hzscl_op (the scale of horizontal assimilation). Hybrid data assimilation was conducted on the D01 wind field data, whereas the D02 data were assimilated through the 3DVAR system.
The background error matrix (B) is always the most complicated part of data assimilation. In GSI, the spatial distribution of the perturbation is conducted by using the recursive filter. It comprises three sets of Gaussian functions to produce the “fat-tailed” pattern in the spectrum of the error covariance to obtain the analysis on a small scale. The scale and amplitude parameters of the Gaussian function can be tuned through two sets of horizontal scale factors called “hzscl_op” and weights “hswgt_op” in the name list. The “hzscl_op” is a set of scale factors for horizontal smoothing. Typically, it determines how far the distance that observation could influence.
This study used the sensitivity of different tuning combinations to evaluate the sensitivity of the horizontal length scale to rainfall forecast and obtain reasonable values. This study used “hzscl_op” to perform the experiments, control, and experimental groups, named WRF-GSI_lidar and WRF-GSI_lidar_hzscl. The design aims to understand how lidar data affect model forecasts through different effect distances. The numerical weather model with a data assimilation system has discovered and tested the effective horizontal radius, which showed an impact on the weather forecast. These articles used similar research methods to achieve this purpose [68,69,70]
The horizontal radii of influence in the control and experimental groups were established. The hzscl_op in the control group was twice as large as that in the experimental group; that is, the range of influence of the observational data in the experimental group was double that of the data in the control group.
- Control group: hzscl_op (3) = [0.09325, 0.1865, 0.375];
- Experiment group: hzscl_op (3) = [0.046625, 0.09325, 0.1875].
Figure 9 demonstrates the strategy of the cycle assimilation experiment, which was a modified version of the NCEP high-resolution rapid refresh system design [56]. A 15 km WRF model grid combined with GSI hybrid data assimilation (later called WRF-GSI) was conducted on D01, providing initial and boundary to the inner grid. The GFS initial field, the GEFS ensemble forecast data, and the GDAS observational data were integrated to generate a 15 km WRF initial field for one full-cycle forecast per 6 h. Each hourly output data point was applied as the D02 initial field. The D02 data underwent lidar assimilation through the GSI 3DVAR system once per hour; apart from the lidar mentioned above, there are no other data to be assimilated into the 3 km grid. However, the 15 km grid assimilated all NCEP GDAS databases, and the coarse grid DA should be able to carry that local data information to the inner grid through interpolation. Therefore, the following four groups of forecasting data were established: (1) 15 km assimilated GDAS data (WRF-GSI), (2) 3 km nonassimilated data (WRF-GSI_noDA), (3) 3 km assimilated lidar data (WRF-GSI_lidar), and (4) 3 km assimilated lidar data with half the radius of influence as (3) (WRF-GSI_lidar_hzscl). Table 1 describes and concludes all data assimilation experiments designed and the reference data.
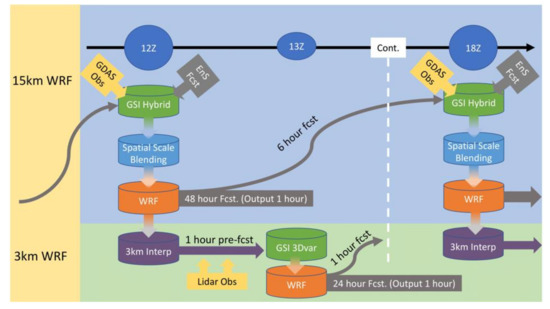
Figure 9.
Assimilation cycle experiment. (Modified and referred from the reference [56]).

Table 1.
Numerical experiment and sensitivity design.
4. Results
The ambient field data recorded by different sources on June 4 were compared, including the initial and forecast fields. The sources were the NCEP GFS and WRF-GSI models. In addition, the changes in the radar echoes and accumulated rainfall after the assimilation of the 3D wind field data were examined.
4.1. General Weather Analysis
4.1.1. Surface Wind Field, Sea-Level Pressure, and Upper-Air Wind Field
Figure 10 and Figure 11 depict the 15 km surface wind field and sea-level pressure at t = 0 (analysis field) and t = 6 (6th-hour forecast), respectively. Until 00:00 UTC, 4 June, eight full-cycle hybrid data assimilations were conducted, starting from 00:00 UTC, 2 June.
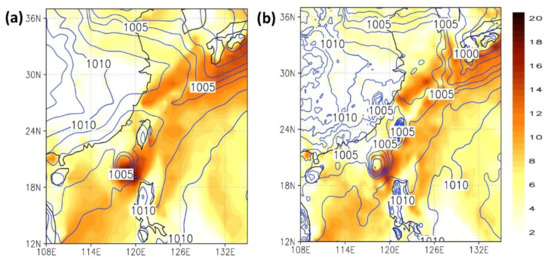
Figure 10.
Surface wind field (m/s) and sea-level pressure (hPa) in the 15 km initial field analysis (t = 0): (a) US National Centers for Environmental Prediction (NCEP) GFS; (b) WRF-GSI.
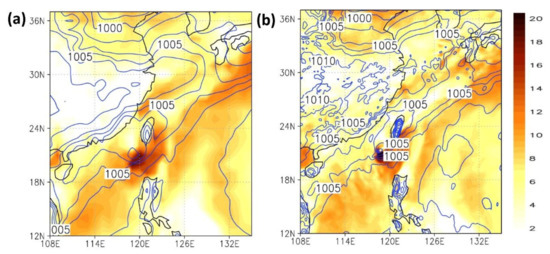
Figure 11.
Surface wind field (m/s) and sea-level pressure (hPa) in the 15 km forecast field analysis (t = 6): (a) NCEP GFS; (b) WRF-GSI.
In the initial field analysis (t = 0), the three models did not differ considerably in their performance. However, the WRF-GSI model exhibited the poorest typhoon prediction because the typhoon data were not adjusted and initialized in the experiment. The three models did not differ substantially in their forecasted fronts’ sizes, locations, and intensities.
The forecast field analysis (t = 6) showed that the three models did not differ substantially in their typhoon and front intensity forecasts. Here, the WRF-GSI produces a slightly stronger typhoon than GFS. Generally, 15 km WRF-GSI shows some mesoscale features in the forecast.
Figure 12 and Figure 13 depict the upper-air wind field and water vapor at 200 hPa at t = 0 (analysis field) and t = 6 (6th-hour forecast). When t = 0, the wind speed reported by the WRF-GSI model was closer to that reported by the GFS even though the two wind speed values differed. When t = 6, the WRF-GSI reported slightly different upper-air wind speed and a wider wind field at 200 hPa over the South-China Sea and the Philippines.
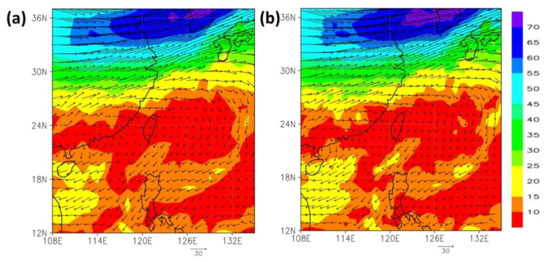
Figure 12.
Upper-air wind field (m/s) and water vapor in the 15 km initial field analysis (t = 0): (a) NCEP GFS; (b) WRF-GSI.
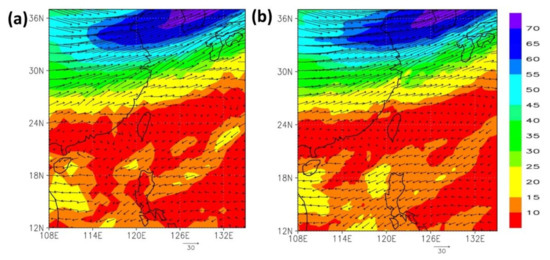
Figure 13.
Upper-air wind field (m/s) and water vapor in the 15 km forecast field analysis (t = 6): (a) NCEP GFS; (b) WRF-GSI.
The surface and upper-air wind speed reported by the WRF-GSI model was weaker than that reported by the other two models in the forecast field analysis. This was conducive to predicting the vertical pull effect and the water vapor accumulation near the surface. In other words, the large-scale ambient field was generally favorable for predicting the development of the convective system in northern Taiwan.
The forecast field analysis results of the WRF-GSI model were closer to those of the NCEP GFS. In other words, the large-scale data field generated by the forecast data assimilation system developed in this study was comparable in quality to that created by competent weather authorities. Accordingly, the 15 km WRF-GSI data field was deemed capable of being used as the initial and boundary data for the 3 km high-resolution forecasting.
4.1.2. Incremental Influence of the 3D Wind Field
Figure 14 presents the incremental results of the control group (larger radius of influence by the 3D wind field), with (a) and (b) illustrating the increments after the profiler data assimilation at the wind fields U and V, respectively. The U and V profiler data on the surface changed by 0–1.5 m/s, indicating a decrease in the surface wind speed by 30–50% after data assimilation. This suggested that the original surface wind field exhibited overestimation, consistent with the general model prediction results.
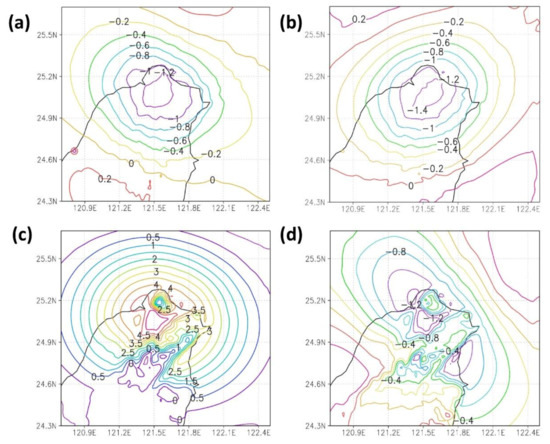
Figure 14.
Three-kilometer U and V wind speed increments in the assimilated profiler data at the 3 km resolution (m/s): (a) surface U wind speed increment; (b) surface V wind speed increment; (c) 850 hPa U wind speed increment; (d) 850 hPa V wind speed increment.
The Doppler wind lidar scanning strategy of Taipei Songshan Airport enables observation to a maximum of 1600 m in height, with 850 hPa being the upper limit of the observational data. Figure 14c,d depicts the wind speed increment at 850 hPa, which differed from the surface. In the U direction, some of the increments were positive. In the upper air of Taipei, the wind speed changed by 5 m/s. The wind speed increased by 50–60% after the data assimilation, indicating that the original model underestimated the wind field U. The wind speed adjustment at the V direction was consistent with that on the surface, indicating that the original model overestimated the wind field V.
Because of the changes in wind speed increments, wind cut in the east-west direction is notable in northern Taiwan, revealing the development and change of the bottom circulation.
Figure 15 illustrates the experimental group’s results, similar to those of the control group but involving half the influence radius. Changes were notable in both distances and wind speed increments. Specifically, the surface and the upper-air wind speed increased by 0.2–0.3 and 0.5 m/s, respectively. It was because of the change in the horizontal scale, which indirectly caused the difference in the covariance. The incremental field analysis revealed that the settings in the data assimilation system affected the initial field analysis substantially, thereby influencing the model forecasts.
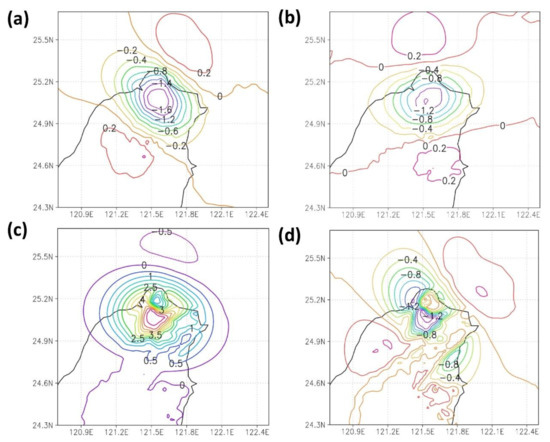
Figure 15.
Three-kilometer U and V wind speed increments with half the radius of influence (hzscl) as the experimental groups: (a) surface U wind speed increment; (b) surface V wind speed increment; (c) 850 hPa U wind speed increment; (d) 850 hPa V wind speed increment.
Figure 16 shows the OMB and OMA statistics from GSI. The variables used in the GSI are U and V wind components. As can be seen from the figure, the OMB is generally greater than OMA. In other words, the results could be improved during the initial analysis when lidar data were included in the simulation. As for the v-component, it even performed better than the u-component wind. Because the lidar is a single profile in this study, it may only have a concise memory in the model and propagate downstream quickly. The study’s primary goal is to focus on the small area and heavy rainfall events in Taipei City. Figure 16 shows that OMA is lower than OMB, which is likely that the lidar data used in the data assimilation system positively impact the model analysis.
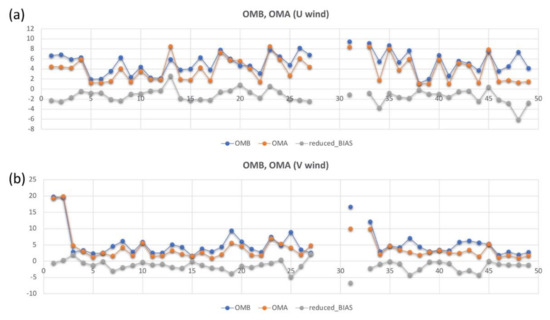
Figure 16.
Results of the OMA and OMB for (a) U component and (b) V component.
4.2. Accumulated Rainfall
Figure 17 presents the accumulated rainfall predicted by the three forecast models from 00:00 to 12:00 UTC on 4 June. Figure 17a shows the actual rain that occurred in the center of Taipei City high amount of precipitation. The heavy rain fell mainly for about two to three hours. Figure 17b illustrates the profiler data without assimilation, which, compared to the accumulated rainfall map in Figure 6 and Figure 17a, reveals that the predicted locations of extreme precipitation were east of the actual locations. After the profiler data were assimilated, as shown in Figure 17c, the predicted locations were calibrated westward, moving closer to the actual locations.
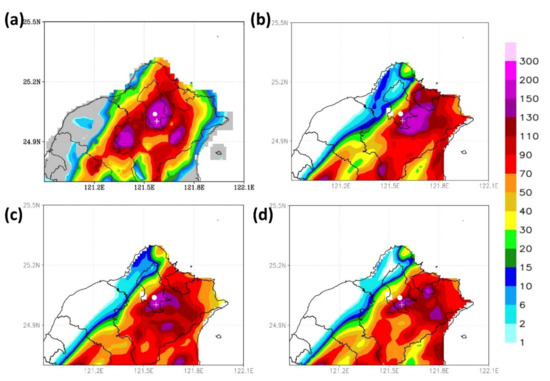
Figure 17.
Three-kilometer accumulated rainfall from 04:00 to 12:00 UTC on 4 June (mm): (a) CWB observed accumulated rainfall; (b) WRF-GSI_noDA; (c) WRF-GSI_lidar; (d) WRF-GSI_lidar_hzscl. The white dot and plus denote the locations of Xin-Yi and WenShan districts, respectively.
Figure 18a illustrates the time series of the accumulated rainfall in the Wenshan district from 00:00 to 12:00 UTC on 4 June. The rain started at 05:00, and by 06:00 UTC, 170 mm of precipitation had accumulated. In the WRF model, rainfall started at 03:00 UTC. However, the assimilated lidar data demonstrated accumulated rainfall higher than that in the nonassimilated data by 10 mm. The result was closer to the accumulated rainfall but still differed from it by 30 mm; specifically, the total rainfall in the Wenshan district at 20:00 was 232.5 mm. Similarly, regarding the accumulated rainfall in the Xinyi district (Figure 18b), the assimilated wind field data were more accurate than the nonassimilated data; specifically, the two data sets differed in accumulated rainfall of 30 mm. The actual total rain in the Xinyi district at 20:00 was 200 mm.
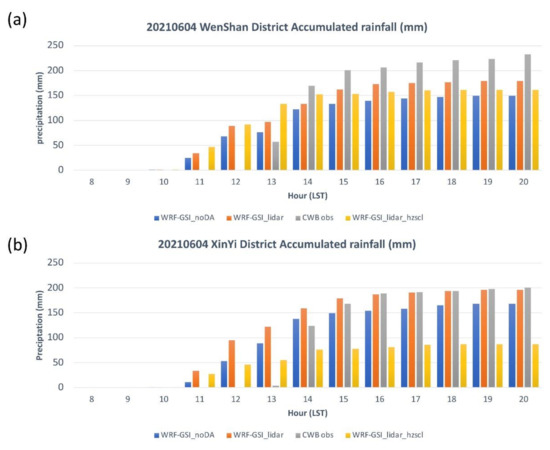
Figure 18.
Predicted and observed accumulated rainfall (mm) from 3 km results on 4 June 2021 in (a) Wenshan district and (b) Xinyi district.
As demonstrated in Figure 17d, the area and intensity of extreme precipitation decreased when the radius of influence was reduced. Relative to the 3 km WRF rainfall forecast by the noDA (Figure 17b), the assimilated wind field data were more accurate in predicting the locations and intensity of extreme precipitation than the nonassimilated data regardless of the radius of influence. Accordingly, the change in the ambient airflow was the main cause of the extreme rainfall.
5. Discussion
This study employed the WRF-GSI model to assimilate 3D wind radar field data to simulate extreme precipitation, yielding a rainfall intensity prediction close to the actual rainfall intensity. This section discusses the effect of 3D wind field data assimilation on the predicted ambient field, convection development, and rainfall intensity.
5.1. Ambient Field
This subsection discusses the changes in the initial (t = 0) and forecast (t = 6) field analyses after data assimilation and the causes of these changes.
5.1.1. Initial Field Analysis
In the initial field analysis on the surface, the typhoon simulated in the WRF-GSI model was particularly weak because the typhoon data were not adjusted and initialized. Generally, because the intensity of a typhoon is unpredictable, most mesoscale models have initialized the data of tropical cyclones, such as their intensity and locations. However, in this study, the typhoon data were not initialized because excessive errors and factors had to be avoided. Consequently, the typhoon’s intensity simulated in the WRF-GSI model was particularly low after multiple data assimilations.
In the initial field analysis in the upper air, the analysis results generated by the WRF-GSI model were close to those generated by the NCEP GFS. Still, the two models differed slightly in wind speed. The WRF-GSI model incorporated the observational field analyses at the time and forecast fields for the first six hours. Data assimilation through the reduction of initial errors enabled the WRF-GSI model to generate reasonable large-scale data. The mesoscale model could generate small-scale and medium-scale systematic initial field data.
5.1.2. Forecast Field Analysis
The two models yielded similar results in the forecast field analysis on the surface with large-scale systems (e.g., typhoons and fronts). After the models were initiated, the typhoon circulation could be initiated through physics parameterization. Moreover, Typhoon Choi-wan exerted a relatively small influence because it was a mild typhoon. In this study, typhoon circulation was initiated. Therefore, the three models did not differ significantly in their forecast field analyses.
The forecast field analysis in the upper air showed that the WRF-GSI predicted a similar wind speed at 200 hPa. Theoretically, excessive wind speed in the upper air affects divergence, causing the vertical pull effect in the atmosphere. It has a high probability of affecting the development of the precipitation system and the locations and movement of front systems. It is discussed later when analyzing the 3 km model results.
5.2. Accumulated Rainfall
The wind field forecast data were analyzed to understand further why the Doppler wind lidar data led to the significant differences between the three models on rainfall predictions. Figure 19 depicts the wind fields at 950 hPa when t = 0 (i.e., 00:00 UTC, 4 June, which was the models’ starting time). After the 3D wind field data were assimilated, the wind speed in Taipei and its west boundary decreased significantly, whereas a weak wake was observed at the northeast coast and the open sea nearby. Comparing the three different model initial conditions, the WRF-GSI_noDA (Figure 19a) gives a more robust wind speed at Taipei City than the other two with lidar data assimilated. After several DA cycles without lidar data, the model produced a higher wind speed at the initial stage (Figure 19b,c).
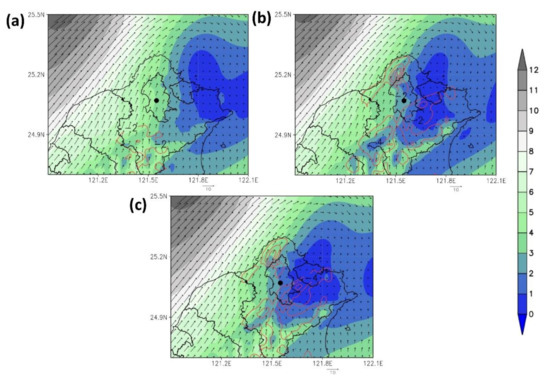
Figure 19.
Three-kilometer initial wind field at 950 hPa (color scale, m/s) and 850 hPa convergence (red dotted line, 1/s) at 8:00 on June 4: (a) WRF-GSI_noDA; (b) WRF-GSI_lidar; (c) WRF-GSI_lidar_hzscl. Black circle is Songshan Airport (longitude = 121.55, latitude = 25.07).
Figure 20 illustrates the forecasts 6 h after the 3D wind radar field data assimilation, which led to a decrease in wind speed. As shown in Figure 20b, the control group, which featured assimilated 3D wind field data with a larger hzscl_op, sustained a particularly long duration and a broader range of data influence. Conversely, the experimental group, which featured half the hzscl_op of the control group, had reduced its range of data influence, leading to more robust sea breeze circulation. This result was partially similar to the forecast results of the nonassimilated profiler data. In the nonassimilated data and the assimilated data with a smaller hzscl_op, the sea breeze at the estuary of Tamsui extended its influence on the city, causing the simulated convective system to be located east of its actual location, leading to the difference between the simulated and actual locations of extreme precipitation.
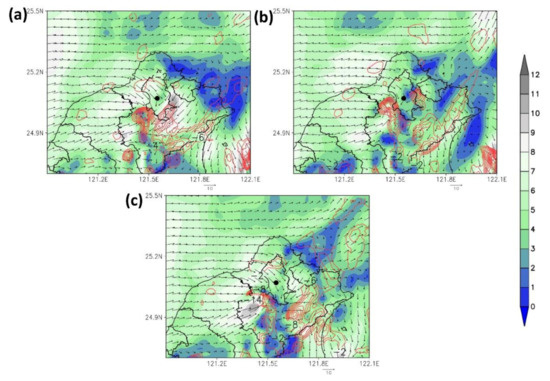
Figure 20.
Three-kilometer wind field at 950 hPa (color scale, m/s) and 850 hPa convergence (red dotted line, 1/s) at 14:00 on June 4: (a) WRF-GSI_noDA; (b) WRF-GSI_lidar; (c) WRF-GSI_lidar_hzscl. Black circle is Songshan Airport (longitude = 121.55, latitude = 25.07).
Figure 21 illustrates the upper boundary layer wind and convergence distribution at 500 hPa. Without lidar data, the winds in the boundary layer near the airport are still strong even though the convection can develop up to 500 hPa. As mentioned earlier (Section 5.1.2), if the winds above are too strong, it will cause the convection to tend to tilt downstream. Figure 17b shows that the WRF-GSI_noDA produced rain area southeastward. Convection could develop vertically without tilting when lidar data assimilation reduces the wind speed vertically. It helps the raindrop drop in the correct location. Again, Figure 17d and Figure 20c indicate that the convection system tilt westward due to increasing wind speed vertically. It is because of the effective radius changes in 3 km grid that the 15 km simulation results by the WRF-GSI model do not substantially vary from those of the NCEP GFS.
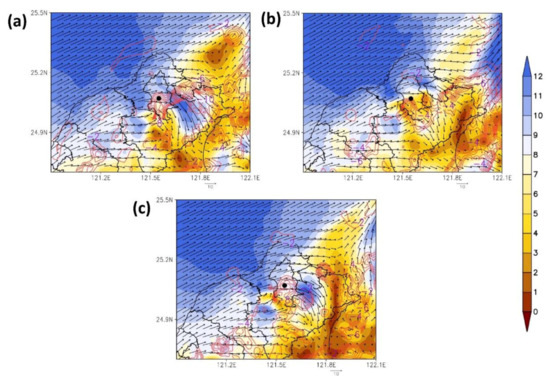
Figure 21.
Three-kilometer wind field at 850 hPa (color scale, m/s) and 500 hPa convergence (green dotted line, 1/s) at 14:00 on June 4: (a) WRF-GSI_noDA; (b) WRF-GSI_lidar; (c) WRF-GSI_lidar_hzscl. Black circle is Songshan Airport (longitude = 121.55, latitude = 25.07).
Under the complex atmospheric conditions during the study period, a front system was located north of Taiwan, while Typhoon Choi-wan was located southwest of Taiwan. The 3 km simulation results substantially differed in these two models, particularly regarding the coastal wind speed different on the northern side of the Taiwan Strait. The wind field simulated by the WRF-GSI_lidar model was much closer to the actual wind field than the WRF-GSI_noDA model due to the wind field along the coast area simulated well.
In summary, assimilation of the Doppler wind lidar data at Taipei Songshan Airport could improve the wind field and thus the forecasting location of the extreme precipitation on 4 June. In other words, once the 3D wind field data within the boundary layer were improved, the convective system’s location could also be predicted accurately. In addition, large-scale initial and boundary data close to the actual synoptic environments are required to achieve such results.
6. Conclusions
This study integrated 3D lidar data on wind fields using advanced data assimilation technology (e.g., hybrid data and 3D variations) to develop a high-resolution, small-scale (e.g., northern Taiwan) data assimilation and weather forecasting system. The results presented in this study use a single doppler wind lidar from the Shongshan Airport to create a case study. A data assimilation forecast analysis was conducted on an extreme precipitation event in Taipei in 2021, leading to the following contributions:
- Two independent grids, which featured 15 and 3 km resolutions, were employed for weather forecasting at different scales. The data were then assimilated for application. Hybrid data assimilation was conducted to acquire a large-scale ambient field as the initial and boundary conditions for high-resolution analyses, thus preventing the disturbance between small-scale and large-scale analysis data.
- According to the large-scale analysis results, the short-duration extreme precipitation of the case event was caused by the interaction between the northeast wind incurred by the large-scale frontal movement, and the humid southerly wind generated by Typhoon Choi-wan, and the regional sea-land breeze circulation in northern Taiwan.
- The introduction of the Doppler wind lidar data improved the prediction of the locations and intensity of small-scale extreme precipitation on 4 June because of the improvement in the 3D wind field data within the boundary layer. Because the lidar data corrected the overestimated wind speed and wind directions in the nonassimilated boundary layer data, the wind fields from the estuary of Tamsui and the valley of Keelung were also calibrated with the ground convergence intensity and locations. Therefore, the locations and intensity of the convective systems were corrected.
- The horizontal length scale experiments showed that rainfall forecasts have different results due to wind lidar data at different length scales. Compared with the WRF-GSI_lidar and WRF-GSI_lidar_hzscl experiment, the results indicated that a smaller length scale (hzscl_op) produces a slightly weaker wind speed zone at Taipei Basin when T=0. However, the forecast showed that a smaller length scale generates stronger wind, making the convection tilt southeastward when T=6. Because of such wind field changes, the rainfall area is narrowed away from the XinYi District. From the results of this case, it would be better to set a bigger length scale when assimilating the wind lidar data.
- Compared to the 3 km high-resolution regional forecast results published by the CWB, the forecast by the WRF-GSI model was more accurate in terms of the locations and intensity of extreme precipitation. Regarding the flood in the Xinyi district, the assimilated wind field data reported accumulated rainfall higher than the nonassimilated data by 30 mm. In other words, the model proposed in this study predicted that the accumulated rainfall in the district was improved more than that of the operational model by 15%.
In summary, the short-duration convective systems in Taipei on 4 June 2021 were caused by atmospheric interactions at varying scales. Two factors must be considered to predict short-duration extreme precipitation accurately: (1) an accurate initial large-scale ambient field, which prevents errors in the locations of dynamic convergence at different scales, and (2) accurate wind field data within the boundary layer. Errors in the wind field data in the boundary layer lead to biases in the locations of dynamic convergence and the intensity of dynamic convergence and divergence, thus inhibiting the accuracy of convective rainfall intensity and accumulated rainfall prediction. The WRF-GSI data assimilation method generated an accurate large-scale ambient field. The Doppler wind lidar data were assimilated to reduce the overestimation of the boundary layer wind speed, effectively correcting the locations and intensities of the simulated convective systems and raising the accuracy of the extreme precipitation prediction.
Author Contributions
Conceptualization, C.-Y.C. and N.-C.Y.; methodology, C.-Y.C. and N.-C.Y.; validation, C.-Y.C.; formal analysis, C.-Y.C. and N.-C.Y.; writing—original draft preparation, N.-C.Y.; writing—review and editing, N.-C.Y., C.-Y.C., and C.-Y.L.; funding acquisition, N.-C.Y. and C.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the MINISTRY OF SCIENCE AND TECHNOLOGY of Taiwan, grant numbers MOST 110-2111-M-344-001, 110-2111-M-001-013 and 110-2811-M-001-573.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data sets of GFS, GDAS, and GEFS used in this study are publicly available in the archives: GFS and GDAS: (NOAA Global Forecast System (GFS)—Registry of Open Data on AWS ), accessed on 01 July 2021. GEFS: (NOAA Global Ensemble Forecast System (GEFS)—Registry of Open Data on AWS ), accessed on 01 July 2021, respectively.
Acknowledgments
The authors want to acknowledge Taiwan’s Air Force Weather Wing for providing the Doppler Wind Lidar data. Also, the authors would like to thank the service from the Ministry of Science and Technology and Chinese Culture University, Data Bank for Atmospheric and Hydrologic Research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Hegerl, G.C. Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J. Clim. 2007, 20, 1419–1444. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q.; Jon Dokken, D.; Ebi, K.L.; Mastrandrea, M.D.; Mach, K.J.; Plattner, G.K.; Allen, S.K.; et al. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambrdige University Press: Cambridge, UK, 2012; ISBN 9781139177245. [Google Scholar] [CrossRef]
- Ratnam, J.; Behera, S.; Ratna, S.B.; Rajeevan, M.; Yamagata, T. Anatomy of Indian heatwaves. Sci. Rep. 2016, 6, 24395. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Pradhan, P.K.; Sinha, T.; Rao, S.V.B.; Chang, H.-P. Interaction of a low-pressure system, an offshore trough, and mid-tropospheric dry air intrusion: The Kerala Flood of august 2018. Atmosphere 2020, 11, 740. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate extremes and compound hazards in a warming world. Annu. Rev. Earth Planet. Sci. 2020, 48, 519–548. [Google Scholar] [CrossRef]
- World Economic Forum. The Global Risks Report 2021, 16th ed.; World Economic Forum: Geneva, Switzerland, 2021; ISBN 9782940631247. [Google Scholar]
- Aristizábal, E.; García, E.F.; Marín, R.J.; Gómez, F.; Guzmán-Martínez, J. Rainfall-intensity effect on landslide hazard assessment due to climate change in north-western Colombian Andes. Rev. Fac. Ing. Univ. Antioquia. 2022, 103, 1–16. [Google Scholar] [CrossRef]
- Aguilar, E.; Peterson, T.; Obando, P.R.; Frutos, R.; Retana, J.A.; Solera, M.; Soley, J.; García, I.G.; Araujo, R.M.; Santos, A.R.; et al. Changes in precipitation and temperature extremes in Central America and northern South America, 1961–2003. J. Geophys. Res. Atmos. 2005, 110, 1–15. [Google Scholar] [CrossRef]
- Ávila, A.; Justino, F.; Wilson, A.; Bromwich, D.; Amorim, M. Recent precipitation trends, flash floods and landslides in southern Brazil. Environ. Res. Lett. 2016, 11, 114029. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Ronchail, J.; Marengo, J.A.; Segura, H. Contrasting North–South changes in Amazon wet-day and dry-day frequency and related atmospheric features (1981–2017). Clim. Dyn. 2019, 52, 5413–5430. [Google Scholar] [CrossRef]
- Ávila, Á.; Guerrero, F.C.; Escobar, Y.C.; Justino, F. Recent precipitation trends and floods in the Colombian Andes. Water. 2019, 11, 379. [Google Scholar] [CrossRef]
- Avila-Diaz, A.; Justino, F.; Lindemann, D.S.; Rodrigues, J.M.; Ferreira, G.R. Climatological aspects and changes in temperature and precipitation extremes in viçosa-Minas Gerais. An. Acad. Bras. Cienc. 2020, 92, 1–19. [Google Scholar] [CrossRef]
- Cerón, W.L.; Kayano, M.T.; Andreoli, R.V.; Avila-Diaz, A.; Ayes, I.; Freitas, E.D.; Martins, J.A.; Souza, R.A.F. Recent intensification of extreme precipitation events in the La Plata Basin in Southern South America (1981–2018). Atmos. Res. 2021, 249, 105299. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Chapter 11: Weather and climate extreme events in a changing climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V.P., Zhai, A., Pirani, S.L., Connors, C., Péan, S., Berger, N., Caud, Y., Chen, L., Goldfarb, M.I., Gomis, M., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; p. 345. [Google Scholar]
- Donat, M.; Alexander, L.V.; Herold, N.; Dittus, A.J. Temperature and precipitation extremes in century-long gridded observations, reanalyses, and atmospheric model simulations. J. Geophys. Res. Atmos. 2016, 121, 11–174. [Google Scholar] [CrossRef]
- Yang, Y.; Gan, T.Y.; Tan, X. Spatiotemporal changes in precipitation extremes over Canada and their teleconnections to large-scale climate patterns. J. Hydrometeorol. 2019, 20, 275–296. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Khadgarai, S.; Kumar, V.; Pradhan, P.K. The connection between extreme precipitation variability over Monsoon Asia and large-scale circulation patterns. Atmosphere 2021, 12, 1492. [Google Scholar] [CrossRef]
- Balmaceda-Huarte, R.; Olmo, M.E.; Bettolli, M.L.; Poggi, M.M. Evaluation of multiple reanalyses in reproducing the spatio-temporal variability of temperature and precipitation indices over southern South America. Int. J. Climatol. 2021, 41, 5572–5595. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; García-Herrera, R.; Peña-Angulo, D.; Tomas-Burguera, M.; Domínguez-Castro, F.; Noguera, I.; Calvo, N.; Murphy, C.; Nieto, R.; Gimeno, L.; et al. Do CMIP models capture long-term observed annual precipitation trends? Clim. Dyn. 2021, 58, 2825–2842. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T. A new paradigm for continental U.S. summer rainfall variability: Asia-North America teleconnection. J. Clim. 2016, 29, 7313–7327. [Google Scholar] [CrossRef]
- Sánchez-Benítez, A.; García-Herrera, R.; Vicente-Serrano, S.M. Revisiting precipitation variability, trends and drivers in the Canary Islands. Int. J. Climatol. 2017, 37, 3565–3576. [Google Scholar] [CrossRef]
- Gao, L.; Huang, J.; Chen, X.; Chen, Y.; Liu, M. Contributions of natural climate changes and human activities to the trend of extreme precipitation. Atmos. Res. 2018, 205, 60–69. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, G.; Wang, X.; Cheng, G. Future Changes in Precipitation Extremes Over Canada: Driving Factors and Inherent Mechanism. J. Geophys. Res. Atmos. 2018, 123, 5783–5803. [Google Scholar] [CrossRef]
- Krishnan, R.; Sanjay, J.; Gnanaseelan, C.; Mujumdar, M.; Kulkarni, A.; Chakraborty, S. Assessment of Climate Change over the Indian Region: A Report of the Ministry of Earth Sciences (MOES), Government of India; Springer Nature: Basingstoke, UK, 2020; p. 226. [Google Scholar]
- Chadwick, R.; Good, P.; Martin, G.; Rowell, D.P. Large rainfall changes consistently projected over substantial areas of tropical land. Nat. Clim. Chang. 2016, 6, 177–181. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Brown, J.M.; Brunet, G.; Lynch, P.; Saito, K.; Schlatter, T.W. 100 Years of progress in forecasting and NWP applications. Meteorol. Monogr. 2019, 59, 13.1–13.67. [Google Scholar] [CrossRef]
- Houze, R.A. 100 Years of research on mesoscale convective systems. Meteorol. Monogr. 2018, 59, 17.1–17.54. [Google Scholar] [CrossRef]
- Prein, A.F.; Langhans, W.; Fosser, G.; Ferrone, A.; Ban, N.; Goergen, K.; Keller, M.; Tölle, M.; Gutjahr, O.; Feser, F.; et al. A review on regional convection-permitting climate modeling: Demonstrations, prospects, and challenges. Rev. Geophys. 2015, 53, 323–361. [Google Scholar] [CrossRef]
- Peters, K.; Hohenegger, C.; Klocke, D. Different Representation of Mesoscale Convective Systems in Convection-Permitting and Convection-Parameterizing NWP Models and Its Implications for Large-Scale Forecast Evolution. Atmosphere 2019, 10, 503. [Google Scholar] [CrossRef]
- Zhang, F.; Odins, A.M.; Nielsen-Gammon, J.W. Mesoscale predictability of an extreme warm-season precipitation event. Weather Forecast 2006, 21, 149–166. [Google Scholar] [CrossRef]
- Kato, T.; Aranami, K. Formation factors of 2004 Niigata-Fukushima and Fukui heavy rainfalls and problems in the predictions using a cloud-resolving model. Sci. Online Lett. Atmos. 2005, 1, 1–4. [Google Scholar] [CrossRef]
- Done, J.; Davis, C.A.; Weisman, M. The next-generation of NWP: Explicit forecasts of convection using the Weather Research and Forecasting (WRF) model. Atmos. Sci. Lett. 2004, 5, 110–117. [Google Scholar] [CrossRef]
- Hristova-Veleva, S.; Zhang, S.Q.; Turk, F.J.; Haddad, Z.S.; Sawaya, R.C. Assimilation of DAWN Doppler wind lidar data during the 2017 convective processes experiment (CPEX): Impact on precipitation and flow structure. Atmos. Meas. Tech. 2021, 14, 3333–3350. [Google Scholar] [CrossRef]
- Kawabata, T.; Seko, H.; Saito, K.; Kuroda, T.; Tamiya, K.; Tsuyuki, T.; Honda, Y.; Wakazuki, Y. An assimilation and forecasting experiment of the Nerima heavy rainfall with a cloud-resolving nonhydrostatic 4-dimensional variational data assimilation system. J. Meteor. Soc. Jpn. 2007, 85, 255–276. [Google Scholar] [CrossRef]
- Rennie, S.J.; Dance, S.L.; Illingworth, A.J.; Ballard, S.P.; Simonin, D. 3D-Var assimilation of insect-derived Doppler radar radial winds in convective cases using a high-resolution model. Mon. Weather Rev. 2011, 139, 1148–1163. [Google Scholar] [CrossRef]
- Tang, W.; Chan, P.W.; Haller, G. Lagrangian Coherent structure analysis of terminal winds detected by lidar. part I: Turbulence structures. J. Appl. Meteorol. Clim. 2011, 50, 325–338. [Google Scholar] [CrossRef]
- Zhang, L.; Pu, Z. Four-dimensional assimilation of multitime wind profiles over a single station and numerical simulation of a mesoscale convective system observed during IHOP_2002. Mon. Weather Rev. 2011, 139, 3369–3388. [Google Scholar] [CrossRef][Green Version]
- Huang, X.-Y.; Xiao, Q.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.; Ma, Z.; et al. Four-dimensional variational data assimilation for WRF: Formulation and preliminary results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef]
- Li, L.; Shao, A.; Zhang, K.; Ding, N.; Chan, P.-W. Low-Level wind shear characteristics and lidar-based alerting at Lanzhou Zhongchuan International Airport, China. J. Meteorol. Res. 2020, 34, 633–645. [Google Scholar] [CrossRef]
- Banta, R.M.; Olivier, L.D.; Gudiksen, P.H.; Lange, R. Implications of small-scale flow features to modeling dispersion over complex terrain. J. Appl. Meteor. 1996, 35, 330–342. [Google Scholar] [CrossRef][Green Version]
- Shun, C.M.; Chan, P.W. Applications of an infrared Doppler lidar in detection of wind shear. J. Atmos. Oceanic Technol. 2008, 25, 637–655. [Google Scholar] [CrossRef]
- Wu, C.-S.; Lin, Y.-F.; Lee, C.-Y. Application of wind profiler by laser. Q. J. Meteorol. 2016, 228, 1–7. (In Chinese) [Google Scholar]
- Zhang, H.; Wu, S.; Wang, Q.; Liu, B.; Yin, B.; Zhai, X. Airport low-level wind shear lidar observation at Beijing Capital International Airport. Infrared Phys. Technol. 2019, 96, 113–122. [Google Scholar] [CrossRef]
- Thobois, L.; Cariou, J.P.; Gultepe, I. Review of lidar-based applications for aviation weather. Pure Appl. Geophys. 2019, 176, 1959–1976. [Google Scholar] [CrossRef]
- Kawabata, T.; Iwai, H.; Seko, H.; Shoji, Y.; Saito, K.; Ishii, S.; Mizutani, K. Cloud-Resolving 4D-Var assimilation of doppler wind lidar data on a meso-gamma-scale convective system. Mon. Weather Rev. 2014, 142, 4484–4498. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3 (No. NCAR/TN-475+STR); University Corporation for Atmospheric Research: Boulder, CO, USA, 2008; p. 113. [Google Scholar] [CrossRef]
- Kleist, D.T.; Parrish, D.F.; Derber, J.C.; Treadon, R.; Wu, W.-S.; Lord, S. Introduction of the GSI into the NCEP global data assimilation system. Weather Forecast 2009, 24, 1691–1705. [Google Scholar] [CrossRef]
- Kanamitsu, M. Description of the NMC Global data assimilation and forecast system. Weather Forecast 1989, 4, 335–342. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Baker, W.E. Global numerical weather prediction at the National Meteorological Center. Bull. Am. Meteor. Soc. 1990, 71, 1410–1428. [Google Scholar] [CrossRef]
- Harris, L.; Chen, X.; Putman, W.; Zhou, L.; Chen, J.-H. A Scientific Description of the GFDL Finite-Volume Cubed-Sphere Dynamical Core; Geophysical Fluid Dynamics Laboratory: Princeton, NJ, USA, 2021; p. 109. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NMC: The generation of perturbations. Bull. Am. Meteor. Soc. 1993, 74, 2317–2330. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M.; Wei, X.; Song, Y.; Toth, Z. Ensemble data assimilation with the NCEP global forecast system. Mon. Weather Rev. 2008, 136, 463–482. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Y.; Hou, D.; Kleist, D. Comparison of the ensemble transform and the ensemble Kalman Filter in the NCEP global ensemble forecast system. Weather Forecast 2016, 31, 2058–2074. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Y.; Hou, D.; Luo, Y.; Peng, J.; Wobus, R. Performance of the New NCEP global ensemble forecast system in a parallel experiment. Weather Forecast 2017, 32, 1989–2004. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell1, D.C.; Grell, G.A.; et al. A North American hourly assimilation and model forecast cycle: The rapid refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Tao, W.-K.; Simpson, J.; McCumber, M. An ice–water saturation adjustment. Mon. Weather Rev. 1989, 117, 231–235. [Google Scholar] [CrossRef]
- Tao, W.-K.; Wu, D.; Lang, S.; Chern, J.-D.; Peters-Lidard, C.; Fridlind, A.; Matsui, T. High-resolution NU-WRF simulations of a deep convective-precipitation system during MC3E: Further improvements and comparisons between Goddard microphysics schemes and observations. J. Geophys. Res. Atmos. 2016, 121, 1278–1305. [Google Scholar] [CrossRef] [PubMed]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long–lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor–Yamada level 3 model: Its numerical stability and application to a regional prediction of advection fog. Bound. Layer Meteor. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteor. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Pleim, J.E.; Xiu, A. Development and testing of a surface flux and planetary boundary layer model for application in mesoscale models. J. Appl. Meteor. 1995, 34, 16–32. [Google Scholar] [CrossRef]
- Pleim, J.E.; Xiu, A. Development of a land surface model. Part II: Data assimilation. J. Appl. Meteor. 2003, 42, 1811–1822. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.-L. Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Weather Forecast 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Pleim, J.E. A Combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing. J. Appl. Meteor. Climatol. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Madala, S.; Srinivas, C.V.; Satyanarayana, A.N.V. Performance of WRF for simulation of mesoscale meteorological characteristics for air quality assessment over tropical coastal city, Chennai. Pure Appl. Geophys. 2018, 175, 501–518. [Google Scholar] [CrossRef]
- Cooperman, A.; Dam, C.P.; Zack, J.; Chen, S.-H.; MacDonald, C. Improving Short-Term Wind Power Forecast. Through Measurements and Modeling of the Tehachapi Wind Resource Area; Publication Number: CEC-500-2018-002; California Energy Commission: Sacramento, CA, USA, 2018; p. 77. [Google Scholar]
- Wu, W.-S.; Purser, R.J.; Parrish, D.F. Three-dimensional variational analysis with spatially inhomogeneous covariances. Mon. Weather Rev. 2002, 130, 2905–2916. [Google Scholar] [CrossRef]
- Purser, R.J.; Wu, W.-S.; Parrish, D.F.; Roberts, N.M. Numerical aspects of the application of recursive filters to variational statistical analysis. Part I: Spatially homogeneous and isotropic Gaussian covariances. Mon. Weather Rev. 2003, 131, 1524–1535. [Google Scholar] [CrossRef]
- Liu, Y.-A.; Huang, H.-L.A.; Gao, W.; Lim, A.H.N.; Liu, C.; Shi, R. Tuning of background error statistics through sensitivity experiments and its impact on typhoon forecast. J. Appl. Remote Sens. 2015, 9, 96051. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).