Prediction Model for Daily Reference Crop Evapotranspiration Based on Hybrid Algorithm in Semi-Arid Regions of China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. FAO-56 PM
2.3. Partial Correlation Analysis
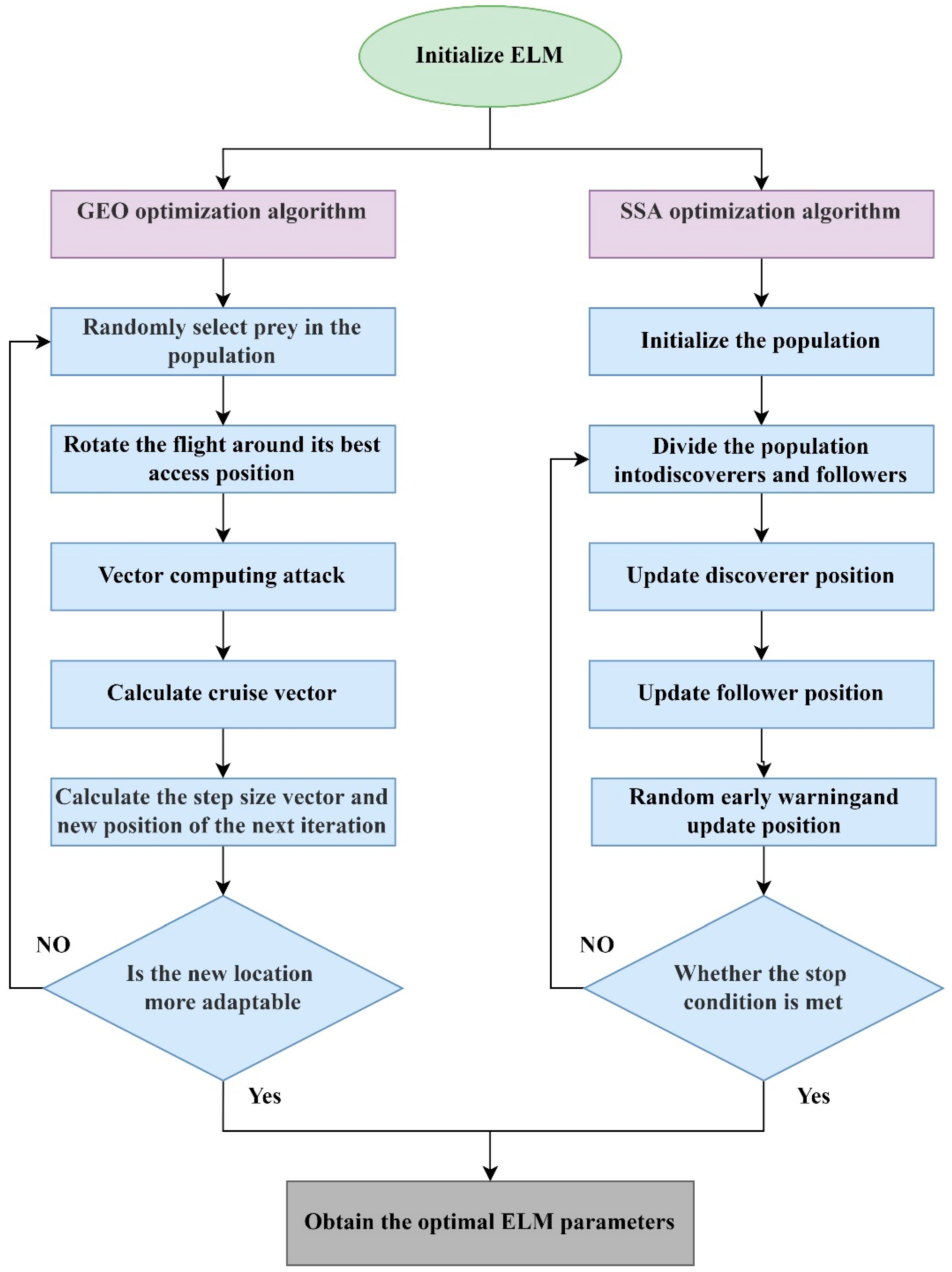
2.4. Development of Two Bionic Optimization Algorithms to Optimize ELM
2.4.1. ELM
2.4.2. GEO
2.4.3. SSA
2.5. Model Prediction Evaluation
3. Results and Discussion
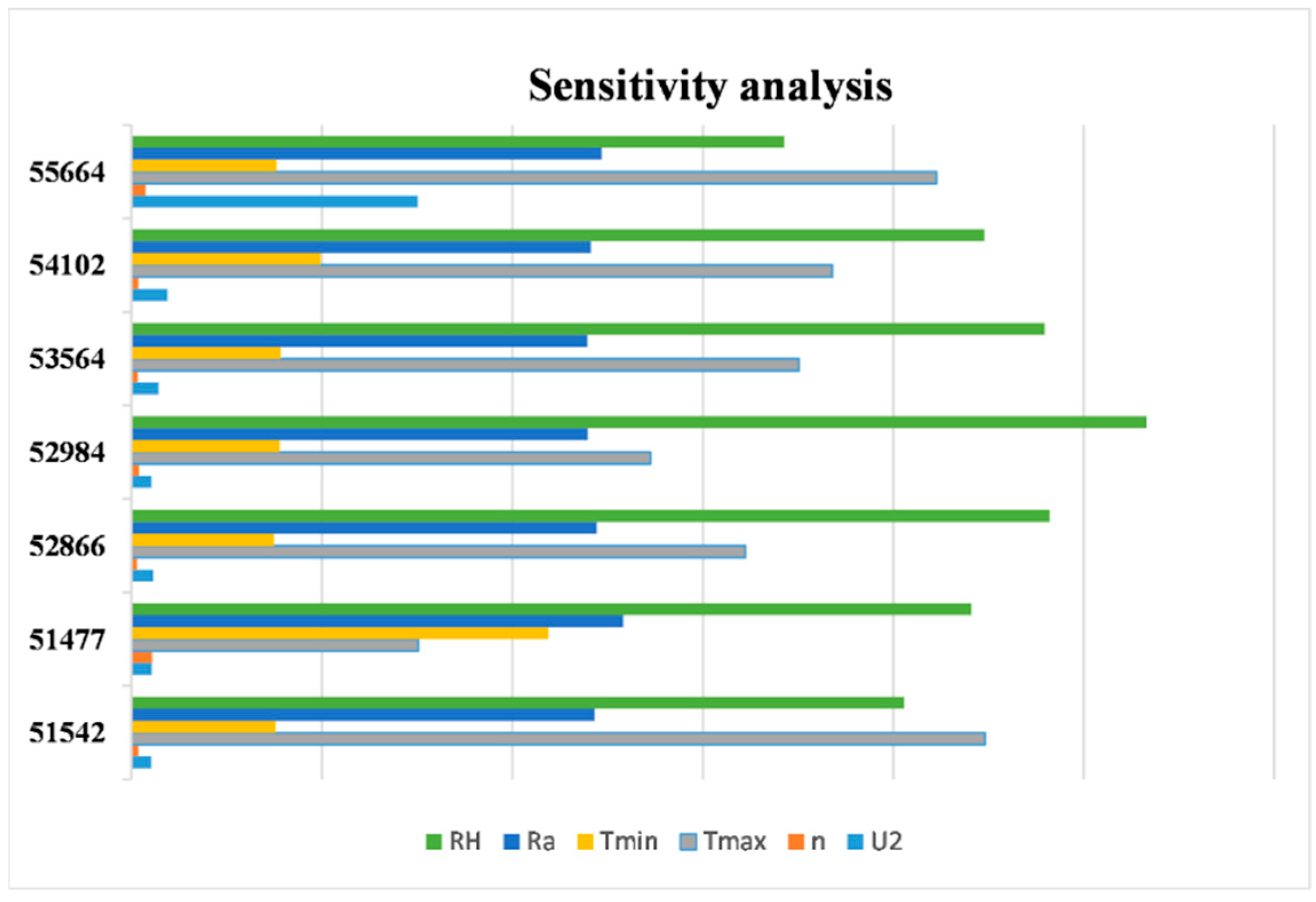
3.1. Selecting Important Weather Factors with Partial Correlation Analysis
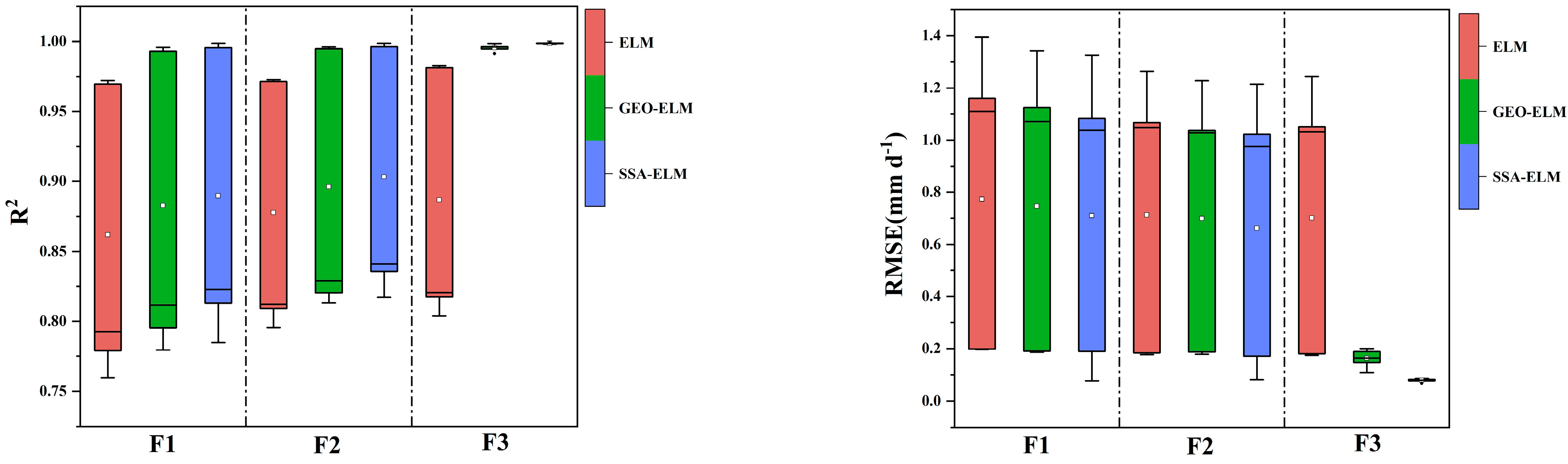
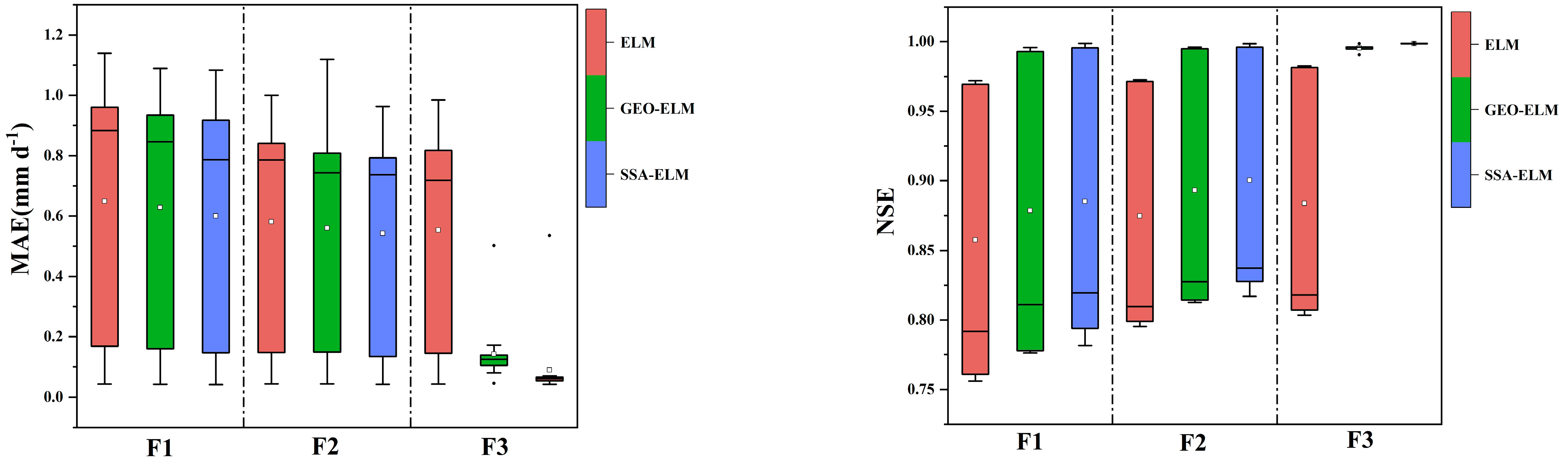
3.2. Analysis of ELM Model Predicting Daily Evapotranspiration
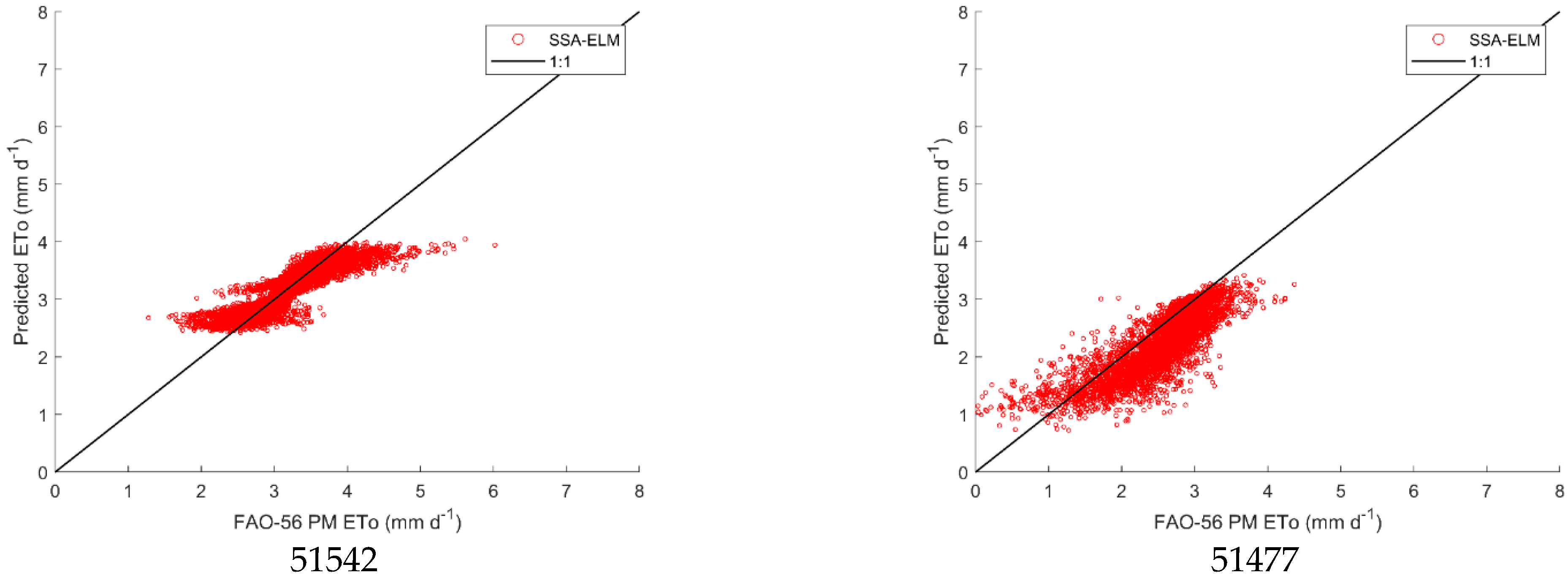
3.3. Applicability of ETO Model in Semi-Arid Region
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Xu, C.; Chen, X. Reference evapotranspiration changes in China: Natural processes or human influences. Theor. Appl. Climatol. 2011, 103, 479–488. [Google Scholar] [CrossRef]
- Miralles, D.; De Jeu, R.; Gash, J.; Holmes, T.; Dolman, A. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
- Awad, M.; Darwish, T. Mapping evapotranspiration to administer water use in Bekaa valley. In Proceedings of the 2015 International Workshop on Evapotranspiration Mapping for Water Security, Washington, DC, USA, 15–17 September 2015. [Google Scholar]
- Allen, G.; Pereira, S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Gavil´an, P.; Berengena, J.; Allen, G. Measuring versus estimating net radiation and soil heat flux: Impact on Penman-Monteith reference ET estimates in semiarid regions. Agric. Water Manag. 2007, 89, 275–286. [Google Scholar] [CrossRef]
- L´opez-Urrea, R.; Olalla, S.; Fabeiro, C.; Moratalla, A. An evaluation of two hourly reference evapotranspiration equations for semiarid conditions. Agric. Water Manag. 2006, 86, 277–282. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, S.; Singh, R. Evaluation of variable-infiltration capacity model and MODIS-terra satellite-derived grid-scale evapotranspiration estimates in a river basin with tropical monsoon-type climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028.1–04017028.16. [Google Scholar] [CrossRef] [Green Version]
- Elbeltagi, A.; Kumari, N.; Dharpure, K.; Mokhtar, A.; Kuriqi, A. Prediction of combined terrestrial evapotranspiration index (ctei) over large river basin based on machine learning approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Nasseri, S.; Ghamarnia, H.; Khosravi, R.; Mohamadi, Y.; Sargordi, F. Evaluation of the accuracy of different combined methods for estimating the potential evapotranspiration in different climates (case study: Iran). Water Irrig. Manag. 2020, 10, 443–452. [Google Scholar]
- Sinclair, T. “Natural Evaporation from Open Water, Bare Soil and Grass” by Harold L. Penman, (1948) A193:120–146. Crop Sci. 2019, 59, 2297–2299. [Google Scholar] [CrossRef]
- Biazar, S.; Dinpashoh, Y.; Singh, V. Sensitivity analysis of the reference crop evapotranspiration in a humid region. Environ. Sci. Pollut. Res. 2019, 26, 32517–32544. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Yue, J.; Ningbo, C.; Lu, Z.; Chen, L.; Daozhi, G. Calibration of Hargreaves model for reference evapotranspiration estimation in Sichuan basin of southwest China. Agric. Water Manag. 2017, 181, 1–9. [Google Scholar]
- Hafeez, M.; Chatha, Z.; Khan, A.; Gulshan, A.; Basit, A.; Tahira, F. Comparative Analysis of Reference Evapotranspiration by Hargreaves and Blaney-Criddle Equations in Semi-Arid Climatic Conditions. Curr. Res. Agric. Sci. 2020, 7, 52–57. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, Y.; Wu, C.; Zheng, H.; Zhang, L.; Cui, Y.; Sun, N.; Wang, L. Evaluation of six equations for daily reference evapotranspiration estimating using public weather forecast message for different climate regions across China. Agric. Water Manag. 2019, 222, 386–399. [Google Scholar] [CrossRef]
- Fernando, F.; Fernando, F.; Marco, A.; Epitácio, J. Performance of estimative models for daily reference evapotranspiration in the city of Cassilândia, Brazil. Eng. Agric. 2017, 37, 173–184. [Google Scholar]
- Irmak, S.; Irmak, A.; Allen, R.G.; Jones, J.W. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates. J. Irrig. Drain. Eng. 2003, 129, 336–347. [Google Scholar] [CrossRef]
- Shakibul, I.; Rashidul, A. Performance evaluation of FAO Penman-Monteith and best alternative models for estimating reference evapotranspiration in Bangladesh. Heliyon 2021, 7, e07487. [Google Scholar]
- Hossein, T.; Ozgur, K.; Azadeh, E.; Hosseinzadeh, T. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444–445, 78–89. [Google Scholar]
- Akpootu, D.; Iliyasu, M. A comparison of various evapotranspiration models for estimating reference evapotranspiration in Sokoto, North Western, Nigeria. Phys. Sci. Int. J. 2017, 14, 1–14. [Google Scholar] [CrossRef]
- Valiantzas, J. Temperature-and humidity-based simplified Penman’s ETO formulae. Comparisons with temperature-based Hargreaves-Samani and other methodologies. Agric. Water Manag. 2018, 208, 326–334. [Google Scholar] [CrossRef]
- Shrestha, N.; Shukla, S. Support vector machine based modeling of evapotranspiration using hydro-climatic variables in a sub-tropical environment. Agric. For. Meteorol. 2015, 200, 172–184. [Google Scholar] [CrossRef]
- Junliang, F.; Wenjun, Y.; Lifeng, W.; Fucang, Z.; Huanjie, C.; Xiukang, W.; Xianghui, L.; Youzhen, X. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar]
- Wu, Z.; Cui, N.; Zhu, B.; Zhao, L.; Wang, X.; Hu, X.; Wang, Y.; Zhu, S. Improved hargreaves model based on multiple intelligent optimization algorithms to estimate reference crop evapotranspiration in humid areas of southwest China. Atmosphere 2020, 12, 15. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Lu, X.; Fan, J.; Wu, L.; Dong, J. Forecasting multi-step ahead monthly reference evapotranspiration using hybrid extreme gradient boosting with grey wolf optimization algorithm. Comput. Model. Eng. Sci. 2020, 125, 699–723. [Google Scholar] [CrossRef]
- Citakoglu, H.; Cobaner, M.; Haktanir, T.; Kisi, O. Estimation of Monthly Mean Reference Evapotranspiration in Turkey. Water Resour. Manag. 2014, 28, 99–113. [Google Scholar] [CrossRef]
- Chia, M.; Huang, Y.; Koo, C. Reference evapotranspiration estimation using adaptive neuro-fuzzy inference system with limited meteorological data. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Tokyo, Japan, 2020; Volume 612, p. 012017. [Google Scholar]
- Han, Y.; Wu, J.; Zhai, B.; Pan, Y.; Zeng, W. Coupling a bat algorithm with xgboost to estimate reference evapotranspiration in the arid and semiarid regions of China. Adv. Meteorol. 2019, 2019, 9575782. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, Z.; Zhang, L.; Lin, Q.; Du, J. Improved online sequential extreme learning machine for simulation of daily reference evapotranspiration. Tecnol. Cienc. Agua 2017, 8, 127–140. [Google Scholar] [CrossRef]
- Samui, P.; Dixon, B. Application of support vector machine and relevance vector machine to determine evaporative losses in reservoirs. Hydrol. Processes 2012, 26, 1361–1369. [Google Scholar] [CrossRef]
- Ahmad, M.J.; Choi, K.S. Influence of climate variables on FAO Penman-Monteith reference evapotranspiration in the Upper Chenab Canal command area of Pakistan. Paddy Water Environ. 2018, 16, 425–438. [Google Scholar] [CrossRef]
- Cui, F.; Zhang, H.; Yao, Q. Influencing factors and prediction models of soil temperature in Yantai based on partial correlation analysis. Shandong Agric. Sci. 2010, 1, 18–21. [Google Scholar]
- Abdullah, S.; Malek, A.; Abdullah, S.; Kisi, O.; Yap, S. Extreme learning machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Mohammadi-Balani, A.; Nayeri, M.; Azar, A.; Taghizadeh-Yazdi, M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Yan, P.; Shang, S.; Zhang, C.; Yin, N. Research on the Processing of Coal Mine Water Source Data by Optimizing BP Neural Network Algorithm with Sparrow Search Algorithm. IEEE Access 2021, 9, 108718–108730. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Yu, H.; Wen, X.; Li, B.; Yang, Z.; Wu, M.; Ma, Y. Uncertainty analysis of artificial intelligence modeling daily reference evapotranspiration in the northwest end of China. Comput. Electron. Agric. 2020, 176, 105653. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Xiang, Y.; Zheng, J. Climate change effects on reference crop evapotranspiration across different climatic zones of China during 1956. J. Hydrol. 2016, 542, 923–937. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, X.; Pan, X.; Shi, Y.; Qiu, Z.; Li, X.; Xing, X.; Bai, J. Prediction of daily reference crop evapotranspiration in different Chinese climate zones: Combined application of key meteorological factors and Elman algorithm. J. Hydrol. 2022, 610, 127822. [Google Scholar] [CrossRef]
- Xing, X.; Liu, Y.; Zhao, W.; Kang, D.; Yu, M.; Ma, X. Determination of dominant weather parameters on reference evapotranspiration by path analysis theory. Comput. Electron. Agric. 2016, 120, 10–16. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Gocic, M.; Petković, D.; Shamshirband, S.; Kamsin, A. Comparative analysis of reference evapotranspiration equations modelling by extreme learning machine. Comput. Electron. Agric. 2016, 127, 56–63. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, X.; Zhou, H.; Wang, X.; Xing, X. Prediction model for daily reference crop evapotranspiration based on hybrid algorithm and principal components analysis in Southwest China. Comput. Electron. Agric. 2021, 190, 106424. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, D. Carbon price forecasting based on improved CEEMDAN and extreme learning machine optimized by sparrow search algorithm. Sustainability 2021, 13, 4896. [Google Scholar] [CrossRef]
- Srivastava, A.; Rodriguez, J.; Saco, P.; Kumari, N.; Yetemen, O. Global Analysis of Atmospheric Transmissivity Using Cloud Cover, Aridity and Flux Network Datasets. Remote Sens. 2021, 13, 1716. [Google Scholar] [CrossRef]
- Kumar, U.; Srivastava, A.; Kumari, N.; Sahoo, B.; Chatterjee, C.; Raghuwanshi, N. Evaluation of spatiotemporal evapotranspiration using satellite-based approach and lysimeter in the agriculture dominated catchment. J. Indian Soc. Remote Sens. 2021, 49, 1939–1950. [Google Scholar] [CrossRef]
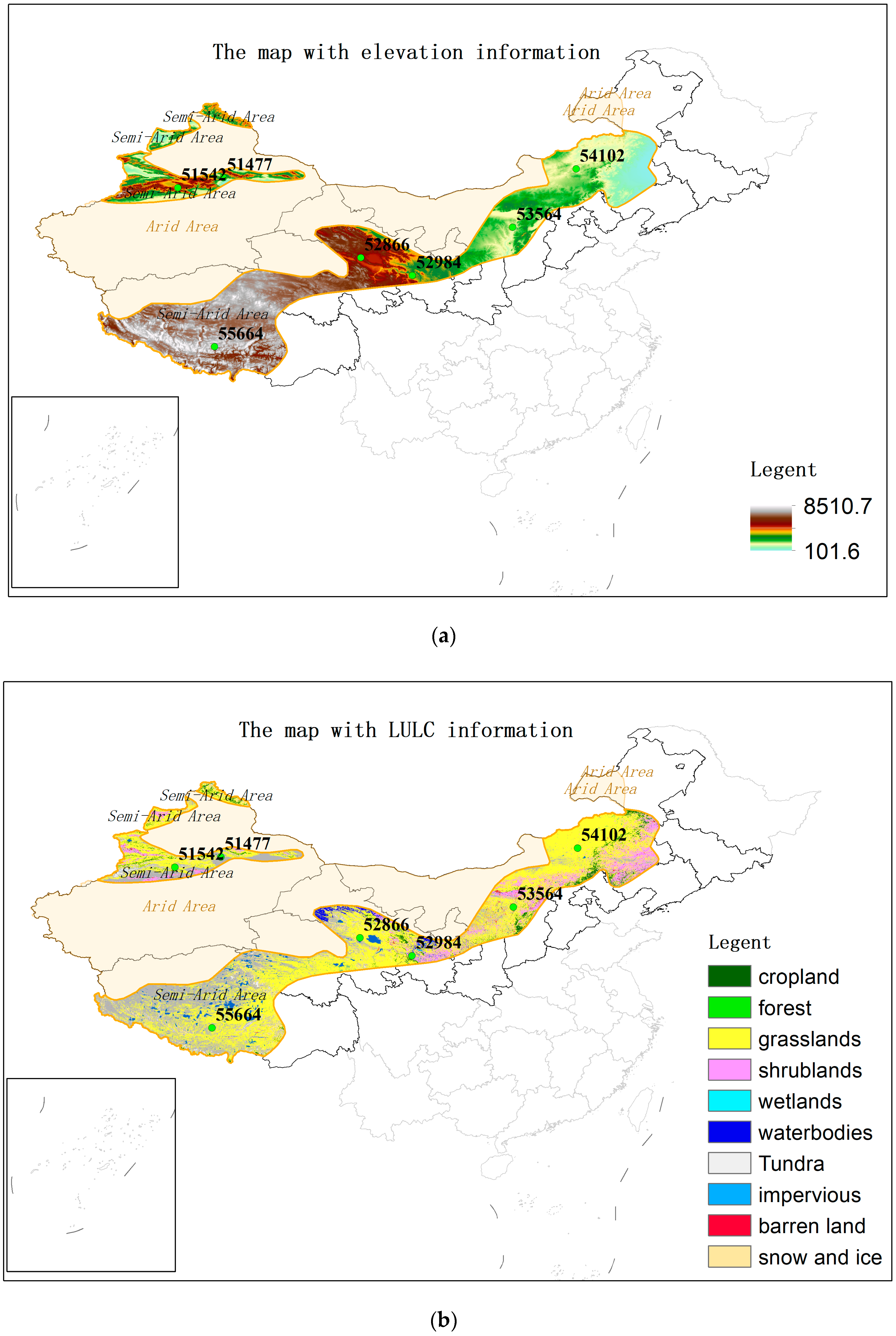
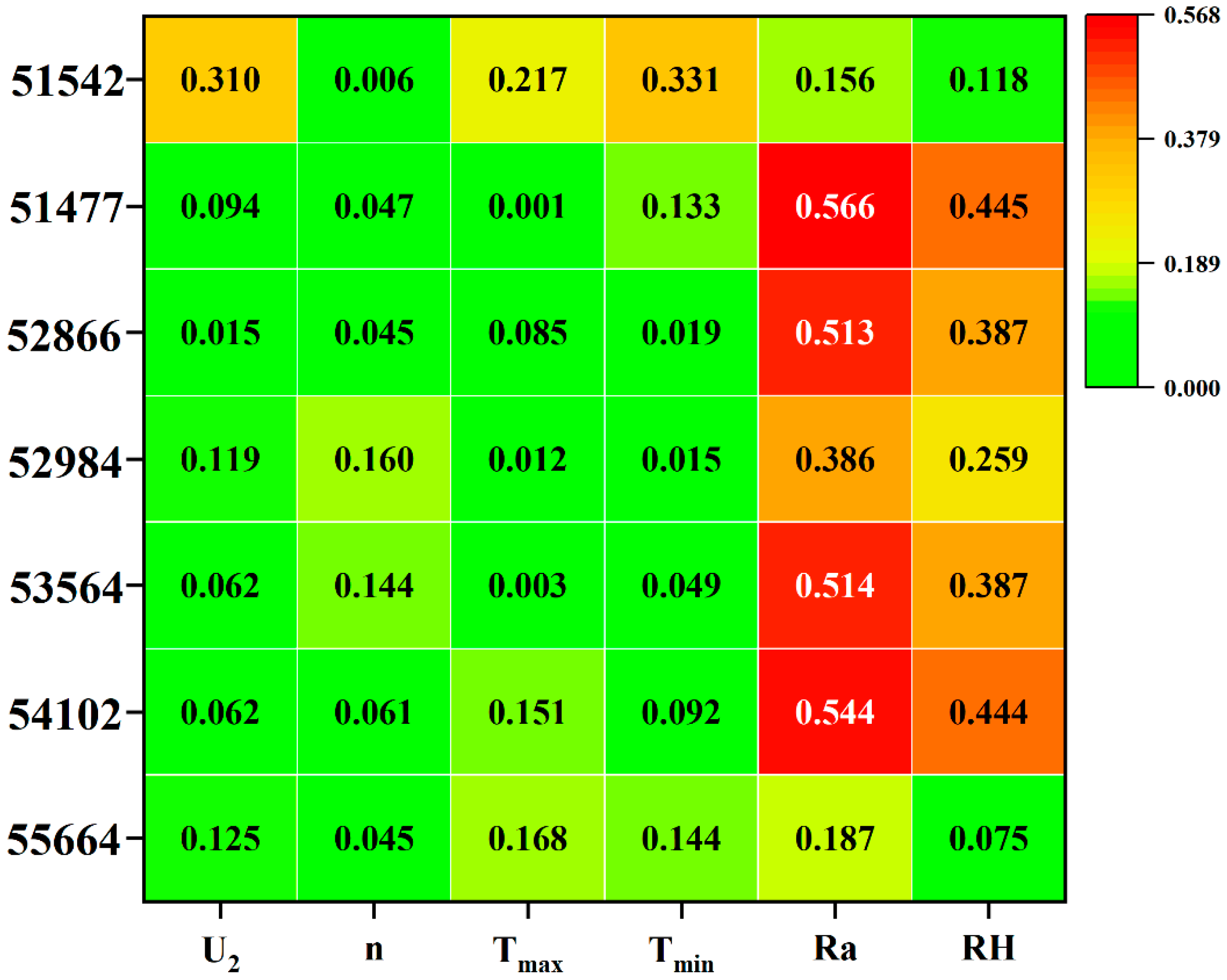
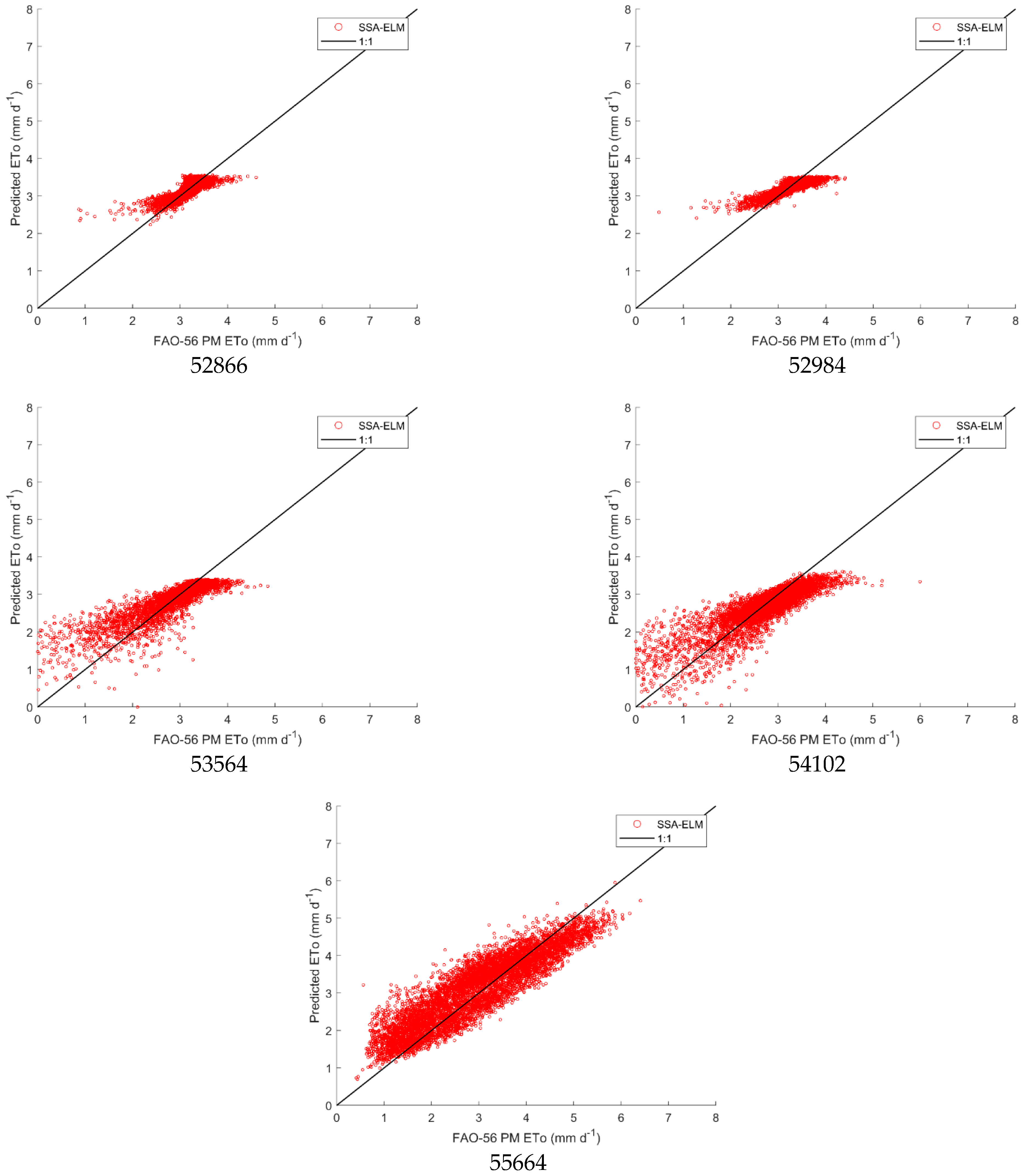
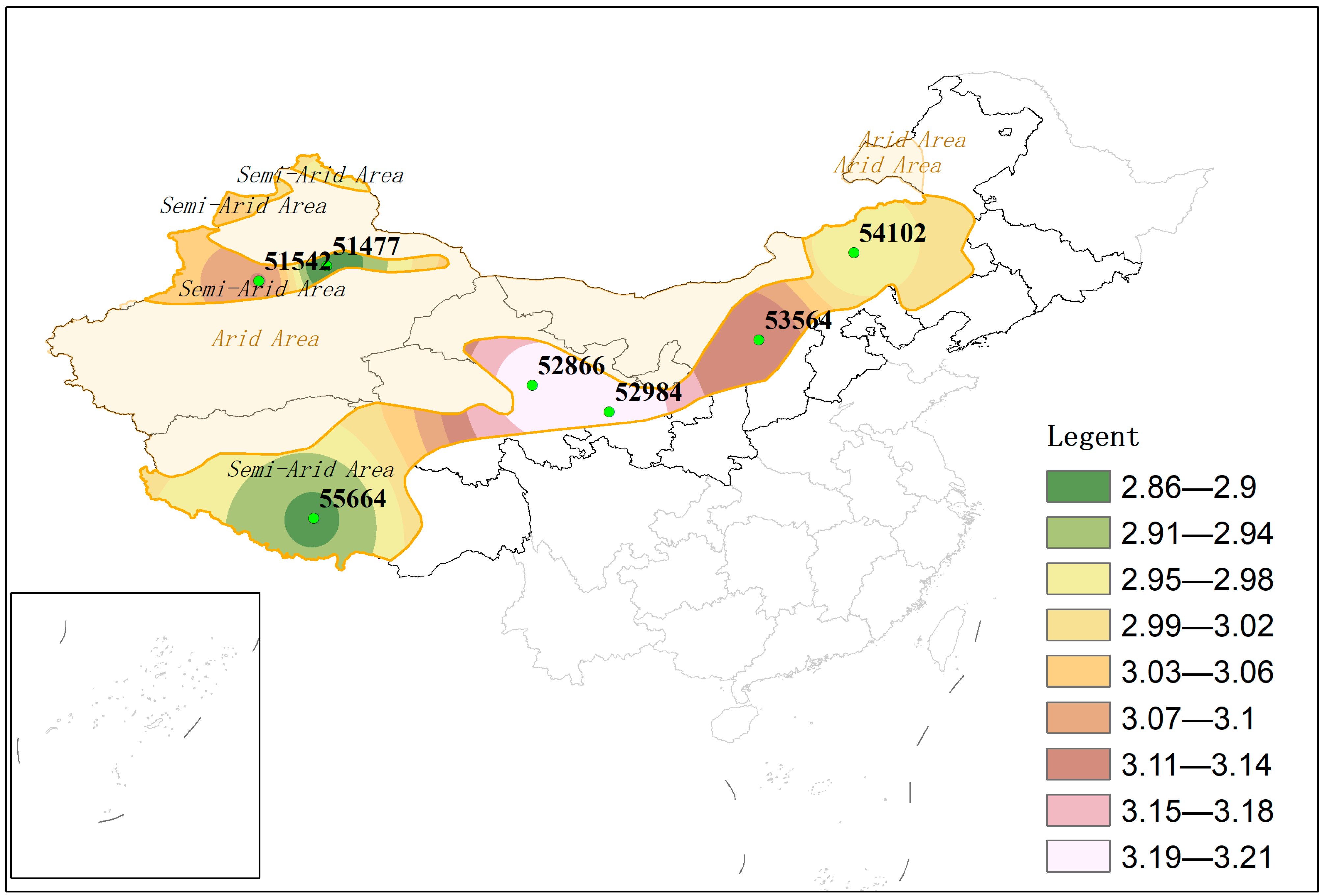
| Station ID | Station Name | Latitude (°N) | Longitude (°E) | Tmax (°C) | Tmin (°C) | RH (%) | U2 (m s−1) | n (h d−1) | ETO (mm d−1) |
|---|---|---|---|---|---|---|---|---|---|
| 51542 | Bayinbuluke | 42.5 | 84.7 | 3.3 | −10.5 | 0.7 | 2.7 | 7.6 | 1.7 |
| 51477 | Dabancheng | 43.3 | 88.3 | 13.1 | −1.1 | 0.3 | 2.6 | 8.4 | 3.1 |
| 52866 | Xining | 36.6 | 101.7 | 14.1 | 0.1 | 0.5 | 1.5 | 7.2 | 2.4 |
| 52984 | Linxia | 35.6 | 103.2 | 14.5 | 1.7 | 0.6 | 1.3 | 6.5 | 2.3 |
| 53564 | Hequ | 39.4 | 111.1 | 16.1 | 2.0 | 0.5 | 1.5 | 7.3 | 2.5 |
| 54102 | Xilinhaote | 44.1 | 116.1 | 10.0 | −3.6 | 0.5 | 3.4 | 8.0 | 2.6 |
| 55664 | Dingri | 28.6 | 87.1 | 11.7 | −5.2 | 0.4 | 2.5 | 9.1 | 2.86 |
| Three-Factor Input | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | ELM | GEO-ELM | SSA-ELM | |||||||||
| RMSE | R2 | MAE | NSE | RMSE | R2 | MAE | NSE | RMSE | R2 | MAE | NSE | |
| 51542 | 0.295 | 0.691 | 0.206 | 0.672 | 0.107 | 0.975 | 0.087 | 0.975 | 0.104 | 0.999 | 0.078 | 0.999 |
| 51477 | 0.418 | 0.630 | 0.267 | 0.406 | 0.153 | 0.973 | 0.128 | 0.959 | 0.148 | 0.996 | 0.116 | 0.996 |
| 52866 | 0.169 | 0.535 | 0.113 | 0.456 | 0.195 | 0.971 | 0.164 | 0.957 | 0.189 | 0.994 | 0.149 | 0.994 |
| 52984 | 0.180 | 0.578 | 0.117 | 0.516 | 0.180 | 0.972 | 0.146 | 0.958 | 0.174 | 0.995 | 0.133 | 0.995 |
| 53564 | 0.429 | 0.681 | 0.233 | 0.632 | 0.196 | 0.971 | 0.165 | 0.971 | 0.190 | 0.995 | 0.150 | 0.995 |
| 54102 | 0.678 | 0.612 | 0.384 | 0.555 | 0.191 | 0.973 | 0.154 | 0.932 | 0.185 | 0.996 | 0.140 | 0.996 |
| 55664 | 0.230 | 0.664 | 0.152 | 0.515 | 1.142 | 0.718 | 0.974 | 0.671 | 1.106 | 0.736 | 0.882 | 0.717 |
| Four-Factor Input | ||||||||||||
| Station | ELM | GEO-ELM | SSA-ELM | |||||||||
| RMSE | R2 | MAE | NSE | RMSE | R2 | MAE | NSE | RMSE | R2 | MAE | NSE | |
| 51542 | 0.295 | 0.689 | 0.207 | 0.670 | 0.107 | 0.975 | 0.086 | 0.975 | 0.103 | 0.999 | 0.078 | 0.999 |
| 51477 | 0.418 | 0.630 | 0.266 | 0.408 | 0.153 | 0.973 | 0.127 | 0.959 | 0.148 | 0.996 | 0.115 | 0.996 |
| 52866 | 0.171 | 0.535 | 0.113 | 0.446 | 0.170 | 0.972 | 0.142 | 0.958 | 0.164 | 0.996 | 0.129 | 0.996 |
| 52984 | 0.181 | 0.572 | 0.117 | 0.511 | 0.180 | 0.972 | 0.146 | 0.958 | 0.174 | 0.995 | 0.132 | 0.995 |
| 53564 | 0.428 | 0.677 | 0.232 | 0.633 | 0.190 | 0.972 | 0.158 | 0.972 | 0.184 | 0.995 | 0.144 | 0.995 |
| 54102 | 0.678 | 0.609 | 0.385 | 0.554 | 0.191 | 0.973 | 0.154 | 0.932 | 0.185 | 0.996 | 0.139 | 0.996 |
| 55664 | 0.233 | 0.608 | 0.154 | 0.498 | 0.168 | 0.971 | 0.141 | 0.930 | 0.163 | 0.994 | 0.128 | 0.994 |
| Five-Factor Input | ||||||||||||
| Station | ELM | GEO-ELM | SSA-ELM | |||||||||
| RMSE | R2 | MAE | NSE | RMSE | R2 | MAE | NSE | RMSE | R2 | MAE | NSE | |
| 51542 | 0.266 | 0.741 | 0.187 | 0.725 | 0.107 | 0.975 | 0.086 | 0.972 | 0.103 | 0.995 | 0.078 | 0.999 |
| 51477 | 0.416 | 0.642 | 0.256 | 0.412 | 0.147 | 0.973 | 0.123 | 0.955 | 0.143 | 0.992 | 0.112 | 0.996 |
| 52866 | 0.166 | 0.541 | 0.109 | 0.475 | 0.151 | 0.973 | 0.128 | 0.956 | 0.146 | 0.993 | 0.116 | 0.997 |
| 52984 | 0.174 | 0.598 | 0.113 | 0.540 | 0.167 | 0.973 | 0.135 | 0.954 | 0.162 | 0.992 | 0.122 | 0.996 |
| 53564 | 0.424 | 0.678 | 0.231 | 0.638 | 0.188 | 0.972 | 0.157 | 0.969 | 0.182 | 0.991 | 0.143 | 0.995 |
| 54102 | 0.657 | 0.632 | 0.363 | 0.574 | 0.172 | 0.973 | 0.138 | 0.927 | 0.167 | 0.993 | 0.125 | 0.997 |
| 55664 | 0.233 | 0.606 | 0.154 | 0.498 | 0.167 | 0.971 | 0.140 | 0.925 | 0.162 | 0.990 | 0.127 | 0.994 |
| Station | ELM | GEO-ELM | SSA-ELM | |||
|---|---|---|---|---|---|---|
| GPI | Ranking | GPI | Ranking | GPI | Ranking | |
| Three-factor input | ||||||
| 51542 | −2.000 | 63 | −1.749 | 62 | −1.687 | 61 |
| 51477 | −1.533 | 60 | −1.338 | 57 | −1.147 | 52 |
| 52866 | −1.303 | 56 | −1.081 | 51 | −0.963 | 45 |
| 52984 | −1.294 | 55 | −1.073 | 49 | −0.928 | 42 |
| 53564 | 1.514 | 35 | 1.722 | 26 | 1.980 | 2 |
| 54102 | 1.589 | 32 | 1.800 | 17 | 1.792 | 19 |
| 55664 | 1.547 | 34 | 1.754 | 22 | 1.750 | 23 |
| Four-factor input | ||||||
| 51542 | −1.462 | 59 | −1.247 | 54 | −1.207 | 53 |
| 51477 | −1.073 | 50 | −0.901 | 40 | −0.747 | 37 |
| 52866 | −1.041 | 48 | −0.839 | 39 | −0.768 | 38 |
| 52984 | −1.038 | 47 | −0.924 | 41 | −0.657 | 36 |
| 53564 | 1.579 | 33 | 1.786 | 20 | 1.973 | 7 |
| 54102 | 1.613 | 30 | 1.815 | 16 | 1.815 | 15 |
| 55664 | 1.593 | 31 | 1.739 | 25 | 1.795 | 18 |
| Five-factor input | ||||||
| 51542 | −1.366 | 58 | 1.936 | 10 | 2.000 | 1 |
| 51477 | −0.981 | 46 | 1.859 | 11 | 1.976 | 5 |
| 52866 | −0.948 | 44 | 1.849 | 12 | 1.979 | 3 |
| 52984 | −0.946 | 43 | 1.831 | 13 | 1.976 | 4 |
| 53564 | 1.666 | 29 | 1.784 | 21 | 1.966 | 9 |
| 54102 | 1.699 | 27 | 1.816 | 14 | 1.973 | 8 |
| 55664 | 1.679 | 28 | 1.747 | 24 | 1.973 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Li, Y.; Zhao, Z.; Xing, X.; Feng, G.; Bai, J.; Wang, Y.; Qiu, Z.; Zhang, J. Prediction Model for Daily Reference Crop Evapotranspiration Based on Hybrid Algorithm in Semi-Arid Regions of China. Atmosphere 2022, 13, 922. https://doi.org/10.3390/atmos13060922
Zhao X, Li Y, Zhao Z, Xing X, Feng G, Bai J, Wang Y, Qiu Z, Zhang J. Prediction Model for Daily Reference Crop Evapotranspiration Based on Hybrid Algorithm in Semi-Arid Regions of China. Atmosphere. 2022; 13(6):922. https://doi.org/10.3390/atmos13060922
Chicago/Turabian StyleZhao, Xinbo, Yuanze Li, Zhenhua Zhao, Xuguang Xing, Guohua Feng, Jiayi Bai, Yuhang Wang, Zhaomei Qiu, and Jing Zhang. 2022. "Prediction Model for Daily Reference Crop Evapotranspiration Based on Hybrid Algorithm in Semi-Arid Regions of China" Atmosphere 13, no. 6: 922. https://doi.org/10.3390/atmos13060922
APA StyleZhao, X., Li, Y., Zhao, Z., Xing, X., Feng, G., Bai, J., Wang, Y., Qiu, Z., & Zhang, J. (2022). Prediction Model for Daily Reference Crop Evapotranspiration Based on Hybrid Algorithm in Semi-Arid Regions of China. Atmosphere, 13(6), 922. https://doi.org/10.3390/atmos13060922






