Abstract
Spatiotemporal particulate matter (PM) concentration prediction using MODIS AOD with significant PM factors in rural and urban landscapes in Thailand is necessary for public health and has been complicated by the limitations of PM monitoring stations. The research objectives were (1) to identify significant factors affecting PM10 concentrations in rural landscapes and PM2.5 in urban landscapes; (2) to predict spatiotemporal PM10 and PM2.5 concentrations using geographically weighted regression (GWR) and mixed-effect model (MEM), and (3) to evaluate a suitable spatiotemporal model for PM10 and PM2.5 concentration prediction and validation. The research methodology consisted of four stages: data collection and preparation, the identification of significant spatiotemporal factors affecting PM concentrations, the prediction of spatiotemporal PM concentrations, and a suitable spatiotemporal model for PM concentration prediction and validation. As a result, the predicted PM10 concentrations using the GWR model varied from 50.53 to 85.79 µg/m3 and from 36.92 to 51.32 µg/m3 in winter and summer, while the predicted PM10 concentrations using the MEM model varied from 50.68 to 84.59 µg/m3 and from 37.08 to 50.81 µg/m3 in both seasons. Likewise, the PM2.5 concentration prediction using the GWR model varied from 25.33 to 44.37 µg/m3 and from 16.69 to 24.04 µg/m3 in winter and summer, and the PM2.5 concentration prediction using the MEM model varied from 25.45 to 44.36 µg/m3 and from 16.68 and 23.75 µg/m3 during the two seasons. Meanwhile, according to Thailand and U.S. EPA standards, the monthly air quality index (AQI) classifications of the GWR and MEM were similar. Nevertheless, the derived average corrected Akaike Information Criterion (AICc) values of the GWR model for PM10 and PM2.5 predictions during both seasons were lower than that of the MEM model. Therefore, the GWR model was chosen as a suitable model for spatiotemporal PM10 and PM2.5 concentration predictions. Furthermore, the result of spatial correlation analysis for GWR model validation based on a new dataset provided average correlation coefficient values for PM10 and PM2.5 concentration predictions with a higher than the expected value of 0.5. Subsequently, the GWR model with significant monthly and seasonal factors could predict spatiotemporal PM 10 and PM2.5 concentrations in rural and urban landscapes in Thailand.
1. Introduction
Air pollution is a significant problem, with profound toxicological impacts on human health and the environment [1]. According to a World Health Organization (WHO) report, 3.7 million premature deaths worldwide were related to ambient air pollution in 2012. Premature deaths increased to 4.2 million worldwide in 2016 [2,3]. Moreover, the Western-Pacific and South-East Asia region (SEAR) had 799,000 deaths in 2012 [4].
The Health Effects Institute [5] presented the increasing number of deaths attributable to PM2.5 in a given year as those deaths that had occurred earlier than would have been expected in the absence of PM2.5, which was computed based on nonlinear integrated-exposure-response (IER) functions, for all ages and sexes combined between 1990 and 2019 in Thailand. These data are presented in Figure 1. However, Apte et al. [6] suggested that exposure to ambient fine particulate matter (PM2.5) air pollution was a significant risk for premature death. However, if PM2.5 in all countries met the WHO’s air quality guideline (10 µg/m3), the estimated life expectancy could increase by a population-weighted median of 0.6 years (interquartile range of 0.2–1.0 years).
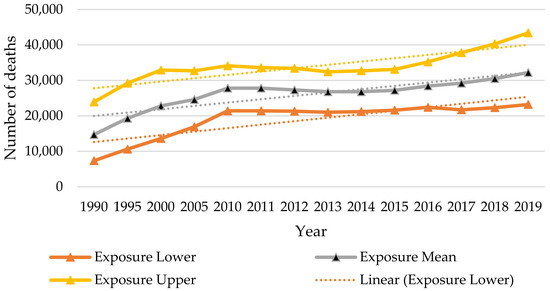
Figure 1.
The number of deaths attributable to PM2.5 in Thailand between 1990 and 2019. Source: Health Effects Institute [5].
Ambient air pollutants include particulate matter (PM), ozone, nitrogen dioxide, sulfur dioxide, and other contaminants. PM is a complex mixture of solid and liquid particles of primary and secondary origin, and contains a wide range of inorganic and organic components. PM mass and composition are also highly variable in spatiotemporal terms and are strongly influenced by climatic and meteorological conditions [7]. PM can be emitted from natural and human-made sources, including forest fires, dust storms, traffic, and industry.
Basically, PM is measured as particles with an aerodynamic diameter of less than 10 μm (PM10) and less than 2.5 μm (PM2.5) [8]. Particles at PM10 are inhalable and may reach the upper part of the airways and lungs, while smaller PM2.5 particles are more able to penetrate the lungs and perhaps reach the alveoli. Ultrafine particles, which have a cut-off at 0.1 μm, may be a small proportion of the total mass but may also have the most significant health impacts due to their ability to pass from the lung directly into the bloodstream and their larger reactive surface area, which may be capable of inducing more significant damage [7].
PM exposure depends on physical characteristics, including breathing mode, rate, and volume of a person’s lungs; particle size has been linked as a leading cause of health problems. Generally, the smaller a particle is, the more deeply and rapidly it can penetrate and deposit on the respiratory tract. In nasal breathing, the cilia and the mucus together act as an active filter for most particulates exceeding 10 μm, or coarse PM. As the coarse PM fraction settles quickly, it tends to lodge in the upper throat or the bronchi. If humans inhale this PM, it will be initially collected in the nose and throat. The body will then react to eliminate these intruding PMs through sneezing and coughing [9].
Furthermore, many researchers studied the effects of air pollution, including PM, on the materials. Varotsos and Cartalis [10] stated that atmospheric pollution accelerates the material deterioration of buildings and other structures and objects of cultural heritage. The corrosive effects of gaseous SO2, NOx, O3, HNO3, PM, and acid rainfall in combination with climatic parameters are crucial, especially for mega-cities such as Athens with unique historic monuments ([10,11]). Tzanis et al. [12] reported nitric acid and particulate matter measurements in Athens, Greece.
In Thailand, PM has had diverse and far-reaching effects on the economy, impacting tourism, property values, and medical treatment costs. According to the Kasikorn Research Centre report in 2019, the smog could cost Thailand THB 6.6 billion in losses due to air pollution in the healthcare and tourism sectors [13]. The Thai Public Broadcasting Service reported the effect of PM2.5 on medical expenses and the loss of tourism opportunities in and around Bangkok if PM2.5 does not ease within a month: Medical expenses per person could reach an average of THB 1000 for each medical visit and THB 22.50 per day for face masks. Total medical costs alone could be in the range of THB 1.6–3.1 million, depending on the intensity of the air pollution [14].
Therefore, the monitoring of PM10 and PM2.5 should be improved in many countries to assess population exposure and to encourage local authorities to improve air quality [15]. However, most pollutant concentration information has been obtained from ground monitoring stations, which have significant limitations: limited in number, unequally distributed, and varied measure frequency ranges. These can affect the geographical and demographic range of studies, resulting in an information bias and a lack of exposure–response studies [2].
The spatiotemporal variations of PM10 and PM2.5 are complex, and continuous monitoring is not possible in many countries and regions. Therefore, satellite-based remote sensing has become a widely used technique for monitoring. It can provide extensive spatial coverage and is cost-effective for studies. In addition, the data is acquired directly from the measured spectral aerosol optical depth (AOD), which is the integration of aerosol light extinction across a vertical path through the atmosphere [16]. However, atmospheric aerosols are a complex mixture of particles (being ubiquitous in air, often observable as dust, smoke, and haze) arising from a large number of discrete natural and anthropogenic sources (e.g., Ondov and Wexler [17]; Murr and Garza [18]; Varotsos and Zellner [19]; Varotsos et al. [20]).
Therefore, a suitable model for spatiotemporal PM concentration prediction in rural and urban landscapes was investigated based on the review article of Chu et al. [2], “A Review on Predicting Ground PM2.5 Concentration Using Satellite Aerosol Optical Depth.” They found that four predicting models were widely used: multiple linear regression (MLR), mixed-effect model (MEM), chemical transport model (CTM) and geographically weighted regression (GWR). Regarding the prediction accuracy, MEM performs the best, while MLR performs the worst. CTM predicts PM2.5 better on a global scale, while GWR performs well on a regional level. Therefore, MEM and GWR models were chosen to examine a suitable model for spatiotemporal PM concentration prediction in rural and urban landscapes. Consequently, spatiotemporal PM concentration predictions using a moderate resolution imaging spectroradiometer (MODIS) AOD with significant PM factors in rural and urban landscapes in Thailand are necessary due to the limitations of PM monitoring stations.
The expected results provide significant spatiotemporal data affecting PM10 and PM2.5 concentrations in rural and urban landscapes. The results can also provide the spatial patterns of PM10 and PM2.5 concentrations in both landscapes at the district level in the winter and summer seasons. Additionally, the results can be used as guidelines for improving air quality and reducing impacts on human health. The objective of this research was to predict spatiotemporal PM10 and PM2.5 concentrations in rural and urban regions during the winter and summer seasons. The specific research concerns were (1) to identify significant factors of PM10 concentrations in rural regions and PM2.5 concentrations in urban landscapes in the winter and summer seasons as well as their interrelationships using the multicollinearity test and an ordinary least squares (OLS) regression analysis; (2) to predict spatiotemporal PM10 and PM2.5 concentrations using GWR and MEM models, and (3) to evaluate a suitable spatiotemporal model for PM10 and PM2.5 concentration prediction and validation.
2. Study Area
Two study areas were chosen for two different studies affecting PM10 concentrations in rural landscapes and PM2.5 concentrations in urban landscapes, as shown in Figure 2. We chose rural and urban landscapes according to recent land use data from Thailand’s Land Development Department [21].
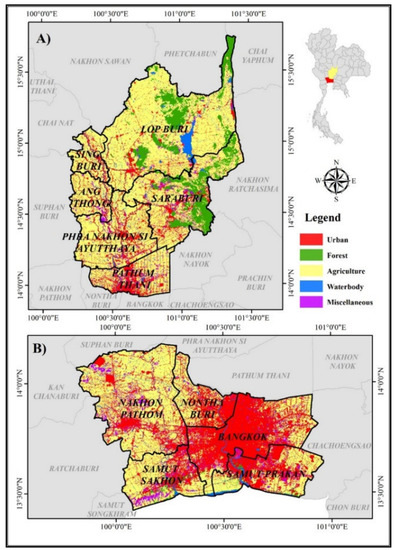
Figure 2.
Land use classification and location map of the study area: (A) Rural landscape and (B) Urban landscape.
According to the Land Development Department [21], more than 65 percent of rural landscapes, which covers approximately 15,827 sq km with 60 districts from 6 provinces (i.e., Ang Thong, Lop Buri, Phra Nakhon Si Ayutthaya, Pathum Thani, Saraburi, and Sing Buri) are agricultural, including features such as paddy fields, field crops, orchards, and perennial trees. Agricultural operations, mainly agricultural debris burning, generate massive sources of PM10 contribution. Arslan and Aybek [22] stated that agricultural field operations caused dust production in conventional crop production, including soil tillage and seedbed preparation, planting, fertilization, pesticide application, harvesting, and post-harvest processes. The high PM10 concentration distribution in the dust is circulated and spread by the wind, especially on the surfaces without cement and asphalt [23].
Meanwhile, urban landscapes cover approximately 6180 sq km with 72 districts from 5 provinces, including Bangkok, Nakhon Pathom, Nonthaburi, Samut Prakan, and Samut Sakhon. This landscape, especially in Bangkok, the capital city of Thailand, has a high-density population and economic activity clusters. Lin et al. [24] stated that high PM2.5 concentrations have primarily been identified in regions with high populations, rapid urban expansion, and local economic growth.
3. Material and Method
The overview framework of the research methodology consisted of four components, including (1) data collection and preparation; (2) identification of significant spatiotemporal factors affecting PM concentrations; (3) prediction of spatiotemporal PM concentrations, and (4) a suitable spatiotemporal model for PM concentration prediction and validation, as shown in Figure 3. Details of each stage are separately described in the following sections.
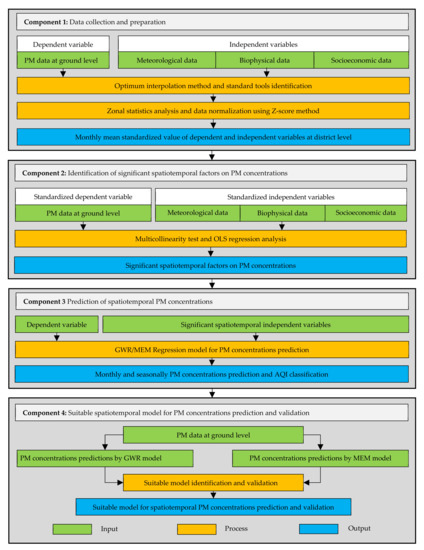
Figure 3.
Overview of the research framework of the study.
3.1. Data Collection and Preparation
Data included ground-level PM data, as dependent variables, and meteorological, biophysical, and socioeconomic data, as independent variables, from October 2019 to May 2020, that were collected from national and international organizations and then prepared using standard tools in the Environmental Systems Research Institute (ESRI) ArcMap software, as summarized in Table 1.

Table 1.
List of data collection and preparation for analysis and modeling in the study.
In this study, available interpolation methods under the ESRI ArcMap software, which many researchers use, were examined to identify an optimal method for specific factors. Seven interpolation methods, namely inverse distance weighted (IDW), global polynomial interpolation (GPI), radial basis functions (RBF), ordinary kriging (OK), ordinary cokriging (OCK), simple kriging (SK), and simple cokriging (SCK), were selected to examine an optimal interpolation method for appropriate dependent and independent variables, including average monthly PM data at ground level, meteorological data (e.g., relative humidity, temperature, wind speed, pressure, visibility), and MODIS fire data (e.g., brightness temperature and radiative firepower) based on the existing data between October 2019 to May 2020 using the average monthly root mean squared error (RMSE) from each method. The RMSE indicates how closely a model predicts measured values. The RMSE value was derived using the following equation:
where n is the number of measured data.
However, appropriate standard tools for the Spatial Analyst tool in ESRI ArcMap software were applied with other independent variables, including MODIS AOD, normalized difference vegetation index (NDVI), built-up index (BUI), road density, factory density, elevation, fire hotspot, population density, and gross provincial product (GPP).
After that, all prepared variables were normalized using the Z-score method to identify significant spatiotemporal factors in PM concentrations in the next stage.
In practice, mean and standard deviation values at the district level of all dependent and independent variables were first extracted using the zonal statistics analysis. Then, they were exported into Microsoft Excel spreadsheets and normalized using the Z-score method as follows:
where Z is the standard score, X is the observed value, μ is the mean of the sample, and σ is the standard deviation of the sample. As a result, the mean values of all variables are zero, and their standard deviation values are one.
3.2. Identification of Significant Spatiotemporal Factors Affecting PM Concentrations and Relationships
Normalized dependent and independent variables affecting PM10 concentrations in rural landscapes and PM2.5 concentrations in urban landscapes in the winter (October 2019–February 2020) and summer (March 2020–May 2020) were applied to identify significant spatiotemporal factors using the multicollinearity test with a variance inflation factor (VIF) and the OLS regression analysis.
VIF measures the amount of multicollinearity in a set of multiple regression variables. A high VIF value indicates that the associated independent variable is redundant with the other variables in the model. Therefore, the VIF value should be lower than 7.5 to avoid multicollinearity, as suggested in ArcGIS 10.3.1 documentation [25], as follows:
where Ri2 comprises multiple coefficients of determination in a regression of the ith predictor on the others.
The main output of the OLS regression analysis was the significant spatiotemporal factors affecting PM10 concentrations in rural landscapes and PM2.5 concentrations in urban landscapes in the winter and summer seasons.
3.3. Prediction of Spatiotemporal PM Concentrations
Under this component, primary input data (MODIS AOD) and significant spatiotemporal independent variables (the output from component 1) affecting PM10 and PM2.5 concentrations in the rural and urban landscapes, respectively, were separately applied to predict monthly PM concentrations in winter and summer seasons using the GWR and MEM models.
In this study, the standard function of the GWR model (as a local model) with an adaptive kernel type and AICc bandwidth was applied to predict PM concentrations in the ESRI ArcMap software environment. The efficiency of the GWR model was automatically reported using the corrected Akaike information criterion (AICc), coefficient of determination (R2), and adjusted R-squared () using the following equations:
Here, L is the maximum likelihood for the estimated model, k is the number of independent variables, n is the number of sample sizes, is the sum of squares of residual or called the residual sum of squares, and is the total sum of squares.
Meanwhile, the MEM model (as a global model) with fixed effects intercepts and scaled identity covariance type was applied to predict PM concentrations using the IBM SPSS statistics software. The efficiency of the models was automatically reported using the AIC, corrected Akaike information criterion (AICc), and Bayesian information criterion (BIC) as follows:
where is the value of the log-likelihood function of the fitted model evaluated at the model estimate, k is the number of fitted model parameters, and N is the recorded measurements.
The results of this analysis were the monthly and seasonally predictive equations for monthly PM10 concentrations in rural landscapes and PM2.5 concentrations in urban landscapes during the winter and summer seasons. Additionally, the air quality index (AQI), based on the monthly PM10 concentrations in rural landscapes and PM2.5 concentrations in urban landscapes over two seasons, and according to Thailand and the U.S. EPA AQI standards, was mapped (see Table 2 and Table 3).

Table 2.
Thailand’s air quality index classification based on affected PM concentrations.

Table 3.
The U.S. EPA air quality index classification based on affected PM concentrations.
3.4. Suitable Spatiotemporal Model for PM Concentration Prediction and Validation
Under this component, a suitable model for spatiotemporal PM10 and PM2.5 concentration predictions between GWR and MEM models was first identified based on their AICc values. (See also Section 3.3). In general, a lower AICc value indicates a better fit model. In practice, average AICc values for PM10 concentrations in rural landscapes, and PM2.5 concentrations in urban landscapes in winter and summers from GWR and MEM models, were calculated to identify a suitable model for spatiotemporal PM10/PM2.5 concentration predictions.
Furthermore, a suitable model for spatiotemporal PM10 and PM2.5 concentration predictions was validated with a new dataset (October 2020–May 2021) using Pearson’s correlation analysis. The expected correlation coefficient value should be equal to or more than 0.5, which indicates a strong linear relationship between the dependent and independent variables [28].
4. Results and Discussion
4.1. Optimal Method for a Specific Variable Identification
The optimal methods for monthly mean PM10 concentrations, PM2.5 concentrations, relative humidity, temperature, wind speed, pressure, visibility, brightness temperature, and radiative firepower interpolation with seven different methods (i.e., IDW, GPI, RBF, OK, OCK, SK, and SCK) based on the average RMSE value under cross-validation are summarized below.
4.1.1. PM10 and PM2.5 Concentrations
The SCK method with either the hole effect or the K-Bessel function could have been used as an optimal method for monthly mean PM10 concentration interpolation since both functions could provide the lowest RMSE value. As a result, the average RMSE value of monthly mean PM10 concentration interpolation was 15.73 µg/m3. The SCK method with the K-Bessel function was chosen as an optimal method for monthly mean PM2.5 concentration interpolation. The average RMSE value of monthly mean PM2.5 concentration interpolation was 15.73 µg/m3. Nevertheless, previous research on a suitable interpolation method for predicting PM10 and PM2.5 concentrations at international and national levels reported success using different methods.
Sajjadi et al. [29] selected four interpolation methods (i.e., IDW, RBF, OK, and UK) to identify an optimal method for predicting PM10 and PM2.5 in Sabzevar City in the Razavi Khorasan Province, Iran, using RMSE, MAE, and MAPE. They found that IDW was the best interpolation method for PM10 and PM2.5 concentration predictions. Meanwhile, Vorapracha et al. [30] selected three methods (i.e., IDW, OK, and UK) to identify a suitable method for predicting PM10 in the central region of Thailand using RMSE. They also found that the most suitable method for PM10 prediction was IDW. Meanwhile, Wong et al. [31] identified OK as a suitable method for PM10 prediction compared to IDW. Likewise, Kumar et al. [32] reported OK as the best interpolation method for PM10 concentration prediction among the three selected methods (i.e., IDW, OK, and spline).
As compared to previous studies, we examined more interpolation methods with various functions to ensure the accuracy and efficiency of our results. After considering seven different methods, namely IDW, GPI, RBF, OK, OCK, SK, and SCK, for use with RMSE, we selected the SCK method, as it applies the covariance between two or more realizations of cross-correlated random fields [33], which would be the most suitable for our research objectives.
4.1.2. Relative Humidity
The SCK method with the J-Bessel function was selected as an optimal method for monthly mean relative humidity interpolation. The average RMSE value of monthly mean relative humidity interpolation was 3.43%.
4.1.3. Temperature
The SCK method with the hole effect function is selected as an optimal method for monthly mean temperature interpolation. The average RMSE value of monthly mean temperature interpolation was 0.79 degrees Celsius.
4.1.4. Wind Speed
The RBF method, with the spline with tension and one sector, was chosen as an optimal method for monthly mean wind speed interpolation. The average RMSE value of monthly mean wind speed interpolation was 1.54 knots.
4.1.5. Pressure
The SCK method with the stable function was selected as an optimal method for monthly mean pressure interpolation. The average RMSE value of monthly mean pressure interpolation was 0.40 hPa.
4.1.6. Visibility
The OCK method with the hole effect function was selected as an optimal method for monthly mean visibility interpolation. The average RMSE value of monthly mean visibility interpolation was 1.32 km.
As reported in Section 4.1.2, Section 4.1.3, Section 4.1.4, Section 4.1.5 and Section 4.1.6, the average RMSE values from the seven interpolation methods of monthly mean meteorological data were similar. In the meantime, the previous studies on a suitable interpolation method for predicting monthly mean meteorological data at international and national levels have reported different methods. Prasomsup [34] found that the SCK was the optimal method for monthly mean temperatures in November, December, February, and March, while OCK was optimal in January and April. Jantakat and Ongsomwang [35] selected OCK for interpolated monthly mean temperatures in January, November, and December, while they selected Distinctive Cokriging (DCK) for February–October. At the same time, Ozturk and Kilic [36] chose OK for interpolated temperature and precipitation during 5-year periods. Similar to what Cao et al. [37] presented, the OK with exponential and spherical had the best interpolation precision.
Likewise, as Keskin and Özdoğu [38] presented, OK performed better overall than the other interpolation methods for wind speed data. In contrast, this study suggested RBF with spline with tension functions; the geometry of the search neighborhood was an ellipse. We followed the study of Gradka and Kwinta [39]. The RBF was conceptually similar to fitting a rubber membrane through the measured sample values while minimizing the surface’s total curvature and selecting one functional parameter to control the surface’s smoothness using cross-validation. In addition, the RBF represented an irregular surface using many linear functions that connected the node with the data point and could be an alternative to kriging.
Equally, the other techniques could be used to interpolate meteorological data. However, the most commonly used have been the kriging technique and the additions of the cross-correlated variables to reduce the estimation error variance [40]. However, Kuo et al. [41] used the kriging method to interpolate the temperature data with a focus on the optimal sample size of the sensors. In addition, Deligiorgi and Philippopoulos [42] reported that the most common kriging method was simple kriging, which assumes a known constant mean, as compared to ordinary kriging, which assumes an unknown constant mean. As well, kriging is also known as the best unbiased linear estimator.
Many suitable interpolation methods are possible for predicting monthly mean meteorological data; the method selected should be based on the objective and parameters involved in the research, as mentioned in Section 4.1.1.
4.1.7. MODIS Brightness Temperature
The SCK method with the stable function was selected as an optimal method for monthly mean brightness temperature interpolation. The average RMSE value of monthly mean brightness temperature interpolation was 4.56 degrees Kelvin.
4.1.8. MODIS Fire Radiative Power
The RBF method with the spline with tension and eight sector functions was selected as an optimal method for monthly mean fire radiative power interpolation. The average RMSE value of monthly mean fire radiative power interpolations was 19.44 MW.
Several methods were used to interpolate MODIS fire data from previous studies. For example, Veraverbeke et al. [43] used kriging for interpolating the MODIS active fire as kriging is based on local variogram analysis and allows uncertainty analysis by spatially estimating the kriging standard error. Similar to Devkota [44], Ponomarev et al. [45] used kriging to interpolate the MODIS fire radiative power data. Loboda et al. [46] used IDW to determine the fire spread from MODIS active fire points data.
As discussed in Section 4.1.1, Section 4.1.2, Section 4.1.3, Section 4.1.4, Section 4.1.5 and Section 4.1.6, the rationale for a suitable interpolation method for predicting monthly mean MODIS fire data should be based on the research objective and required parameters.
4.2. Suitable Method for Specific Factors Preparation
Standard tools under ESRI ArcMap software were applied to prepare other independent variables, including MODIS AOD, NDVI, BUI, road density, factory density, elevation, fire hotspot, population density, and GPP, as summarized in Table 4.

Table 4.
Summary of the standard tools for other independent variable preparation.
All prepared dependent and independent variables with Z-score normalization were further applied to identify significant spatiotemporal factors affecting PM concentrations using the multicollinearity test and the OLS regression analysis.
4.3. Significant Spatiotemporal Factors Affecting PM10 Concentrations in Rural Landscapes
The multicollinearity test of independent factors affecting PM10 concentrations after normalization is reported in Table 5. The results showed that the uncorrelated factors varied by 8–10 factors per month. In addition, NDVI, BUI, road density, and population density were redundant in PM10 concentrations every month. Therefore, the next step would exclude the correlated factors with a VIF value equal to or more than 7.5 for the OLS regression analysis.

Table 5.
Multicollinearity test of explanatory variables for PM10 concentrations.
The results of the OLS regression analysis for significant factors in PM10 concentrations identification are summarized in Table 6. The results indicated significant differences among the monthly factors for PM10 concentrations. The number of significant factors affecting PM10 concentrations in winter and summer was five each season, and they varied per season. Three common factors impacting PM10 concentrations were temperature, visibility, and MODIS AOD that were identified in both seasons. Two significant factors affecting PM10 concentrations only found during the winter season included wind speed and fire radiative power. In contrast, factory density and brightness temperature were the only factors during the summer season. These findings indicated that factory density (FD) related to human activity in April might be managed to reduce the impact on PM10 concentrations in rural landscapes.

Table 6.
Monthly and seasonally significant factors affecting PM10 concentrations.
The significant factors affecting PM10 concentrations in this study were similar to those found in a previous study by Harnkijroong and Panich [47]. They reported that PM10 concentrations on the roadsides of Bangkok were most relevant to the temperature, followed by the wind speed. They also found that rainfall did not influence PM10 concentrations.
Furthermore, Unal et al. [48] suggested that PM10 concentrations were associated with wind speed, and high PM10 concentrations were found in high pressure and low wind speed. Likewise, the most significant meteorological factors, including planetary boundary layer height, temperature, wind speed, and precipitation influenced by the seasonal dynamics of PM10 concentrations, were reported by Czernecki et al. [49].
In addition, many studies reported the relationship between MODIS AOD and PM10 concentrations [50,51,52,53]. Ferrero et al. [51] found a strong relationship between the two and developed a high accuracy algorithm to predict ground PM concentrations based on AOD mixing height and wind speed. Similarly, Kanabkaew [53] reported that the relationship between AOD and hourly PM improved accuracy when corrected with meteorological factors, including relative humidity and temperature data.
4.4. Significant Spatiotemporal Factors Affecting PM2.5 Concentrations in Urban Landscapes
The multicollinearity test of independent factors affecting PM2.5 concentrations after normalization in urban landscapes in the winter and summer seasons is reported in Table 7. The uncorrelated factors varied by 5–10 factors per month. In addition, NDVI, BUI, road density, population density, and GPP were redundant with PM2.5 concentrations every month. Therefore, the next step would exclude the correlated factors with a VIF value equal to or more than 7.5 in the OLS regression analysis.

Table 7.
Multicollinearity test of explanatory variables affecting PM2.5 concentrations.
The results of the OLS regression analysis for significant factors affecting PM2.5 concentration identification are summarized in Table 8. The significant factors affecting PM2.5 in winter and summer were ten and eight, respectively. Many meteorological factors significantly influenced PM2.5, as compared to PM10 concentrations [54]. This study found seven common factors affecting PM2.5 concentrations in both seasons: wind speed, visibility, brightness temperature, fire radiative power, MODIS AOD, fire hotspot, and elevation. Three significant factors affecting PM2.5 concentrations were only found in the winter season: relative humidity, temperature, and pressure. In contrast, one significant factor affecting PM2.5 concentrations, factory density, was only identified in the summer season. These findings imply that factory density (FD), MODIS brightness temperature (BT), MODIS fire radiative power (FRP), and MODIS fire hotspot (FH) factors that are related to human activities which are found in a specific month might be managed to reduce the impact on PM2.5 concentrations.

Table 8.
Monthly and seasonally significant factors affecting PM2.5 concentrations.
The findings showed similar results to the previous study of Guo and Zhang [55], who had reported that PM2.5 concentrations were most relevant to visibility, followed by wind speed. The least pertinent factors were temperature and relative humidity. Likewise, these findings were consistent with Chen et al. [54], who showed the strong influence of wind speed on local PM2.5 concentrations. They also observed strong interactions between wind speed and other meteorological factors influencing PM2.5 concentrations. Galindo et al. [56] found that the winter wind speed was the main influence on the dilution of atmospheric aerosols, while temperature and solar radiation strongly influenced coarser particles. This indicated that the meteorological data and the solar heating at the Earth’s surface via the active fire data were significantly related to PM2.5 concentrations. In addition, MODIS AOD had a strong correlation to PM2.5 concentrations [57,58]. Similarly, Lee et al. [59] reported potentially helpful methods for predicting PM2.5 concentrations. Chudnovsky et al. [60] predicted PM2.5 concentrations with MODIS AOD and improved the accuracy when land use and meteorological data were included. However, Chu et al. [2] suggested using AOD data with higher resolution to obtain a more accurate estimation of PM2.5 concentrations in relatively small areas.
4.5. Prediction of PM10 Concentrations in Rural Landscapes Using GWR and MEM Models
The generic equations for PM10 concentrations in winter and summer in rural landscapes using the GWR model as a local model are shown in Equations (9) and (10):
where denotes intercept value at district i, month j; denotes the coefficients of temperature; denotes the coefficients of wind speed; denotes the coefficients of visibility; denotes the coefficients of fire radiative power; denotes the coefficients of MODIS AOD; denotes the coefficients of brightness temperature; denotes the coefficients of factory density, and is residual values. TEMP, WS, VIS, FRP, AOD, BT, and FD as significant factors on PM10 concentrations, which were identified using multicollinearity test and OLS regression analysis (see Table 6), were applied to predict monthly and seasonal PM10 concentrations in winter and summer seasons using Equations (9) and (10).
Table 9 shows an example of the predictive equations and their predicted PM10 concentrations using the GWR model in rural landscapes in December 2019.

Table 9.
The predictive equations of PM10 concentrations and coefficient values in December 2019 using the GWR model.
As shown in Table 9, the model performance indicated that AICc, R-square, and adjusted R-square values were 123.24, 0.90, and 0.80, respectively. The maximum value of the predicted PM10 in December 2019 was 55.03 µg/m3 in Chaloem Phra Kiat District, Saraburi Province. In contrast, the minimum value was 50.53 µg/m3 in Mueang Pathum Thani District, Pathum Thani Province. Meanwhile, the classification of the AQI of the predicted PM10 concentrations using the GWR model is displayed in Figure 4.
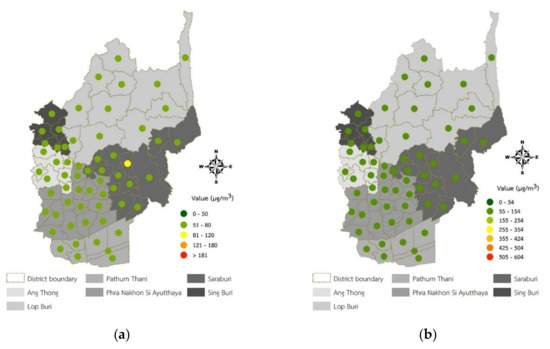
Figure 4.
The AQI classification map of PM10 concentration predictions in December 2019 using the GWR model: (a) Thailand AQI standard and (b) U.S. EPA AQI standard.
Comparatively, the generic equations for PM10 concentrations in winter and summer in rural landscapes using the MEM model as a global model are shown in Equations (11) and (12):
where is the averaged PM10 concentrations at district i on month j; is the fixed intercept; − are coefficients of fixed effect for independent variables; is the temperature on month j; is the wind speed at district i on month j; is visibility at district i on month j; is fire radiative power at district i on month j; is MODIS AOD at district i on month j; is brightness temperature at district i on month j; is factory density at district i on month j, and is the residual error.
The results of the predicted PM10 concentrations for each month and season by the district in rural landscapes using the MEM model are reported in Table 10.

Table 10.
The predictive value of PM10 concentrations in each month and season using the MEM model.
As shown in Table 10, the maximum value of the predicted PM10 in December 2019 was 79.97 µg/m3 in Chaloem Phra Kiat District, Pathum Thani Province. In contrast, the minimum value was 73.47 µg/m3 in Sam Khok District, Pathum Thani Province. The classifications of the AQI maps of predicted values for PM10 concentrations in December 2019 using the MEM model are displayed in Figure 5.
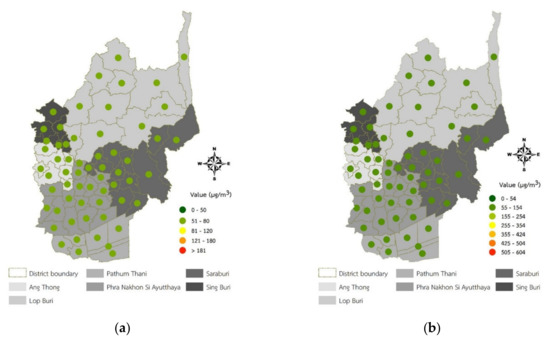
Figure 5.
The AQI classification map of PM10 concentration predictions in December 2019 using the MEM model: (a) Thailand AQI standard and (b) U.S. EPA AQI standard.
4.6. Prediction of PM2.5 Concentrations in Urban Landscapes Using GWR and MEM Models
Similarly to Section 4.4, the generic equations for PM2.5 concentrations in winter and summer in urban landscapes using the GWR model as a local model are shown in Equations (13) and (14):
where denotes intercept value at district , month ; denotes the coefficients of relative humidity; denotes the coefficients of temperature; denotes the coefficients of wind speed; denotes the coefficients of pressure; denotes the coefficients of visibility; denotes the coefficients of brightness temperature; denotes the coefficients of fire radiative power; denotes the coefficients of fire hotspot; denotes the coefficients of MODIS AOD; denotes the coefficients of elevation; denotes the coefficients of factory density, and is residual values. RH, TEMP, WS, P, VIS, BT, FRP, FH, AOD, ELEV, and FD as significant factors on PM2.5 concentrations, which were identified using multicollinearity test and OLS regression analysis (see Table 8), were applied to predict monthly and seasonal PM2.5 concentrations in winter and summer seasons using Equations (13) and (14).
Table 11 shows an example of the predictive equations and their predicted PM2.5 concentrations in urban landscapes in December 2019 using the GWR model.

Table 11.
The predictive equations of PM2.5 concentrations and coefficient values in December 2019 using the GWR model.
As shown in Table 11, the model performance showed that the AICc, R-square, and adjusted R-square values were 24.44, 0.97, and 0.95, respectively. The maximum predicted value of PM2.5 concentrations was 40.52 µg/m3 in Kamphaeng Saen District, Nakhon Pathom Province. In contrast, the minimum value was 38.76 µg/m3 in Bang Bo District, Samut Prakan province. The classifications of AQI of the predicted PM2.5 concentrations in December 2019 using the GWR model are displayed in Figure 6.
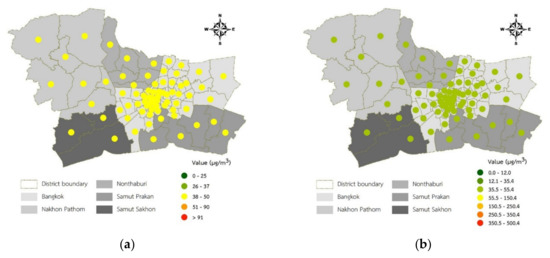
Figure 6.
The AQI classification map of PM2.5 concentration predictions in December 2019 using the GWR model: (a) Thailand AQI standard and (b) U.S. EPA AQI standard.
In contrast, the generic equations for PM2.5 concentrations in winter and summer in urban landscapes using the MEM model as a global model are shown in Equations (15) and (16):
Here, is the averaged PM2.5 concentrations at district i on month j in the winter season; is the fixed intercept; − are coefficients of fixed effect for independent variables; , , , , , , , , , are relative humidity, temperature, wind speed, pressure, visibility, brightness temperature, fire radiative power, fire hotspot, MODIS AOD, elevation at district i on month j, respectively, and is the residual error.
Here, is the averaged PM2.5 concentrations at district i on month j in the summer season; is the fixed intercept; − are coefficients of fixed effect for independent variables; , , , , , , , are visibility, wind speed, brightness temperature, fire radiative power, fire hotspot, MODIS AOD, factory density, and elevation at district i on month j, respectively, and is the residual error.
The results of the predicted PM2.5 concentrations in each month and season by the district in rural landscapes using the MEM model are shown in Table 12.

Table 12.
The predictive value of PM2.5 concentrations in each month and season using the MEM model.
As shown in Table 12, the maximum value of the predicted PM2.5 in December 2019 was 43.80 µg/m3 in Mueang Nakhon Pathom District, Samut Prakan Province. In contrast, the minimum value was 43.30 µg/m3 in Phra Samut Chedi District, Samut Prakan Province. The classifications of AQI of the predicted values for PM10 concentrations in December 2019 using the MEM model are displayed in Figure 7.
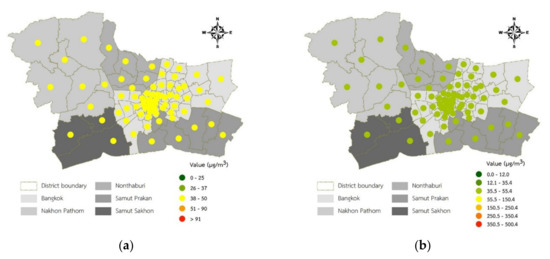
Figure 7.
The AQI classification map of PM2.5 concentration predictions in December 2019 using the MEM model: (a) Thailand AQI standard and (b) U.S. EPA AQI standard.
4.7. Comparison of Spatiotemporal Patterns of PM Concentrations Using GWR and MEM Models
The spatiotemporal patterns of PM10 and PM2.5 concentrations using the GWR model as a local model and MEM model as a global model are summarized in terms of similarity/dissimilarity based on the derived results in Section 4.5 and Section 4.6.
4.7.1. Monthly Air Quality Index Classification
Overall monthly AQI classification according to Thailand and U.S. EPA standards of PM10 and PM2.5 concentrations using the GWR and MEM models are summarized in Table 13 and Table 14.

Table 13.
Comparison of monthly AQI classifications according to Thailand and U.S. EPA standards of PM10 concentrations using the GWR and MEM models.

Table 14.
Comparison of monthly AQI classifications according to Thailand and U.S. EPA standards of PM2.5 concentrations using the GWR and MEM models.
Monthly AQI classifications according to Thailand and U.S. EPA standards were similar. The interpretation of each AQI class from two standards yielded quantitative information in corresponding tables due to the number of AQI classes and the quantity of PM10 and PM2.5 concentrations being slightly different. Nevertheless, as a local model, the GWR model provided the predictive equation for each district.
4.7.2. Seasonal Air Quality Index Classification
According to Thailand and the U.S. EPA standards of PM10 and PM2.5 concentrations and using the GWR and MEM models, seasonally, AQI classifications are summarized in Table 15.

Table 15.
Comparison of seasonal AQI classifications according to Thailand and U.S. EPA standards of PM10 and PM2.5 concentrations using the GWR and MEM models.
As shown in Table 15, seasonal AQI classifications according to Thailand and U.S. EPA standards were similar. As mentioned in Section 4.7.1, the interpretation of each AQI class from two standards yielded the quantitative information in corresponding tables due to the number of AQI classes and the quantity of PM10 and PM2.5 concentrations being slightly different. However, the predicted value of PM10 and PM2.5 concentrations should be further classified according to WHO air quality guidelines for long-term prevention of PM exposure.
4.8. Suitable Model for Spatiotemporal PM Concentration Predictions
Suitable models for spatiotemporal PM10 and PM2.5 concentration predictions are summarized and discussed in the following section.
4.8.1. Suitable Models for Spatiotemporal PM10 Concentration Prediction
The AICc values of PM10 concentration prediction in sixty districts with rural landscapes during the winter and summer seasons and compared between the GWR and MEM models are summarized in Table 16. The average AICc values of PM10 concentrations in the winter and summer seasons using the GWR model were lower than in the MEM model. Therefore, the GWR model was suitable for spatiotemporal PM10 concentration prediction in both seasons.

Table 16.
Monthly AICc values and the average for two competing models for PM10 concentration prediction in the winter and summer.
4.8.2. Suitable Models for Spatiotemporal PM2.5 Concentration Prediction
The AICc values of PM2.5 concentration prediction on seventy-two districts in urban landscapes in the winter and summer seasons and compared between GWR and MEM models are reported in Table 17.

Table 17.
Monthly AICc values and the average for two competing models for PM2.5 concentration prediction in the winter and summer.
As shown in Table 17, the average AICc values of PM2.5 concentrations in the winter and summer seasons using the GWR model were lower than in the MEM model. Therefore, the GWR model was suitable for spatiotemporal PM2.5 concentration prediction in both seasons.
In summary, we concluded that the GWR model was suitable for monthly PM10 and PM2.5 concentration predictions in rural and urban landscapes in the winter and summer seasons. This finding was consistent with many previous studies. Chu et al. [2] concluded that GWR was suitable for PM2.5 concentration prediction at a regional scale. Similarly, Wei et al. [61] suggested that the GWR model could provide a better spatiotemporal PM2.5 concentration prediction than the MEM model. In addition, Gu [57] stated that the GWR generated the best performance compared with the mixed linear regression (MEM) model.
However, statistical methods, such as artificial neural networks, nonlinear regression, support vector machine, and multiple linear regression have been used for PM concentrations in recent years (Hoi et al. [62]; Li et al. [63]; Zhang et al. [64]). Therefore, these developed methods should be examined in future studies. For example, Zaman et al. [65] applied machine learning models (random forest and support vector regression) to predict PM2.5 concentrations at a national scale in Malaysia by combining satellite aerosol retrievals with ground-based pollutants and meteorological factors.
4.9. Validation of a Suitable Model for Spatiotemporal PM Concentration Predictions
Under this section, a newly collected and prepared dataset in the winter and summer seasons (between October 2020 and May 2021) was reapplied to validate the spatiotemporal PM10 and PM2.5 concentration predictions using the GWR model as a suitable model.
4.9.1. Validation of PM10 Concentration Prediction
Using the GWR as a suitable model, the predictive values of monthly PM10 concentrations at the centroid of each district in the winter and summer seasons from the existing dataset (October 2019–February 2020) and the new dataset (October 2020–February 2021) were extracted for the spatial correlation analysis. The results of the spatial correlation analysis between the predictive values of the monthly PM10 concentrations in the winter and summer seasons from the existing dataset and the new dataset are summarized in Table 18.

Table 18.
The correlation coefficient values for PM10 concentrations in the winter and summer seasons between the existing and new datasets.
According to Table 18, the correlation coefficient values for PM10 concentrations in the winter season between the existing dataset and the new dataset varied from 0.81 to 0.91, with an average value of 0.87. Similarly, the correlation coefficient values between the existing dataset and the new dataset in the summer season varied from 0.75 to 0.94, with an average value of 0.82. As suggested by Chowdhury et al. [66], these values showed a strong positive relationship. Therefore, we concluded that the predicted PM10 concentrations during two seasons in rural landscapes using the GWR model could be accepted in the current study.
Additionally, these findings indicated that the identified significant monthly factors affecting the PM10 concentrations in two seasons from the existing dataset could be managed to mitigate the PM10 concentrations in rural landscapes. For example, fire radiative power due to burning activity as a significant factor affecting PM10 concentrations in February should be reduced by setting up a schedule for burning agricultural debris.
4.9.2. Validation of PM2.5 Concentration Prediction
Similar to the PM10 concentration prediction, the predictive values of the monthly PM2.5 concentrations during the winter and summer seasons at the centroid of each district from the existing dataset and the new dataset were extracted using the GWR model for spatial correlation analysis. The results of the spatial correlation analysis between the predictive values of monthly PM2.5 concentrations in both seasons from the existing dataset and the new dataset are summarized in Table 19.

Table 19.
The correlation coefficient values for PM2.5 concentrations in the winter and summer seasons between the existing and new datasets.
According to Table 19, the correlation coefficient values for PM2.5 concentrations in the winter season between the existing dataset and the new dataset varied from 0.67 to 0.92, with an average value of 0.77. Similarly, the correlation coefficient values between the existing dataset and the new dataset in the summer season varied from 0.67 to 0.84, with an average value of 0.77. Chowdhury et al. [66] suggested that these values showed a strong positive relationship. Therefore, we concluded that the predicted PM2.5 concentrations during two seasons in urban landscapes using the GWR model could be accepted in the current study as the expected correlation coefficient value should be equal to or more than 0.5.
Additionally, these findings indicated that the significant monthly factors affecting PM2.5 concentrations in two seasons from the existing dataset could be managed to mitigate PM2.5 concentrations in urban landscapes. For example, brightness temperature, fire radiative power, and fire hotspots as significant factors affecting PM2.5 concentrations in October should lead to reduced burning activities in the agricultural areas, particularly in Nakhon Pathom Province.
Moreover, AOD data of AErosol RObotic NETwork (AERONET) strongly correlated with PM concentrations with a coefficient of determination (R2) of 0.81, RMSE of 0.13, and an overall overestimation of only 1% [67] which can be downloaded to validate the spatiotemporal PM10 and PM2.5 concentration predictions using the GWR model. Kondratyev et al. [68] mentioned that global AERONET with regular surface observations contributed substantially to raising the adequate level of aerosol models.
5. Conclusions
A suitable interpolation method was identified among seven methods (IDW, GPI, RBF, OK, OCK, SK, and SCK) for variable preparation based on the average RMSE value from October to May under the ESRI ArcMap software. As a result, the SCK method with either the hole effect or the K-Bessel function was suitable for monthly mean PM10 concentration with an average RMSE value of 15.73 µg/m3. The SCK method with the K-Bessel function was suitable for monthly mean PM2.5 concentration with an average RMSE value of 15.73 µg/m3. The SCK method with the J-Bessel function was suitable for monthly mean relative humidity with an average RMSE value of 3.43%. The SCK method with the hole effect function was suitable for monthly mean temperature with an average RMSE value of 0.79 degrees Celsius. The RBF method with the spline with tension and one sector was suitable for monthly mean wind speed with an average RMSE value of 1.54 knots. The SCK method with the stable function was suitable for monthly mean pressure with an average RMSE value of 0.40 hPa. The OCK method with the hole effect function was suitable for monthly mean visibility with an average RMSE value of 1.32 km. The SCK method with the stable function was suitable for monthly mean MODIS brightness temperature with an average RMSE value of 4.56 degrees Kelvin. The RBF method with the spline with tension and eight sector function was suitable for monthly mean MODIS fire radiative power with an average RMSE value of 19.44 MW.
For spatiotemporal significant PM concentration identification using multicollinearity test and PLS regression analysis, the significant factors on PM10 concentrations in winter and summer were five and five. Herein, three common factors on PM10 concentrations: temperature, visibility, and MODIS AOD, were identified in both seasons. Two significant factors on PM10 concentrations were only found in the winter season, including wind speed and fire radiative power. On the contrary, two significant factors of PM10 concentrations, factory density and brightness temperature, were only found in the summer season. In the meantime, there were seven common factors on PM2.5 concentrations in both seasons: wind speed, visibility, brightness temperature, fire radiative power, MODIS AOD, fire hotspot, and elevation. Three significant factors on PM2.5 concentrations were only found in the winter season, including relative humidity, temperature, and pressure. In contrast, one significant factor in PM2.5 concentrations, factory density, was only found in the summer season.
The identified significant factors on PM10 and PM2.5 concentrations were further applied to predict monthly concentrations in rural and urban landscapes in the winter and summer seasons using the GWR and MEM models. The predicted PM10 concentrations using the GWR model varied from 50.53 to 85.79 µg/m3 and from 36.92 to 51.32 µg/m3 in winter and summer, while the predicted PM10 concentrations using the MEM model varied from 50.68 to 84.59 µg/m3 and from 37.08 to 50.81 µg/m3 in both seasons. At the same time, the PM2.5 concentration prediction using the GWR model varied from 25.33 to 44.37 µg/m3 and from 16.69 to 24.04 µg/m3 in winter and summer, and the PM2.5 concentration prediction using the MEM model varied from 25.45 to 44.36 µg/m3 and from 16.68 and 23.75 µg/m3 during the two seasons. The average AICc values of the GWR model for spatiotemporal PM10 and PM2.5 concentration predictions were 97.92 and 73.86 in the winter season and 113.03 and 122.55 in the summer season, respectively; while the average AICc values of the MEM model for spatiotemporal PM10 and PM2.5 concentration predictions were 155.49 and 168.61 in the winter season and 164.77 and 186.67 in the summer season, respectively. As a result, the average AICc values of the GWR model for spatiotemporal PM10 and PM2.5 concentration predictions in two seasons were lower than the MEM model. Thus, this study chose the GWR model as a suitable model for spatiotemporal PM10 and PM2.5 concentration predictions. The validation of the GWR model for PM10 and PM2.5 concentration predictions based on existing and new datasets using spatial correlation analysis showed a strong correlation with average correlation coefficient values of 0.87 and 0.77 in the winter season and 0.82 and 0.77 in the summer, respectively. Therefore, spatiotemporal PM10 and PM2.5 concentration predictions using the GWR model were accepted as expected, with a correlation coefficient value of more than 0.5. The prediction of the PM concentrations using the GWR model could provide significant information to the public in rural areas without relying on PM monitoring stations.
Author Contributions
Conceptualization, S.O. and P.T.; methodology, S.O.; software, P.T.; validation, S.O. and P.T.; formal analysis, S.O. and P.T.; investigation, S.O. and P.T.; resources, P.T.; data curation, P.T.; writing—original draft preparation, P.T.; writing—review and editing, S.O.; visualization, P.T.; supervision, S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Suranaree University of Technology, Kamphaeng Phet Rajabhat University, Thai Pollution Control Department, and Thai Meteorological department for supporting the facilities and data to undertake this research. Special thanks from the authors go to anonymous reviewers for their valuable comments and suggestions that improved our manuscript from various perspectives.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghorani, A.A.; Riahi, Z.B.; Balali, M.M. Effects of air pollution on human health and practical measures for prevention in Iran. J. Res. Med. Sci. 2016, 21, 65. [Google Scholar]
- Chu, Y.; Liu, Y.; Li, X.; Liu, Z.; Lu, H.; Lu, Y.; Mao, Z.; Chen, X.; Li, N.; Ren, M.; et al. A Review on Predicting Ground PM2.5 Concentration Using Satellite Aerosol Optical Depth. Atmosphere 2016, 7, 129. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Leeuw, G.d.; Yang, Z.; Chen, X.; Su, X.; Jiao, J. Estimating Spatio-Temporal Variations of PM2.5 Concentrations Using VIIRS-Derived AOD in the Guanzhong Basin, China. Remote Sens. 2019, 11, 2679. [Google Scholar] [CrossRef] [Green Version]
- Sonwani, S.; Maurya, V. Impact of Air Pollution on the Environment and Economy; Saxena, P., Naik, V., Eds.; CAB International: Oxfordshire, UK, 2019; p. 235. [Google Scholar]
- Health Effects Institute. Health Impact. Available online: https://www.stateofglobalair.org/ (accessed on 19 June 2021).
- Apte, J.S.; Brauer, M.; Cohen, A.J.; Ezzati, M.; Pope, C.A. Ambient PM2.5 Reduces Global and Regional Life Expectancy. Environ. Sci. Technol. Lett. 2018, 5, 546–551. [Google Scholar] [CrossRef] [Green Version]
- Wiseman, C.L.S.; Zereini, F. Airborne Particulate Matter: Sources, Composition and Concentration; Springer: Berlin/Heidelberg, Germany, 2010; p. 656. [Google Scholar] [CrossRef]
- Kulshreshtha, P. Effects of Air Pollution on Human Health; CAB International: Oxfordshire, UK, 2019; p. 235. [Google Scholar]
- Kim, K.H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef]
- Varotsos, C.; Cartalis, C. Re-evaluation of surface ozone over Athens, Greece, for the period 1901–1940. Atmos. Res. 1991, 26, 303–310. [Google Scholar] [CrossRef]
- Cartalis, C.; Varotsos, C. Surface ozone in Athens, Greece, at the beginning and at the end of the 20th-century. Atmos. Environ. 1994, 28, 3–8. [Google Scholar] [CrossRef]
- Tzanis, C.; Varotsos, C.; Ferm, M.; Christodoulakis, J.; Assimakopoulos, M.N.; Efthymiou, C. Nitric acid and particulate matter measurements at Athens, Greece, in connection with corrosion studies. Atmos. Chem. Phys. 2009, 9, 8309–8316. [Google Scholar] [CrossRef] [Green Version]
- The Thaiger & The Nation. Bangkok Smog to Hit Thailand in the Tourism Pocket. Available online: https://thethaiger.com/news/bangkok/bangkok-smog-to-hit-thailand-in-the-tourism-pocket (accessed on 19 June 2021).
- Thai PBS WORLD. Prolonged Air Pollution can Cause Economic Loss Up to 6 Billion Baht. Available online: https://www.thaipbsworld.com/prolonged-air-pollution-can-cause-economic-loss-up-to-6-billion-baht/ (accessed on 19 June 2021).
- World Health Organization. Health Effects of Particulate Matter: Policy Implications for Countries in Eastern Europe, Caucasus and Central Asia; WHO Regional Office for Europe: Copenhagen, Denmark, 2013; p. 20. [Google Scholar]
- Levy, R.C. The Dark-Land MODIS Collection 5 Aerosol Retrieval: Algorithm Development and Product Evaluation; Association with Praxis Publishing: New York, NY, USA, 2009; p. 398. [Google Scholar]
- Ondov, J.M.; Wexler, A.S. Where Do Particulate Toxins Reside? An Improved Paradigm for the Structure and Dynamics of the Urban Mid-Atlantic Aerosol. Environ. Sci. Technol. 1998, 32, 2547–2555. [Google Scholar] [CrossRef]
- Murr, L.E.; Garza, K.M. Natural and anthropogenic environmental nanoparticulates: Their microstructural characterization and respiratory health implications. Atmos. Environ. 2009, 43, 2683–2692. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Zellner, R. A new modeling tool for the diffusion of gases in ice or amorphous binary mixture in the polar stratosphere and the upper troposphere. Atmos. Chem. Phys. 2010, 10, 3099–3105. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, C.; Ondov, J.; Tzanis, C.; Öztürk, F.; Nelson, M.; Ke, H.; Christodoulakis, J. An observational study of the atmospheric ultra-fine particle dynamics. Atmos. Environ. 2012, 59, 312–319. [Google Scholar] [CrossRef]
- Land Development Department. Provincial Land Use in Thailand. Available online: http://www1.ldd.go.th/ldd_en/en-US/land-use-planning/ (accessed on 1 October 2020).
- Arslan, S.; Aybek, A. Particulate Matter Exposure in Agriculture; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Chen, X.; Yuan, X.; Zeng, G.; León, T.; Liang, J.; Chen, G.; Yuan, X. Characteristics of Particulate Pollution (PM2.5 and PM10) and Their Spacescale-Dependent Relationships with Meteorological Elements in China. Sustainability 2017, 9, 2330. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Fu, J.; Jiang, D.; Hu, W.; Dong, D.; Huang, Y.; Zhao, M. Spatio-Temporal Variation of PM2.5 Concentrations and Their Relationship with Geographic and Socioeconomic Factors in China. Int. J. Environ. Res. Public Health 2014, 11, 173–186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ESRI. ArcGIS 10.3.1 Help. In Regression Analysis Basics; Environmental Systems Research Institute, Inc.: Redlands, CA, USA, 2015. [Google Scholar]
- Pollution Control Department. Thailand’s Air Quality Information. Available online: http://air4thai.pcd.go.th/webV2/ (accessed on 19 June 2021).
- U.S. Environmental Protection Agency. Technical Assistance Document for the Reporting of Daily Air Quality—The Air Quality Index (AQI); Research Triangle Park, NC, USA, 2018; p. 22. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: New York, NY, USA, 1988; p. 78. [Google Scholar]
- Sajjadi, S.A.; Zolfaghari, G.; Adab, H.; Allahabadi, A.; Delsouz, M. Measurement and modeling of particulate matter concentrations: Applying spatial analysis and regression techniques to assess air quality. MethodsX 2017, 4, 372–390. [Google Scholar] [CrossRef]
- Vorapracha, P.; Phonprasert, P.; Khanaruksombat, S.; Pijarn, N. A Comparison of Spatial Interpolation Methods for predicting concentrations of Particle Pollution (PM10). Int. J. Chem. Environ. Biol. Sci. 2015, 3, 302–306. [Google Scholar]
- Wong, D.W.; Yuan, L.; Perlin, S.A. Comparison of spatial interpolation methods for the estimation of air quality data. J. Expo. Anal. Environ. Epidemiol. 2004, 14, 404–415. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Gupta, I.; Brandt, J.; Kumar, R.; Dikshit, A.K.; Patil, R.S. Air quality mapping using GIS and economic evaluation of health impact for Mumbai City, India. J. Air Waste Manag. Assoc. 2016, 66, 470–481. [Google Scholar] [CrossRef] [Green Version]
- Giraldo, R.; Herrera, L.; Leiva, V. Cokriging Prediction Using as Secondary Variable a Functional Random Field with Application in Environmental Pollution. Mathematics 2020, 8, 1305. [Google Scholar] [CrossRef]
- Prasomsup, W. Spatial Evaluation and Prediction of Urban Heat Island Phenomena In Bangkok and Its Vicinity; Suranaree University of Technology: Nakhon Ratchasima, Thailand, 2017. [Google Scholar]
- Jantakat, Y.; Ongsomwang, S. Assessing The Effect Of Incorporating Topographical Data With Geostatistical Interpolation For Monthly Rainfall And Temperature In Ping Basin, Thailand. Suranaree J. Sci. Technol. 2011, 18, 123–139. [Google Scholar]
- Ozturk, D.; Kilic, F. Geostatistical Approach for Spatial Interpolation of Meteorological Data. Ann. Braz. Acad. Sci. 2016, 88, 2121–2136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, W.; Hu, J.; Yu, X. A Study on Temperature Interpolation Methods Based on GIS. In Proceedings of the 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–5. [Google Scholar]
- Keskin, M.; Özdoğu, K. Comparison of Interpolation Methods for Meteorological Data. Bachelor Thesis, Istanbul Technical University, Istanbul, Turkey, 2011. [Google Scholar]
- Gradka, R.; Kwinta, A. A Short Review Of Interpolation Methods Used For Terrain Modeling. Geomat. Land Manag. Landsc. 2018, 4, 29–47. [Google Scholar] [CrossRef]
- Yalçin, E. Cokriging and its effect on the estimation precision. J. S. Afr. Inst. Min. Metall. 2005, 105, 223–228. [Google Scholar]
- Kuo, P.-F.; Huang, T.-E.; Putra, I.G.B. Comparing Kriging Estimators Using Weather Station Data and Local Greenhouse Sensors. Sensors 2021, 21, 1853. [Google Scholar] [CrossRef] [PubMed]
- Deligiorgi, D.; Philippopoulos, K. Spatial Interpolation Methodologies in Urban Air Pollution Modeling: Application for the Greater Area of Metropolitan Athens, Greece. Adv. Air Pollut. 2011, 17, 341–362. [Google Scholar]
- Veraverbeke, S.; Sedano, F.; Hook, S.J.; Randerson, J.T.; Jin, Y.; Rogers, B.M. Mapping the daily progression of large wildland fires using MODIS active fire data. Int. J. Wildland Fire 2014, 23, 655–667. [Google Scholar] [CrossRef] [Green Version]
- Devkota, J.U. Statistical analysis of active fire remote sensing data: Examples from South Asia. Environ. Monit. Assess. 2021, 193, 1–14. [Google Scholar] [CrossRef]
- Ponomarev, E.I.; Shvetsov, E.G.; Usataya, Y.O. Determination of the Energy Properties of Wildfires in Siberia by Remote Sensing. Atmos. Ocean. Phys. 2018, 54, 979–985. [Google Scholar] [CrossRef] [Green Version]
- Loboda, T.V.; Hall, J.V.; Baer, A. ABoVE: Wildfire Date of Burning within Fire Scars across Alaska and Canada, 2001–2019; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2017. [Google Scholar]
- Harnkijroong, T.; Panich, N. Influence of Meteorological Factors on PM10 at Roadside of Bangkok. In Proceedings of the 10th National Kasetsart University Kamphaeng Saen Conference, Nakhon Pathom, Thailand, 6–7 December 2013; pp. 2543–2550. [Google Scholar]
- Unal, Y.S.; Toros, H.; Deniz, A.; Incecik, S. Influence of meteorological factors and emission sources on spatial and temporal variations of PM10 concentrations in Istanbul metropolitan area. Atmos. Environ. 2011, 45, 5504–5513. [Google Scholar] [CrossRef]
- Czernecki, B.; Półrolniczak, M.; Kolendowicz, L.; Marosz, M.; Kendzierski, S.; Pilguj, N. Influence of the atmospheric conditions on PM10 concentrations in Poznań, Poland. J. Atmos. Chem. 2017, 74, 115–139. [Google Scholar] [CrossRef] [Green Version]
- Syafrijon; Marzuki; Emriadi; Pratama, R. Relationship Between MODIS-based Aerosol Optical Depth and PM10 over Sumatra to Overcome the Limitations of Air Quality Monitoring Data Availability. Orient. J. Chem. 2018, 34, 2163–2169. [Google Scholar] [CrossRef] [Green Version]
- Ferrero, L.; Riccio, A.; Ferrini, B.S.; D’Angelo, L.; Rovelli, G.; Casati, M.; Angelini, F.; Barnaba, F.; Gobbi, G.P.; Cataldi, M.; et al. Satellite AOD conversion into ground PM10, PM2.5 and PM1 over the Povalley (Milan, Italy) exploiting information on aerosol vertical profiles, chemistry, hygroscopicity and meteorology. Atmos. Pollut. Res. 2019, 10, 1895–1912. [Google Scholar] [CrossRef]
- Grgurić, S.; Križan, J.; Gašparac, G.; Antonić, O.; Špirić, Z.; Mamouri, R.E.; Christodoulou, A.; Nisantzi, A.; Agapiou, A.; Themistocleous, K.; et al. Relationship between MODIS based Aerosol Optical Depth and PM10 over Croatia. Cent. Eur. J. Geosci. 2014, 6, 2–16. [Google Scholar] [CrossRef]
- Kanabkaew, T. Prediction of Hourly Particulate Matter Concentrations in Chiangmai, Thailand Using MODIS Aerosol Optical Depth and Ground-Based Meteorological Data. Environ. Asia 2013, 6, 65–70. [Google Scholar]
- Chen, Z.; Cai, J.; Gao, B.; Xu, B.; Dai, S.; He, B.; Xie, X. Detecting the causality influence of individual meteorological factors on local PM2.5 concentration in the Jing-Jin-Ji region. Sci. Rep. 2017, 7, 40735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Zhang, X. Analysis of the Pollution Characteristics and Influence Factors of PM2.5 in Chinese main capital city. Adv. Mater. Res. 2014, 1023, 247–251. [Google Scholar] [CrossRef]
- Galindo, N.; Varea, M.; Gil-Moltó, J.; Yubero, E.; Nicolás, J. The Influence of Meteorology on Particulate Matter Concentrations at an Urban Mediterranean Location. Water Air Soil Pollut. 2011, 215, 365–372. [Google Scholar] [CrossRef]
- Gu, Y. Estimating PM2.5 Concentrations Using 3 km MODIS AOD Products: A Case Study in British Columbia, Canada; University of Waterloo: Waterloo, ON, Canada, 2019. [Google Scholar]
- Kong, L.; Xin, J.; Zhang, W.; Wang, Y. The empirical correlations between PM2.5, PM10 and AOD in the Beijing metropolitan region and the PM2.5, PM10 distributions retrieved by MODIS. Environ. Pollut. 2016, 216, 350–360. [Google Scholar] [CrossRef]
- Lee, H.J.; Liu, Y.; Coull, B.A.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef] [Green Version]
- Chudnovsky, A.A.; Koutrakis, P.; Kloog, I.; Melly, S.; Nordio, F.; Lyapustin, A.; Wang, Y.; Schwartz, J. Fine particulate matter predictions using high resolution Aerosol Optical Depth (AOD) retrievals. Atmos. Environ. 2014, 89, 189–198. [Google Scholar] [CrossRef] [Green Version]
- Wei, Q.; Zhang, L.; Duan, W.; Zhen, Z. Global and Geographically and Temporally Weighted Regression Models for Modeling PM2.5 in Heilongjiang, China from 2015 to 2018. Environ. Res. Public Health 2019, 16, 5107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoi, K.I.; Yuen, K.V.; Mok, K.M. Prediction of daily averaged PM10 concentrations by statistical time-varying model. Atmos. Environ. 2009, 43, 2579–2581. [Google Scholar] [CrossRef]
- Li, L.; Chen, B.; Zhang, Y.; Zhao, Y.; Xian, Y.; Xu, G.; Zhang, H.; Guo, L. Retrieval of Daily PM2.5 Concentrations Using Nonlinear Methods: A Case Study of the Beijing–Tianjin–Hebei Region, China. Remote Sens. 2018, 10, 2006. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, Y.; Shi, R.; Yao, Q. Evaluation of PM10 forecasting based on the artificial neural network model and intake fraction in an urban area: A case study in Taiyuan City, China. J. Air Waste Manag. Assoc. 2013, 63, 755–763. [Google Scholar] [CrossRef] [Green Version]
- Zaman, N.A.F.K.; Kanniah, K.D.; Kaskaoutis, D.G.; Latif, M.T. Evaluation of Machine Learning Models for Estimating PM2.5 Concentrations across Malaysia. Appl. Sci. 2021, 11, 7326. [Google Scholar] [CrossRef]
- Chowdhury, A.K.; Debsarkar, A.; Chakrabarty, S. Novel Methods for Assessing Urban Air Quality: Combined Air and Noise Pollution Approach. J. Atmos. Pollut. 2015, 3, 1–8. [Google Scholar]
- Kanniah, K.D.; Zaman, N.A.F.K.; Kaskaoutis, D.G.; Latif, M.T. COVID-19’s impact on the atmospheric environment in the Southeast Asia region. Sci. Total Environ. 2020, 736, 139658. [Google Scholar] [CrossRef]
- Kondratyev, K.Y.; Ivlev, L.S.; Krapivin, V.F.; Varotsos, C.A. Atmospheric Aerosol Properties: Formation, Processes and Impacts; Springer: Berlin/Heidelberg, Germany, 2006; p. 572. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).