Automatic Detection of Electric Field VLF Electromagnetic Wave Abnormal Disturbance on Zhangheng-1 Satellite
Abstract
:1. Introduction
2. Materials and Methods
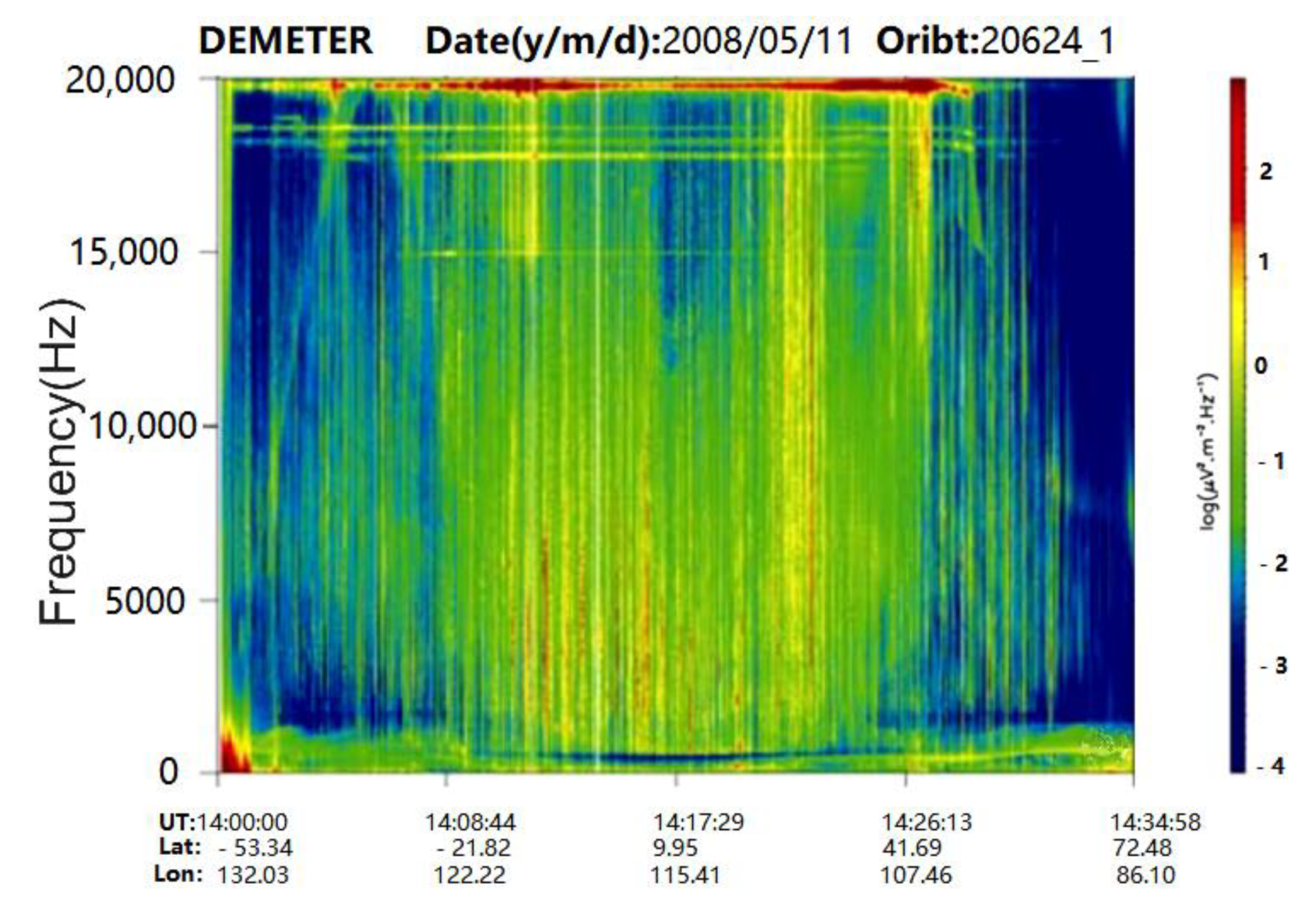
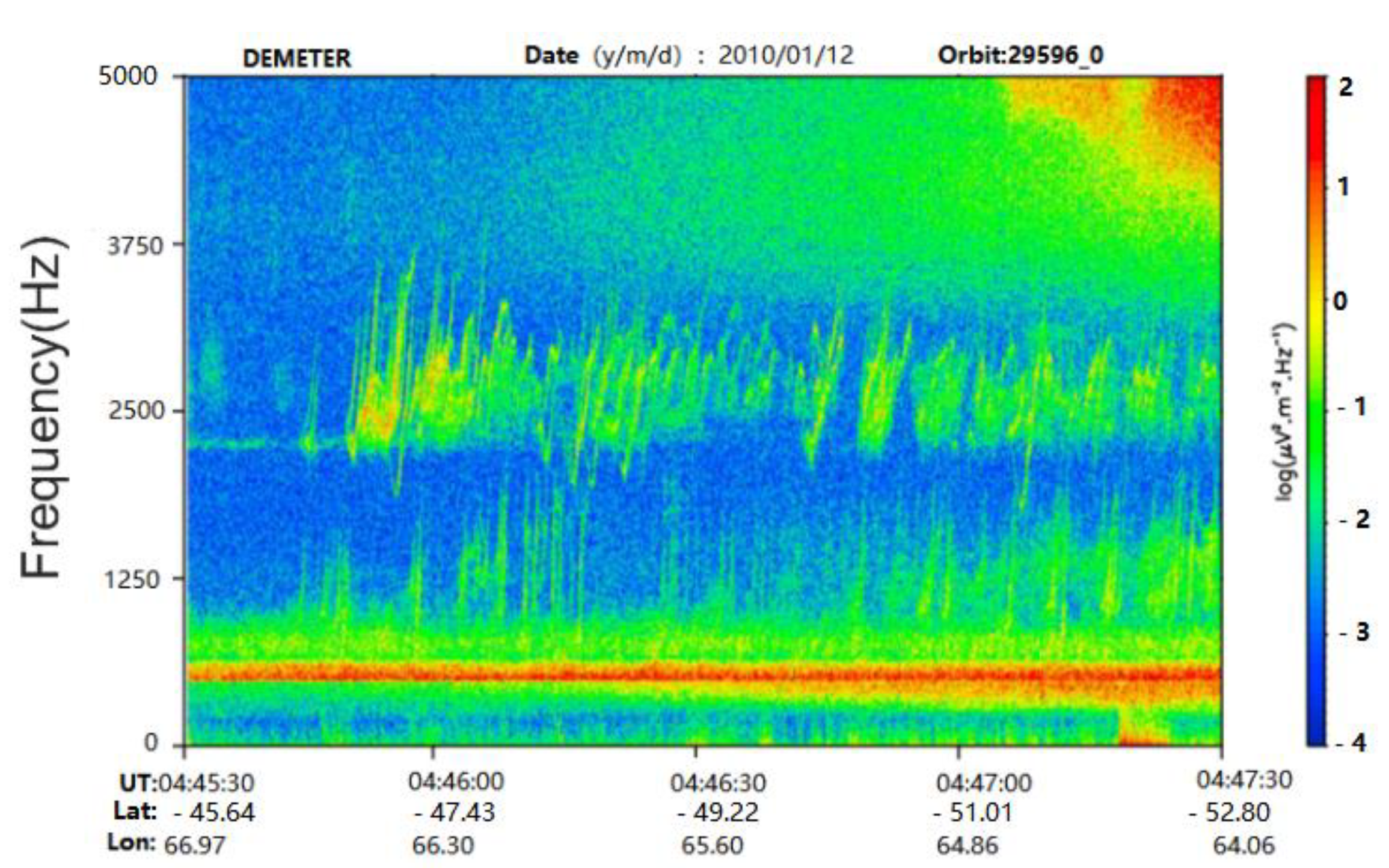
2.1. Data Collection
2.2. Gray Processing
2.3. Horizontal Edge Feature Extraction
2.4. Binarization
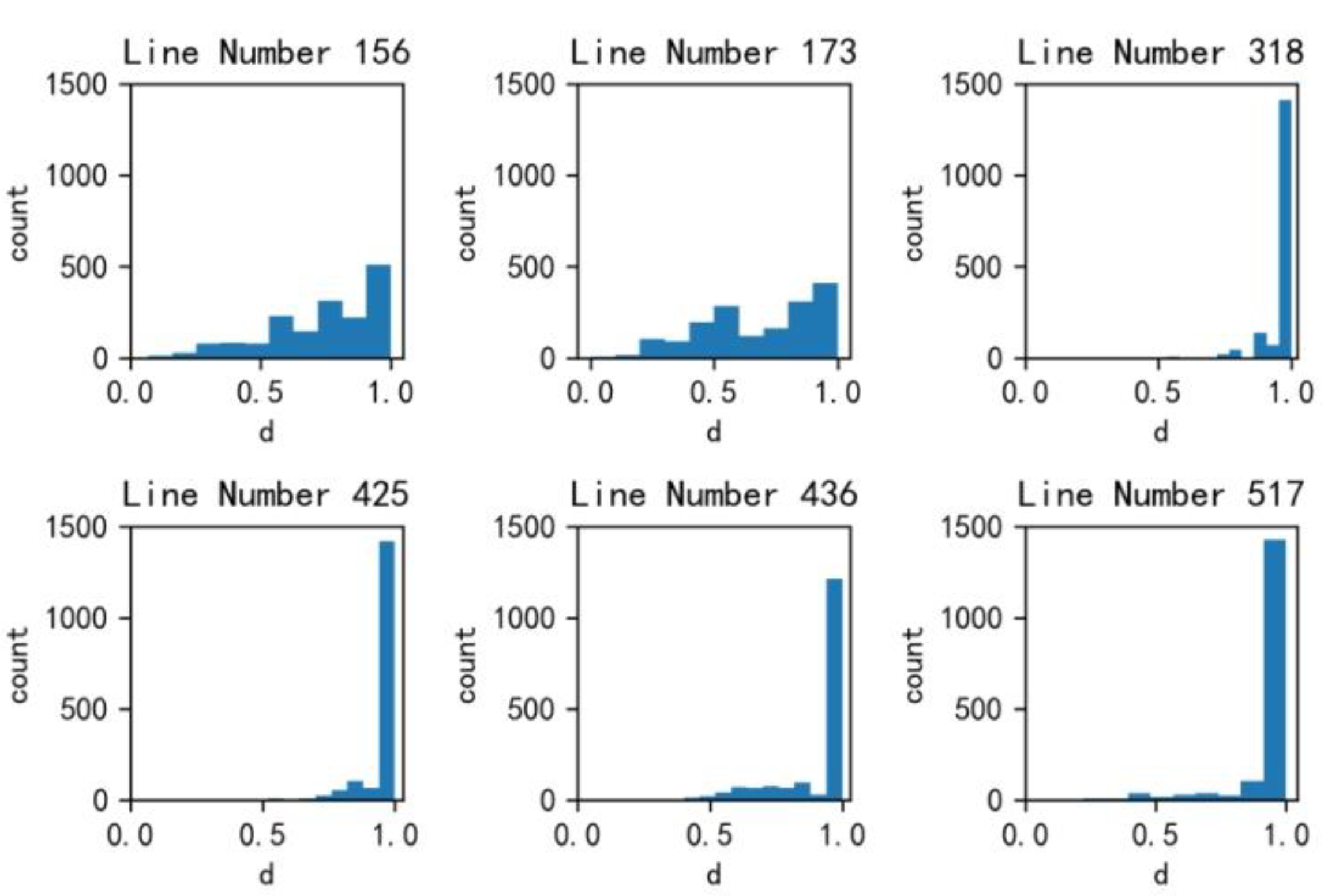
2.5. Horizontal Line Detection Based on Unsupervised Learning
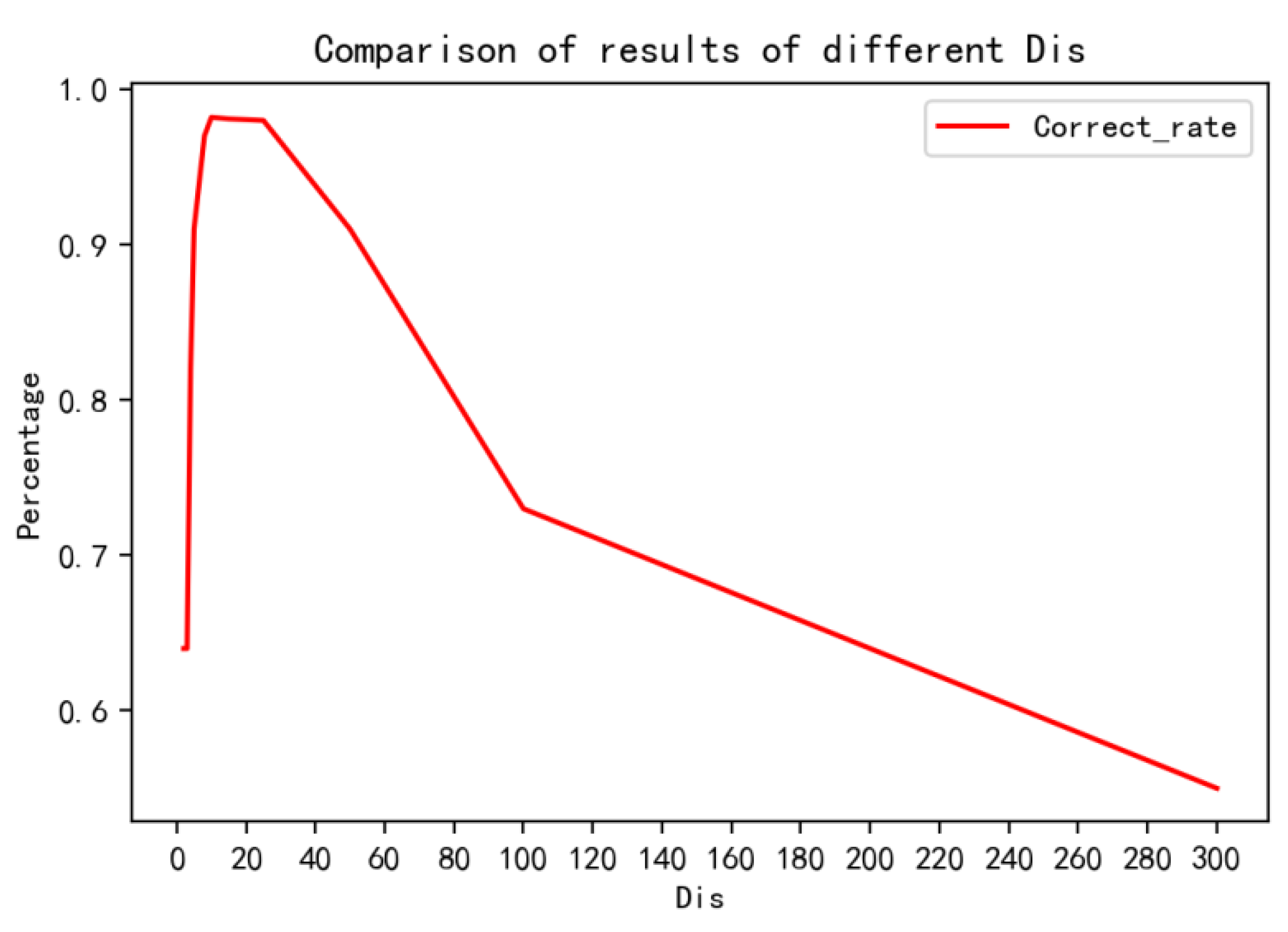
2.6. Selection of Abnormal Window on Horizontal Line
2.7. Abnormal Disturbance Identification
3. Results
3.1. Experimental Method
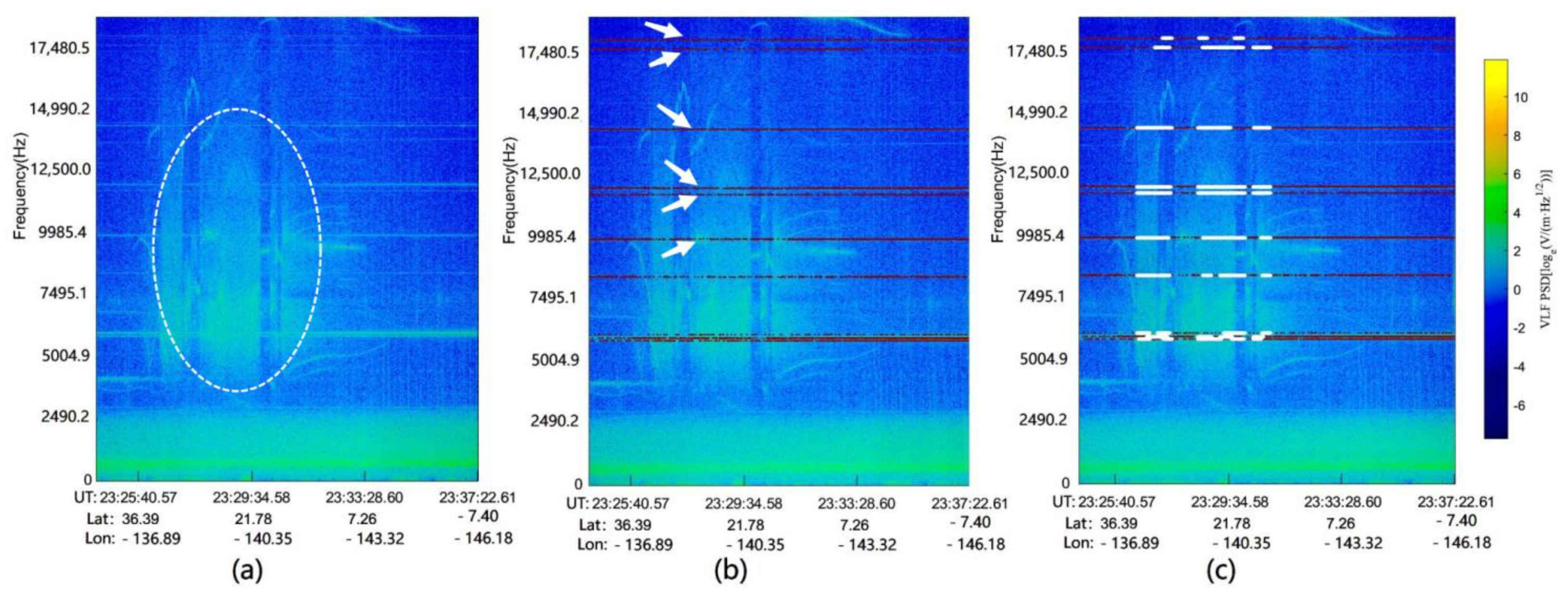
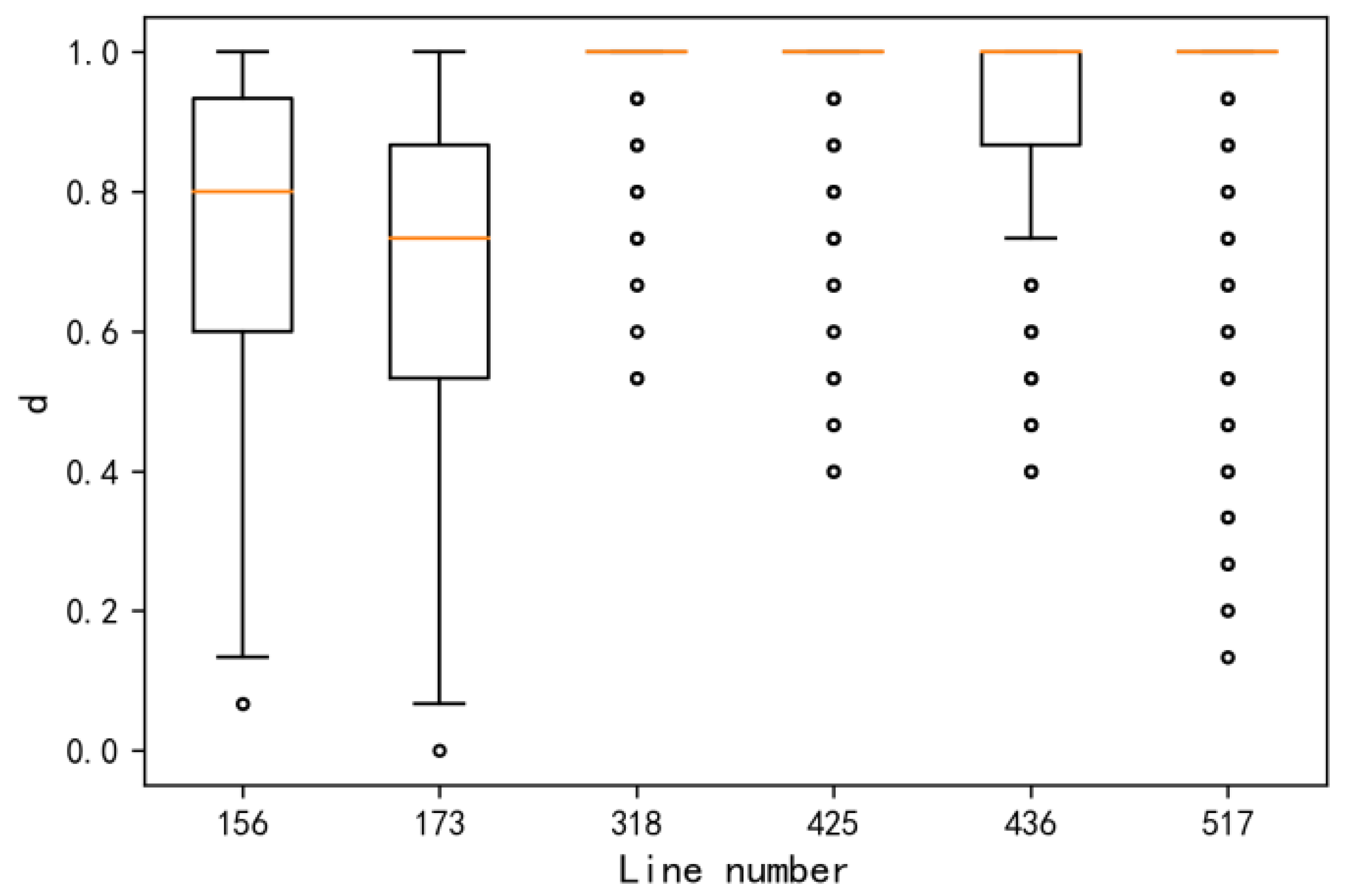
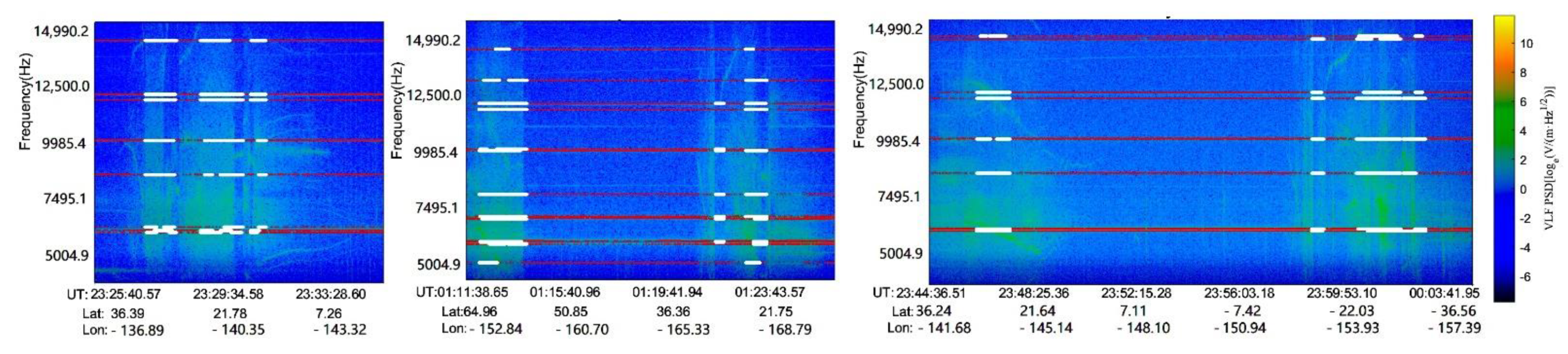
3.2. Experimental Results and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parrot, M.; Berthelier, J.J.; Lebreton, J.P.; Sauvaud, J.A.; Santolik, O.; Blecki, J. Examples of unusual ionospheric observations made by the DEMETER satellite over seismic regions. Phys. Chem. Earth Parts 2006, 31, 486–495. [Google Scholar] [CrossRef]
- Larkina, V.I.; Nalivaiko, A.V.; Gershenzon, N.I.; Gokhberg, M.B.; Liperovskii, V.A.; Shalimov, S.L. Intercosmos-19 observation of VLF emissions associated with seismic activity. Geomagn. Aeron. 1983, 23, 842–846. [Google Scholar]
- Chmyrev, V.; Isaev, N.; Bilichenko, S.; Stanev, G. Observation by space-borne detectors of electric fields and hydromagnetic waves in the ionosphere over an earthquake centre. Phys. Earth Planet. Inter. 1989, 57, 110–114. [Google Scholar] [CrossRef]
- Parrot, M.; Mogilevsky, M. VLF emissions associated with earthquakes and observed in the ionosphere and the magnetosphere. Phys. Earth Planet. Inter. 1989, 57, 86–99. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Legen’Ka, A.D. Spatial–Temporal Characteristics of Large Scale Disturbances of Electron Density Observed in the Ionospheric F-Region before Strong Earthquakes. Cosm. Res. 2003, 41, 221–230. [Google Scholar] [CrossRef]
- Liu, Y.M.; Wang, J.S.; Xiao, Z.; Suo, Y. A Possible Mechanism of Typhoon Effects on the Ionospheric F2 Layer. Chin. J. Space Sci. 2006, 26, 92–97. [Google Scholar]
- Juntao, C.; Guo, Z.Z.; Yan, Z.; Tang, J.; Chen, X.B. The study on ionospheric disturbances during earthquakes. Prog. Geophys. 2007, 22, 695–701. [Google Scholar]
- Parrot, M. DEMETE Robservations of manmade waves that propagate in the ionosphere. Comptes Rendus Phys. 2018, 19, 26–35. [Google Scholar] [CrossRef]
- Ryu, K.; Lee, E.; Chae, J.S.; Parrot, M.; Pulinets, S. Seismo-ionospheric coupling appearing as equatorial electron density enhancements observed via DEMETER electron density measurements. J. Geophys. Res. Space Phys. 2014, 119, 8524–8542. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zeren, Z.M.; Shen, X.H.; Jun, C.; Zhao, S.; Xiong, P.; Chen, H.; Ouyang, X. Analysis on variation of electric field spectrum at cut-off frequency before strong earthquakes: Taking 2006 Tonga M_W8.0 earthquake as an example. Acta Seismol. Sin. 2011, 33, 451–460. [Google Scholar]
- He, Y.F.; Yang, D.M.; Chen, H.R. Demeter satellite detected the signal-to-noise ratio change of ground VLF transmitting station signal that may be related to Wenchuan earthquake. Chin. Sci. Part D 2009, 39, 403–4122009. [Google Scholar]
- Zhang, X.M.; Shen, X.H.; Ouyang, X.Y.; Cai, J.A.; Huang, J.P.; Liu, J.; Zhao, S.F. Ionosphere VLF electric field anomalies before Wenchuan M 8 earthquake. Dianbo Kexue Xuebao Chin. J. Radio Sci. 2009, 24, 1024–1032. [Google Scholar]
- Zeren, Z.M. Electromagnetic Waves Induced by Strong Earthquake and Non-Earthquake Sources in Geospace. Ph.D. Thesis, Beijing University of Aeronautics and Astronautics, Beijing, China, 2014. [Google Scholar]
- Zhang, X.M.; Qian, J.D.; Ying, Y.; Zhao, S.-F.; Lou, W.-Y. Space Electromagnetic Disturbances Induced by High-voltage Power Lines. Earthquake 2019, 39, 11. [Google Scholar]
- Parrot, M.; Manninen, J.; Santolík, O.; Němec, F.; Turunen, T.; Raita, T.; Macúšová, E. Simultaneous observation on board a satellite and on the ground of large-scale magnetospheric line radiation. Geophys. Res. Lett. 2007, 34, L19102. [Google Scholar] [CrossRef]
- Shen, X.H.; Zong, Q.G.; Zhang, X.M. Introduction to special section on the China Seismo-Electromagnetic Satellite and initial results. Earth Planet. Phys. 2018, 2, 3–7. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Huang, J.; Yin, H.; Jia, J. Research on Pre-Seismic Feature Recognition of SpatialElectric Field Data Recorded by CSES. Atmosphere 2022, 13, 179. [Google Scholar] [CrossRef]
- Cao, J.B.; Yang, J.Y.; Lu, L. Non-seismic Induced Electromagnetic Waves in the Near Earth Space. Earthquakes 2008, 29, 17–25. (In Chinese) [Google Scholar]
- Wang, Z.; Zhou, C.; Zhao, S.; Xu, X.; Liu, M.; Liu, Y.; Liao, L.; Shen, X. Numerical Study of Global ELF Electromagnetic Wave Propagation with Respect to Lithosphere–Atmosphere–Ionosphere Coupling. Remote Sens. 2021, 13, 4107. [Google Scholar] [CrossRef]
- Wang, L.; Hu, Z.; Shen, X. Data processing methods and procedures of CSES satellite. J. Remote Sens. 2018, 22, 39–55. [Google Scholar]
- Zhou, B.; Cheng, B. Development and calibration of high-precision magnetometer of the China Seismo-Electromagnetic satellite. Natl. Remote Sens. Bull. 2018, 22, 64–73. [Google Scholar]
- Diego, P.; Huang, J.; Piersanti, M.; Badoni, D.; Zeren, Z.; Yan, R.; Rebustini, G.; Ammendola, A.; Candidi, M.; Guan, Y.-B.; et al. The Electric Field Detector on Board the China Seismo Electromagnetic Satellite-In-Orbit Results and Validation. Instruments 2020, 5, 1. [Google Scholar] [CrossRef]
- Lu, H.X.; Shen, X.H.; Zhao, S.F.; Liao, L.; Lin, J.; Huang, J.; Zeren, Z.; Sun, F.; Guo, F. Typical event observation of the tri-band beacon onboard the CSES (ZH-1) satellite. Chin. J. Radio Sci. 2022, 36, 1–8. [Google Scholar]
- Liu, C.; Guan, Y.; Zheng, X.; Zhang, A.; Piero, D.; Sun, Y. The technology of space plasma in-situ measurement on the China Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2018, 62, 829–838. [Google Scholar] [CrossRef]
- Yan, R.; Shen, X.H.; Huang, J.X.; Wang, Q.; Chu, W.; Liu, D.; Xu, S. Examples of unusual ionospheric observations by the CSES prior to earthquakes. Earth Planet. Phys. 2018, 2, 515–526. [Google Scholar] [CrossRef]
- Rui, Y.; Zhe, H.; Wang, L.; Guan, Y.; Liu, C. Preliminary data inversion method of Langmuir probe onboard CSES. Acta Seismol. Sin. 2017, 39, 239–247. [Google Scholar]
- Zhou, B.; Yang, Y.; Zhang, Y.; Gou, X.; Cheng, B.; Wang, J.; Li, L. Magnetic field data processing methods of the China Seismo-Electromagnetic Satellite. Earth Planet. Phys. 2018, 2, 455–461. [Google Scholar]
- Wang, L.; Shen, X.; Zhang, Y.; Zhang, X.; Hu, Z.; Yan, R.; Yuan, S.; Zhu, X. Developing progress of China Seismo-Electromagnetic Satellite project. Acta Seismol. Sin. 2016, 38, 376–385+509. [Google Scholar]
- Wang, X.T.; Yang, D.H.; Zhou, Z.H.; Cui, J.; Zhou, N.; Shen, X. Features of topside ionospheric background over China and its adjacent areas obtained by the ZH-1 satellite. Chin. J. Geophys. 2021, 64, 391–409. [Google Scholar]
- Shen, X.; Zhang, X.; Cui, J.; Zhou, X.; Jiang, W.L.; Gong, L.X.; Liu, Q.Q. Remote sensing application in earthquake science research and geophysical fields exploration satellite mission in China. Natl. Remote Sens. Bull. 2018, 22, 1–16. [Google Scholar]
- Ma, M.; Lei, J.; Li, C. Design Optimization of Zhangheng-1 Space Electric Field Detector. J. Vac. Sci. Technol. 2018, 38, 582–589. [Google Scholar]
- Yuan, J.; Wang, Q.; Yang, D.H. Automatic recognition algorithm of lightning whistlers observed by the Search Coil Magnetometer onboard the Zhangheng-1 Satellite. Chin. J. Geophys. 2021, 64, 3905–3924. [Google Scholar] [CrossRef]
- Han, Y.; Yuan, J.; Feng, J.L.; Yang, D.; Huang, J.; Wang, Q.; Zeren, Z. Automatic detection of “horizontal” electromagnetic wave disturbance in the data of EFD on ZH-1. Prog. Geophys. 2021, 36, 2303–2311. [Google Scholar]
- Han, Y.; Yuan, J.; Feng, J.L.; Yang, D.; Huang, J.; Wang, Q.; Zeren, Z. Automatic detection of horizontal electromagnetic wave disturbance in Zhangheng-1 EFD data based on horizontal convolution kernel. Prog. Geophys. 2022, 37, 11–18. [Google Scholar]
- Wu, Q.H.; Ding, G.R.; Sun, J.C. Electromagnetic Spectrum Data Mining Theories and Applications; Science Press: Beijing, China, 2020. [Google Scholar]
- Zhang, Y.J. A Course of Image Processing and Analysis, 2nd ed.; People Post Press: Beijing, China, 2016. [Google Scholar]


| Name | Content | Type | Size | Unit |
|---|---|---|---|---|
| A133_W | Z | 64-bit floating | N × 2048 | mV/m |
| Dis | Correct Rate | Error Rate | Missed Rate |
|---|---|---|---|
| Dis = 15 | 0.982 ± 0.01 | 0.018 ± 0.003 | 0.005 ± 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Yuan, J.; Huang, J.; Li, Z.; Shen, X. Automatic Detection of Electric Field VLF Electromagnetic Wave Abnormal Disturbance on Zhangheng-1 Satellite. Atmosphere 2022, 13, 807. https://doi.org/10.3390/atmos13050807
Han Y, Yuan J, Huang J, Li Z, Shen X. Automatic Detection of Electric Field VLF Electromagnetic Wave Abnormal Disturbance on Zhangheng-1 Satellite. Atmosphere. 2022; 13(5):807. https://doi.org/10.3390/atmos13050807
Chicago/Turabian StyleHan, Ying, Jing Yuan, Jianping Huang, Zhong Li, and Xuhui Shen. 2022. "Automatic Detection of Electric Field VLF Electromagnetic Wave Abnormal Disturbance on Zhangheng-1 Satellite" Atmosphere 13, no. 5: 807. https://doi.org/10.3390/atmos13050807
APA StyleHan, Y., Yuan, J., Huang, J., Li, Z., & Shen, X. (2022). Automatic Detection of Electric Field VLF Electromagnetic Wave Abnormal Disturbance on Zhangheng-1 Satellite. Atmosphere, 13(5), 807. https://doi.org/10.3390/atmos13050807






