Innovative Trend Analysis of High-Altitude Climatology of Kashmir Valley, North-West Himalayas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.3. MK and Sen’s Slope Tests
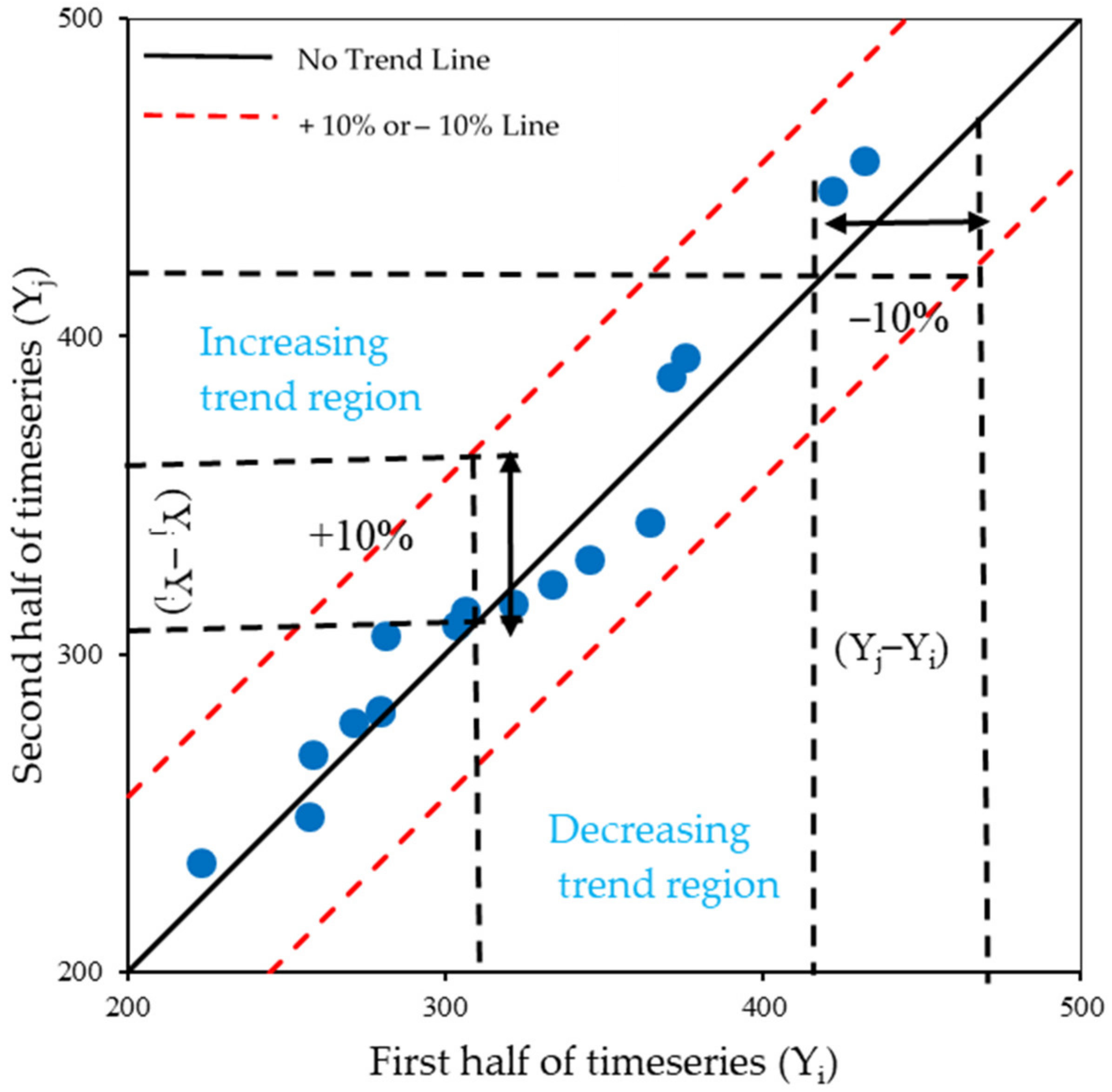
2.4. Innovative Trend Analysis (ITA) Method
3. Results
3.1. Spatio-Temporal Variations of Tmax, Tmin and Precipitation for Kashmir Valley Stations
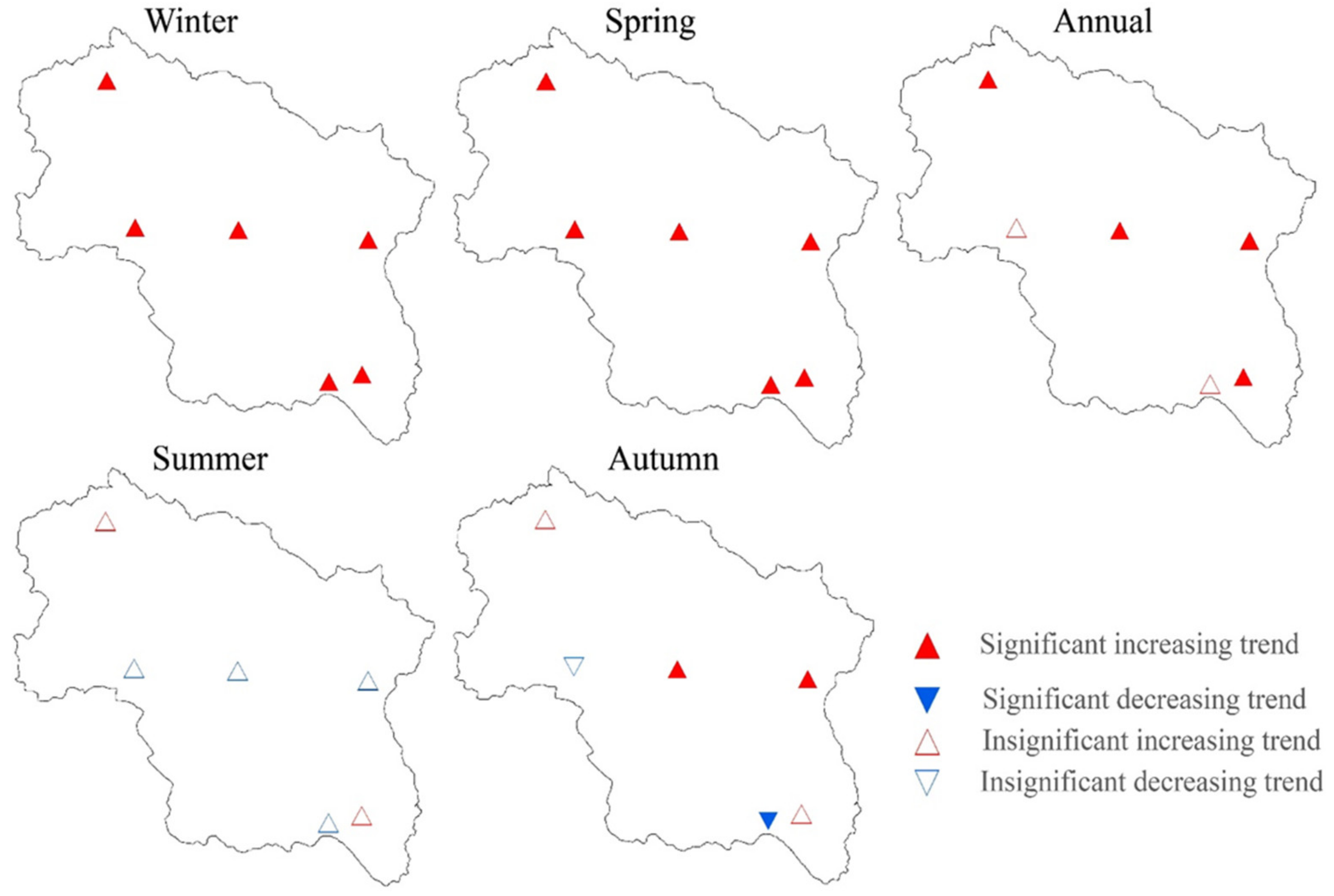
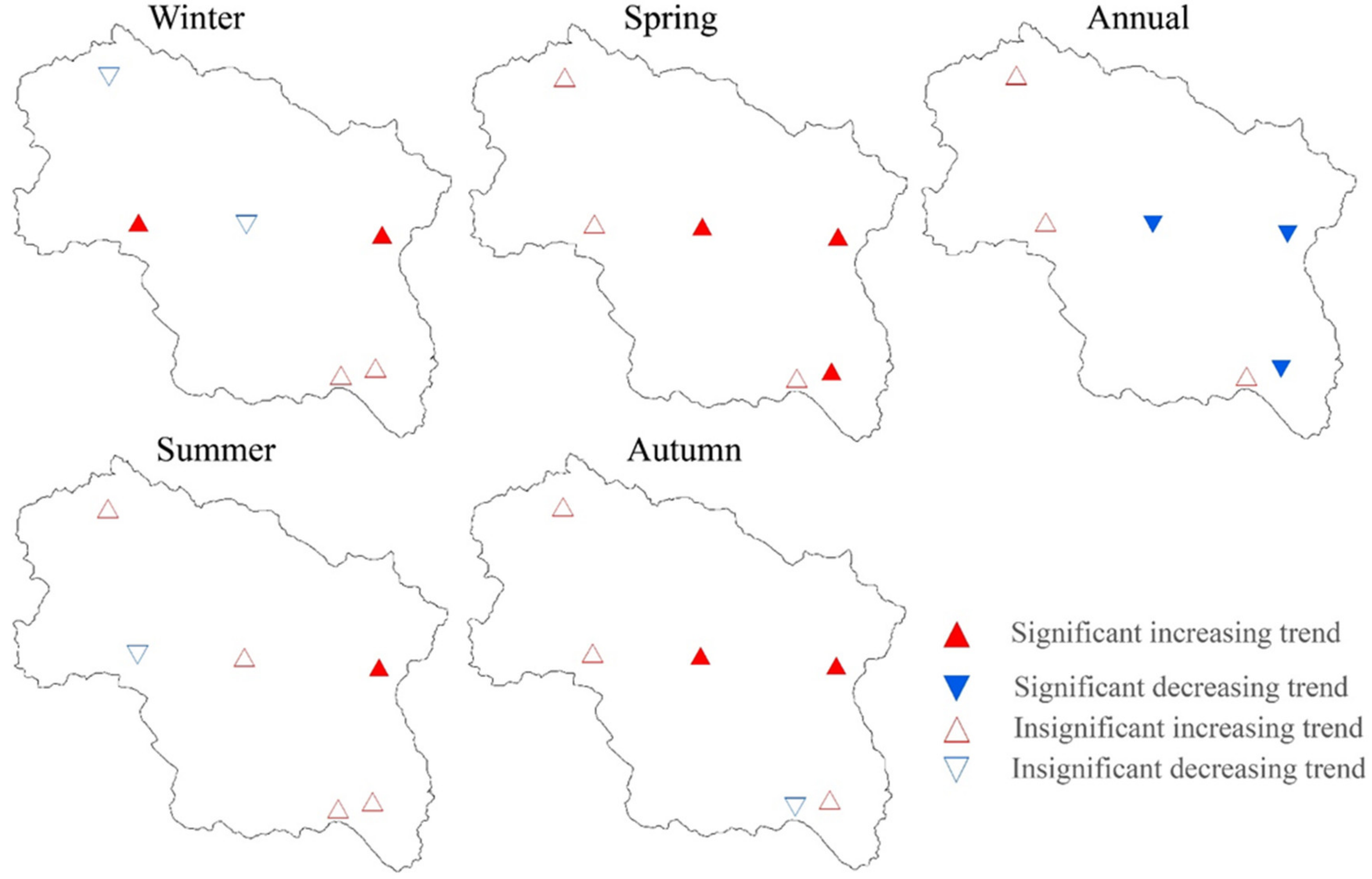
3.2. Annual and Seasonal Tmax Variations over Time
3.3. Annual and Seasonal Tmin Variations
3.4. Annual and Seasonal Precipitation Variations over Time
3.5. Comparison of ITA, MK, and Sen Slope Estimation Approach Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahmat, A.; Zaki, M.K.; Effendi, I.; Mutolib, A.; Yanfika, H.; Listiana, I. Effect of global climate change on air temperature and precipitation in six cities in Gifu Prefecture, Japan. J. Phys. Conf. Ser. 2019, 1155, 012070. [Google Scholar] [CrossRef]
- Arora, N.K.; Fatima, T.; Mishra, I.; Verma, M.; Mishra, J.; Mishra, V. Environmental sustainability: Challenges and viable solutions. Environ. Sustain. 2018, 1, 309–340. [Google Scholar] [CrossRef]
- Aamir, M.; Rai, K.K.; Dubey, M.K.; Zehra, A.; Tripathi, Y.N.; Divyanshu, K.; Samal, S.; Upadhyay, R.S. Impact of Climate Change on Soil Carbon Exchange, Ecosystem Dynamics, and Plant–Microbe Interactions. In Climate Change and Agricultural Ecosystems; Elsevier: Amsterdam, The Netherlands, 2019; pp. 379–413. [Google Scholar]
- Le Quéré, C.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Korsbakken, J.I.; Peters, G.P.; Manning, A.C.; Boden, T.A.; Tans, P.P.; Houghton, R.A.; et al. Global carbon budget. Earth Syst. Sci. Data 2016, 8, 605–649. [Google Scholar] [CrossRef] [Green Version]
- Cui, L.; Wang, L.; Lai, Z.; Tian, Q.; Liu, W.; Li, J. Innovative trend analysis of annual and seasonal air temperature and rainfall in the Yangtze River Basin, China during 1960–2015. J. Atmos. Sol. Terr. Phys. 2017, 164, 48–59. [Google Scholar] [CrossRef]
- Higashino, M.; Stefan, H.G. Trends and correlations in recent air temperature and precipitation observations across Japan (1906–2005). Theor. Appl. Climatol. 2020, 140, 517–531. [Google Scholar] [CrossRef]
- Thuiller, W. Patterns and uncertainties of species’ range shifts under climate change. Glob. Chang. Biol. 2004, 10, 2020–2027. [Google Scholar] [CrossRef]
- Walsh, K.J.; McBride, J.L.; Klotzbach, P.J.; Balachandran, S.; Camargo, S.J.; Holland, G.; Knutson, T.R.; Kossin, J.P.; Lee, T.C.; Sobel, A.; et al. Tropical cyclones and climate change. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 65–89. [Google Scholar] [CrossRef]
- Ren, Y.-Y.; Ren, G.-Y.; Sun, X.-B.; Shrestha, A.B.; You, Q.-L.; Zhan, Y.-J.; Rajbhandari, R.; Zhang, P.-F.; Wen, K.-M. Observed changes in surface air temperature and precipitation in the Hindu Kush Himalayan region over the last 100-plus years. Adv. Clim. Chang. Res. 2017, 8, 148–156. [Google Scholar] [CrossRef]
- Gedefaw, M.; Yan, D.; Wang, H.; Qin, T.; Girma, A.; Abiyu, A.; Batsuren, D. Innovative trend analysis of annual and seasonal rainfall variability in Amhara regional state, Ethiopia. Atmosphere 2018, 9, 326. [Google Scholar] [CrossRef] [Green Version]
- Shyam, G.M.; Taloor, A.K.; Singh, S.K.; Kanga, S. Sustainable water management using rainfall-runoff modeling: A geospatial approach. Groundw. Sustain. Dev. 2021, 15, 100676. [Google Scholar] [CrossRef]
- Piao, S.L.; Ciais, P.; Huang, Y.; Shen, Z.H.; Peng, S.S.; Li, J.S.; Zhou, L.P.; Liu, H.Y.; Ma, Y.C.; Ding, Y.H.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wu, X.; Finlayson, B.L.; Webber, M.; Wei, T.; Li, M.; Chen, Z. Variability and trend in the hydrology of the Yangtze River, China: Annual precipitation and runoff. J. Hydrol. 2014, 513, 403–412. [Google Scholar] [CrossRef]
- Wang, R.; Chen, J.; Chen, X.; Wang, Y. Variability of precipitation extremes and dryness/wetness over the southeast coastal region of China, 1960–2014. Int. J. Climatol. 2017, 37, 4656–4669. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Processes 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Sen, Z. Partial trend identification by change-point successive average methodology (SAM). J. Hydrol. 2019, 571, 288–299. [Google Scholar] [CrossRef]
- Dong, Z.; Jia, W.; Sarukkalige, R.; Fu, G.; Meng, Q.; Wang, Q. Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China. Water 2020, 12, 3293. [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Flügel, W.-A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 015101. [Google Scholar] [CrossRef]
- You, Q.; Min, J.; Kang, S. Rapid warming in the Tibetan Plateau from observations and CMIP5 models in recent decades. Int. J. Climatol. 2016, 36, 2660–2670. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. A J. R. Meteorol. Soc. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Shrestha, A.B.; Devkota, L.P. Climate Change in the Eastern Himalayas: Observed Trends and Model Projections; International Centre for Integrated Mountain Development (ICIMOD): Kathmandu, Nepal, 2010. [Google Scholar]
- Ren, G. Climate changes of China’s mainland over the past half century. Acta Meteorol. Sin. 2005, 63, 942–955. [Google Scholar]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global increasing trends in annual maximum daily precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef] [Green Version]
- Pingale, S.M.; Khare, D.; Jat, M.K.; Adamowski, J. Spatial and temporal trends of mean and extreme rainfall and temperature for the 33 urban centers of the arid and semi-arid state of Rajasthan, India. Atmos. Res. 2014, 138, 73–90. [Google Scholar] [CrossRef]
- Martinez-Austria, P.F.; Bandala, E.R.; Patiño-Gómez, C. Temperature and heat wave trends in northwest Mexico. Phys. Chem. Earth Parts A/B/C 2016, 91, 20–26. [Google Scholar] [CrossRef]
- Gemmer, M.; Fischer, T.; Jiang, T.; Su, B.; Liu, L.L. Trends in precipitation extremes in the Zhujiang River basin, South China. J. Clim. 2011, 24, 750–761. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Gujree, I.; Wani, I.; Muslim, M.; Farooq, M.; Meraj, G. Evaluating the variability and trends in extreme climate events in the Kashmir Valley using PRECIS RCM simulations. Modeling Earth Syst. Environ. 2017, 3, 1647–1662. [Google Scholar] [CrossRef]
- Shafiq, M.U.; Rasool, R.; Ahmed, P.; Dimri, A. Temperature and precipitation trends in Kashmir Valley, north western Himalayas. Theor. Appl. Climatol. 2019, 135, 293–304. [Google Scholar] [CrossRef]
- Dad, J.M.; Muslim, M.; Rashid, I.; Rashid, I.; Reshi, Z.A. Time series analysis of climate variability and trends in Kashmir Himalaya. Ecol. Indic. 2021, 126, 107690. [Google Scholar] [CrossRef]
- Ahmad, T.; Pandey, A.C.; Kumar, A. Long-term precipitation monitoring and its linkage with flood scenario in changing climate conditions in Kashmir valley. Geocarto Int. 2021, 1–26. [Google Scholar] [CrossRef]
- Zaz, S.N.; Romshoo, S.A.; Krishnamoorthy, R.T.; Viswanadhapalli, Y. Analyses of temperature and precipitation in the Indian Jammu and Kashmir region for the 1980–2016 period: Implications for remote influence and extreme events. Atmos. Chem. Phys. 2019, 19, 15–37. [Google Scholar] [CrossRef] [Green Version]
- Sabzevari, A.A.; Zarenistanak, M.; Tabari, H.; Moghimi, S. Evaluation of precipitation and river discharge variations over southwestern Iran during recent decades. J. Earth Syst. Sci. 2015, 124, 335–352. [Google Scholar] [CrossRef]
- Sen, Z. Trend identification simulation and application. J. Hydrol. Eng. 2014, 19, 635–642. [Google Scholar] [CrossRef]
- Elouissi, A.; Şen, Z.; Habi, M. Algerian rainfall innovative trend analysis and its implications to Macta watershed. Arab. J. Geosci. 2016, 9, 303. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Investigation of trend analysis of monthly total precipitation by an innovative method. Theor. Appl. Climatol. 2015, 120, 617–629. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Kisi, O. Trend analysis of maximum hydrologic drought variables using Mann–Kendall and Şen’s innovative trend method. River Res. Appl. 2017, 33, 597–610. [Google Scholar] [CrossRef]
- Wu, H.; Qian, H. Innovative trend analysis of annual and seasonal rainfall and extreme values in Shaanxi, China, since the 1950s. Int. J. Climatol. 2017, 37, 2582–2592. [Google Scholar] [CrossRef]
- Romshoo, S.; Zaz, S.; Ali, N. Recent Climate Variability in Kashmir Valley, India and its Impact on Streamflows of the Jhelum River. J. Res. Dev. 2018, 17, 1–22. [Google Scholar]
- Zaz, S.N.; Romshoo, S.A. Recent variation in temperature trends in Kashmir Valley (India). J. Himal. Ecol. Sustain. Dev. 2013, 8, 42–63. [Google Scholar]
- Ahsan, S.; Bhat, M.S.; Alam, A.; Ahmed, N.; Farooq, H.; Ahmad, B. Assessment of trends in climatic extremes from observational data in the Kashmir basin, NW Himalaya. Environ. Monit. Assess. 2021, 193, 649. [Google Scholar] [CrossRef]
- Kumar, V.; Jain, S.K. Trends in seasonal and annual rainfall and rainy days in Kashmir Valley in the last century. Quat. Int. 2010, 212, 64–69. [Google Scholar] [CrossRef]
- Romshoo, S.A.; Dar, R.A.; Rashid, I.; Marazi, A.; Ali, N.; Zaz, S.N. Implications of shrinking cryosphere under changing climate on the streamflows in the Lidder catchment in the Upper Indus Basin, India. Arct. Antarct. Alp. Res. 2015, 47, 627–644. [Google Scholar] [CrossRef]
- Bagnouls, F. Bioclimatic Types of South-East Asia; Institute Francais de Pondichery: Pondicherry, India, 1959. [Google Scholar]
- Dar, R.A.; Romshoo, S.A.; Chandra, R.; Ahmad, I. Tectono-geomorphic study of the Karewa Basin of Kashmir Valley. J. Asian Earth Sci. 2014, 92, 143–156. [Google Scholar] [CrossRef]
- Iqbal, M.J.; Ilyas, K. Influence of Icelandic Low pressure on winter precipitation variability over northern part of Indo-Pak Region. Arab. J. Geosci. 2013, 6, 543–548. [Google Scholar] [CrossRef]
- Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the Upper Indus Basin, global teleconnections and hydrological implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Li, P.; Zhao, B.; Xu, R.; Zhao, G.; Sun, W.; Mu, X. Use of double mass curves in hydrologic benefit evaluations. Hydrol. Processes 2017, 31, 4639–4646. [Google Scholar] [CrossRef]
- Ahmad, I.; Zhang, F.; Tayyab, M.; Anjum, M.N.; Zaman, M.; Liu, J.; Saddique, Q. Spatiotemporal analysis of precipitation variability in annual, seasonal and extreme values over upper Indus River basin. Atmos. Res. 2018, 213, 346–360. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of Statistical Analysis in Climate Research. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Douglas, E.; Vogel, R.; Kroll, C. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Sen, Z. Innovative trend analysis methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation trends over time using Mann-Kendall and spearman’s rho tests in swat river basin, Pakistan. Adv. Meteorol. 2015, 2015, 431860. [Google Scholar] [CrossRef] [Green Version]
- Mann, H. Non-Parametric Tests against Trend. Econmetrica J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, K. Thin-film peeling-the elastic term. J. Phys. D Appl. Phys. 1975, 8, 1449. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherlands, 1992; Volume 49. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Ohlson, J.A.; Kim, S. Linear valuation without OLS: The Theil-Sen estimation approach. Rev. Account. Stud. 2015, 20, 395–435. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Processes Int. J. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Jeelani, G.; Deshpande, R. Isotope fingerprinting of precipitation associated with western disturbances and Indian summer monsoons across the Himalayas. J. Earth Syst. Sci. 2017, 126, 108. [Google Scholar] [CrossRef] [Green Version]
- Singh, D.; Sharma, V.; Juyal, V. Observed linear trend in few surface weather elements over the Northwest Himalayas (NWH) during winter season. J. Earth Syst. Sci. 2015, 124, 553–565. [Google Scholar] [CrossRef] [Green Version]
- Meraj, G.; Romshoo, S.A.; Yousuf, A.; Altaf, S.; Altaf, F. Assessing the influence of watershed characteristics on the flood vulnerability of Jhelum basin in Kashmir Himalaya. Nat. Hazards 2015, 77, 153–175. [Google Scholar] [CrossRef]
- Meraj, G.; Farooq, M.; Singh, S.K.; Islam, M.; Kanga, S. Modeling the sediment retention and ecosystem provisioning services in the Kashmir valley, India, Western Himalayas. Modeling Earth Syst. Environ. 2021, 1–26. [Google Scholar] [CrossRef]
- Rather, M.A.; Meraj, G.; Farooq, M.; Shiekh, B.A.; Kumar, P.; Kanga, S.; Singh, S.K.; Sahu, N.; Tiwari, S.P. Identifying the Potential Dam Sites to Avert the Risk of Catastrophic Floods in the Jhelum Basin, Kashmir, NW Himalaya, India. Remote Sens. 2022, 14, 1538. [Google Scholar] [CrossRef]
- Altaf, S.; Meraj, G.; Romshoo, S.A. Morphometry and land cover based multi-criteria analysis for assessing the soil erosion susceptibility of the western Himalayan watershed. Environ. Monit. Assess. 2014, 186, 8391–8412. [Google Scholar] [CrossRef] [PubMed]
- Altaf, F.; Meraj, G.; Romshoo, S.A. Morphometric analysis to infer hydrological behaviour of Lidder watershed, Western Himalaya, India. Geogr. J. 2013, 2013, 178021. [Google Scholar] [CrossRef]
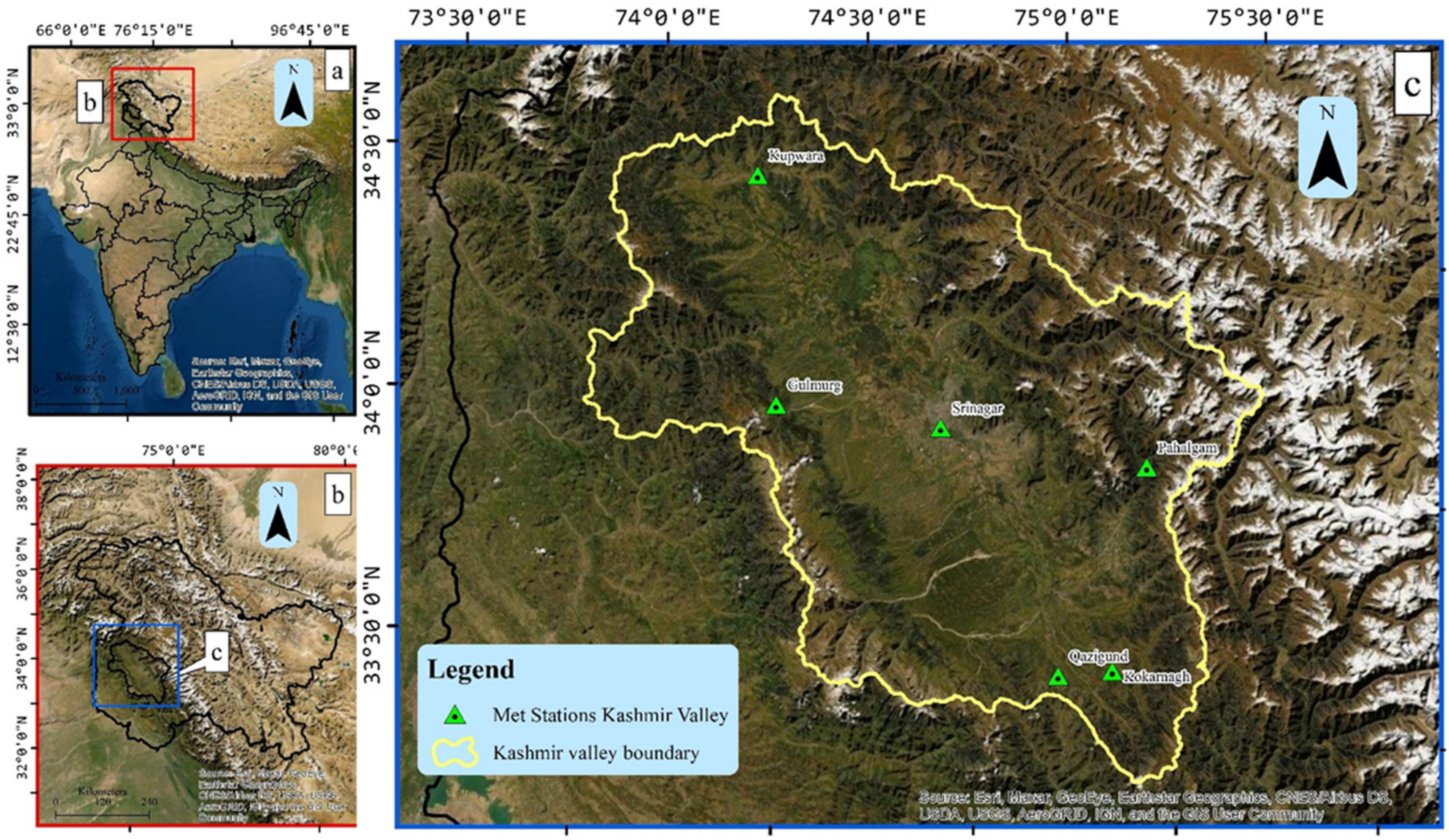


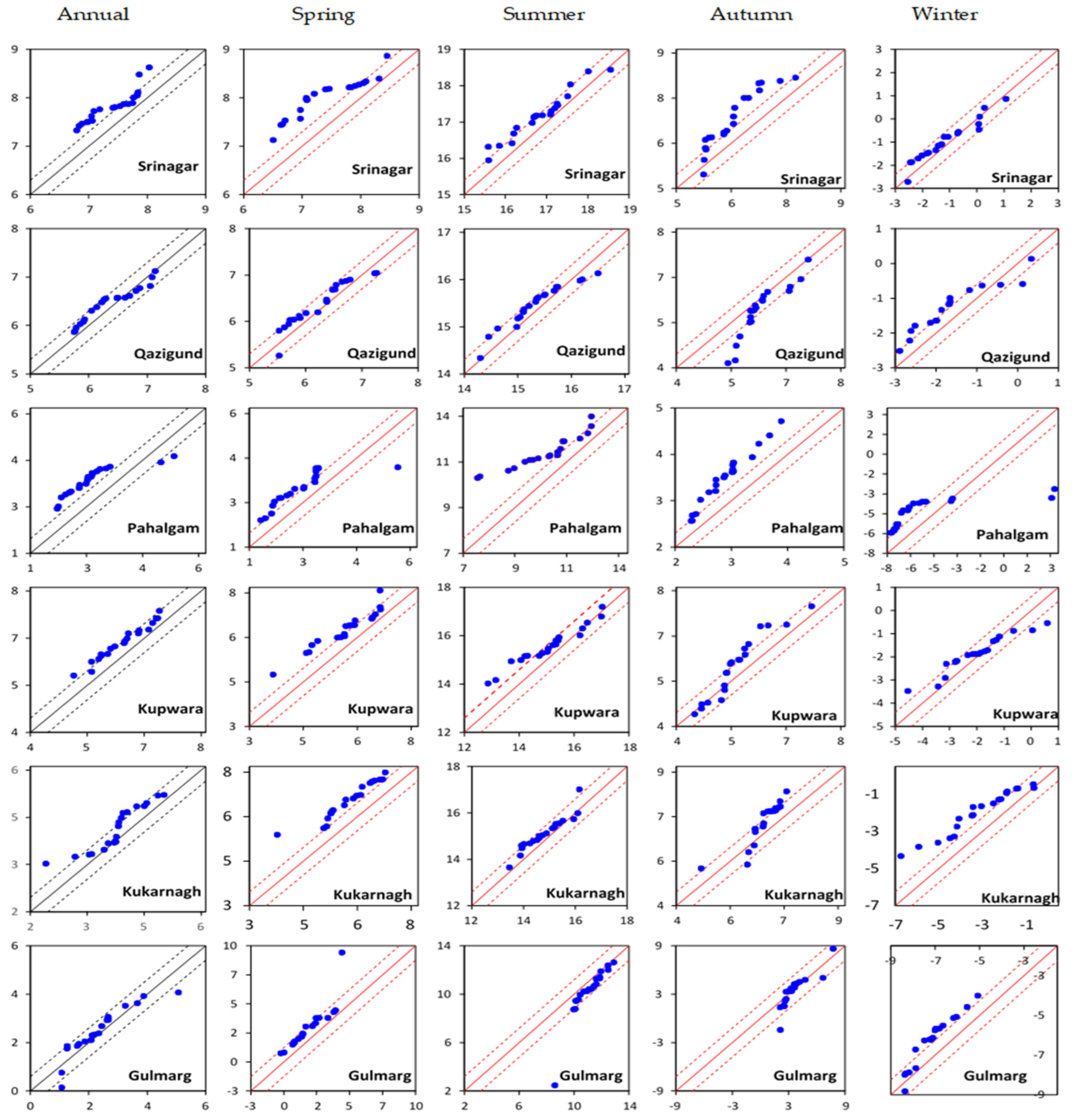

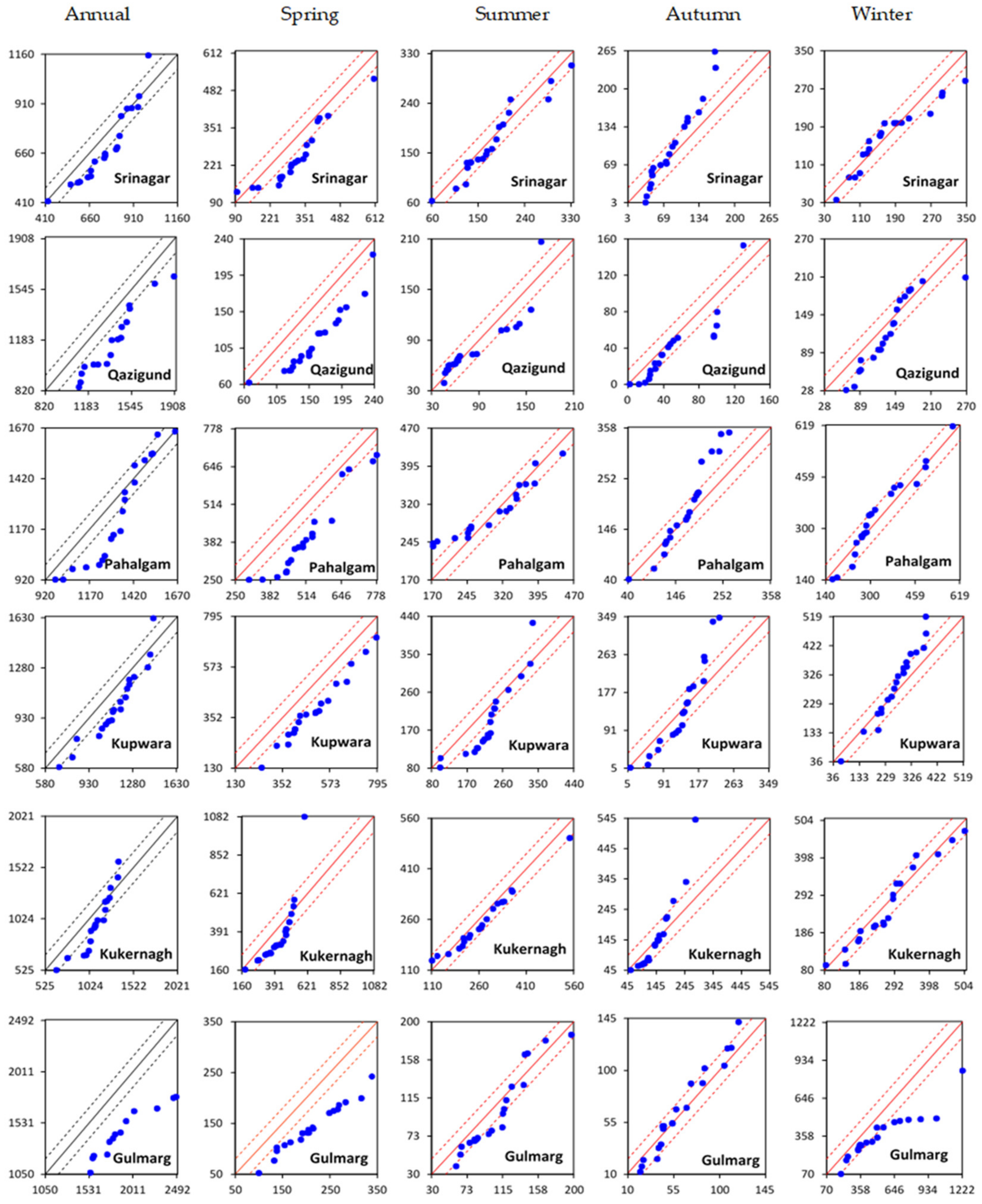
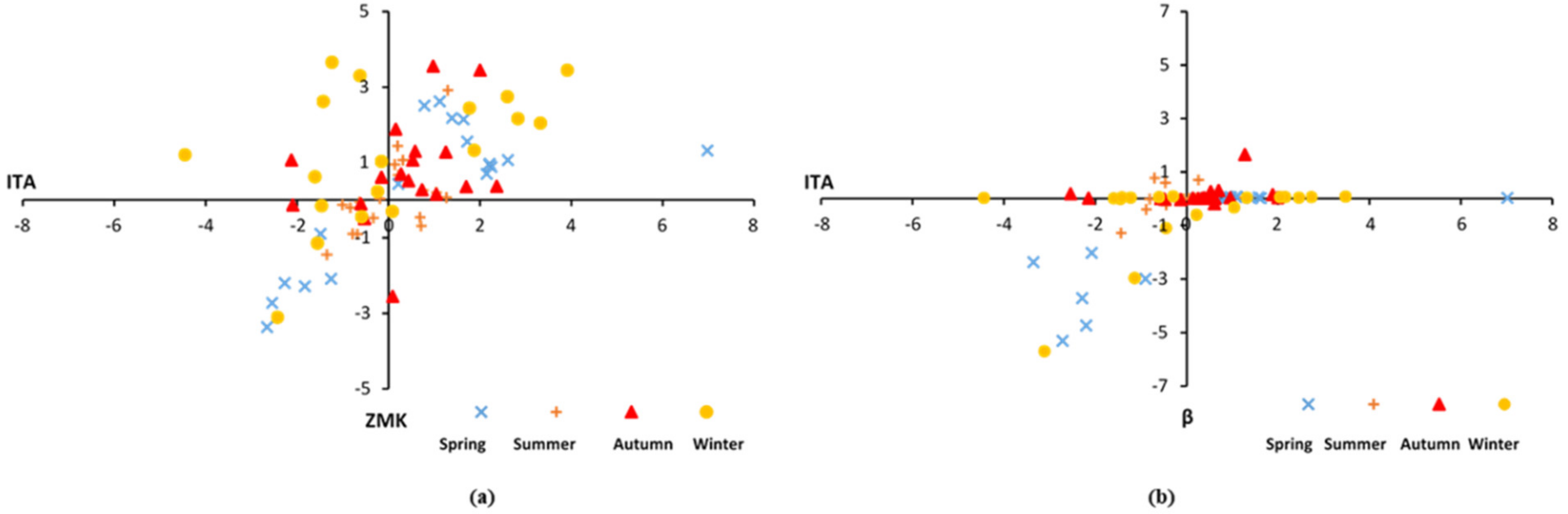
| S.No. | Met Stations | Latitude | Longitude | Resolution | Time Period | Variables |
|---|---|---|---|---|---|---|
| 1 | Srinagar | 34.05 | 74.80 | Monthly | 1980–2019 | Tmax, Tmin, Precp |
| 2 | Gulmarg | 34.06 | 74.39 | Monthly | 1980–2019 | Tmax, Tmin, Precp |
| 3 | Kupwara | 34.53 | 74.27 | Monthly | 1980–2019 | Tmax, Tmin, Precp |
| 4 | Phalgham | 34.02 | 75.33 | Monthly | 1980–2019 | Tmax, Tmin, Precp |
| 5 | Qazigund | 33.60 | 75.17 | Monthly | 1980–2019 | Tmax, Tmin, Precp |
| 6 | Kukarnagh | 33.59 | 75.30 | Monthly | 1980–2019 | Tmax, Tmin, Precp |
| Stations Name | Seasons | Tmax | Tmin | Mean-Temperature | Precipitation |
|---|---|---|---|---|---|
| 1980–2019 | 1980–2019 | 1980–2019 | 1980–2019 | ||
| Srinagar | Annual | 20.0 | 7.6 | 13.8 | 723.8 |
| Spring | 20.1 | 7.7 | 13.9 | 281.0 | |
| Summer | 29.3 | 17.0 | 23.2 | 173.0 | |
| Autumn | 21.7 | 6.7 | 14.2 | 93.0 | |
| Winter | 8.8 | −1.1 | 3.9 | 172.5 | |
| Qazigund | Annual | 19.3 | 6.4 | 12.8 | 1212.7 |
| Spring | 19.4 | 6.3 | 12.8 | 135.9 | |
| Summer | 27.7 | 15.3 | 21.5 | 82.5 | |
| Autumn | 21.4 | 5.8 | 13.6 | 43.8 | |
| Winter | 8.7 | −1.9 | 3.4 | 129.1 | |
| Pahalgam | Annual | 16.6 | 3.1 | 9.8 | 1288.9 |
| Spring | 16.6 | 2.9 | 9.7 | 463.9 | |
| Summer | 25.0 | 11.2 | 18.1 | 300.1 | |
| Autumn | 18.6 | 3.2 | 10.9 | 181.6 | |
| Winter | 6.1 | −4.9 | 0.6 | 332.6 | |
| Kupwara | Annual | 20.1 | 6.3 | 13.2 | 1081.2 |
| Spring | 19.8 | 6.2 | 13.0 | 442.4 | |
| Summer | 29.5 | 15.3 | 22.4 | 207.7 | |
| Autumn | 22.5 | 5.6 | 14.1 | 138.9 | |
| Winter | 8.6 | −1.9 | 3.3 | 281.4 | |
| Kukarnagh | Annual | 18.1 | 4.1 | 11.1 | 1080.2 |
| Spring | 18.4 | 6.4 | 12.4 | 394.3 | |
| Summer | 27.0 | 14.9 | 21.0 | 259.3 | |
| Autumn | 19.9 | 6.8 | 13.3 | 151.2 | |
| Winter | 7.1 | −2.1 | 2.5 | 267.7 | |
| Gulmarg | Annual | 11.7 | 2.4 | 7.0 | 1485.1 |
| Spring | 10.8 | 1.9 | 6.4 | 176.3 | |
| Summer | 20.0 | 10.7 | 15.3 | 104.3 | |
| Autumn | 13.2 | 3.1 | 8.2 | 63.3 | |
| Winter | 2.6 | −6.0 | −1.7 | 439.6 |
| S.No. | Station Name | Annual | Spring | Summer | Autumn | Winter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ||
| 1 | Srinagar | 0.57 | 2.92 ** | 0.04 | 0.88 | 2.23 * | 0.05 | 0.04 | −0.20 | 0.00 | 0.37 | 2.34 * | 0.04 | 2.17 | 2.81 ** | 0.06 |
| 2 | Qazigund | 0.22 | 1.13 | 0.01 | 0.70 | 2.16 * | 0.04 | −0.06 | −0.62 | 0.00 | −0.13 | −2.11 * | −0.03 | 1.32 | 1.85 + | 0.04 |
| 3 | Pahalgam | 0.56 | 2.80 ** | 0.04 | 0.94 | 2.21 * | 0.05 | −0.13 | −1.00 | −0.01 | 0.36 | 1.68 + | 0.03 | 3.45 | 3.93 *** | 0.08 |
| 4 | Kupwara | 0.58 | 3.18 ** | 0.04 | 1.06 | 2.62 ** | 0.07 | 0.20 | 1.06 | 0.02 | 0.15 | 1.06 | 0.02 | 2.04 | 3.30 *** | 0.06 |
| 5 | Kukarnagh | 0.60 | 2.57 * | 0.04 | 0.96 | 2.20 * | 0.06 | 0.07 | 1.25 | 0.01 | 0.27 | 0.73 | 0.01 | 2.75 | 2.57 * | 0.06 |
| 6 | Gulmarg | 0.25 | 0.85 | 0.01 | 1.55 | 1.71 + | 0.05 | −0.20 | −0.83 | −0.02 | −0.50 | −0.52 | −0.01 | 2.44 | 1.78 + | 0.04 |
| S.No. | Station Name | Annual | Spring | Summer | Autumn | Winter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ||
| 1 | Srinagar | 0.58 | 2.83 ** | 0.02 | 0.80 | 2.50 * | 0.02 | 0.20 | 1.43 | 0.01 | 0.96 | 3.55 *** | 0.04 | −1.47 | −0.15 | 0.00 |
| 2 | Qazigund | 0.14 | 0.85 *** | 0.00 | 0.21 | 0.43 | 0.00 | 0.11 | 0.94 | 0.01 | −0.59 | −0.10 | 0.00 | −1.61 | 0.62 | 0.01 |
| 3 | Pahalgam | 2.72 | 3.66 ** | 0.04 | 1.62 | 2.14 * | 0.03 | 1.27 | 2.91 ** | 0.05 | 2.01 | 3.45 *** | 0.03 | −1.23 | 2.18 * | 0.04 |
| 4 | Kupwara | 0.62 | 1.27 | 0.04 | 1.10 | 1.62 | 0.07 | 0.31 | 0.97 | 0.02 | 0.53 | 1.06 | 0.02 | −0.63 | −0.48 | 0.06 |
| 5 | Kukarnagh | 0.77 | 2.27 | 0.02 | 1.41 | 2.18 * | 0.03 | 0.21 | 0.66 | 0.01 | 0.60 | 1.29 | 0.01 | −4.44 | 1.20 | 0.03 |
| 6 | Gulmarg | 0.40 | 0.97 | 0.01 | 7.00 | 1.32 | 0.03 | −0.81 | −0.90 | −0.02 | −2.14 | 1.06 | 0.02 | −1.45 | 2.62 ** | 0.05 |
| S.No. | Station Name | Annual | Spring | Summer | Autumn | Winter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ITA | Zmk | Sen Slope (β) | ||
| 1 | Srinagar | −0.78 | −0.36 | −1.08 | −2.09 | −1.27 | −2.02 | −0.48 | −0.34 | −0.22 | 1.88 | 0.15 | 0.15 | −0.30 | 0.08 | 0.09 |
| 2 | Qazigund | −1.64 | −1.18 | −5.59 | −2.72 | −2.53 * | −5.31 | −0.46 | 0.66 | 0.60 | −2.55 | 0.10 | 0.18 | −1.14 | −1.55 | −2.96 |
| 3 | Pahalgam | −0.61 | −0.42 | −1.29 | −2.20 | −2.28 * | −4.73 | 0.26 | 0.77 | 0.70 | 1.27 | 1.26 | 1.65 | 0.23 | −0.26 | −0.60 |
| 4 | Kupwara | −1.03 | −1.57 | −5.57 | −2.28 | −1.85 + | −3.71 | −1.45 | −1.35 | −1.28 | 0.61 | −0.17 | −0.19 | 1.03 | −0.17 | −0.32 |
| 5 | Kukarnagh | −0.58 | −0.20 | −0.68 | −0.90 | −1.50 | −2.99 | −0.68 | 0.70 | 0.77 | 0.69 | 0.27 | 0.31 | −0.44 | −0.61 | −1.09 |
| 6 | Gulmarg | −2.42 | −2.34 * | −12.30 | −3.36 | −2.64 ** | −2.37 | −0.90 | −0.69 | −0.40 | 0.51 | 0.45 | 0.27 | −3.10 | −2.41 * | −5.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gujree, I.; Ahmad, I.; Zhang, F.; Arshad, A. Innovative Trend Analysis of High-Altitude Climatology of Kashmir Valley, North-West Himalayas. Atmosphere 2022, 13, 764. https://doi.org/10.3390/atmos13050764
Gujree I, Ahmad I, Zhang F, Arshad A. Innovative Trend Analysis of High-Altitude Climatology of Kashmir Valley, North-West Himalayas. Atmosphere. 2022; 13(5):764. https://doi.org/10.3390/atmos13050764
Chicago/Turabian StyleGujree, Ishfaq, Ijaz Ahmad, Fan Zhang, and Arfan Arshad. 2022. "Innovative Trend Analysis of High-Altitude Climatology of Kashmir Valley, North-West Himalayas" Atmosphere 13, no. 5: 764. https://doi.org/10.3390/atmos13050764
APA StyleGujree, I., Ahmad, I., Zhang, F., & Arshad, A. (2022). Innovative Trend Analysis of High-Altitude Climatology of Kashmir Valley, North-West Himalayas. Atmosphere, 13(5), 764. https://doi.org/10.3390/atmos13050764









