Abstract
Precipitation, as an important part of the hydrological cycle, is often related to flood and drought. In this study, we collected daily rainfall data from 21 rainfall stations in Shaanxi Province from 1961 to 2017, and calculated eight extreme climate indices. Annual and seasonal concentration indices (CI) were also calculated. The trends in the changes in precipitation were calculated using the M–K test and Sen’s slope. The results show that the precipitation correlation index and CI (concentration index) in Shaanxi Province are higher in the south and lower in the north. For the annual scale, the CI value ranges from 0.6369 to 0.6820, indicating that Shaanxi Province has a high precipitation concentration and an uneven distribution of annual precipitation. The eight extreme precipitation indices of most rainfall stations showed a downward trend during the study period, and more than half of the stations passed the 0.05 confidence interval test. Among them, the Z value of PRCPTOT (annual total precipitation in wet days) at Huashan station reached −6.5270. The lowest slope of PRCPTOT reached −14.3395. This shows that annual rainfall in Shaanxi Province has been decreasing in recent decades. These findings could be used to make decisions about water resources and drought risk management in Shaanxi Province, China.
1. Introduction
The hydrological cycle in many watersheds and regions of the world is undergoing major changes due to climate change and the intensification of human activities [1,2,3]. The probability of extreme precipitation events has increased in the context of climate change, and they usually lead to catastrophic flash floods, soil erosion [4,5] and threaten water balances [6]. Because of its impact on natural ecosystems, social economies, human settlements, and agricultural production, changes in extreme precipitation have attracted increasing attention from many fields such as agriculture, disaster prevention, environmental policy and water resources management, which has resulted in a growing amount of research on related issues [7,8,9,10,11]. In recent years, many researchers have analyzed precipitation changes at different spatial scales, and most studies have found that extreme precipitation events have increased [12,13,14,15,16]. According to certain research, the percentage of severe precipitation in regard to total yearly precipitation is rising [17,18].
Globally, with every one degree increase in temperature, average precipitation is predicted to rise by two to three percent, because it is mainly a process with limited energy [19]. The frequency of extreme precipitation events will increase due to the combined effect of thermodynamics and storm dynamics, with temperatures increasing by 7% or more for every degree increase [20,21,22,23].
At the intercontinental and international level, the northwest of Mexico, Australia, the arid and semi-arid regions of Asia, Paraguay, the subtropical Argentina, the Arctic, the Northeast Pacific, the northern half of Europe, Brazil, and the source of intermediate water between North America and Antarctica, have shown an increase in annual precipitation. In temperate Asia, northern Asia, the Southwest Pacific, southern Europe and tropical Africa, the annual precipitation has been found to show a decreasing trend [24]. In addition, annual precipitation in tropical areas such as Japan and Colombia has no significant trends [4,25].
The mainland of China has an obvious continental monsoon climate with diverse landforms and climatic characteristics. The climate of China is greatly influenced by the East Asian monsoon [26]. Of course, large-scale atmospheric circulations, such as the Indian Ocean Dipole (IOD), El Niño Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), and the Pacific Decadal Oscillation (PDO) also have an impact on China’s climate. Seasons, inter-years, and decadals all demonstrate non-stationary patterns in regard to precipitation [27,28,29]. Therefore, for decision makers to create disaster reduction measures, a comprehensive study on variations in severe precipitation in different areas of China and the factors that affect these variations is critical [30,31,32]. Gu et al. [33] used daily monitoring data from 728 weather stations in China to calculate and evaluate the changes in extreme precipitation. Guo et al. [12] analyzed precipitation concentration at 780 rainfall stations in China from 1961 to 2016, and its potential association with drought. The results showed that the annual drought trend is decreasing. Shi et al. [34] discussed the precipitation trends and temporal and spatial periodic changes at 31 stations in the Lancang River Basin during 1960–2010. Hsu et al. [35] analyzed the impact of boreal summer intra-seasonal oscillations on extreme precipitation events in Southern China. Song et al. [36] investigated the non-stationarity of severe precipitation occurrences using daily precipitation data from the Beijing–Tianjin–Hebei (BTH) area of China. There are regional disparities in the frequency and severity of severe precipitation due to variances in climatic and geographical factors in different parts of China [37].
Researchers have done a great deal of research on extreme precipitation, but there is little data on the number of days it rains or the concentration of the precipitation. As a result, various precipitation concentration indices have arisen [9]. Among them, the concentration index (CI) [38] can be used to examine precipitation concentrations on a daily scale. Trend analysis is a key method for forecasting future extreme precipitation [39]. The M–K test is one of the most popular trend test methods and has been widely used around the world [40]. For example, Longobardi et al. conducted an M–K test on the non-perennial and annual rainfall data in the Mediterranean area [41]. Vishwakarma et al. used the M–K method to provide the trends in rainfall and temperature at different time scales in the Sagar District, India [42].
Rainfall in China shows significant regional variations due to complex atmospheric circulation and topography. In fact, the proxy data used in previous studies primarily reflect the moisture variability in the warm season. Generally, the North–South mode coupled with the West–East mode represents a warm season tripolar hydroclimatic pattern in China with three centers located in the arid region (Xinjiang), semi-arid region (North China), and humid region (South China) during the last millennium [43]. Shaanxi Province is in the transition zone between the semi-aridzone and humid zone. There are great spatial differences in climate in Shaanxi Province [44]. Research on extreme precipitation events in Shaanxi Province could provide a reference for a response to climate change and the formulation of disaster prevention and mitigation plans in the province. Therefore, the objectives of this study were: (i) to use the daily precipitation dataset for Shaanxi Province from 1961 to 2017 to examine the temporal and geographic properties of the precipitation indices; (ii) to use the concentration index (CI) to analyze the uneven temporal distribution of precipitation and the link between precipitation concentration and precipitation structure, and (iii) to study the trends in the precipitation CI by using the Mann–Kendall trend test and Sen’s slope. Figure 1 presents the flowchart of the methodology.
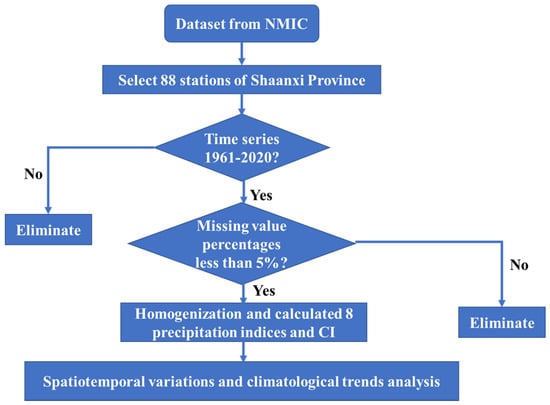
Figure 1.
Flowchart of the methodology.
2. Materials and Methods
2.1. Study Area
Shaanxi Province (105°29′–111°15′ E, 31°42′–39°35′ N) is located in northwestern China (Figure 2). Shaanxi Province is landlocked and is surrounded by eight provinces, the largest number of neighboring provinces in China. Its advantage is that it connects the east with the west. The topography of Shaanxi is generally high in the north and south and low in the centre. The average elevation of Shaanxi Province is 1127 m; the highest average elevation of each city in Shaanxi is Baoji City at a height of 1351 m, and the city with the lowest average elevation is Weinan City at a height of 675 m. Shaanxi is divided into three natural zones by the Beishan and Qinling Mountains: the Northern Shaanxi Plateau in the north, the Guanzhong Plain in the center, and the Qinba Mountains in the south.
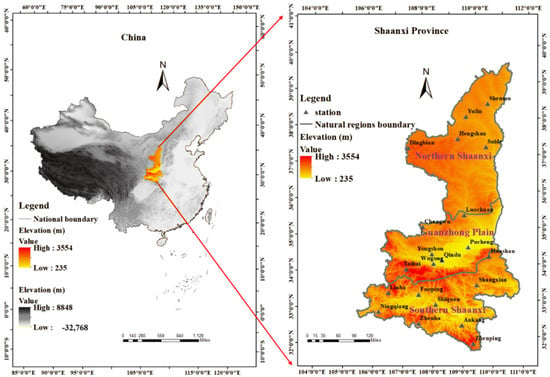
Figure 2.
Study area and stations.
2.2. Data
The National Meteorological Information Center (http://data.cma.cn/) provided the total daily rainfall data (accessed on 1 March 2022) for 21 stations (Table 1) in Shaanxi Province from 1961 to 2017. Quality checks and controls were carried out before the data release. Less than 5% of the selected data series was missing.

Table 1.
Stations’ name and coordinates.
2.3. Homogenization of Data
Inhomogeneity in a precipitation time series might be a long-term trend or an abrupt change [45]. When researching climate change, a homogeneous time series is required to eliminate the effects of nonclimatic elements such as changes in observation locations, timing, and instruments [46].
To assess the homogeneity of data, the RHtests dlyPrcp software package was utilized [47]. The RHtests dlyPrcp software program [48] is comparable to the RHtestsV3 and RHtestsV4 tools, but it is tailored to homogenize daily precipitation data time series [49,50,51]. Only two stations detected significant changepoints at 0.05 significant level. Each precipitation series with significant changepoints was then adjusted to the most recent segment of the data series using RHtests dlyPrcp’s mean-adjustments [52]. Finally, we obtained the homogenized daily precipitation time series at each of the two locations.
2.4. Methods
2.4.1. Extreme Precipitation Indices
The five extreme precipitation indicators (Table 2) employed in this study were chosen from ETCCDI’s (http://cccma.seos.uvic.ca/ETCCDMI) 27 core extreme indicators (accessed on 20 March 2021) [53], which were established based on daily temperature and precipitation data [33,54]. In addition, R25 and R50 were also applied in this study. Rain events with daily rainfall of more than 25 mm are called heavy rains and an event with a daily rainfall of more than 50 mm is called a rainstorm; therefore, we think they can represent extreme rainfall characteristics to some extent. Wet days (annual count of days when RR ≥ 1 mm) were also used in this study.

Table 2.
Definitions of the 8 selected extreme precipitation indices.
2.4.2. Concentration Index (CI)
The concentration index (CI) is an index representing the contribution of high intensity daily precipitation to annual total precipitation. The specific calculation steps are as follows. First of all, the dry and wet days are distinguished within the limit of 1 mm/d; Second, the new precipitation sequence is reordered from small to large. Then, the following formulas are used to calculate Xj and Yj.
where n is the accumulated number of wet days, P is accumulated precipitation; N is the total number of wet days; Xj is the percentage of accumulated wet days to annual total precipitation days; Yj is the percentage of accumulated precipitation to annual total precipitation.
Finally, the Lorentz curve is drawn on the Cartesian coordinate system with Xj as the horizontal axis and Yj as the vertical axis. The calculation formula for CI is as follows:
where A is the area of the graph enclosed by the Lorentz curve and the X-axis and Y = 1. For more details, please refer to previous studies [14,55].
2.4.3. Trend Test Methods
Because it is less sensitive to outliers than parameter statistics and does not need normality or linear assumptions, the M–K test [56] is commonly employed in the assessment of hydrometeorological time series. The calculation of the Mann–Kendall test is as follows:
where e is the number of tied groups and ti is the number of data values in the ith group.
The statistical S test is as follows:
where
The statistical value S and variance value Var(S) are used to perform the normal approximation Z test. The formula is as follows:
The absolute value of Z indicates the significance of the sequence trend. A Z value of plus or minus indicates an upward or downward trend.
2.4.4. Spatial Interpolation
Since it is a superior unbiased linear estimator with little spatial variation, the kriging technique was chosen to do the spatial interpolation of local data [57]. The generic kriging was employed in this study as previous research has demonstrated no substantial difference between the most advanced geostatistics and the most basic kriging approach, with good overall results in all circumstances [57,58,59].
3. Result
3.1. Spatial Analysis of Precipitation Indices
Figure 3 depicts the kriging interpolated distribution of eight precipitation indices in Shaanxi Province from 1961 to 2017. In Shaanxi Province, all eight index values exhibit a declining geographical distribution tendency from south to north. This means that among the three regions in Shaanxi Province, the eight index values are the largest in Qinba Mountains, the second largest are in Guanzhong and the smallest in Northern Shaanxi Plateau. The lowest values of the five indices were observed in the Northern Shaanxi Plateau in the state of Dingbian, with 364 mm of PRCPTOT, 66 wet days, 2.1 days of R25, 0.5 day of R50, 5.5 mm/day of SDII, 4.14 days of CWD, 39.7 mm of Rx1day, 52.3 mm of Rx3day. While the maximum value of wet days and rx3day occurred at Ningqiang station, the maximum value of all other indicators appeared in Zhenba station, ofwhich PRCPTOT was 1311 mm, R25 was 12.5 days, R50 was 5.26 days, SDII was 9.4 mm/day, CWD was 7.57 days, Rx1day was 87.06 mm and Rx3day was 181.41 mm.
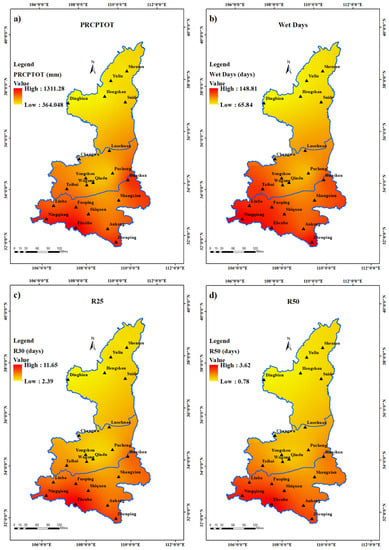
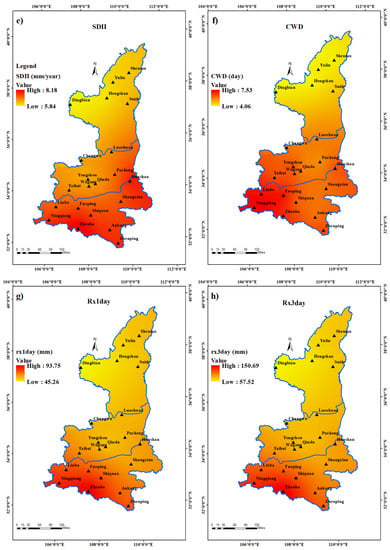
Figure 3.
Spatial distribution of (a) PRCPTOT, (b) wet days, (c) R25, (d) R50 and (e) SDII, (f) CWD, (g) Rx1day, (h) Rx3day.
The spatial differences in the precipitation index may be caused by the differences in latitude, climate, geography and geomorphology of the three regions in Shaanxi Province. The distribution of yearly precipitation is more concentrated in the south and less concentrated in the north, which is heavily influenced by mountain terrain. The Qinling Mountains restrict humid air from the south, resulting in less precipitation in the Guanzhong Plain and northern Shaanxi Plateau. The Qinba Mountains area, which is south of the Qinling Mountains is not affected by this. What is more, the humidity that reaches the southern foot of the Qinling Mountains under the influence of the monsoon is lifted by the terrain due to the movement of the air. The water vapor in the air cools down with the elevation to form precipitation, making the precipitation in Qinba Mountains higher than Northern Shaanxi Plateau and Guanzhong Plain.
The values of the eight indices at the 21 stations at the annual level are shown in Figure 4. The extreme maximum value of PRCPTOT (Figure 4a) was observed at Huashan station as 2678 mm in the year of 1973 and the lowest value was observed at Shenmu station in 1965, with 215.2 mm. The highest values for wet days (Figure 4b), R25 (Figure 4c) and R50 (Figure 4d) were observed at Ningqiang station, with values of 205 days in 1964, and 20 days and 14 days in 1981, respectively. The lowest number of wet days (Figure 4b) was 42 days at Yulin station in 1995. The minimum and maximum values of SDII (Figure 4e) were observed at Shenmu and Huashan stations and were 1.84 mm/day in 1965 and 24.3 mm/day in 1973, respectively. The minimum and maximum values of CWD (Figure 4f) appeared in Suide (2 days) and Liuba (18 days), for Rx1day (Figure 4g) they appeared in Shenmu (15 mm) and Zhenba (253.3 mm), and for Rx3day (Figure 4h) they appeared in Dingbian (19.6 mm) and Zhenba (388.6 mm), respectively.
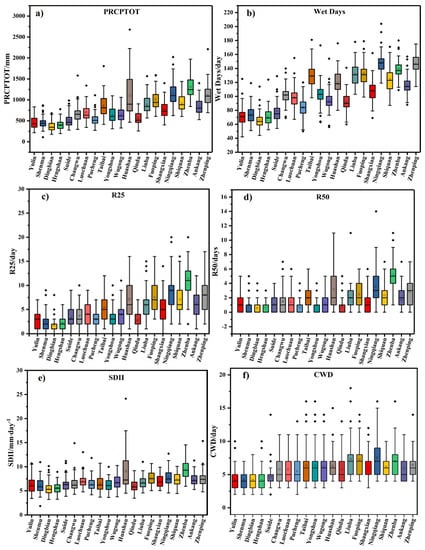
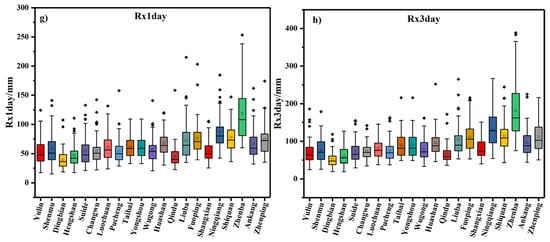
Figure 4.
The values of (a) PRCPTOT, (b) wet days, (c) R25, (d) R50 and (e) SDII, (f) CWD, (g) Rx1day, (h) Rx3day at the 21 stations at the annual level.
In the three regions, the degree of dispersion of the eight indices was highest in Southern Shaanxi, second in the Guanzhong Plain, and lowest in the Northern Shaanxi Plateau. The highest dispersion of PRCPTOT (Figure 4a), wet days (Figure 4b) and SDII (Figure 4e) occurred at Huashan Station, while the highest dispersion of R25 (Figure 4c) and R50 (Figure 4d) occurred at Ningqiang Station. It is worth noting that both Huashan Station and Ningqiang Station are located in the Qinba Mountains.
3.2. Trend Analysis of Extreme Rainfall Indices
The trends in the eight extreme precipitation indices from 1961 to 2017 are depicted in Figure 5. During the research period, the five extreme precipitation indices of the three natural areas in Shaanxi Province showed a fluctuating, decreasing tendency. However, CWD, Rx1day and Rx3day are on the rise. In addition, the five precipitation indices are largest in Southern Shaanxi, followed by Guanzhong, and smallest in Northern Shaanxi.
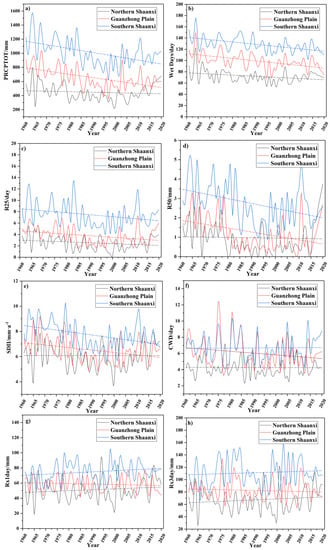
Figure 5.
Extreme precipitation index curves for three natural regions from 1961 to 2020: (a) PRCPTOT, (b) wet days, (c) R25, (d) R50 and (e) SDII, (f) CWD, (g) Rx1day, (h) Rx3day.
Table 3 shows the changepoints in PRCPTOT from 1961 to 2017. It can be seen that most of the transformation took place in the 1960s and 1970s.

Table 3.
Changepoints of PRCPTOT obtained by M–K test.
Figure 6 and Table 4 show the Mann–Kendall trend test distribution of eight precipitation indicators from 1961 to 2017. It can be seen from the figure that the spatial distribution of the eight precipitation indices over 57 years are roughly the same. In the northern Shaanxi and Guanzhong regions, six indices (except for Rx1day and Rx3day) show different degrees of decrease. Only a few locations in southern Shaanxi demonstrated an upward trend.
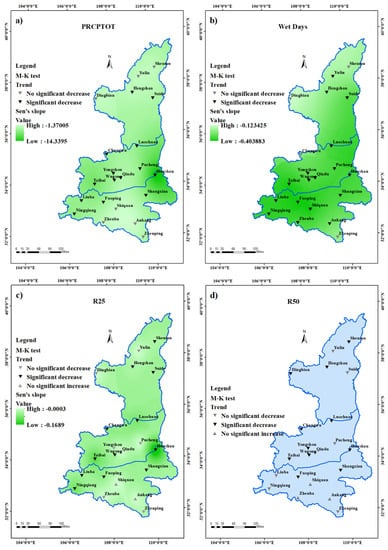
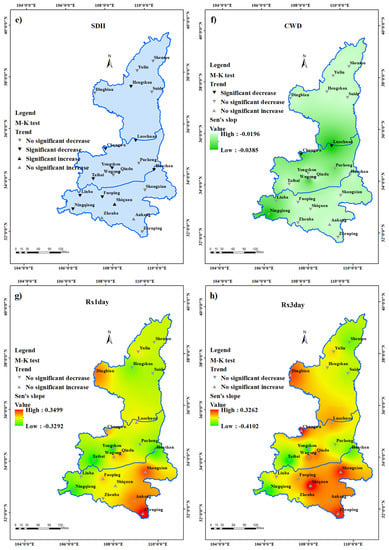
Figure 6.
Mann–Kendall trend test and Sen’s slope distribution of (a) PRCPTOT, (b) wet days, (c) R25, (d) R50 and (e) SDII, (f) CWD, (g) Rx1day, (h) Rx3day. (Note: Since the Sen’s slope value of R50 and SDII is extremely small, with the absolute value fluctuating around 0.01, kriging interpolation is not able to show their differences, thus the slope results of these two indices were not evaluated).

Table 4.
Z value of precipitation-related indices.
PRCPTOT (Figure 6a) and wet days (Figure 6b) decreased significantly at all stations in the Guanzhong region. In the southern part of northern Shaanxi and the northern part of southern Shaanxi, PRCPTOT (Figure 6a) and wet days (Figure 6b) showed a substantial decreasing trend. Regarding R25 (Figure 6c), except for the two stations (Shi Quan, An Kang) in southern Shaanxi that showed a non-significant increasing trend, all other sites showed a decreasing trend. R50 (Figure 6d) shows basically the same trend as R25, with three stations (Zhenba, Shiquan, Ankang) showing an increasing trend, and other stations showing a decreasing trend. The trend in the SDII (Figure 6e) varies greatly among the stations. The SDII of Hengshan Station in northern Shaanxi exhibited a substantial decline, whereas other stations showed a non-significant decreasing trend. The SDII of three stations in Guanzhong exhibited a non-significant decreasing trend, while four stations showed a significant downward trend. In the nine stations in southern Shaanxi, four kinds of trend appeared. Among them, four stations (Liuba, Fuoping, Huashan, Ningqiang) showed a significant declining trend, two stations (Shangxian, Zhenping) showed a non-significant declining trend, two stations (Ankang, Zhenba) showed a non-significant rising trend, and one station (Shiquan) showed a significant rising trend. The CWD of all stations showed a downward trend, but only Changwu and Luochuan showed a significant decline. Rx1day and Rx3day have different trends at different stations, but neither showed a significant trend.
3.3. Temporal and Spatial Distribution of Precipitation Concentration Index
Figure 7 displays the regional distribution of Shaanxi Province’s average CI value from 1961 to 2017. The maximum CI was found in the south (Zhenba station) and the minimum CI appears in the north (around Dingbian station) whether it is the annual CI or the CI for each season. For seasonal CI, the spring CI at the annual scale (Figure 7a), ranges between 0.4634 and 0.6251, the summer CI (Figure 7b) is between 0.5805 and 0.6461, the autumn CI (Figure 7c) is between 0.5099 and 0.6301, and the winter CI (Figure 7d) ranges between 0.2103 and 0.5465. At the annual scale (Figure 7e), the CI value ranges between 0.6364–0.6824. The biggest difference between the North and South occurs in the winter CI (Figure 7d). The winter CI of five stations located in northern Shaanxi is 0.2104–0.2601, while the winter CI of the other 16 stations located in southern Shaanxi and Guanzhong ranges from 0.3459 to 0.5461. The Northern Shaanxi Plateau is a typically arid area where annual precipitation is low, the precipitation is mostly concentrated in the summer, and it is dry in winter. Therefore, the winter CI value in northern Shaanxi is lower than that in Guanzhong and the southern part of Shanxi Province.
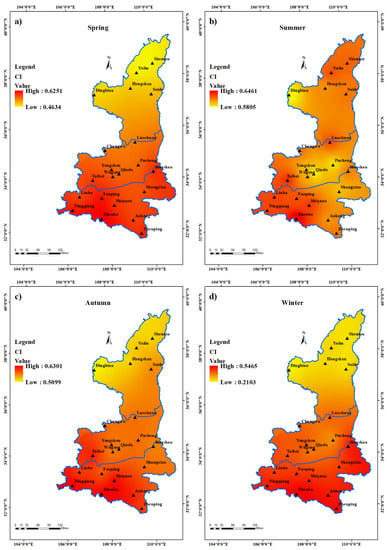
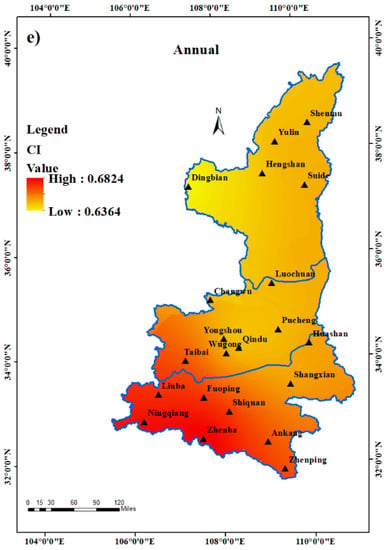
Figure 7.
The spatial distribution of the average CI value of (a) spring, (b) summer, (c) autumn, (d) winter and (e) annually from 1961 to 2020.
The yearly CI trend (Figure 8e) at five stations revealed a significant downward trend, whereas the trend at nine stations was non-significant. The other seven stations exhibited an upward trend that was not statistically significant (Figure 8e). Figure 8e also demonstrates that the Sen’s slope in Shaanxi Province ranges from −0.0011 to 0.0005, with the geographical distribution of the yearly Sen’s slope values indicating that the north is small and the south is big.
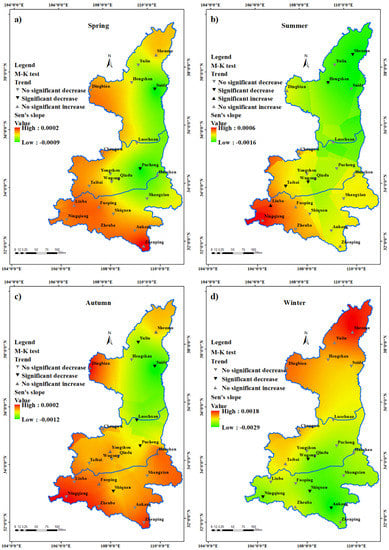
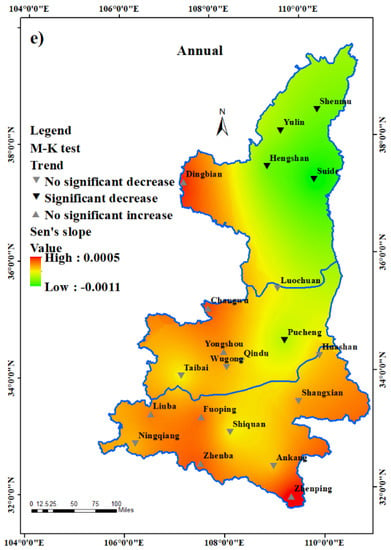
Figure 8.
The CI trend in (a) spring, (b) summer, (c) autumn, (d) winter and (e) annually in Shanxi Province.
In various seasons, the geographical distribution of Sen’s slope values exhibits significant changes. In particular, in summer (Figure 8b) and winter (Figure 8d), they show an almost completely opposite spatial distribution. In summer (Figure 8b), the Sen’s slope is higher in the south of the province and lower in the north. In winter (Figure 8d), it is lower in the south and higher in the north. The Sen’s slope in spring (Figure 8a) and autumn (Figure 8c) showed relatively similar spatial distribution characteristics, with the highest in the south, the second in the north, and the lowest in the middle.
The M–K trend test of the four seasons showed roughly the same spatial distribution as the Sen’s slope. Stations with a significant decrease in CI basically appeared in places with low Sen’s slope values. The spring CI (Figure 8a) of two stations showed a significant reduction, 14 stations demonstrated a non-significant decrease, and five sites demonstrated a non-significant upward trend. In terms of the summer CI (Figure 8b), four stations exhibited a significant reduction, 11 stations showed no statistically significant decrease, and six stations showed no significant increasing trend. The CI of five stations showed a significant reduction in the autumn (Figure 8c), 11 stations exhibited a non-significant decreasing, and five stations displayed a non-significant upward trend. In the winter, the CI at four sites demonstrated a highly substantial decline, eleven showed a non-significant decline, and six showed a non-significant increasing trend. Table 5 displays the CI Z values for each station.

Table 5.
Z value of CI.
4. Discussion
In Shaanxi Province, the geographical distribution of precipitation and precipitation-related indicators is characterized by a high in the south and a low in the north. This is consistent with other research in China [60,61,62,63,64,65]. Many scholars have studied the climate change in Shaanxi Province. Some researchers have looked at changes in drought indices and found that under climate change conditions, the drought severity increases with the decline in precipitation and higher water demand as a result of the temperature increase [60]. Zhang et al. [66] combined with hourly precipitation data from automatic stations and deformation satellite data from the climate Prediction Center from 2008 to 2015, the diurnal variation and difference in precipitation and precipitation frequency in southern Shaanxi and northern Shaanxi were analyzed. The results showed that the frequency and amount of rainfall showed a decreasing trend from south to north, and the zonal variation under topography was the most important feature.In our study, we calculated 8 precipitation indices and CI. PRCPTOT and wet days both exhibited a downward trend in Shaanxi Province over the research period. However, SDII has shown an increasing trend in some stations in the south of Shaanxi Province, such as the Shiquan station, which has shown a significant increasing trend. The R30 and R50 at more than half of the stations indicated a substantial downward trend. In summary, the precipitation-related indices for most of the stations in Shaanxi Province show a downward trend. This is consistent with previous research [67]. The reduction in precipitation in the basin will seriously affect the ecosystem and hydrological cycle. Specifically, changes in precipitation will cause changes in runoff and affect the recharge rate of groundwater, power generation in hydropower stations, thus affecting the water supply system. On the agriculture demand side, insufficient soil moisture caused by low precipitation may threaten both paddy fields and dry land. Ultimately, the natural and social processes of the entire Shaanxi Province will be influenced by the temporal and geographical distribution of precipitation [68,69].
Annual and seasonal CI spatial distributions exhibited the same features as PRCPTOT. However, the trend of annual CI and PRCPTOT shows a positive correlation at 14 stations, and a negative correlation at 7 stations. As pointed out by Li et al. [30], the positive trend in PRCPTOT and CI may increase the flood risk, because a large amount of precipitation and a high concentration index indicate that heavy rainfall is possible. On the contrary, low PRCPTOT and high CI indicate that more dry periods can be observed.
Understanding how ENSO influences the full course of the seasonal rainfall in East Asia is just as essential as concentrating on the wettest season [65]. The rainband in East Asia exhibits a considerable meridional excursion with the season [26,70]. Given the significant yearly movement, it is plausible to assume that the ENSO-affected region shifts with the seasons. Furthermore, in certain places, spring and autumn rainfall are a significant portion of total annual rainfall, which makes seasonal variability crucial. In southern China, spring rainfall and variability are comparable to summer, whereas in central Japan, fall rainfall and fluctuation are comparable to summer. [71]. In certain epochs, the Indian monsoon circulation interacted with regional circulations in northern China, whereas in others, such connection was disrupted. When the interaction was active, ENSO-related changes in the Indian monsoon, such as those caused by El Nino or La Nina, were extended to effect rainfall variations in northern China, resulting in a teleconnection between ENSO and northern China rainfall. Jiang et al. [72] found that the El Niño Southern Oscillation (ENSO) exerted greater impacts on PRCPTOT than other EPIs and greater in the Guanzhong Plain than northern Shaanxi and southern Shaanxi Province. The ENSO influence waned when the connection was weak or non-existent [73]. This might explain why CI in Shaanxi Province is seasonal.
In our work, two types of PRCPTOT and precipitation CI relationships were observed. On the one hand, a decrease in PRCPTOT was accompanied by an increase in the CI, whereas the other type of relationship showed a decrease in PRCPTOT, and the CI also decreased. The first type of relationship was observed at seven stations, one of which was in northern Shaanxi, two in Guanzhong, and four in southern Shaanxi. The second relationship was observed at 14 stations. A station that exhibits the first relationship between PRCPTOT and CI may have an increased risk of drought and/or flood disasters events near the station. In addition, more than half of the stations with the first relationship between PRCPTOT and CI are located in southern Shaanxi. The climate characteristics of southern Shaanxi are already very humid and the annual rainfall is relatively high (more than 1300 mm/year). So, there may be a greater risk of flood disasters at stations that show the first type of relationship between PRCPTOT and CI in the rainy season. However, stations in northern Shaanxi that show the first type of relationship between PRCPTOT and CI should pay attention to the threat of drought in the dry season. As there is not much rainfall, the more concentrated precipitation may cause more aridity in the non-rainy season. Previous studies have shown that precipitation and temperature in the region will increase from south to north in the future, with the largest increase in the west [74]. In the middle and late twenty-first century, due to significant increases in temperature, the aridification trend in northern Shaanxi may be aggravated.
The second relationship between precipitation and CI may mean that precipitation will become more uniform and lesser. However, attention should be paid to flood prevention at some stations, such as Shiquan and Ankang. Although the annual precipitation and CI at these stations show a decreasing trend, R30 and R50 are increasing, implying that the frequency of severe precipitation occurrences may rise, and these places still have a higher risk of flood disasters.
Our research found that at most stations in Shaanxi Province, the five extreme precipitation indicators all showed a downward trend from 1961 to 2017. The CI values for practically all stations in the study region, indicate an increasing trend, which correlates to a considerable rise in severe precipitation occurrences in recent years. Global warming may be one of the main factors contributing to this phenomenon [75]. Research on the relationship between precipitation concentration and climate change is helpful for dealing with natural disasters caused by climate change. Precipitation concentration and the elements that govern it have received less attention in earlier research on the distribution of precipitation throughout time and space. In future research, we should pay more attention to this.
5. Conclusions
Shaanxi Province is in the transition zone between a semi-arid and a humid zone. There are great spatial differences in climate in Shaanxi Province. There are few studies on long time series extreme precipitation indices and precipitation concentration in Shaanxi Province. Research on extreme precipitation events in Shaanxi Province could provide a reference for responses to climate change and the formulation of disaster prevention and mitigation plans in the province. The temporal–spatial variation features of precipitation and its concentration at various sites in Shaanxi Province, China, were investigated in this research from 1961 to 2017. The following conclusions can be drawn from this study.
(1) All of the precipitation-related indices considered in this study have a geographical distribution. That is, the southern value is large and the northern value is small. In terms of changing trends in the northern Shaanxi and Guanzhong regions, the precipitation-related indices all show decreasing trends, only a few stations in southern Shaanxi show an increasing trend.
(2) The spatial distribution of the CI in Shaanxi Province and the precipitation-related index are basically the same. Both the annual CI and seasonal CI trends showed a decreasing trend in more than two-thirds of the stations in the study area. This means that the precipitation concentration in most parts of Shaanxi Province is developing in a decreasing direction.
(3) Considering the precipitation-related index and CI, there are mainly two types of relationships between the development trends of the two in Shaanxi Province. The first relationship (a decrease in PRCPTOT accompanied by an increase in the CI) may mean an increased risk of drought and/or flood disasters events. The other type of relationship (a decrease in PRCPTOT, and a decrease in CI) may mean that precipitation becomes more uniform. However, at some special stations, we should still be alert to the threat of flood disasters because the analysis of R30 and R50 found that the frequency of extreme precipitation events in these areas has an increasing trend.
Author Contributions
Conceptualization, S.W. and P.L.; methodology, S.W.; software, S.W.; validation, P.L.; formal analysis, Z.C.; investigation, P.L.; resources, P.L.; data curation, S.W. and W.Z.; writing—original draft preparation, S.W.; writing—review and editing, P.L.; visualization, Z.C.; supervision, P.L.; project administration, P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support was provided by National Key R&D Program of China (2018YFE0103800), the Fundamental Research Fund for the Central Universities, CHD (300102299302).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All precipitation data created or used during this study are openly available from the China Meteorological Data Service Center at http://data.cma.cn/ (accessed on 1 March 2022).
Acknowledgments
Financial support was provided by National Key R&D Program of China (2018YFE0103800), the Fundamental Research Fund for the Central Universities, CHD (300102299302).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grill, G.; Lehner, B.; Lumsdon, A.E.; MacDonald, G.K.; Zarfl, C.; Liermann, C.R. An index-based framework for assessing patterns and trends in river fragmentation and flow regulation by global dams at multiple scales. Environ. Res. Lett. 2015, 10, 015001. [Google Scholar] [CrossRef]
- Haddeland, I.; Heinke, J.; Biemans, H.; Eisner, S.; Flörke, M.; Hanasaki, N.; Konzmann, M.; Ludwig, F.; Masaki, Y.; Schewe, J.; et al. Global water resources affected by human interventions and climate change. Proc. Natl. Acad. Sci. USA 2013, 111, 3251–3256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zha, X.; Luo, P.; Zhu, W.; Wang, S.; Lyu, J.; Zhou, M.; Huo, A.; Wang, Z. A bibliometric analysis of the research on Sponge City: Current situation and future development direction. Ecohydrology 2021, 14, e2328. [Google Scholar] [CrossRef]
- Tank, A.M.G.K.; Peterson, T.C.; Quadir, D.A.; Dorji, S.; Zou, X.; Tang, H.; Santhosh, K.; Joshi, U.R.; Jaswal, A.K.; Kolli, R.K.; et al. Changes in daily temperature and precipitation extremes in central and south Asia. J. Geophys. Res. Earth Surf. 2006, 111, D16105. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, J.; He, C.; Ding, G. Linking wind erosion to ecosystem services in drylands: A landscape ecological approach. Landsc. Ecol. 2017, 32, 2399–2417. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol. 2009, 379, 92–110. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2015, 6, 166–171. [Google Scholar] [CrossRef]
- Piras, M.; Mascaro, G.; Deidda, R.; Vivoni, E.R. Quantification of hydrologic impacts of climate change in a Mediterranean basin in Sardinia, Italy, through high-resolution simulations. Hydrol. Earth Syst. Sci. 2014, 18, 5201–5217. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.-P.; Sun, J.-Q.; Li, H.-X. Future changes in precipitation extremes over China using the NEX-GDDP high-resolution daily downscaled data-set. Atmos. Ocean. Sci. Lett. 2017, 10, 403–410. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, B. Predictability of summer extreme precipitation days over eastern China. Clim. Dyn. 2017, 51, 4543–4554. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in Total Precipitation and Frequency of Daily Precipitation Extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Guo, E.; Wang, Y.; Jirigala, B.; Jin, E. Spatiotemporal variations of precipitation concentration and their potential links to drought in mainland China. J. Clean. Prod. 2020, 267, 122004. [Google Scholar] [CrossRef]
- Mastrangelo, D.; Horvath, K.; Riccio, A.; Miglietta, M. Mechanisms for convection development in a long-lasting heavy precipitation event over southeastern Italy. Atmos. Res. 2011, 100, 586–602. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Regano, A. An observational and numerical study of a flash-flood event over south-eastern Italy. Nat. Hazards Earth Syst. Sci. 2008, 8, 1417–1430. [Google Scholar] [CrossRef]
- van Oldenborgh, G.J.; Otto, F.E.; Haustein, K.; Cullen, H. Climate change increases the probability of heavy rains like those of storm Desmond in the UK–an event attribution study in near-real time. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 13197–13216. [Google Scholar] [CrossRef]
- Frei, C.; Schöll, R.; Fukutome, S.; Schmidli, J.; Vidale, P.L. Future change of precipitation extremes in Europe: Intercomparison of scenarios from regional climate models. J. Geophys. Res. Earth Surf. 2006, 111, 986–991. [Google Scholar] [CrossRef] [Green Version]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Tank, A.M.G.K.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1042–1063. [Google Scholar] [CrossRef] [Green Version]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G. Erratum: Corrigendum: Human contribution to more-intense precipitation extremes. Nature 2013, 498, 526. [Google Scholar] [CrossRef] [Green Version]
- Schneider, T.; O’Gorman, P.A.; Levine, X.J. Water Vapor and the Dynamics of Climate Changes. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef] [Green Version]
- Demaria, E.M.C.; Hazenberg, P.; Scott, R.L.; Meles, M.B.; Nichols, M.; Goodrich, D. Intensification of the North American Monsoon Rainfall as Observed from a Long-Term High-Density Gauge Network. Geophys. Res. Lett. 2019, 46, 6839–6847. [Google Scholar] [CrossRef] [Green Version]
- Fischer, E.; Knutti, R. Observed heavy precipitation increase confirms theory and early models. Nat. Clim. Chang. 2016, 6, 986–991. [Google Scholar] [CrossRef]
- Loriaux, J.M.; Lenderink, G.; De Roode, S.R.; Siebesma, A.P. Understanding Convective Extreme Precipitation Scaling Using Observations and an Entraining Plume Model. J. Atmos. Sci. 2013, 70, 3641–3655. [Google Scholar] [CrossRef]
- Molnar, P.; Fatichi, S.; Gaál, L.; Szolgay, J.; Burlando, P. Storm type effects on super Clausius–Clapeyron scaling of intense rainstorm properties with air temperature. Hydrol. Earth Syst. Sci. 2015, 19, 1753–1766. [Google Scholar] [CrossRef]
- Dore, M.H. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Takeuchi, K.; Ishidaira, H. Monotonic trend and step changes in Japanese precipitation. J. Hydrol. 2003, 279, 144–150. [Google Scholar] [CrossRef]
- Ding, Y. Monsoons over China; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993; Volume 16. [Google Scholar]
- Chen, A.; He, X.; Guan, H.; Zhang, X. Variability of seasonal precipitation extremes over China and their associations with large-scale ocean-atmosphere oscillations. Int. J. Clim. 2018, 39, 613–628. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Singh, V.P.; Shi, P. Changes in magnitude and frequency of heavy precipitation across China and its potential links to summer temperature. J. Hydrol. 2017, 547, 718–731. [Google Scholar] [CrossRef] [Green Version]
- Xiao, M.; Zhang, Q.; Singh, V.P. Spatiotemporal variations of extreme precipitation regimes during 1961-2010 and possible teleconnections with climate indices across China. Int. J. Clim. 2016, 37, 468–479. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Z.; Zhang, X.; Li, L. On the Emergence of Anthropogenic Signal in Extreme Precipitation Change over China. Geophys. Res. Lett. 2018, 45, 9179–9185. [Google Scholar] [CrossRef] [Green Version]
- Robledo, F.; Vera, C.; Penalba, O. Multi-scale features of the co-variability between global sea surface temperature anomalies and daily extreme rainfall in Argentina. Int. J. Clim. 2019, 40, 4289–4299. [Google Scholar] [CrossRef]
- Zhao, N.; Jiao, Y.; Ma, T.; Zhao, M.; Fan, Z.; Yin, X.; Liu, Y.; Yue, T. Estimating the effect of urbanization on extreme climate events in the Beijing-Tianjin-Hebei region, China. Sci. Total Environ. 2019, 688, 1005–1015. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; Zhang, Q.; Li, J.; Singh, V.P.; Sun, P. Impact of urbanization on nonstationarity of annual and seasonal precipitation extremes in China. J. Hydrol. 2019, 575, 638–655. [Google Scholar] [CrossRef]
- Shi, W.; Yu, X.; Liao, W.; Wang, Y.; Jia, B. Spatial and temporal variability of daily precipitation concentration in the Lancang River basin, China. J. Hydrol. 2013, 495, 197–207. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Lee, J.-Y.; Ha, K.-J. Influenfce of boreal summer intraseasonal oscillation on rainfall extremes in southern China. Int. J. Clim. 2015, 36, 1403–1412. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Zou, X.; Mo, Y.; Zhang, J.; Zhang, C.; Tian, Y. Nonstationary bayesian modeling of precipitation extremes in the Beijing-Tianjin-Hebei Region, China. Atmos. Res. 2020, 242, 105006. [Google Scholar] [CrossRef]
- Onyutha, C.; Willems, P. Space-time variability of extreme rainfall in the River Nile basin. Int. J. Clim. 2017, 37, 4915–4924. [Google Scholar] [CrossRef]
- Martin-Vide, J. Spatial distribution of a daily precipitation concentration index in peninsular Spain. Int. J. Clim. 2004, 24, 959–971. [Google Scholar] [CrossRef]
- Stefanidis, S.; Stathis, D. Spatial and Temporal Rainfall Variability over the Mountainous Central Pindus (Greece). Climate 2018, 6, 75. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xu, Y.; Tabari, H.; Wang, J.; Wang, Q.; Song, S.; Hu, Z. Innovative trend analysis of annual and seasonal rainfall in the Yangtze River Delta, eastern China. Atmos. Res. 2019, 231, 104673. [Google Scholar] [CrossRef]
- Longobardi, A.; Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial and temporal distribution of precipitation in a Mediterranean area (southern Italy). Environ. Earth Sci. 2016, 75, 189. [Google Scholar] [CrossRef]
- Vishwakarma, A.; Choudhary, M.K.; Chauhan, M.S. Applicability of SPI and RDI for forthcoming drought events: A non-parametric trend and one way ANOVA approach. J. Water Clim. Chang. 2020, 11, 18–28. [Google Scholar] [CrossRef]
- Huang, W.; Liu, C.; Cao, J.; Chen, J.; Feng, S. Changes of hydroclimatic patterns in China in the present day and future. Sci. Bull. 2020, 65, 1061–1063. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, H.; Luo, H.; Yi, S. Decadal change in ENSO related seasonal precipitation over southern China under influences of ENSO and its combination mode. Clim. Dyn. 2020, 54, 1973–1986. [Google Scholar] [CrossRef]
- Li, Z.; Cao, L.; Zhu, Y.; Yan, Z. Comparison of Two Homogenized Datasets of Daily Maximum/Mean/Minimum Temperature in China during 1960–2013. J. Meteorol. Res. 2016, 30, 55–68. [Google Scholar] [CrossRef]
- Li, Z.; Yan, Z.; Tu, K.; Wu, H. Changes of precipitation and extremes and the possible effect of urbanization in the Beijing metropolitan region during 1960–2012 based on homogenized observations. Adv. Atmos. Sci. 2015, 32, 1173–1185. [Google Scholar] [CrossRef]
- Cao, L.; Zhao, P.; Yan, Z.; Jones, P.; Zhu, Y.; Yu, Y.; Tang, G. Instrumental temperature series in eastern and central China back to the nineteenth century. J. Geophys. Res. Atmos. 2013, 118, 8197–8207. [Google Scholar] [CrossRef]
- Wang, X.L.; Feng, Y. RHtests_dlyPrcp User Manual. 2014. Available online: http://etccdi.pacificclimate.org/software.shtml (accessed on 15 April 2022).
- Wang, X.L.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New Techniques for the Detection and Adjustment of Shifts in Daily Precipitation Data Series. J. Appl. Meteorol. Clim. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Wang, X.L. Accounting for autocorrelation in detecting mean shifts in climate data series using the penalized maxi-mal t or F test. J. Appl. Meteorol. Climatol. 2008, 47, 2423–2444. [Google Scholar] [CrossRef]
- Wang, X.L. Penalized Maximal F Test for Detecting Undocumented Mean Shift without Trend Change. J. Atmos. Ocean. Technol. 2008, 25, 368–384. [Google Scholar] [CrossRef]
- Cao, L.; Yan, Z.; Zhao, P.; Zhu, Y.; Yu, Y.; Tang, G.; Jones, P. Climatic warming in China during 1901–2015 based on an extended dataset of instrumental temperature records. Environ. Res. Lett. 2017, 12, 064005. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wires Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Li, X. Flash droughts in a typical humid and subtropical basin: A case study in the Gan River Basin, China. J. Hydrol. 2017, 551, 162–176. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank correlation methods. Br. J. Psychol. 1990, 25, 86–91. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Catalini, C.G.; Guillen, N.F.; Bazzano, F.M.; García, C.M.; Baraquet, M.M. Web Mapping of Extreme Daily Rainfall Data in Central and Northern Argentina. J. Hydrol. Eng. 2021, 26, 05021013. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef] [Green Version]
- Jiang, R.; Xie, J.; He, H.; Luo, J.; Zhu, J. Use of four drought indices for evaluating drought characteristics under climate change in Shaanxi, China: 1951–2012. Nat. Hazards 2015, 75, 2885–2903. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, S.; Luo, P.; Zha, X.; Cao, Z.; Lyu, J.; Zhou, M.; He, B.; Nover, D. A Quantitative Analysis of the Influence of Temperature Change on the Extreme Precipitation. Atmosphere 2022, 13, 612. [Google Scholar] [CrossRef]
- Wei, X.D.; Yang, J.; Luo, P.P.; Lin, L.G.; Lin, K.L.; Guan, J.M. Assessment of the variation and influencing factors of vegetation NPP and carbon sink capacity under different natural conditions. Ecol. Indic. 2022, 112, 108834. [Google Scholar] [CrossRef]
- Luo, P.; Mu, Y.; Wang, S.; Zhu, W.; Mishra, B.K.; Huo, A.; Zhou, M.; Lyu, J.; Hu, M.; Duan, W.; et al. Exploring sustainable solutions for the water environment in Chinese and Southeast Asian cities. AMBIO 2021, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Xu, C.; Kang, S.; Huo, A.; Lyu, J.; Zhou, M.; Nover, D. Heavy metals in water and surface sediments of the Fenghe River Basin, China: Assessment and source analysis. Water Sci. Technol. 2021, 84, 3072–3090. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Wang, N.; Luo, P.; Yang, J.; Zhang, J.; Lin, K. Spatiotemporal Assessment of Land Marketization and Its Driving Forces for Sustainable Urban–Rural Development in Shaanxi Province in China. Sustainability 2021, 13, 7755. [Google Scholar] [CrossRef]
- Zhang, H.F.; Li, J.K.; Pan, L.J.; Lu, S. Diurnal variation characteristics and north-south differences of precipitation in warm season in Shaanxi Province. Arid Land Geogr. 2020, 43, 889–898. [Google Scholar]
- Liu, W.; Zhang, M.; Wang, S.; Wang, B.; Li, F.; Che, Y. Changes in precipitation extremes over Shaanxi Province, northwestern China, during 1960–2011. Quat. Int. 2013, 313, 118–129. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Xiao, W.; Chen, L.-H.; Yan, D.-H.; Zhou, Y.-Y.; Jiang, D.-C.; Yang, M.-Z. Spatial and Temporal Variability in the Precipitation Concentration in the Upper Reaches of the Hongshui River Basin, Southwestern China. Adv. Meteorol. 2018, 2018, 4329757. [Google Scholar] [CrossRef] [Green Version]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate Extremes: Observations, Modeling, and Impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [Green Version]
- Tao, S.-Y. A review of recent research on the East Asian summer monsoon in China. Monsoon Meteorol. 1987, 60–92. [Google Scholar]
- Juneng, L.; Tangang, F.T. Evolution of ENSO-related rainfall anomalies in Southeast Asia region and its relationship with atmosphere–ocean variations in Indo-Pacific sector. Clim. Dyn. 2005, 25, 337–350. [Google Scholar] [CrossRef]
- Jiang, R.; Xie, J.; Zhao, Y.; He, H.; He, G. Spatiotemporal variability of extreme precipitation in Shaanxi province under climate change. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2016, 130, 831–845. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q. Variations in the teleconnection of ENSO and summer rainfall in northern China: A role of the Indian summer monsoon. J. Clim. 2004, 17, 4871–4881. [Google Scholar] [CrossRef]
- Wang, X.; Zhuo, L.; Li, C.; Engel, B.A.; Sun, S.; Wang, Y. Temporal and spatial evolution trends of drought in northern Shaanxi of China: 1960–2100. Theor. Appl. Climatol. 2020, 139, 965–979. [Google Scholar] [CrossRef]
- Wasko, C.; Sharma, A.; Westra, S. Reduced spatial extent of extreme storms at higher temperatures. Geophys. Res. Lett. 2016, 43, 4026–4032. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).