GAN-rcLSTM: A Deep Learning Model for Radar Echo Extrapolation
Abstract
:1. Introduction
2. Materials and Methods
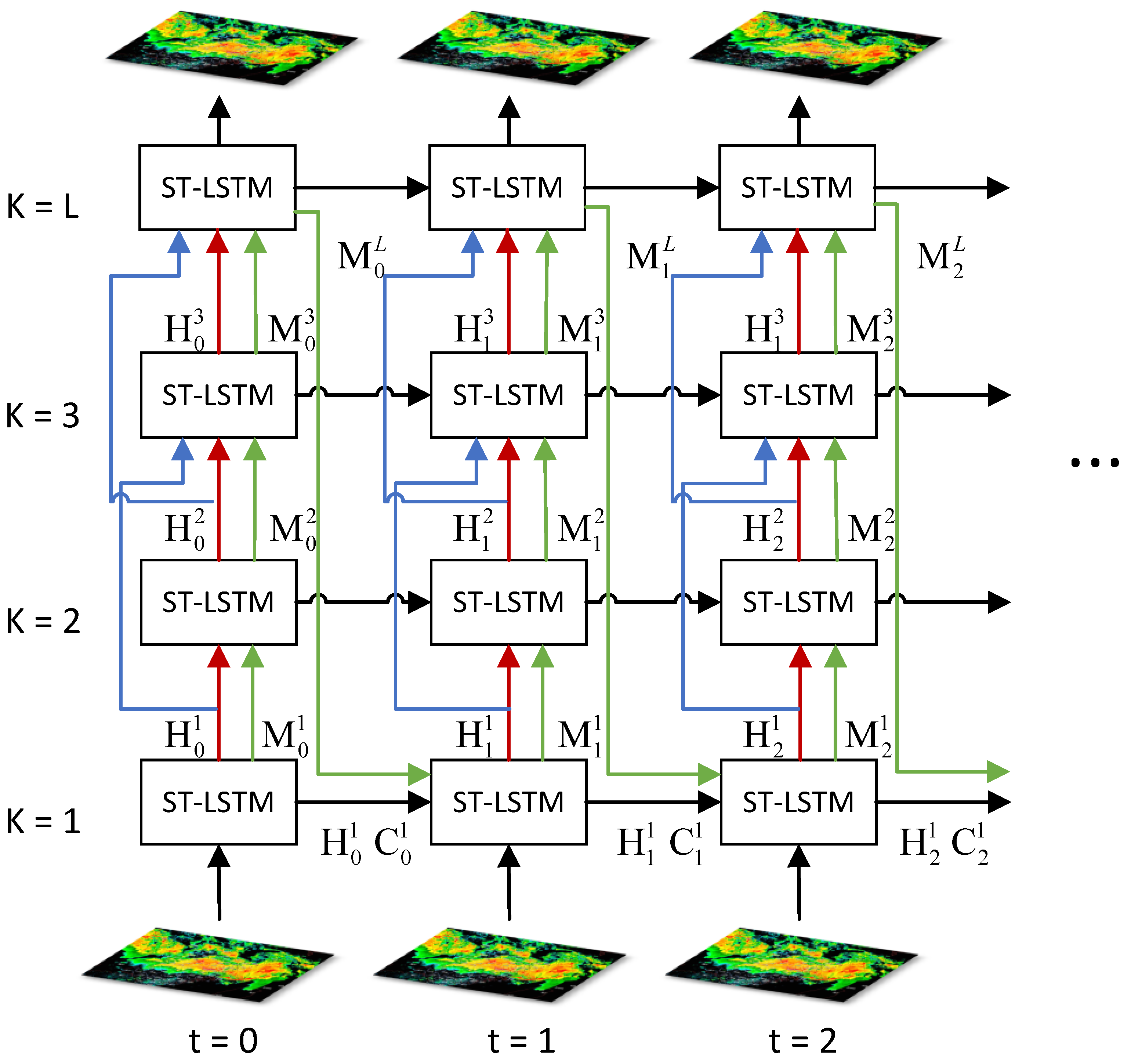
2.1. rcLSTM
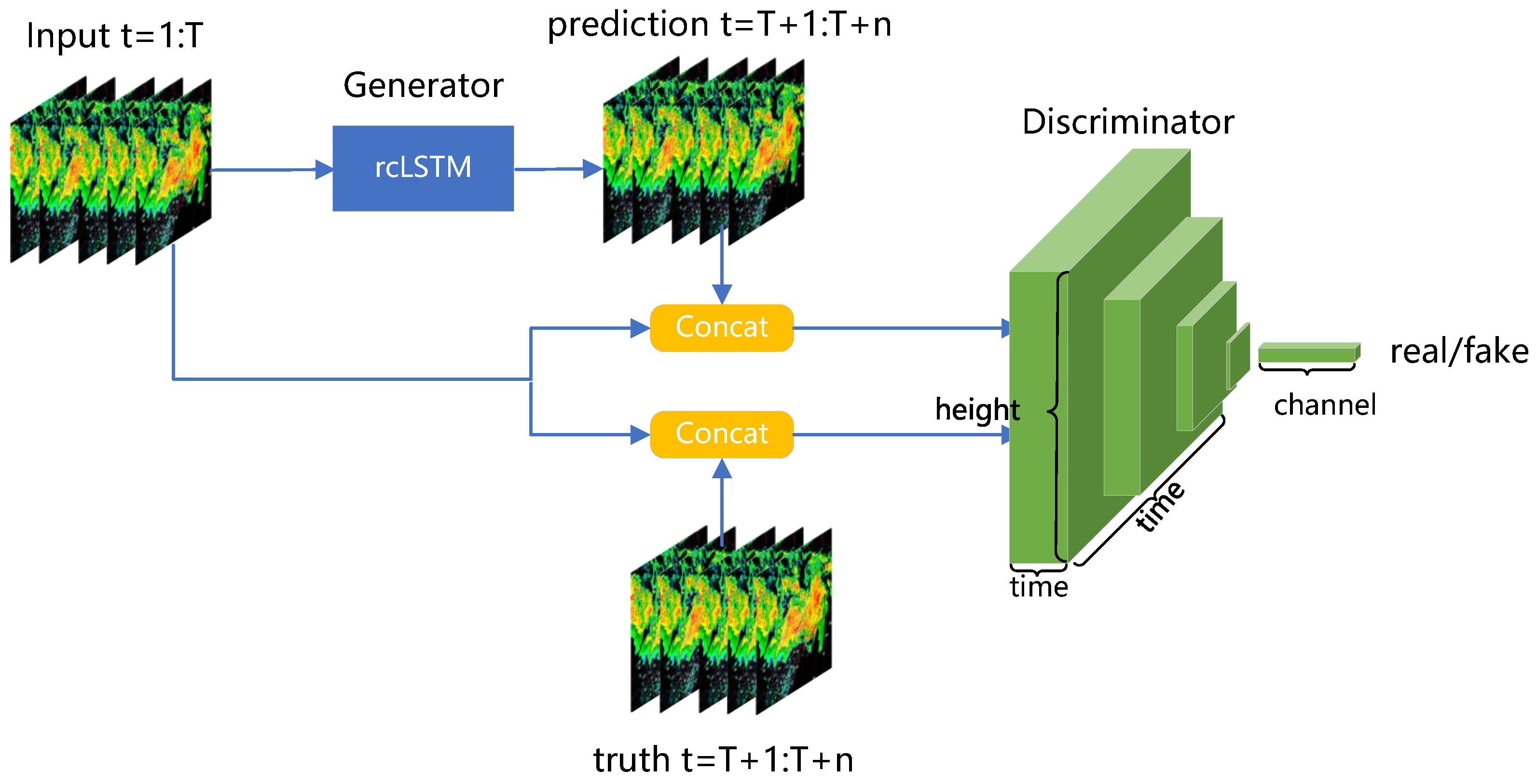
2.2. GAN-rcLSTM
| Algorithm 1: Minibatch stochastic gradient descent training of GAN-rcLSTM. The hyperparameter k for the number of steps applied to the discriminator is set to 4. |
|
2.3. Data
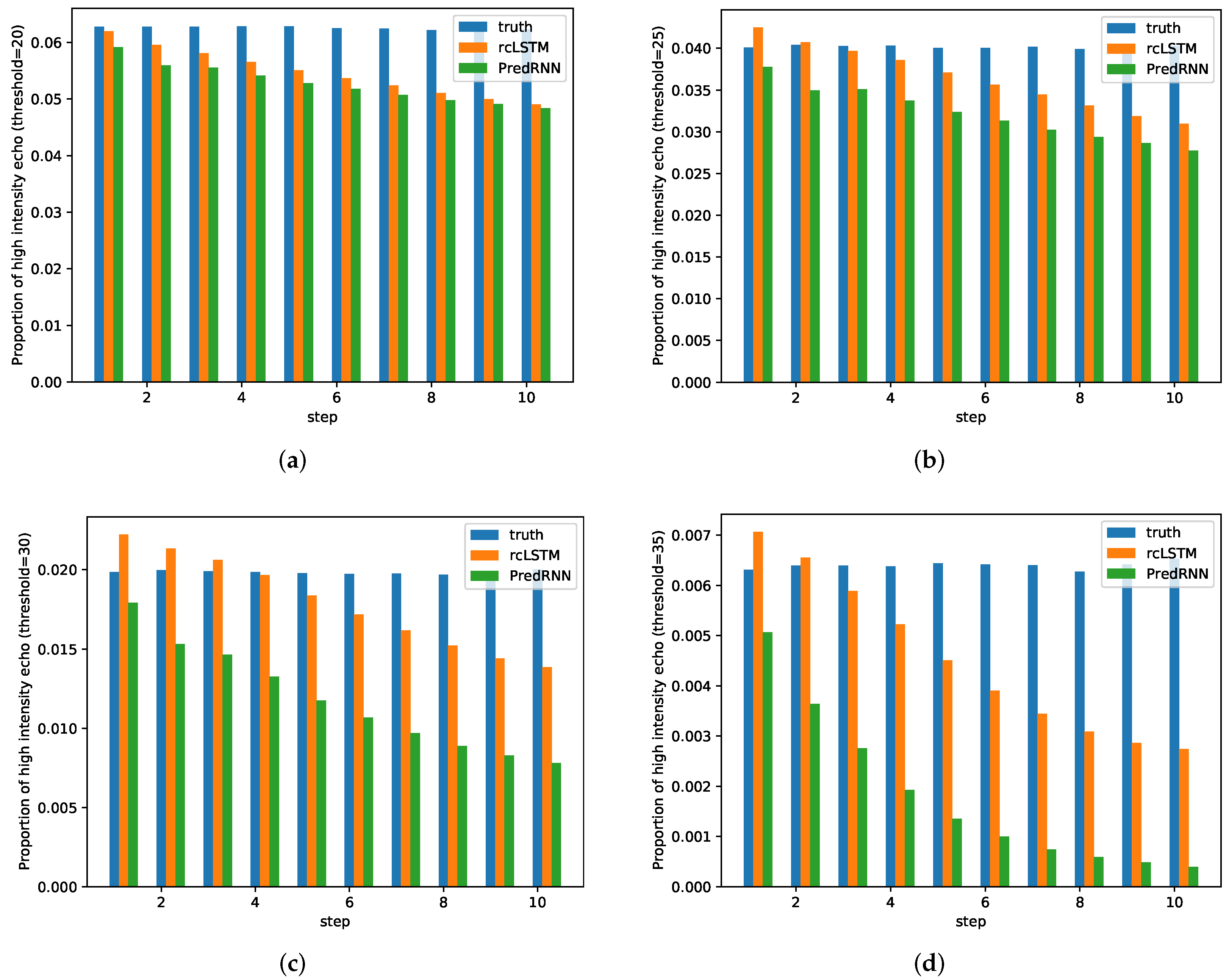
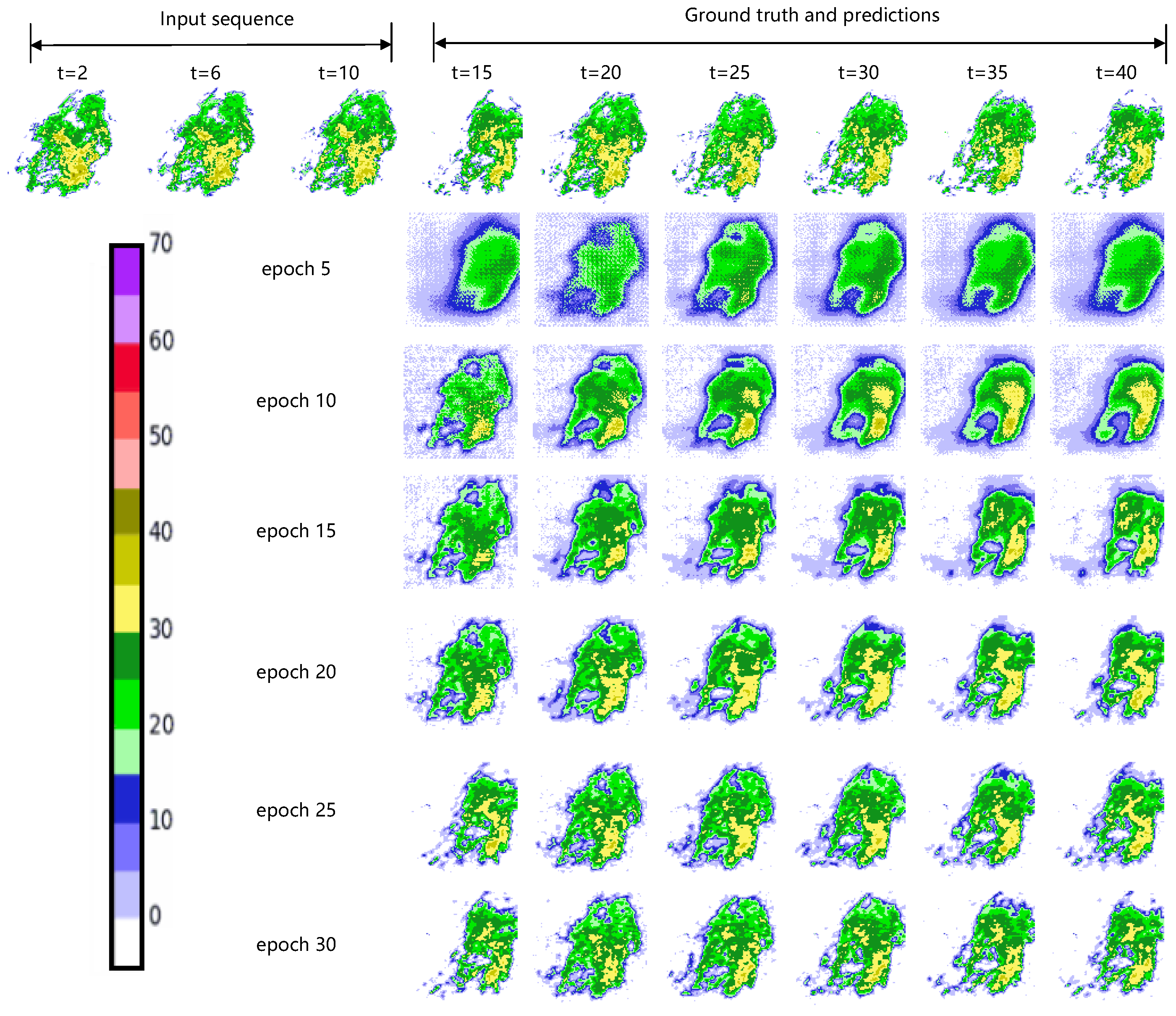
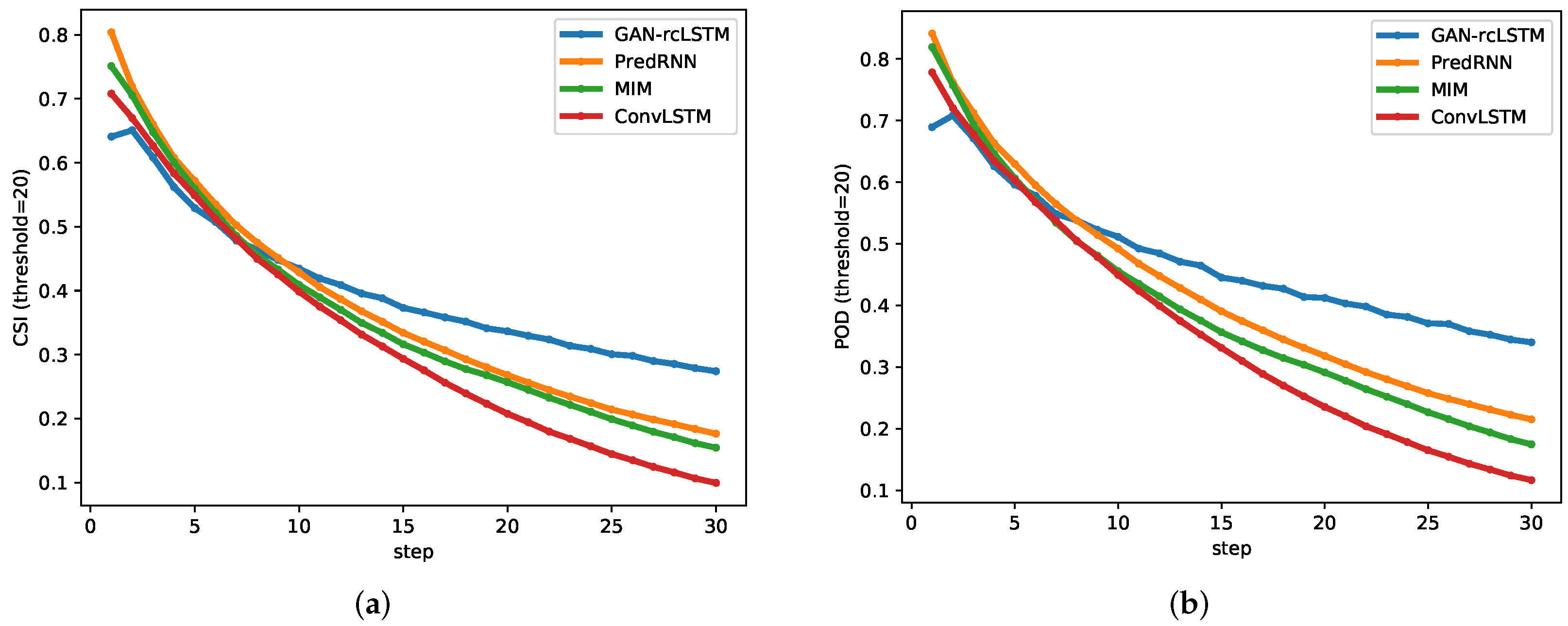
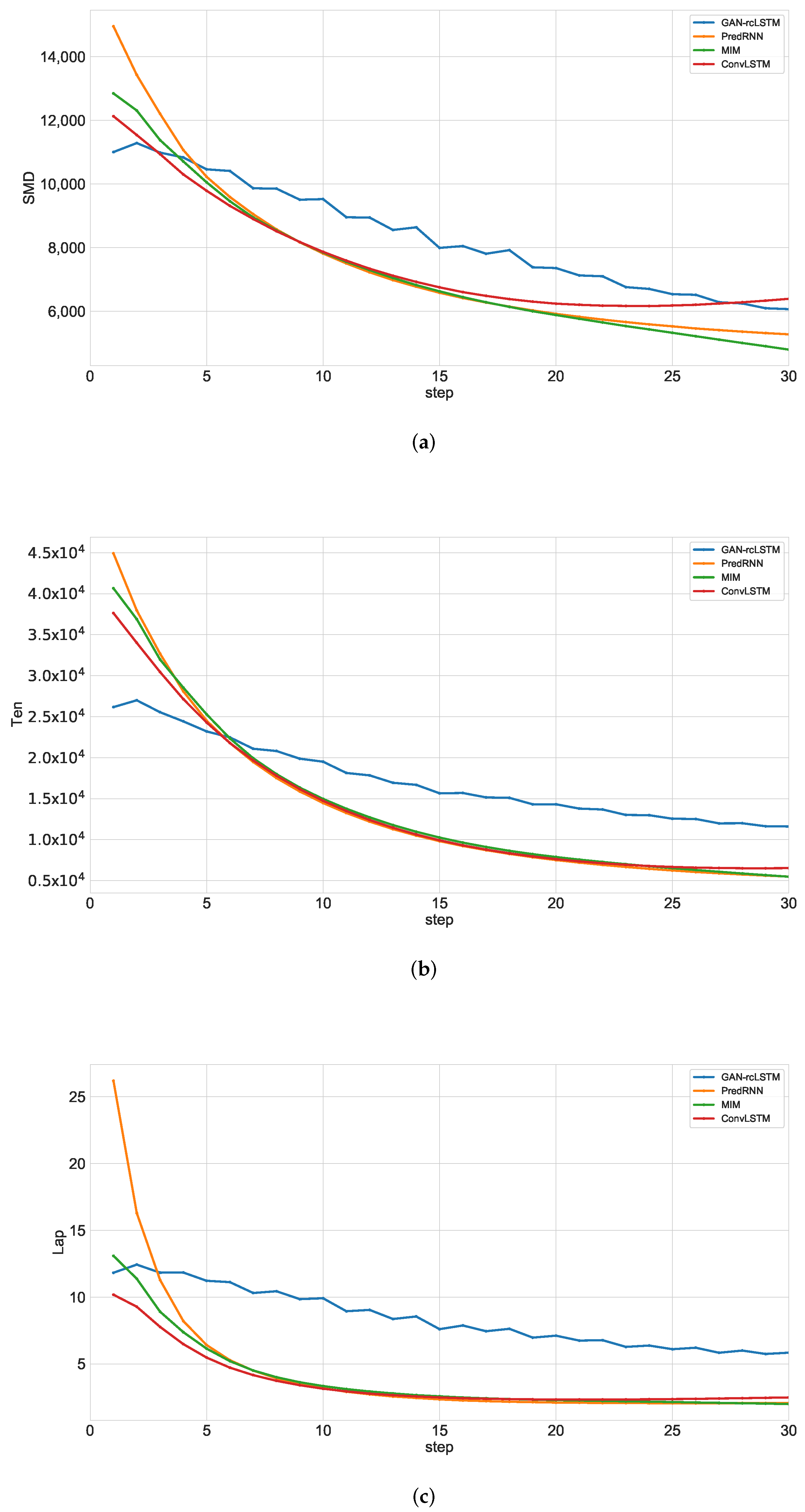
3. Results
3.1. Implementation
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, J.; MacKeen, P.; Witt, A.; Mitchell, E.; Stumpf, G.; Eilts, M.; Thomas, K. The Storm Cell Identification and Tracking Algorithm: An Enhanced WSR-88D Algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef] [Green Version]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A Radar-based Methodology. J. Atmos. Ocean. Technol. 1993, 10, 785. [Google Scholar] [CrossRef]
- Li, L.; Schmid, W.; Joss, J. Nowcasting of Motion and Growth of Precipitation with Radar over a Complex Orography. J. Appl. Meteorol. 1995, 34, 1286–1300. [Google Scholar] [CrossRef] [Green Version]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Farneback, G. Very high accuracy velocity estimation using orientation tensors, parametric motion, and simultaneous segmentation of the motion field. In Proceedings of the IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; Volume 1, pp. 171–177. [Google Scholar] [CrossRef] [Green Version]
- Sakaino, H. Spatio-Temporal Image Pattern Prediction Method Based on a Physical Model With Time-Varying Optical Flow. IEEE Trans. Geoence Remote Sens. 2013, 51, 3023–3036. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale-Dependence of the Predictability of Precipitation from Continental Radar Images. Part I: Description of the Methodology. Mon. Weather Rev. 2001, 130, 2859–2873. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Weinzaepfel, P.; Revaud, J.; Harchaoui, Z.; Schmid, C. DeepFlow: Large Displacement Optical Flow with Deep Matching. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1385–1392. [Google Scholar] [CrossRef] [Green Version]
- Wulff, J.; Black, M.J. Efficient sparse-to-dense optical flow estimation using a learned basis and layers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 120–130. [Google Scholar] [CrossRef]
- Elsayed, N.; Maida, A.S.; Bayoumi, M. Reduced-Gate Convolutional LSTM Architecture for Next-Frame Video Prediction Using Predictive Coding. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2019; pp. 1–9. [Google Scholar] [CrossRef]
- Kalchbrenner, N.; Oord, A.; Simonyan, K.; Danihelka, I.; Vinyals, O.; Graves, A.; Kavukcuoglu, K. Video Pixel Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1771–1779. [Google Scholar]
- Lotter, W.; Kreiman, G.; Cox, D. Deep predictive coding networks for video prediction and unsupervised learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Oliu, M.; Selva, J.; Escalera, S. Folded Recurrent Neural Networks for Future Video Prediction. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 716–731. [Google Scholar] [CrossRef] [Green Version]
- Denton, E.; Birodkar, V. Unsupervised learning of disentangled representations from video. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 4417–4426. [Google Scholar]
- Ham, Y.; Kim, J.; Luo, J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Oh, J.; Guo, X.; Lee, H.; Lewis, R.; Singh, S. Action-conditional video prediction using deep networks in Atari games. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Montreal, QC, USA, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; Volume 28, pp. 2863–2871. [Google Scholar]
- Villegas, R.; Yang, J.; Zou, Y.; Sohn, S.; Lin, X.; Lee, H. Learning to generate long-term future via hierarchical prediction. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3560–3569. [Google Scholar]
- He, W.; Xiong, T.; Wang, H.; He, J.; Ren, X.; Yan, Y.; Tan, L. Radar Echo Spatiotemporal Sequence Prediction Using an Improved ConvGRU Deep Learning Model. Atmosphere 2022, 13, 88. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, S.; Geng, H.; Chen, Y.; Zhang, C.; Min, J. Strong Spatiotemporal Radar Echo Nowcasting Combining 3DCNN and Bi-Directional Convolutional LSTM. Atmosphere 2020, 11, 569. [Google Scholar] [CrossRef]
- Geng, H.; Geng, L. MCCS-LSTM: Extracting Full-Image Contextual Information and Multi-Scale Spatiotemporal Feature for Radar Echo Extrapolation. Atmosphere 2022, 13, 192. [Google Scholar] [CrossRef]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Merrienboer, B.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar] [CrossRef]
- Srivastava, N.; Mansimov, E.; Salakhutdinov, R. Unsupervised learning of video representations using LSTMs. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 843–852. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Montreal, QC, USA, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; Volume 1, pp. 802–810. [Google Scholar]
- Brabandere, B.; Jia, X.; Tuytelaars, T.; Van Gool, L. Dynamic Filter Networks. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29, pp. 667–675. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 5622–5632. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent Neural Networks for Predictive Learning using Spatiotemporal LSTMs. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 879–888. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, H.; Yu, P.S. PredRNN++: Towards A Resolution of the Deep-in-Time Dilemma in Spatiotemporal Predictive Learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 5123–5132. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training very deep networks. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Montreal, QC, USA, 7–12 December 2015; Volume 28, pp. 2377–2385. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in Memory: A Predictive Neural Network for Learning Higher-Order Non-Stationarity From Spatiotemporal Dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9154–9162. [Google Scholar]
- Wang, Y.; Jiang, L.; Yang, M.; Li, L.; Long, M.; Li, F. Eidetic 3D LSTM: A Model for Video Prediction and Beyond. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Cun, L.; Boser, Y.; Denker, B.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Backpropagation Applied to Handwritten zip code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar]
- Szegedy, C.; Wei, L.; Yangqing, J.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, K.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5353–5360. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Highway Networks. arXiv 2015, arXiv:1505.00387. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014; Volume 27, pp. 2672–2680. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Jarvis, R. Focus optimisation criteria for computer image processing. Microscope 1976, 24, 163–180. [Google Scholar]
- Krotkov, E. Focusing. Int. J. Comput. Vis. 1987, 1, 223–227. [Google Scholar] [CrossRef]
- Pech-Pacheco, J.; Cristobal, G.; Chamorro-Martinez, J.; Fernandez-Valdivia, J. Diatom autofocusing in brightfield microscopy: A comparative study. In Proceedings of the 15th International Conference on Pattern Recognition., Barcelona, Spain, 3–7 September 2000; Volume 3, pp. 314–317. [Google Scholar] [CrossRef]
- Nayar, S.; Nakagawa, Y. Shape from focus system. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 824–831. [Google Scholar] [CrossRef] [Green Version]



| Forecast Types | Period Validity |
|---|---|
| nowcasting | 0–2 h |
| short-term forecasting | 0–12 h |
| short-range forecasting | 1–3 days |
| medium-range forecasting | 4–10 days |
| long-range forecasting | >30 days |
| Radar Parameters | Value |
|---|---|
| Band | S |
| Wavelength | 10 cm |
| Frequency | 2.86 GHZ |
| Pulse recurrence frequency | 322–1014 Hz |
| Pulse width | 1.57 s |
| Peak power | 650 KW |
| Antenna gain | 44 dB |
| Antenna aperture | 8.5 m |
| Beam width | 0.95° |
| Operation mode | STSR |
| Volume scan mode | PPI |
| Sagittal resolution | 250 m |
| Depth | ConvLSTM | PredRNN | MIM | rcLSTM |
|---|---|---|---|---|
| 1 | 21.32 | - | - | - |
| 2 | 20.58 | 18.18 | 18.61 | 18.16 |
| 3 | 18.29 | 17.66 | 16.98 | 17.32 |
| 4 | 17.04 | 16.33 | 15.95 | 15.76 |
| 5 | 17.12 | 16.51 | 15.49 | 15.35 |
| 6 | 17.03 | 17.28 | 16.73 | 15.28 |
| 7 | 19.28 | 17.13 | 16.98 | 15.16 |
| Model | MSE | CSI | POD | FAR |
|---|---|---|---|---|
| ConvLSTM | 34.629 | 0.323 | 0.360 | 0.268 |
| PredRNN | 33.508 | 0.373 | 0.424 | 0.298 |
| MIM | 31.366 | 0.356 | 0.395 | 0.235 |
| GAN-rcLSTM | 32.662 | 0.402 | 0.472 | 0.259 |
| Model | SMD | Tenengrad | Laplacian |
|---|---|---|---|
| ConvLSTM | 7582 | 1,370,620 | 3.582 |
| PredRNN | 7534 | 1,394,062 | 4.441 |
| MIM | 7300 | 1,408,276 | 3.824 |
| GAN-rcLSTM | 8356 | 1,719,049 | 8.406 |
| Model | Time Required to Predict 10 Frames (GPU/CPU) | Time Required to Predict 20 Frames (GPU/CPU) | Time Required to Predict 30 Frames (GPU/CPU) |
|---|---|---|---|
| ConvLSTM | 0.7 s/48.5 s | 1.0 s/75.4 s | 2.3 s/126.8 s |
| PredRNN | 0.9 s/51.2 s | 1.5 s/78.3 s | 2.2 s/131.9 s |
| MIM | 1.8 s/57.8 s | 2.9 s/94.8 s | 3.9 s/143.0 s |
| GAN-rcLSTM | 0.9 s/51.4 s | 1.5 s/82.0 s | 2.3 s/134.2 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, H.; Wang, T.; Zhuang, X.; Xi, D.; Hu, Z.; Geng, L. GAN-rcLSTM: A Deep Learning Model for Radar Echo Extrapolation. Atmosphere 2022, 13, 684. https://doi.org/10.3390/atmos13050684
Geng H, Wang T, Zhuang X, Xi D, Hu Z, Geng L. GAN-rcLSTM: A Deep Learning Model for Radar Echo Extrapolation. Atmosphere. 2022; 13(5):684. https://doi.org/10.3390/atmos13050684
Chicago/Turabian StyleGeng, Huantong, Tianlei Wang, Xiaoran Zhuang, Du Xi, Zhongyan Hu, and Liangchao Geng. 2022. "GAN-rcLSTM: A Deep Learning Model for Radar Echo Extrapolation" Atmosphere 13, no. 5: 684. https://doi.org/10.3390/atmos13050684
APA StyleGeng, H., Wang, T., Zhuang, X., Xi, D., Hu, Z., & Geng, L. (2022). GAN-rcLSTM: A Deep Learning Model for Radar Echo Extrapolation. Atmosphere, 13(5), 684. https://doi.org/10.3390/atmos13050684






