A Heuristic Method for Modeling Odor Emissions from Open Roof Rectangular Tanks
Abstract
1. Introduction
2. Material and Methods
2.1. Passive Odor Sources
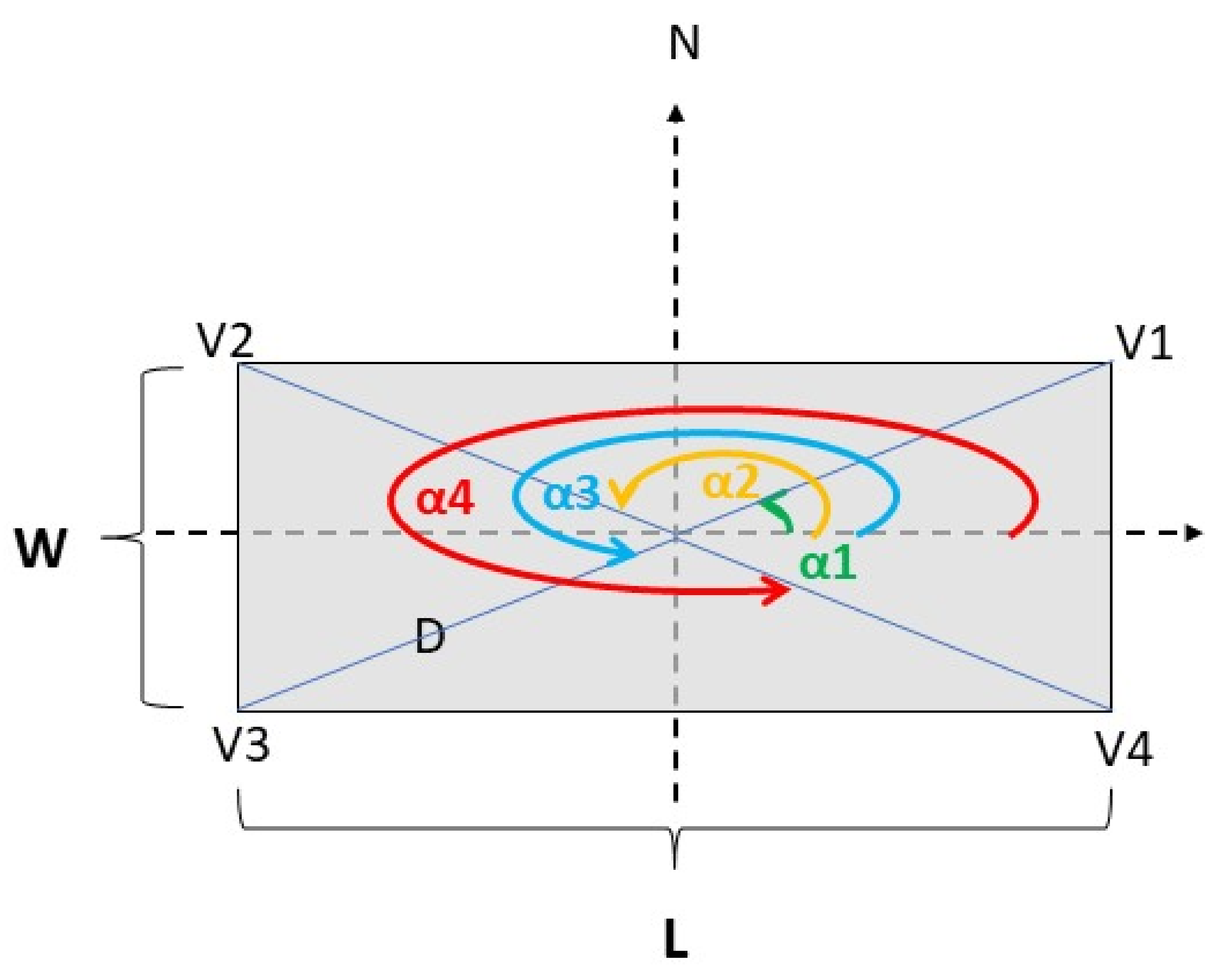
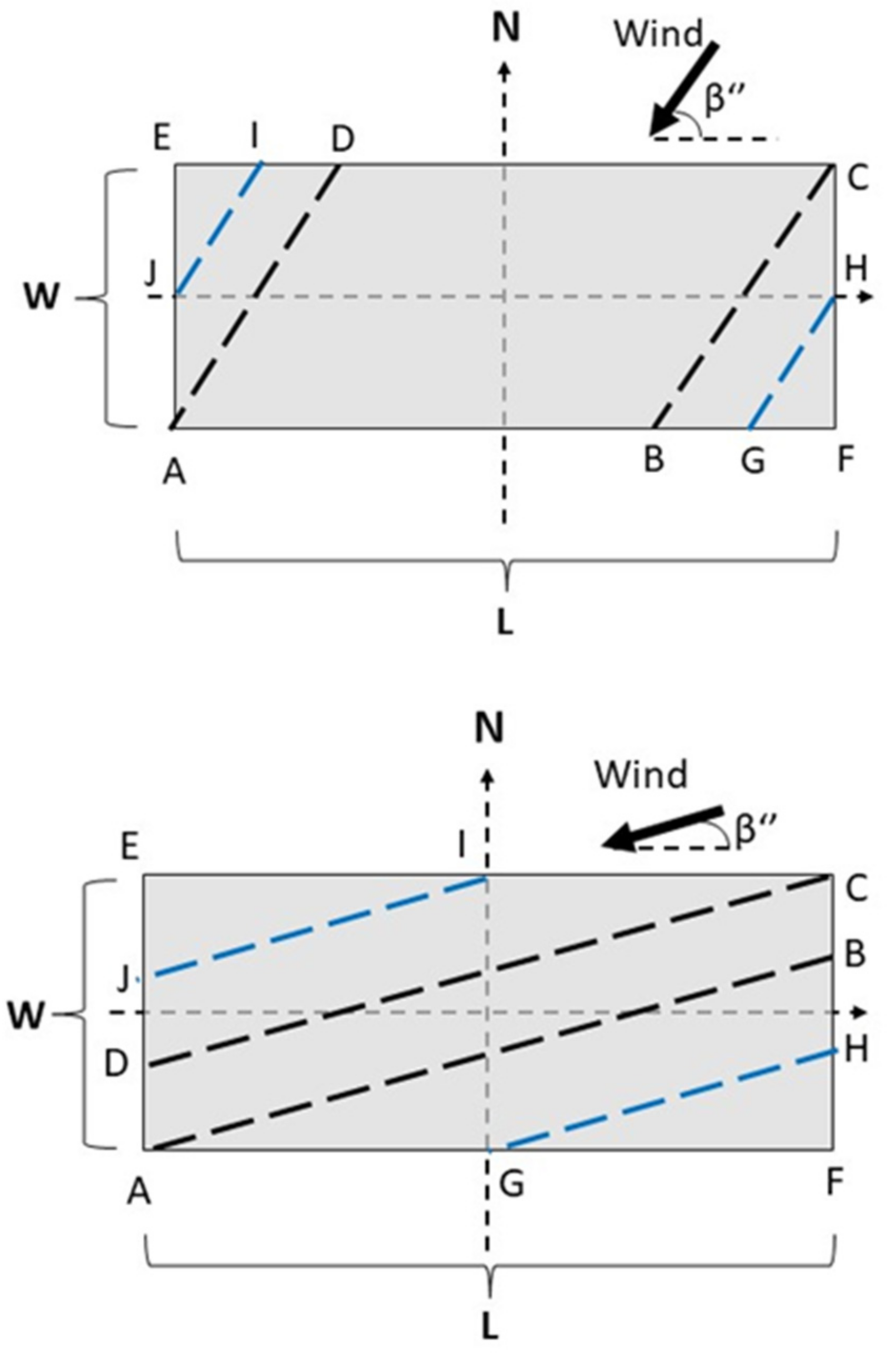
2.2. Wind Speed over the Emitting Surface
2.3. The LAPMOD Dispersion Model
2.4. Meteorology
2.5. Source Term
2.6. Simulation Domain
3. Results and Discussion
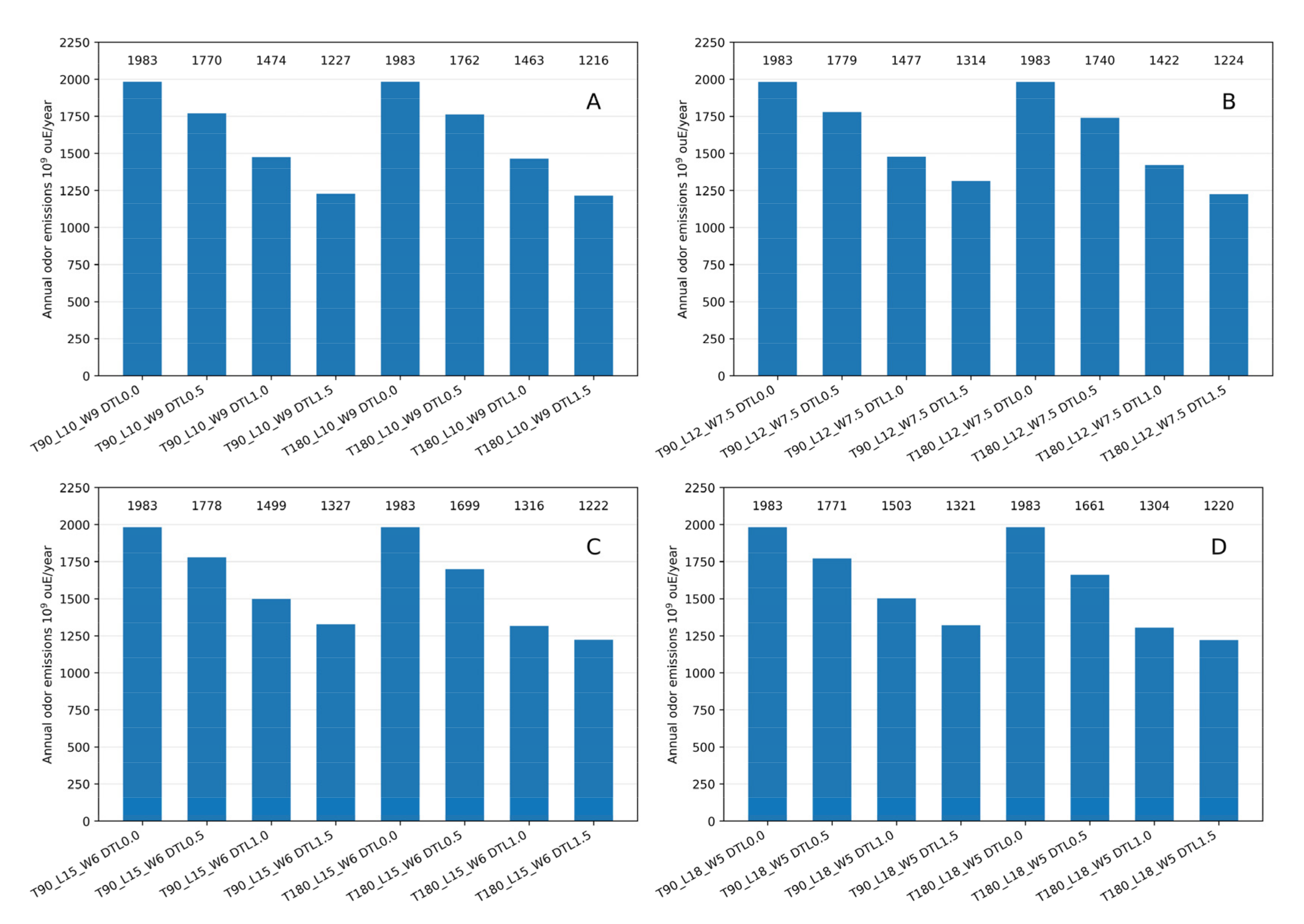
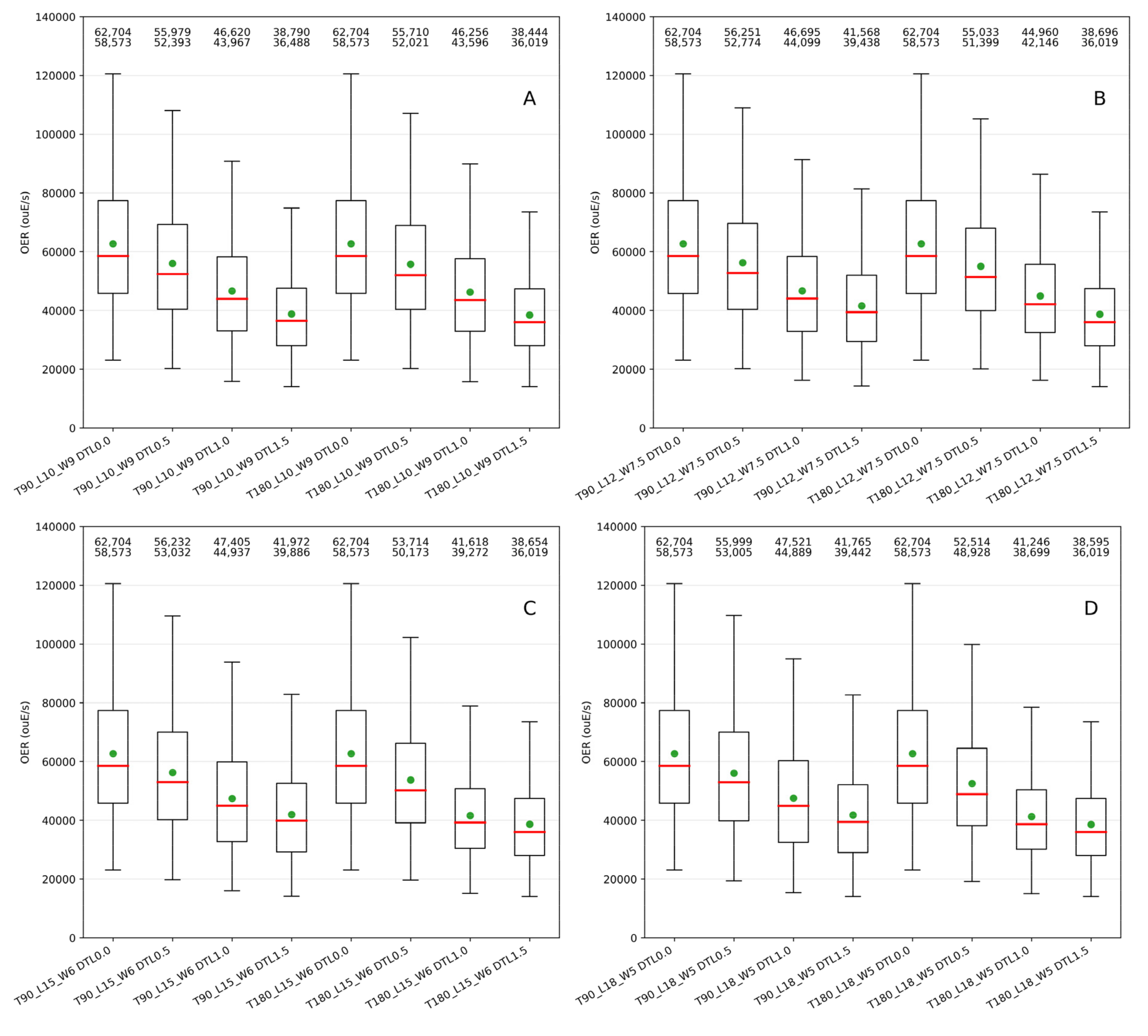
3.1. Emissions
3.2. Separation Distances
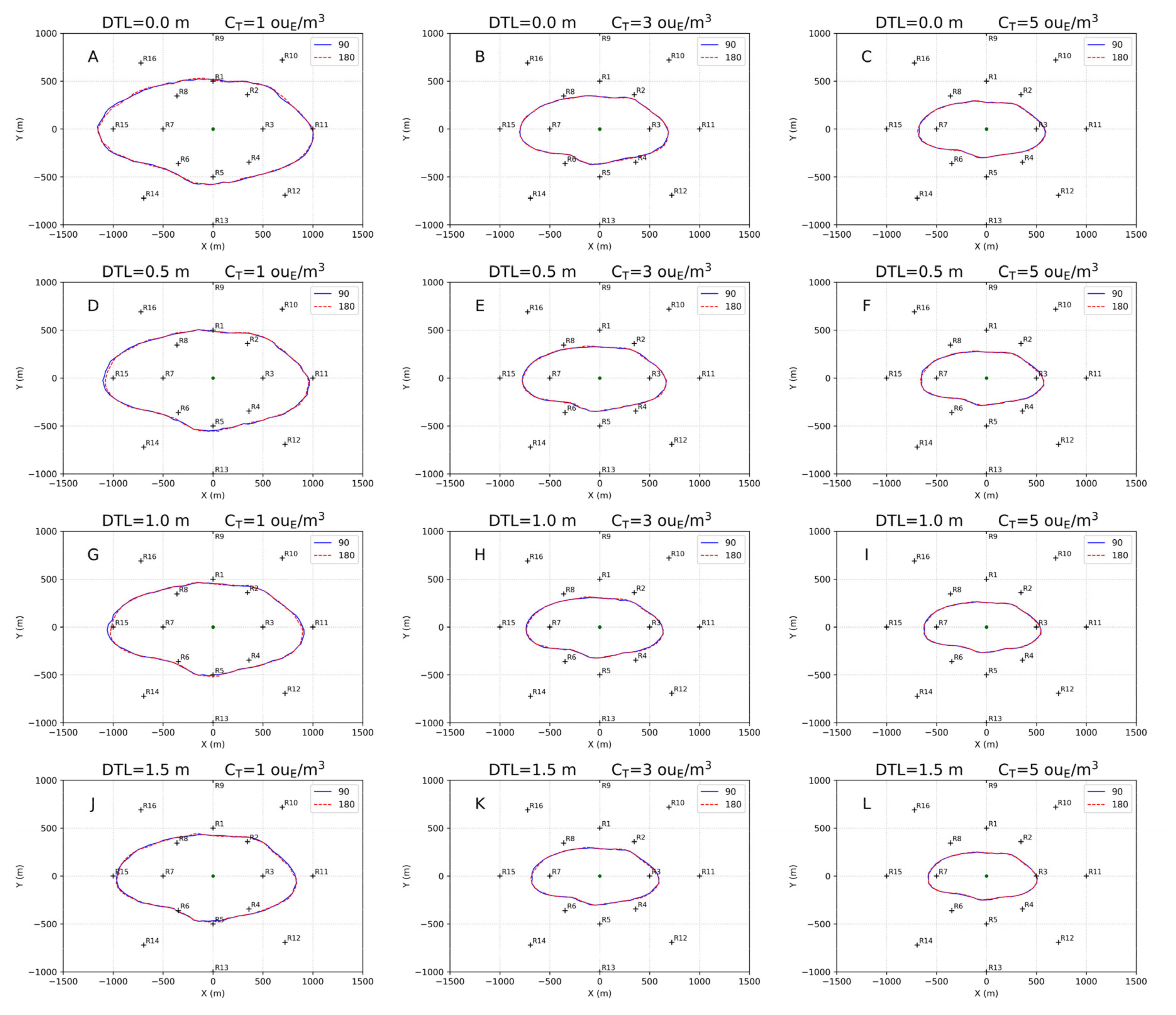
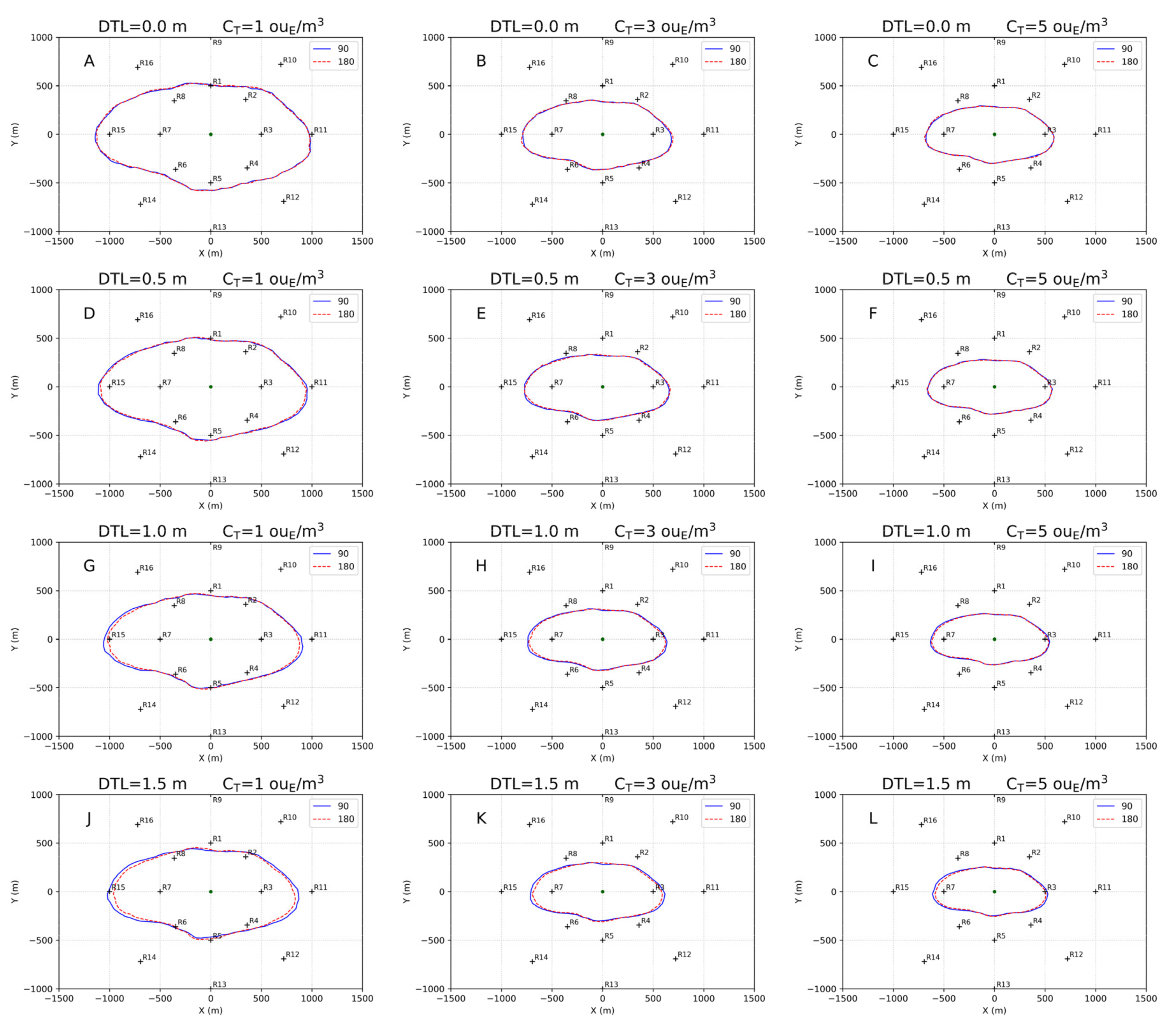
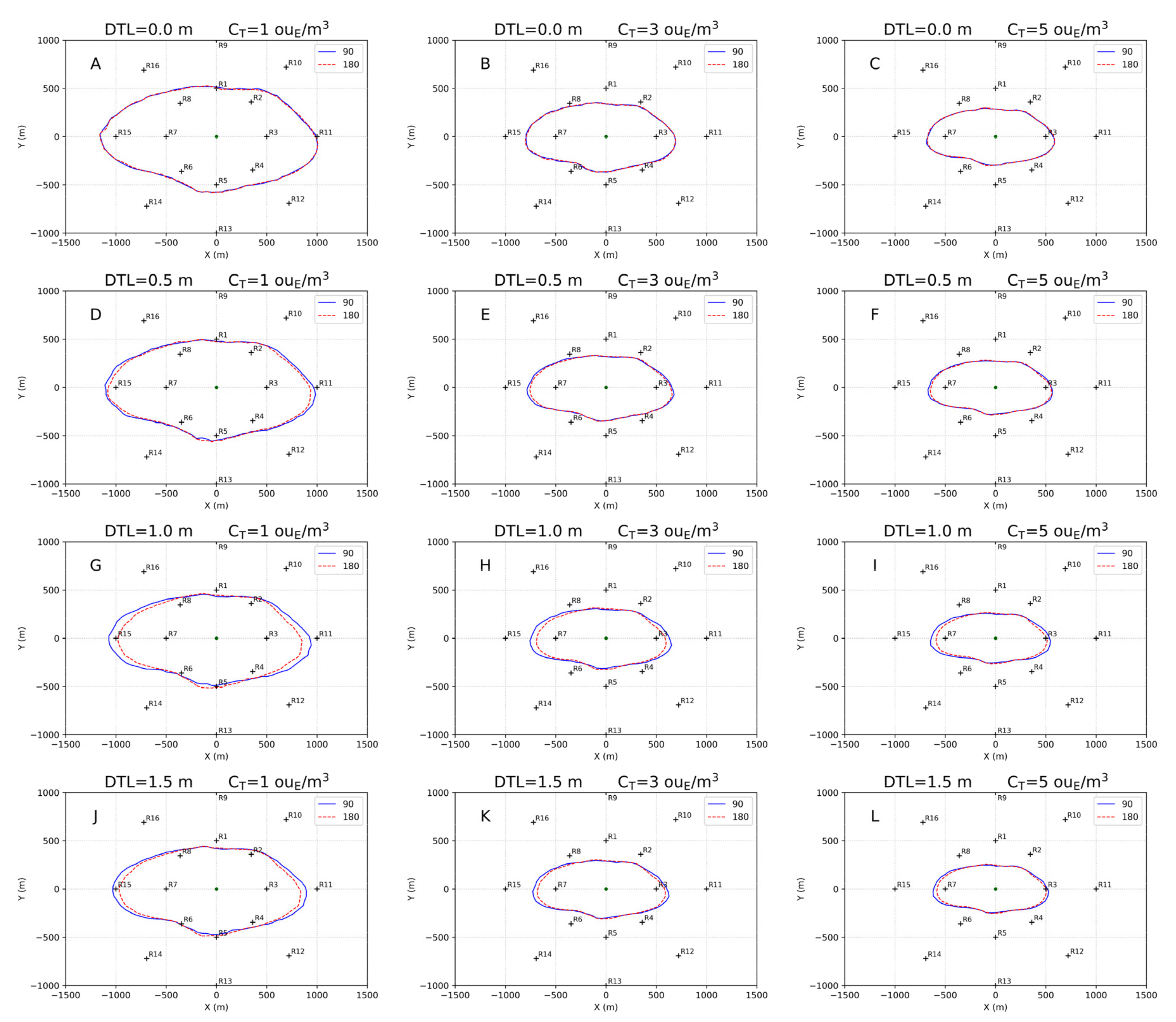
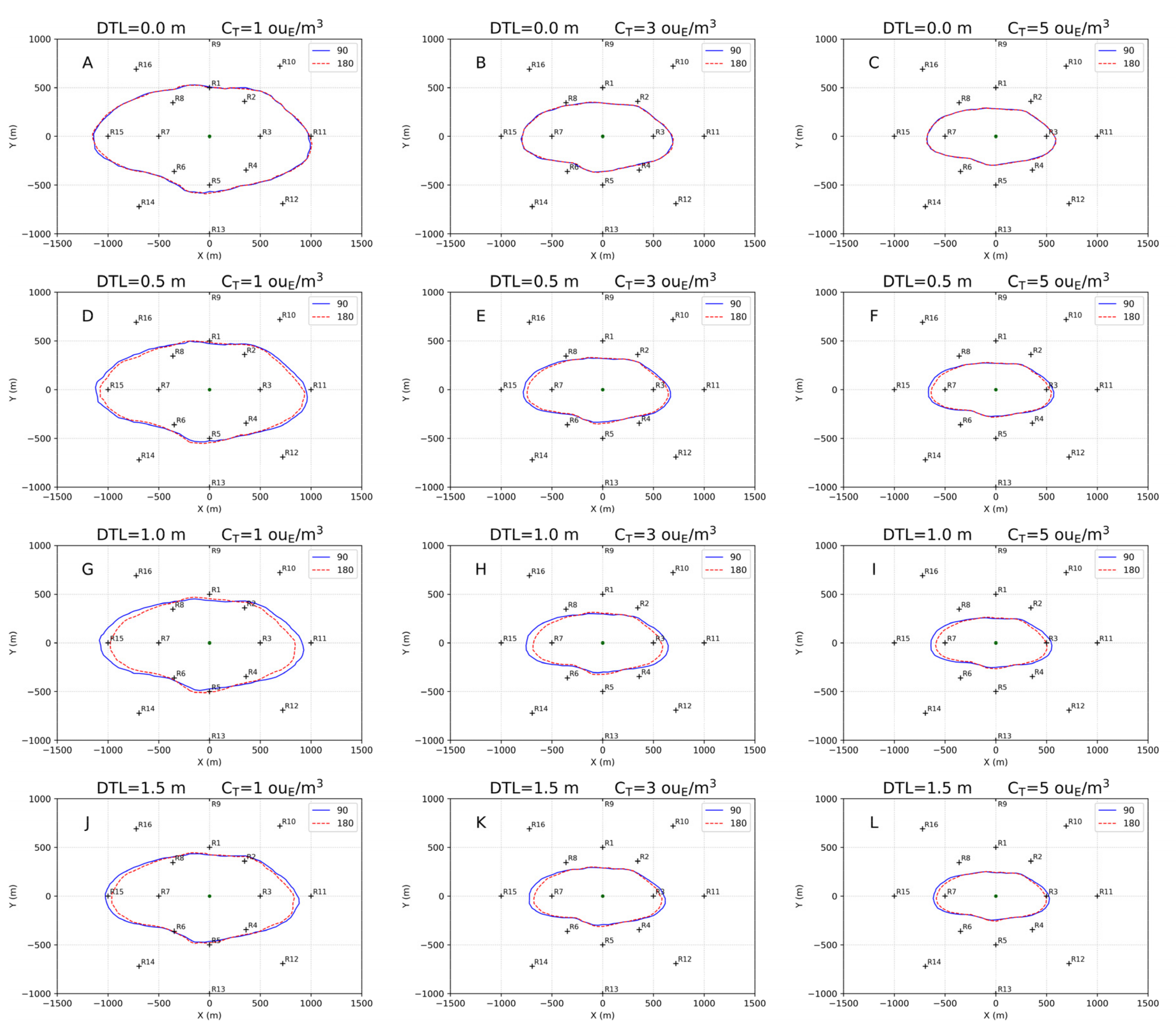
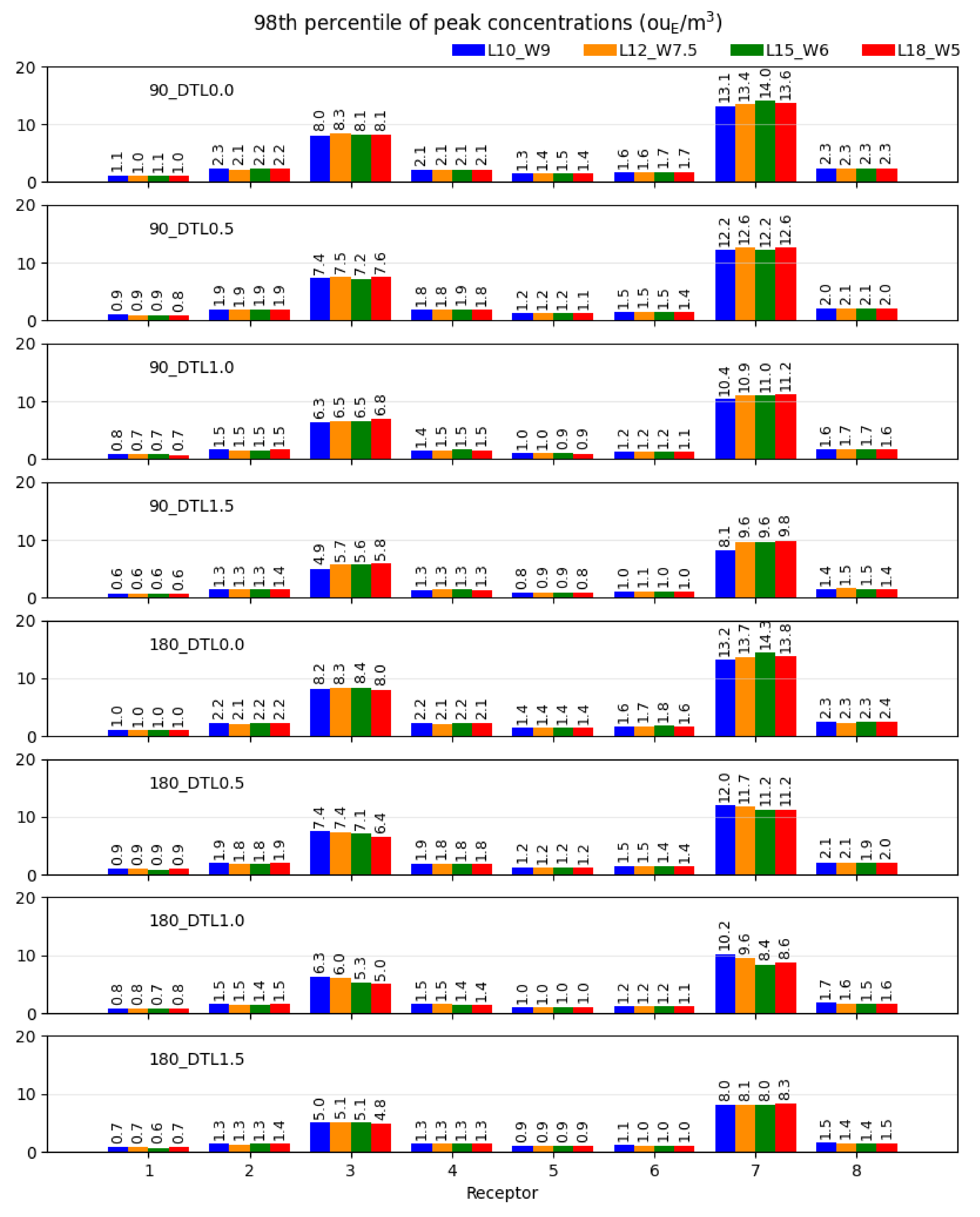
3.3. Results at Discrete Receptors
3.4. Evaluation of Uncertainties
- The proportionality factor (k = 3) between the DTL and the distance of the impingement point from the leading edge, or the distance from the separation point and the trailing edge of the cavity, used in Equation (6).
- The roughness length (z0 = 0.01 m) used in Equation (5) for determining the flow velocity close to the emitting surface.
- The height (h0 = 0.1 m) above the odor-emitting surface at which the wind speed is evaluated, Equation (5).
- The correction factor (μ = 0.8) used in Equation (5) for determining the flow velocity close to the emitting surface.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- DEQ Nuisance Odor Report. State of Oregon. Department of Environmental Quality, 24 March 2014. Available online: https://www.oregon.gov/deq/FilterDocs/NuisanceOdorReport.pdf (accessed on 11 January 2022).
- Aatamila, M.; Verkasalo, P.K.; Korhonen, M.J.; Suominen, A.L.; Hirvonen, M.-R.; Viluksela, M.K.; Nevalainen, A. Odour annoyance and physical symptoms among residents living near waste treatment centres. Environ. Res. 2011, 111, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Invernizzi, M.; Capelli, L.; Sironi, S. Proposal of Odor Nuisance Index as Urban Planning Tool. Chem. Senses 2017, 42, 105–110. [Google Scholar] [CrossRef]
- Guadalupe-Fernandez, V.; De Sario, M.; Vecchi, S.; Bauleo, L.; Michelozzi, P.; Davoli, M.; Ancona, C. Industrial odour pollution and human health: A systematic review and meta-analysis. Environ. Heal. 2021, 20, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Brancher, M.; Hieden, A.; Baumann-Stanzer, K.; Schauberger, G.; Piringer, M. Performance evaluation of approaches to predict sub-hourly peak odour concentrations. Atmos. Environ. X 2020, 7, 100076. [Google Scholar] [CrossRef]
- Barclay, J.; Diaz, C.; Galvin, G.; Bellasio, R.; Tinarelli, G.; Díaz-Robles, L.A.; Schauberger, G.; Capelli, L. New International Handbook on the Assessment of Odour Exposure Using Dispersion Modelling. Chem. Eng. Trans. 2021, 85, 175–180. [Google Scholar]
- Carrera-Chapela, F.; Donoso-Bravo, A.; Souto, J.A.; Ruiz-Filippi, G. Modeling the Odor Generation in WWTP: An Integrated Approach Review. Water Air Soil Pollut. 2014, 225, 1932. [Google Scholar] [CrossRef]
- Ravina, M.; Bruzzese, S.; Panepinto, D.; Zanetti, M. Analysis of Separation Distances under Varying Odour Emission Rates and Meteorology: A WWTP Case Study. Atmosphere 2020, 11, 962. [Google Scholar] [CrossRef]
- Martínez-Solano, F.J.; Iglesias Rey, P.L.; Gualtieri, C.; López-Jiménez, P.A. Modelling flow and concentration field in a 3D rectangular water tank. In Proceedings of the 2010 International Congress on Environmental Modelling and Software, Ottawa, ON, Canada, 5–8 July 2010. [Google Scholar]
- Jing, W.; Feng, H.; Cheng, X. Dynamic Responses of Liquid Storage Tanks Caused by Wind and Earthquake in Special Environment. Appl. Sci. 2019, 9, 2376. [Google Scholar] [CrossRef]
- Sun, X.; Li, W.; Huang, Q.; Zhang, J.; Sun, C. Large eddy simulations of wind loads on an external floating-roof tank. Eng. Appl. Comput. Fluid Mech. 2020, 14, 422–435. [Google Scholar] [CrossRef]
- Invernizzi, M.; Sironi, S. Odour Emission Rate Estimation Methods for Hydrocarbon Storage Tanks. Chem. Eng. Trans. 2020, 82, 67–72. [Google Scholar]
- UE-EPA. AP-42: Compilation of Air Emissions Factors; US-EPA: Research Triangle Park, NC, USA, 2020. Available online: https://www.epa.gov/air-emissions-factors-and-quantification/ap-42-compilation-air-emissions-factors (accessed on 19 February 2022).
- TANKS Emissions Estimation Software, Version 4.09D. Available online: https://www3.epa.gov/ttnchie1/software/tanks/ (accessed on 19 February 2022).
- Invernizzi, M.; Ilare, J.; Capelli, L.; Sironi, S. Proposal of a Method for Evaluating Odour Emissions from Refinery Storage Tanks. Chem. Eng. Trans. 2018, 68, 49–54. [Google Scholar]
- Rong, L.; Nielsen, P.V.; Zhang, G. Experimental and Numerical Study on Effects of Airflow and Aqueous Ammonium Solution Temperature on Ammonia Mass Transfer Coefficient. J. Air Waste Manag. Assoc. 2010, 60, 419–428. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cook, N. The Deaves and Harris ABL model applied to heterogeneous terrain. J. Wind Eng. Ind. Aerodyn. 1997, 66, 197–214. [Google Scholar] [CrossRef]
- Liu, Q.; Bundy, D.S.; Hoff, S.J. A study on the air flow and odor emission rate from a simplified open manure storage tank. Trans. ASAE 1995, 38, 1881–1886. [Google Scholar] [CrossRef]
- Bellasio, R.; Bianconi, R.; Mosca, S.; Zannetti, P. Formulation of the Lagrangian particle model LAPMOD and its evaluation against Kincaid SF6 and SO2 datasets. Atmos. Environ. 2017, 163, 87–98. [Google Scholar] [CrossRef]
- Bellasio, R.; Bianconi, R.; Mosca, S.; Zannetti, P. Incorporation of Numerical Plume Rise Algorithms in the Lagrangian Particle Model LAPMOD and Validation against the Indianapolis and Kincaid Datasets. Atmosphere 2018, 9, 404. [Google Scholar] [CrossRef]
- Region Lombardy. D.g.r. 15 Febbraio 2012–n. IX/3018. Determinazioni Generali in Merito Alla Caratterizzazione Delle Emissioni Gassose in Atmosfera Derivanti da Attività a Forte Impatto Odorigeno; Region Lombardy: Milan, Italy, 2012. (In Italian) [Google Scholar]
- Jiang, K.; Kaye, R. Comparison study on portable wind tunnel system and isolation chamber for determination of VOCs from areal sources. Water Sci. Technol. 1996, 34, 583–589. [Google Scholar] [CrossRef]
- Scire, J.S.; Robe, F.R.; Fernau, M.E.; Yamartino, R.J. A User’s Guide for the CALMET Meteorological Model (Version 5.0); Earth Tech Inc.: Concord, MA, USA, January 2000; Available online: http://www.src.com/calpuff/download/CALMET_UsersGuide.pdf (accessed on 19 February 2022).
- Arya, S.P. Air Pollution Meteorology and Dispersion; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- EPA. User’s Guide for the Industrial Source Complex (ISC3) Dispersion Model; Description of Model Algorithms; Report EPA-454/B-95-003b; US-EPA: Research Triangle Park, NC, USA, 1995; Volume II.
- Soulhac, L.; Perkins, R.J.; Salizzoni, P. Flow in a Street Canyon for any External Wind Direction. Bound.-Layer Meteorol. 2007, 126, 365–388. [Google Scholar] [CrossRef]
- Hotchkiss, R.S.; Harlow, F.H. Air Pollution Transport in Street Canyons; EPA-R4-73-029; US-EPA: Research Triangle Park, NC, USA, 1973.
- Yamartino, R.J.; Wiegand, G. Development and evaluation of simple models for the flow, turbulence and pollutant concentration fields within an urban street canyon. Atmos. Environ. 1986, 20, 2137–2156. [Google Scholar] [CrossRef]
- Berkowicz, R.; Hertel, O.; Larsen, S.E.; Sørensen, N.N.; Nielsen, M. Modelling Traffic Pollution in Streets; National Environmental Research Institute: Roskilde, Denmark, 1997. [Google Scholar]
- Huang, L.; Zhao, K.; Liang, J.; Kopiev, V.; Belyaev, I.; Zhang, T. A Numerical Study of the Wind Speed Effect on the Flow and Acoustic Characteristics of the Minor Cavity Structures in a Two-Wheel Landing Gear. Appl. Sci. 2021, 11, 11235. [Google Scholar] [CrossRef]
- Crook, S.D.; Lau, T.C.W.; Kelso, R.M. Three-dimensional flow within shallow, narrow cavities. J. Fluid Mech. 2013, 735, 587–612. [Google Scholar] [CrossRef]
- Ashcroft, G.; Zhang, X. Vortical structures over rectangular cavities at low speed. Phys. Fluids 2005, 17, 015104. [Google Scholar] [CrossRef]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Haq, A.U.; Nadeem, Q.; Farooq, A.; Irfan, N.; Ahmad, M.; Ali, M.R. Assessment of Lagrangian particle dispersion model “LAPMOD” through short range field tracer test in complex terrain. J. Environ. Radioact. 2019, 205-206, 34–41. [Google Scholar] [CrossRef]
- Invernizzi, M.; Brancher, M.; Sironi, S.; Capelli, L.; Piringer, M.; Schauberger, G. Odour impact assessment by considering short-term ambient concentrations: A multi-model and two-site comparison. Environ. Int. 2020, 144, 105990. [Google Scholar] [CrossRef] [PubMed]
- Vitali, L.; Monforti, F.; Bellasio, R.; Bianconi, R.; Sachero, V.; Mosca, S.; Zanini, G. Validation of a Lagrangian dispersion model implementing different kernel methods for density reconstruction. Atmos. Environ. 2006, 40, 8020–8033. [Google Scholar] [CrossRef]
- Mylne, K.R.; Mason, P.J. Concentration fluctuation measurements in a dispersing at a range up to 1000 m. Q. J. R. Meteorol. Soc. 1991, 117, 177–206. [Google Scholar] [CrossRef]
- Weather Research and Forecasting Model. Available online: https://www.mmm.ucar.edu/weather-research-and-forecasting-model (accessed on 11 January 2022).
- Bellasio, R. Analysis of wind data for airport runway design. J. Airl. Airpt. Manag. 2014, 4, 97–116. [Google Scholar] [CrossRef]
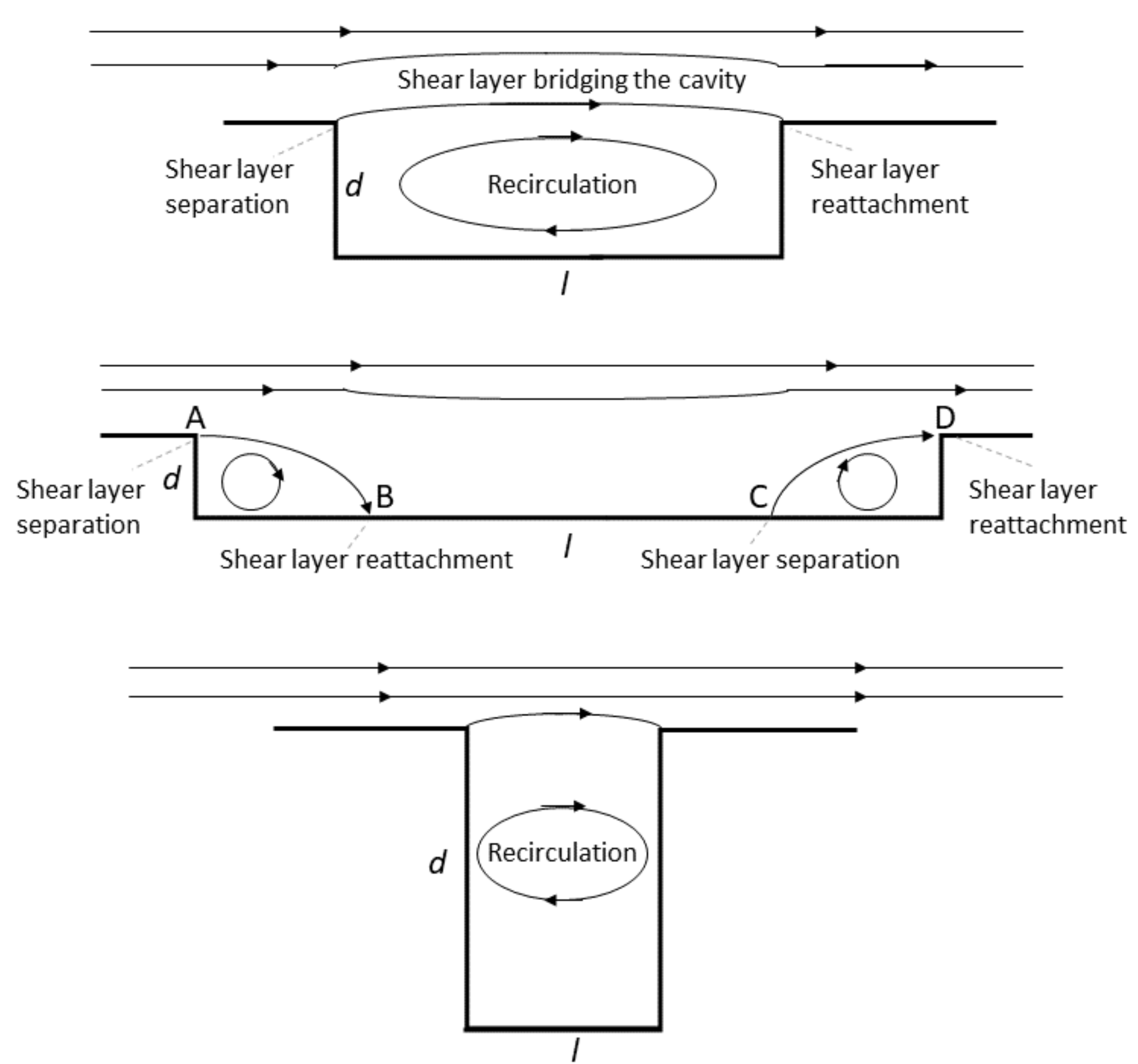
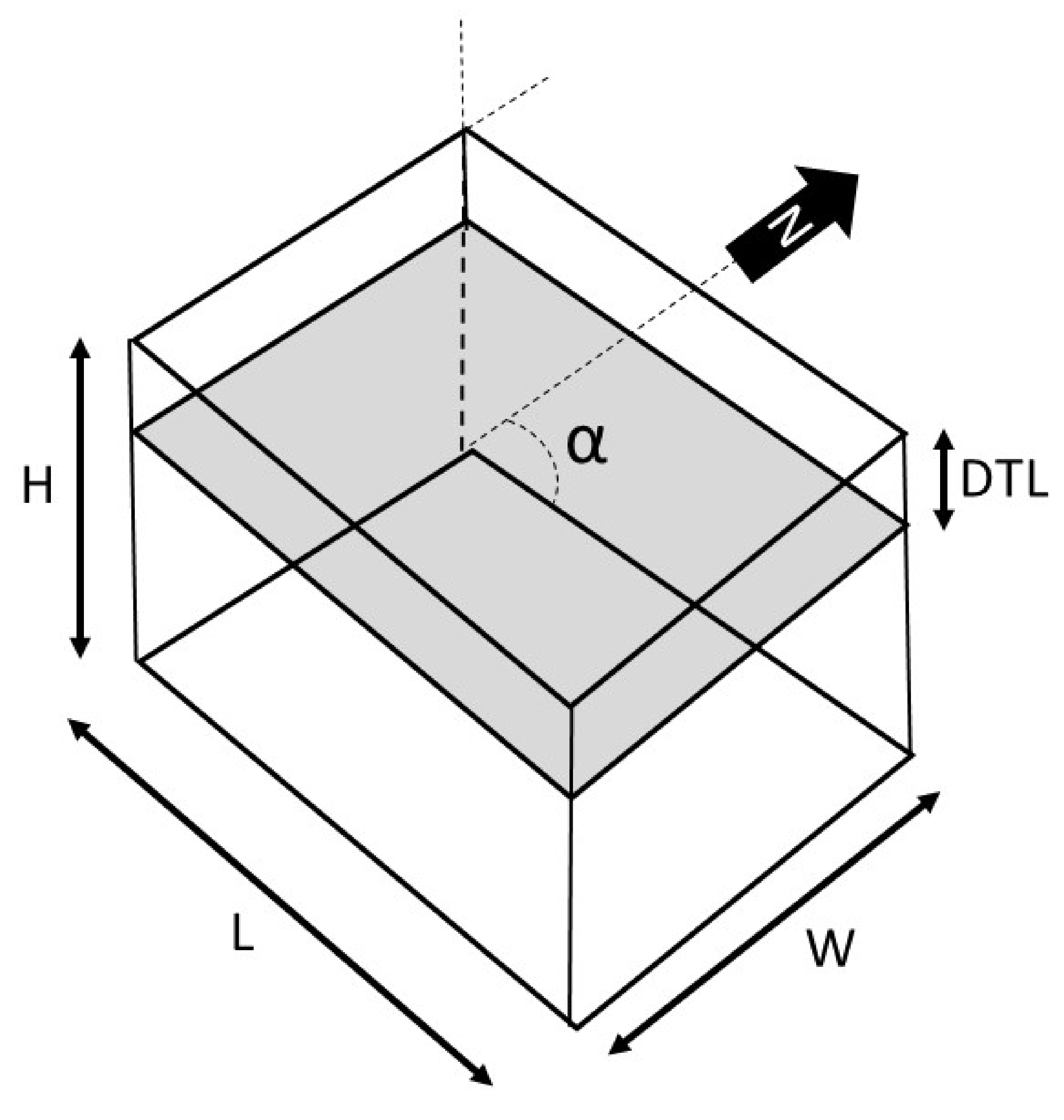
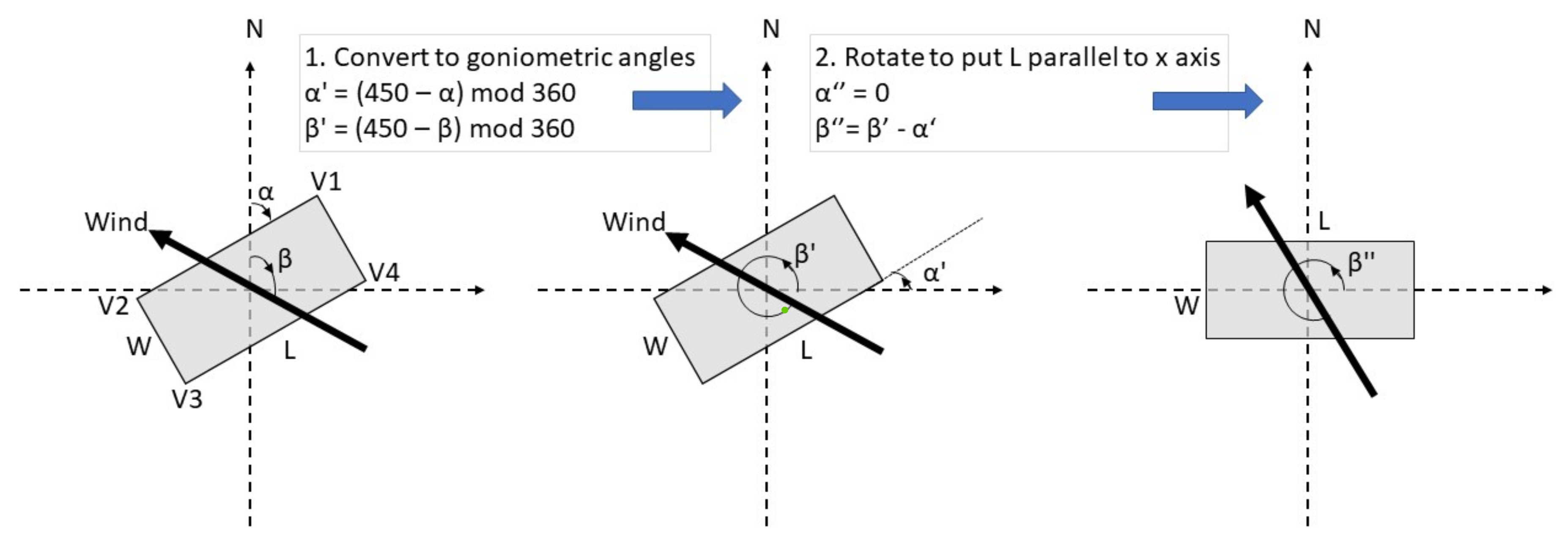

| Stability Class | Rural Terrain | Urban Terrain |
|---|---|---|
| A | 0.07 | 0.15 |
| B | 0.07 | 0.15 |
| C | 0.10 | 0.20 |
| D | 0.15 | 0.25 |
| E | 0.35 | 0.30 |
| F | 0.55 | 0.30 |
| Tank | Length (m) | Width (m) | L/W |
|---|---|---|---|
| L10_W9 | 10.0 | 9.0 | 1.11 |
| L12_W7.5 | 12.0 | 7.5 | 1.60 |
| L15_W6 | 15.0 | 6.0 | 2.50 |
| L18_W5 | 18.0 | 5.0 | 3.60 |
| Parameter | Value |
|---|---|
| Height (m) | 3 |
| DTLs (m) | 0.0, 0.5, 1.0, 1.5 |
| Orientations (degrees) | 90, 180 |
| SOER (ouE/m2/s) | 80 |
| DTL (m) | L10_W9 (%) | L12_W7.5 (%) | L15_W6 (%) | L18_W5 (%) |
|---|---|---|---|---|
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.5 | 0.5 | 2.2 | 4.5 | 6.2 |
| 1.0 | 0.8 | 3.7 | 12.2 | 13.2 |
| 1.5 | 0.9 | 6.9 | 7.9 | 7.6 |
| Tank | Wind from N or S | Wind from E or W | Ratio |
|---|---|---|---|
| T90_L18_W5 DTL0.5 | 120,431 | 132,688 | 1.10 |
| T180_L18_W5 DTL0.5 | 135,547 | 115,769 | 0.85 |
| T90_L18_W5 DTL1.0 | 92,659 | 121,976 | 1.32 |
| T180_L18_W5 DTL1.0 | 120,043 | 88,844 | 0.74 |
| T90_L18_W5 DTL1.5 | 88,831 | 109,379 | 1.23 |
| T180_L18_W5 DTL1.5 | 100,162 | 85,174 | 0.85 |
| Tank | Wind from N or S | Wind from E or W | Ratio |
|---|---|---|---|
| T90_L18_W5 DTL0.5 | 44,425 | 64,633 | 1.45 |
| T180_L18_W5 DTL0.5 | 50,364 | 56,966 | 1.13 |
| T90_L18_W5 DTL1.0 | 34,138 | 58,231 | 1.71 |
| T180_L18_W5 DTL1.0 | 45,301 | 43,770 | 0.97 |
| T90_L18_W5 DTL1.5 | 32,728 | 50,221 | 1.53 |
| T180_L18_W5 DTL1.5 | 38,940 | 41,962 | 1.08 |
| CT = 1 ouE/m3 | CT = 3 ouE/m3 | CT = 5 ouE/m3 | ||||||
|---|---|---|---|---|---|---|---|---|
| Tank | Or. (degrees) | DTL (m) | ΔX (%) | ΔY (%) | ΔX (%) | ΔY (%) | ΔX (%) | ΔY (%) |
| L10_W9 | 90 | 0.5 | −4.3 | −4.4 | −3.1 | −6.9 | −2.7 | −4.2 |
| L10_W9 | 180 | 0.5 | −7.0 | −3.3 | −3.1 | −6.9 | −2.7 | −4.2 |
| L10_W9 | 90 | 1.0 | −9.1 | −13.3 | −8.5 | −13.8 | −8.2 | −14.6 |
| L10_W9 | 180 | 1.0 | −11.8 | −12.2 | −8.5 | −13.8 | −8.2 | −14.6 |
| L10_W9 | 90 | 1.5 | −16.0 | −17.8 | −14.6 | −17.2 | −14.5 | −20.8 |
| L10_W9 | 180 | 1.5 | −16.0 | −17.8 | −14.6 | −17.2 | −14.5 | −20.8 |
| L12_W7.5 | 90 | 0.5 | −2.7 | −4.4 | −2.3 | −3.6 | −3.6 | −4.3 |
| L12_W7.5 | 180 | 0.5 | −4.3 | −3.3 | −2.3 | −3.6 | −3.6 | −4.3 |
| L12_W7.5 | 90 | 1.0 | −7.6 | −13.3 | −6.2 | −14.3 | −7.2 | −10.9 |
| L12_W7.5 | 180 | 1.0 | −11.4 | −12.2 | −8.5 | −12.5 | −9.0 | −10.9 |
| L12_W7.5 | 90 | 1.5 | −10.8 | −18.9 | −10.1 | −19.6 | −10.8 | −17.4 |
| L12_W7.5 | 180 | 1.5 | −16.2 | −14.4 | −13.2 | −14.3 | −15.3 | −15.2 |
| L15_W6 | 90 | 0.5 | −4.8 | −4.4 | −0.8 | −7.0 | −1.8 | −6.5 |
| L15_W6 | 180 | 0.5 | −7.0 | −3.3 | −4.7 | −7.0 | −5.4 | −4.3 |
| L15_W6 | 90 | 1.0 | −7.5 | −15.6 | −5.4 | −15.8 | −5.4 | −13.0 |
| L15_W6 | 180 | 1.0 | −15.5 | −11.1 | −14.0 | −12.3 | −13.5 | −10.9 |
| L15_W6 | 90 | 1.5 | −10.7 | −20.0 | −8.5 | −19.3 | −9.0 | −17.4 |
| L15_W6 | 180 | 1.5 | −16.6 | −16.7 | −14.0 | −15.8 | −14.4 | −15.2 |
| L18_W5 | 90 | 0.5 | −1.6 | −7.8 | −2.3 | −8.8 | −1.8 | −8.7 |
| L18_W5 | 180 | 0.5 | −5.9 | −4.4 | −7.7 | −3.5 | −6.4 | −4.3 |
| L18_W5 | 90 | 1.0 | −4.9 | −16.7 | −5.4 | −17.5 | −5.5 | −15.2 |
| L18_W5 | 180 | 1.0 | −14.6 | −12.2 | −14.6 | −10.5 | −12.7 | −10.9 |
| L18_W5 | 90 | 1.5 | −9.7 | −20.0 | −9.2 | −17.5 | −9.1 | −15.2 |
| L18_W5 | 180 | 1.5 | −15.7 | −16.7 | −15.4 | −12.3 | −13.6 | −13.0 |
| CT = 1 ouE/m3 | CT = 3 ouE/m3 | CT = 5 ouE/m3 | |||||
|---|---|---|---|---|---|---|---|
| Tank | DTL (m) | ΔX (%) | ΔY (%) | ΔX (%) | ΔY (%) | ΔX (%) | ΔY (%) |
| L10_W9 | 0.5 | −2.8 | 1.2 | 0.0 | 0.0 | 0.0 | 0.0 |
| L10_W9 | 1.0 | −2.9 | 1.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| L10_W9 | 1.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| L12_W7.5 | 0.5 | −1.7 | 1.2 | 0.0 | 0.0 | 0.0 | 0.0 |
| L12_W7.5 | 1.0 | −4.1 | 1.3 | −2.5 | 2.1 | −1.9 | 0.0 |
| L12_W7.5 | 1.5 | −6.1 | 5.5 | −3.4 | 6.7 | −5.1 | 2.6 |
| L15_W6 | 0.5 | −2.2 | 1.2 | −3.9 | 0.0 | −3.7 | 2.3 |
| L15_W6 | 1.0 | −8.7 | 5.3 | −9.0 | 4.2 | −8.6 | 2.5 |
| L15_W6 | 1.5 | −6.6 | 4.2 | −5.9 | 4.3 | −5.9 | 2.6 |
| L18_W5 | 0.5 | −4.4 | 3.6 | −5.5 | 5.8 | −4.6 | 4.8 |
| L18_W5 | 1.0 | −10.2 | 5.3 | −9.8 | 8.5 | −7.7 | 5.1 |
| L18_W5 | 1.5 | −6.6 | 4.2 | −6.8 | 6.4 | −5.0 | 2.6 |
| Tank | Or. (degrees) | DTL (m) | Mean (ouE/s) | Median (ouE/s) | Min (ouE/s) | Max (ouE/s) | StdDev (ouE/s) | Calculated (ouE/s) |
|---|---|---|---|---|---|---|---|---|
| L10_W9 | 90 | 0.5 | 41,691 | 41,730 | 39,328 | 43,251 | 684 | 41,767 |
| L10_W9 | 90 | 1.0 | 36,288 | 36,415 | 31,091 | 39,967 | 1528 | 36,429 |
| L10_W9 | 90 | 1.5 | 27,370 | 27,604 | 20,275 | 33,146 | 2388 | 29,891 |
| L10_W9 | 180 | 0.5 | 41,258 | 41,315 | 38,950 | 43,141 | 763 | 41,326 |
| L10_W9 | 180 | 1.0 | 35,070 | 35,209 | 28,745 | 39,154 | 1777 | 35,273 |
| L10_W9 | 180 | 1.5 | 27,352 | 27,557 | 20,467 | 32,972 | 2364 | 27,610 |
| L12_W7.5 | 90 | 0.5 | 42,396 | 42,438 | 40,587 | 43,739 | 556 | 42,418 |
| L12_W7.5 | 90 | 1.0 | 38,010 | 38,108 | 34,226 | 40,998 | 1202 | 38,099 |
| L12_W7.5 | 90 | 1.5 | 32,844 | 32,982 | 25,411 | 37,563 | 2047 | 33,017 |
| L12_W7.5 | 180 | 0.5 | 40,336 | 40,403 | 37,131 | 42,602 | 946 | 40,432 |
| L12_W7.5 | 180 | 1.0 | 32,633 | 32,865 | 24,711 | 37,868 | 2271 | 32,837 |
| L12_W7.5 | 180 | 1.5 | 27,270 | 27,388 | 20,250 | 32,841 | 2293 | 27,610 |
| L15_W6 | 90 | 0.5 | 43,003 | 43,035 | 41,594 | 44,107 | 448 | 43,060 |
| L15_W6 | 90 | 1.0 | 39,647 | 39,715 | 36,613 | 41,875 | 915 | 39,698 |
| L15_W6 | 90 | 1.5 | 35,756 | 35,837 | 30,559 | 39,342 | 1506 | 35,872 |
| L15_W6 | 180 | 0.5 | 38,941 | 39,052 | 34,346 | 41,877 | 1224 | 39,051 |
| L15_W6 | 180 | 1.0 | 28,550 | 28,787 | 21,321 | 34,182 | 2421 | 28,800 |
| L15_W6 | 180 | 1.5 | 27,469 | 27,700 | 20,323 | 32,682 | 2355 | 27,610 |
| L18_W5 | 90 | 0.5 | 43,447 | 43,470 | 42,238 | 44,396 | 370 | 43,483 |
| L18_W5 | 90 | 1.0 | 40,677 | 40,738 | 38,233 | 42,544 | 743 | 40,729 |
| L18_W5 | 90 | 1.5 | 37,590 | 37,654 | 33,897 | 40,379 | 1173 | 37,656 |
| L18_W5 | 180 | 0.5 | 37,513 | 37,639 | 32,277 | 41,190 | 1498 | 37,620 |
| L18_W5 | 180 | 1.0 | 28,509 | 28,653 | 21,226 | 34,121 | 2468 | 28,800 |
| L18_W5 | 180 | 1.5 | 27,380 | 27,633 | 20,473 | 32,808 | 2362 | 27,610 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellasio, R.; Bianconi, R. A Heuristic Method for Modeling Odor Emissions from Open Roof Rectangular Tanks. Atmosphere 2022, 13, 367. https://doi.org/10.3390/atmos13030367
Bellasio R, Bianconi R. A Heuristic Method for Modeling Odor Emissions from Open Roof Rectangular Tanks. Atmosphere. 2022; 13(3):367. https://doi.org/10.3390/atmos13030367
Chicago/Turabian StyleBellasio, Roberto, and Roberto Bianconi. 2022. "A Heuristic Method for Modeling Odor Emissions from Open Roof Rectangular Tanks" Atmosphere 13, no. 3: 367. https://doi.org/10.3390/atmos13030367
APA StyleBellasio, R., & Bianconi, R. (2022). A Heuristic Method for Modeling Odor Emissions from Open Roof Rectangular Tanks. Atmosphere, 13(3), 367. https://doi.org/10.3390/atmos13030367






