Abstract
One of the main current challenges is detecting changes in the climate at the regional level. The present study tried to address this issue by looking for some influence of large-scale climate oscillations on the climate of a small and complex topography basin in Central Mexico. We collected temperature and precipitation data from 44 climate stations within an area of up to 20 km around the Apatlaco River sub-basin (~30 km south of Mexico City) during the period 1950–2013. Posteriorly, quality analysis and homogenization of the climate databases were performed by using the Climatol algorithm. We analyzed the trend of five ETCCDI climate indices through several statistical tests. Finally, we calculated simple Pearson correlations of those indices with four climate oscillation indices that have affected Mexico’s climate in the recent past. The results revealed that the Atlantic Multidecadal Oscillation had a clear influence on four of the five indices analyzed in the study area. The summer days and the extreme maximum and minimum temperatures accounted for a small increase in the temperature of the middle east (urban) basin compared to the middle west (rural), which could be a manifestation of the heat island effect or the difference in soil type (and therefore albedo) of the two zones. As expected, the midsummer drought effect predominated in most of the sub-basin, with only the uppermost part showing monsoon-type precipitation during a typical year.
1. Introduction
In search of a better comprehension of global climate variability, research interests have extended from global warming to internal climate variability [1].
Internal climate variability comprises various timescales, such as the interannual, decadal, and multidecadal. The sea surface temperature changes related to the dominant internal climate variability are the El Niño–Southern Oscillation (ENSO), the Pacific Decadal Oscillation (PDO), and the Atlantic Multidecadal Oscillation (AMO), which run at 2–7-year, decadal, and multidecadal (65–80-year) time scales, respectively [2,3,4].
The decadal to multidecadal internal climate variability is critical for understanding the timing and magnitude of changes in the global mean surface temperature [5,6], regional climate [4,7,8], and climate extremes [9].
The interannual climate variability of Mexico is determined by the dynamics of the Intertropical Convergence Zone (ITCZ) [10,11], the ENSO [12,13,14,15,16,17], the Madden–Julian Oscillation (MJO) [18,19,20], the PDO [16,17,21,22,23], the North Atlantic Oscillation (NAO) [24,25], and the AMO [21,26].
Climate variability in central Mexico is driven primarily by the PDO/ENSO and the AMO/NAO signals [27]. The first attempts to relate the precipitation and temperature behavior with low-frequency oscillations (ENSO, PDO, AMO) in Mexico were reported in [26,28], respectively. Ref. [21] stated that the AMO probably lost much of its influence in Central Mexico at the beginning of the 20th century, and since then, the PDO has driven the major changes in the climate. The force of the Atlantic plays an important role in regulating summer rains in central Mexico [29]. The difficulty in detecting the AMO could be due to the influence of the PDO/ENSO, which complicates the pattern of climate changes related to the AMO [30,31].
One way to study recent changes in climate and its extremes is through the climate change indices recommended by the now extinct CCl/WCRP/JCOMM Expert Team on Climate Change Detection and Indices (ETCCDI). Within the agreements of the 17th edition of the WMO Commission on Climatology, the ETCCDI was suspended, and the new group in charge of the now Sector-Specific Climate Indices (SCI) is the Commission for Weather, Climate, Water, and Related Environmental Services and Applications (SERCOM)—Expert Team on Climate Information for Decision-Making [32].
On a global scale, several studies have applied the ETCCDI indices to monitor changes in climatic extremes [33,34] and explain the pause in global warming in the 2010s [35]. The ETCCDI indices have also been used for the regional analysis of extreme weather events (both historical and future); for example, in China [36,37,38,39,40], India [41,42], Europe [43,44], Africa [45,46], and the Middle East [47], among others.
In Mexico, there are several relatively recent studies that analyzed climatic extremes of surface temperature and precipitation with the ETCCDI indices. In the case of surface temperature, practically all the studies showed a clear warming signal at the regional level, particularly in the last decades. For instance, [48] found, in the central and southern parts of Mexico, positive trends for extreme maximum temperatures and negative trends for extreme minimum temperatures. Another study found, for most of northern Mexico (above 20° N), an increase in the maximums of minimum temperatures that was even greater than extreme maximum temperatures [49]. Ref. [50] analyzed the behavior of some climate indices for two basins, one in the north (arid) and the other in the south (humid) of Mexico, and found an increase in the Diurnal Temperature Range (DTR) in both basins; the same results were found in another study in Zacatecas, in the north central part of Mexico [51].
For precipitation, no conclusive results have been found in Mexico. For instance, the study in [48] found no appreciable change in the precipitation mean, but there was in the extremes, since humid and very humid days increased. Another study found no statistically significant data for precipitation trends in Mexico [49]. Ref. [23] found that the variability of the precipitation annual indices was partially linked to natural variations of the combined effects of ENSO/PDO, and that most of the trends were explained by the PDO. Finally, two recent studies on Zacatecas reached contrasting conclusions regarding the precipitation trend, probably due to differences in the database period, since one of them argued that precipitation increased (period 1976–2015) [51] and the other that it decreased (period 1961–2014) [52].
The objective of this study was to contribute to a better understanding of the mechanisms that drive climate variability in the central part of Mexico. To achieve this, we performed quality and homogenization analyzes on a set of climate stations around the Apatlaco River sub-basin, located 30 km south of the Mexico City metropolitan area, to improve data reliability. Finally, we calculated some ETCCDI indices for surface temperature and precipitation, analyzed the results, and correlated them with some of the main climate oscillations mentioned above in the period of 1950–2013.
Details of how this was done are explained in the next section.
2. Materials and Methods
2.1. Data and Study Domain
The Apatlaco River sub-basin, which belongs to the Amacuzac River basin, is between the geographical coordinates 18°36′40″and 19°11′40″ north latitude, and 99°09′40″ and 99°21′00″ west longitude, about 30 km south of Mexico City. It covers an area of approximately 806 km2, with 88% in the State of Morelos and the rest in the State of Mexico and Mexico City [53]. Despite its small size, the sub-basin has a very steep slope, ranging from 900 m above sea level (masl) in the southern part of it to more than 3000 masl in the northern part (Figure 1, bottom left).
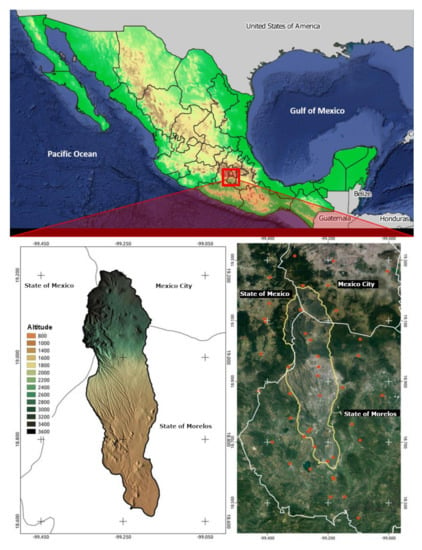
Figure 1.
Location and topography of the Apatlaco River sub-basin (bottom left), and location of the 44 climatic stations (bottom right) analyzed in this study, 14 of which were within the limits of the sub-basin.
According to the topography, the sub-basin was divided into an upper part (limited by the 2000 masl level contour), medium part (limited to the south by the 1200 masl level contour), and lower part (below the 1200 masl level). In addition, the middle part was subdivided into urban (middle east) and rural (middle west) areas based on land use, leaving at the end four study areas within the sub-basin.
Information on precipitation and daily maximum and minimum temperature was collected from 44 climatic stations located in an area of up to 20 km around the Apatlaco River sub-basin, with only 14 of them within the sub-basin (Figure 1, bottom right). The 20 km area around the sub-basin was used to make the data interpolation more accurate within the sub-basin area. The source of the data was the Mexican climatological database of the National Meteorological Service of Mexico (SMN). The available data from the 44 climatic stations covered 49% of the total data in the precipitation time series, and 46% in the temperature series for the base period of 1950–2013.
2.2. Quality Control Analysis and Homogenization of Climate Data
The series of meteorological observations are of great importance for the study of climate variability. One of the main problems is that the series can be affected by nonclimatic factors, whether they are errors in taking measurements, changes in instrumentation, or in the environment of the station. These alterations are known as inhomogeneities, and they mask the genuine changes in the climate, causing the study of climatic series to lead to erroneous conclusions.
The process of quality control, homogenization, and in-filling of the missing data from the climatic databases was carried out using the Climatol software [54], version 3.1, executed in the R programming language. This method allowed in-filling the gaps in the time series due to climatic conditions, in addition to detecting anomalous values, which may have occurred due to the errors mentioned above. Climatol uses the method of Paulhus and Kohler [55] to fill in daily series through averages of nearby stations; and normalizes data by dividing by its mean, subtracting means, or full standardization. The key problem with this method is that the means of the series in the study period are not known if they are not complete, which is common in a series of real data. To solve this problem, Climatol calculates these parameters with available data in each series, fills in missing data using the provisional means and standard deviations, and recalculates them with the filled series. Subsequently, the initially missing data are recalculated, obtaining new means and standard deviations, repeating until the mean does not change when rounding with the initial precision of the data [54].
Once the means are stabilized, all the data are normalized, and they are estimated using the following expression:
where is a data item estimated from the corresponding nearest n data available at each time step, and is the weight assigned to them [54]. The weight comes from the application of the technique of Paulhus and Kohler, which is used by Climatol [54] to interpolate missing precipitation records in mountainous regions by using the normal-ratio method [55].
To check the homogeneity of the climatic series, Climatol uses the Standard Normal Homogeneity Test (SNHT) [56]. This process and the spatial interpolation described above make it possible to correct the inhomogeneities mentioned above. The daily homogenized data per station were interpolated to a regular mesh of 0.02 × 0.02 degrees (~ 20 × 20 km) of resolution per cell covering the entire study area.
2.3. Calculation of the ETCCDI Indices
The homogenized database was used to calculate the climatic indices recommended by the ETCCDI [57] using the ClimPACT2 software.
In this study, we present the results of five indices for analysis:
- a.
- SU. Summer days.
Let Txij be the maximum daily temperature on day i, period j. Count the number of days when:
- b.
- Txx. Extreme maximum temperature.
Let Txkj be the maximum daily temperature in month k, period j. The maximum daily maximum temperature each month is then:
- c.
- Tnn. Extreme minimum temperature.
Let Tnkj be the minimum daily temperature in month k, period j. The minimum daily minimum temperature each month is then:
- d.
- PcpT. Total precipitation.
Let RRij be the daily amount of precipitation on day i, period j. If I represents the number of days in j, then:
- e.
- r20 mm. Days with rain greater than 20 mm.
Let RRij be the daily amount of precipitation on day i, period j. Count the number of days where:
To suppress the differences between the total accumulated values of the ETCCDI indices for the different study areas, their standardized anomalies were obtained.
2.4. Trend Analysis of the ETCCDI Indices and Serial Correlation
Since the time series of the five previous indices did not necessarily fulfill the assumption of normality, nonparametric methods generally give better results. Two of the most robust methods in finding trends, the Mann–Kendall test [58] and Spearman’s rank correlation coefficient test (also known as Spearman’s rho test) [59,60], were applied in this study. Slopes were calculated by the Sen’s method [61], which is another nonparametric method. The two previous tests and the Sen’s slope method are widely used for the analysis of hydrometeorological time series [62]. All the above parameters were applied at a significance level of α = 0.05 to assess whether the results were statistically significant (p ≤ 0.05).
However, it is known that results are seriously affected when the time series are serially correlated [63]. To test the serial correlation in the data, the lag-1 serial correlation coefficients were calculated in the same way as in [63]. For the series that were serially correlated, the Mann–Kendall and Spearman’s rho tests were not sufficient. Since there is no universal method of considering the serial correlation present in the time series, five additional statistical tests were applied in the same way as in [63], and we confirmed that there was a trend if at least three of the five tests were favorable with at least 95% confidence. The tests carried out were:
- Prewhitening Mann–Kendall (PWMK) [64,65];
- Trend-free prewhitening Mann–Kendall (TFPWMK) [66];
- Bias correction applied to prewhitening (BCPW) [67];
- Variance correction approach suggested by Hamed and Ramachandra (MMKH) [68];
- Variance correction approach suggested by Yue and Wang (MMKY) [69].
These tests are extensively discussed in [63], so we will not repeat them here.
2.5. Calculation of the Pearson Correlations between ETCCDI Indices and Climate Oscillation Indices, and Their Statistical Significance
Finally, the time series of various oscillation indices were obtained through the NOAA Physical Sciences Laboratory website for the given study period. The climatic indices were chosen based on those teleconnections that have had some influence on the climatology of Mexico according to the literature (e.g., AMO, PDO, NAO, ENSO).
The time series of the oscillation indices were correlated with the time series of the standardized anomalies of the ETCCDI indices. It was preferred to make comparisons with the standardized anomalies and not with the direct values of the indices in order to make a better comparison between the different areas in which the sub-basin was subdivided. Correlations between ETCCDI indices and those between oscillation indices were also obtained. Finally, correlations with statistical significance of up to 95% confidence (p ≤ 0.05) were obtained following a standard statistical method.
The results are shown below.
3. Results
3.1. Homogenization and Climatology of the Apatlaco River Sub-Basin
Some results about the quality control and homogenization procedures applied to the 44 climatological stations in the neighborhood of the Apatlaco River sub-basin using Climatol are given in the Supplementary Materials. However, it is worth mentioning that 38.6% of the stations presented inhomogeneities for precipitation (a total of 27 break points; Table S1), 79.5% of the stations presented inhomogeneities for maximum temperature (a total of 139 break points; Table S2), and 70.4% of the stations presented inhomogeneities for minimum temperature (a total of 94 break points; Table S3).
Using the homogenized mesh database (~ 20 × 20 km spatial resolution), the mean annual precipitation (mm/year) and the mean annual maximum and minimum temperature (°C) are presented during the period of 1950–2013 for the Apatlaco River sub-basin (Figure 2).
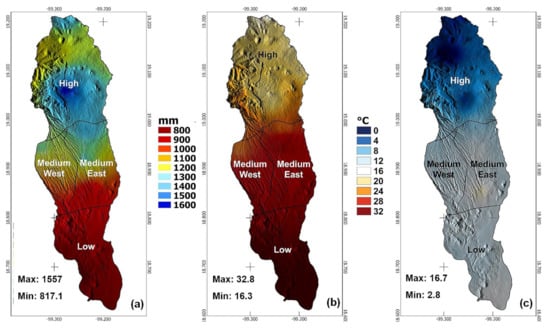
Figure 2.
(a) Annual mean precipitation (mm/year), (b) mean annual maximum temperature (°C), and (c) mean annual minimum temperature (°C) and their maximum and minimum values for the Apatlaco River sub-basin obtained with the database homogenized in mesh for the period 1950–2013. The four study areas (high, middle east, middle west, and low) for this work are also delimited.
Given the size and shape of the sub-basin and its remarkable orographic gradient, the found behavior of the three variables analyzed agreed with the expectations based on general climatological knowledge. Precipitation was lower in the lower part of the sub-basin and higher in the upper part. Higher values were also noted in the northern part of the middle east zone (compared to the middle west zone at the same latitude), which was the urbanized zone (metropolitan zone of the city of Cuernavaca) and where a potential effect related to the heat island caused higher rainfall in that area.
For the maximum and minimum temperatures, the behavior was basically defined by the topography, with temperatures (both maximum and minimum) higher in the lower part of the basin and lower in the upper part. Similarly, the thermal gradient in the northern part of the mideast zone is more pronounced than in the midwest zone, with the possibility of generating stronger convective events, particularly during the rainy season.
The annual cycles of the analyzed variables are shown through climograms for each study region (Figure 3). The greatest differences are shown in the precipitation values, in which we see that a monsoon-type behavior predominated (maximum rainfall in summer and minimum in winter) for the entire basin, which was defined by the relatively high rainfall in the upper part of the basin. There was also a minor difference when comparing the two middle zones: in the eastern (urban) zone, the second maximum of precipitation was delayed until September, which is the typical maximum in the tropical zone of Mexico due to the influence of tropical cyclones.
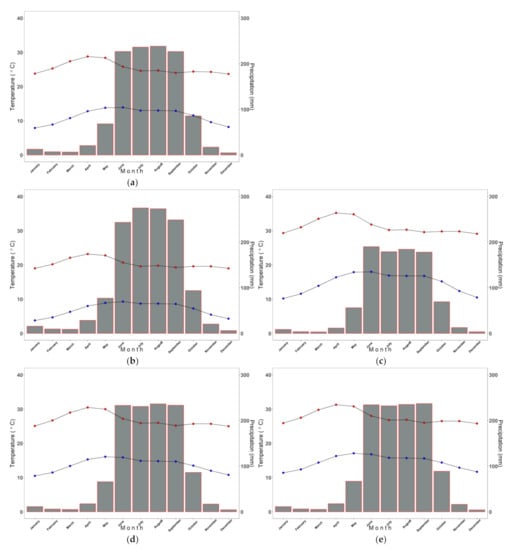
Figure 3.
Climograms with the annual precipitation cycle (mm, gray bars) and maximum temperature (°C) (red lines) and minimum (blue lines) for the (a) entire sub-basin, (b) upper zone, (c) lower zone, (d) middle west zone, and (e) middle east zone of the Apatlaco River sub-basin.
As expected, the general behavior of the annual temperature cycle was more uniform, although there were differences in the magnitude of the values for the different regions. Thus, for the maximum temperature, the maximum values were in April and the minimums were in December. For the minimum temperature, the maximum values were in June and the minimums again were in December for all areas.
3.2. Climate Indices
Using the homogenized precipitation and temperature databases of the Apatlaco River sub-basin, the five indices of climate change mentioned above were calculated. The time series of the averaged climate change indices for the sub-basin are presented in Figure 4.
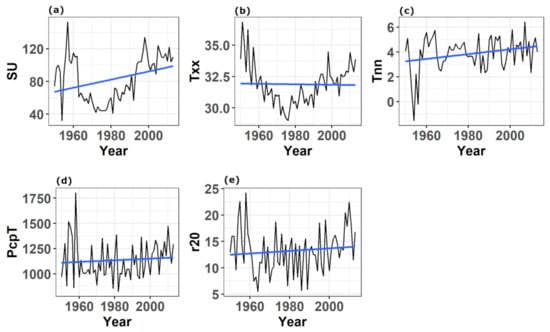
Figure 4.
Time series of (a) days of summer (SU), (b) extreme maximum temperature (Txx, in °C), (c) extreme minimum temperature (Tnn, in °C), (d) total precipitation (PcpT, in mm/year), and (e) days with rain greater than 20 mm (r20), averaged annually for the Apatlaco River sub-basin. The slope of a simple linear regression is also shown.
The summer days (SU) time series showed relatively high values (>80 days) for most of the 1950s, despite a very sharp minimum in 1954 (discussed later) (Figure 4a). Subsequently, the values declined and remained low until the early 1990s, when they increased again until the end of the period in the early 2010s. The value of a simple linear trend for the entire period showed a positive slope of 0.5 days/year (Table 1).

Table 1.
Calculation of different parameters and statistical tests for the five ETCCDI indices analyzed here (SU, Txx, Tnn, PcpT, and r20). The results for the linear trend (Trend), the Mann–Kendall (MK) test, the slope of Sen (SS), and the Spearman’s rho correlation test (SRC), without considering the possible serial correlation (SC) of the time series, are given; as well as for the prewhitening Mann–Kendall (PWMK); trend-free prewhitening Mann–Kendall (TFPWMK), bias-correction applied to prewhitening (BCPW), variance correction approach suggested by Hamed and Ramachandra (MMKH), and variance correction approach suggested by Yue and Wang (MMKY). Results that were statistically significant with 95% confidence are highlighted in bold.
The time series for the extreme maximum temperature (Txx) showed the highest values (>35 °C) at the beginning of the period, and the values decreased almost monotonically until the mid-1970s, and from there they rose again until the end of the period (Figure 4b). The linear trend for the entire period of this index was practically zero (Table 1).
The extreme minimum temperature (Tnn) presented very low values for several years in the 1950s (Figure 4c), especially in 1954, which coincided precisely with the minimum of SU mentioned above, which reinforced a plausible explanation. Since the 1960s and throughout the period, the average value was around 4 °C. The value of the slope for the linear trend was slightly positive (~0.02 °C/year).
For total precipitation (Figure 4d), the highest values clearly were found in the 1950s (>1250 mm/year), then lower values until the mid-1990s, and then they increased slightly again toward the end of the period. The linear trend for the entire period was practically zero, given the average annual values of total precipitation for the sub-basin (Table 1).
Finally, the behavior of days with precipitation greater than 20 mm was very similar to that of total precipitation, with the highest values (>20 days) during the 1950s, lower values in the next three decades, and a rise again in the last period (Figure 5d). Again, the value of the linear trend was negligible (Table 1).
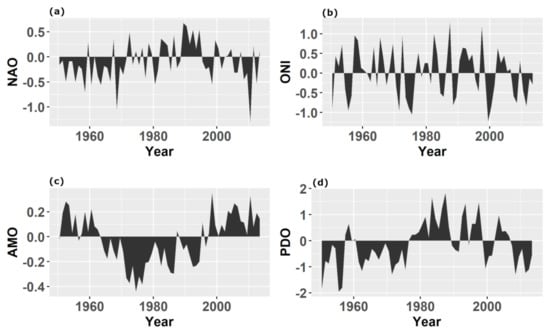
Figure 5.
Time series of the annual averages of the indices of four climate oscillations for the period 1950–2013: (a) NAO; (b) ONI; (c) AMO; (d) PDO.
As mentioned above, the nonparametric Mann–Kendall (MK) and Spearman’s rho (SRC) tests are more robust for trend detection if the data are not serially correlated. The calculation of the new slope was made using the nonparametric method of Sen. The results (Table 1) showed that only the summer days had a statistically significant trend, with a slope of 0.76 days/year confirmed by both methods (MK and SRC). These results did not consider the serial correlation of the data.
After calculating the serial correlation coefficient for lag-1, only the SU and Txx series were the ones that turned out to have a serial correlation. In this way, the five tests mentioned above in the Materials and Methods section were applied. For Txx, which did not show any trend, only the TFPWMK test showed statistical significance, and for SU, the TFPWMK and MMKY tests showed statistical significance. In none of the cases were three or more tests statistically significant. Therefore, we concluded that none of the climate change indices showed a statistically significant linear trend.
3.3. Climate Oscillations and ETCCDI Indices
3.3.1. Climate Oscillations
Given that no significant linear trend was found in the ETCCDI indices for the Apatlaco River sub-basin, we looked for an explanation of its behavior with the climate oscillations that have affected the climatology of Mexico in the past (e.g., NAO, PDO, AMO, and ENSO).
The time series of the annual averages of the indices of the four previous climate oscillations (ONI representing ENSO) are presented in Figure 5 for the period 1950–2013. It was observed that the NAO (Figure 5a) prevailed, with a negative phase from 1950 to 1972, then passing through a transitory phase from 1972 to 1982, a mainly positive phase from 1982 to 1996, and finally another predominantly negative phase from 1996 to 2013. The ENSO, represented here by ONI (Figure 5b), showed the typical interannual variability of this phenomenon, with an irregular cycle of 2–7 years [70], and the influence of the most intense El Niño and La Niña events also was reflected. Regarding the AMO (Figure 5c), a positive phase was observed in the period of 1950–1962, while a negative phase (cold) was observed from 1962 to 1999, then returning to the warm phase from 1999 until the end of the record. Finally, in the case of the PDO (Figure 5d), we can see that it was mostly in a negative (cold) phase from 1950 to 1978, a period of almost 30 years. Subsequently, a period of approximately 22 years (1978–1999) of positive (hot) phase was recorded, and from 2000 to the end of the record, it fluctuated every 2–3 years from cold to hot.
3.3.2. Correlations between Climate Oscillations and ETCCDI Indices
We then calculated the Pearson correlations of the NAO, PDO, AMO, and ONI indices (the latter representing ENSO) versus the ETCCDI indices analyzed here (SU, Txx, Tnn, PcpT, and r20). The results are shown in Figure 6, where the correlated values between the climate oscillations themselves and between the same climatic indices of the ETCCDI are also shown. Note that all the correlation values shown in Figure 6 are statistically significant (p ≤ 0.05), and they were obtained with a standard statistical method.
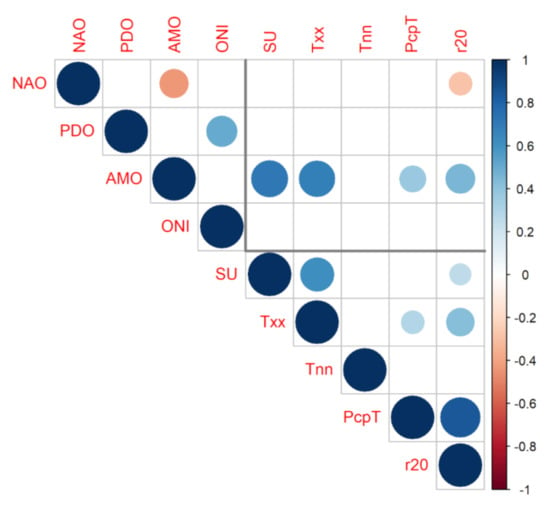
Figure 6.
Statistically significant Pearson correlations (95% confidence) for the Apatlaco River sub-basin between the climate oscillations (NAO, PDO, AMO, and ONI) (upper left), the climatic indices of the ETCCDI (SU, Txx, Tnn, PcpT and r20) (lower right), and between both groups (inside the rectangle at the top right after the gray line). The results are for the entire period of 1950–2013. Shades in blue show positive correlations, and those in red show negative correlations. Blank cells indicate the correlation was not statistically significant.
The results revealed a correlation of −0.44 between the NAO and the AMO, and a correlation of +0.5 between the PDO and ONI. This type of correspondence has already been documented before; for example, in the southwestern United States, the PDO tended to substantially modulate the strength of the ENSO teleconnections, which implied a positive correlation between these two indices [71]. On the other hand, as expected, SU and Txx had an important positive correlation, and in the same way, PcpT and r20 did as well. A more modest positive correlation existed between Txx and r20, and an even lesser one between Txx and PcpT and between SU and r20.
However, the most relevant result found in this work was the strong statistically significant correlation between the AMO with four (of the five) ETCCDI indices analyzed here (except for Tnn) for the Apatlaco River sub-basin. The strongest correlations were those of the AMO with the two indices related to the maximum temperature, SU and Txx, with values of 0.79 and 0.74, respectively (Table 2). The AMO with r20 and PcpT also had statistically significant correlations for the sub-basin, although they were considerably lower (0.39 and 0.34, respectively). These results agreed with the aforementioned important role of the Atlantic forcing in the summer precipitation in Central Mexico [29]. A modest negative correlation of −0.29 was found between the NAO and r20 for the sub-basin.

Table 2.
Statistically significant Pearson correlation values between the mean annual values of climate oscillations and the annual values of some climatic indices of the ETCCDI for the Apatlaco River sub-basin in the period of 1950–2013. Titles are for the entire sub-basin (ALL), the upper part (HG), the lower part (LW), the middle west (MW), and the middle east (ME).
Another interesting aspect was that the correlations of the AMO with the different climatic indices of the ETCCDI were maintained practically for all the subregions of the study. A clear exception could be the noninclusion of the correlation of the AMO and SU for the upper zone of the sub-basin, but this result was thus given by the definition taken here for summer days when the condition of Txij > 30 °C was fulfilled for a few days a year in that area, and therefore it was not significant. Another interesting aspect of the AMO results was that the correlations were higher for the lower part of the basin compared to the upper part, and higher in the middle east (urban) regarding the middle west (rural) for the maximum temperature indices. The NAO maintained its statistically significant negative correlation with r20 for the upper and lower zones, and both the NAO and the PDO had low but significant correlations with Txx only for the lower zone.
4. Discussion
The average values of precipitation and surface temperature shown here (Figure 2 and Figure 3) were a clear example that, on certain occasions, they could lead us to a wrong idea about the typical behavior of a region, since the bimodal behavior of midsummer drought clearly prevailed in three of the four sub-regions (instead of the monsoon type shown for the entire sub-basin), which is also a typical rainfall pattern for Central and Southern Mexico [15].
Urban effects in the climate of some large Central Mexico cities, such as Mexico City [72,73,74,75] and others [76,77], have been reported. An increasing trend in the total precipitation and in the frequency of intense rain showers of Mexico City compared to the suburban areas was reported for the period of 1941–1985 [72]. Even though it was not the main purpose here to study urban effects on climate, the higher values of total mean precipitation in the northern part of the middle east zone (Cuernavaca metropolitan area) compared to those in the middle west zone (rural) (Figure 2) might be another manifestation of the so-called rain-island effect in a tropical city. Three key factors were initially proposed in [78] as possible causes for urban-induced changes in precipitation: (i) mechanical turbulence resulting from increased surface roughness; (ii) the addition of sensible heat from the urban warm air; and (iii) the anthropogenic condensation nuclei floating in the urban air. On the other hand, [73] describes the climatology of the near-surface urban heat island of Mexico City. The author mentions that the less-frequent daytime heat islands may have been caused by differences in evaporative cooling from the wet surface during the wet season. In addition, he showed that the average urban/rural thermal contrasts were positive throughout the year, varying from 5 °C in the middle of the dry season to 1–3 °C during the wet season. The results here do not present an analysis of the heat-island effect, but reveal that the thermal gradient in the northern part of the mideast zone was larger than in the midwest zone (Figure 2). As we know, the heat-island effect is favored by the change in land use in large cities, and the population of Mexico went from 25.8 million inhabitants (42.6% urban, 57.4% rural) in 1950 to 119.5 million inhabitants in 2015 (77% urban, 23% rural) [79].
The results of the SU and Tnn temperature indices analyzed here were consistent with the study in [48], which found a clear warming trend for the period of 1961–2003 in areas close to the study region. However, the Txx analysis did not corroborate this result, since we found a slightly negative and nonsignificant trend for the Apatlaco region.
On the other hand, [80] reported an analysis of various temperature and precipitation indices for 14 urban stations in Mexico. The station of this study that was closest to the Apatlaco River sub-basin was Milpa Alta, south of Mexico City and very close to the north of Apatlaco. The authors of [80] mentioned that the behavior of the indices, particularly those related to surface temperature, was radically different from those found in the rest of the country. They attributed the negative trends in several of the temperature indices in Mexico City to the increase in air pollution and the continuous emissions from the Popocatépetl volcano. The results found here for the Apatlaco sub-basin contrasted with those found in [80]. On the one hand, the slightly negative but not significant Txx slope reported here for the Apatlaco sub-basin was consistent with the results from the Mexico City stations reported in [80], although that study reported a high statistical significance. However, for Tnn and SU, [80] reported negative trends, contrary to the positive and significant trends found here for the Apatlaco sub-basin.
For precipitation, [48,81] reported nonsignificant negative trends for areas close to the study region, which differed somewhat from the positive but nonsignificant trend found here. Although the Apatlaco results were consistent with the positive trend found for Milpa Alta in the study in [80], the difference was that they found a high statistical significance of the slope.
The present results showed an inverse relationship between NAO and r20 (Table 2). The NAO negative phase reinforced strong precipitation for our study region. This result agreed with some precipitation patterns found in North America [82,83]. The AMO influence during its positive phase supported an increment in SU, Txx, PcpT, and r20. Similar results were found in [84] for the temperature and precipitation of Central America and Southeast Mexico, where AMO was pointed out as a low-frequency teleconnection; this was associated with the tropical Pacific-originated atmospheric variability [85]. The influence of the AMO was quite significant for the extreme maximum temperatures in most of the Mexican territory; for example, in the case of the state of Zacatecas [86], in the north center of the country, the behavior in the temporal evolution, as well as the correlation values, were quite similar to those obtained for the Apatlaco sub-basin.
The results shown here supported that the AMO positive phase produced an increment in the temperature and precipitation. On the other hand, the relationship of PDO and ENSO with precipitation was not detected in the present study, contrary to the results reported in [27]; these oscillations had a higher frequency compared to the AMO oscillation. This no-signal (on the PDO and ENSO) was attributed to the local factors’ influences on the temperature and precipitation [83,87]. The above suggests that the homogenization process improved the data quality and allowed the influence of local factors on the climate variables to be found.
The results presented here for this small region in Central Mexico basically contradicted the argument in [21], which stated that the AMO probably lost much of its influence in Central Mexico at the beginning of the 20th century, nor did they agree with the supposed difficulty in detecting AMO due to the influence of PDO/ENSO [30,31].
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atmos13020339/s1, Table S1: Precipitation break points, Table S2: Maximum temperature break points, Table S3: Minimum temperature break points.
Author Contributions
Conceptualization, M.J.M.-M.; methodology, M.J.M.-M. and O.P.-D.; validation, M.J.M.-M. and O.P.-D.; formal analysis, M.J.M.-M., O.P.-D. and M.A.-V.; investigation, M.J.M.-M. and O.P.-D.; writing—original draft preparation, M.J.M.-M. and O.P.-D.; writing—review and editing, M.J.M.-M., O.P.-D. and M.A.-V.; visualization, M.J.M.-M. and O.P.-D.; supervision, M.J.M.-M.; discussion, M.J.M.-M., O.P.-D. and M.A.-V.; funding acquisition, M.A.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Projects of Cátedra-CONACYT under program number 945 (M.A.-V.).
Acknowledgments
We acknowledge José Antonio Guijarro from AEMET for developing and maintaining the Climatol package for quality control, homogenization, and missing data in-filling of climatological series.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, H.; Wei, Y.; Zhang, Q.; Liu, X.; Huang, J.; Feng, T.; Zhang, M. Multi-model assessment of global temperature variability on different time scales. Int. J. Climatol. 2020, 40, 273–291. [Google Scholar] [CrossRef]
- Gershunov, A.; Barnett, T.P. Interdecadal modulation of ENSO teleconnections. Bull. Am. Meteorol. Soc. 2010, 79, 2715–2726. [Google Scholar] [CrossRef] [Green Version]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Knight, J.R.; Folland, C.K.; Scaife, A.A. Climate impacts of the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2006, 33, L17706. [Google Scholar] [CrossRef] [Green Version]
- Kosaka, Y.; Xie, S. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Fyfe, J.C.; Xie, S.P.; Dai, X. Decadal modulation of global surface temperature by internal climate variability. Nat. Clim. Change 2015, 5, 555–559. [Google Scholar] [CrossRef]
- Folland, C.K.; Parker, D.E.; Palmer, T.N. Sahel rainfall and worldwide sea temperatures 1901–85. Nature 1986, 320, 602–607. [Google Scholar] [CrossRef]
- Power, S.; Casey, T.; Folland, C.; Colman, A.; Mehta, V. Inter-decadal modulation of the impact of ENSO on Australia. Clim. Dynam. 1999, 15, 319–324. [Google Scholar] [CrossRef]
- Seager, R.; Hoerling, M.; Schubert, S.; Wang, H.; Lyon, B.; Kumar, A.; Nakamura, J.; Henderson, N. Causes of the 2011–14 California drought. J. Clim. 2015, 28, 6997–7024. [Google Scholar] [CrossRef]
- Metcalfe, S.E. Historical data and climatic change in Mexico: A review. Geogr. J. 1987, 153, 211–222. [Google Scholar] [CrossRef]
- Waliser, D.E.; Gautier, C. A satellite-derived climatology of the ITCZ. J. Clim. 1993, 6, 2162–2174. [Google Scholar] [CrossRef]
- Cavazos, T.; Hastenrath, S. Convection and rainfall over Mexico and their modulation by the Southern Oscillation. Int. J. Climatol. 1990, 10, 377–386. [Google Scholar] [CrossRef]
- Dilley, M. Synoptic controls on precipitation in the Valley of Oaxaca, Mexico. Int. J. Climatol. 1996, 16, 1019–1031. [Google Scholar] [CrossRef]
- Pavia, E.G.; Graef, F. The recent rainfall climatology of the Mediterranean Californias. J. Clim. 2002, 15, 2697–2701. [Google Scholar] [CrossRef]
- Magaña, V.O.; Vázquez, J.L.; Pérez, J.L.; Pérez, J.B. Impact of El Niño on precipitation in Mexico. Geofís. Int. 2003, 42, 313–330. [Google Scholar]
- Andrade-Velázquez, M.; Medrano-Pérez, R. Precipitation patterns in Usumacinta and Grijalva basins (southern Mexico) under a changing climate. Rev. Bio Cienc. 2020, 7, e905. [Google Scholar] [CrossRef]
- Andrade-Velázquez, M.; Medrano-Pérez, R. Historical precipitation patterns in the South-Southeast region of Mexico and future projections. Earth Sci. Res. J. 2021, 25, 69–84. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. Modulation of hurricane activity in the Gulf of Mexico by the Madden-Julian oscillation. Science 2000, 287, 2002–2004. [Google Scholar] [CrossRef] [PubMed]
- Aiyyer, A.; Molinari, J. MJO and tropical cyclogenesis in the Gulf of Mexico and eastern Pacific: Case study and idealized numerical modeling. J. Atmos. Sci. 2008, 65, 2691–2704. [Google Scholar] [CrossRef] [Green Version]
- Camargo, S.J.; Wheeler, M.C.; Sobel, A.H. Diagnosis of the MJO modulation of tropical cyclogenesis using an empirical index. J. Atmos. Sci. 2009, 66, 3061–3074. [Google Scholar] [CrossRef]
- Park, J.; Byrne, R.; Böhnel, H. The combined influence of Pacific decadal oscillation and Atlantic multidecadal oscillation on central México since the early 1600s. Earth Planet. Sc. Lett. 2017, 464, 1–9. [Google Scholar] [CrossRef]
- Goodrich, G.B. Influence of the Pacific decadal oscillation on winter precipitation and drought during years of neutral ENSO in the western United States. Weather Forecast. 2007, 22, 116–124. [Google Scholar] [CrossRef]
- Arriaga-Ramírez, S.; Cavazos, T. Regional trends of daily precipitation indices in northwest Mexico and southwest United States. J. Geophys. Res.-Atmos. 2010, 115, D14111. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. North American precipitation and temperature patterns associated with the El Niño/Southern Oscillation (ENSO). Mon. Weather Rev. 1986, 114, 2352–2362. [Google Scholar] [CrossRef] [Green Version]
- Portis, D.H.; Walsh, J.E.; El Hamly, M.; Lamb, P.J. Seasonality of the North Atlantic oscillation. J. Clim. 2001, 14, 2069–2078. [Google Scholar] [CrossRef]
- Englehart, P.J.; Douglas, A.V. Characterizing regional-scale variations in monthly and seasonal surface air temperature over Mexico. Int. J. Climatol. 2004, 24, 1897–1909. [Google Scholar] [CrossRef]
- Stahle, D.W.; Burnette, D.J.; Diaz, J.V.; Heim, R.R.; Fye, F.K.; Paredes, J.C.; Soto, R.A.; Cleaveland, M.K. Pacific and Atlantic influences on Mesoamerican climate over the past millennium. Clim. Dynam. 2012, 39, 1431–1446. [Google Scholar] [CrossRef]
- Douglas, A.V.; Englehart, P.J. Warm season rainfall in eastern Mexico: Interannual variability of tropical cyclone and non-tropical cyclone rainfall as modulated by ENSO and the AMO. In Proceedings of the 26th Annual Climate Diagnostics and Prediction Workshop, La Jolla, CA, USA, 23–27 October 2001; US Department of Commerce, NOAA: Washington, DC, USA, 2002. [Google Scholar]
- Méndez, M.; Magaña, V. Regional aspects of prolonged meteorological droughts over Mexico and Central America. J. Clim. 2010, 23, 1175–1188. [Google Scholar] [CrossRef] [Green Version]
- Mo, K.C.; Schemm, J.K.E.; Yoo, S.H. Influence of ENSO and the Atlantic multidecadal oscillation on drought over the United States. J. Clim. 2009, 22, 5962–5982. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Feng, S. AMO-and ENSO-driven summertime circulation and precipitation variations in North America. J. Clim. 2012, 25, 6477–6495. [Google Scholar] [CrossRef] [Green Version]
- Expert Team on Climate Information for Decision-Making. Available online: https://community.wmo.int/governance/commission-membership/commission-weather-climate-water-and-related-environmental-service-applications-sercom/commission-services-officers/sercom-management-group/standing-committee-climate-services/expert-team-climate-information-decision (accessed on 13 January 2022).
- Peterson, T.C.; Manton, M.J. Monitoring changes in climate extremes: A tale of international collaboration. Bull. Am. Meteorol. Soc. 2008, 89, 1266–1271. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Caesar, J. Global land-based datasets for monitoring climatic extremes. Bull. Am. Meteorol. Soc. 2013, 94, 997–1006. [Google Scholar] [CrossRef] [Green Version]
- Sillmann, J.; Donat, M.G.; Fyfe, J.C.; Zwiers, F.W. Observed and simulated temperature extremes during the recent warming hiatus. Environ. Res. Lett. 2014, 9, 64023. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Pepin, N.; Flügel, W.A.; Yan, Y.; Xu, Y.; Zhang, Y.; Huang, J. Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim. Dynam. 2011, 36, 2399–2417. [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, L.; Chen, D.; Xu, J.; Zhang, H. Comparison between past and future extreme precipitations simulated by global and regional climate models over the Tibetan Plateau. Int. J. Climatol. 2018, 38, 1285–1297. [Google Scholar] [CrossRef]
- Hui, P.; Tang, J.; Wang, S.; Niu, X.; Zong, P.; Dong, X. Climate change projections over China using regional climate models forced by two CMIP5 global models. Part I: Evaluation of historical simulations. Int. J. Climatol. 2018, 38, e57–e77. [Google Scholar] [CrossRef]
- Hui, P.; Tang, J.; Wang, S.; Niu, X.; Zong, P.; Dong, X. Climate change projections over China using regional climate models forced by two CMIP5 global models. Part II: Projections of future climate. Int. J. Climatol. 2018, 38, e78–e94. [Google Scholar] [CrossRef]
- Sui, Y.; Lang, X.; Jiang, D. Projected signals in climate extremes over China associated with a 2 °C global warming under two RCP scenarios Int. J. Climatol. 2018, 38, e678–e697. [Google Scholar] [CrossRef]
- Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting representative climate models for climate change impact studies: An advanced envelope-based selection approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef] [Green Version]
- Panda, D.K.; Panigrahi, P.; Mohanty, S.; Mohanty, R.K.; Sethi, R.R. The 20th century transitions in basic and extreme monsoon rainfall indices in India: Comparison of the ETCCDI indices. Atmos. Res. 2016, 181, 220–235. [Google Scholar] [CrossRef]
- Gallego, M.C.; Trigo, R.M.; Vaquero, J.M.; Brunet, M.; García, J.A.; Sigró, J.; Valente, M.A. Trends in frequency indices of daily precipitation over the Iberian Peninsula during the last century. J. Geophys. Res.-Atmos. 2011, 116, D02109. [Google Scholar] [CrossRef]
- van den Besselaar, E.J.M.; Klein Tank, A.M.G.; Buishand, T.A. Trends in European precipitation extremes over 1951–2010. Int. J. Climatol. 2013, 33, 2682–2689. [Google Scholar] [CrossRef]
- Filahi, S.; Tramblay, Y.; Mouhir, L.; Diaconescu, E.P. Projected changes in temperature and precipitation indices in Morocco from high-resolution regional climate models. Int. J. Climatol. 2017, 37, 4846–4863. [Google Scholar] [CrossRef]
- Barry, A.A.; Caesar, J.; Klein Tank, A.M.G.; Aguilar, E.; McSweeney, C.; Cyrille, A.M.; Nikiema, M.P.; Narcisse, K.B.; Sima, F.; Stafford, G.; et al. West Africa climate extremes and climate change indices. Int. J. Climatol. 2018, 38, e921–e938. [Google Scholar] [CrossRef]
- Athar, H. Trends in observed extreme climate indices in Saudi Arabia during 1979–2008. Int. J. Climatol. 2014, 34, 1561–1574. [Google Scholar] [CrossRef]
- Aguilar, E.; Peterson, T.C.; Obando, P.R.; Frutos, R.; Retana, J.A.; Solera, M.; Soley, J.; García, I.G.; Araujo, R.M.; Santos, A.R.; et al. Changes in precipitation and temperature extremes in Central America and northern South America, 1961–2003. J. Geophys. Res.-Atmos. 2005, 110, D23107. [Google Scholar] [CrossRef]
- Peterson, T.C.; Zhang, X.; Brunet-India, M.; Vázquez-Aguirre, J.L. Changes in North American extremes derived from daily weather data. J. Geophys. Res.-Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Montero-Martínez, M.J.; Santana-Sepúlveda, J.S.; Pérez-Ortiz, N.I.; Pita-Díaz, Ó.; Castillo-Liñan, S. Comparing climate change indices between a northern (arid) and a southern (humid) basin in Mexico during the last decades. Adv. Sci Res. 2018, 15, 231–237. [Google Scholar] [CrossRef]
- Pita-Díaz, O.; Ortega-Gaucin, D. Analysis of Anomalies and Trends of Climate Change Indices in Zacatecas, Mexico. Climate 2020, 8, 55. [Google Scholar] [CrossRef] [Green Version]
- Ortiz-Gómez, R.; Muro-Hernández, L.J.; Flowers-Cano, R.S. Assessment of extreme precipitation through climate change indices in Zacatecas, Mexico. Theor. Appl. Climatol. 2020, 141, 1541–1557. [Google Scholar] [CrossRef]
- Astudillo, C.; Peña, A.; Suárez, M.A.; Aguilar, E.; Bravo, J.A. Caracterización de la cuenca del Río Apatlaco. In Impacto del Cambio Climático para la Gestión Integral de la Cuenca Hidrológica del Río Apatlaco; Soares, D., Peña, A., Eds.; IMTA: Jiutepec, México, 2018; pp. 57–107. [Google Scholar]
- Guijarro, J.A. Homogenization of Climatic Series with Climatol; Versión 3.1.1; Agencia Estatal de Meteorología (AEMET): D.T. en Islas Baleares, España; Available online: https://www.researchgate.net/profile/Jose_Guijarro/publication/325203476_Homogenization_of_climatic_series_with_Climatol/links/5afda3fea6fdcc3a5a90bd5b/Homogenization-of-climatic-series-with-Climatol.pdf (accessed on 13 January 2022).
- Paulhus, J.H.L.; Kohler, M.A. Interpolation of missing precipitation records. Mon. Weather Rev. 1952, 80, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Alexandersson, H. A homogeneity test applied to precipitation data. Int. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, F. RClimDex (1.0) User Guide; Climate Research Branch Environment Canada: Downsview, ON, Canada, 2004. Available online: http://etccdi.pacificclimate.org/RClimDex/RClimDexUserManual.doc (accessed on 13 January 2022).
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1948. [Google Scholar]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Lehmann, E.L.; D’Abrera, H.J. Nonparametrics Statistical Methods Based on Ranks; Holden-Day: San Francisco, CA, USA, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Fonseca, D.; Calvalho, M.J.; Marta-Almeida, M.; Melo-Goncalves, P.; Rocha, A. Recent trends of extreme temperature indices for the Iberian Peninsula. Phys. Chem. Earth Pt. A/B/C 2016, 94, 66–76. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; Muthiah, K.; Sridhar, V. Long-term homogeneity, trend, and change-point analysis of rainfall in the arid district of Ananthapuramu, Andhra Pradesh State. India. Water 2020, 12, 211. [Google Scholar] [CrossRef] [Green Version]
- Von Storch, H.; Navarra, A. Misuses of Statistical Analysis in Climate Research. In Analysis of Climate Variability-Applications of Statistical Techniques; Springer: Berlin/Heidelberg, Germany, 1995; pp. 11–26. [Google Scholar]
- Kulkarni, A.; von Storch, H. Monte Carlo experiments on the effect of serial correlation on the Mann-Kendall test of trend. Meteorol. Zeitschrift 1995, 4, 82–85. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Hamed, K.H. Enhancing the effectiveness of prewhitening in trend analysis of hydrologic data. J. Hydrol. 2009, 368, 143–155. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Lau, K.M.; Bua, W. Mechanisms of monsoon-Southern Oscillation coupling: Insights from GCM experiments. Clim. Dynam. 1998, 14, 759–779. [Google Scholar] [CrossRef]
- Brown, D.P.; Comrie, A.C. A winter precipitation ‘dipole’ in the western United States associated with multidecadal ENSO variability. Geophys. Res. Lett. 2004, 31, L09203. [Google Scholar] [CrossRef] [Green Version]
- Jáuregui, E.; Romales, E. Urban effects on convective precipitation in Mexico City. Atmos. Environ. 1996, 30, 3383–3389. [Google Scholar] [CrossRef]
- Jauregui, E. Heat island development in Mexico City. Atmos. Environ. 1997, 31, 3821–3831. [Google Scholar] [CrossRef]
- Jáuregui, E. The heat spells of Mexico City. Invest. Geog. 2009, 70, 71–76. Available online: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0188-46112009000300005&lng=es&nrm=iso (accessed on 13 January 2022).
- Cui, Y.Y.; De Foy, B. Seasonal variations of the urban heat island at the surface and the near-surface and reductions due to urban vegetation in Mexico City. J. Appl. Meteorol. Clim. 2012, 51, 855–868. [Google Scholar] [CrossRef]
- Jauregui, E.; Godinez, L.; Cruz, F. Aspects of heat-island development in Guadalajara, Mexico. Atmos. Environ. B-Urb. 1992, 26, 391–396. [Google Scholar] [CrossRef]
- Jáuregui, E. Possible impact of urbanization on the thermal climate of some large cities in México. Atmósfera 2005, 18, 249–252. [Google Scholar]
- Chandler, T. The Climate of London; Hutchinson: London, UK, 1965. [Google Scholar]
- INEGI. Población. Available online: https://www.inegi.org.mx/temas/estructura/ (accessed on 13 January 2022).
- García-Cueto, O.R.; Santillán-Soto, N.; López-Velázquez, E.; Reyes-López, J.; Cruz-Sotelo, S.; Ojeda-Benítez, S. Trends of climate change indices in some Mexican cities from 1980 to 2010. Theor. Appl. Climatol. 2019, 137, 775–790. [Google Scholar] [CrossRef]
- Mateos, E.; Santana, J.S.; Montero-Martínez, M.J.; Deeb, A.; Grunwaldt, A. Possible climate change evidence in ten Mexican watersheds. Phys. Chem. Earth Pt A/B/C 2016, 91, 10–19. [Google Scholar] [CrossRef]
- Zhang, W.; Mei, X.; Geng, X.; Turner, A.G.; Jin, F. A nonstationary ENSO–NAO relationship due to AMO modulation, J. Climate 2019, 32, 33–43. [Google Scholar] [CrossRef]
- Myoung, B.; Kim, S.H.; Kim, J.; Kafatos, M.C. On the Relationship between the North Atlantic Oscillation and Early Warm Season Temperatures in the Southwestern United States. J. Clim. 2015, 28, 5683–5698. [Google Scholar] [CrossRef]
- Andrade-Velázquez, M.; Medrano-Pérez, O.R.; Montero-Martínez, M.J.; Alcudia-Aguilar, A. Regional Climate Change in Southeast Mexico-Yucatan Peninsula, Central America and the Caribbean. Appl. Sci. 2021, 11, 8284. [Google Scholar] [CrossRef]
- Lin, P.; Yu, Z.; Lü, J.; Ding, M.; Hu, A.; Liu, H. Two regimes of Atlantic multidecadal oscillation: Cross-basin dependent or Atlantic-intrinsic. Sci. Bull. 2019, 64, 198–204. [Google Scholar] [CrossRef] [Green Version]
- Pita-Díaz, O. Variabilidad de Temperatura y Precipitación en el Estado de Zacatecas y su Posible Relación con Oscilaciones de Baja Frecuencia. In Proceedings of the 10° Congreso Nacional en Investigación en Cambio Climático y 2° Congreso Latino de Investigación en Cambio Climático, Mexico City, Mexico, 19 October 2020; Available online: https://www.facebook.com/PINCCDELAUNAM/videos/382234066289676 (accessed on 13 January 2022).
- Alfaro, E.J.; Gershunov, A.; Cayan, D. Prediction of Summer Maximum and Minimum Temperature over the Central and Western United States: The Roles of Soil Moisture and Sea Surface Temperature. J. Clim. 2006, 19, 1407–1421. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).