Extreme Low Flow Estimation under Climate Change
Abstract
:1. Introduction
2. Data and Methodology
2.1. Description of the Watershed
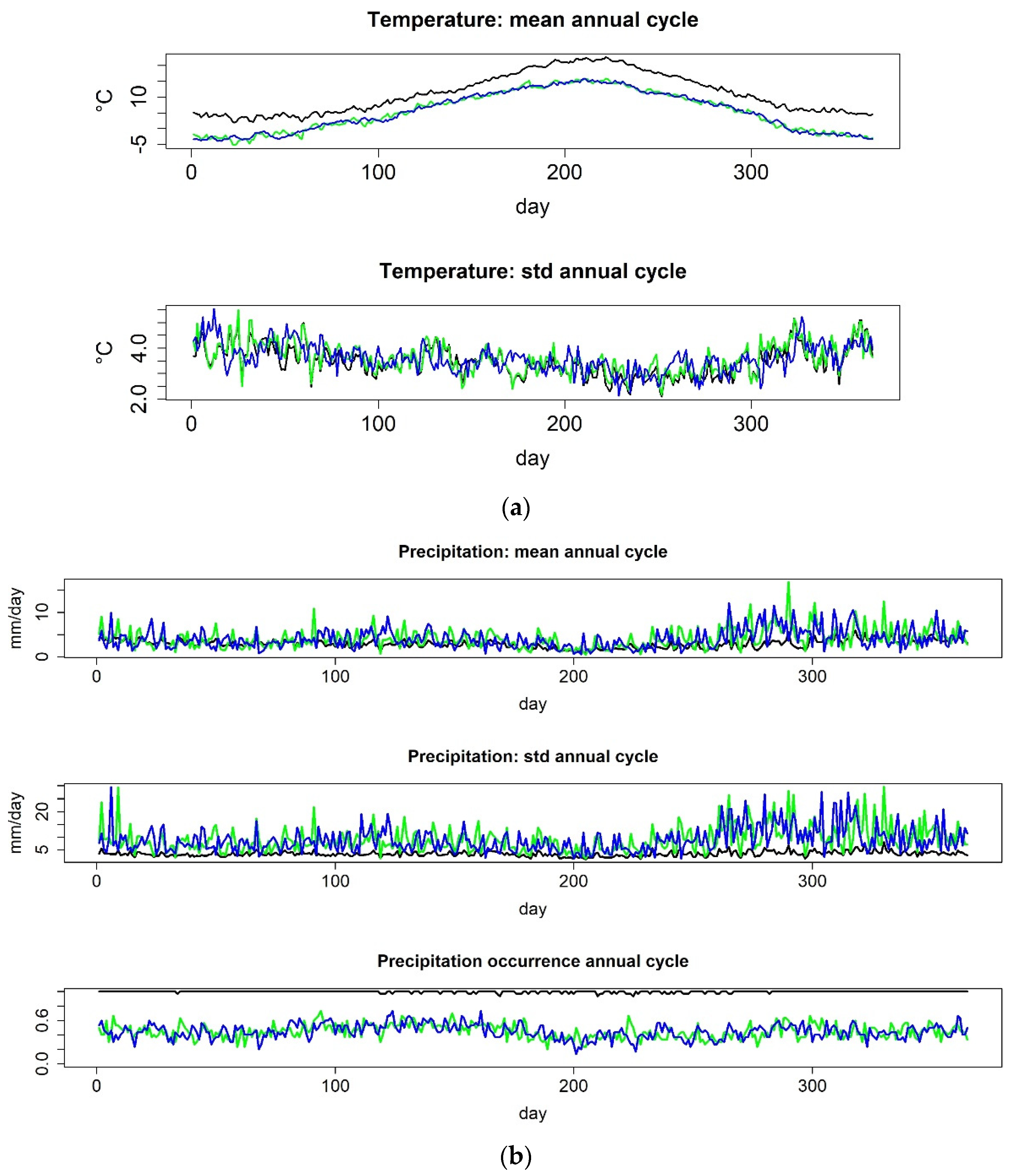
2.2. The Non-Homogenous Hidden Markov Model
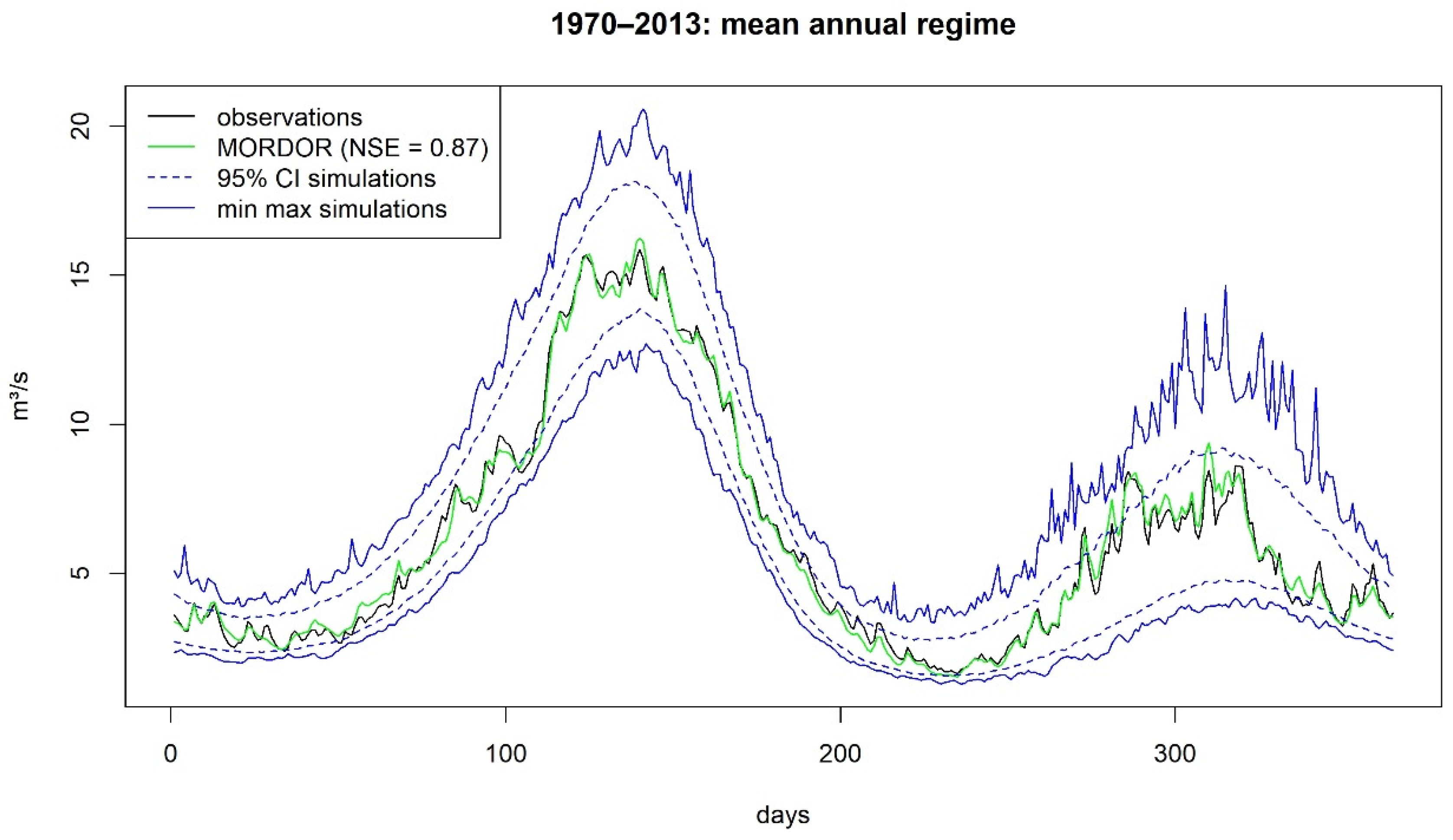
2.3. The Hydrological Model MORDOR
- -
- a snow accumulation function calculated from the temperature and a rain–snow transition curve;
- -
- a snowmelt function based on an improved degree-day formulation;
- -
- an evaporation function that determines the potential evaporation as a function of the air temperature;
- -
- a rainfall excess and soil moisture accounting storage that contribute to the actual evaporation and to the direct runoff;
- -
- an evaporating storage filled by a part of the indirect runoff component that contributes to the actual evaporation;
- -
- an intermediate storage that determines the partitioning between a direct runoff, an indirect runoff and the percolation to a deep storage.
- -
- a deep storage that determines a baseflow component;
- -
- a unit hydrograph that determines the routing of the total runoff.
2.4. Simulation Strategy and Return Level Estimation
3. Results
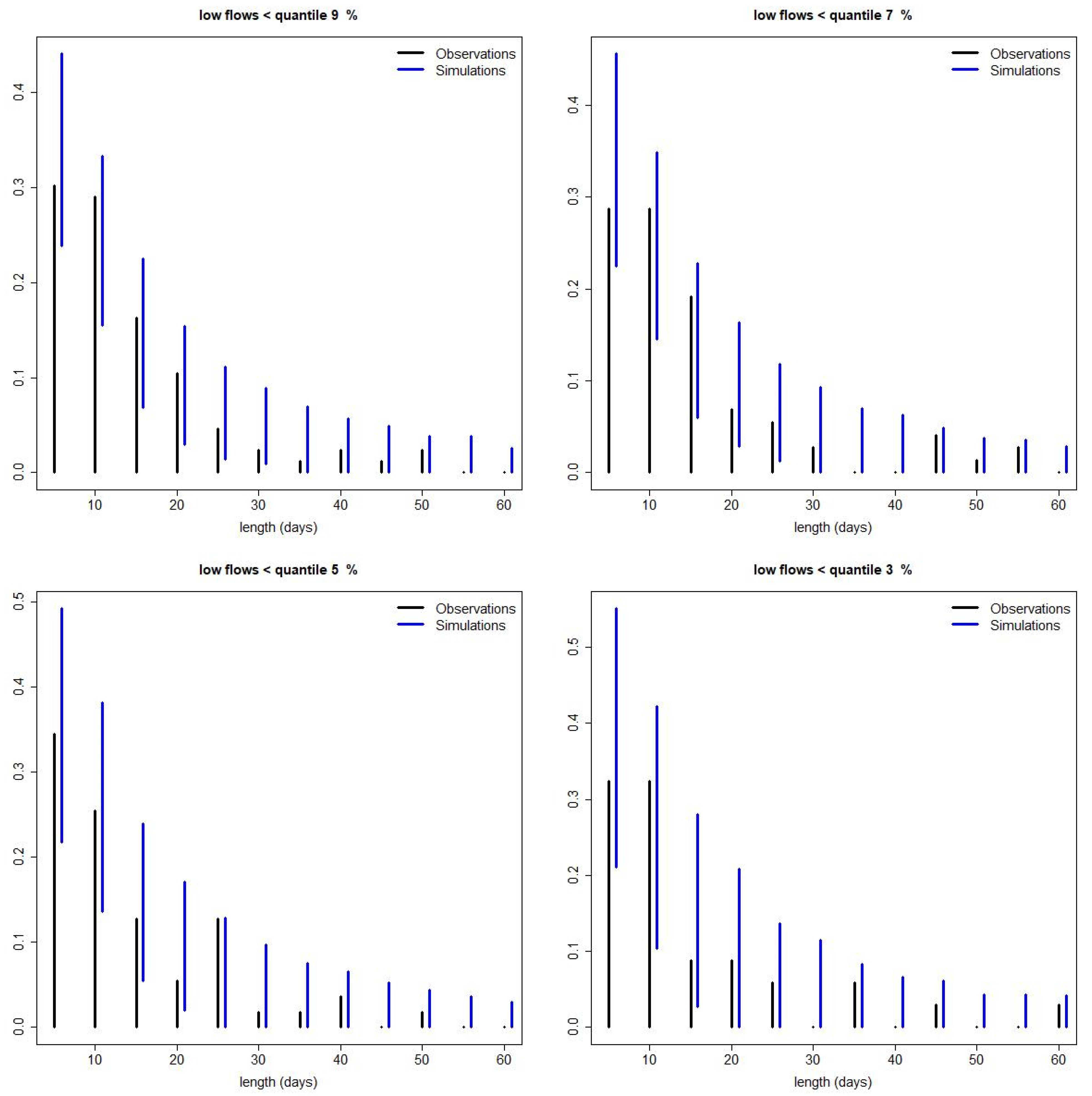
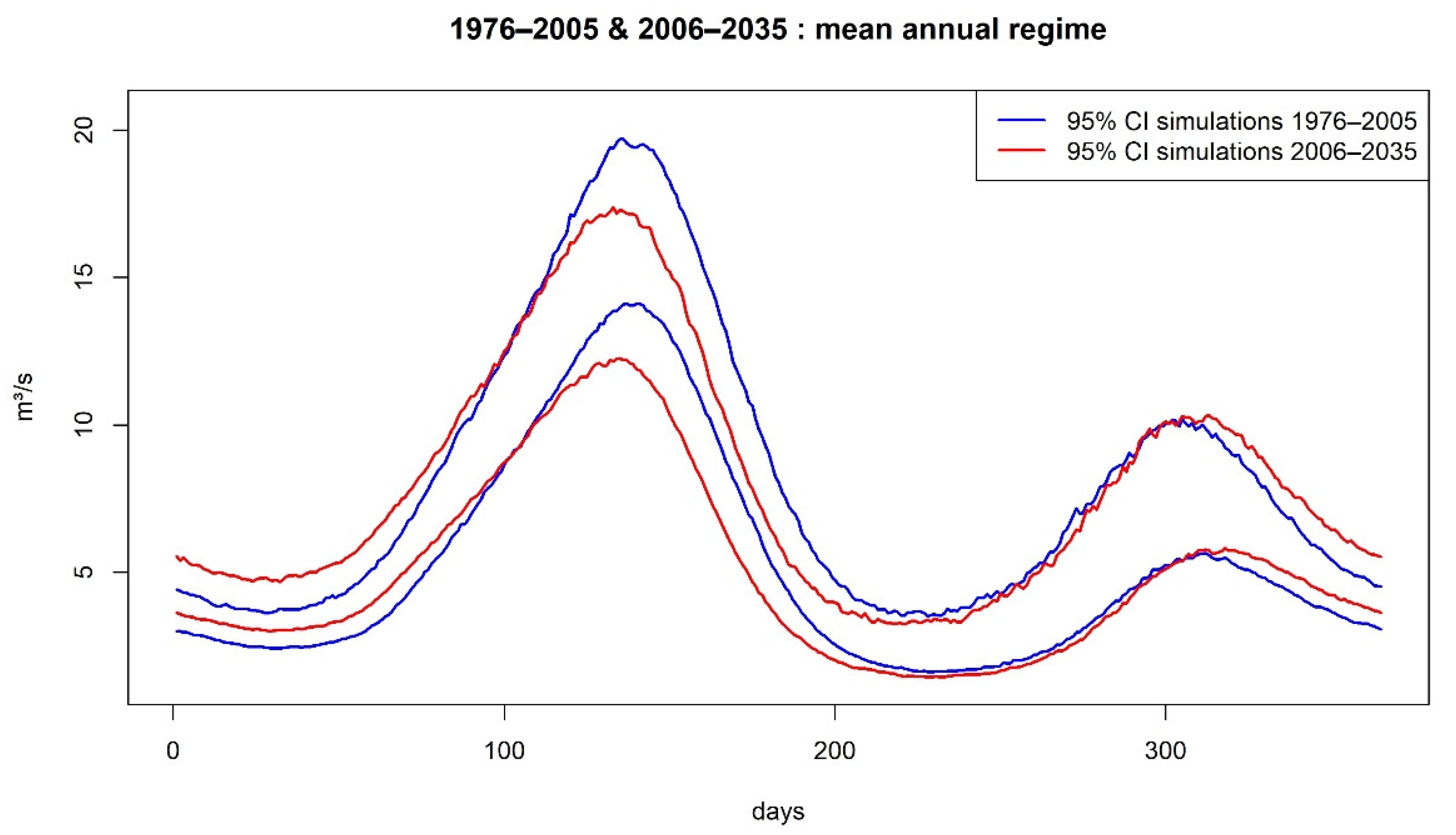
3.1. Validation over the Historical Period
3.2. Extreme Low Flow Estimation
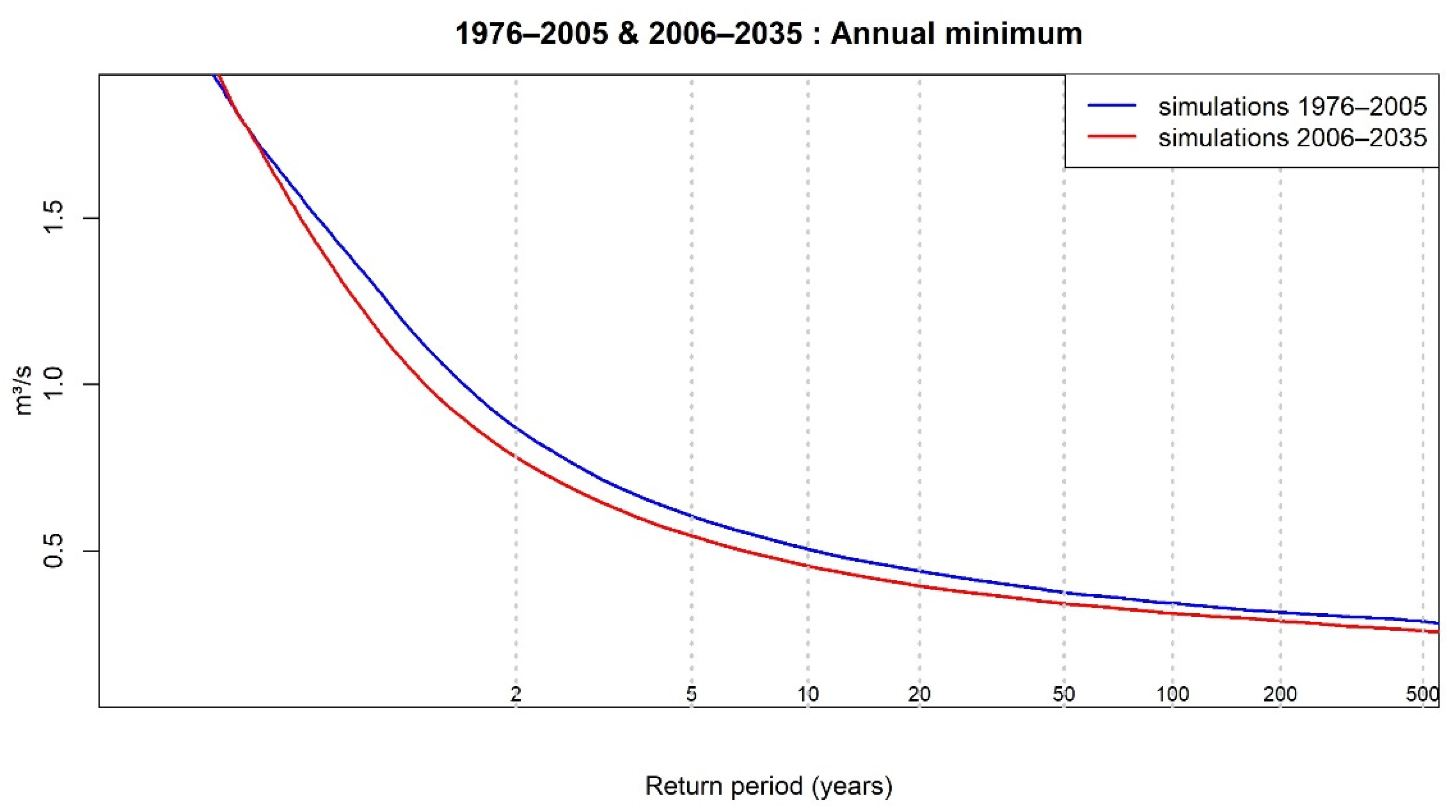
3.3. Future Extreme Low Flow
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krysanova, V.; Vetter, T.; Eisner, S.; Huang, S.; Pechlivanidis, I.; Strauch, M.; Gelfan, A.; Kumar, R.; Aich, V.; Arheimer, B.; et al. Intercomparison of regional-scale hydrological models and climate change impacts projected for 12 large river basins worldwide—A synthesis. Environ. Res. Lett. 2017, 12, 105002. [Google Scholar] [CrossRef]
- Marx, A.; Kumar, R.; Thober, S.; Rakovec, O.; Wanders, N.; Zink, M.; Wood, E.F.; Pan, M.; Sheffield, J.; Samaniego, L. Climate change alters low flows in Europe under global warming of 1.5, 2, and 3 °C, Hydrol. Earth Syst. Sci. 2018, 22, 1017–1032. [Google Scholar] [CrossRef] [Green Version]
- Donnelly, C.; Greuell, W.; Andersson, J.; Gerten, D.; Pisacane, G.; Roudier, P.; Ludwig, F. Impacts of climate change on European hydrology at 1.5, 2 and 3 degrees mean global warming above preindustrial level. Clim. Change 2017, 143, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Oo, H.T.; Zin, W.W.; Kyi, C.T. Analysis of Streamflow Response to Changing Climate Conditions Using SWAT Model. Civ. Eng. J. 2020, 6, 194–209. [Google Scholar] [CrossRef]
- AlSafi, H.I.J.; Sarukkalige, P.R. The application of conceptual modelling to assess the impacts of future climate change on the hydrological response of the Harvey River catchment. J. Hydro-Environ. Res. 2020, 28, 22–33, ISSN 1570-6443. [Google Scholar] [CrossRef]
- Kay, A.L.; Watts, G.; Wells, S.C.; Allen, S. The impact of climate change on U.K. river flows: A preliminary comparison of two generations of probabilistic climate projections. Hydrol. Process. 2020, 34, 1081–1088. [Google Scholar] [CrossRef]
- Alodah, A.; Seidou, O. Assessment of Climate Change Impacts on Extreme High and Low Flows: An Improved Bottom-Up Approach. Water 2019, 11, 1236. [Google Scholar] [CrossRef] [Green Version]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Leadbetter, M.R. Extremes and local dependence in stationary sequences. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 1983, 65, 291–306. [Google Scholar] [CrossRef]
- Richardson, C.W. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Wilks, D.S.; Wilby, R.L. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Fletcher, C.; Naveau, P.; Allard, D.; Brisson, N. A stochastic daily weather generator for skewed data. Water Resour. Res. 2010, 46, W07519. [Google Scholar] [CrossRef]
- Vrac, M.; Stein, M.; Hayhoe, K. Statistical downscaling of precipitation through nonhomogeneous stochastic weather typing. Clim. Res. 2007, 34, 169–184. [Google Scholar] [CrossRef]
- Zucchini, W.; Guttorp, P. A hidden Markov model for space-time precipitation. Water Resour. Res. 1991, 27, 1917–1923. [Google Scholar] [CrossRef]
- Kirshner, S. Modeling of Multivariate Time Series Using Hidden Markov Models. Ph.D. Thesis, University of California, Irvine, CA, USA, 2005. [Google Scholar]
- Ailliot, P.; Pene, F. Consistency of the maximum likelihood estimate for non-homogeneous markov-switching models. ESAIM Probab. Stat. 2015, 19, 268–292. [Google Scholar] [CrossRef] [Green Version]
- Ailliot, P.; Monbet, V. Markov-switching autoregressive models for wind time series. Environ. Model. Softw. 2012, 30, 92–101. [Google Scholar] [CrossRef] [Green Version]
- Hugues, J.P.; Guttorp, P. A class of stochastic models for relating synoptic atmospheric patterns to regional hydrologic phenomena. Water Resour. Res. 1994, 30, 1535–1546. [Google Scholar] [CrossRef]
- Hugues, J.P.; Guttorp, P.; Charles, S.P. A non-homogeneous hidden Markov model for precipitation occurrence. J. R. Stat. Soc. Ser. C 1999, 48, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Peleg, N.; Fatichi, S.; Paschalis, A.; Molnar, P.; Burlando, P. An advanced stochastic weather generator for simulating 2-d high-resolution climate variables. J. Adv. Modeling Earth Syst. 2017, 9, 1595–1627. [Google Scholar] [CrossRef]
- Dubrovsky, M.; Huth, R.; Dabhi, H.; Rotach, M.W. Parametric gridded weather generator for use in present and future climates: Focus on spatial temperature characteristics. Theor. Appl. Climatol. 2020, 139, 1031–1044. [Google Scholar] [CrossRef]
- Touron, A. Consistency of the maximum likelihood estimator in seasonal hidden markov models. Stat. Comput. 2019, 29, 1055–1075. [Google Scholar] [CrossRef] [Green Version]
- Alodah, A.; Seidou, O. The adequacy of stochastically generated climate time series for water resources systems risk and performance assessment. Stoch. Environ. Res. Risk Assess. 2019, 33, 253–269. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. Available online: http://www.jstor.org/stable/2958889 (accessed on 25 October 2021). [CrossRef]
- Garavaglia, F.; Le Lay, M.; Gottardi, F.; Garçon, R.; Gailhard, J.; Paquet, E.; Mathevet, T. Impact of model structure on flow simulation and hydrological realism: From a lumped to a semi-distributed approach. Hydrol. Earth Syst. Sci. 2017, 21, 3937–3952. [Google Scholar] [CrossRef] [Green Version]
- Panagoulia, D.; Economou, P.; Caroni, C. Stationary and nonstationary generalized extreme value modelling of extreme precipitation over a mountainous area under climate change. Environmetrics 2014, 25, 29–43. [Google Scholar] [CrossRef]
- Michelangeli, P.-A.; Vrac, M.; Loukos, H. Probabilistic downscaling approaches: Application to wind cumulative distribution functions. Geophys. Res. Lett. 2009, 36, L11708. [Google Scholar] [CrossRef]
- Guo, T.; Mehan, S.; Gitau, M.W.; Wang, Q.; Kuczek, T.; Flanagan, D.C. Impact of number of realizations on the suitability of simulated weather data for hydrologic and environmental applications. Stoch. Environ. Res. Risk Assess. 2017, 32, 2405–2421. [Google Scholar] [CrossRef]
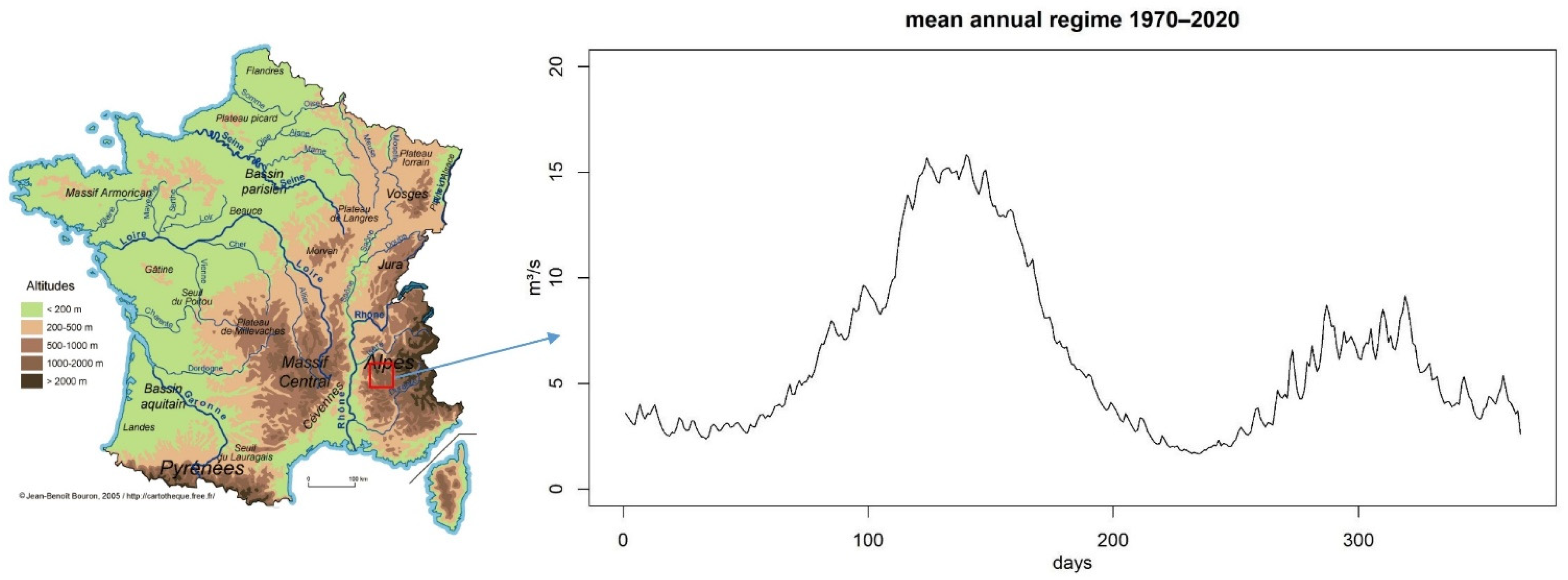

| Hydrological Budget (mm/Year) | Descriptors | ||
|---|---|---|---|
| Precipitation | 1421 | Drainage Area | 214 km2 |
| Rainfall | 911 | Mean Elevation | 1628 m |
| Snow | 510 | Maximum Elevation | 2790 m |
| Actual Evapotranspiration | 522 | Minimum Elevation | 854 m |
| Runoff | 899 | ||
| 1976–2005 | 2006–2035 | |
|---|---|---|
| Mean number of events per year | 0.80 | 1.02 |
| 2-year return level | 0.743 [0.742; 0.744] | 0.679 [0.678; 0.681] |
| 10-year return level | 0.496 [0.495; 0.498] | 0.448 [0.446; 0.450] |
| 20-year return level | 0.436 [0.434; 0.438] | 0.392 [0.390; 0.394] |
| 50-year return level | 0.374 [0.371; 0.377] | 0.340 [0.338; 0.342] |
| 100-year return level | 0.342 [0.340; 0.344] | 0.311 [0.309; 0.314] |
| 200-year return level | 0.315 [0.312; 0.318] | 0.289 [0.286; 0.292] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parey, S.; Gailhard, J. Extreme Low Flow Estimation under Climate Change. Atmosphere 2022, 13, 164. https://doi.org/10.3390/atmos13020164
Parey S, Gailhard J. Extreme Low Flow Estimation under Climate Change. Atmosphere. 2022; 13(2):164. https://doi.org/10.3390/atmos13020164
Chicago/Turabian StyleParey, Sylvie, and Joël Gailhard. 2022. "Extreme Low Flow Estimation under Climate Change" Atmosphere 13, no. 2: 164. https://doi.org/10.3390/atmos13020164
APA StyleParey, S., & Gailhard, J. (2022). Extreme Low Flow Estimation under Climate Change. Atmosphere, 13(2), 164. https://doi.org/10.3390/atmos13020164







