Numerical Simulation of Atmospheric Boundary Layer Turbulence in a Wind Tunnel Based on a Hybrid Method
Abstract
1. Introduction
2. Hybrid Numerical Simulation Method
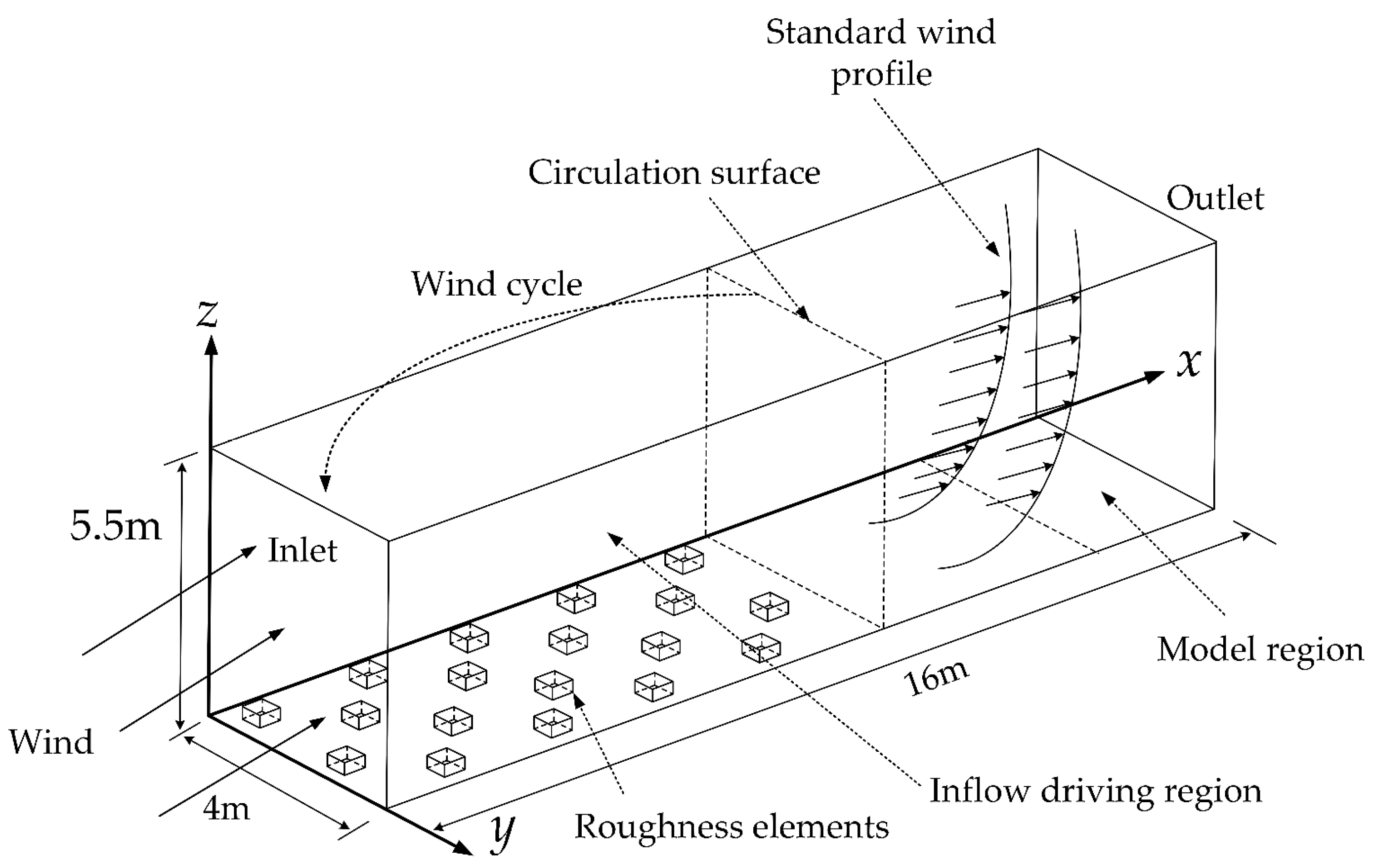
2.1. Simulation Target
2.2. Simulation Strategy
3. Simulation Setups
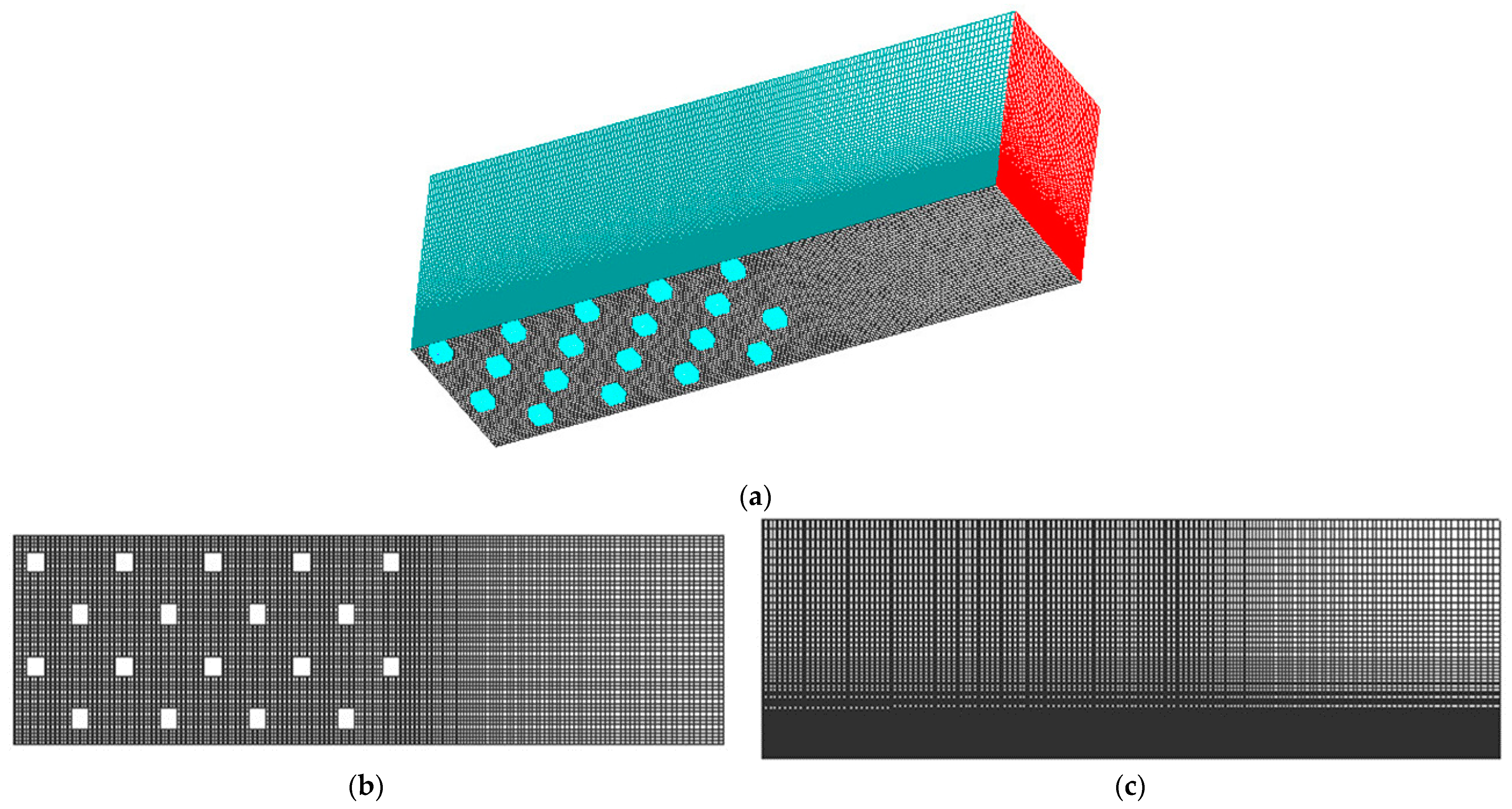
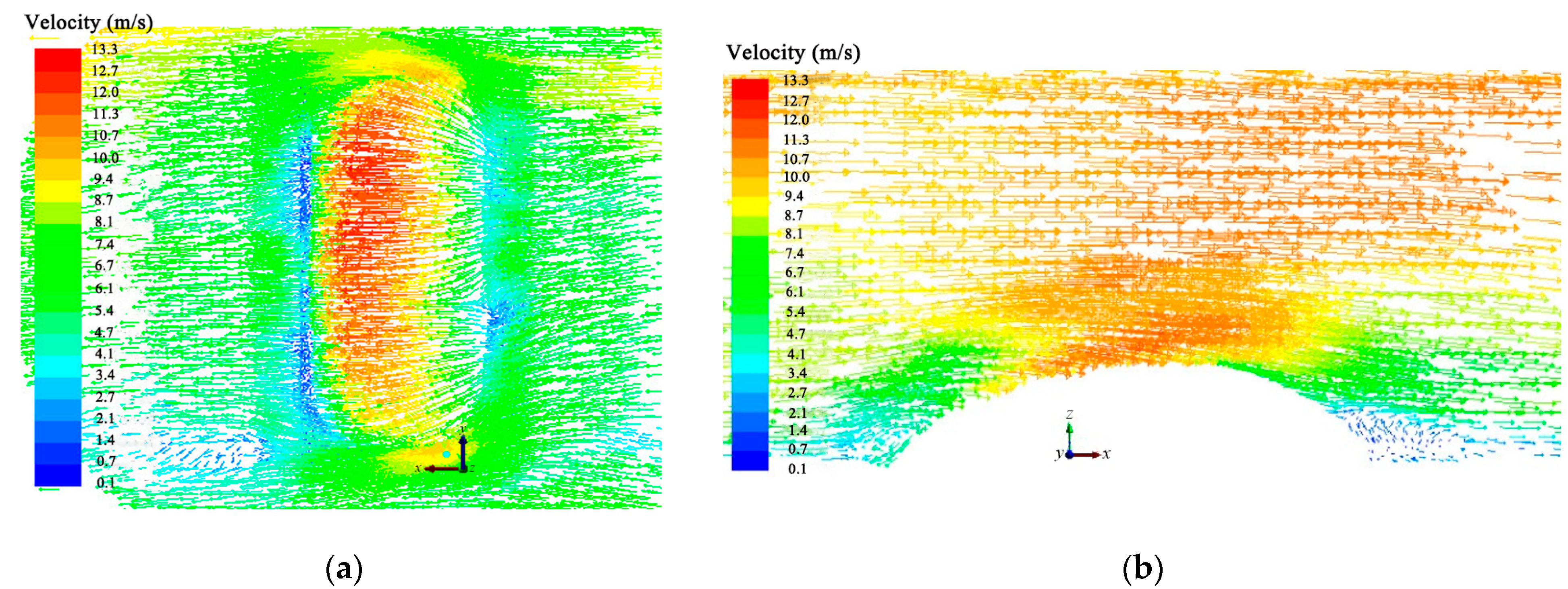
3.1. Calculation Domain and Grids
3.2. Boundary Conditions and Solution Settings
4. Parametric Analysis
4.1. Effect of Grid Number
4.2. Suggestion for Building Model Position
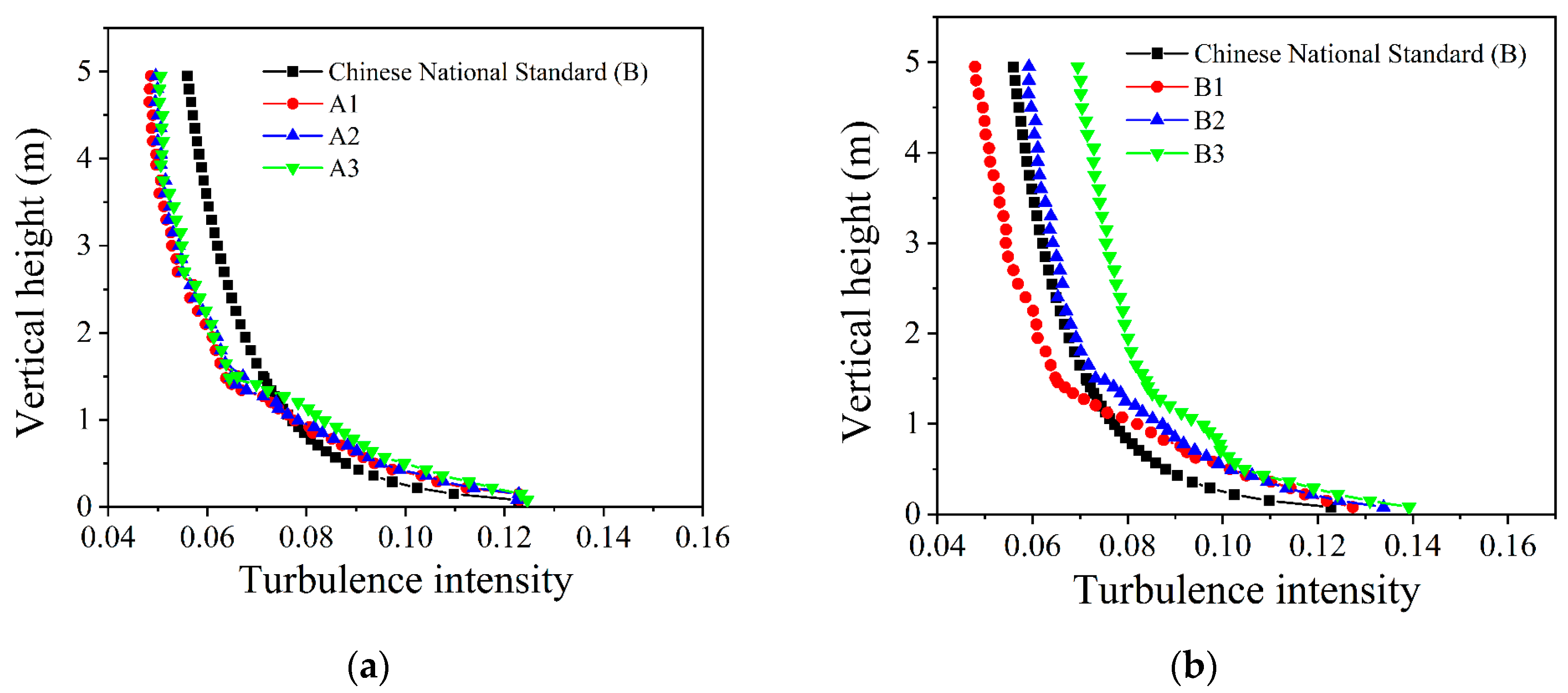
4.3. The Influence of the Radom Number Parameters
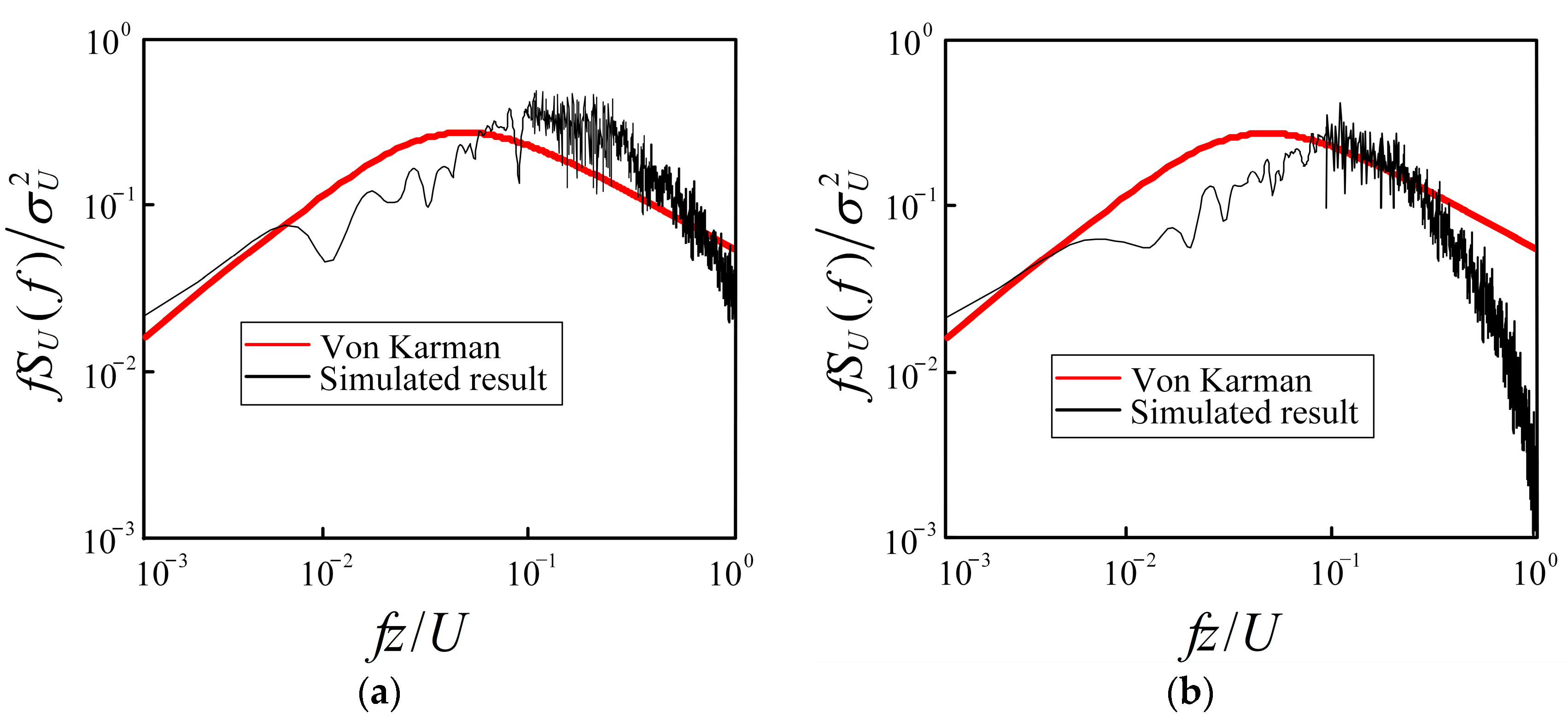
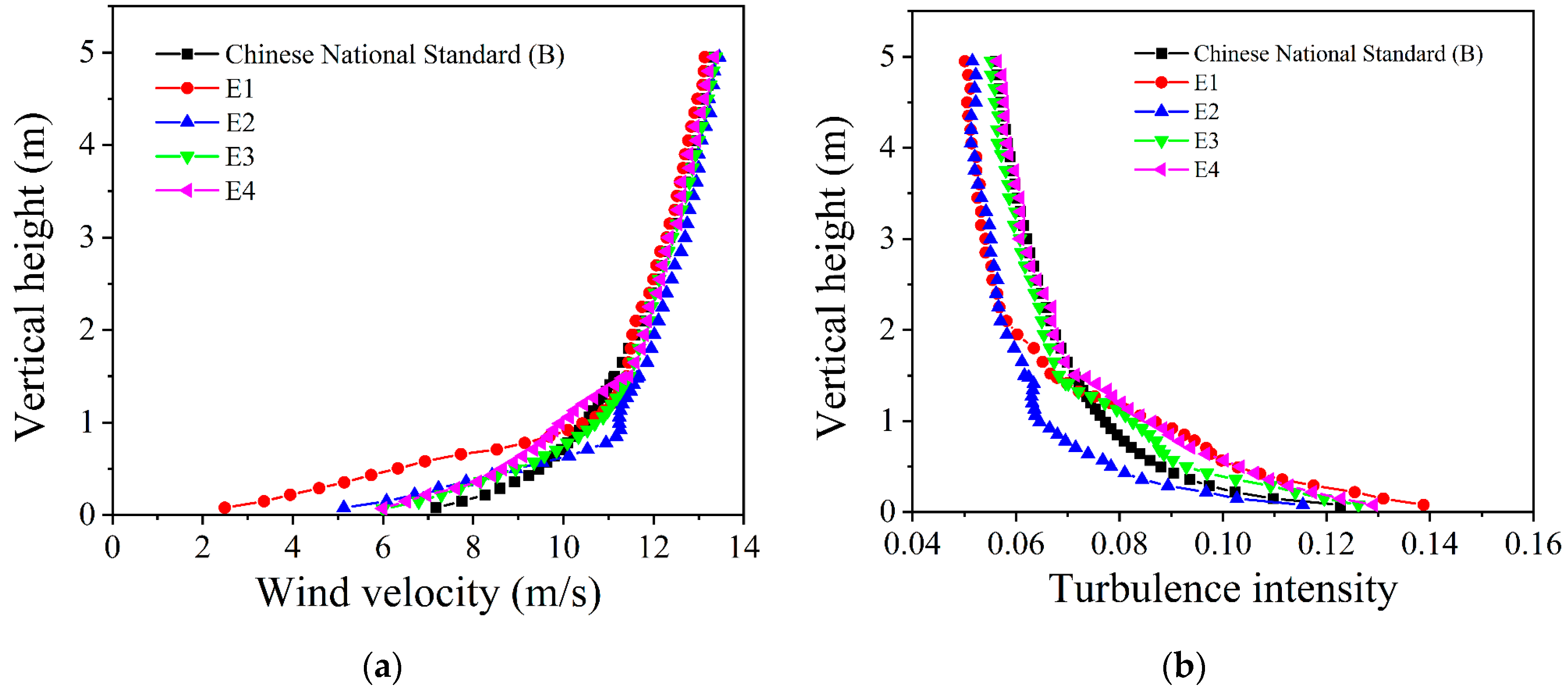
4.4. The Influence of Solution Methods
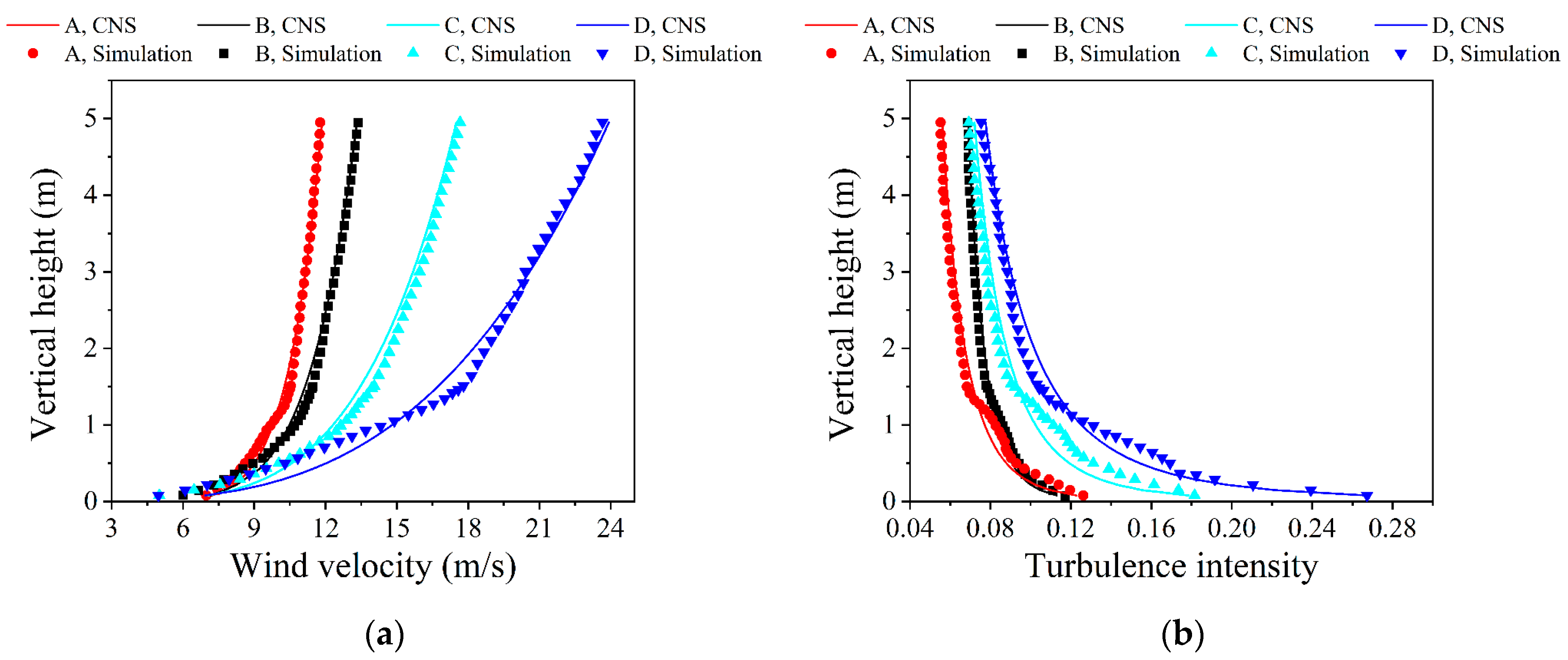
4.5. Recommendation Simulation of Standard Terrains
5. Engineering Application and Verification
5.1. Detials of Wind Tunnel Test and Numerical Simulation
5.2. Comparisons of Wind Tunnel Test and Numerical Simulation
6. Conclusions
- (1)
- Combined with the large eddy simulation technique, roughness elements array, random perturbation technique, circulation surface wind velocity reintroduction technique, and the internal and external grid fusion technique, the wind fields meeting the CNS terrains are generated in the numerical wind tunnels. The wind field simulation strategies are provided.
- (2)
- For random number assignment parameters, the normal distribution range does not typically affect the flow field, whereas the assignment direction has a significant effect. The free-stream turbulence intensity is positively correlated with the standard deviation of random number and negatively correlated with the assignment height. The influence height of the roughness element on turbulence intensity is about 6 times as high as its height.
- (3)
- The effectiveness of the simulation method is validated by a practical engineering example of inflatable membrane structure in this paper. In terms of distribution and values, the wind pressure coefficients of inflatable membrane structure obtained from simulation show good agreement with the wind tunnel test. It is anticipated that the numerical wind tunnel simulation method proposed in this paper can be helpful for subsequent research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kataoka, H.; Ono, Y.; Enoki, K. Applications and prospects of CFD for wind engineering fields. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104310. [Google Scholar] [CrossRef]
- Paula, C.; José, C.; Leorlen, M.; Daniel, G.; Alexandre, C.; Teresa, S. Wind Resource Assessment in Building Environment: Benchmarking of Numerical Approaches and Validation with Wind Tunnel Data. Wind 2022, 2, 659–690. [Google Scholar] [CrossRef]
- Toja-Silva, F.; Kono, T.; Peralta, C.; Lopez-Garcia, O.; Chen, J. A review of computational fluid dynamics (CFD) simulations of the wind flow around buildings for urban wind energy exploitation. J. Wind Eng. Ind. Aerodyn. 2018, 180, 66–87. [Google Scholar] [CrossRef]
- Zhang, Z.; Bao, X. Research Status on Inflow turbulence generation method with Large Eddy Simulation of CFD numerical wind tunnel. IOP Conf. Ser. Mater. Sci. Eng. 2019, 490, 032015. [Google Scholar] [CrossRef]
- Phillips, D.A.; Soligo, M.J. Will CFD ever replace wind tunnels for building wind simulations? Int. J. High-Rise Build. 2019, 8, 107–116. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- García-Sánchez, C.; van Beeck, J.; Gorlé, C. Predictive large eddy simulations for urban flows: Challenges and opportunities. Build. Environ. 2018, 139, 146–156. [Google Scholar] [CrossRef]
- Vasaturo, R.; Kalkman, I.; Blocken, B.; Van Wesemael, P. Large eddy simulation of the neutral atmospheric boundary layer: Performance evaluation of three inflow methods for terrains with different roughness. J. Wind Eng. Ind. Aerodyn. 2018, 173, 241–261. [Google Scholar] [CrossRef]
- Neves, T.; Fisch, G.; Raasch, S. Local convection and turbulence in the Amazonia using large eddy simulation model. Atmosphere 2018, 9, 399. [Google Scholar] [CrossRef]
- Takadate, Y.; Uematsu, Y. Steady and unsteady aerodynamic forces on a long-span membrane structure. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103946. [Google Scholar] [CrossRef]
- Wijesooriya, K.; Mohotti, D.; Chauhan, K.; Dias-da-Costa, D. Numerical investigation of scale resolved turbulence models (LES, ELES and DDES) in the assessment of wind effects on supertall structures. J. Build. Eng. 2019, 25, 100842. [Google Scholar] [CrossRef]
- Hassan, S.; Akter, U.H.; Nag, P.; Molla, M.M.; Khan, A.; Hasan, M.F. Large-Eddy Simulation of Airflow and Pollutant Dispersion in a Model Street Canyon Intersection of Dhaka City. Atmosphere 2022, 13, 1028. [Google Scholar] [CrossRef]
- De Nayer, G.; Breuer, M.; Boulbrachene, K. FSI simulations of wind gusts impacting an air-inflated flexible membrane at Re = 100,000. J. Fluids Struct. 2022, 109, 103462. [Google Scholar] [CrossRef]
- De Nayer, G.; Apostolatos, A.; Wood, J.N.; Bletzinger, K.U.; Wüchner, R.; Breuer, M. Numerical studies on the instantaneous fluid–structure interaction of an air-inflated flexible membrane in turbulent flow. J. Fluids Struct. 2018, 82, 577–609. [Google Scholar] [CrossRef]
- Auvinen, M.; Boi, S.; Hellsten, A.; Tanhuanpää, T.; Järvi, L. Study of Realistic Urban Boundary Layer Turbulence with High-Resolution Large-Eddy Simulation. Atmosphere 2020, 11, 201. [Google Scholar] [CrossRef]
- Wu, X. Inflow turbulence generation methods. Annu. Rev. Fluid Mech. 2017, 49, 23–49. [Google Scholar] [CrossRef]
- Thordal, M.S.; Bennetsen, J.C.; Koss, H.H.H. Review for practical application of CFD for the determination of wind load on high-rise buildings. J. Wind Eng. Ind. Aerodyn. 2019, 186, 155–168. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celik, I. Random Flow Generation Technique for Large Eddy Simulations and Particle-Dynamics Modeling. J. Fluids Eng. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Castro, H.G.; Paz, R.R. A time and space correlated turbulence synthesis method for Large Eddy Simulations. J. Comput. Phys. 2013, 235, 742–763. [Google Scholar] [CrossRef]
- Adler, M.C.; Gonzalez, D.R.; Stack, C.M.; Gaitonde, D.V. Synthetic generation of equilibrium boundary layer turbulence from modeled statistics. Comput. Fluids 2018, 165, 127–143. [Google Scholar] [CrossRef]
- Lee, Y.-T.; Gutti, L.K.; Lim, H.-C. Numerical Study of the Influence of the Inlet Turbulence Length Scale on the Turbulent Boundary Layer. Appl. Sci. 2021, 11, 5177. [Google Scholar] [CrossRef]
- Perret, L.; Delville, J.; Manceau, R.; Bonnet, J.-P. Generation of turbulent inflow conditions for large eddy simulation from stereoscopic PIV measurements. Int. J. Heat Fluid Flow 2006, 27, 576–584. [Google Scholar] [CrossRef]
- Maruyama, Y.; Tamura, T.; Okuda, Y.; Ohashi, M. LES of fluctuating wind pressure on a 3D square cylinder for PIV-based inflow turbulence. J. Wind Eng. Ind. Aerodyn. 2013, 122, 130–137. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, H.; Huang, Q.; Xue, H.; Lin, K. A multi-scale synthetic eddy method for generating inflow data for LES. Comput. Fluids 2017, 156, 103–112. [Google Scholar] [CrossRef]
- Ji, B.; Lei, W.; Xiong, Q. An inflow turbulence generation method for large eddy simulation and its application on a standard high-rise building. J. Wind Eng. Ind. Aerodyn. 2022, 226, 105048. [Google Scholar] [CrossRef]
- Yoshie, R.; Jiang, G.; Shirasawa, T.; Chung, J. CFD simulations of gas dispersion around high-rise building in non-isothermal boundary layer. J. Wind Eng. Ind. Aerodyn. 2011, 99, 279–288. [Google Scholar] [CrossRef]
- Thordal, M.S.; Bennetsen, J.C.; Capra, S.; Koss, H.H.H. Engineering approach for a CFD inflow condition using the precursor database method. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104210. [Google Scholar] [CrossRef]
- Pimont, F.; Dupuy, J.-L.; Linn, R.R.; Sauer, J.A.; Muñoz-Esparza, D. Pressure-Gradient Forcing Methods for Large-Eddy Simulations of Flows in the Lower Atmospheric Boundary Layer. Atmosphere 2020, 11, 1343. [Google Scholar] [CrossRef]
- Spalart, P.R. Direct simulation of a turbulent boundary layer up to Rθ = 1410. J. Fluid Mech. 1988, 187, 61–98. [Google Scholar] [CrossRef]
- Lund, T.S.; Wu, X.; Squires, K.D. Generation of Turbulent Inflow Data for Spatially-Developing Boundary Layer Simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef]
- Nozawa, K.; Tamura, T. Simulation of rough-wall turbulent boundary layer for LES inflow data. In Proceedings of the Second Symposium on Turbulence and Shear Flow Phenomena, Stockholm, Sweden, 27–29 June 2001; pp. 443–448. [Google Scholar] [CrossRef]
- Kataoka, H.; Mizuno, M. Numerical flow computation around aeroelastic 3D square cylinder using inflow turbulence. Wind Struct. 2002, 5, 379–392. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Cao, S.; Cao, J. Iteration-Based Recycling and Reshaping Method for Inflow Turbulence Generation and Its Evaluation. Atmosphere 2022, 13, 72. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012. Available online: https://scholar.google.com/scholar_lookup?title=Load%20Code%20for%20Design%20of%20Building%20Structures%2C%20China%20National%20Standard%20(CNS).%20GB%2050009-2012&author=National%20Standard%20Committee&publication_year=2012 (accessed on 10 August 2022). (In Chinese)
- AIJ-RLB-2004; Recommendations for Loads on Buildings. Architecture Institute of Japan: Tokyo, Japan, 2004. Available online: https://scholar.google.com/scholar?q=Architectural%20Institute%20of%20Japan,%202004.%20Recommendations%20for%20loads%20on%20buildings.%20Architectural%20Institute%20of%20Japan%20 (accessed on 10 August 2022).
- Xie, S.; Zheng, J.; Xiao, B.; Hu, H.; Cao, X.; Wang, X.; Zhang, L. Numerical Simulation and Wind Tunnel Test on the Wind-Induced Response of Three Typical Types of Greenhouse Main Structures. Agriculture 2022, 12, 1294. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Q. Large eddy simulation of atmospheric boundary layer flow based on FLUENT. Chin. J. Comput. Mech. 2012, 29, 734–739. Available online: https://sc.panda321.com/scholar?hl=zh-CN&as_sdt=0%2C5&q=Wang%2C+T.%3B+Yang%2C+Q.+Large+eddy+simulation+of+atmospheric+boundary+layer+flow+based+on+FLUENT.+Chinese+Journal+of+Computational+Mechanics+2012%2C+29%2C+734-739%2C+&btnG= (accessed on 1 May 2022). (In Chinese with English Abstract).
- Oakland, J.S. Statistical Process Control, 6th ed.; Routledge: London, UK, 2007; pp. 88–89. [Google Scholar] [CrossRef]
- Ricci, M.; Patruno, L.; de Miranda, S. Wind loads and structural response: Benchmarking LES on a low-rise building. Eng. Struct. 2017, 144, 26–42. [Google Scholar] [CrossRef]
- Feng, C.; Gu, M.; Zheng, D. Numerical simulation of wind effects on super high-rise buildings considering wind veering with height based on CFD. J. Fluids Struct. 2019, 91, 102715. [Google Scholar] [CrossRef]
- Qiu, Y.; Sun, Y.; Wu, Y.; San, B.; Tamura, Y. Surface roughness and Reynolds number effects on the aerodynamic forces and pressures acting on a semicylindrical roof in smooth flow. J. Struct. Eng. 2018, 144, 04018140. [Google Scholar] [CrossRef]

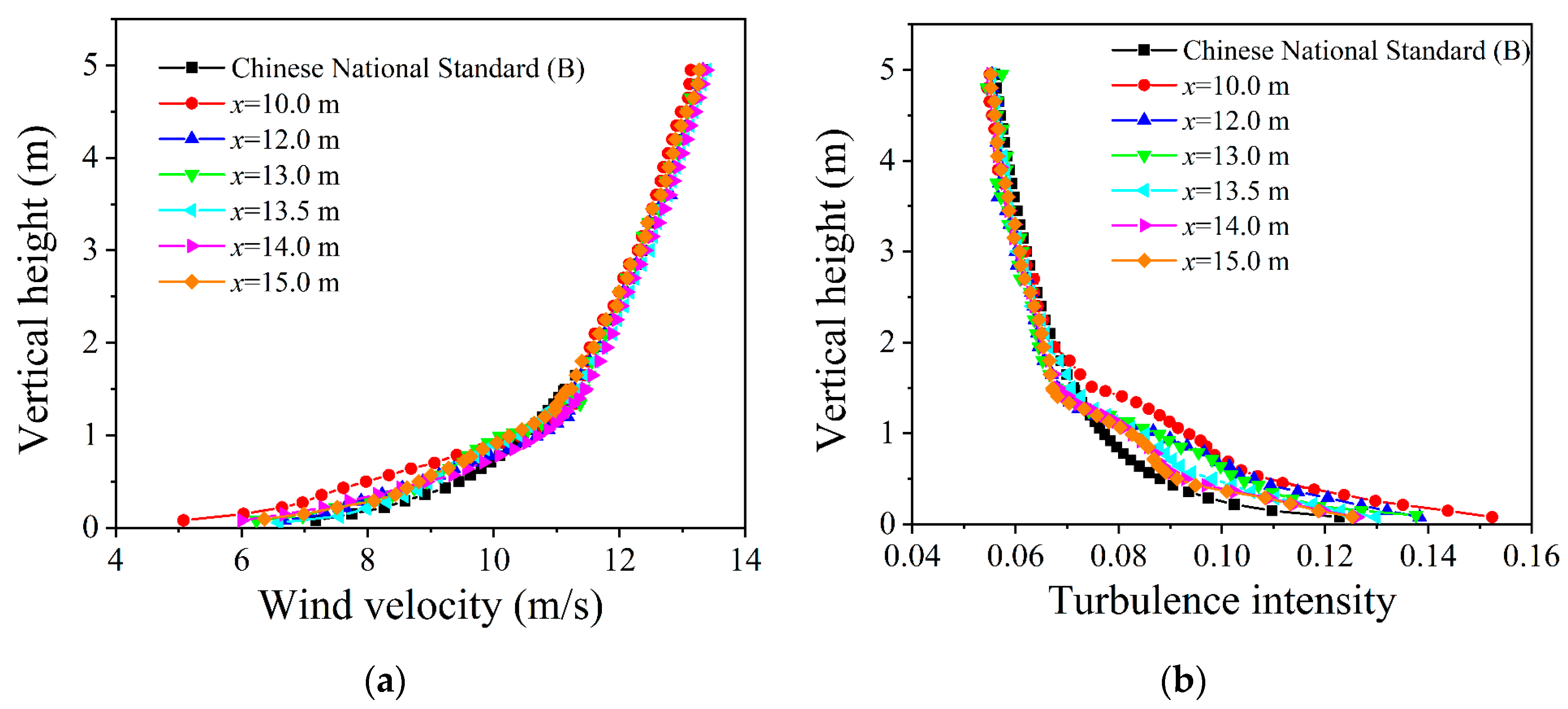


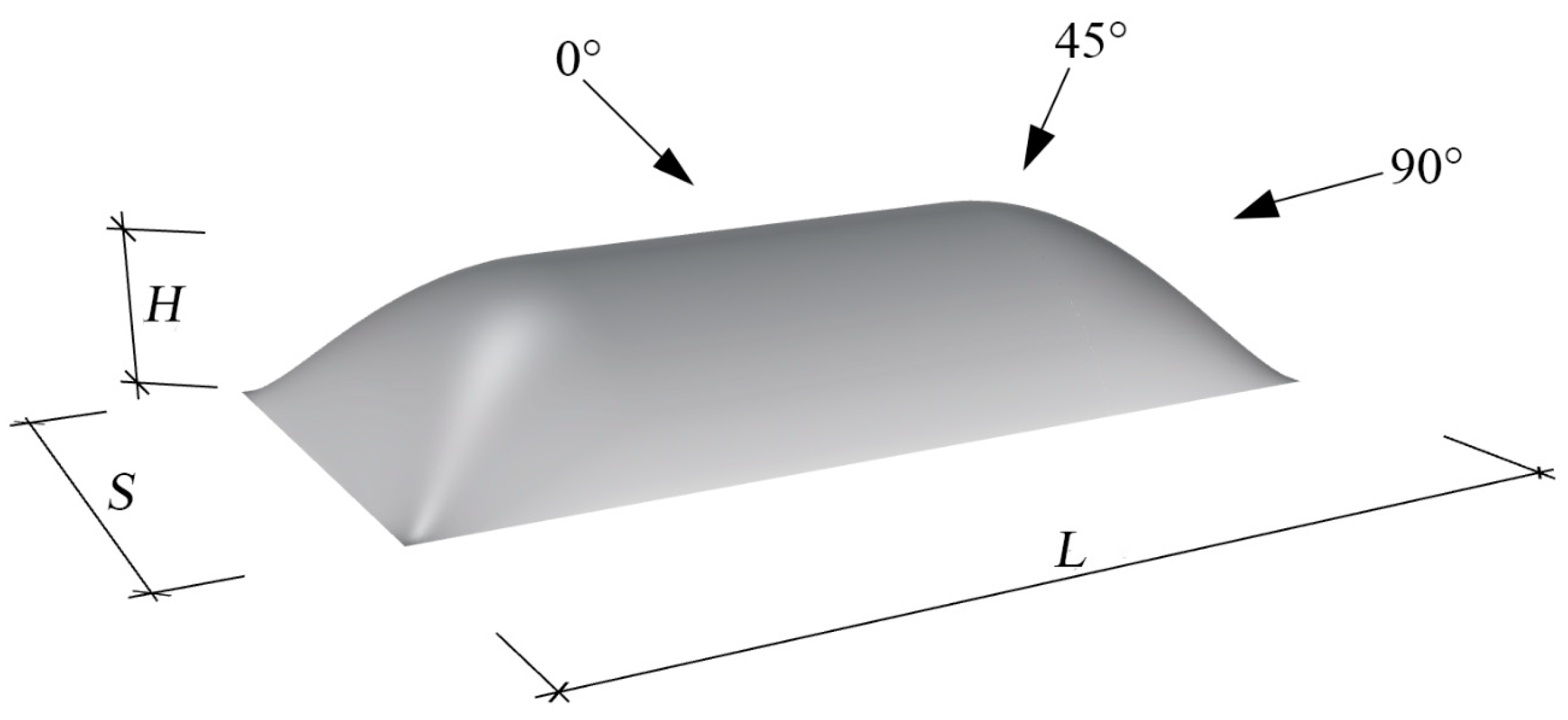


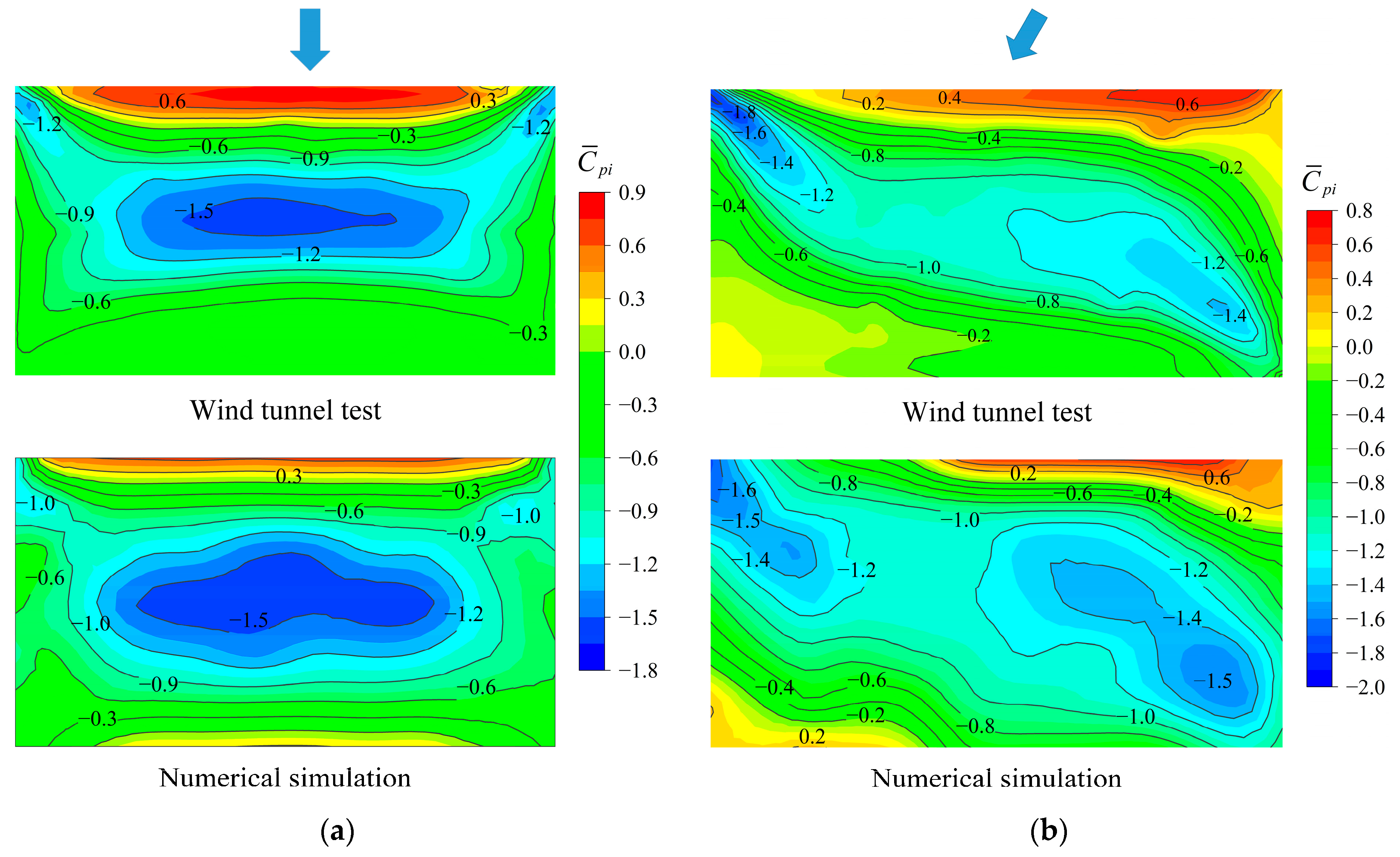
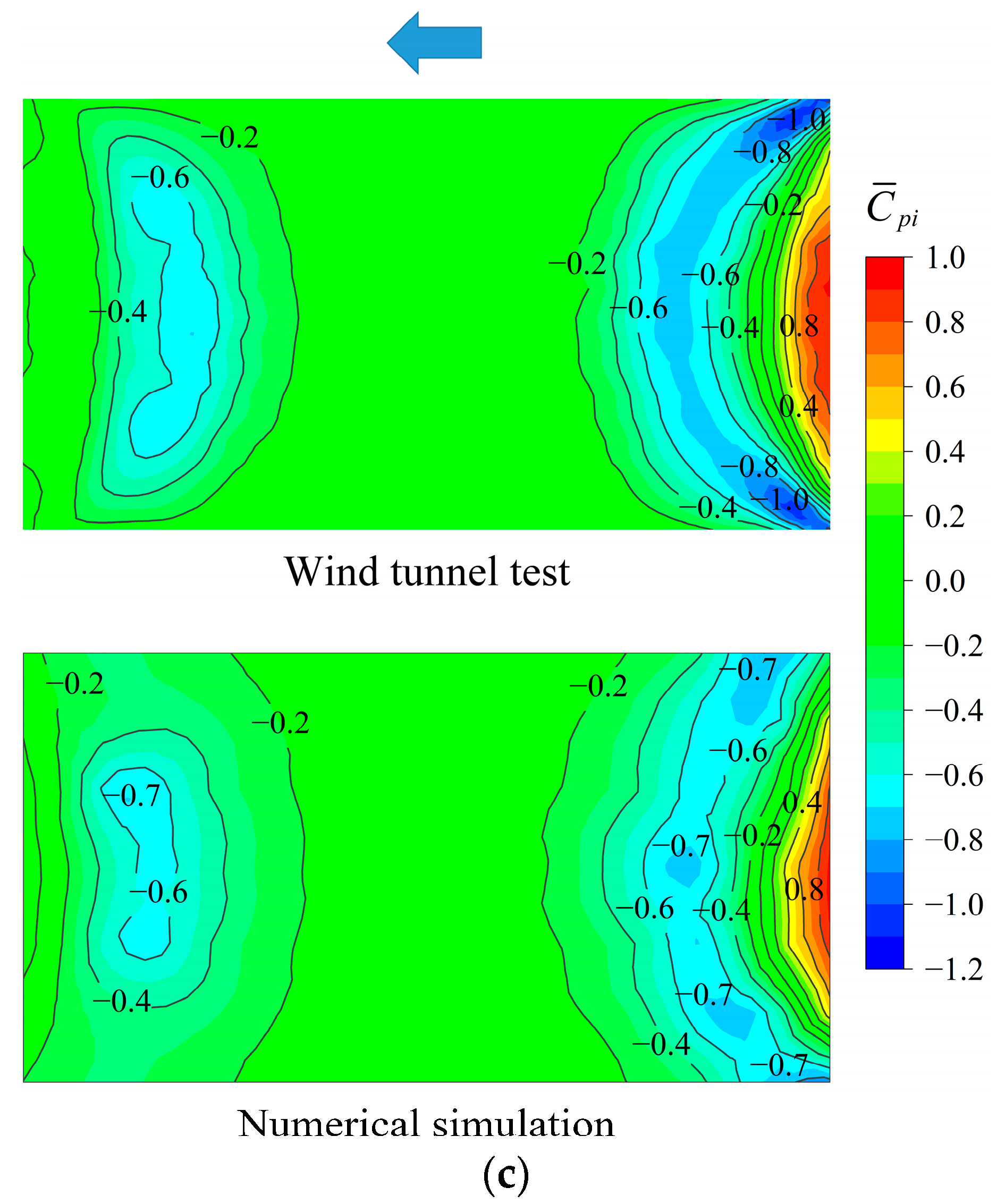
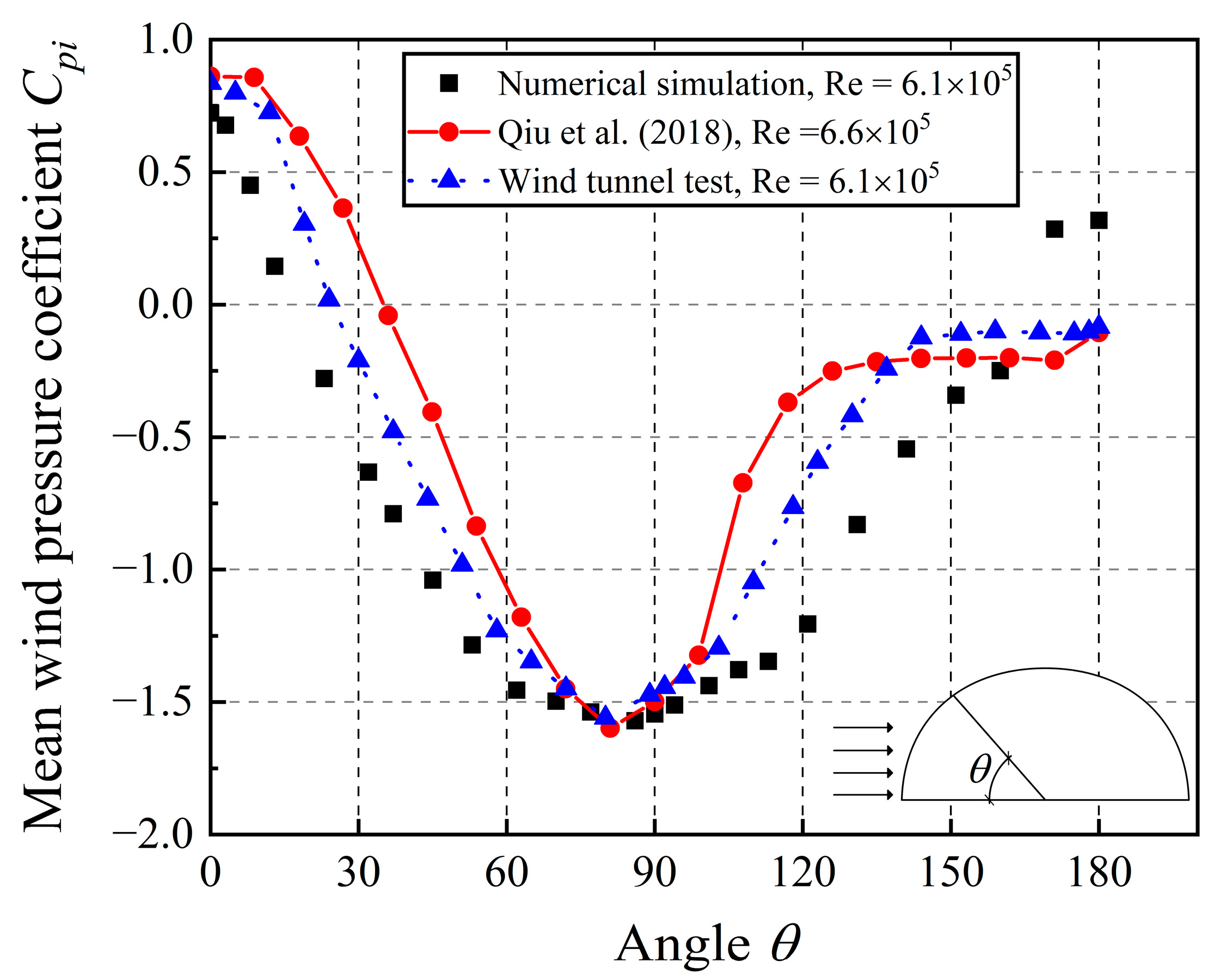
| Terrain | Roughness Index α | Boundary Layer Height (m) | Nominal Turbulence Intensity I0 | Reference Height z0 (m) |
|---|---|---|---|---|
| A | 0.12 | 300 | 0.12 | 10 |
| B | 0.15 | 350 | 0.14 | |
| C | 0.22 | 450 | 0.23 | |
| D | 0.30 | 500 | 0.39 |
| Scheme | The Near-Wall Spacing | Grid Growth Rate | Grid Number (x × y × z) | Total Grid Number |
|---|---|---|---|---|
| 1 | 0.0005 m | 1.09 | 261 × 128 × 56 | 1.87 million |
| 2 | 0.001 m | 1.10 | 208 × 88 × 56 | 1.02 million |
| Boundary Surface | Boundary Condition |
|---|---|
| Inlet and circulation surfaces | Pseudo-periodic boundary conditions |
| Lateral spread | Periodic boundary conditions |
| Top surface | Slip boundary condition (Specified-shear wall) |
| Computational domain bottom, roughness element surface | Non-slip boundary condition (No-slip wall) |
| Case | Height of Roughness Elements (m) | Standard Deviation | Assignment Height (m) | Assignment Direction | Normal Distribution Range |
|---|---|---|---|---|---|
| A1 | 0.25 | 1.3 | Over 1.3 | x | (−1.5σ, 1.5σ) |
| A2 | (−2σ, 2σ) | ||||
| A3 | (−3σ, 3σ) | ||||
| B1 | No | 1.3 | Over 0.25 | x | (−3σ, 3σ) |
| B2 | 1.4 | ||||
| B3 | 1.5 | ||||
| B4 | 0.25 | 1.3 | Over 1.3 | x | (−3σ, 3σ) |
| B5 | 1.4 | ||||
| B6 | 1.5 | ||||
| C1 | 0.25 | 1.4 | Over 1.3 | x | (−3σ, 3σ) |
| C2 | x, y | ||||
| C3 | x, z | ||||
| D1 | 0.25 | 1.3 | Over 1.0 | x | (−3σ, 3σ) |
| D2 | Over 1.3 | ||||
| D3 | Over 1.7 |
| Case | Momentum Discrete Forma | Transient Term Format |
|---|---|---|
| E1 | First-order upwind | Bounded second-order implicit |
| E2 | First-order upwind (adding dissipation velocity) | |
| E3 | Bounded central difference | |
| E4 | Second-order upwind |
| Terrain | Boundary Layer Height (m) | Height of Roughness Elements (m) | Standard Deviation | Assignment Height (m) | Assignment Direction |
|---|---|---|---|---|---|
| A | 3.0 | 0.22 | 1.114 | Over 1.2 | x |
| B | 3.5 | 0.25 | 1.393 | Over 1.3 | x |
| C | 4.5 | 0.37 | 1.953 | Over 0.9 | x |
| D | 5.5 | 0.48 | 2.794 | Over 0.9 | x, y, z |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wei, C.; Chen, Z.; Wang, S.; Tang, L. Numerical Simulation of Atmospheric Boundary Layer Turbulence in a Wind Tunnel Based on a Hybrid Method. Atmosphere 2022, 13, 2044. https://doi.org/10.3390/atmos13122044
Chen Z, Wei C, Chen Z, Wang S, Tang L. Numerical Simulation of Atmospheric Boundary Layer Turbulence in a Wind Tunnel Based on a Hybrid Method. Atmosphere. 2022; 13(12):2044. https://doi.org/10.3390/atmos13122044
Chicago/Turabian StyleChen, Zhaoqing, Chao Wei, Zhuozhuo Chen, Shuang Wang, and Lixiang Tang. 2022. "Numerical Simulation of Atmospheric Boundary Layer Turbulence in a Wind Tunnel Based on a Hybrid Method" Atmosphere 13, no. 12: 2044. https://doi.org/10.3390/atmos13122044
APA StyleChen, Z., Wei, C., Chen, Z., Wang, S., & Tang, L. (2022). Numerical Simulation of Atmospheric Boundary Layer Turbulence in a Wind Tunnel Based on a Hybrid Method. Atmosphere, 13(12), 2044. https://doi.org/10.3390/atmos13122044









