Study on Surface Characteristic Parameters and Surface Energy Exchange in Eastern Edge of the Tibetan Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Introduction of Study Area and Data
2.2. Method
2.2.1. Eddy Correlation Method
2.2.2. Zero Plane Displacement
2.2.3. Aerodynamic Roughness and Thermodynamic Roughness
2.2.4. Momentum Flux Transport Coefficient and Sensible Heat Flux Transport Coefficient
2.2.5. Calculation Method of Surface Soil Heat Flux (TDEC)
2.2.6. Surface Energy Balance Equation
2.2.7. Analysis Method of the Degree of Closure of the Surface Energy Balance
3. Results and Analysis
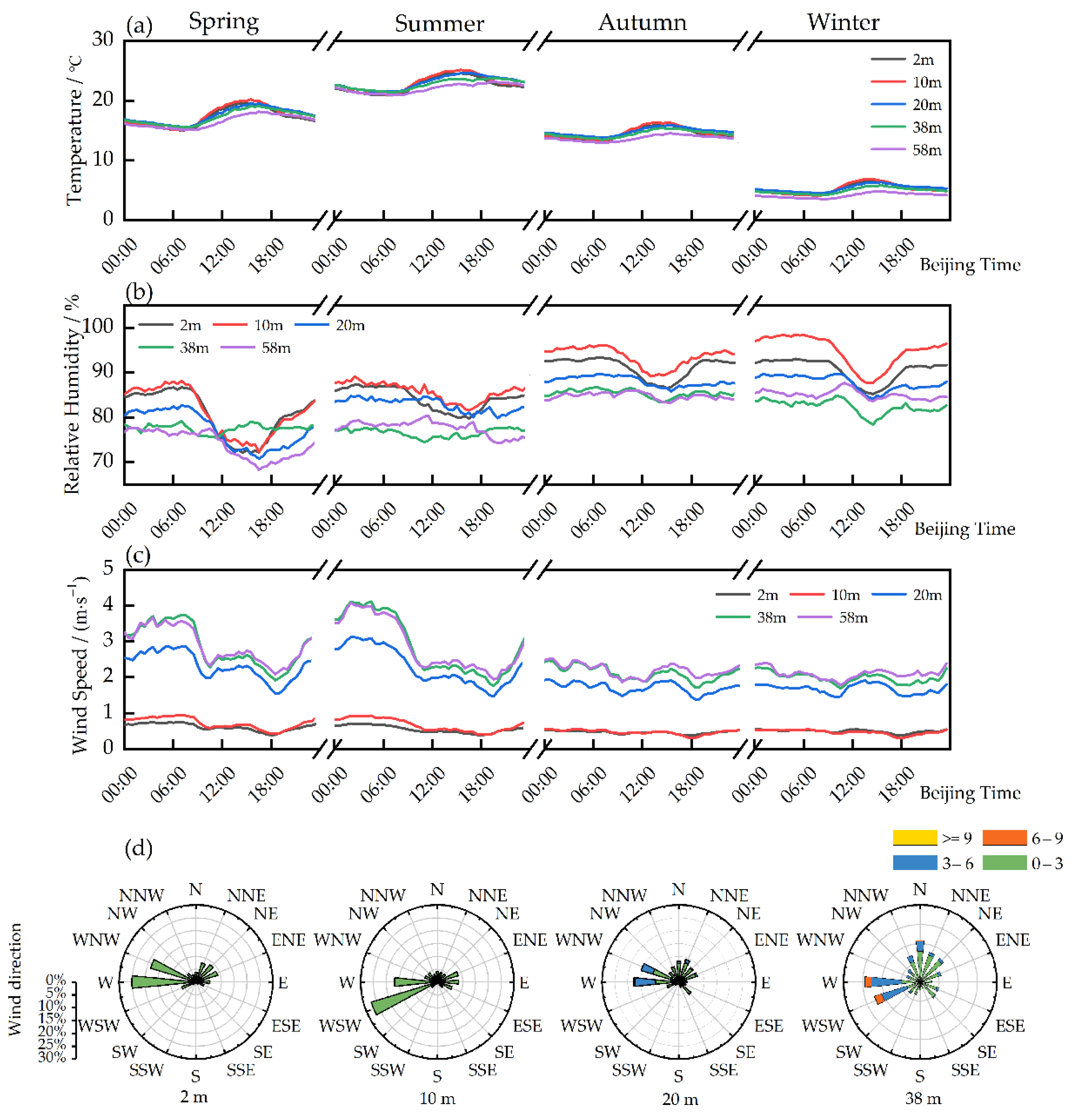
3.1. Characteristics of Changes in Near-Surface Meteorological Elements
3.2. Aerodynamic and Thermodynamic Parameters
3.2.1. Zero Plane Displacement , Aerodynamic Roughness and Thermodynamic Roughness
3.2.2. The Momentum Flux Transport Coefficient and the Sensible Heat Flux Transport Coefficient
3.3. The Similarity Relationship of Dimensionless Wind Speed Fluctuation Variance
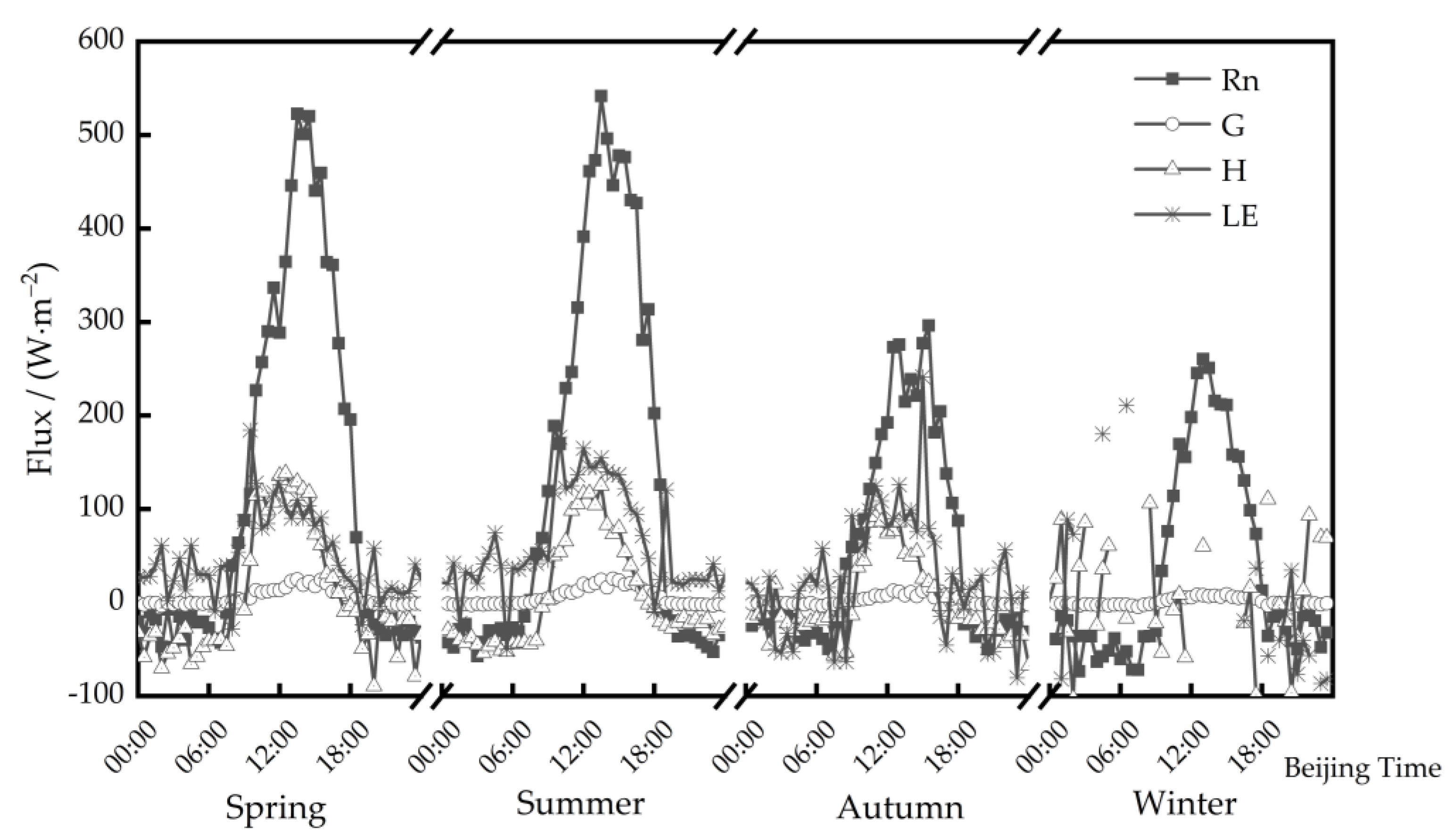
3.4. The Variation Characteristics of Surface Energy
3.4.1. The Variation Characteristics of Each Component of Surface Balance
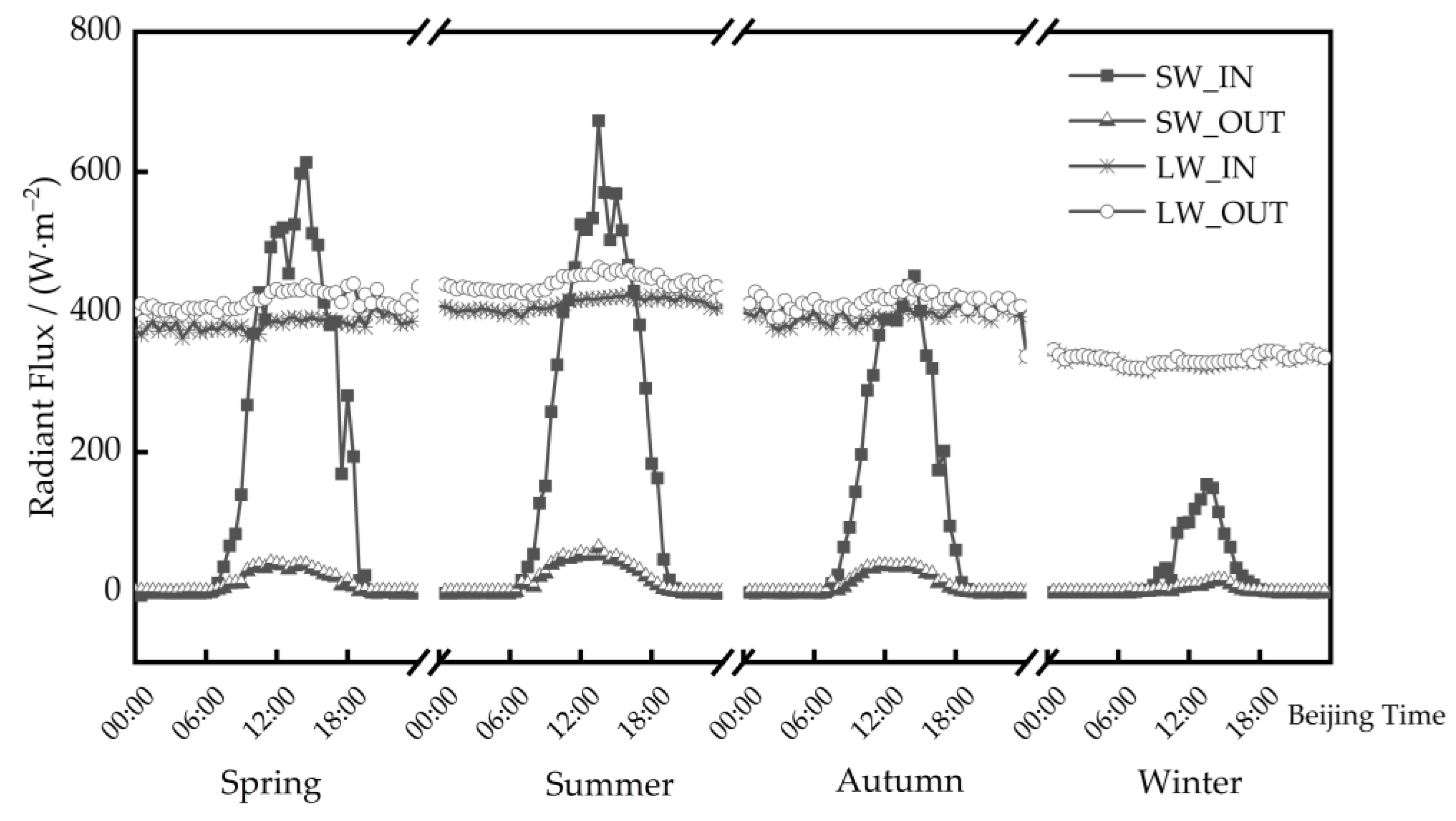
3.4.2. Surface Radiation Budget Characteristics
3.4.3. Variation Characteristics of Surface Albedo
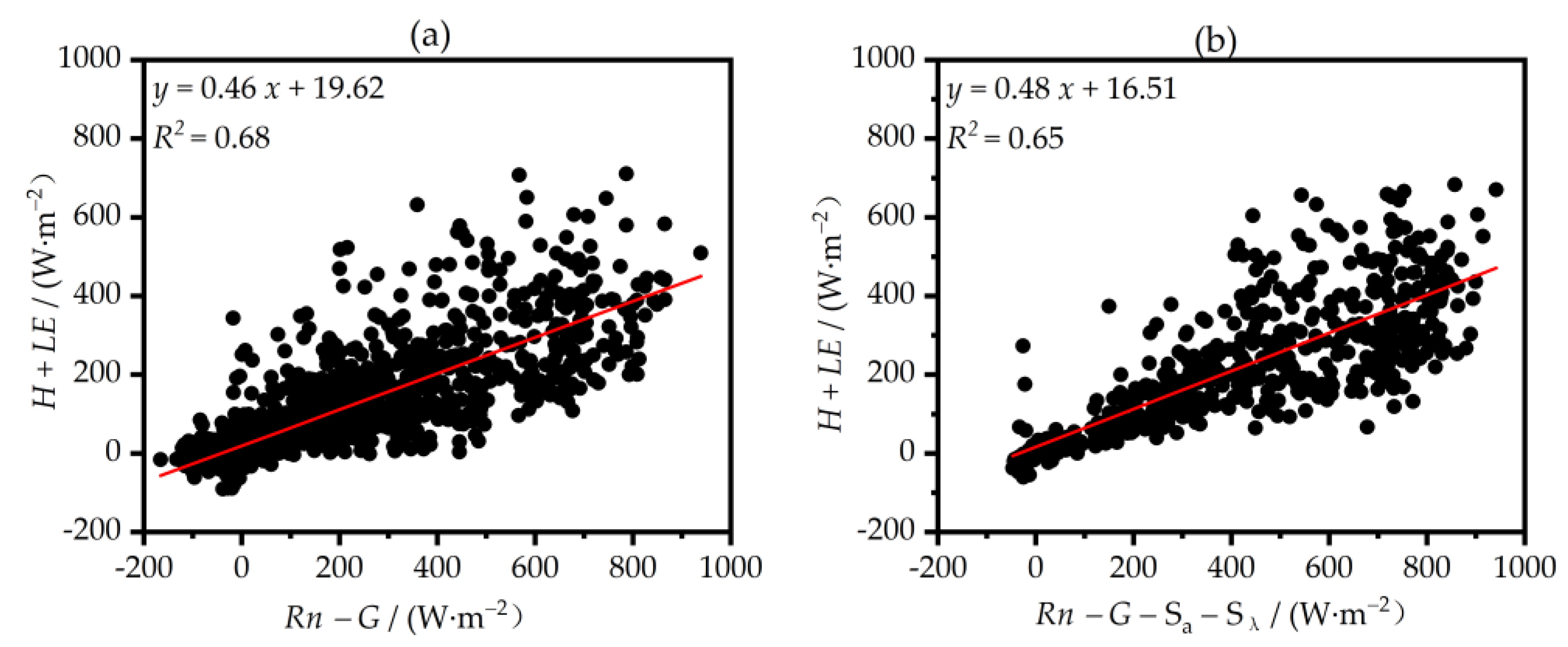
3.4.4. Characteristics of Changes in the Degree of Energy Balance Closure
4. Conclusions
- (1)
- The annual average value of zero-plane displacement calculated is 10.45 . Aerodynamic roughness basically does not change with seasons, and aerodynamic thermal roughness fluctuates slightly with seasons. The annual average values of aerodynamic roughness and aerothermal roughness obtained by calculation are 1.65 and 9.95 , respectively. The annual average values of momentum flux transport coefficient and sensible heat flux transport coefficient are and , respectively.
- (2)
- Under unstable stratification, the dimensionless vertical wind fluctuation variance in the Mount Emei area can better conform to the 1/3rd power law of Monin–Obukhov similar theory, while the dimensionless horizontal wind fluctuation variance does not conform to the 1/3rd power law of Monin–Obukhov similar theory. This is caused by the topographic relief and the difference in the physical characteristics of the underlying surface. Under the stable stratification condition, the dimensionless wind fluctuation variance does not conform to the 1/3 order law of Monin–Obukhov similar theory. In the near-neutral case, the dimensionless velocity variance in the vertical direction in this area is 1.314.
- (3)
- The sensible heat flux in spring is slightly greater than the latent heat flux, the latent heat flux in summer is dominant, the dominant position of latent heat flux in autumn is gradually reduced, the difference between sensible heat flux and latent heat flux is small, and the sensible heat flux in winter is dominant.
- (4)
- The average surface albedo of the Mount Emei area in each season in the daytime has little difference, ranging from 0.05 to 0.08. The surface albedo in winter is slightly smaller than that in other seasons, which is 0.05. The station is a forest underlay, so its albedo is less than most stations on the plateau.
- (5)
- The non-closure phenomenon is significant in the Mount Emei area. Before considering the canopy thermal storage, the energy closure rate of the Mount Emei station was 46%, and after considering the canopy thermal storage, the energy closure rate increased to 48%. The possible reason for the energy non-closure in this area is that the influence of horizontal advection and vertical advection on the energy closure is not considered. Second, consider the effects of the leaf heat storage, branch heat storage in the canopy on the energy closure, and the more significant errors in the estimated soil heat fluxes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Boston, MA, USA, 1988; pp. 3–666. [Google Scholar]
- Ding, A.J. Study on Variation Characteristics and Transport of Air Pollutants at Low Level in East Asia. Ph.D. Thesis, Nanjing University, Nanjing, China, 2004. [Google Scholar]
- Wu, G.X.; Liu, X.; Zhang, Q.; Qian, Y.F.; Mao, J.Y.; Liu, Y.M.; Li, W.P. Progresses in the Study of the Climate Impacts of the Elevated Heating over the Tibetan Plateau. Clim. Environ. Res. 2002, 7, 184–201. [Google Scholar]
- Duan, A.M.; Wu, G.X. Weakening trend in the atmospheric heat source over the Tibetan Plateau during recent decades. Part I: Observations. J. Clim. 2010, 21, 3149–3164. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.G.; Tang, W.J.; Chen, Y.Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. J. Agric. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Foken, T.; Wimmer, F.; Mauder, M. The Energy Balance Closure Problem: An Overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Oncley, S.; Foken, T.; Vogt, R.; Kohsiek, W.; DeBruin, H.A.; Bernhofer, C.; Christen, A.; Van Gorsel, E.; Grantz, D.; Feigenwinteret, C.; et al. The energy balance experimentEBEX-2020. Part I: Overview and energy balance. Bound.-Layer Meteor. 2007, 123, 1–28. [Google Scholar] [CrossRef]
- Jacobs, A.; Heusinkveld, B.; Holtslag, A. Towards closing the surface energy budget of a mid-latitude grassland. Int. J. Climatol. 2010, 9, 30. [Google Scholar] [CrossRef]
- Xu, X.D.; Chen, L.S. Advances of the Study on Tibetan Plateau Experiment of Atmospheric Sciences. J. Appl. Meteor. Sci. 2006, 6, 756–772. [Google Scholar]
- Li, D.L.; Zhang, J.J.; Wu, H.B. A diagnostic study on surface sensible heat flux anomaly in summer over the Qinghai-Xizang Plateau. Plateau Meteor. 1997, 16, 367–375. [Google Scholar]
- Li, G.P.; Duan, T.Y.; Wu, G.F. The Intersity of Surface Heat Source and Surface Heat Balance on the Western Qinghai-Xizang Plateau. Sci. Geogr. Sin. 2003, 23, 13–18. [Google Scholar]
- Ma, Y.M.; Yao, T.D.; Wang, J.M. Experimental Study of Energy and Water Cycle in Tibetan Plateau--The Progress Introduction on the Study of GAME/Tibet and CAMP/Tibet. Plateau Meteor. 2006, 25, 344–351. [Google Scholar]
- Li, M.S.; Ma, Y.M.; Hu, Z.Y.; Ma, W.Q.; Wang, J.M.; Ogino, S. Study on Characteristics of ABL over Naqu Region of Northern Tibetan Plateau. Plateau Meteor. 2004, 23, 728–773. [Google Scholar]
- Li, M.S.; Yang, Y.X.; Ma, Y.M.; Sun, F.L.; Chen, X.L.; Wang, B.B.; Zhu, Z.K. Analyses on Turbulence Data Control and Distribution of Surface Energy Flux in Namco Area of Tibetan Plateau. Plateau Meteor. 2012, 31, 875–884. [Google Scholar]
- Chen, X.L.; Ma, Y.M.; Li, M.S.; Ma, W.Q.; Wang, H. Analyses on Near Surface Layer Atmospheric Characteristics and Soil Features in Northern Tibetan Plateau. Plateau Meteor. 2008, 27, 941–948. [Google Scholar]
- Li, M.S.; Babel, W.; Tanaka, K.; Foken, T. Note on the application of planar-fit rotation for non-omnidirectional sonic anemometers. Atmos. Meas. Tech. 2012, 5, 7323–7340. [Google Scholar] [CrossRef]
- Li, M.S.; Ma, Y.M.; Sun, F.L.; Zhao, Y.Z.; Wang, Y.J.; Lv, Y.Q. Characteristics of Micrometeorology and Exchange of Surface Energy in the Namco Region. Plateau Meteor. 2008, 27, 727–732. [Google Scholar]
- Li, Y.; Li, Y.Q.; Zhao, X.B. Analyses of turbulent fluxes and micrometeorological characteristics in the surface layer at Litang of the eastern Tibetan Plateau. Acta Meteor. Sin. 2009, 67, 417–425. [Google Scholar]
- Zhao, X.B.; Liu, C.W.; Tong, B.; Li, Y.B.; Wang, L.L.; Ma, Y.M.; Gao, Z.Q. Study on Surface Process Parameters and Soil Thermal Parameters at Shiquanhe in the Western Qinghai-Xizang Plateau. Plateau Meteor. 2021, 40, 711–723. [Google Scholar]
- Fu, W.; Li, M.S.; Yin, S.C.; Lv, Z.; Wang, L.Z.; Shu, L. Study on the ABL Structure of the QinghaiXizang Plateau under the South Branch of the Westerly Wind and the Plateau Monsoon Circulation Field. Plateau Meteor. 2022, 41, 190–203. [Google Scholar]
- Gromke, C.; Manes, C.; Walter, B.; Lehning, M.; Guala, M. Aerodynamic Roughness Length of Fresh Snow. Bound.-Layer Meteorol. 2011, 141, 21–34. [Google Scholar] [CrossRef]
- Kubota, A.; Sugita, M. Radiometrically determined skin temperature and scalar roughness to estimate surface heat flux. Part I: Parameterization of radiometric scalar roughness. Bound.-Layer Meteorol. 1994, 69, 397–416. [Google Scholar] [CrossRef]
- Graf, A.; Boer, A.; Moene, A.; Vereecken, H. Intercomparison of Methods for the Simultaneous Estimation of Zero-Plane Displacement and Aerodynamic Roughness Length from Single-Level Eddy-Covariance Data. Bound.-Layer Meteorol. 2014, 151, 373–387. [Google Scholar] [CrossRef]
- Babić, N.; Večenaj, Ž.; De Wekker, S.F.J. Flux–Variance Similarity in Complex Terrain and Its Sensitivity to Different Methods of Treating Non-stationarity. Bound.-Layer Meteorol. 2016, 159, 123–145. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Dimensionless characteristics of turbulence in the atmospheric surface layer. Dokl. Akad. Nauk SSSR 1953, 93, 223–226. [Google Scholar]
- Liu, H.Z.; Hong, Z.X. Turbulent Characteristics in the Surface Layer over Gerze Area in the Tibetan Plateau. Chinese J. Atmos. Sci. 2000, 24, 289–300. [Google Scholar]
- Chen, Y.G.; Zhang, Y.; Wang, S.Y. Seasonal variation of turbulence characteristics over alpine meadow ecosystem. Plateau Meteor. 2014, 33, 585–595. [Google Scholar]
- Liwei, Y.A.N.G.; Xiaoqing, G.A.O.; Xiaoying, H.U.I.; Na, G.A.O.; Ya, Z.H.O.U.; Xuhong, H.O.U. Study on turbulence characteristics in the atmospheric surface layer over Nyainrong grassland in central Qinghai-Tibetan Plateau. Plateau Meteor. 2017, 36, 875–885. [Google Scholar]
- Ma, Y.; Ma, W.; Hu, Z.; Li, M.; Wang, J.; Ishikawa, H.; Tsukamoto, O. Similarity analysis of atmospheric turbulent intensity over grassland surface of Qinghai-Xizang Plateau. Plateau Meteor. 2002, 21, 514–517. [Google Scholar]
- Franceschi, M.D.; Zardi, D.; Tagliazucca, M.; Tampieri, F. Analysis of second-order moments in surface layer turbulence in an Alpine valley. Q. J. R. Meteorol. Soc. 2010, 135, 1750–1765. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.Q.; Zhao, X.B. The Comparison and Analysis of ABL observational data between the East of Tibetan Plateau and Chengdu Plain (I). Plateau Mt. Meteor Res. 2008, 28, 30–35. [Google Scholar]
- Lv, Z.; Li, M.S.; Liu, X.R.; Yin, S.C.; Song, X.Y.; Fu, W.; Wang, L.Z.; Shu, L. Characteristics of Surface Energy Exchange in Emei Mountain Area on the Eastern Qinghai-Tibetan Plateau in Winter. Plateau Meteor. 2020, 39, 445–458. [Google Scholar]
- Chang, N.; Li, M.S.; Wang, L.Z.; Gong, M.; Fu, W.; Shu, L. Study on Micrometeorological Characteristics of Near Surface Layer in Emei Mount Area. Plateau Meteor. 2022, 41, 226–240. [Google Scholar]
- Mahrt, L. Flux sampling errors for aircraft and towers. J. Atmos. Ocean. Technol. 1998, 15, 416–429. [Google Scholar] [CrossRef]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Yu, G.R.; Sun, X.M. Principles and Methods of Flux Observation in Terrestrial Ecosystems, 2nd ed.; Higher Education Press: Beijing, China, 2006; pp. 1–335. [Google Scholar]
- Feng, J.W.; Liu, H.Z.; Wang, L.; Du, Q.; Shi, L.Q. Seasonal and inter-annual variation of surface roughness length and bulk transfer coefficients in a semiarid area. Sci. China Earth Sci. 2011, 42, 24–33. [Google Scholar] [CrossRef]
- Yue, P.; Zhang, Q.; Zhao, W.; Wang, S.; Shi, J.S.; Wang, R.A. Characteristics of Turbulence Transfer in Surface Layer over Semi-Arid Grassland in Loess Plateau in Summer. Plateau Meteor. 2015, 34, 21–29. [Google Scholar]
- Yue, P.; Zhang, Q.; Li, Y.H.; Wang, R.Y.; Wang, S.; Sun, X.Y. Bulk transfer coefficients of momentum and sensible heat over semiarid grassland surface and their parameterization scheme. Acta Phys. Sin. 2013, 62, 527–535. [Google Scholar]
- Yang, K.; Wang, J.M. A temperature prediction-correction method for estimating surface soil heat flux from soil temperature and moisture data. Sci. China Ser. D-Earth Sci. 2008, 51, 721–729. [Google Scholar] [CrossRef]
- Tian, Z.W.; Wang, W.Z.; Wang, J.M. Analyzing the effects of energy storage terms in vegetation-atmosphere system on energy balance closure. J. Glaciol. Geocryol. 2016, 38, 794–803. [Google Scholar]
- Sun, C.; Jiang, H.; Chen, J.; Liu, Y.L.; Niu, X.D.; Chen, X.F.; Fang, C.Y. Energy flux and balance analysis of Phyllostachys edulis forest ecosystem in subtropical China. Acta Ecol. Sinica. 2015, 35, 4128–4136. [Google Scholar]
- Liu, H.P.; Liu, S.H.; Zhu, T.Y.; Jin, C.J.; Kong, F.Z.; Guan, D.X. Determination of Aerodynamic Parameters of Changbai Mountain Forest. Acta Scicntiarum Nat. Univ. Pekin. 1997, 33, 116–122. [Google Scholar]
- Liu, Y.J.; Wei, Z.G.; Chen, C.; Dong, W.J.; Zhu, X.; Chen, G.Y.; Liu, Y.J. Comparison of Meteorological Elements in Dry and Wet Seasons and Parameterization of Momentum and Sensible Heat Exchange Coefficients near the Underlying Surface of the Zhuhai Phoenix Mountain Forest. Clim. Environ. Res. 2020, 25, 457–468. [Google Scholar]
- Li, M.; Ma, Y.; Ma, W.; Hu, Z.; Ishikawa, H.; Su, Z.; Sun, F. Analysis of turbulence characteristics over the northern Tibetan Plateau area. Adv. Atmos. Sci. 2006, 23, 579–585. [Google Scholar] [CrossRef]
- Hui-zhi, L.I.U.; Jian-wu, F.E.N.G.; Han, Z.O.U.; Ai-guo, L.I. Turbulent characteristics of the surface layer in Rongbuk Valley on the northern slope of Mt. Qomolangma. Plateau Meteor. 2007, 26, 1151–1161. [Google Scholar]
- Zhang, G.; Zheng, N.; Zhang, J.S.; Meng, P. Turbulence micro-meteorological characteristics over the plantation canopy. Chin. J. Appl. Ecol. 2018, 29, 1787–1796. [Google Scholar]
- Xu, J.Q.; Chen, B.Y.; Sui, X.X. Observational Analysis on Turbulent Characteritics of the Atmospheric Surface Layer Above Forest. J. Arid. Meteor. 2014, 32, 1–9. [Google Scholar]
- Qi, Y.Q.; Wang, J.M.; Jia, L.; Liu, W.; Ma, Y.M.; Ren, Y.X. A Study of Turbulent Transfer Characteristics in Wudaoliang Area of Qinghai-Xizang Plateau. Plateau Meteor. 1996, 15, 43–48. [Google Scholar]
- Panofsky, H.A.; Tennekes, H.; Lenschow, D.H.; Wyngaard, J.C. The characteristics of turbulent velocity components in the surface layer under convective conditions. Bound.-Layer Meteorol. 1977, 11, 355–361. [Google Scholar] [CrossRef]
- Chen, J.B.; Lv, S.H.; Yu, Y. Comparison of heat and matter transfer characteristics in the surface layers of oasis and Gobi. Chinese J. Geophys. 2012, 55, 1817–1830. [Google Scholar]
- Ji, G.L.; Jiang, H.; Lv, L.Z. Characteristics of Longwave Radiation over the Qinghai-Xizang Plateau. Plateau Meteor. 1995, 14, 68–75. [Google Scholar]
- Guan, D.X.; Jin, M.S.; Xu, H. Reflectivity of broad-leaved Korean pine forest in growing season on Changbai Mountain. Chin. J. Appl. Ecol. 2002, 13, 1544–1546. [Google Scholar]
- Zhong, L.; Ma, Y.M.; Li, M.S. An Analysis of Atmosphere Turbulence and Energy Transfer Characteristics of Surface Layer over Rongbu Valley in Mt. Qomolangma Area. Chinese J. Atmos Sci. 2007, 31, 48–56. [Google Scholar]
- Li, Y.; Hu, Z.Y. A Preliminary Study on Land-Surface Albedo in Northern Tibetan Plateau. Plateau Meteor. 2006, 25, 1034–1041. [Google Scholar]
- Yang, L.W.; Gao, X.Q.; Hui, X.Y.; Zhou, Y.; Hou, X.H. A study on energy balance and transfer in the surface layer over semi-arid grassland of Nyainrong area in central Tibetan Plateau in summer. Clim. Environ. Res. 2017, 22, 335–345. (In Chinese) [Google Scholar]
- Hu, Y.Y.; Zhou, L.; Ma, Y.M.; Zou, B.J.; Huang, Z.Y.; Xu, K.P.; Feng, L. Model estimation and validation of the surface energy fluxes at typical underlying surfaces over the Qinghai Tibetan Plateau. Plateau Meteor. 2018, 37, 1499–1510. [Google Scholar]
- Li, Q.; Zhang, X.Z.; Shi, P.L.; He, Y.T.; Xu, L.L.; Sun, W. Study on the Energy Balance Closure of Alpine Meadow on Tibetan Plateau. J. Nat. Resour. 2008, 23, 391–399. [Google Scholar]
- Lu, X.C.; Wen, J.; Yang, Y.; Tian, H.; Liu, W.H.; W, Y.Y.; Jiang, Y.Q. Research on the Influence of Horizontal Thermal Advection on Surface Energy Balance in Zoige Alpine Wetland. Plateau Meteor. 2022, 41, 122–131. [Google Scholar]




| Observation Site | Wind Direction | Canopy Height/m | Source | ||||
|---|---|---|---|---|---|---|---|
| Changbai Mountain | / | 26 | 19.5 | 1.60 | 6.66 | 6.4 | [44] |
| Gaize | / | 0.05 | / | / | 2.31 | 2.15 | [27] |
| Phoenix Mountain | 315°~45° | 18 | 30.29 | 1.80 | 50 | 5.5 | [45] |
| Phoenix Mountain | 45°~135° | 18 | 8.24 | 0.67 | 5.5 | 3.0 | [45] |
| Phoenix Mountain | 135°~225° | 18 | 16.46 | 1.35 | 22 | 4.0 | [45] |
| Phoenix Mountain | 225°~315° | 18 | / | / | / | / | [45] |
| Emei Mount | / | 14 | 10.45 | 1.65 | 15.8 | 3.79 | this paper |
| Site | Observation Time | Canopy Height | Observation Height | Source | |||
|---|---|---|---|---|---|---|---|
| Mount Emei | December 2019–November 2020 | 14 | 38 | / | / | 1.314 | this paper |
| Xiaolangdi plantation observation area | 2015. Spring | 10.1 | 30 | 3.31 | 3.17 | 1.84 | [48] |
| 2016. Summer | 10.1 | 30 | 2.04 | 2.62 | 1.57 | [48] | |
| Changbai Mountain | September 2003 | 26 | 42 | 2.47 | 2.47 | 1.47 | [49] |
| Gaize | June–July 1998 | 0.05 | 2.57 | 3.21 | 2.69 | 1.46 | [27] |
| Wudaoliang | June–July 1994 | 0.05 | 2.9 | 2.98 | 2.91 | 1.35 | [50] |
| Plain area | / | / | / | 2.4 | 1.9 | 1.25 | [51] |
| Litang | January 2006 | 0.05 | 4 | 3.7 | 3.29 | 0.92 | [19] |
| Litang | July 2006 | 0.05 | 4 | 4.44 | 4.28 | 0.96 | [19] |
| Jinta Oasis, Gansu | June–August 2008 | 1–2 | 10 | 2.4 | 2.5 | 1.3 | [52] |
| Jinta Gobi, Gansu | June–August 2008 | 1–2 | 1.84 | 2.8 | 2.7 | 1.1 | [52] |
| Anduo | July 1998 | 0.05 | 2.9 | 4.01 | 3.85 | 1.43 | [30] |
| Site (Underpad Surface) | Longitude and Latitude | Altitude | Spring | Summer | Autumn | Winter | Source |
|---|---|---|---|---|---|---|---|
| D105 (alpine Grassland) | 32.69° N, 91.94° E | 5020 m | 0.28 | 0.22 | 0.23 | 0.32 | [56] |
| Anduo (alpine Grassland) | 32.24° N, 91.64° E | 4700 m | 0.27 | 0.22 | 0.23 | 0.33 | [56] |
| Naqu (alpine Grassland) | 31.37° N, 91.90° E | 4534 m | 0.24 | 0.18 | 0.18 | 0.35 | [56] |
| Pailong (gravel and grass) | 30.04° N, 95.61° E | 2058 m | 0.14 | 0.13 | 0.14 | 0.14 | [33] |
| Danka (grass) | 29.89° N, 95.68° E | 2701 m | 0.14 | 0.13 | 0.14 | 0.17 | [33] |
| Mount Emei (grass) | 29.52° N, 103.34° E | 3070 m | 0.18 | 0.16 | 0.18 | 0.31 | [33] |
| Mount Emei (forest) | 29.52° N, 103.34° E | 970 m | 0.07 | 0.06 | 0.06 | 0.04 | This paper |
| Observation Site | Longitude and Latitude | Altitude/m | Underpad Surface | Closure Rate/% | Source |
|---|---|---|---|---|---|
| Nyainrong Station | 32.17° N, 92.30 E | 4607 | alpine grassland | 74.0 | [57] |
| Nagqu Station | 32.37 N, 91.90 E | 4509 | alpine grassland | 66.4 | [58] |
| Dangxiong Grassland Station | 30.51 N, 91.05 E | 4333 | alpine meadows | 53.0 | [59] |
| Everest Station | 28.36 N, 86.95 E | 4276 | river beach sand and gravel grass | 40.0 | [58] |
| Pai Lung Station | 30.04 N, 95.61 E | 2058 | gravel and grass | 57.2 | [33] |
| Emei Mountain (grass) | 29.52 N, 103.34 E | 3070 | grass | 64.5 | [33] |
| Emei Mountain (forest) | 29.16 N, 103.36 E | 970 | forest | 48 | This paper |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, N.; Li, M.; Gong, M.; Xu, P.; Ma, Y.; Sun, F.; Yang, Y. Study on Surface Characteristic Parameters and Surface Energy Exchange in Eastern Edge of the Tibetan Plateau. Atmosphere 2022, 13, 1749. https://doi.org/10.3390/atmos13111749
Chang N, Li M, Gong M, Xu P, Ma Y, Sun F, Yang Y. Study on Surface Characteristic Parameters and Surface Energy Exchange in Eastern Edge of the Tibetan Plateau. Atmosphere. 2022; 13(11):1749. https://doi.org/10.3390/atmos13111749
Chicago/Turabian StyleChang, Na, Maoshan Li, Ming Gong, Pei Xu, Yaoming Ma, Fanglin Sun, and Yaoxian Yang. 2022. "Study on Surface Characteristic Parameters and Surface Energy Exchange in Eastern Edge of the Tibetan Plateau" Atmosphere 13, no. 11: 1749. https://doi.org/10.3390/atmos13111749
APA StyleChang, N., Li, M., Gong, M., Xu, P., Ma, Y., Sun, F., & Yang, Y. (2022). Study on Surface Characteristic Parameters and Surface Energy Exchange in Eastern Edge of the Tibetan Plateau. Atmosphere, 13(11), 1749. https://doi.org/10.3390/atmos13111749







