Multi-Hazard Assessment of a Flood Protection Levee
Abstract
1. Introduction
2. Data and Methods
2.1. Case Study Presentation
2.2. Liquefaction Hazard Potential
2.3. Frequency Analysis
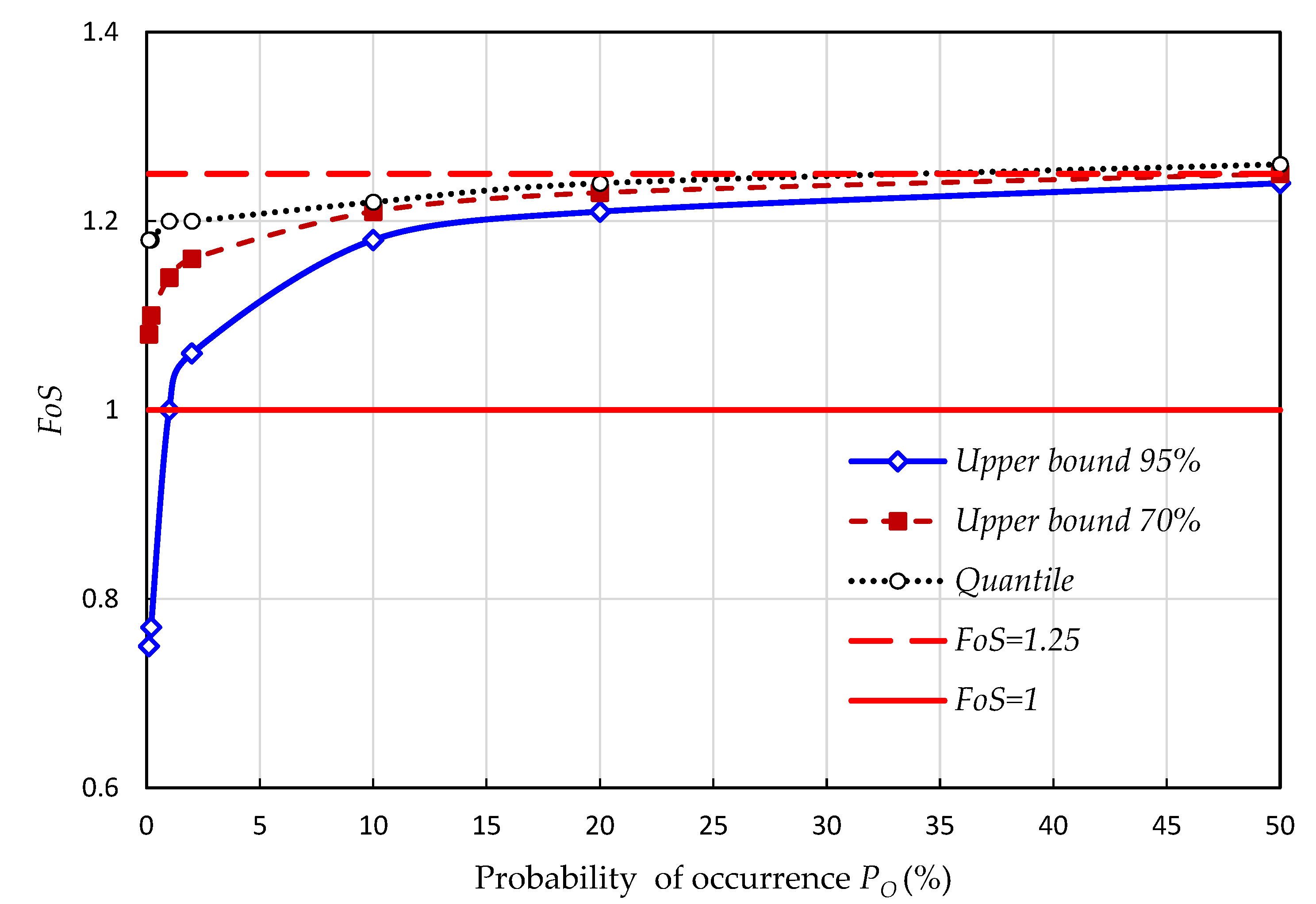
3. Results and Discussion
3.1. Conventional Liquefaction Hazard Assessment
- Total vertical overburden stress
- Pore water pressure
- Effective vertical overburden stress
- Normalized friction ratio in % ()
- Normalized cone resistance.
- Soil behavior type index.
- Normalized penetration resistance.
- Correction factor for the cone resistance
- Clean sand normalized penetration resistance.
- Cyclic resistance ratio for an earthquake of a magnitude 7.5Magnitude Scaling Factor.
- Cyclic resistance ratio for a magnitude MwCyclic stress ratio.
- Depth-dependent stress reduction factorFactor of safety against liquefaction.
3.2. Probabilistic Approach
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ASCE. So, You Live behind a Levee! American Society of Civil Engineers: Reston, VA, USA, 2009. [Google Scholar]
- Barbetta, S.; Camici, S.; Bertuccioli, P.; Palladino, M.R.; Moramarco, T. Levee body seepage: A refinement of an expeditious procedure for fragility curves and vulnerability diagrams’ assessment. Hydrol. Res. 2017, 48, 763–775. [Google Scholar] [CrossRef]
- Mallakpour, I.; Sadegh, M.; AghaKouchak, A. Changes in the exposure of California’s levee-protected critical infrastructure to flooding hazard in a warming climate. Environ. Res. Lett. 2020, 15, 064032. [Google Scholar] [CrossRef]
- Kwak, D.Y.; Mikami, A.; Brandenberg, S.J.; Stewart, J.P. Ground motion estimation for evaluation of levee performance in past earthquakes. In Proceedings of the 9th International Conference on Urban Earthquake Engineering/4th Asia Conference on Earthquake Engineering, Tokyo Institute of Technology, Tokyo, Japan, 6–8 March 2012. [Google Scholar]
- Serre, D.; Maurel, P.; Peyras, L.; Diab, Y. A spatial decision support system to optimize inspection, maintenance and reparation operations of river levees. In Proceedings of the International Conference on Computing and Decision Making in Civil and Building Engineering, Montréal, Canada, QC, 14–16 June 2006. [Google Scholar]
- Jasim, F.H.; Vahedifard, F.; Alborzi, A.; Moftakhari, H.; AghaKouchak, A. Effect of Compound Flooding on Performance of Earthen Levees. In Proceedings of the Geo-Congress GSP 316, Minneapolis, MN, USA, 25–28 February 2020. [Google Scholar]
- Chen, J.; O-tani, H.; Takeyama, T.; Oishi, S.; Hori, H.M. A Probabilistic Liquefaction Hazard Assessment for Urban Regions Based on Dynamics Analysis Considering Soil Uncertainties. J. Earth Sci. 2021, 32, 1129–1138. [Google Scholar] [CrossRef]
- Seed, R.B.; Bea, R.G.; Abdelmalak, R.I.; Athanasopoulos-Zekkos, A.; Boutwell, G.P.; Briaud, J.L.; Cheung, C.; Cobos-Roa, D.; Ehrensing, L.; Govindasamy, A.V.; et al. New Orleans and Hurricane Katrina. I: Introduction, Overview, and East Flank. J. Geotech. Geoenviron. Eng. 2008, 134, 701–717. [Google Scholar] [CrossRef]
- Sasaki, Y.; Towhata, I.; Miyamoto, K.; Sherato, M.; Narita, A.; Sasaki, T.; Sako, S. Reconnaissance report on damage in and around river levees caused by the 2011 off the pacific coast of Tohoku earthquake. Soils Found. 2012, 52, 1016–1032. [Google Scholar] [CrossRef]
- Kramer, S. Geotechnical Earthquake Engineering; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M.; Andrus, R.D.; Arango, I.; Castro, G.; Christian, J.T.; Dobry, R.; Liam Finn, W.D.; Harder, L.F., Jr.; Hynes, M.E.; et al. Liquefaction resistance of soils summary report from 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef]
- Ulusay, R.; Kuru, T. 1998 Adana-Ceyhan (Turkey) earthquake and a preliminary microzonation based on liquefaction potential for Ceyhan town. Nat. Hazards 2004, 32, 59–88. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Soil Liquefaction during Earthquakes; Earthquake Engineering Research Institute: Oakland, CA, USA, 2008. [Google Scholar]
- Dixit, J.; Dewaikar, D.M.; Janjid, R.S. Assessment of liquefaction potential index for Mumbai city. Nat. Hazards Earth Syst. Sci. 2012, 12, 2759–2768. [Google Scholar] [CrossRef]
- Juang, C.H.; Ching, J.; Wang, L.; Khoshnevisan, S.; Ku, C.S. Simplified procedure for estimation of liquefaction-induced settlement and site-specific probabilistic settlement exceedance curve using cone penetration test (CPT). Can. Geotech. J. 2013, 500, 1055–1066. [Google Scholar] [CrossRef]
- Chung, J.W.; Rogers, J.D. Influence of assumed groundwater depth on mapping liquefaction potential. Environ. Eng. Geosci. 2013, 19, 377–389. [Google Scholar] [CrossRef]
- Molina-Gómez, F.; Bulla-Cruz, L.A.; Moreno-Anselmi, L.A.; Ruge, J.C.; Arévalo-Daza, C. Assessment of groundwater level variations using multivariate statistical methods. Ing. Investig. 2019, 39, 36–42. [Google Scholar] [CrossRef]
- Tyagunov, S.; Vorogushyn, S.; Jimenez, C.M.; Stefano Parolai, S.; Fleming, K. Mult-hazard fragility analysis for fluvial dikes in earthquake- and flood-prone areas. Nat. Hazards Earth Syst. Sci. 2018, 18, 2345–2354. [Google Scholar] [CrossRef]
- Chang, M.; Chan, M.S.; Huang, R.C.; Upomo, T.C.; Kusumawardani, R. Assignment of groundwater table in liquefaction analysis of soils. In Advancement in Geotechnical Engineering; The official 2020 publications of the Soil-Structure Interaction Group in Egypt (SSIGE), Egypt; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–18. [Google Scholar]
- Haase, J.S.; Choi, Y.S.; Nowack, R.L. Liquefaction hazard near the Ohio River from Midwestern scenario earthquakes. Environ. Eng. Geosci. 2011, 17, 165–181. [Google Scholar] [CrossRef]
- Holzer, T.L.; Noce, T.E.; Bennett, M.J. Liquefaction probability curves for surficial geologic deposits. Environ. Eng. Geosci. 2011, 17, 1–21. [Google Scholar] [CrossRef]
- Robertson, P.K.; Campanella, R.G.; Gillespie, D.; Greig, J. Use of Piezometer Cone data. In Proceedings of the ASCE, In-Situ’86 Use of Ins-itu testing in Geotechnical Engineering, Blacksburg, VA, USA, 23–25 June 1986; pp. 1263–1280. [Google Scholar]
- Robertson, P.K.; Wride, C. Evaluating Cyclic Liquefaction Potential Using the Cone Penetration Test. Can. Geotech. J. 1998, 35, 442–459. [Google Scholar] [CrossRef]
- Liao, S.S.C.; Veneziano, D.; Whitman, R.V. Regression model for evaluating liquefaction probability. J. Geotech. Eng. 1988, 114, 389–410. [Google Scholar] [CrossRef]
- Seed, R.B.; Idriss, I.M. Ground Motions and Soil Liquefaction during Earthquakes; Engineering monographs on earthquake criteria, structural design and strong motion records; Earthquake Engineering Research Institute: Berkeley, CA, USA, 1982. [Google Scholar]
- Weibull, W. A statistical theory of strength of materials. Ingeniôrsvetenskapsakademiens Handl. 1939, 151, 1–45. [Google Scholar]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1928; Volume 24, pp. 180–190. [Google Scholar]
- Iai, S.; Tsuchida, H.; Koizumi, K. A new criterion for assessing liquefaction potential using grain size accumulation curve and N-value. Rep. Port Harb. Res. Inst. 1986, 25, 125–234. [Google Scholar]
- Robertson, P.K. Soil classification using the cone penetration test. Can. Geotech. J. 1990, 27, 151–158. [Google Scholar] [CrossRef]
- Das, S.K.; Muduli, P.K. Probability-based method for assessing liquefaction potential of soil using genetic programming. In Proceedings of the International Symposium on Engineering under Uncertainty: Safety Assessment and Management (ISEUSAM), Kolkata, India, 4 January 2013. [Google Scholar]
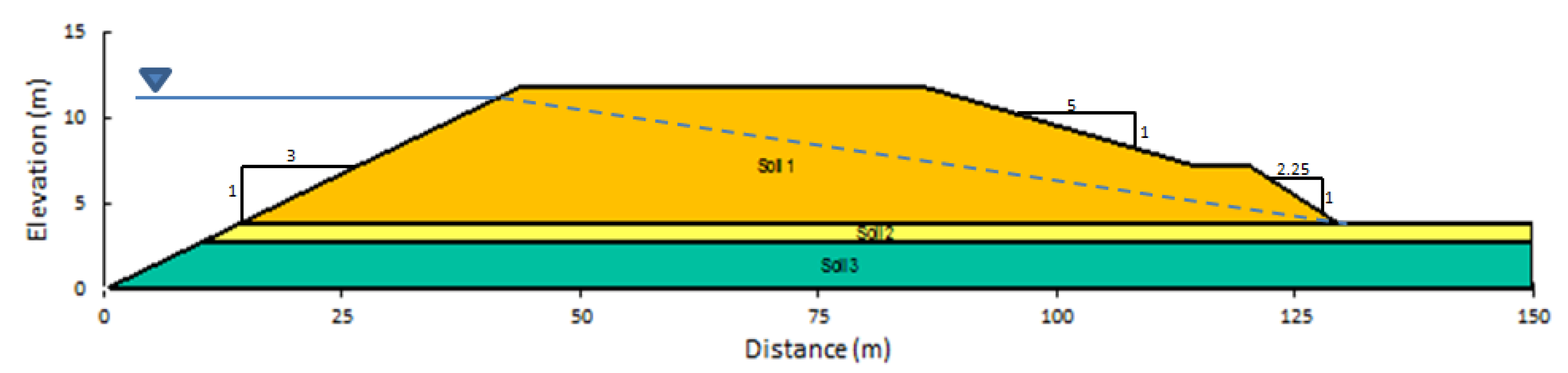
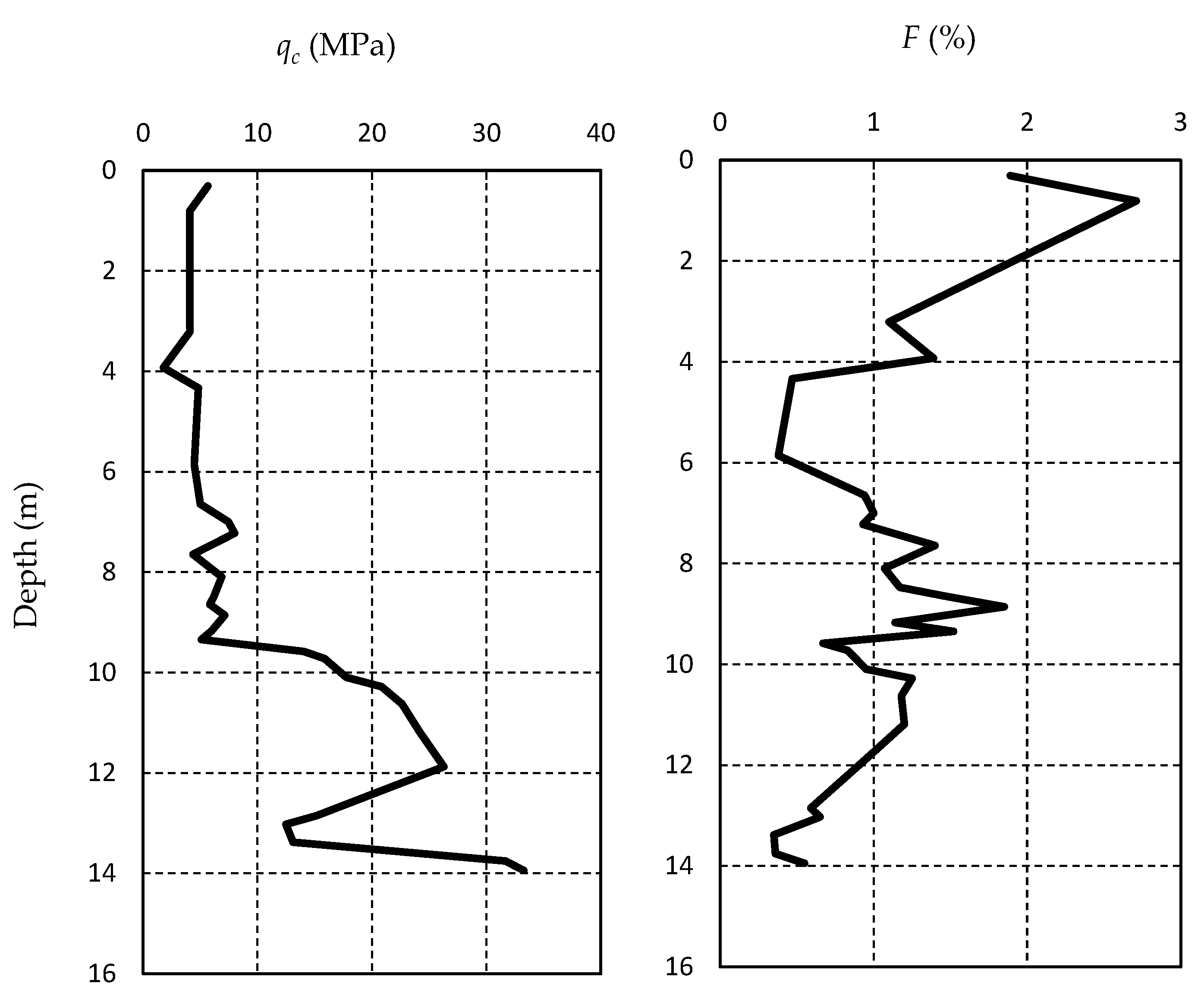
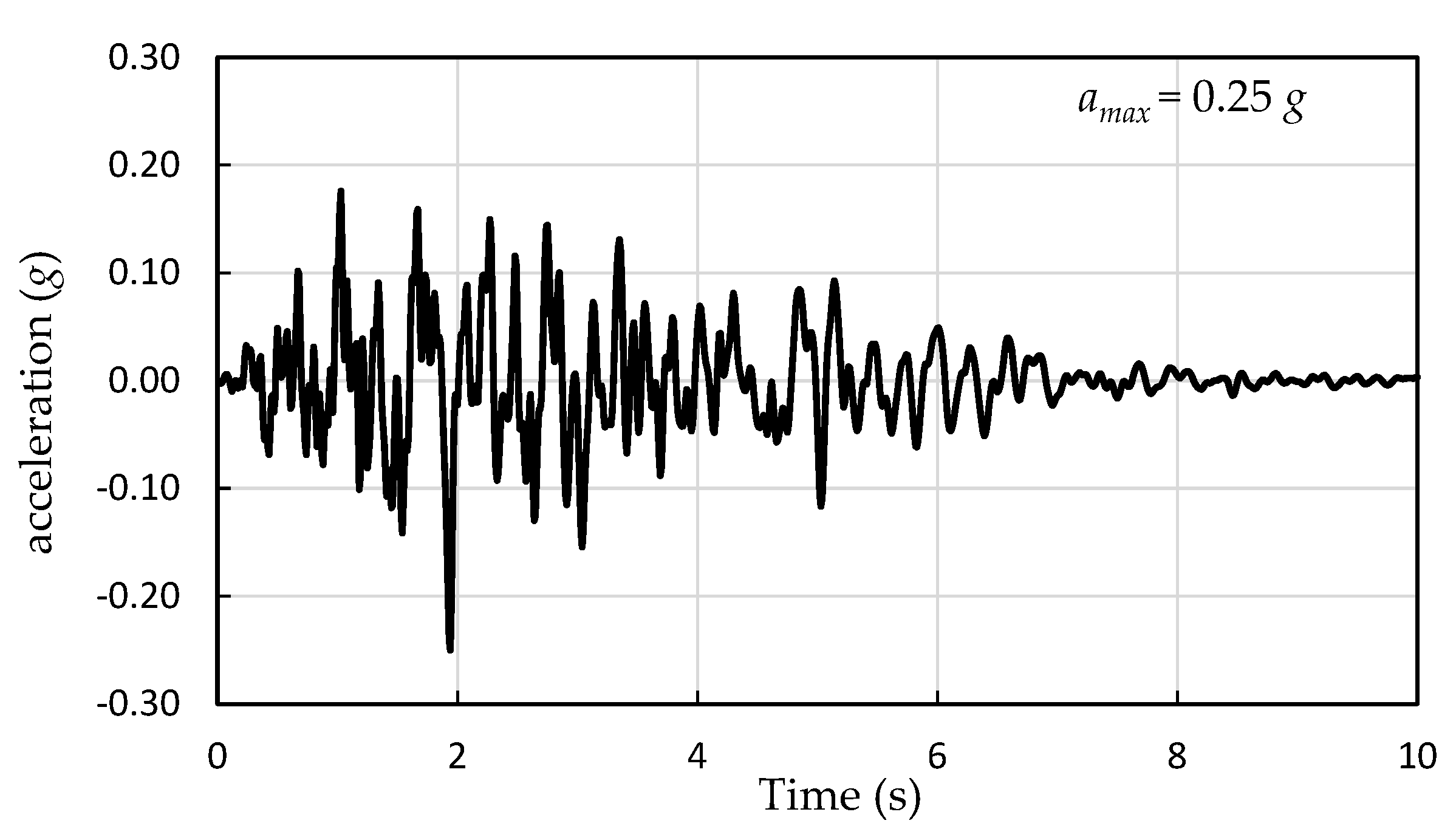
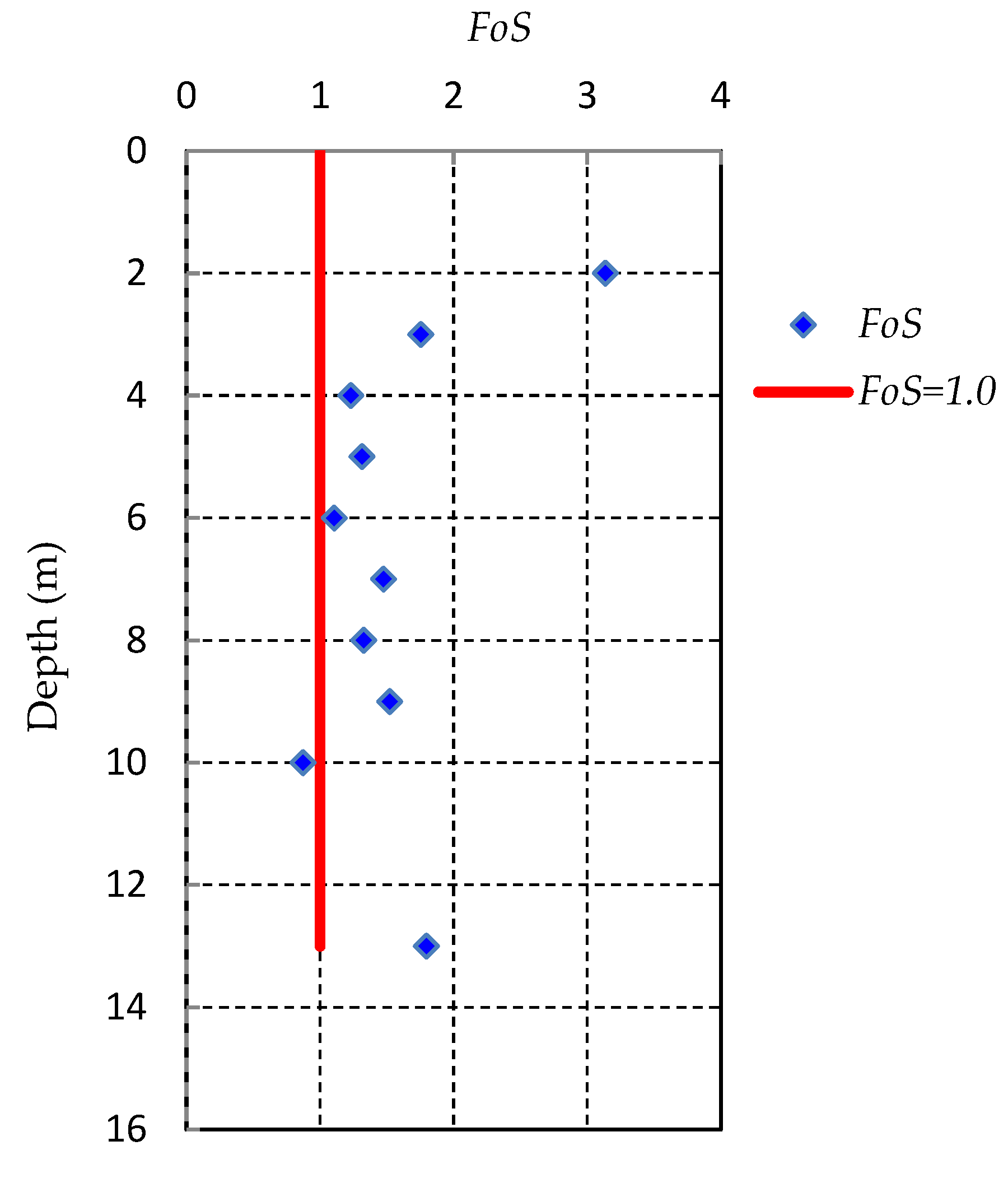

| Soil | Thickness (m) | ||||
|---|---|---|---|---|---|
| Soil 1 | 10 | 22 | 25 | 28 | |
| Soil 2 | 1 | 19 | 0 | 35 | |
| Soil 3 | 3 | 20 | 0 | 38 |
| Depth (m) | (kPa) | (%) | (n = 0.5) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 22.00 | - | 22.00 | 2.58 | 84.11 | 2.03 | 86.35 | 2.24 | 0.50 | 2.24 | 86.35 | 1.77 | 152.80 | 0.41 | 2.43 | 1.01 |
| 2.0 | 44.00 | - | 44.00 | 1.91 | 91.84 | 2.13 | 60.92 | 2.26 | 0.50 | 2.26 | 60.92 | 1.82 | 110.77 | 0.21 | 2.43 | 0.51 |
| 3.0 | 66.00 | - | 66.00 | 1.24 | 61.08 | 2.14 | 49.62 | 2.21 | 0.50 | 2.21 | 49.62 | 1.69 | 83.66 | 0.13 | 2.43 | 0.33 |
| 4.0 | 88.00 | - | 88.00 | 1.23 | 25.22 | 2.45 | 23.66 | 2.47 | 0.50 | 2.47 | 23.66 | 2.63 | 62.22 | 0.10 | 2.43 | 0.25 |
| 5.0 | 110.00 | - | 110.00 | 0.99 | 41.52 | 2.21 | 43.55 | 2.20 | 0.50 | 2.20 | 43.55 | 1.66 | 72.32 | 0.12 | 2.43 | 0.28 |
| 6.0 | 132.00 | - | 132.00 | 0.83 | 28.73 | 2.31 | 33.01 | 2.26 | 0.50 | 2.26 | 33.01 | 1.83 | 60.25 | 0.10 | 2.43 | 0.25 |
| 7.0 | 154.00 | - | 154.00 | 1.00 | 47.44 | 2.17 | 58.87 | 2.09 | 0.50 | 2.09 | 58.87 | 1.44 | 84.86 | 0.14 | 2.43 | 0.34 |
| 8.0 | 176.00 | - | 176.00 | 1.14 | 34.99 | 2.31 | 46.42 | 2.21 | 0.50 | 2.21 | 46.42 | 1.69 | 78.47 | 0.12 | 2.43 | 0.31 |
| 9.0 | 198.00 | 9.81 | 188.19 | 1.53 | 34.12 | 2.39 | 46.81 | 2.28 | 0.50 | 2.28 | 46.81 | 1.89 | 88.70 | 0.14 | 2.43 | 0.36 |
| 10.0 | 217.00 | 19.62 | 197.38 | 0.92 | 7.65 | 2.84 | - | - | 1.00 | 2.84 | 7.65 | 5.17 | 39.57 | 0.08 | 2.43 | 0.20 |
| 10.5 | 226.50 | 24.53 | 201.98 | 1.21 | 9.76 | 2.80 | - | - | 1.00 | 2.80 | 9.76 | 4.79 | 46.79 | 0.09 | 2.43 | 0.22 |
| 11.0 | 236.50 | 29.43 | 207.07 | 1.19 | 13.12 | 1.92 | 162.79 | 1.81 | 0.50 | 1.81 | 162.79 | 1.11 | 180.98 | 0.63 | 2.43 | 1.55 |
| 12.0 | 256.50 | 39.24 | 217.26 | 0.90 | 13.22 | 1.84 | 166.89 | 1.71 | 0.50 | 1.71 | 166.89 | 1.05 | 174.84 | 0.58 | 2.43 | 1.42 |
| 13.0 | 276.50 | 49.05 | 227.45 | 0.64 | 55.34 | 2.01 | 83.47 | 1.86 | 0.50 | 1.86 | 83.47 | 1.15 | 96.14 | 0.16 | 2.43 | 0.40 |
| 14.0 | 296.50 | 58.86 | 237.64 | 0.63 | 32.41 | 1.69 | 204.12 | 1.54 | 0.50 | 1.54 | 204.12 | 1.00 | 204.12 | 0.87 | 2.43 | 2.14 |
| Depth (m) | KPa | (kPa) | KPa | |||
|---|---|---|---|---|---|---|
| 1.0 | 22.00 | - | 22.00 | 0.99 | 0.16 | 6.21 |
| 2.0 | 44.00 | - | 44.00 | 0.98 | 0.16 | 3.14 |
| 3.0 | 66.00 | 9.81 | 56.19 | 0.98 | 0.19 | 1.75 |
| 4.0 | 88.00 | 19.62 | 68.38 | 0.97 | 0.20 | 1.23 |
| 5.0 | 110.00 | 29.43 | 80.57 | 0.96 | 0.21 | 1.31 |
| 6.0 | 132.00 | 39.24 | 92.76 | 0.95 | 0.22 | 1.11 |
| 7.0 | 154.00 | 49.05 | 104.95 | 0.95 | 0.23 | 1.47 |
| 8.0 | 176.00 | 58.86 | 117.14 | 0.94 | 0.23 | 1.33 |
| 9.0 | 198.00 | 68.67 | 129.33 | 0.93 | 0.23 | 1.52 |
| 10.0 | 217.00 | 78.48 | 138.52 | 0.91 | 0.23 | 0.87 |
| 10.5 | 226.50 | 83.39 | 143.12 | 0.89 | 0.23 | 0.94 |
| 11.0 | 236.50 | 88.29 | 148.21 | 0.88 | 0.23 | Non-liquefiable |
| 12.0 | 256.50 | 98.10 | 158.40 | 0.85 | 0.22 | Non-liquefiable |
| 13.0 | 276.50 | 107.91 | 168.59 | 0.83 | 0.22 | 1.79 |
| 14.0 | 296.50 | 117.72 | 178.78 | 0.80 | 0.22 | Non-liquefiable |
| Class | Description of Likelihood | |
|---|---|---|
| 5 | ≥0.85 | Almost certain that it will liquefy |
| 4 | 0.65 ≤ < 0.85 | Very likely to liquefy |
| 3 | 0.35 ≤ < 0.65 | Liquefaction and no liquefaction are equally likely |
| 2 | 0.15 ≤ < 0.35 | Unlikely to liquefy |
| 1 | < 0.15 | Almost certain that it will not liquefy |
| Return Period (Years) | Quantiles | Upper Bound 70% | Upper Bound 95% | |
|---|---|---|---|---|
| 2 | 50 | 1.26 | 1.25 | 1.24 |
| 5 | 20 | 1.25 | 1.23 | 1.21 |
| 10 | 10 | 1.22 | 1.21 | 1.18 |
| 50 | 2 | 1.20 | 1.16 | 1.06 |
| 100 | 1 | 1.20 | 1.14 | 1.00 |
| 500 | 0.2 | 1.18 | 1.10 | 0.77 |
| 1000 | 0.1 | 1.18 | 1.08 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selmi, M.; Hamdi, Y.; Moiriat, D. Multi-Hazard Assessment of a Flood Protection Levee. Atmosphere 2022, 13, 1741. https://doi.org/10.3390/atmos13101741
Selmi M, Hamdi Y, Moiriat D. Multi-Hazard Assessment of a Flood Protection Levee. Atmosphere. 2022; 13(10):1741. https://doi.org/10.3390/atmos13101741
Chicago/Turabian StyleSelmi, Mbarka, Yasser Hamdi, and Denis Moiriat. 2022. "Multi-Hazard Assessment of a Flood Protection Levee" Atmosphere 13, no. 10: 1741. https://doi.org/10.3390/atmos13101741
APA StyleSelmi, M., Hamdi, Y., & Moiriat, D. (2022). Multi-Hazard Assessment of a Flood Protection Levee. Atmosphere, 13(10), 1741. https://doi.org/10.3390/atmos13101741







