Global Ionospheric Disturbance Propagation and Vertical Ionospheric Oscillation Triggered by the 2022 Tonga Volcanic Eruption
Abstract
1. Introduction
2. Materials and Methods
2.1. STEC Data
2.2. COSMIC-2 Profile Data
2.3. Methods for Extracting Disturbance
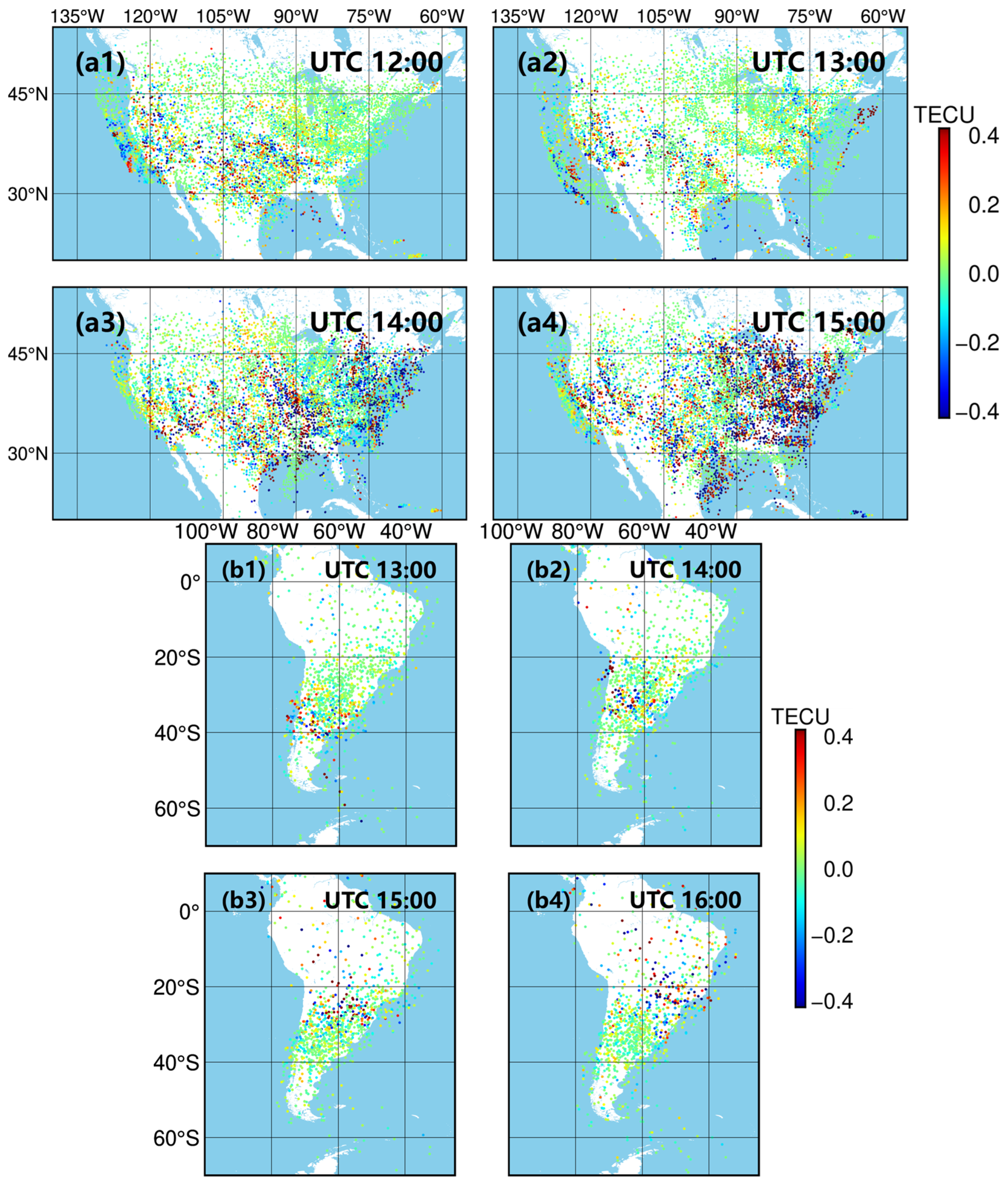
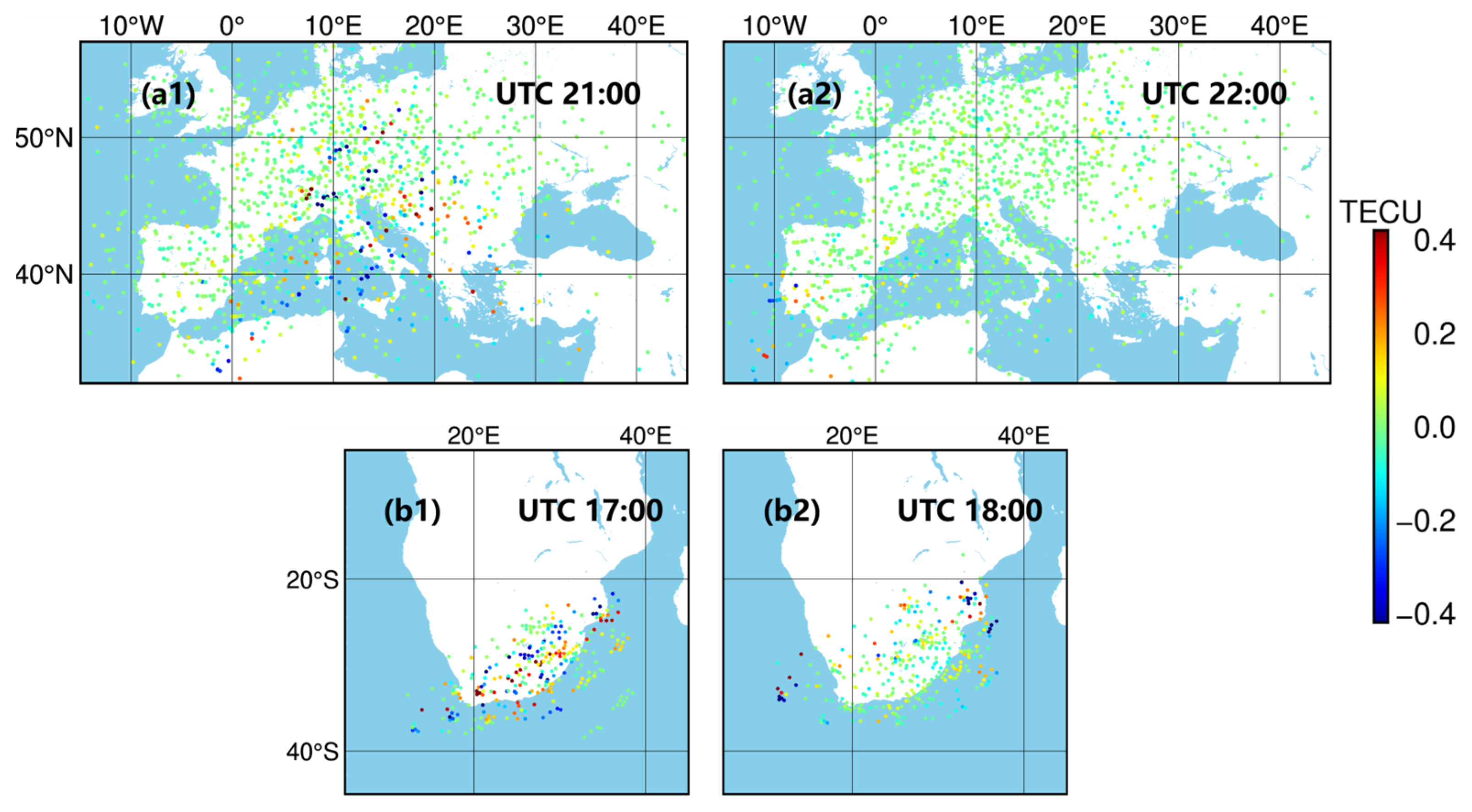
3. Global TID Dissemination Captured by STEC
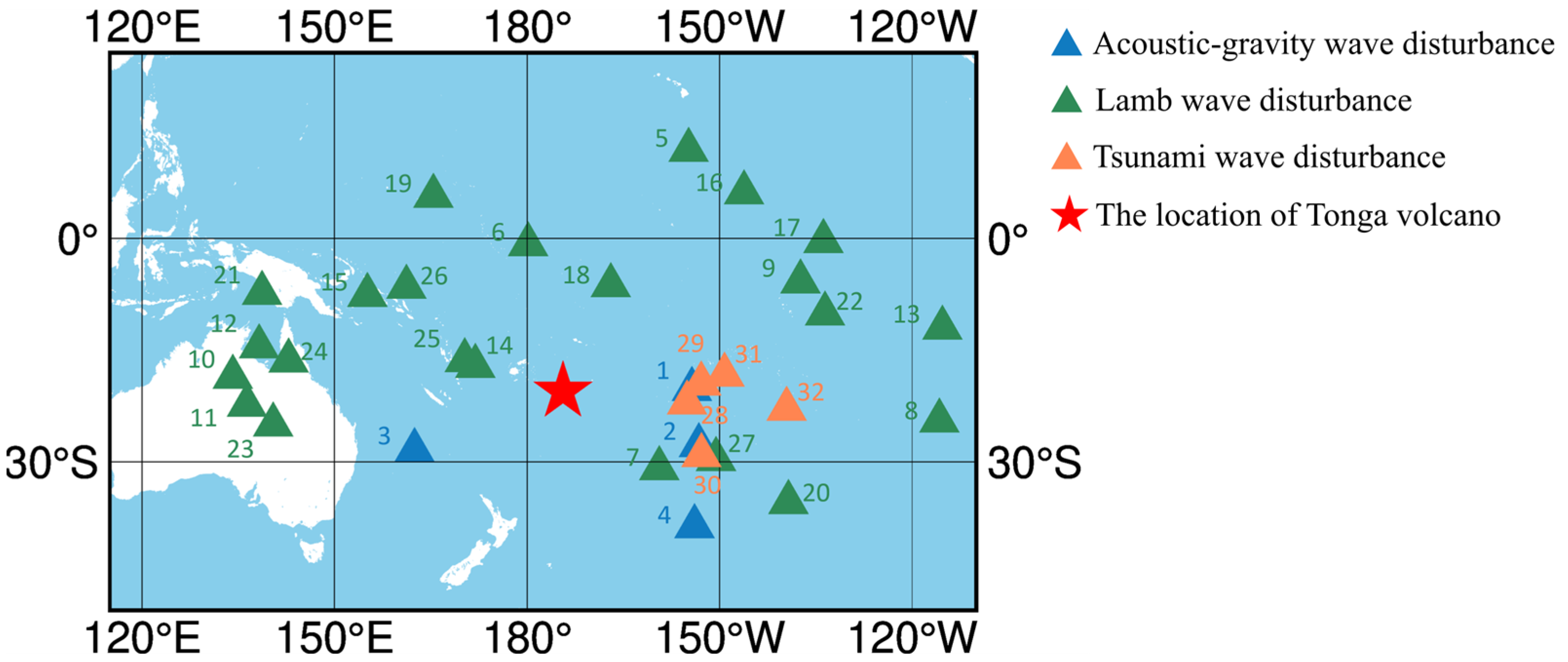
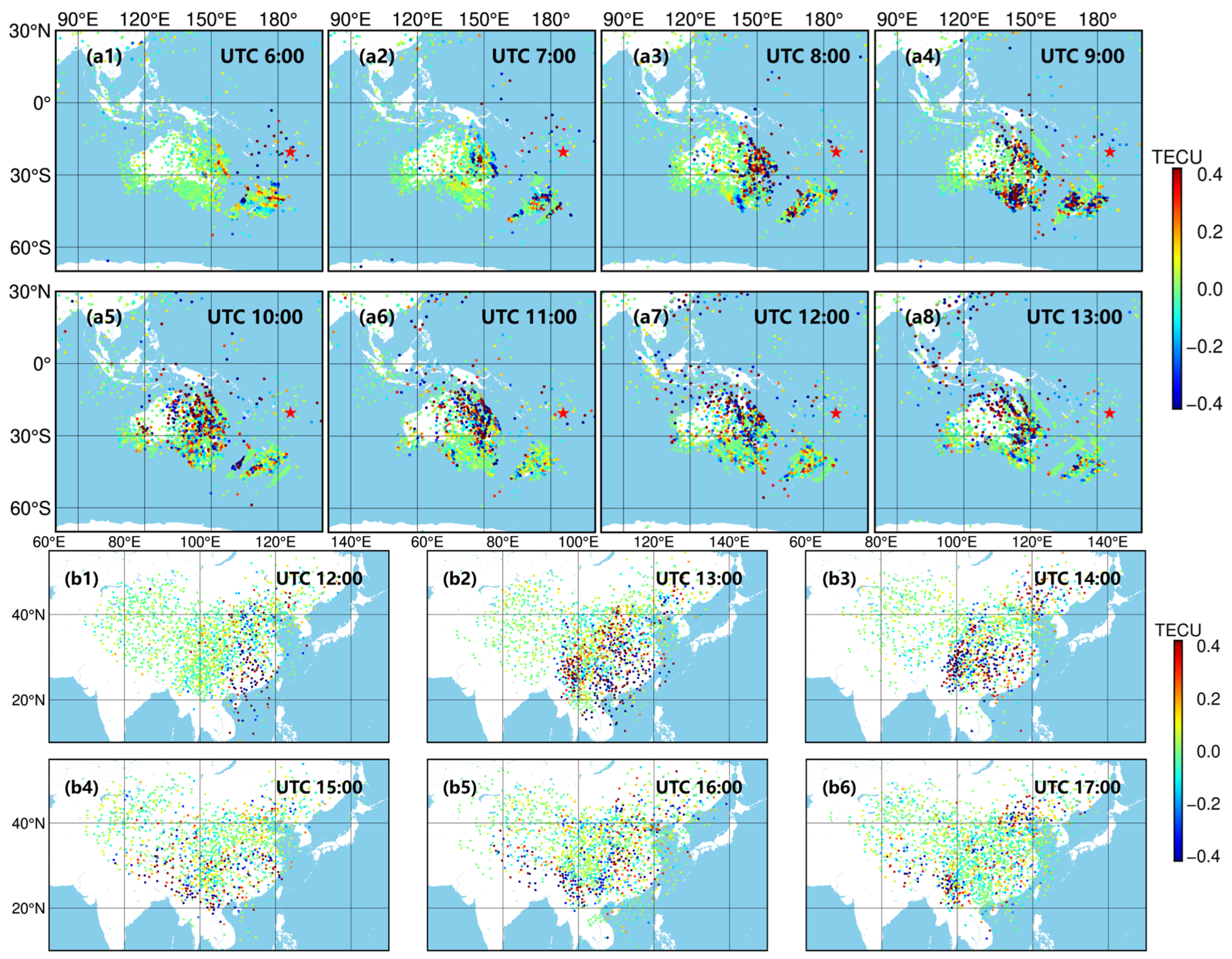
3.1. Disturbance Propagation in the Pacific Rim
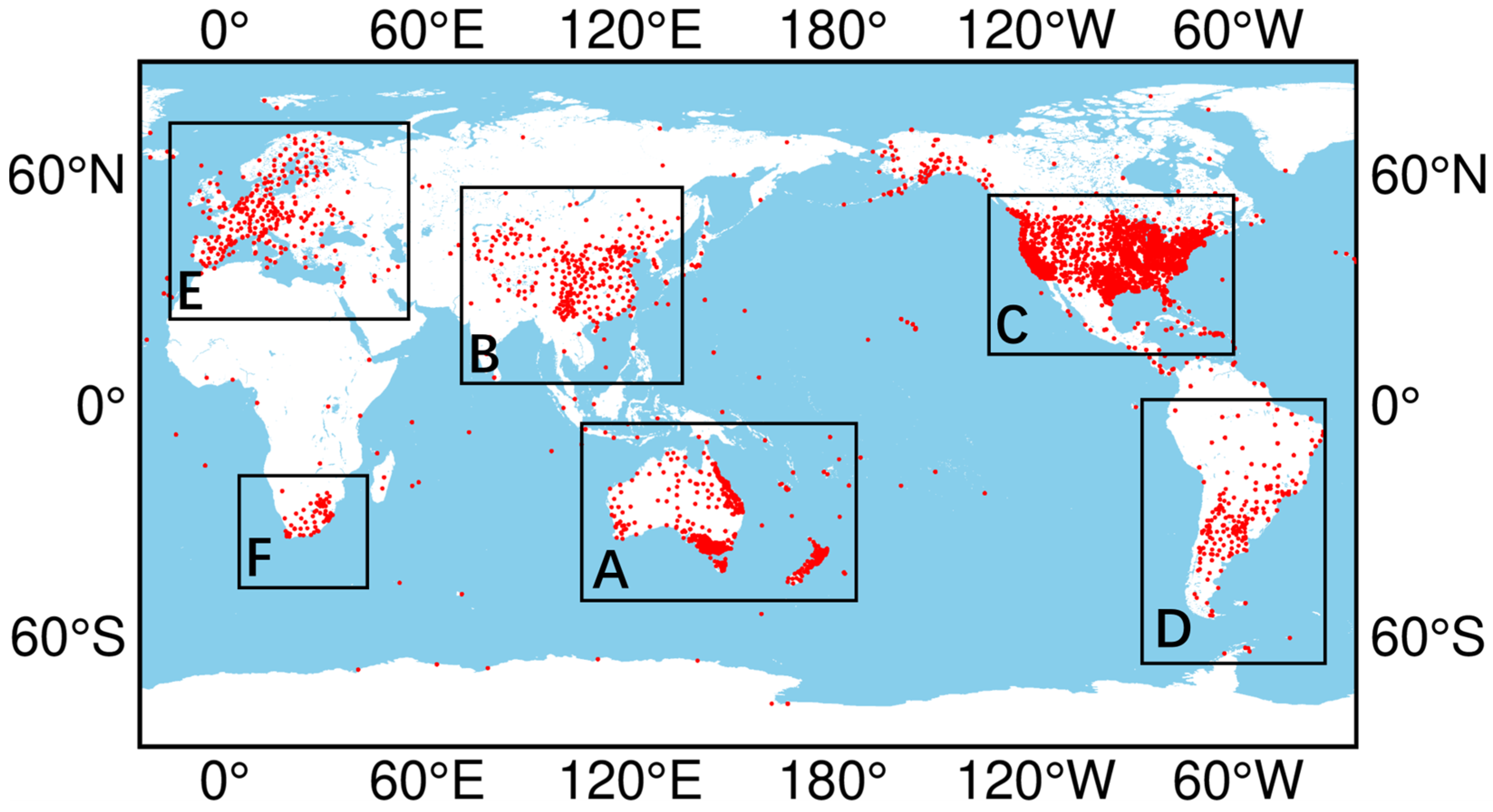
3.2. Disturbance Propagation in Europe and South Africa
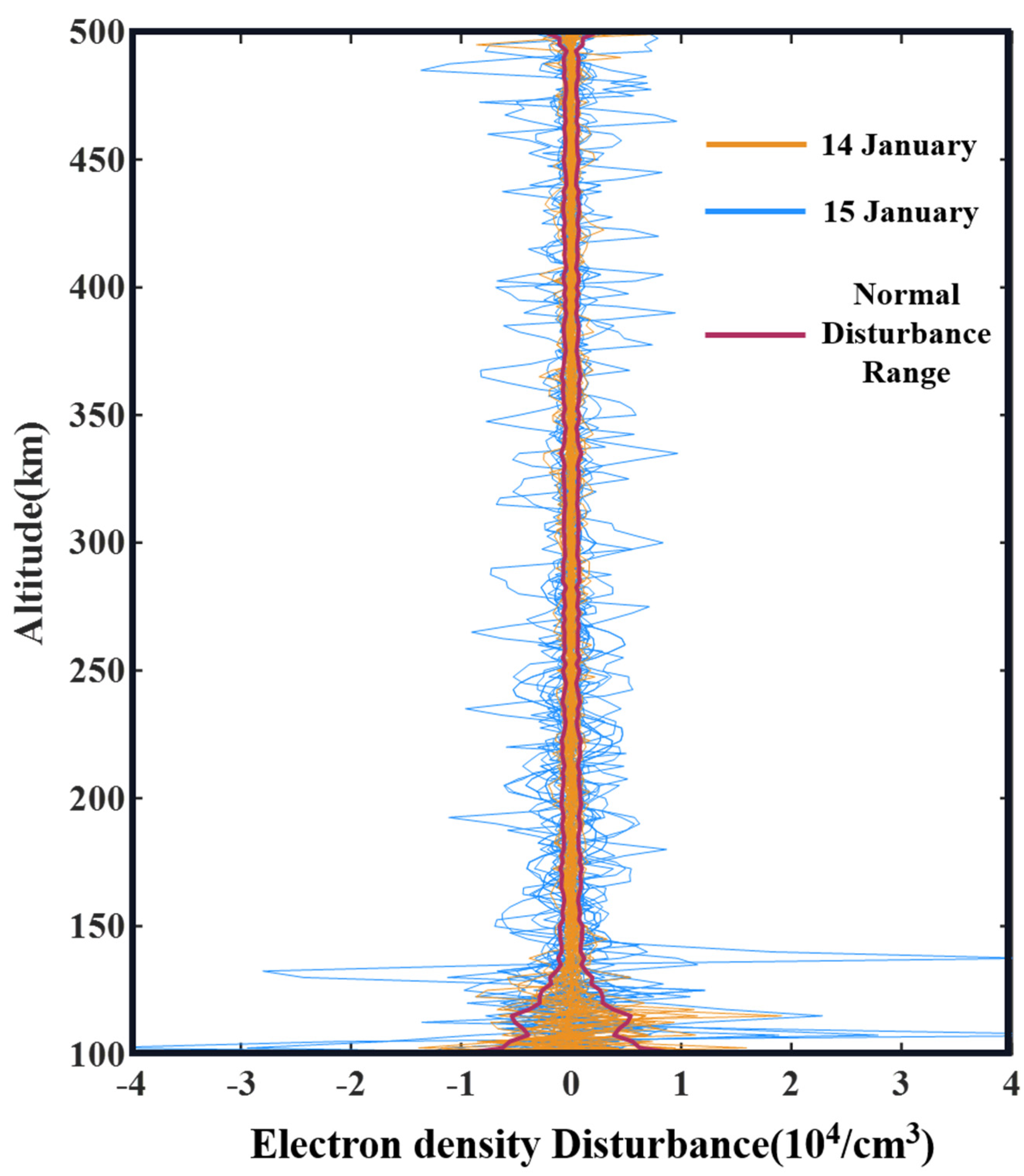
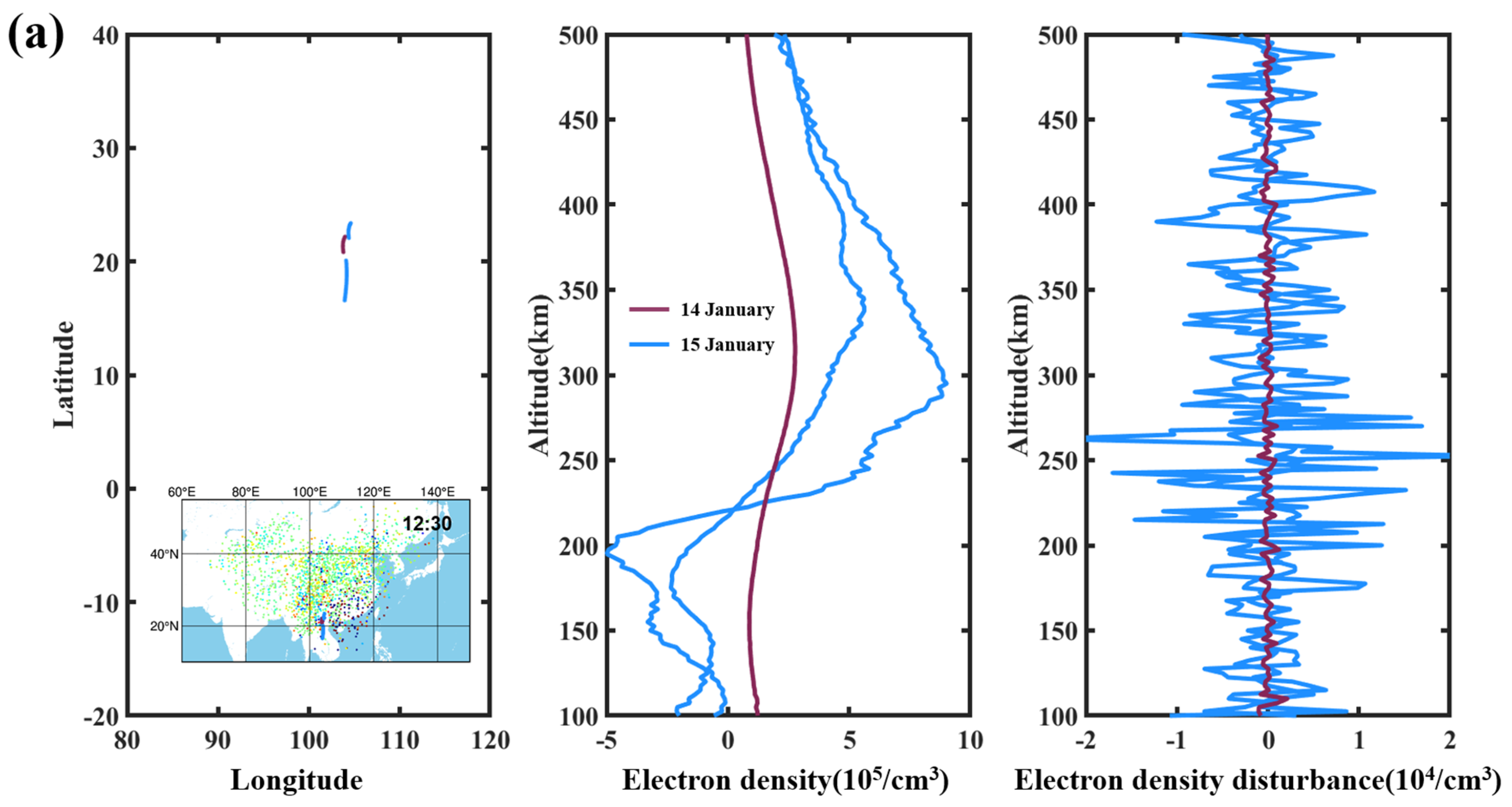
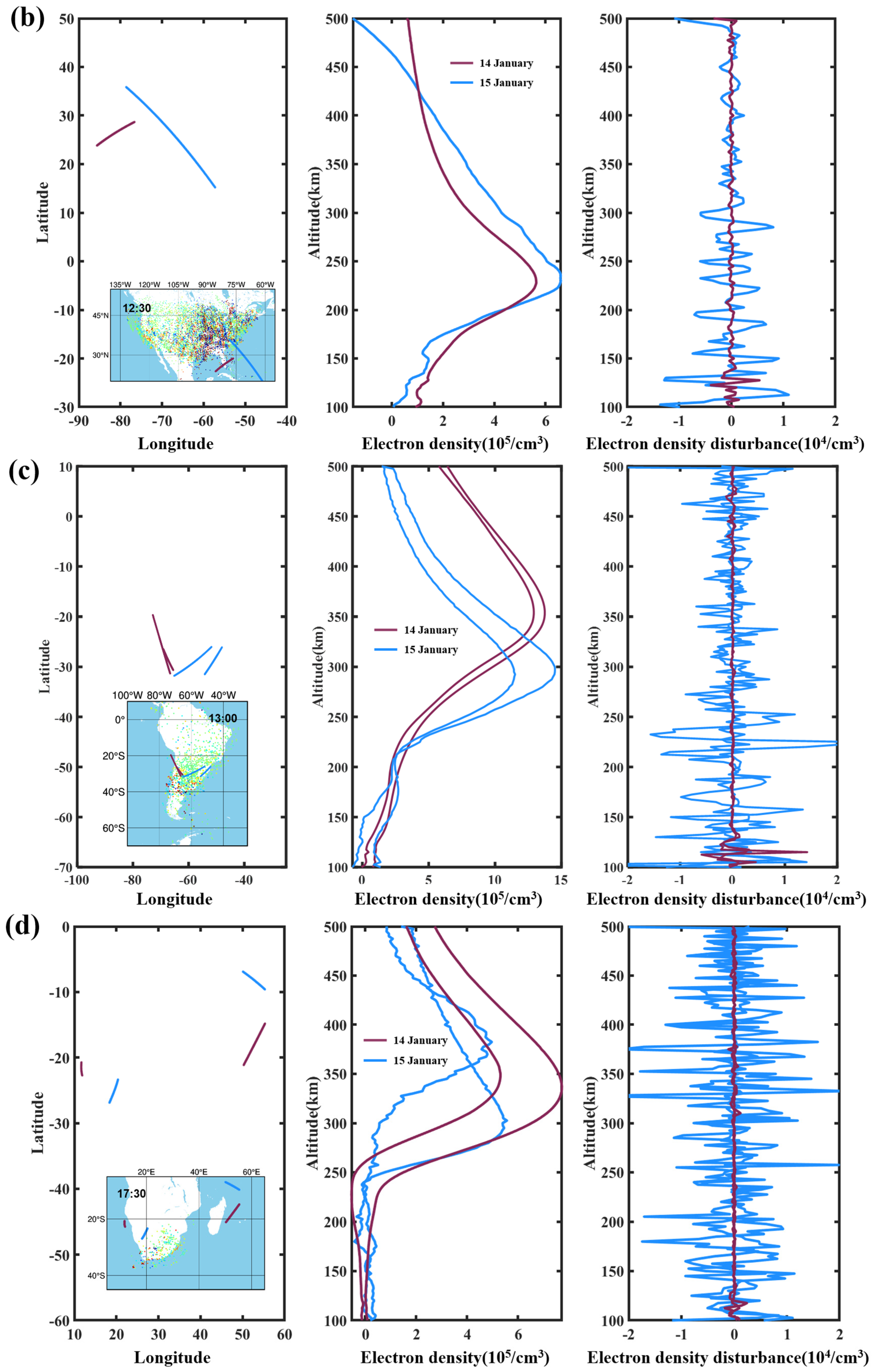
4. Effects of Multiple Atmospheric Wave Disturbances in Near-Field TID Recorded by COSMIC-2 RO
5. Discussion
6. Conclusions
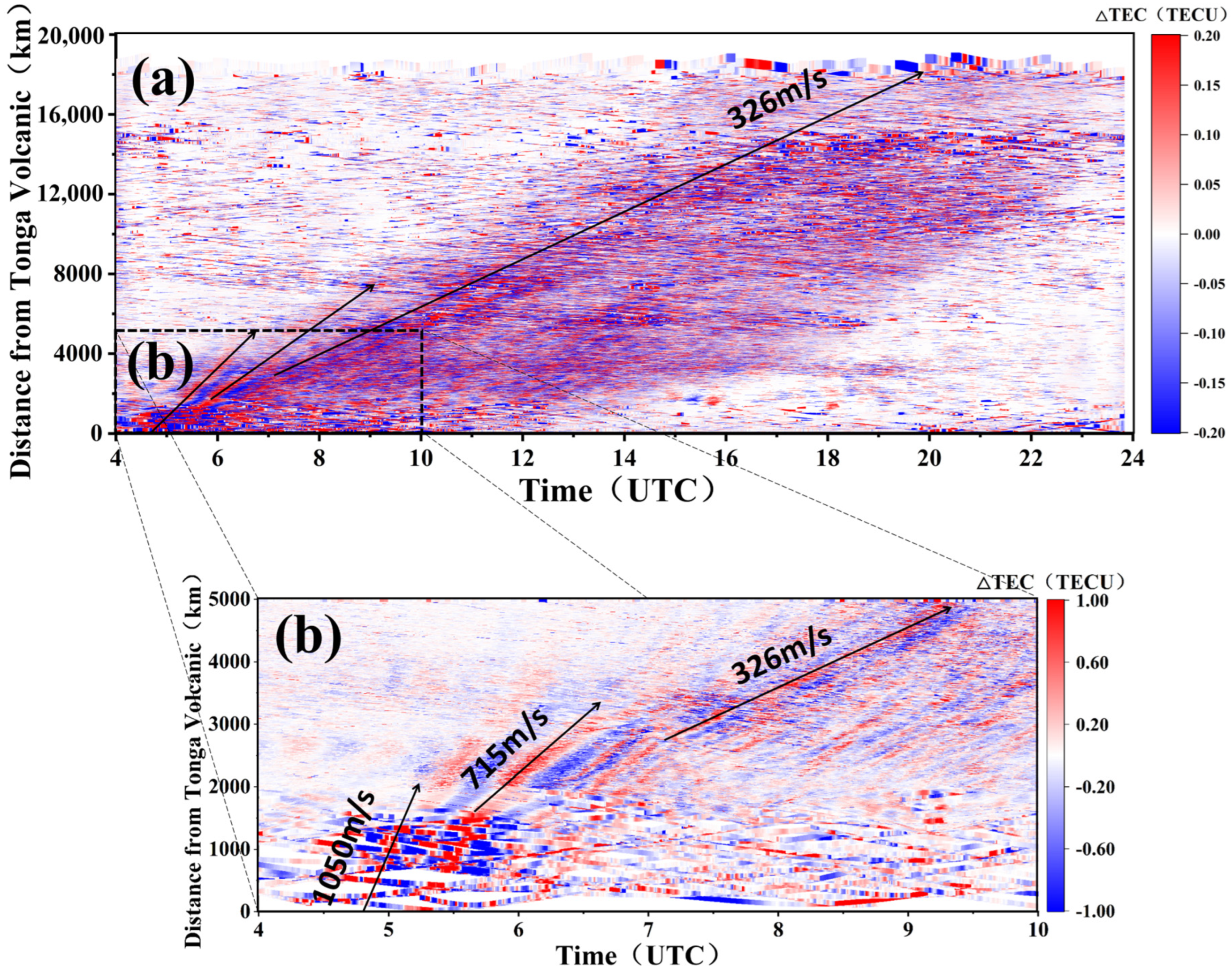
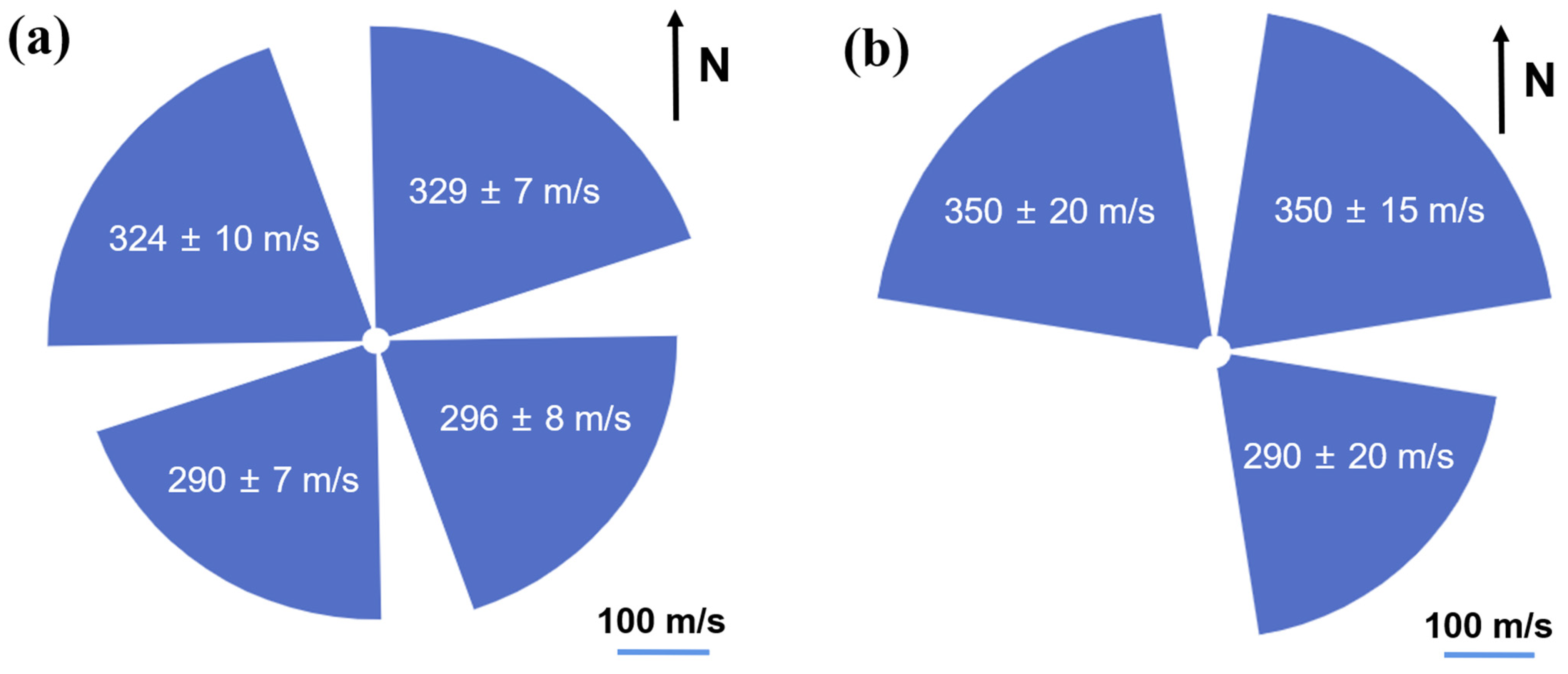
- The disturbance of the ionosphere by the volcanic eruption of Tonga in 2022 can be divided into three processes: acoustic-gravity wave disturbance with a disturbance speed of about 1050 m/s, affecting a range of 3500 km; Lamb wave disturbance with a disturbance speed of about 326 m/s, affecting a range of 16,000 km; and tsunami wave disturbance with a disturbance speed of about 200 m/s.
- Both acoustic-gravity waves and Lamb waves can cause high-frequency oscillations in the ionosphere in the vertical direction and cause short-wave fluctuations of 20 km, while tsunami waves cause long-wave fluctuations in the ionosphere of about 220 km, and the amplitude of the disturbance is much smaller than that of acoustic-gravity waves and Lamb waves.
- There are local features in the TID propagation process, including the TID conjugation in Australia and the TID rapid attenuation phenomenon in Europe.
- The propagation velocity of ionospheric disturbances induced by Lamb waves is different in the southward and northward directions, and is influenced by the magnetic field, besides, its propagation velocity to the northern hemisphere is higher than to the southern hemisphere in both the near and far fields.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matoza, R.S.; Fee, D.; Assink, J.D.; Iezzi, A.M.; Green, D.N.; Kim, K.; Toney, L.; Lecocq, T.; Krishnamoorthy, S.; Lalande, J.M.; et al. Atmospheric waves and global seismoacoustic observations of the January 2022 Hunga eruption, Tonga. Science 2022, 377, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Kubota, T.; Saito, T.; Nishida, K. Global fast-traveling tsunamis driven by atmospheric Lamb waves on the 2022 Tonga eruption. Science 2022, 377, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.H.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and predicting the Earth’s ionosphere using the Global Positioning System. Ph.D. Dissertation, Astronomical Institute of the University of Bernese, Bernese, Switzerland, 1999. [Google Scholar]
- Yuan, Y.B. Study on theories and methods of correcting ionospheric delay and monitoring ionosphere based on GPS. Ph.D. Dissertation, Institute of Geodesy and Geophysics, Chinese Academy of Science, Wuhan, China, 2002. [Google Scholar] [CrossRef]
- Yuan, Y.; Huo, X.; Ou, J.; Zhang, K.; Chai, Y.; Wen, D.; Grenfell, R. Refining the Klobuchar ionospheric coefficients based on GPS observations. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1498–1510. [Google Scholar] [CrossRef]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Gómez-Cama, J.M. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geodesy 2018, 92, 691–706. [Google Scholar] [CrossRef]
- Artru, J.; Ducic, V.; Kanamori, H.; Lognonné, P.; Murakami, M. Ionospheric detection of gravity waves induced by tsunamis. Geophys. J. Int. 2005, 160, 840–848. [Google Scholar] [CrossRef]
- Heki, K.; Ping, J. Directivity and apparent velocity of the coseismic ionospheric disturbances were observed with a dense GPS array. Earth Planet. Sci. Lett. 2005, 236, 845–855. [Google Scholar] [CrossRef]
- Fukao, Y.; Kobayashi, N.; Nishida, K. Background Lamb waves in the Earth’s atmosphere. Geophys. J. Int. 2014, 196, 312–316. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Vierinen, J.; Aa, E.; Goncharenko, L.P.; Erickson, P.J.; Rideout, W.; Coster, A.J.; Spicher, A. 2022 Tonga Volcanic Eruption Induced Global Propagation of Ionospheric Disturbances via Lamb Waves. Front. Astron. Space Sci. 2022, 9. [Google Scholar] [CrossRef]
- Themens, D.R.; Watson, C.; Žagar, N.; Vasylkevych, S.; Elvidge, S.; McCaffrey, A.; Prikryl, P.; Reid, B.; Wood, A.; Jayachandran, P.T. Global Propagation of Ionospheric Disturbances Associated With the 2022 Tonga Volcanic Eruption. Geophys. Res. Lett. 2022, 49. [Google Scholar] [CrossRef]
- Otsuka, S. Visualizing Lamb Waves From a Volcanic Eruption Using Meteorological Satellite Himawari-8. Geophys. Res. Lett. 2022, 49. [Google Scholar] [CrossRef]
- Yue, X.A.; Guo, Y.H.; Zeng, Z.; Wan, W.X. GNSS radio occultation technique for near-Earth space environment detection. Chin. J. Geophys.-Chin. Ed. 2016, 59, 1161–1188. [Google Scholar] [CrossRef]
- An, M.Z.; Yang, Z.H.; Yu, Z.R.; Zhai, Y.F.; Gao, K. Experimental study on the tensile performance of reactive powder concrete. J. China Railw. Soc. 2010, 32, 54–58. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, C.Y.; Sun, Y.Y.; Lee, I.T.; Chum, J. Fluctuations on vertical profiles of the ionospheric electron density perturbed by the March 11, 2011 M9.0 Tohoku earthquake and tsunami. GPS Solut. 2019, 23, 76. [Google Scholar] [CrossRef]
- Shi, K.; Guo, J.; Zhang, Y.; Li, W.; Kong, Q.; Yu, T. Multi-Dimension and Multi-Channel Seismic-Ionospheric Coupling: Case Study of Mw 8.8 Concepcion Quake on 27 February 2010. Remote Sens. 2021, 13, 2724. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, S. Ionospheric Rayleigh Wave Disturbances Following the 2018 Alaska Earthquake from GPS Observations. Remote Sens. 2019, 11, 901. [Google Scholar] [CrossRef]
- Yuan, Y.; Ou, J. Auto-covariance estimation of variable samples (ACEVS) and its application for monitoring random ionospheric disturbances using GPS. J. Geodesy 2001, 75, 438–447. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Themens, D.R.; Jayachandran, P.T.; Langley, R.B.; MacDougall, J.W.; Nicolls, M.J. Determining receiver biases in GPS-derived total electron content in the auroral oval and polar cap region using ionosonde measurements. GPS Solut. 2012, 17, 357–369. [Google Scholar] [CrossRef]
- Yuan, Y.; Ou, J. A generalized trigonometric series function model for determining ionospheric delay. Prog. Nat. Sci. 2004, 14, 1010–1014. [Google Scholar] [CrossRef]
- Yuan, Y.B.; Tscherning, C.C.; Knudsen, P.; Xu, G.; Ou, J.K. The ionospheric eclipse factor method (IEFM) and its application to determining the ionospheric delay for GPS. J. Geodesy 2008, 82, 1–8. [Google Scholar] [CrossRef]
- Shi, K.P.; Liu, X.; Guo, J.Y.; Liu, L.; You, X.Z.; Wang, F.J. Pre-Earthquake and Coseismic Ionosphere Disturbances of the Mw 6.6 Lushan Earthquake on 20 April 2013 Monitored by CMONOC. Atmosphere 2019, 10, 216. [Google Scholar] [CrossRef]
- Jin, R.; Jin, S.; Feng, G. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geodesy 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Schumann, G.P.; Muhlhausen, J.; Andreadis, K.M. Rapid Mapping of Small-Scale River-Floodplain Environments Using UAV SfM Supports Classical Theory. Remote Sens. 2019, 11, 982. [Google Scholar] [CrossRef]
- Zhang, S.R.; Erickson, P.J.; Coster, A.J.; Rideout, W.; Vierinen, J.; Jonah, O.; Goncharenko, L.P. Subauroral and Polar Traveling Ionospheric Disturbances During the 7–9 September 2017 Storms. Space Weather 2019, 17, 1748–1764. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Guo, J.; Shi, K.; Liu, X.; Sun, Y.; Li, W.; Kong, Q. Singular spectrum analysis of ionospheric anomalies preceding great earthquakes: Case studies of Kaikoura and Fukushima earthquakes. J. Geodyn. 2019, 124, 1–13. [Google Scholar] [CrossRef]
- Bretherton, F.P. Lamb waves in a nearly isothermal atmosphere. Q. J. R. Meteorol. Soc. 1969, 95, 754–757. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Blake, D. Lamb waves in the presence of realistic distributions of temperature and dissipation. J. Geophys. Res. 1972, 77, 2166–2176. [Google Scholar] [CrossRef]
- Lin, J.T.; Rajesh, P.K.; Lin, C.C.; Chou, M.Y.; Liu, J.Y.; Yue, J.; Hsiao, T.Y.; Tsai, H.F.; Chao, H.M.; Kung, M.M. Rapid Conjugate Appearance of the Giant Ionospheric Lamb Wave Signatures in the Northern Hemisphere After Hunga-Tonga Volcano Eruptions. Geophys. Res. Lett. 2022, 49. [Google Scholar] [CrossRef]
- Shinbori, A.; Otsuka, Y.; Sori, T.; Nishioka, M.; Perwitasari, S.; Tsuda, T.; Nishitani, N. Electromagnetic conjugacy of ionospheric disturbances after the 2022 Hunga Tonga-Hunga Ha’apai volcanic eruption as seen in GNSS-TEC and SuperDARN Hokkaido pair of radars observations. Earth Planets Space 2022, 74, 1–17. [Google Scholar] [CrossRef]
- Chou, M.Y.; Yue, J.; Lin, C.C.; Rajesh, P.K.; Pedatella, N.M. Conjugate Effect of the 2011 Tohoku Reflected Tsunami-Driven Gravity Waves in the Ionosphere. Geophys. Res. Lett. 2022, 49. [Google Scholar] [CrossRef]
- Hao, Y.; Li, Q.; Guo, J.; Zhang, X.; Yang, G.; Zhang, D.; Xiao, Z. Imaging of the large-scale ionospheric disturbances induced by seismic waves using GPS network in China. Chin. J. Geophys.-Chin. Ed. 2021, 64, 3925–3932. [Google Scholar] [CrossRef]
- Gardner, L.C.; Schunk, R.W. Generation of traveling atmospheric disturbances during pulsating geomagnetic storms. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Lei, X.L.; Fu, Y.; Xue, Z.G.; Du, X.Y.; Yan, W.; Lu, X. Validation of global VTEC maps constructed using data derived from COSMIC constellation. Chin. J. Space Sci. 2011, 31, 754–764. [Google Scholar] [CrossRef]
- Heki, K.; Fujimoto, T. Atmospheric modes excited by the 2021 August eruption of the Fukutoku-Okanoba volcano, Izu–Bonin Arc, observed as harmonic TEC oscillations by QZSS. Earth Planets Space 2022, 74, 27. [Google Scholar] [CrossRef]
- Liu, C.H.; Klostermeyer, J.; Yeh, K.C.; Jones, T.B.; Robinson, T.; Holt, O.; Leitinger, R.; Ogawa, T.; Sinno, K.; Kato, S.; et al. Global dynamic responses of the atmosphere to the eruption of Mount St. Helens on May 18, 1980. J. Geophys. Res. 1982, 87, 6281–6290. [Google Scholar] [CrossRef]
- Roberts, D.H.; Klobuchar, J.A.; Fougere, P.F.; Hendrickson, D.H. A large-amplitude traveling ionospheric disturbance produced by the May 18, 1980, explosion of Mount St. Helens. J. Geophys. Res. 1982, 87, 6291–6301. [Google Scholar] [CrossRef]
- Hao, Y.Q.; Xiao, Z.; Zhang, D.H. Responses of the ionosphere to the Great Sumatra earthquake and volcanic eruption of Pinatubo. Chin. Phys. Lett. 2006, 23, 1955–1957. [Google Scholar] [CrossRef]
- Li, W.; Guo, J.; Yue, J.; Shen, Y.; Yang, Y. Total electron content anomalies associated with global VEI4+ volcanic eruptions during 2002–2015. J. Volcanol. Geotherm. Res. 2016, 325, 98–109. [Google Scholar] [CrossRef]
- Chen, P.; Yao, Y.; Yao, W. On the coseismic ionospheric disturbances after the Nepal Mw7.8 earthquake on April 25, 2015 using GNSS observations. Adv. Space Res. 2017, 59, 103–113. [Google Scholar] [CrossRef]
- Figueiredo, C.A.O.B.; Takahashi, H.; Wrasse, C.M.; Otsuka, Y.; Shiokawa, K.; Barros, D. Medium-Scale Traveling Ionospheric Disturbances Observed by Detrended Total Electron Content Maps Over Brazil. J. Geophys. Res. Space Phys. 2018, 123, 2215–2227. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Q.; Li, C.; Shi, K.; Guo, J.; Han, J.; Wang, T.; Bai, Q.; Chen, Y. Global Ionospheric Disturbance Propagation and Vertical Ionospheric Oscillation Triggered by the 2022 Tonga Volcanic Eruption. Atmosphere 2022, 13, 1697. https://doi.org/10.3390/atmos13101697
Kong Q, Li C, Shi K, Guo J, Han J, Wang T, Bai Q, Chen Y. Global Ionospheric Disturbance Propagation and Vertical Ionospheric Oscillation Triggered by the 2022 Tonga Volcanic Eruption. Atmosphere. 2022; 13(10):1697. https://doi.org/10.3390/atmos13101697
Chicago/Turabian StyleKong, Qiaoli, Changsong Li, Kunpeng Shi, Jinyun Guo, Jingwei Han, Tianfa Wang, Qi Bai, and Yanfei Chen. 2022. "Global Ionospheric Disturbance Propagation and Vertical Ionospheric Oscillation Triggered by the 2022 Tonga Volcanic Eruption" Atmosphere 13, no. 10: 1697. https://doi.org/10.3390/atmos13101697
APA StyleKong, Q., Li, C., Shi, K., Guo, J., Han, J., Wang, T., Bai, Q., & Chen, Y. (2022). Global Ionospheric Disturbance Propagation and Vertical Ionospheric Oscillation Triggered by the 2022 Tonga Volcanic Eruption. Atmosphere, 13(10), 1697. https://doi.org/10.3390/atmos13101697







