A PM2.5 Concentration Prediction Model Based on CART–BLS
Abstract
1. Introduction
- (1)
- CART algorithm has good performance in dealing with data classification. BLS network has the advantages of high prediction accuracy, fast operation speed and simple structure. We combined the advantages of both to propose the CART-BLS model.
- (2)
- We used the CART algorithm to optimize the data set so that the data has a more detailed range and avoid the confusion of the data.
- (3)
- It is proved that the prediction accuracy of the CART–BLS model is high.
2. Methods
2.1. CART Algorithm
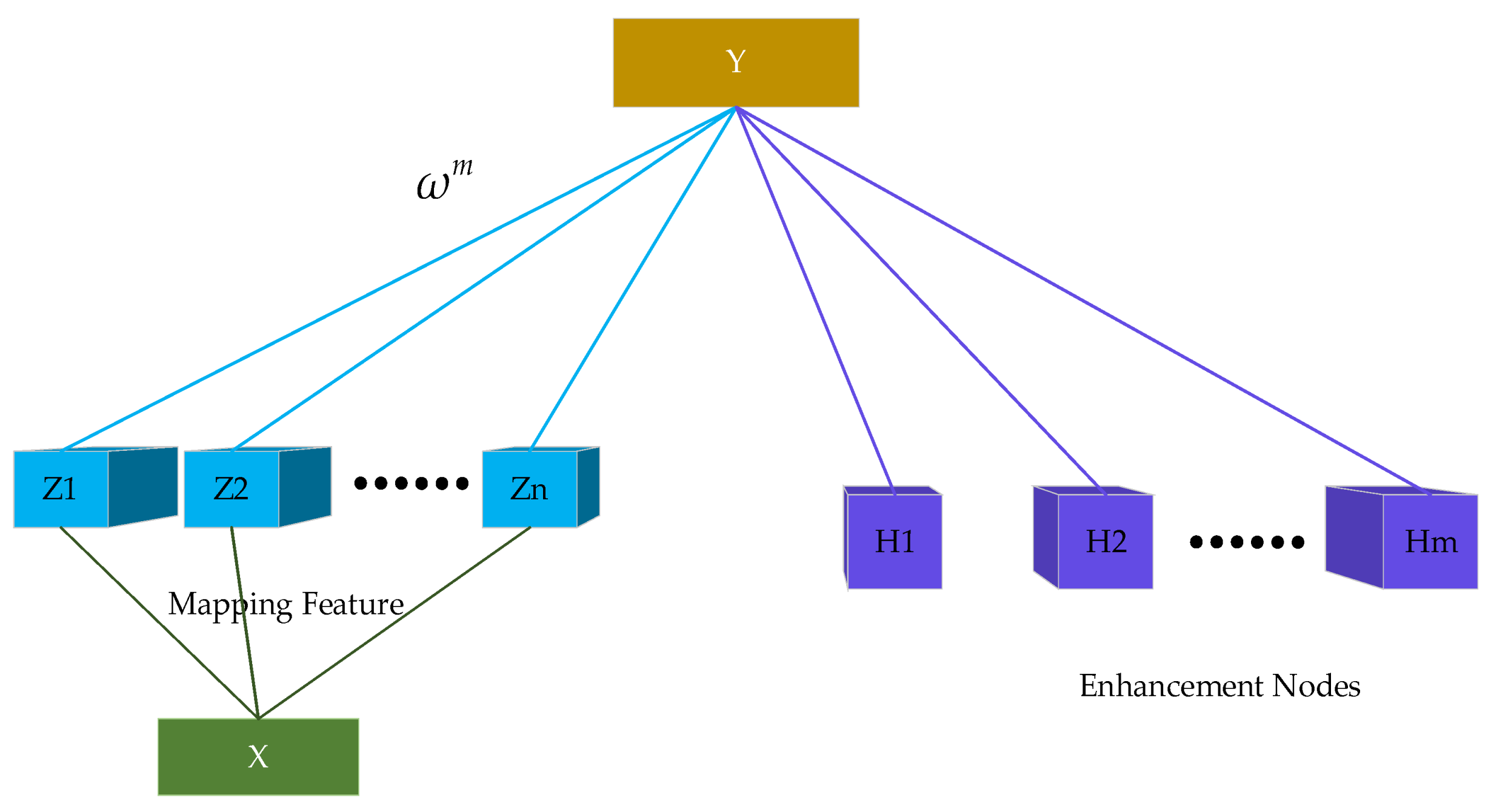
2.2. BLS
2.3. CART–BLS
- (1) Build the CART tree. We use the CART algorithm to train our collected data. The data build a tree in layers. Since the depth of the tree may be affected by outliers, it is necessary to set the maximum depth of the tree when building the regression tree. Each node in the partitioned tree has its own training set. We need to train a local model on each child node, so we need to set a minimum number of samples on each child node to ensure that there are enough data samples for training the local model.
- (2) Use the relevant samples to train the BLS. Before training the BLS, we first classify the data on each node divided by the CART and then use these node samples to train the BLS parameters. The model is globally trained using the data samples of the root node. The root node data are used as the training set data, and the data on each leaf node are used as the verification data to determine the model parameters separately. Local model training of the BLS uses internal node data samples of decision trees. The internal node data are used as training data, and the leaf node data with the internal node as the root node are used as verification data. A local model is trained on each leaf node using its own data samples.
- (3) Compare the global and local BLS models. For the global model, we compare the prediction performance of several global models at the root node. For local models, we compare the prediction effects of several local models on leaf nodes. With this in mind, we select the optimal prediction model.
3. Data and Experimental Results
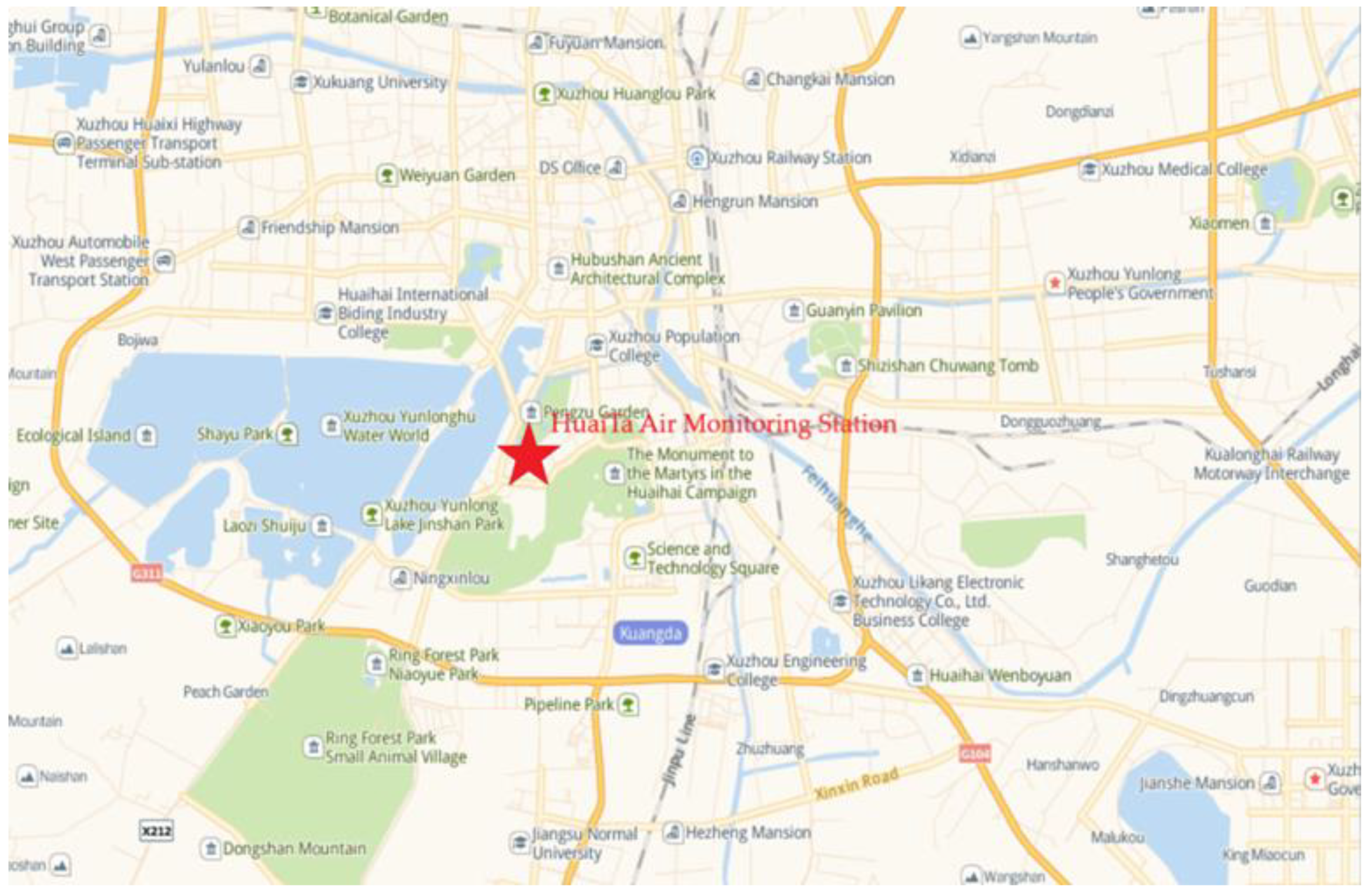
3.1. Data
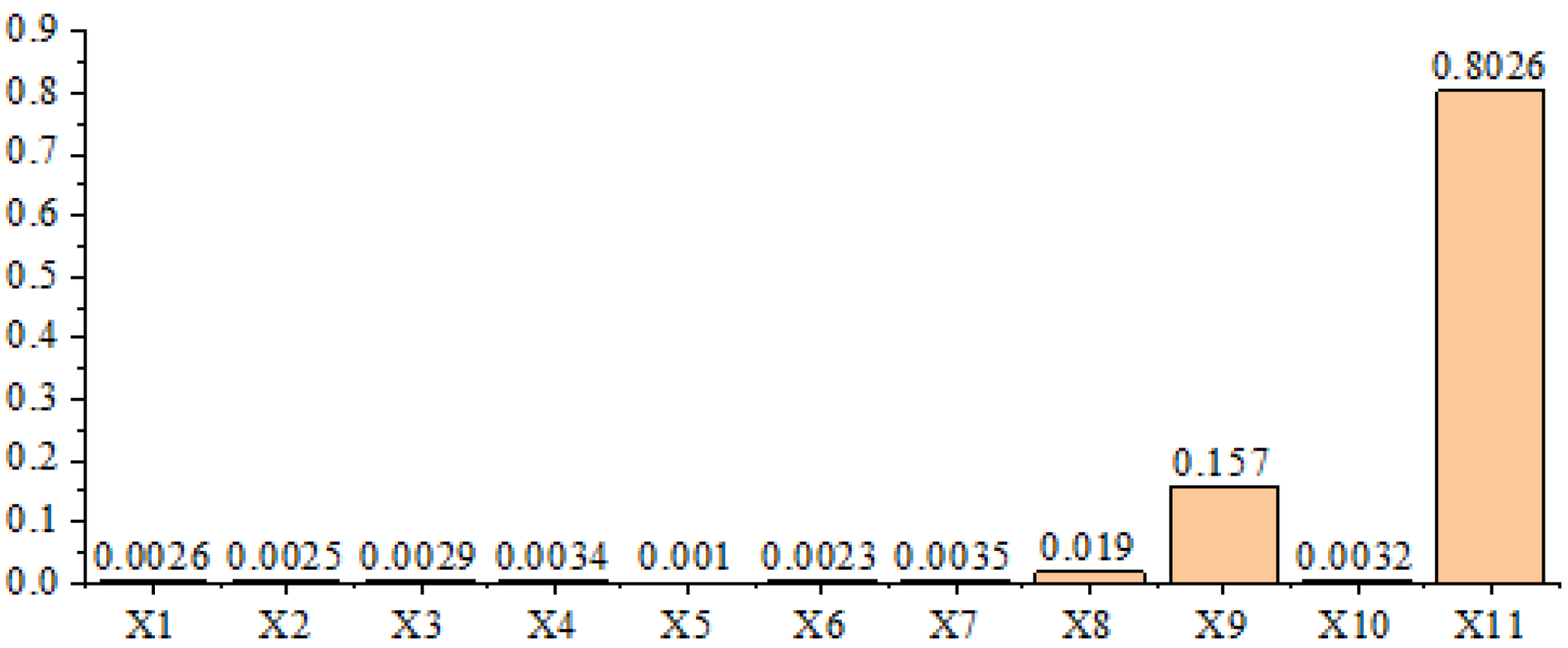
3.2. RF Selection Input Variable
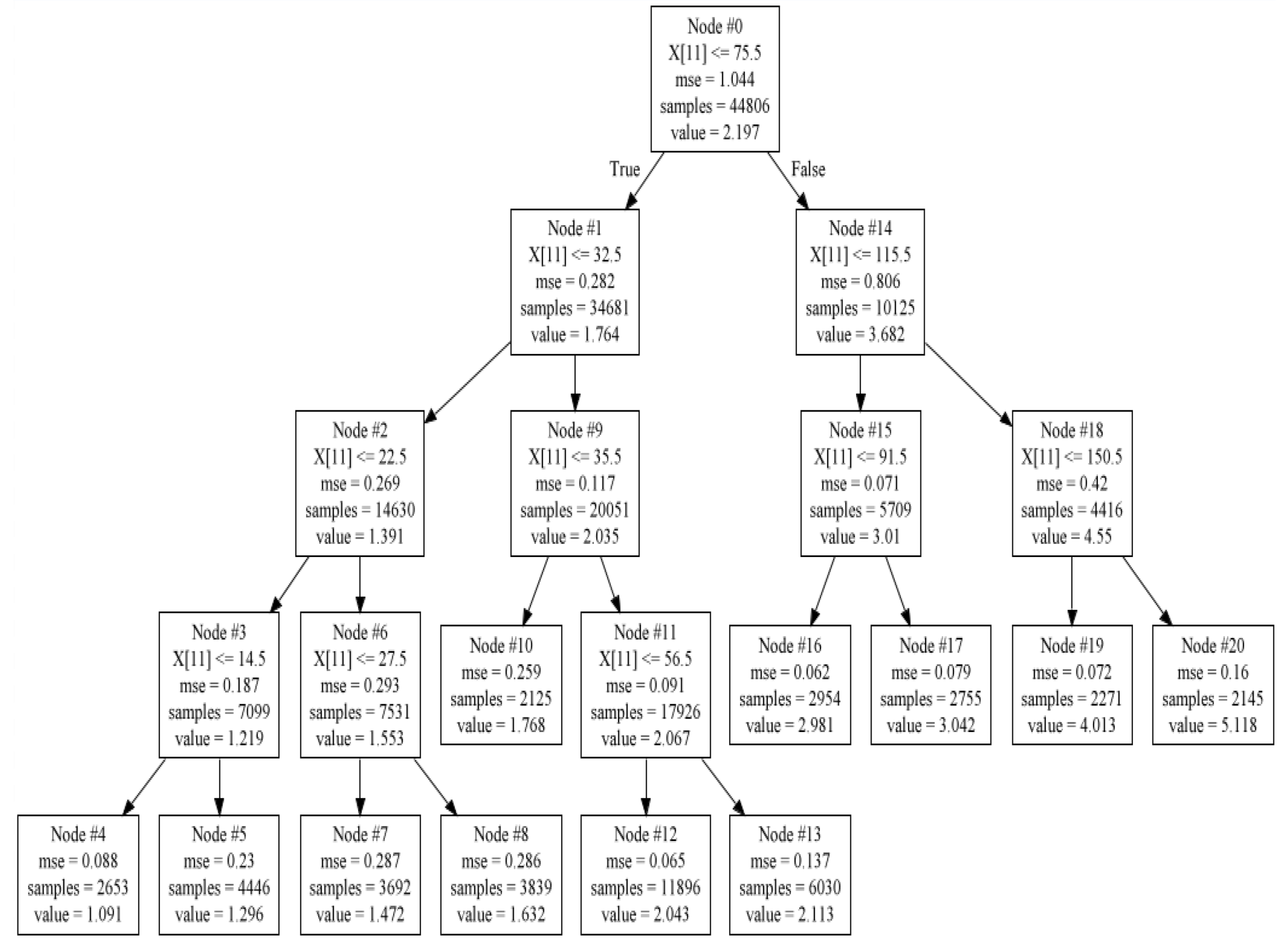
3.3. Splitting the Dataset Using the CART Decision Tree
3.4. Prediction Model Based on CART–BLS
3.4.1. Global Model
3.4.2. Local Model
3.5. Analysis of Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thomaidis, N.S.; Bakeas, E.B.; Siskos, P.A. Characterization of lead, cadmium, arsenic and nickel in PM2.5 particles in the Athens atmosphere, Greece. Chemosphere 2003, 52, 959–966. [Google Scholar] [CrossRef]
- Zhou, Q.P.; Jiang, H.Y.; Wang, J.Z.; Zhou, J.L. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Maftei, C.; Muntean, R.; Poinareanu, I. The Impact of Air Pollution on Pulmonary Diseases: A Case Study from Brasov County, Romania. Atmosphere 2022, 13, 902. [Google Scholar] [CrossRef]
- Byun, D.; Schere, K.L. Review of the Governing Equations, Computational Algorithms, and Other Components of the Models-3 Community Multiscale Air Quality (CMAQ) Modeling System. Appl. Mech. Rev. 2006, 59, 51–77. [Google Scholar] [CrossRef]
- Pouyaei, A.; Choi, Y.; Jung, J.; Sadeghi, B.; Song, C.H. Concentration trajectory route of air pollution with an integrated Lagrangian model (C-TRAIL model v1. 0) derived from the community Multiscale Air quality model (CMAQ model v5. 2). Geosci. Model Dev. 2020, 13, 3489–3505. [Google Scholar] [CrossRef]
- Lee, M.; Brauer, M.; Wong, P. Land use regression modelling of air pollution in high density high rise cities: A case study in Hong Kong. Sci. Total Environ. 2017, 592, 306. [Google Scholar] [CrossRef]
- Zafra, C.; Ángel, Y.; Torres, E. ARIMA analysis of the effect of land surface coverage on PM10 concentrationsin a high-altitude megacity. Atmos. Pollut. Res. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Lira, T.S.; Barrozo, M.A.S.; Assis, A.J. Air quality prediction in Uberlndia, Brazil, using linear models and neural networks. Elsevier 2007, 24, 51–56. [Google Scholar]
- Zhai, L.; Sang, H.; Zhang, J. Estimating the spatial distribution of PM2.5 concentration by integrating geographic data and field measurements. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W4, 209–213. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Zhou, C.; Wang, S.; Li, M. The Impacts of Urban Form on PM2.5 Concentrations: A Regional Analysis of Cities in China from 2000 to 2015. Atmosphere 2022, 13, 963. [Google Scholar] [CrossRef]
- Dong, Y.; Hui, W.; Lin, Z. An improved model for PM2.5 inference based on support vector machine. In Proceedings of the IEEE/ACIS International Conference on Software Engineering, Shanghai, China, 30 May–1 June 2016. [Google Scholar]
- Mogoll´on-Sotelo, C.; Casallas, A.; Vidal, S.; Celis, N.; Ferro, C.; Belalcazar, L.C. A support vector machine model to forecast ground-level PM2.5 in a highly populated city with a complex terrain. Air Qual. Atmos. Health 2021, 13, 399–409. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, J.; Zhang, W.; Sun, D. Short-term effects of air pollution on lower respiratory diseases and forecasting by the group method of data handling. Atmos. Environ. 2012, 51, 29–38. [Google Scholar] [CrossRef]
- Jan, K.D.; Rasa, Z.; Mario, G. Modeling PM2.5 Urban Pollution Using Machine Learning and Selected Meteorological Parameters. J. Electr. Comput. Eng. 2017, 2017, 1–14. [Google Scholar]
- Cobourn, W.G. An enhanced PM2.5 air quality forecast model based on nonlinear regression and back-trajectory concentrations. Atmos. Environ. 2010, 44, 3015–3023. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, T.; He, L. Study on prediction and spatial variation of PM2.5 pollution by using improved BP artificial neural network model of computer technology and GIS. Comput. Model. New Technol. 2014, 18, 107–115. [Google Scholar]
- Linbo, L.; Lilong, L.; Junyu, L. Prediction of PM2.5 Mass Concentration Using GA-BP Neural Network Combined with Water Vapor Factor. J. Guilin Univ. Technol. 2019, 039, 420–426. [Google Scholar]
- Chen, L.; Pai, T.Y. Comparisons of GM(1,1), and BPNN for predicting hourly particulate matter in Dali area of Taichung City, Taiwan. Atmos. Pollut. Res. 2015, 6, 572–580. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Z. Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef]
- E, C.R.; Yuan, C.; Sun, Y.L.; Liu, Z.L.; Chen, L. Research progress of broad learning systems. Comput. Appl. Res. 2021, 38, 2258–2267. [Google Scholar]
- Tang, J.; Deng, C.; Huang, G.B. Extreme learning machine for multilayer perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 809–821. [Google Scholar] [CrossRef]
- Chen, M.; Xu, Z.; Weinberger, K. Marginalized Denoising Autoencoders for Domain Adaptation. Comput. Sci. 2012, 1206, 1627–1634. [Google Scholar]
- Gong, M.; Liu, J.; Li, H.; Cai, Q.; Su, L. A multiobjective sparse feature learning model for deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3263–3277. [Google Scholar] [CrossRef]
- Shuang, F.; Chen, C. Transactions on Fuzzy Systems 1 A Fuzzy Restricted Boltzmann Machine: Novel Learning Algorithms Based on Crisp Possibilistic Mean Value of Fuzzy Numbers. IEEE Trans. Fuzzy Syst. 2016, 99, 1063–6706. [Google Scholar]
- Chen, C.L.P.; Zhang, C.Y.; Chen, L.; Gan, M. Fuzzy restricted Boltzmann machine for the enhancement of deep learning. IEEE Trans. Fuzzy Syst. 2015, 23, 2163–2173. [Google Scholar] [CrossRef]
- Yu, Z.; Li, L.; Liu, J.; Han, G. Hybrid adaptive classifier ensemble. IEEE Trans. Cybern. 2015, 45, 177–190. [Google Scholar]
- He, J.J.; Gong, S.L.; Yu, Y.; Yu, L.J.; Wu, L.; Mao, H.J. Air pollution characteristics and their relation to meteorological conditions during 2014–2015 in major Chinese cities. Environ. Pollut. 2017, 223, 484–496. [Google Scholar] [CrossRef] [PubMed]
- Mckendry, I.G. Evaluation of artificial neural networks for fine particulate pollution ([PM10] and [PM2.5]) forecasting. J. Air Waste Manag. Assoc. 2002, 52, 1096. [Google Scholar] [CrossRef] [PubMed]
- Yeo, I.; Choi, Y.; Lops, Y. Efficient PM2.5 forecasting using geographical correlation based on integrated deep learning algorithms. Neural Comput. Appl. 2021, 33, 15073–15089. [Google Scholar] [CrossRef]
- Li, S.; Xie, G.; Ren, J. Urban PM2.5 Concentration Prediction via Attention Based CNN–LSTM. Appl. Sci. 2020, 10, 1953. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H.; Zhou, F. Prediction of Air Pollutant Concentration Based on One-Dimensional Multi-Scale CNN-LSTM Considering Spatial-Temporal Characteristics: A Case Study of Xi’an, China. Atmosphere 2021, 12, 1626. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef]
- Celis, N.; Casallas, A.; Lopez-Barrera, E.; Martinez, H.; Peña, C.A.; Arenas, R.; Ferro, C. Design of an early alert system for PM2.5 through a stochastic method and machine learning models. Environ. Sci. Policy 2022, 127, 241–252. [Google Scholar] [CrossRef]
- Habibi, R.; Alesheikh, A.A.; Mohammadinia, A. An Assessment of Spatial Pattern Characterization of Air Pollution: A Case Study of CO and PM2.5 in Tehran, Iran. Int. J. Geo-Inf. 2017, 6, 270. [Google Scholar] [CrossRef]
- Jin, Y.J. Imputation adjustment method for missing data. Appl. Stat. Manag. 2001, 5, 47–53. [Google Scholar]
- Cheng, J.; Sun, J.; Yao, K.S.; Xu, M.; Cao, Y. A variable selection method based on mutual information and variance inflation factor. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 268, 1386–1425. [Google Scholar] [CrossRef]
- D, H.; Vu, K.M.; Muttaqi, A.P. A variance inflation factor and backward elimination based robust regression model for forecasting monthly electricity demand using climatic variables. Appl. Energy 2015, 140, 385–394. [Google Scholar]
- Thunis, P.; Pederzoli, A.; Pernigotti, D. Performance criteria to evaluate air quality modeling applications. Atmos. Environ. 2012, 59, 476–482. [Google Scholar] [CrossRef]

| Input Vector | Feature |
|---|---|
| X1, X2…, X11 | Temp, DPT, pressure, WD, WS, CO, NO2, O3, PM10, SO2, PM2.5 |
| Input Vector | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| VIF | 3.67 | 1.11 | 19,98 | 3.68 | 4.69 | 10.16 | 7.61 | 4.29 | 9.94 | 2.94 | 9.47 |
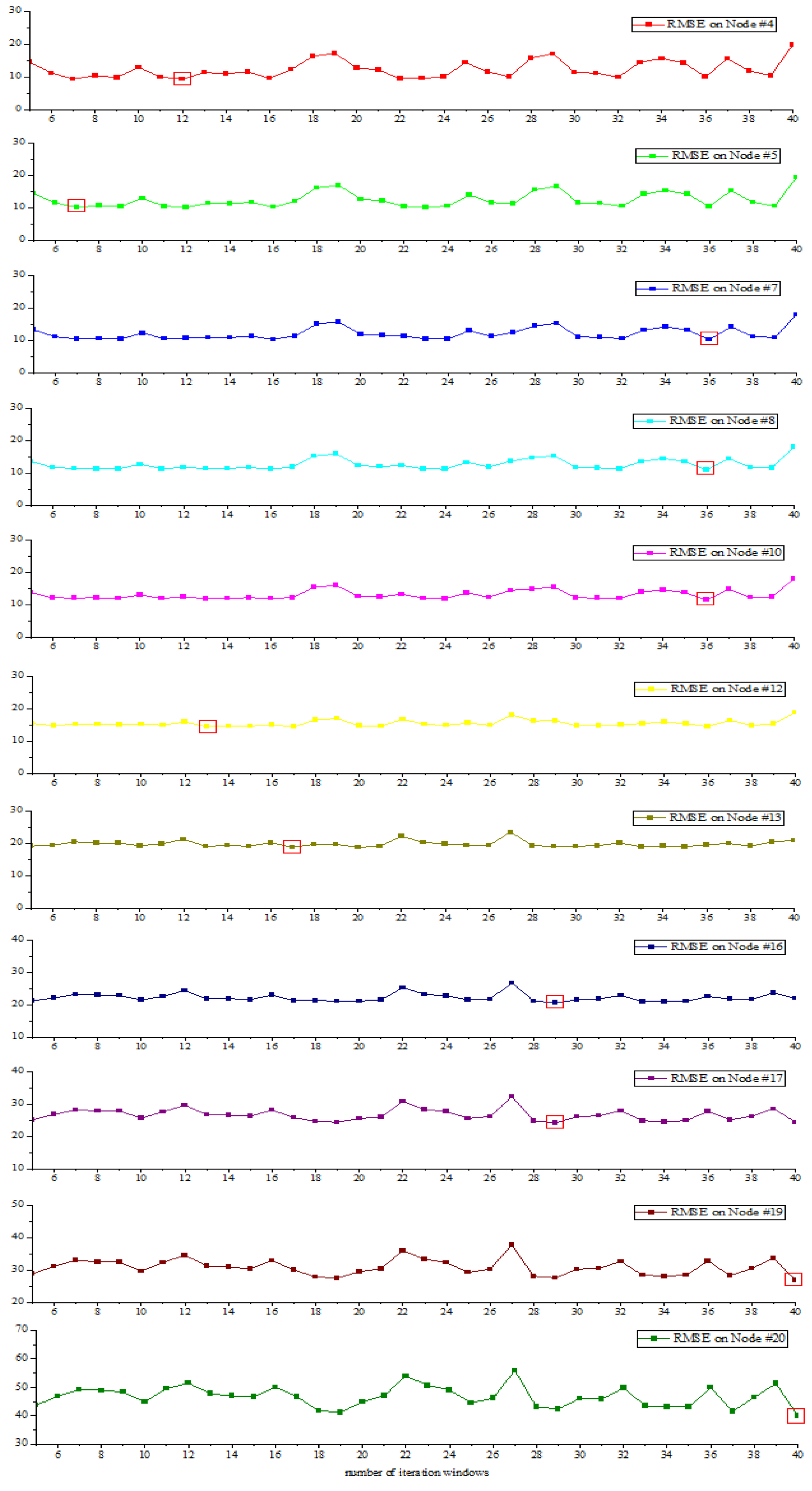
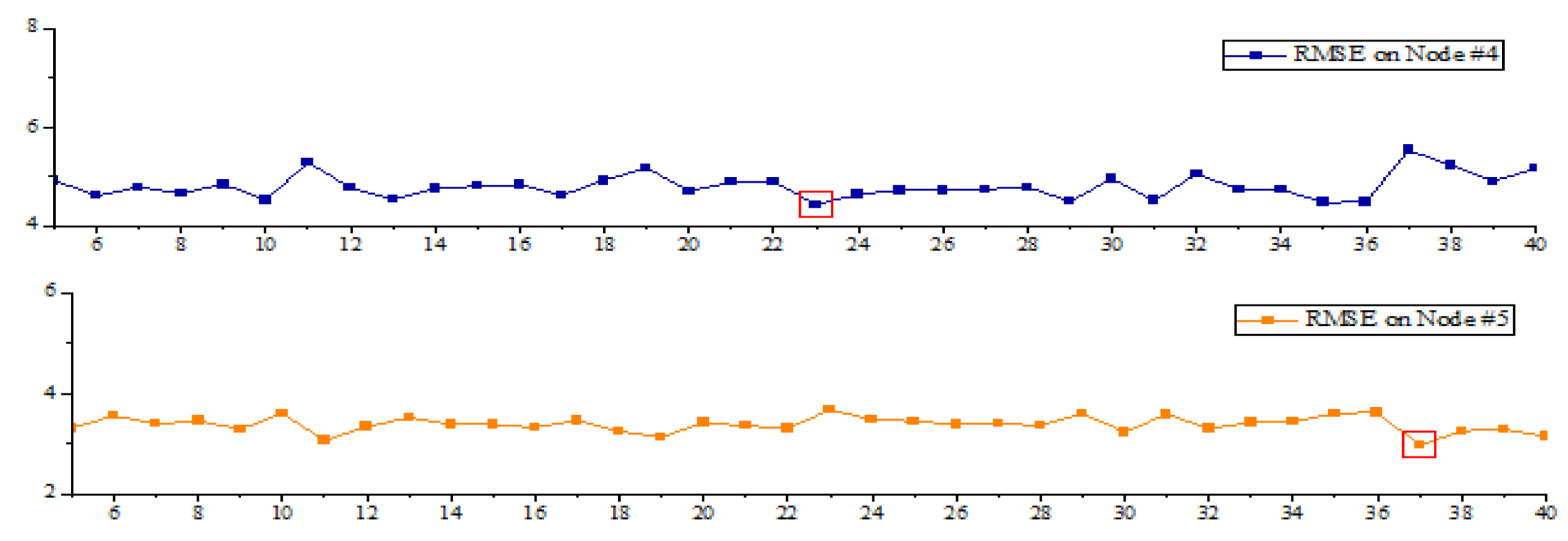
| Model | Testing RMSEs on the Leaf Nodes/μg·m−3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| #4 | #5 | #7 | #8 | #10 | #12 | #13 | #16 | #17 | #19 | #20 | |
| RF | 2.92 | 2.33 | 1.58 | 1.59 | 0.90 | 5.96 | 5.57 | 4.96 | 6.99 | 9.84 | 26.03 |
| V-SVR | 3.44 | 2.36 | 1.62 | 1.54 | 0.93 | 5.56 | 5.56 | 4.77 | 7.02 | 9.86 | 41.26 |
| Seasonal BLS | 3.59 | 2.25 | 1.46 | 1.38 | 0.77 | 6.03 | 5.42 | 4.66 | 6.89 | 9.89 | 40.27 |
| CART–BLS | 3.54 | 2.25 | 1.45 | 1.38 | 0.77 | 6.03 | 5.40 | 4.64 | 6.86 | 9.87 | 41.24 |
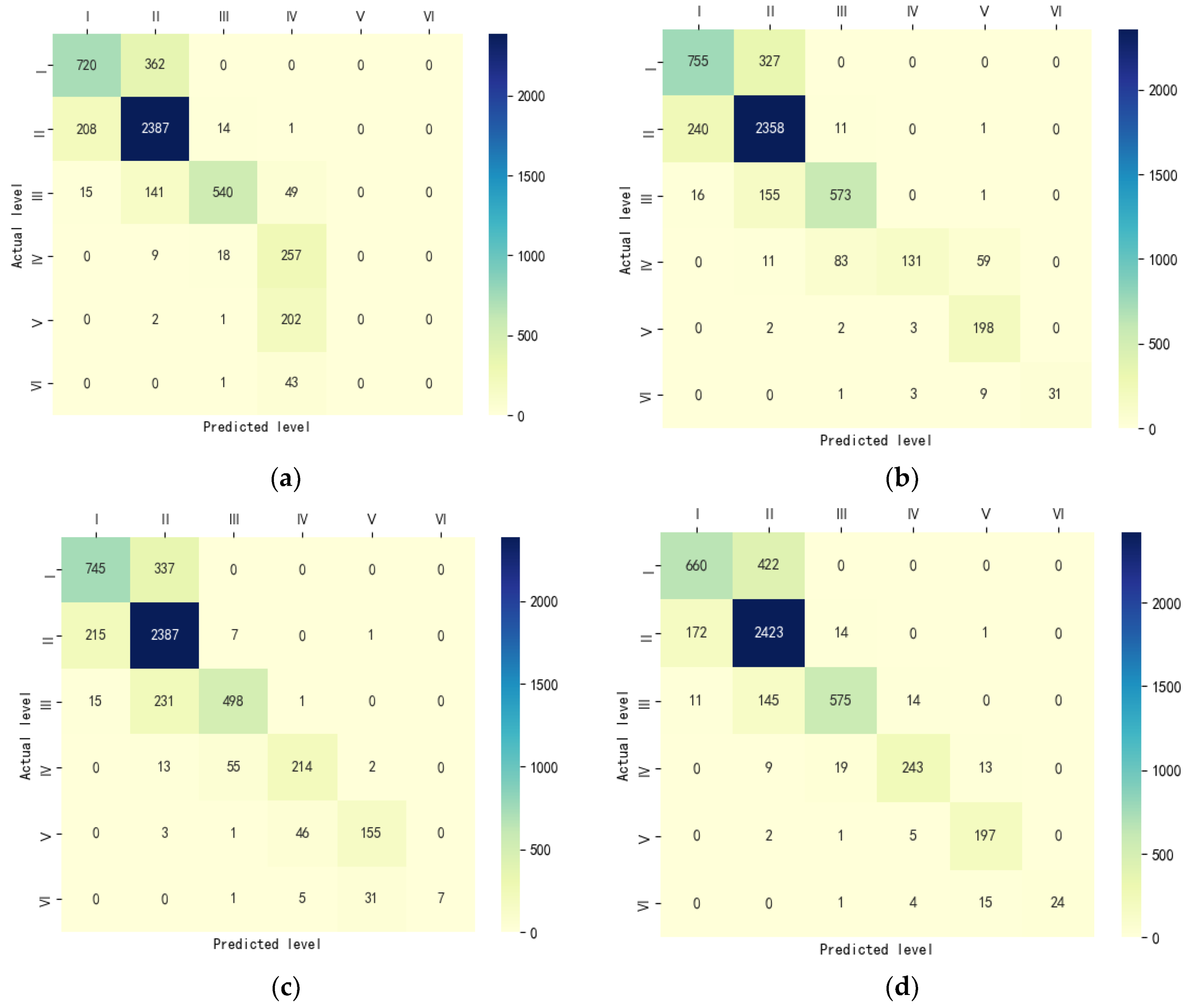
| Model | Testing MAE/μg·m−3 | Testing MAPE/% | R2 |
|---|---|---|---|
| RF | 0.170 | 6.201 | 0.8146 |
| V-SVR | 0.166 | 8.349 | 0.8419 |
| Seasonal BLS | 0.129 | 7.451 | 0.8517 |
| CART–BLS | 0.068 | 4.481 | 0.9362 |
| PM2.5 Concentrations/μg·m−3 | [0,35] | (35,75] | (75,115] | (115,150] | (150,250] | (250, +∞) |
|---|---|---|---|---|---|---|
| Level | I | II | III | IV | V | VI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, Y.; Chen, J.; Shen, X. A PM2.5 Concentration Prediction Model Based on CART–BLS. Atmosphere 2022, 13, 1674. https://doi.org/10.3390/atmos13101674
Wang L, Wang Y, Chen J, Shen X. A PM2.5 Concentration Prediction Model Based on CART–BLS. Atmosphere. 2022; 13(10):1674. https://doi.org/10.3390/atmos13101674
Chicago/Turabian StyleWang, Lin, Yibing Wang, Jian Chen, and Xiuqiang Shen. 2022. "A PM2.5 Concentration Prediction Model Based on CART–BLS" Atmosphere 13, no. 10: 1674. https://doi.org/10.3390/atmos13101674
APA StyleWang, L., Wang, Y., Chen, J., & Shen, X. (2022). A PM2.5 Concentration Prediction Model Based on CART–BLS. Atmosphere, 13(10), 1674. https://doi.org/10.3390/atmos13101674





