Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method †
Abstract
1. Introduction
2. Three-Variable Forms of Saltzman’s Model
2.1. Spectral Form of Solution
2.2. Amplitude Equations
- Lorenz’s nondimensional is roughly 15 times greater than Saltzman’s nondimensional ,
- Lorenz’s nondimensional and are equal to Saltzman’s nondimensional and ,
- Lorenz’s nondimensional is roughly 2 times less than Saltzman’s nondimensional and
- Lorenz’s nondimensional is roughly 200 times less than Saltzman’s nondimensional
3. Dynamics of 3-Mode Systems: S-LOM (3) and L-LOM (3)
3.1. Overview
3.2. Nonchaotic Regime: , ( for Water at
3.3. Chaotic Regime: ,
4. Design of Observation Network
4.1. Model and Forecast Sensitivities
4.2. Forecast Error
4.3. Observations and Cost Function
4.4. Observation Placement
4.4.1. Observations in Time Alone
4.4.2. Observations Taken in Space and Time
- (1)
- Pick such that and are maximum
- (2)
- Let be four time instances where the squares of are maximum. Determine the respective ’s. Then, the final Gramian is given by
5. Data Assimilation Experiments
5.1. Experiment I: Nonchaotic Data Assimilation Process (Lorenz Scaling)
5.2. Experiment II: Nonchaotic Data Assimilation Process (Saltzman Scaling)
5.3. Experiment III: Chaotic Data Assimilation Process (Lorenz Scaling)
5.4. Experiment IV: Data Assimilation in Time and Space (x, z)
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Saltzman, B. Finite Amplitude Free Convection as an Initial Value Problem-I. J. Atmos. Sci. 1962, 19, 329–341. [Google Scholar] [CrossRef]
- Bénard, M. Les Tourbillions cellulaires dans une nape liquide. Rev. Générale Des Sci. Pures Et Appl. 1990, 11, 1261–1271, 1309–1328. [Google Scholar]
- Rayleigh, L. Convection currents in a horizontal layer of fluid, when higher temperature is on the underside. Philos. Mag. 1916, 32, 529–546. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 220–241. [Google Scholar] [CrossRef]
- Saravanan, R. The Climate Demon: Past, Present, and Future of Climate Change; Cambridge University Press: Cambridge, UK, 2022; 379p. [Google Scholar]
- Lewis, J.M.; Lakshmivarahan, S.; Dhall, S.K. Dynamic Data Assimilation: A Least Squares Approach; Cambridge University Press: Cambridge, UK, 2006; 654p. [Google Scholar]
- Lakshmivarahan, S.; Lewis, J.M.; Hu, J. On Controlling the Shape of the Cost Functional in Dynamic Data Assimilation: Guidelines for Placement of Observations and Application to Saltzman’s Model of Convection. J. Atmos. Sci. 2020, 77, 2969–2989. [Google Scholar]
- Lakshmivarahan, S.; Lewis, J.M.; Maryada, S.K.R. Observability Gramian and its Role in the Placement of Observations in Dynamic Data Assimilation. In Data Assimilation for Atmospheric, Oceanic and Hydrographic Applications; Park, S.K., Xu, L., Eds.; Springer: Cham, Switzerland, 2022; Volume IV, pp. 215–257. [Google Scholar]
- Lewis, J.M.; Lakshmivarahan, S.; Maryada, S.K.R. Placement of observations for variational data assimilation: Application to Burgers’ Equation and seiche phenomenon. In Data Assimilation for Atmospheric, Oceanic and Hydrographic Applications; Park, S.K., Xu, L., Eds.; Springer: Cham, Switzerland, 2022; Volume IV, pp. 215–257. [Google Scholar]
- Lakshmivarahan, S.; Lewis, J.M.; Hu, J. Saltzman’s Model: Complete Characterization of Solution Properties. J. Atmos. Sci. 2019, 76, 1587–1608. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford at the Clarendon Press: Oxford, UK, 1961; 654p. [Google Scholar]
- Turner, J.S. Buoyancy Effects in Fluids; Cambridge University Press: Cambridge, UK, 1973; 368p. [Google Scholar]
- Lewis, J.M.; Lakshmivarahan, S. Derivation of Saltzman’s spectral equations for Rayleigh-Bénard convection in terms of two variable parameters, Rayleigh and Prandtl numbers. Tech. Rep. 2019; Unpublished. [Google Scholar]
- Kuo, H.-L. Solution of the nonlinear equations of cellular convection and heat transport. J. Fluid Mech. 1961, 10, 611–634. [Google Scholar] [CrossRef]
- Lakshmivarahan, S.; Lewis, J.M. Forward Sensitivity Based Approach to Dynamic Data Assimilation. Adv. Meteorol. 2010, 2010, 375615. [Google Scholar] [CrossRef]
- Lakshmivarahan, S.; Lewis, J.M.; Jabrzemski, R. Forecast Error Correction Using Dynamic Data Assimilation; Springer: Berlin/Heidelberg, Germany, 2017; 270p. [Google Scholar]
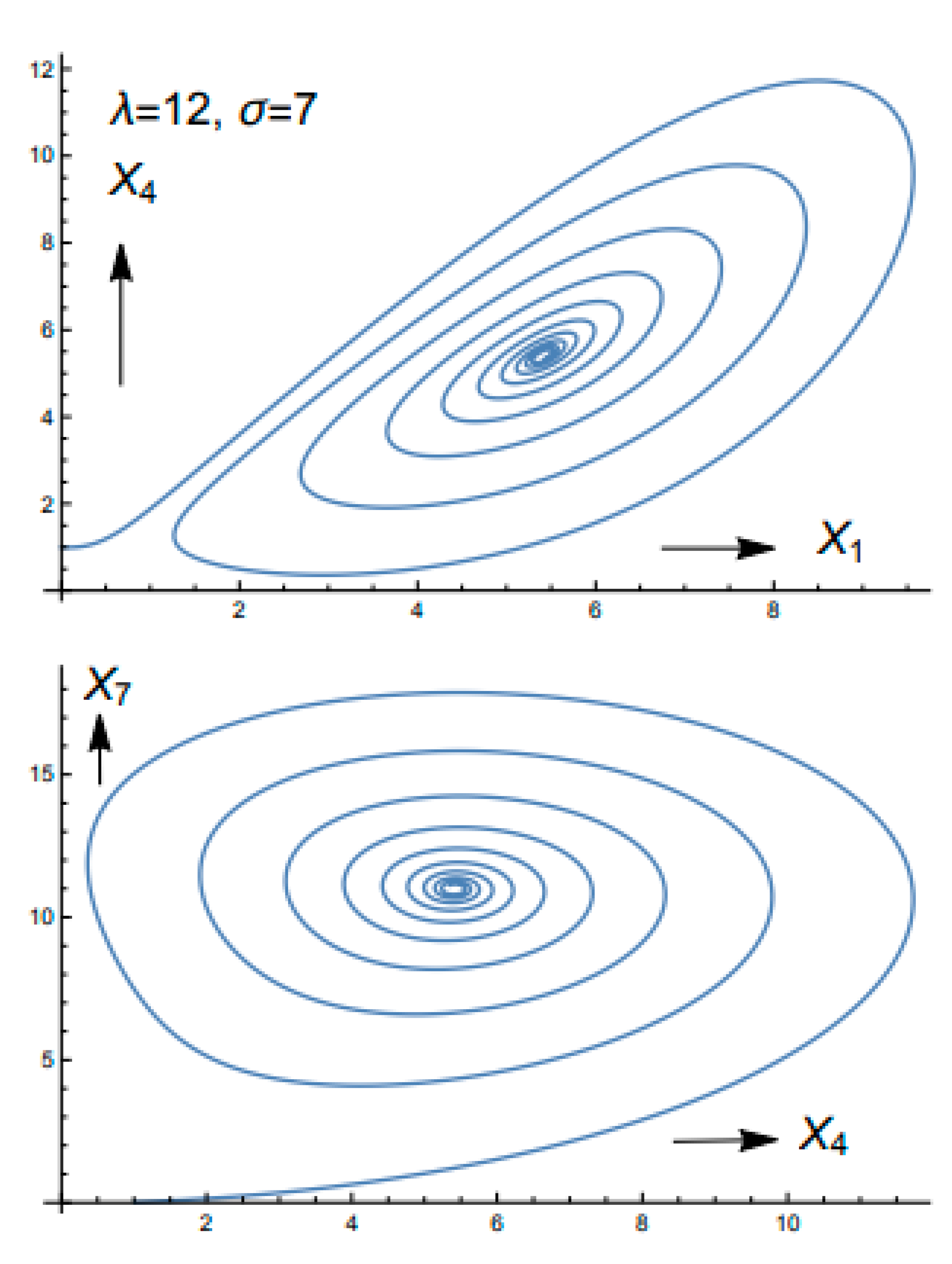
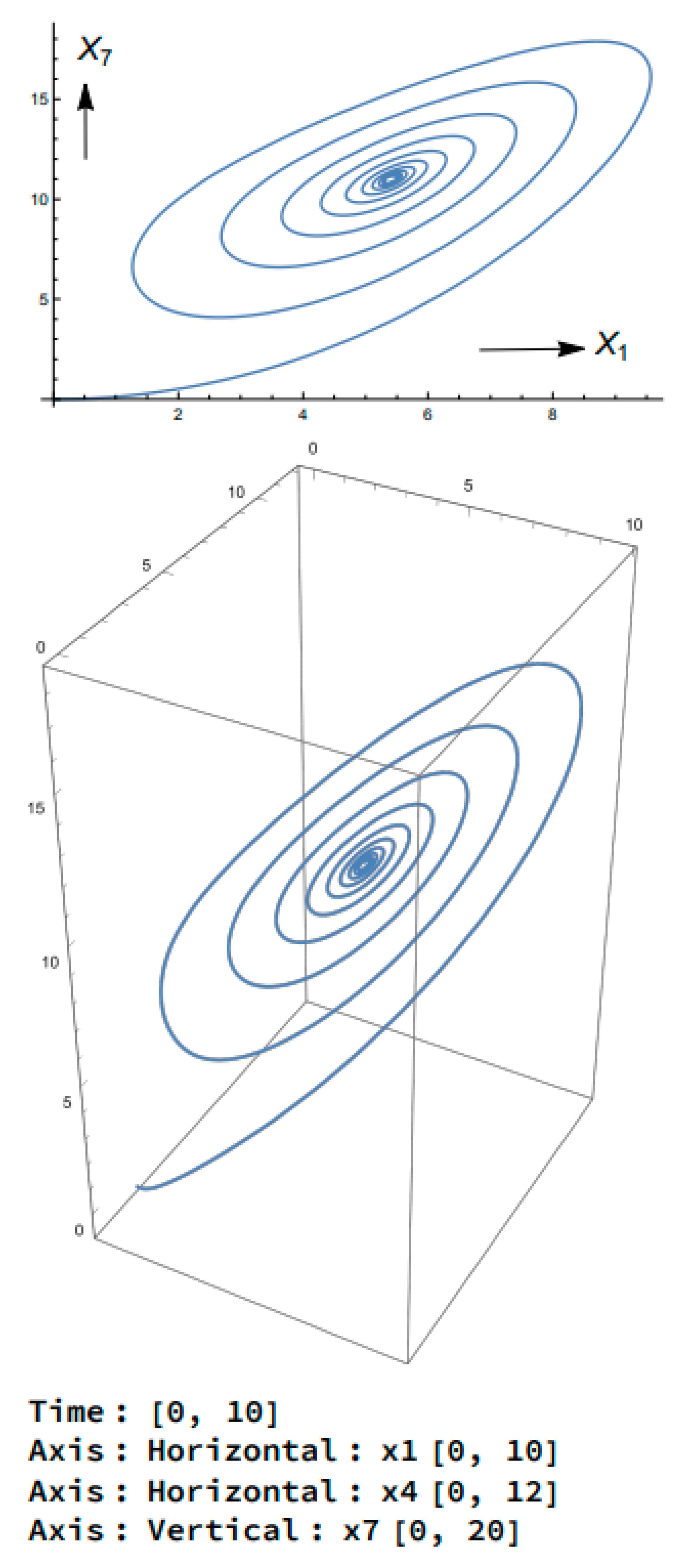
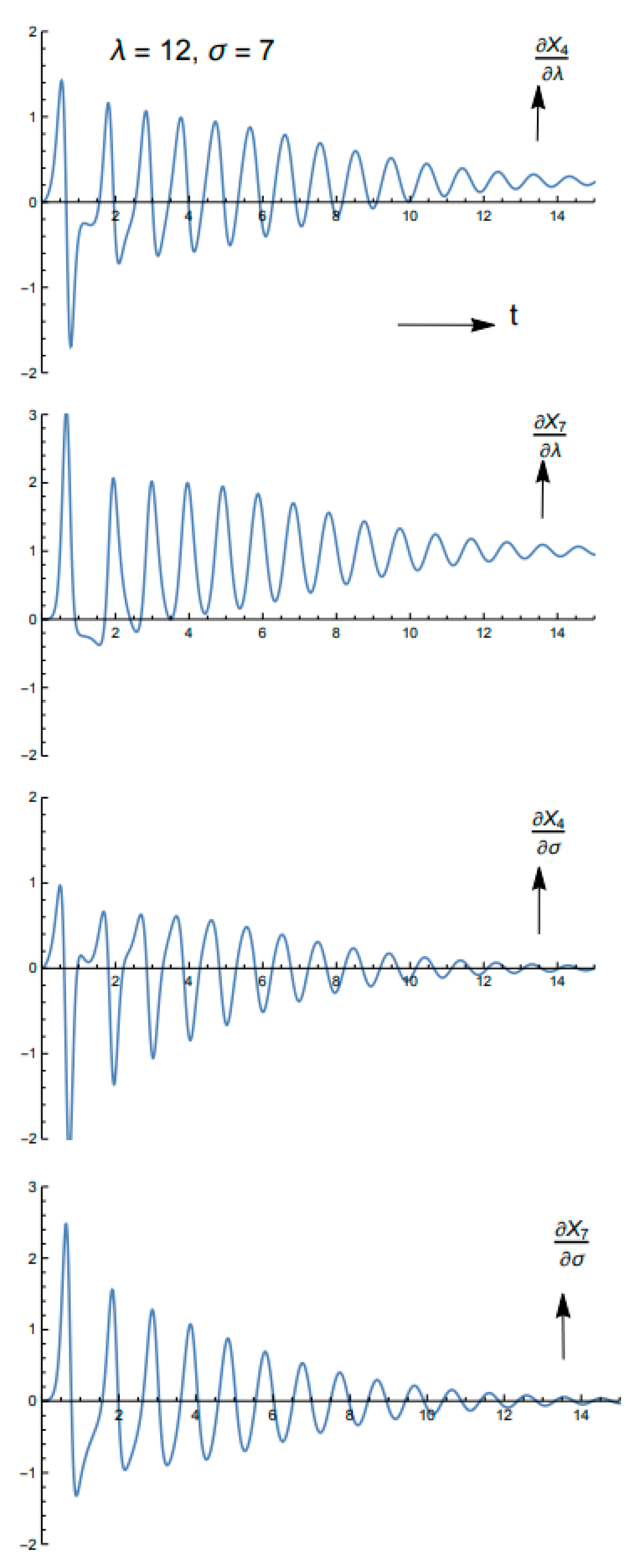
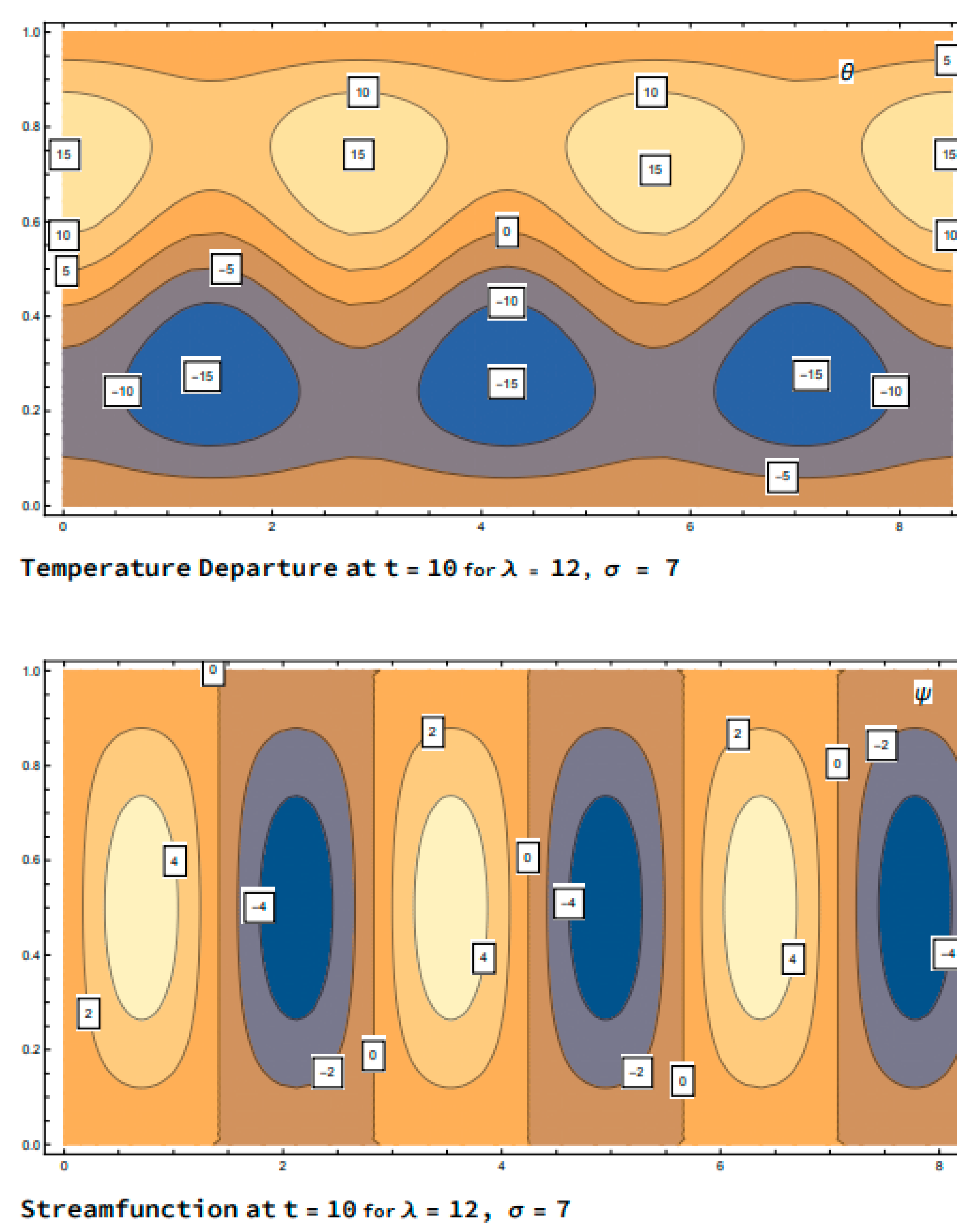
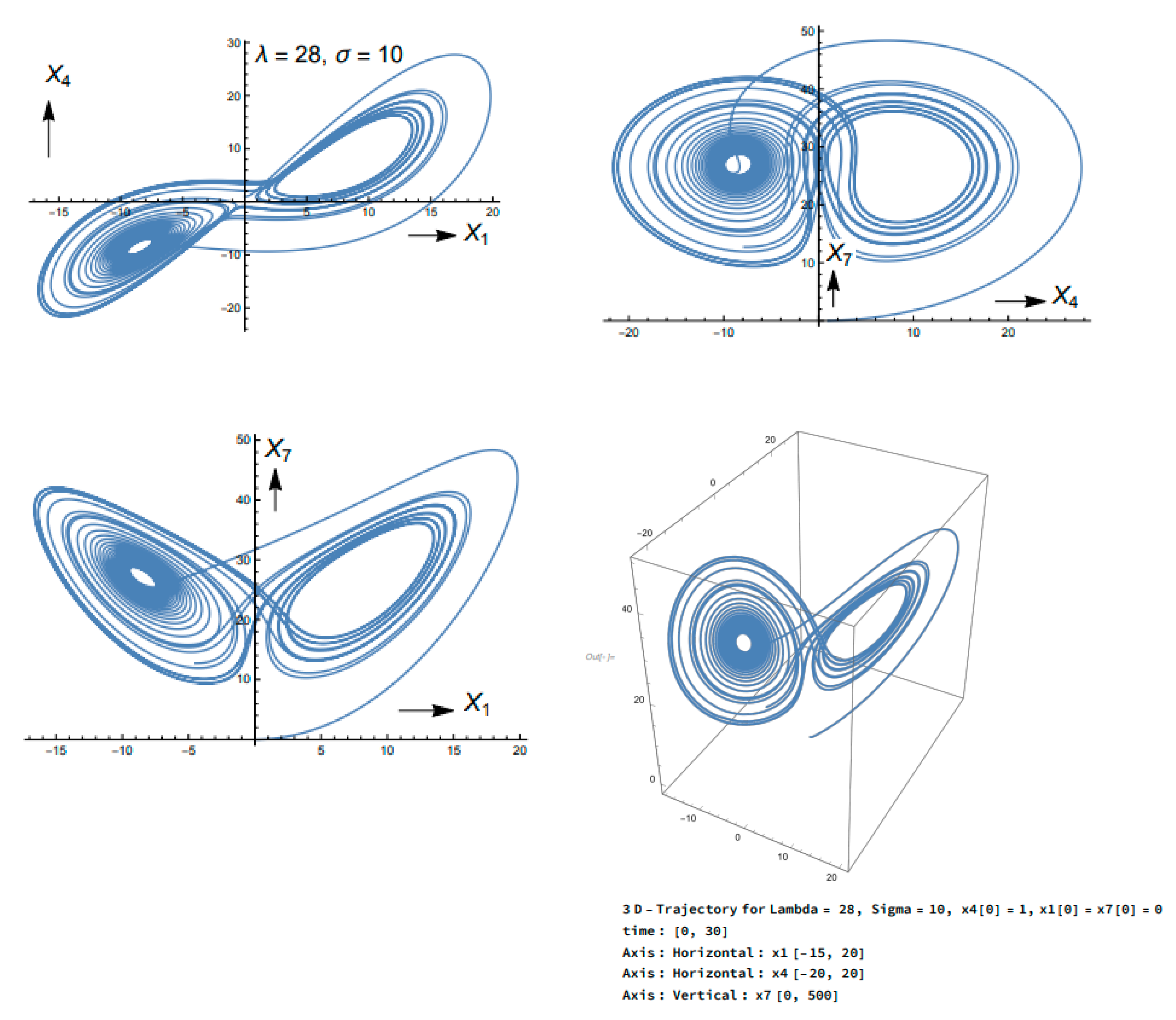
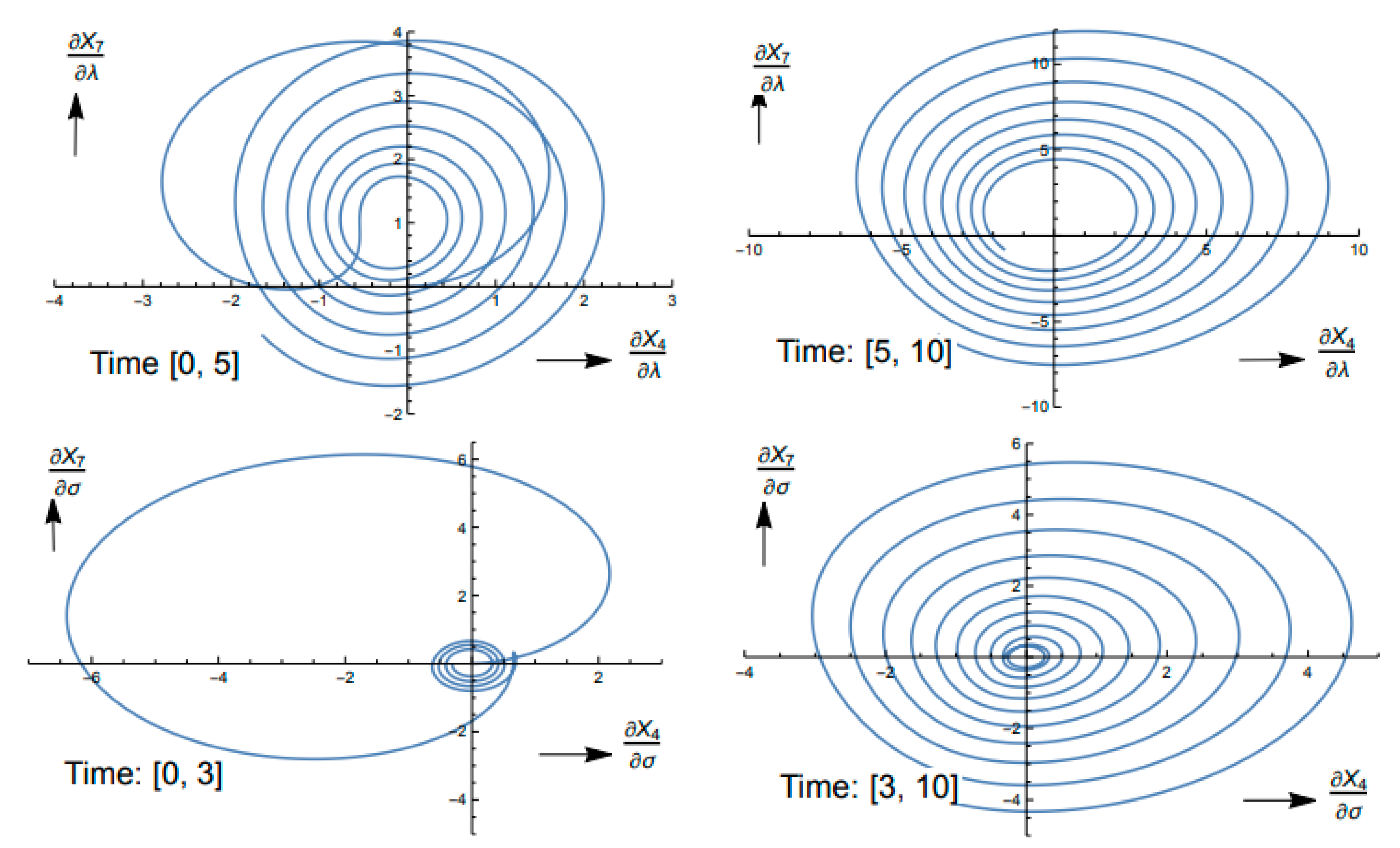

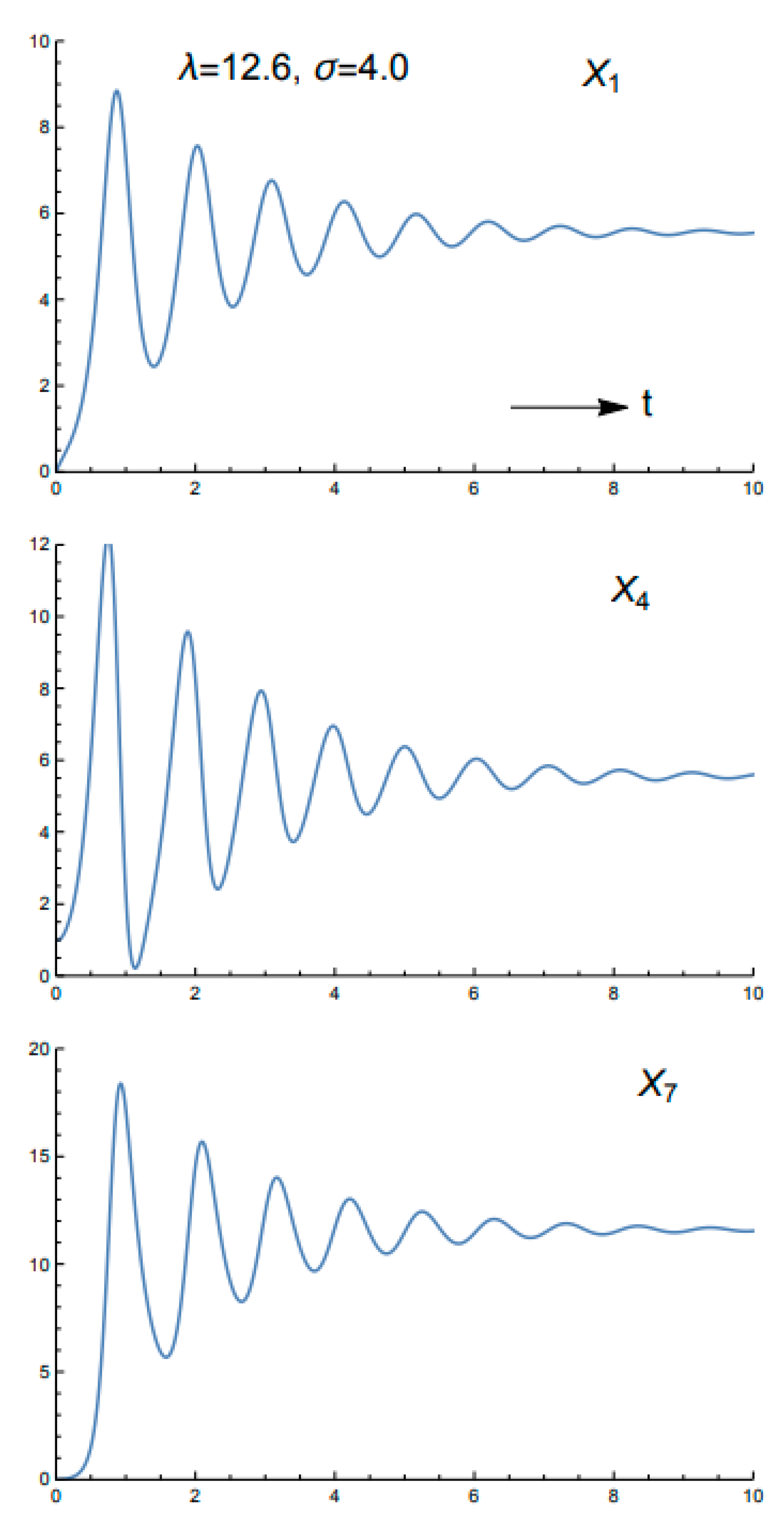

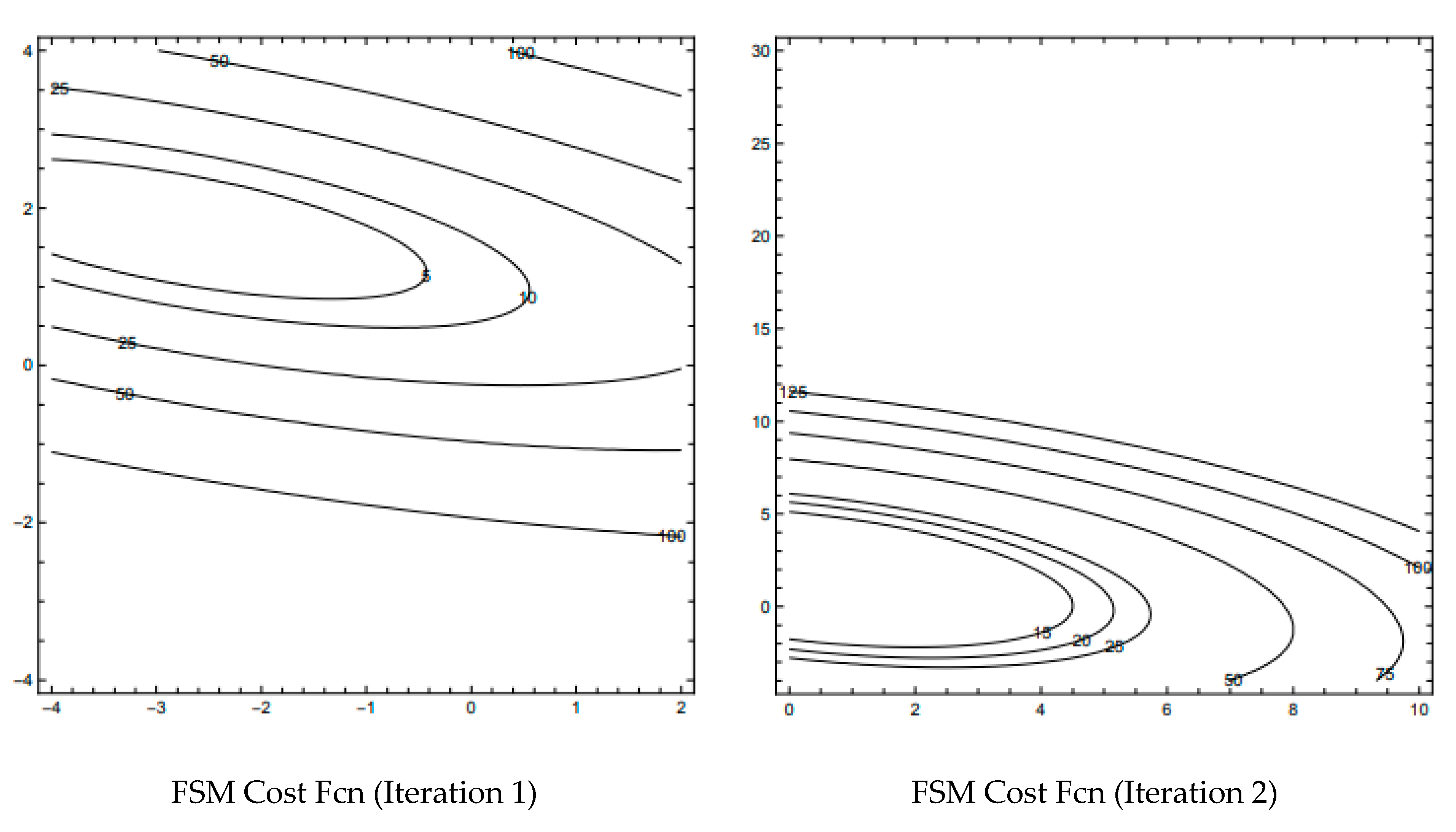
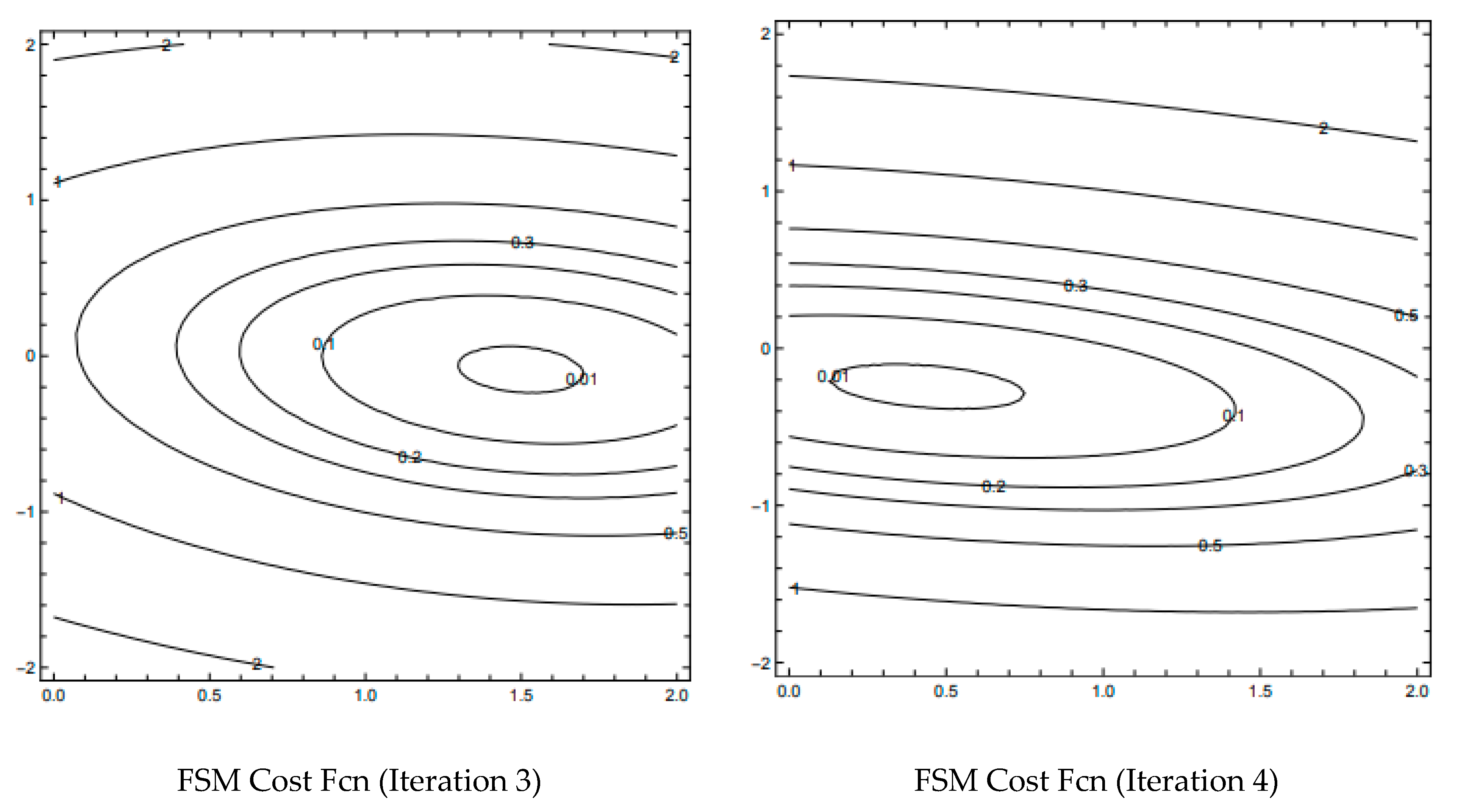
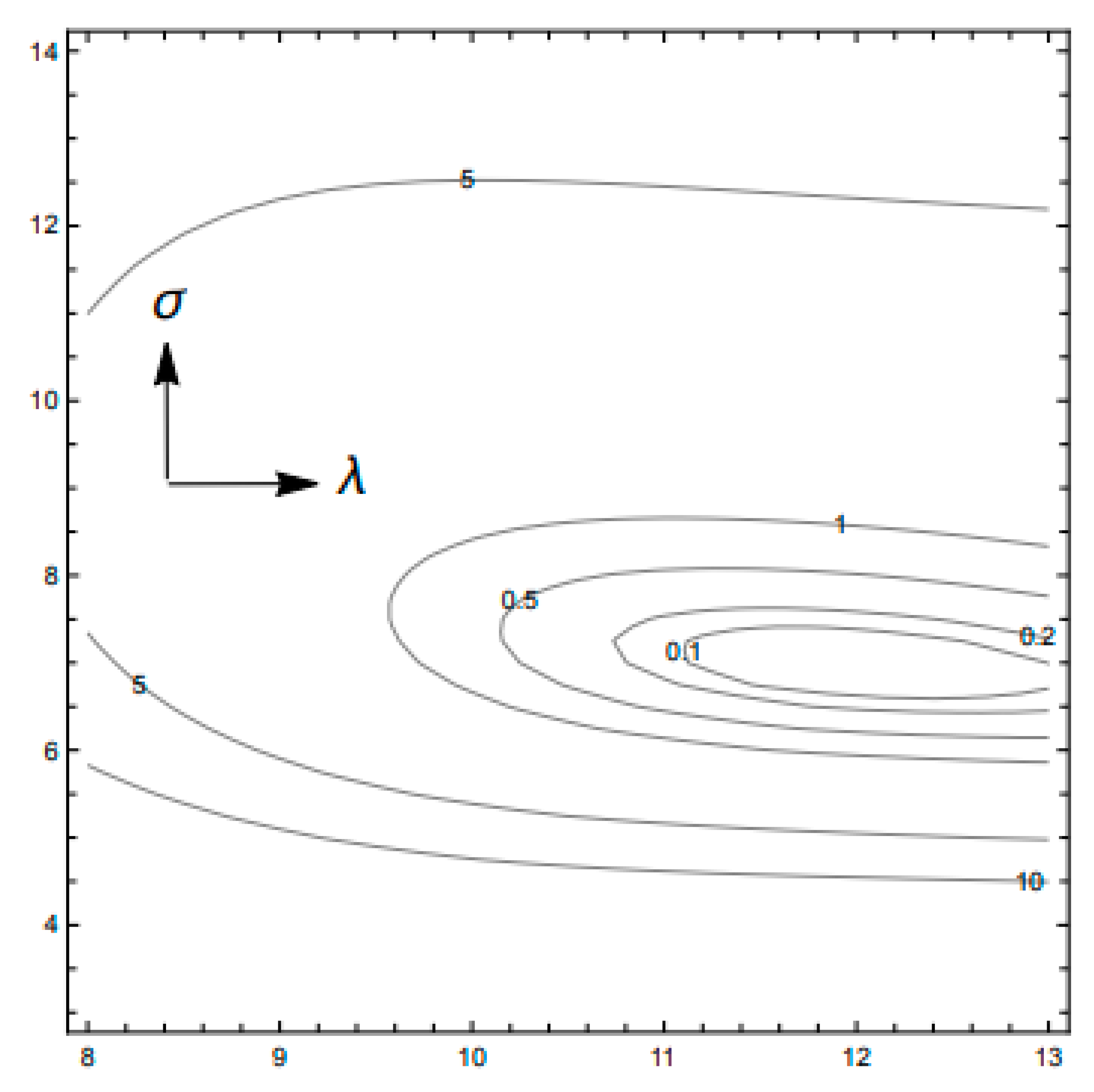
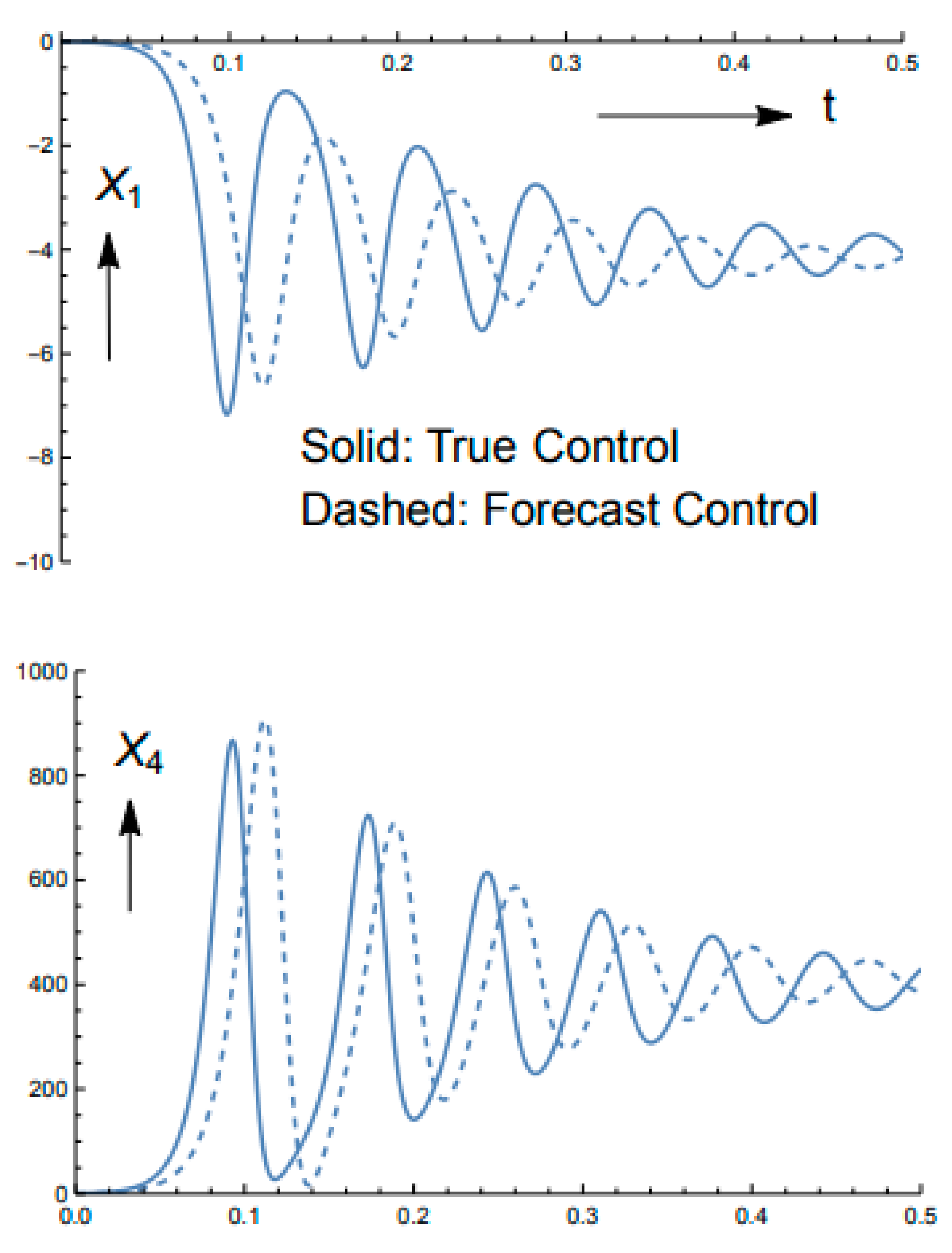
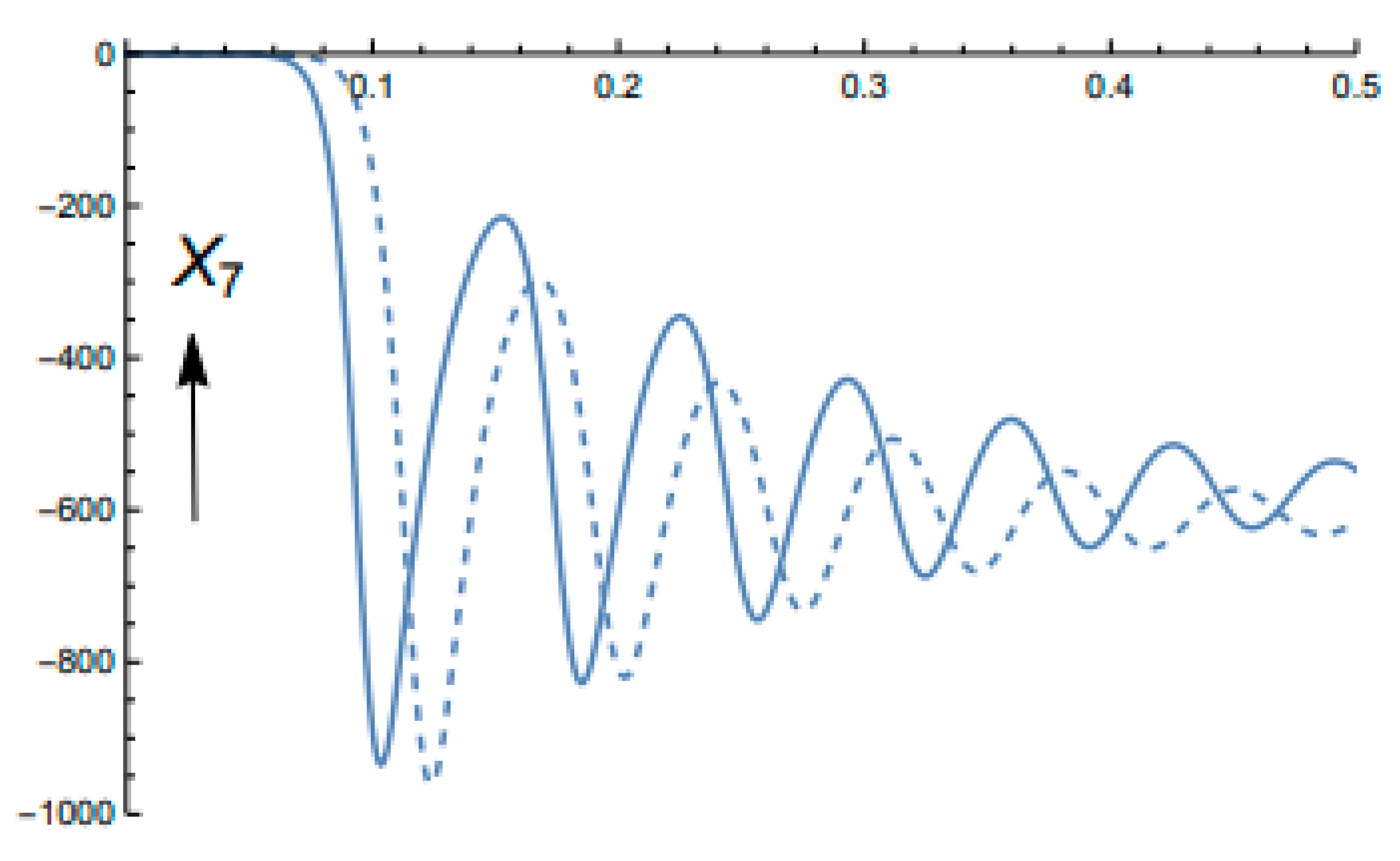

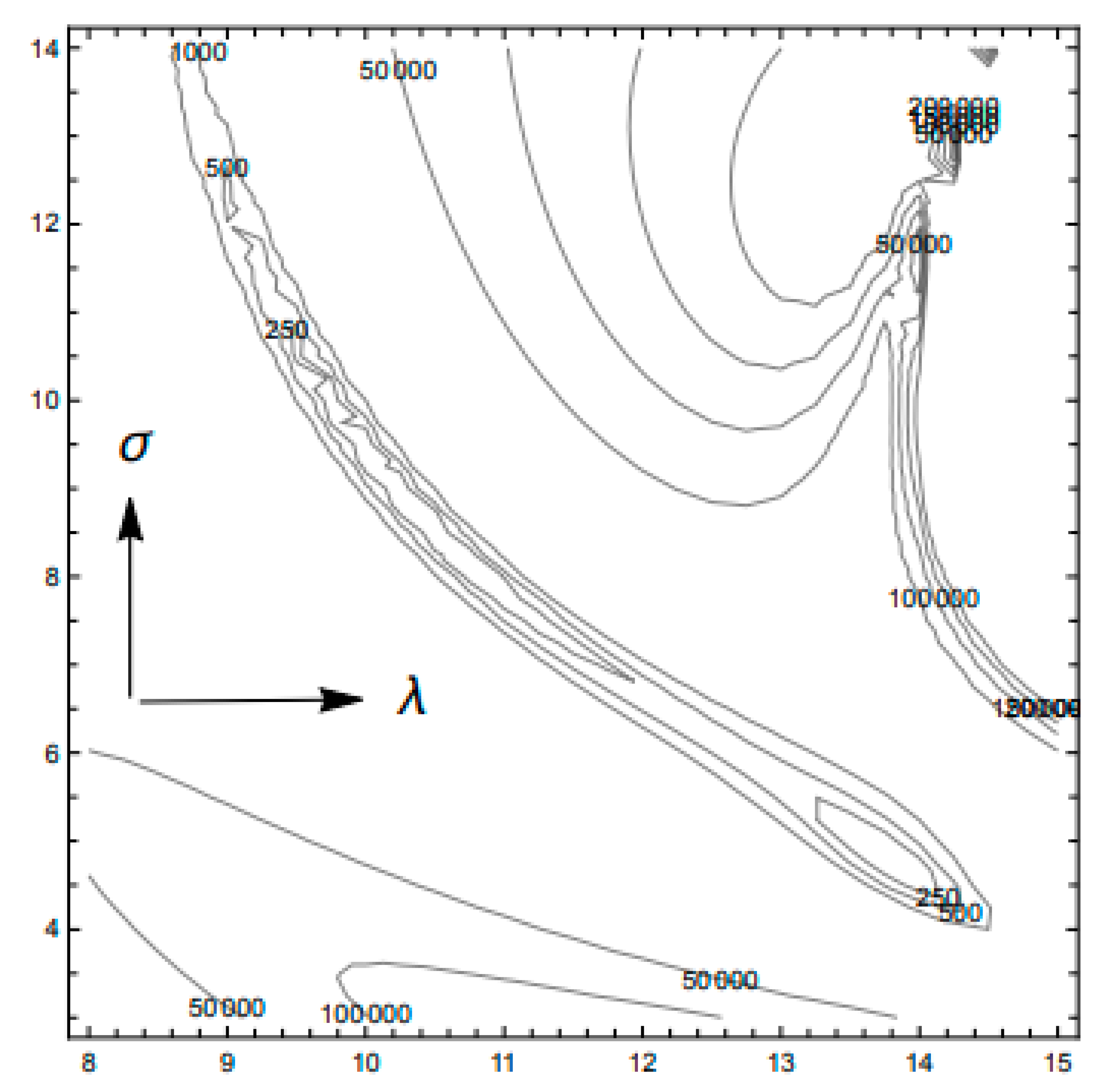

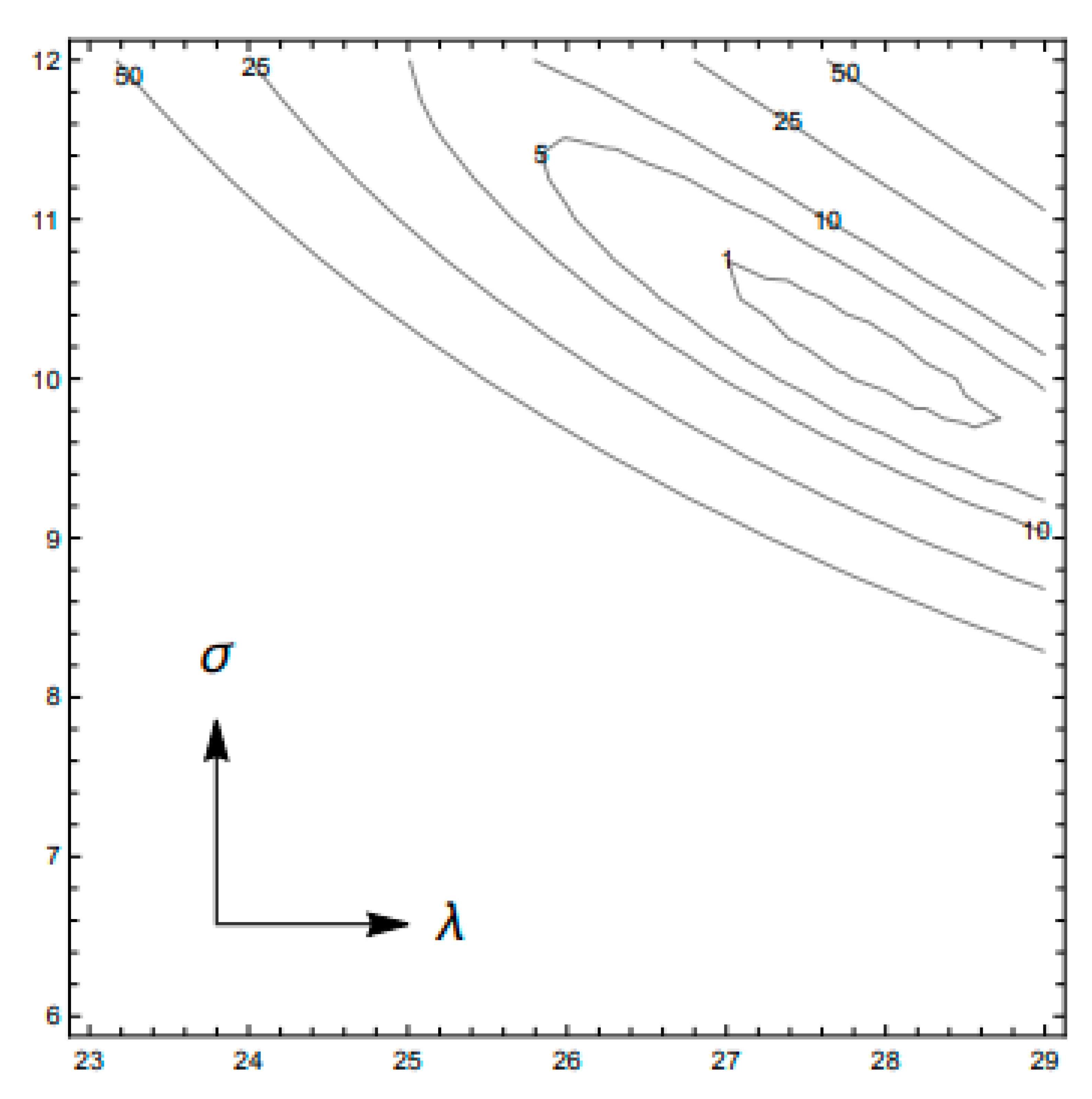
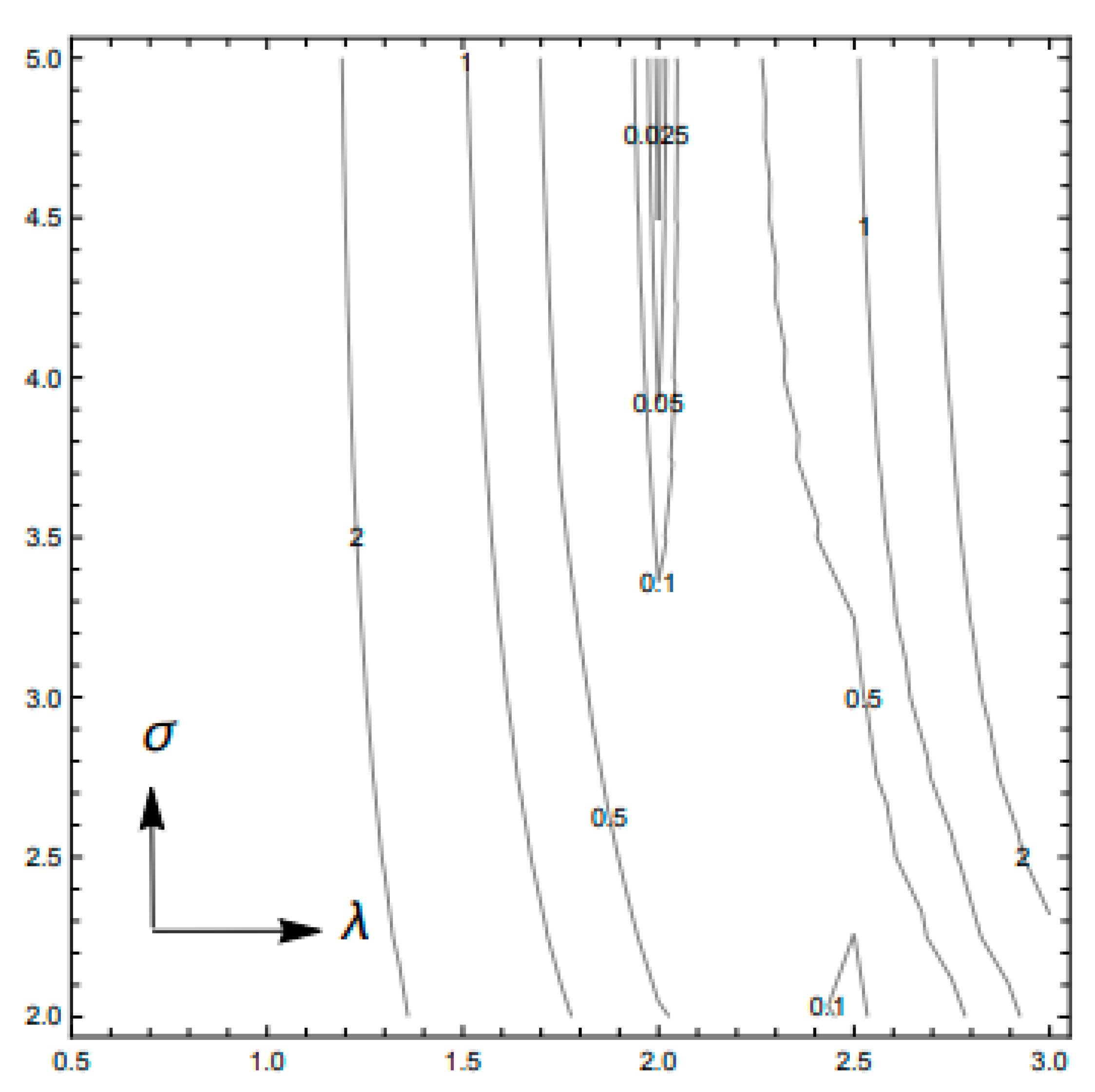
| Saltzman | Lorenz |
|---|---|
| , | , |
| i | Cost Fcn | ||||||
|---|---|---|---|---|---|---|---|
| 0 | — | — | 12.600 | 4.000 | −1.987 | −5.831 | 18.957 |
| 1 | −2.787 | 1.735 | 9.813 | 5.735 | −2.245 | −1.456 | 3.580 |
| 2 | 0.252 | 1.579 | 10.065 | 7.309 | −1.048 | 0.113 | 0.555 |
| 3 | 1.499 | −0.087 | 11.559 | 7.213 | −0.210 | 0.172 | 0.037 |
| 4 | 0.439 | −0.243 | 11.997 | 6.969 | −0.002 | −0.005 |
| i | Cost Fcn | ||||||
|---|---|---|---|---|---|---|---|
| 0 | — | — | 12.600 | 4.000 | 191.857 | 63.905 | |
| 1 | 2.397 | −0.102 | 15.000 | 3.900 | −52.480 | 58.896 | |
| 2 | −1.054 | 0.638 | 13.943 | 4.536 | 4.627 | 10.944 | |
| 3 | −0.135 | 0.218 | 13.807 | 4.754 | 0.750 | 0.742 | |
| 4 | −0.006 | 0.018 | 13.801 | 4.771 | 0.006 | 0.004 |
| i | Cost Fcn | ||||||
|---|---|---|---|---|---|---|---|
| 0 | — | — | 29.000 | 8.000 | −5.732 | 10.712 | 73.801 |
| 1 | −4.419 | 3.130 | 24.581 | 11.130 | 0.773 | 7.839 | 31.024 |
| 2 | 3.003 | −0.815 | 27.584 | 10.315 | 0.294 | 0.258 | |
| 3 | 0.251 | −0.136 | 27.835 | 10.178 | −0.008 | 0.011 | |
| 4 | 0.000 | 0.002 | 27.835 | 10.180 | 9 |
| i | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | — | — | 2.500 | 3.000 | 0.076 | −0.638 | 0.138 | −0.599 |
| 1 | −0.412 | 0.824 | 2.087 | 3.824 | −0.032 | 0.056 | −0.034 | 0.051 |
| 2 | 0.004 | 0.334 | 2.091 | 4.158 | −0.002 | 0.006 | −0.002 | 0.005 |
| 3 | 0.002 | 0.009 | 2.093 | 4.167 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewis, J.M.; Lakshmivarahan, S. Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method. Atmosphere 2022, 13, 1647. https://doi.org/10.3390/atmos13101647
Lewis JM, Lakshmivarahan S. Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method. Atmosphere. 2022; 13(10):1647. https://doi.org/10.3390/atmos13101647
Chicago/Turabian StyleLewis, John M., and Sivaramakrishnan Lakshmivarahan. 2022. "Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method" Atmosphere 13, no. 10: 1647. https://doi.org/10.3390/atmos13101647
APA StyleLewis, J. M., & Lakshmivarahan, S. (2022). Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method. Atmosphere, 13(10), 1647. https://doi.org/10.3390/atmos13101647








