Abstract
Wildfires are well known as annual disasters in Indonesia. More than 3 million ha was burned in the last 5 years. During an extreme event such as in 2019, carbon emissions can cause smog disasters in neighboring countries such as Malaysia and Singapore. Though difficult to predict, many hotspots that appear can be used to indicate the emergence of large-scale wildfires. The objective of this research is to provide suggestions in terms of used variables when analyzing fire event indication (hotspot), fire event scale (burned area), and fire event impact (carbon emissions). This research provides a spatio-temporal analysis and dependency between drought (precipitation and its derivative variables) and fire indicators (hotspot, burned area, and carbon emission). This research provides the different characteristics of each indicator when used to find joint patterns of burned areas, hotspots, and carbon emissions. Overall, using potential evapotranspiration and precipitation to calculate climate water balance gives great results in all analysis. Precipitation anomalies give the best joint spatial pattern to describe wildfire events in the area with monsoonal rainfall. Meanwhile, precipitation gives better results by capturing more wildfire events in a temporal pattern, even on robust analysis.
1. Introduction
Wildfires are annual disasters that occur on Indonesian territory from pre-independence to post-independence times with various scales of events [1]. Areas where wildfires often occurred in Indonesia were Riau, Jambi, North Sumatra, South Sumatra, West Kalimantan, East Kalimantan, and South Kalimantan [2,3,4]. The wildfires usually occur during each respective dry season from August to October and during its transitional period of the dry season [5]. For the last 40 years, severe wildfires occurred in 1982, 1983, 1991, 1994, 1997, 1998, 2006, 2015, and 2019 [1].
The World Bank Group released a report that the losses experienced by Indonesia due to wildfires in 2015 were more than 16 billion USD, or equivalent to 221 trillion Rupiah [6]. South Sumatra, Kalimantan, Papua, Riau, and Jambi were included in the areas with the highest burned area from June to October 2015, with accumulation reaching 93% of the total land damage [7]. A climate anomaly caused by the 2015 forest fires, namely the El Nino Southern Oscillation (ENSO) phenomenon in the Pacific Ocean, caused Indonesia’s drought [8]. One of the most dangerous impacts of wildfire disasters is carbon emissions. In total, 0.35–0.6 Pg C was estimated to be released into the atmosphere from 2015’s event [9], which significantly affected global warming [10].
The climate is one of the natural factors that can cause wildfires. The climatic conditions (temperature, humidity, rainfall, and wind speed) can affect the level of dryness of surface fuels, the amount of oxygen, and the speed of fire spread [11]. Wildfires can be analyzed using several indicators such as the area burned as the primary measurement of the fires event scale, hotspots mainly used as fire detection [12,13,14], and produced carbon emissions affecting global greenhouse gases [10,15]. A combined analysis of wildfires with drought indicators will help to understand their relationship. Many researchers have analyzed wildfire patterns in Indonesia using various climate indicators and methods, such as precipitation and its anomaly [3,4,8,16,17], as well as dry spells [5,8]. However, there is still no research comparing many indicators in one go. Besides precipitation and its derived indicators, potential evapotranspiration is an essential indicator of droughts in terms of atmospheric conditions.
The potential evapotranspiration denotes the atmospheric potential to receive water and regulates its water stress conditions [18]. Thus, it is widely used in drought analysis and monitoring, especially regarding the extreme climate impacts of global warming [19,20,21,22]. There are many evapotranspiration-based indicators to represent the drought condition, such as the Daily Evapotranspiration Deficit Index (DEDI) [23], Palmer Drought Severity Index [24], Reconnaissance Drought Index (RDI) [25], Standardized Precipitation Evapotranspiration Index (SPEI) [25] and the Evaporative Drought Index (EDI) [26], the Drought Severity Index [27], and so on. However, there is still a lack of research that utilizes evapotranspiration to analyze wildfire events. Even more, not all those indexes are effective, depending on the analyzed region. Previous research shows that the SPEI analysis was ineffective compared to other analyzed drought indexes in Antalya [28]. In order to get a better understanding of evapotranspiration’s impact on wildfire, evapotranspiration in this research is used as a standalone variable. The result will be compared with results from precipitation–evapotranspiration and precipitation and analyzed derived precipitation variables.
The objective of this research is to identify the relationship as well as to compare various paired drought–wildfire indicators. Furthermore, we also explained the different characteristics of each indicator when used to find the typical pattern of burned areas, hotspots, and carbon emissions. The drought indicators are the potential evapotranspiration, total precipitation, number of days without rain (dry spell), and the precipitation anomaly. In order to get a joint pattern between the wildfire and drought indicators, this research uses the empirical orthogonal function (EOF). The EOF is a method for determining the dominant data patterns that evolve in space and time. The EOF is said to be a technique to simplify a data set by reducing its dimensions to a smaller size [4,5,17].
In this research, the singular value decomposition (SVD)-based EOF method was used to reduce the composite matrix of drought indicator data and the impact of wildfires. This research uses maximal correlation based on the alternating conditional expectation (ACE) to get the dependency [29], Pearson correlation to get the linear correlation [30], Spearman correlation to get the monotonic correlation [31], as well as Chatterjee’s xi correlation to get the nonlinear correlation [32]. This research provides different characteristics for each climate indicator when paired with various wildfire indicators. Moreover, this research provides additional information about how evapotranspiration behaves when used as a standalone indicator and paired with precipitation to analyze wildfire events.
2. Materials and Methods
Wildfire is defined as a fire event, both natural and man-made, which is characterized by the free spread of fire. Efforts to control wildfires are all efforts that include prevention, suppression, and post-event actions [33]. Control will be effective if the factors that affect the area of the wildfires are known [34]. Wildfire indicator research can assist in the decision-making, management, and prevention of the appropriate incidents [35]. This research uses burned areas, carbon emissions, and hotspots as wildfire indicators. We use monthly data from January 1997 to December 2020 with a spatial resolution of 0.25° × 0.25°. The analyzed region is the whole area of Indonesia, which is from 6° N to 10° S, as well as 95° E–141° E.
2.1. Variable Definition
The burned area describes how large an area burnt during a fire event is in hectares (ha). Meanwhile, carbon emissions show the fire emissions measured in g C m−2. Both the burned area and carbon emissions data are obtained from the Global Fire Emissions Database, Version 4 (GFED4), described in [36] for the burned area and [37] for carbon emissions. Hotspots are indicators of wildfires that detect a location with a relatively high temperature compared to its surroundings. The emergence of hotspots is an early indication of fire events in location and time [38]. Used monthly hotspot data are derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) sensors of the Terra and Aqua Satellites with a spatial resolution of 0.25° × 0.25°, with a confidence level > 80% according to the standard data of the forest fire indicator [39].
This research uses total precipitation, precipitation anomaly, dry spell, and potential evapotranspiration as drought indicators. Total precipitation and precipitation anomaly are derived from ERA5 monthly averaged data on single levels produced by ECMWF [40]. Meanwhile, dry spell data are derived from ERA5-and hourly data and converted into daily data [41]. Dry spell data count the days without rain with a threshold of 1mm daily precipitation. Meanwhile, the potential evapotranspiration is calculated using a formula described in [42,43].
with:
- : Surface nett radiation [MJ m−2 day−1];
- : Mean daily air temperature at 2 m height [;
- : Dewpoint temperature [;
- : Maximum daily air temperature at 2 m height [;
- : Minimum daily air temperature at 2 m height [;
- : Wind speed at 2 m height [m s−1];
- : Height of location [m];
- : Soil heat flux density [MJ m−2 day−1].
All the necessary data in Equations (1)–(6) are obtained from ERA5 monthly averaged data on single levels produced by ECMWF [40]. Furthermore, we also declare a new variable to represent the deviation between precipitation and evapotranspiration following the equation below:
A list of the names of used indicators for wildfire as well as drought indicators are:
- -
- : Deviation between total precipitation & potential evapotranspiration [mm];
- -
- : Potential evapotranspiration [mm];
- -
- : Dry spell (number of days without rain) [days];
- -
- : Total precipitation [mm];
- -
- : Negative precipitation anomaly [mm];
- -
- : Burned area [ha];
- -
- : Carbon emissions [g C m−2];
- -
- : Number of hotspots [unit hotspot].
2.2. Empirical Orthogonal Function Based on Singular Value Decomposition
The joint pattern between wildfire and drought indicators is obtained using the EOF based on SVD. The denote matrix and represent forest fire and drought conditions, respectively. The rows of both matrices represent the spatial dimension, while columns represents the time (temporal) dimension. Defined matrix . The singular value decomposition of is
and are orthogonal matrices that represent the temporal patterns of matrices and , respectively [44]. Meanwhile, is a diagonal matrix which contains the singular value of the joint pattern. The spatial pattern of matrices and is obtained using equation as well as [45]. Meanwhile, the SCF value that represents the contribution of mode-i to the whole data is obtained using the equation below:
2.3. Dependency and Correlation Analysis
Dependency analysis in this research is measured using maximal correlation based on the ACE algorithm [46]. This algorithm calculates optimal transformations by a fast boxcar averaging of rank-ordered data. Both and is transformed using the ACE algorithm, resulting in and . The dependency is measured using the equation described in [24]:
Correlation is one of the most important indicators in the modelling problem. Therefore, information about the type of correlation between paired indicators are important. This research uses three types of correlation, which are linear, monotonic, and nonlinear. Linear correlation between and is calculated using the Pearson correlation [30] following the equation below:
Meanwhile, the monotonic correlation between and is calculated using the Spearman correlation [31] following the equation below:
and are the standard deviations of rank and rank . Monotonicity is “less restrictive” than that of a linear relationship. The nonlinear correlation is calculated using the equation below, as described in [32]:
First, rearrange the data as , so that . is the rank of which is the number of such that . Meanwhile, is the number of such that [33]. Dependency and both correlation methods will be used to measures relationships between wildfire with drought indicators in all data, joint spatial pattern data, as well as joint temporal pattern data.
3. Results
3.1. Burned Area
Burned area was the primary indicator to reflect the scale of the wildfire event. Figure 1 shows a joint spatial pattern between the burned area () and each used drought indicator (). The analysis is focused on seven different locations across the Indonesia region, which are Northern Sumatra (Loc 1), Southern Sumatra (Loc 2), West Kalimantan province (Loc 3), Central and South Kalimantan province (Loc 4), East Kalimantan province (Loc 5), East Nusa Tenggara (Loc 6), and Merauke (Loc 7). Since the first mode SCF of all indicators is already more than 99%, the analysis is focused on how well each paired variable describes all wildfire events using only the first mode. Therefore, we can summarize their performance in a robust analysis, such as describing wildfire events in areas with multiple precipitation patterns. Each indicator shows noticeable differences in describing the drought conditions in Indonesia (Figure 1). In order to make an easier comparison between each drought indicator, we removed the units of the drought indicators. Therefore, the value is in the range of [0, 1] and the value represents the severity of the drought season according to each indicator.
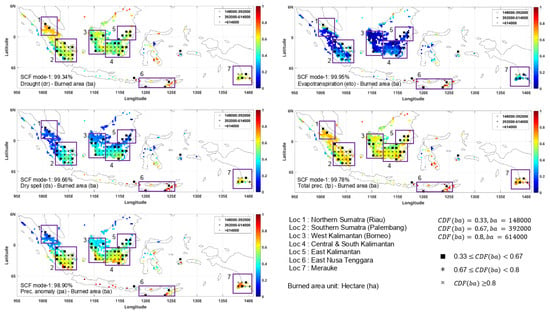
Figure 1.
Joint spatial pattern of burned area paired with drought indicators.
In plain view, tp has the best result when describing the location of ba from all indicators (Figure 1). tp shows a severe drought indication in most of the high numbers of ba. However, it is hard to differentiate and determine which location can lead to higher numbers of ba since most of those analyzed show a similar severity according to tp (around 0.6). Meanwhile, pa gives an apparent differentiation from the tp joint spatial pattern, especially around Loc 1. A high number of ba not only occurred in areas with a severity value of more than 0.6 but also in areas with a severity value close to 0. This behavior indicates that the ba in Loc 1 happened when other Indonesian regions experienced a wet season. A similar pattern with pa was obtained from ds and eto but with a less noticeable separation. Both the ds and eto spatial pattern seem to be dominated by drought conditions in Loc 6 and 7, which have less precipitation than other locations.
Meanwhile, dr, which carried both tp and eto characteristics, resulted in a similar pattern with tp but with some apparent differentiation. dr gives a less severity value in Loc 2, 3, 4, 5, and 7 compared to Loc 1 and 6. This behavior indicates that Loc 1 and 6 have noticeable differences in land characteristics and climate conditions than other locations.
Regarding the first temporal pattern, eto has the best representation of all wildfire events from 1997 to 2020, with an average error of only 0.48. Even though pa has the best spatial pattern, it has the worst temporal pattern with an average error value of 7.2%. This average error value is related to the SCF value of each indicator. The higher the SCF value of the paired indicators, the higher the number of ba that the first mode can represent. Therefore, it can result in a smaller average error value. The negative value represents that the first mode underestimates the actual condition, while the positive value represents overestimating the natural condition. The highest error is obtained in the year 1997 and 1998. The fires event anomaly occurred in 1998, where a high number of ba occurred in the early years, while most of the events occurred at half of the end of each year. Therefore, many drought indicators failed to capture the 1998 fires event except tp and eto. Most temporal patterns also have a similar behavior, with a high negative error followed by a high positive error. The consistent negative error shows that the ba occurred and spread exponentially during the drought. Meanwhile, the following high positive error shows that there are extinguishing attempts to reduce the ba. Since drought indicators rarely increased exponentially and were not affected by local human behavior, the temporal pattern cannot represent the number of ba perfectly.
3.2. Carbon Emissions
Carbon emission is an indicator that can describe the impact of a wildfire event on the burned area and the surrounding area. Therefore, it is expected to have a more marked location than the burned area. The spatial pattern of all drought indicators in Figure 2 is similar to that in Figure 1. Therefore, the analysis will be focused on how well the separation of the spatial pattern value describes the carbon emission (ce) pattern.
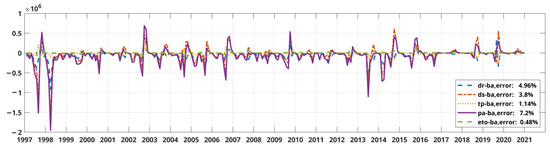
Figure 2.
Difference between raw data and joint temporal pattern of burned area.
The best separation of the spatial pattern value was obtained from the ds indicator where most of the carbon emissions in the range of 3000–5000 g C m−2 occurred on the ds area with a severity value of more than 0.4, except on Loc 7 (Figure 3). On Loc 1–5, the expected behavior appears where more carbon emissions are spotted in the area without a marked ba spatial pattern. However, the opposite behavior occurred on Loc 6 and 7, where the number of marked locations of ce is less than that in the ba. Moreover, no marked ce on Loc 6 shows that the fire event produced significantly less ce. This result indicates that the burned area occurred on non-dry land and vegetation, such as grass or a tropical forest. Unlike the wildfire event on Loc 2–4, where most of the fires occurred on peat land, it produced a massive amount of ce.
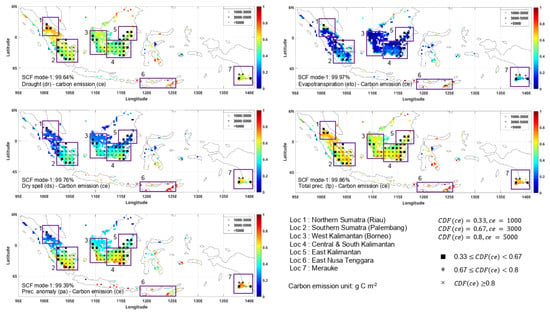
Figure 3.
Joint spatial pattern of carbon emissions paired with drought indicators.
The joint temporal pattern of each drought indicator with ce has a similar behavior in describing carbon emission, where the slightest error obtained is from eto, and the most error is obtained from pa (Figure 4). Compared to Figure 2, the difference occurred on dr and ds. The dr temporal pattern in Figure 4 has less errors than ds, which is opposite to Figure 2. Moreover, the most errors did not occur in 1997 and 1998, but in 2013. All temporal patterns failed to capture the high ce in the 2013 fires event. This behavior indicates that the fire event in 2013 produced a significantly high amount of ce for a similar amount of burned area in other years. A similar behavior of high negative errors also occurred in the ce temporal pattern. However, it is not always followed by a high number of errors. Even more, most of the errors are in the negative value range. This behavior shows that the extinguishing attempt cannot always significantly reduce produced ce from the fire event. These results indicate that prevention is more critical than extinguishing attempts. Even though the ba can be reduced significantly, the produced ce is much harder to handle since it is more related to tp and eto (less value of errors).
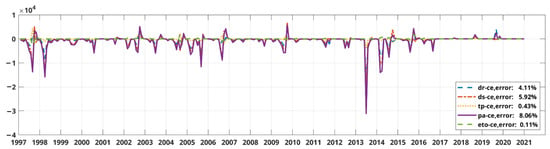
Figure 4.
Difference between raw data and joint temporal pattern of carbon emissions.
3.3. Hotspot
A Hotspot is an indicator that can be used for the early detection of a fire event. However, it cannot be used directly to predict the scale of the fire event since not all hotspots transform into extensive burning. Some of the hotspots result in small-scale fires that go out quickly or even disappear due to the wetness of the area where the hotspots appear. Therefore, the spatial pattern is expected to have more marked hotspots than other variables.
Figure 5 shows that the spatial pattern of dr and tp can describe hotspot occurrence better than the other three indicators. dr and tp have more hotspot markers on Loc 1 than the other three indicators. However, ds and pa describe better which hotspot leads to the high burned area or not. Using ds and pa, we can ignore the hotspot that occurred in areas with less severe drought conditions (blue color). As expected, more square markers occurred, representing the hotspot number of 200–400, especially on Loc 1 and 3. In reverse, there are fewer marked hotspots on Loc 5, 6, and 7. This result indicates that the burned areas on Loc 5, 6, and 7 are mainly caused by unnatural deforestation. Therefore, it is straight up, resulting in a large area with a high temperature detected as a burned area instead of a hotspot.
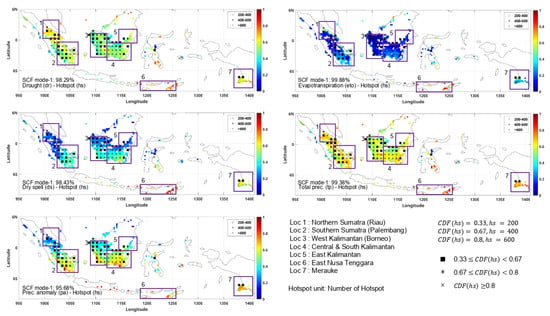
Figure 5.
Joint spatial pattern of hotspots paired with drought indicators.
The joint temporal pattern behavior of all drought indicators in Figure 6 is similar to Figure 4. The maximum average error is obtained from pa with 8.2%, while the minimum one is obtained from eto with 0.22%. However, the error value fluctuates more than the other two fire indicators (ba and ce). The most error was obtained in 2013 and 2014. This result indicates that multiple factors influence hs occurrence and cannot be described by only one dominant mode in robust analysis. The example shows the resulting high negative error early to mid-year (Figure 6). Compared to ba and ce, hs has a much higher error in early to mid-year events. This behavior shows that hotspots occurred early to mid-year, while the dominant precipitation pattern is still in the wet season. Therefore, it cannot be captured by the joint pattern.
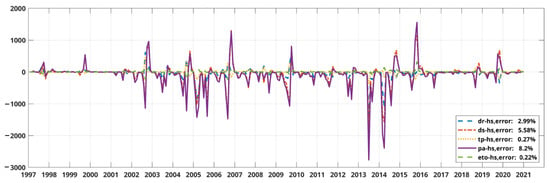
Figure 6.
Difference between raw data and joint temporal pattern of hotspots.
3.4. Dependency and Correlation Measurement
Figure 2, Figure 4, and Figure 6 show that a wildfire in Indonesia occurs almost every year. Even though ba and hs can be reduced by extinguishing action, ce cannot be reduced quickly. Predicting and anticipating the fire event is much more critical than managing the event’s impact. Therefore, dependency and correlation analysis help researchers understand each indicator’s behavior. Dependency and correlation are essential to model development. Thus, the researcher can use the correct method to develop the prediction model. This research measures the raw data and the dependency and correlation between the data obtained from the joint spatial pattern and the joint temporal pattern. By measuring dependency and correlation from the joint pattern, we can determine whether the resulting pattern is dominated by one of the indicators. The results of the measurement are shown in Table 1.

Table 1.
Dependency and correlation of paired wildfires with drought indicator.
Using the maximum correlation based on the ACE algorithm gives a dependency value of 1 (close to 1). This result shows that all three wildfire indicators depend on all of the analyzed drought conditions. Each drought indicator can be used to model the wildfire indicators. In raw data measurement, pa has the highest average linear correlation with wildfire indicators, followed by dr, tp, ds, and eto. ds has the highest average correlation in a nonlinear correlation, followed by pa, tp, eto, and dr. Meanwhile, ba consistently has the highest linear correlation compared to ce and hs when paired with drought indicators. Wildfire indicators consistently have the highest nonlinear correlation is hs up to 0.775 when paired with ds.
The story of measured data obtained from the joint spatial and temporal pattern differs from the raw data analysis. Using the joint spatial pattern, only ds and pa has an average of more than 0.25 for either a linear or nonlinear correlation. The correlations of wildfire with dr and tp are reduced significantly compared to the raw data. The hs correlation is significantly reduced for both linear and nonlinear variables across all of the paired variables. This result indicates that the analyzed region needs to be separated to get a better spatial pattern, especially when analyzing hs. The exciting result is obtained when ba or ce is paired with ds or pa. The joint spatial pattern can increase the linear correlation while reducing the nonlinear correlation, except for ds and hs. This behavior also occurs when measuring the joint temporal pattern.
In the analysis of the joint temporal pattern, all of the paired show a give similar behavior where the linear correlation value increases and the nonlinear correlation value decreases. This increase is significant with up to double the correlation value of the raw data. This behavior is essential since it can reduce the complexity of the method used when modelling the paired indicators. Therefore, the researcher can use more variables to get more accurate results without significantly increasing the analysis’s complexity.
3.5. Distribution Analysis of Climate Indicators
The previous section shows that some of the analyzed climate indicators show a unique behavior while responding to the wildfire indicators. Even though tp and eto can give a more accurate joint pattern (less error in the temporal pattern), both indicators have less correlation in dependency analysis than the ds indicator. Therefore, it is hard to determine which indicator should be used in the modelling. The analysis in this section explains the difference between dr, tp, eto, and ds. We excluded pa from the analysis since pa shows a similar behavior in both joint spatial and temporal patterns and in the majority of dependency analyses. We also give a scatter plot between climate indicators and hotspots to get a general threshold from each indicator that caused a high number of hs. The result is shown in Figure 7. The analysis is only focused on hs since it is the essential wildfire indicator as an early warning to prevent a big-scale wildfire event.
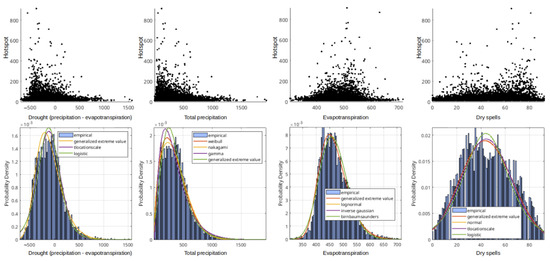
Figure 7.
Scatter plot between hotspot and climate indicators (drought, total precipitation, evapotranspirartion, and dry spells) as well as climate indicators distribution.
The analysis is only carried out on data with a hotspot value of more than 10. This filter is applied to remove data points with 0 hotspots or a small number of the hotspot. Figure 7 shows that each indicator has a unique scatter plot paired with hs and a unique distribution. dr has a distribution shape that is very skewed to the left, while eto and ds have a more centered distribution shape. All of them can be fitted well using generalized extreme value distribution. However, the dry spells variable is the most challenging indicator to be fitted using one distribution in robust analysis. Visually, there are two peaks of the ds value around 30–40 and 60. This result indicates two different characteristics of ds in the data. These two characteristic can be seen clearly in the scatter plot of ds–hs.
There are two groups of a high number of hs in the scatter plot of ds–hs. The first one has a ds value of around 20–40, while the second one has a ds value of around 60–80. This result shows that ds cannot be used easily in the robust analysis without separating the observed area. Both groups referred to two rainfall patterns in Indonesia, which are the equatorial and monsoonal patterns. Equatorial patterns produce two dry seasons in one year with a duration of about 2–3 months, while monsoonal patterns produce one dry season annually with a duration of around 6 months. This behavior did not appear in the other indicators (Figure 7). Eto can not be used efficiently to get a certain threshold for hotspot occurrence. Even though most of the hotspots occur when the eto value is in the range of 400–600, it is more centered, which does not represent extreme drought conditions.
When used to represent extreme drought conditions, dr and eto have a better distribution shape than the other two. The high number of hotspots occurs when 3 months of precipitation is only around 500–600 mm. The number of hs is even higher when the top value is lower than that threshold. However, this threshold cannot generally represent the drought conditions across Indonesian regions. Besides the two precipitation patterns mentioned before, multiple local conditions can affect drought in each region of Indonesia. The downside of using tp in the distribution analysis is that it is located on the left side of the distribution, where the top value is close to 0. The left side of the distribution is too steep, so it is harder to fit in a parametric distribution analysis. This downside is dissipated when using the dr indicators. Although the distribution is not as extreme as tp, dr still gives a threshold value for a high number of hotspots, around 250 mm in 3 months of accumulation.
4. Discussion
Section 3.1, Section 3.2 and Section 3.3 shows that wildfires in Indonesia are hard to analyze robustly. These results represent that wildfire events in Indonesia are influenced by many factors [47,48]. There are many variations between each focused region in terms of rain season characteristics and the type of land where the fire event occurred [5]. Each focused region has a different threshold for the hotspot occurrence, resulting in burned areas and carbon emissions. The same drought condition can lead to different impacts for all three fire indicators [8]. Therefore, using one standardized measurement for all of the areas in Indonesia can lead to misleading modelling results.
Figure 1, Figure 3 and Figure 5 show that ds and eto will give less accurate results when used to analyze wildfires in areas with multiple ranges of drought conditions, such as in Loc 6 and Loc 4. Since both share similar patterns with pa, all three indicators will give less accurate results when used to analyze fire indicators in areas with multiple precipitation patterns, such as in Loc 1 and 2. Areas with a less than 0.3 value of severity in all pa spatial patterns are areas that have a low rainfall season [49]. Meanwhile, the rainfall season in an area with a higher than 0.3 value of severity is heavily influenced by monsoonal wind [50]. However, it did not mean pa, ds, or eto are not valuable for robust wildfire analysis. In reverse, they are handy to separate wildfire events that occur in different drought seasons, such as in areas with equatorial and monsoonal rainfall [8].
tp is well known as the primary indicator reflecting Indonesia’s dry season. Many indicators are derived from tp that can be used to measure multiple impacts of extreme rain and dry conditions. Pairing tp with wildfire indicators will result in principal components that can capture almost all wildfire events with a minimal error, regardless of the precipitation pattern of the analyzed area. This result is beneficial in early analysis, where we were not sure there were multiple wildfire patterns related to the precipitation patterns in the analyzed variable [5,8]. Since it is the primary indicator, it can be beneficial as an early warning measurement to predict hotspot occurrence in time series analysis [51]. Most of the marked hotspots appear when the severity of the drought condition (according to to tp) is more than 0.5, except on Loc 6 and 7.
By definition, dr carried characteristics of tp and eto. Therefore, using dr should give a middle result between using tp and eto. The result of using dr is quite promising. dr can capture all wildfire events while showing different precipitation characteristics between regions. The spatial pattern of dr shows that Loc 2, 3, 4, and 5 have a similar behavior in terms of drought severity that triggers large-scale wildfires event. The severity value of those four locations is lower than Loc 1, 6, and 7. This result shows that Loc 2, 3, 4, and 5 are more sensitive to wildfires [5,8]. The high sensitivity means that the probability of hotspot occurrence during the regular dry season is higher than that with a lower sensitivity [5,8]. This result is reinforced by the fact that wildfires in Loc 2, 3, 4, and 5 happened almost annually [3,4]. There is still a lack of research that utilizes potential evapotranspiration to analyze wildfires in Indonesia. Since it is much more complicated than other derived precipitation indicators, much work is still needed to test whether it is better than other climate indicators that are usually used.
4.1. 1997–1998 Wildfire Event Anomaly
One of the reasons why the error obtained in the temporal pattern is very high is that wildfires happened in 1997–1998 (Figure 2 and Figure 4). During 1997–1998, Southeast Asia suffered from a powerful El Nino impact from late 1997 to mid-1998 [52]. Many people in Southeast Asia started to consider the El Niño Southern Oscillation (ENSO) impact on wildfires in the context of the Indonesian fires of 1997 [53]. On East Kalimantan alone, 2.35 million ha of natural concession, 0.88 million ha of forest plantation, 0.38 million ha of estate crop, 0.44 million of total protected, and 1.16 million of undefined land use area were burned from 1997 to 1998 [54]. Of the 5.2 million burned area total, 0.8 million ha was primary forest, and 1.4 million ha was logged-over forest [55].
The reason analyzed drought indicators underestimate the scale of the events is that while the weather conditions that create drought and flammable forests are pretty natural, the factors that have turned those events into a disaster are man-made [53]. Some of the factors are the extent of logging which pre-disposes the forests to burn, the increasing numbers of transmigrants who often use fires carelessly to clear additional land when their allotted land area proves too tiny or too infertile to support the household, as well as the conflicts created by the imposition of these two newer kinds of land-use on the original population and its right to forest, which is reasserted through fire. [47,53] state that the total cost needed to mitigate the event of the fire by Indonesia was estimated to be 2.315 billion USD for tangible assets and 2.546 billion USD for intangible assets. The condition of the extinguisher program is even worse than in previous fires (1982–1983), since Indonesia suffered an economic crisis in July 1997 [56]. This financial crisis happened across Asian countries resulting in GDP dropping, unemployment rising, wages eroding, and prices increasing dramatically [57,58].
4.2. 2013 and 2014 Wildfire Event Anomaly
Figure 2, Figure 4 and Figure 6 show that almost all drought indicators consistently underestimated all of the analyzed wildfire indicators during 2013 and 2014. The reason is that both events only happened around Riau, while most (annual) wildfires did not happen on Riau. Moreover, Riau is the only focused region with an equatorial rainfall pattern, as mentioned before. One reason for the hotspot occurrence is deforestation, which increased dramatically in 2013 and 2014. There has been an increase in the number of hotspots and fire areas in Riau, with its peak in 2014 [59]. The number of hotspots in 2011 were (6849), 2012 (7826), 2013 (15,089), 2014 (22,588), and 2015 (7262). Then the amount of land burnt in Riau was in 2011 (74.50 ha), 2012 (1060 ha), 2013 (1077.50 ha), 2014 (1077.50 ha), and 2015 (6301.10 ha) [59].
Like in 1997–1998, weather conditions also created drought and flammable forests. During 2013’s peak event, the observed rainfall was 56.08 mm in one month, which is far below the normal amount (the average of 30 years is 145.06 mm) [60]. Meanwhile, Riau is suffering from the intertropical convergence zone (ICTZ) anomaly, resulting in an increase in dry spells for the area around Riau and Singapore [61]. Besides that, the Madden–Julian Oscillation (MJO) also influenced drought conditions in Riau. During the Riau dry season, MJO can lead to more severe drought conditions in phases 5–8 [62].
4.3. Potential Evapotranspiration in Wildfires Research
Evapotranspiration has become more frequent in scientific literature to refer to the integrated land surface latent heat flux since 2000 [63]. Using actual evapotranspiration and precipitation to calculate water balance would improve the ability to guide restoration toward wildfire structure and behavior [64]. The climatic water balance can be defined as the deviation between precipitation and potential evapotranspiration at a given site during a specific period [65]. In this research, it is called a dr indicator. Even though the uses of actual evapotranspiration can result in more accurate water balance conditions, there are no actual evapotranspiration data on Indonesia that is long enough to be used in robust research. However, previous research shows some advantages when using potential evapotranspiration [66]. Using potential evapotranspiration is valid for both humid and arid climates, producing reliable estimations of drought severity compared to precipitation and actual evapotranspiration [66].
The analysis in Section 3 shows that dr is not always the best indicator to represent wildfire indicators. However, dr performs well in all fundamental analyses, especially in Section 3.5. This result suggested that dr can be used as a primary indicator to represent wildfire events. The result will be improved if we homogenized the analyzed area, such as in other research. In southwest America, water balance and tp have the highest correlation (0.78 value of person correlation) with ba compared to various climate indicators [67]. When separating the forest and non-forest area, water balance has a higher correlation in forest ba than that precipitation. Meanwhile, precipitation has a higher correlation in a non-forest area [67]. For drier forest types, eto and water balance deficit were the most important variables explaining ba in the Pacific Northwest, USA [68].
Besides the left side distribution having steeped (Figure 7), the issue of using tp is that warm season precipitation often co-occurs with lightning-induced ignition events, inherently dampening the correlation between tp and ba [69]. Kane et al. found that water balance and actual evapotranspiration were the most influential environmental predictors for structure following a wildfire and burn severity [64]. In Australia, the climatic water balance sets the necessary boundary conditions for the critical aspects of fire regimes (e.g., the fire activity levels and return intervals, intensity range, and the season) [70]. While the previous research presented analyses on wildfires outside of Indonesia, they proved that potential evapotranspiration and water balance are useful in wildfire analysis. Moreover, water balance is essential in wildfires analysis since many researchers have proven that wildfires affect the post-fire water balance [71,72,73,74,75]. Therefore, we proposed to use evapotranspiration (potential/actual) and water balance for wildfire analysis rather than regular derived precipitation indicators in the future. Many observations need to be done to get the best result and can be used in the robust analysis.
5. Conclusions
Wildfires in Indonesia are well known as a very complex problem. Analysis in this research shows that each paired wildfire and drought indicator has different characteristics and behavior in response to each other. From the analysis, we can conclude that the burned area variable performs better in describing the wildfires event. However, the downside of using a hotspot is not significant. Since the availability of hotspot data is much faster, the hotspot can be used as an excellent indicator to describe ongoing wildfire events or even predict the upcoming event. Total precipitation is the best indicator for capturing wildfire events as a temporal pattern. Meanwhile, the dry spell has a better performance in separating areas with similar spatial characteristics, such as what happened in Riau and South Sumatra. However, dry spells become the second worst indicator to describe temporal characteristics.
From the analysis, we can conclude that wildfire and drought indicators did not have a significant linear correlation in robust analysis. Paired variables consistently have a higher monotonic and nonlinear correlation. Therefore, we suggest using a modelling method based on monotonic and nonlinear correlation. Analyzing the spatial pattern often decreases the linear correlation between paired variables, except when using dry spells and precipitation anomalies. This result shows that each wildfire region has different spatial characteristics and needs to be classified to get a higher correlation. When classified, the linear correlation increases significantly, such as when calculating the temporal correlation.
In this research, evapotranspiration gives some exciting results that can become the best indicator in all analyses when used as the climate water balance with precipitation. Even though it never becomes the best indicator in all analyses, they perform well in spatial, temporal, and correlation analysis. Moreover, it dominates other indicators in distribution analysis. When used as a standalone indicator, evapotranspiration gives a unique spatial and temporal pattern compared to other analyzed indicators. We conclude that climate water balance using potential evapotranspiration and precipitation is the best overall indicator in this research.
Author Contributions
Conceptualization, S.N. and A.S.; methodology, A.S. and P.S.; software, M.R.A. and P.S.; validation, S.N., A.S., and P.S.; formal analysis, S.N. and M.R.A.; investigation, A.S.; resources, S.N. and A.S.; data curation, M.R.A.; writing—original draft preparation, P.S.; writing—review and editing, S.N.; visualization, P.S.; supervision, S.N. and A.S.; project administration, S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Department of Mathematics, IPB University, and the Meteorological, Climatological, and Geophysical Agency (BMKG) for their invaluable support and assistance throughout this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samsuri, S.; Surati Jaya, I.N.; Syaufina, L. Spatial Model of Land and Forest Fire Risk Index, Case Study in Undefined. Master’s Thesis, Central Kalimantan Province, IPB University, Bogor, Indonesia, August 2008. [Google Scholar]
- Tan, Z.D.; Carrasco, L.R.; Taylor, D. Spatial correlates of wildfires in Indonesia. Int. J. Wildland Fire 2020, 29, 1088–1099. [Google Scholar] [CrossRef]
- Septiawan, P.; Nurdiati, S.; Sopaheluwakan, A. Numerical Analysis using Empirical Orthogonal Function Based on Multivariate Singular Value Decomposition on Indonesian Forest Fire Signal. IOP Conf. Ser. Earth Environ. Sci. 2019, 303, 012053. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Agustina, A.; Septiawan, P. Multivariate analysis on Indonesian forest fire using combined empirical orthogonal function and covariance matrices. IOP Conf. Ser. Earth Environ. Sci. 2019, 299, 012048. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Septiawan, P. Spatial and temporal analysis of El Niño impact on land and forest fire on Kalimantan and Sumatra. Agromet 2021, 35, 1–10. [Google Scholar] [CrossRef]
- World Bank Group. The Cost of Fire: An Economic Analysis of Indonesia’s 2015 Fire Crisis; World Bank: Jakarta, ID, Indonesia; Available online: https://olc.worldbank.org/content/cost-fire-economic-analysis-indonesia%E2%80%99s-2015-fire-crisis (accessed on 2 August 2022).
- Miettinen, J.; Shi, C.; Liew, S.C. 2015 land cover map of south-east Asia at 250-m spatial resolution. Remote Sens. Lett. 2016, 7, 701–710. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Septiawan, P. Joint Pattern Analysis of Forest Fire and Drought Indicators in Southeast Asia Associated with ENSO and IOD. Atmosphere 2022, 13, 1198. [Google Scholar] [CrossRef]
- Nechita, N.B.; Krol, M.; van der Werf Guido, R.; Johannes, W.K.; Pandey, S.; Huijnen, V.; Clerbaux, C.; Coheur, P.; Merritt, N.D.; Röckmann, T. Monitoring emissions from the 2015 Indonesian fires using CO satellite data. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 1760. [Google Scholar] [CrossRef]
- Prinz, D. Contributor and Victim—Indonesia’s Role in Global Climate Change with Special Reference to Kalimantan. Sains Environ. Technol. J. Indones. 2009, 1, 139–153. [Google Scholar] [CrossRef]
- Benson, R.P.; Roads, J.O.; Weise, D.R. Climatic and Weather Factors Affecting Fire Occurrence and behaviour. Dev. Environ. Sci. 2009, 8, 37–59. [Google Scholar] [CrossRef]
- Plank, S.; Fuchs, E.M.; Frey, C. A Fully Automatic Instantaneous Fire Hotspot Detection Processor Based on AVHRR Imagery—A TIMELINE Thematic Processor. Remote Sens. 2017, 9, 30. [Google Scholar] [CrossRef]
- Suryaningsih, N.; Prasetyowati, A.; Busalim, F. Performance of fire hotspot detection system with sensor based on angle width and voltage difference monitoring for forest security. IOP Conf. Ser. Earth Environ. Sci. 2021, 880, 012030. [Google Scholar] [CrossRef]
- Kato, S.; Miyamoto, H.; Amici, S.; Oda, A.; Matsushita, H.; Nakamura, R. Automated classification of heat sources detected using SWIR remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102491. [Google Scholar] [CrossRef]
- Datta, A.; Krishnamoorti, R. Understanding the Greenhouse Gas Impact of Deforestation Fires in Indonesia and Brazil in 2019 and 2020. Front. Clim. 2022, 4, 799632. [Google Scholar] [CrossRef]
- Fanin, T.; Van der Werf, R.G. Precipitation–fire linkages in Indonesia (1997–2015). Biogeosciences 2017, 14, 3995–4008. [Google Scholar] [CrossRef]
- Lestari, I.L.; Nurdiati, S.; Sopaheluwakan, A. Analysis of Empirical Orthogonal Function (Eof) based Singular Value Decomposition (Svd) to Rainfall Data in Indonesia. J. Math. Its Appl. 2016, 15, 13–22. [Google Scholar] [CrossRef]
- McEvoy, D.J.; Huntington, J.L.; Hobbins, M.T.; Wood, A.; Morton, C.; Anderson, M.; Hain, C. The evaporative de-mand drought index. Part II: CONUS-wide assessmentagainst common drought indicators. J. Hydrome-Teorol. 2016, 17, 1763–1779. [Google Scholar] [CrossRef]
- Zhang, X.; Li, M.X.; Ma, Z.G.; Yang, Q.; Lv, M.X.; Clark, R. Assessment of an evapotranspirationdeficit drought index in relation to impacts on ecosystems. Adv. Atmos. Sci 2019, 36, 1273–1287. [Google Scholar] [CrossRef]
- Mohammed, R.; Scholz, M. Impact of Evapotranspiration Formulations at Various Elevations on the Reconnaissance Drought Index. Water Resour. Manag. 2017, 31, 531–548. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Estimating evapotranspiration and drought stress with ground-based thermal remote sensing in agriculture: A review. J. Exp. Bot. 2002, 63, 4671–4712. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, Y.; Duan, J.; Jian, D.; Ma, Z. A daily drought index based on evapotranspiration and its application in regional drought analyses. Sci. China Earth Sci. 2022, 65, 317–336. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological droughts. U.S. Department of Commerce. Weather. Bur. Res. Pap. 1965, 45, 58. [Google Scholar]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional Drought Assessment Based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K. Monitoring droughtover the conterminous United States using MODIS and NCEP Reanalysis-2 data. J. Appl. Meteor. Clim. 2010, 49, 1665–1680. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Kimball, J.S.; McDowell, N.G.; Running, S.W. A Remotely Sensed Global Terrestrial Drought Severity Index. Bull. Am. Meteorol. Soc. 2013, 94, 83–98. [Google Scholar] [CrossRef]
- Varol, T.; Ertuğrul, M.; Özel, H.B. Drought-Forest Fire Relationships. In Mediterranean Identities—Environment, Society, Culture; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Tjostheim, D.; Otneim; Stove, B. Statistical dependence: Beyond Pearson’s ρ. arXiv 2018, arXiv:1809.10455v1. [Google Scholar] [CrossRef]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Chatterjee, S. A New Coefficient of Correlation. J. Am. Stat. Assoc. 2021, 116, 2009–2022. [Google Scholar] [CrossRef]
- Gunadi, A.; Gunardi, M. The Law of Forest in Indonesia: Prevention and Suppression of Forest Fires. Bina Huk. Lingkung. 2019, 1, 113. [Google Scholar] [CrossRef][Green Version]
- Cahyono, S.A.; Warsito, S.P.; Andayani, W.; Darwanto, D.H. Factors Affecting Forest Fires in Indonesia and Its Policy Implications. J. Sylva Lestari 2015, 3, 103–112. [Google Scholar] [CrossRef]
- Zahran, E.S.M.M.; Shams, S.; Said, S.N.M.B.M. Validation of forest fire hotspot analysis in GIS using forest fire contributory factors. Syst. Rev. Pharm. 2020, 11, 249–255. [Google Scholar] [CrossRef]
- Giglio, L.; Randerson, J.T.; van der Werf, G.R. Analysis of daily, monthly, and annual burned area using the fourth-generation global fire emissions database (GFED4). J. Geophys. Res. Biogeosci. 2013, 118, 317–328. [Google Scholar] [CrossRef]
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; van Leeuwen, T.T.; Chen, Y.; Rogers, B.M.; Mu, M.; van Marle, M.J.E.; Morton, D.C.; Collatz, G.J.; et al. Global fire emissions estimates during 1997–2016. Earth Syst. Sci. Data 2017, 9, 697–720. [Google Scholar] [CrossRef]
- Turmudi, T.; Kardono, P.; Hartanto, P.; Ardhitasari, Y. wildfire Prevention Through the Hotspot Movement Pattern Approach. IOP Conf. Ser. Earth Environ. Sci. 2018, 123, 012027. [Google Scholar] [CrossRef]
- Ardiansyah, M.; Boer, R.; Situmorang, A.P. Typology of land and forest fire in South Sumatra, Indonesia Based on Assessment of MODIS Data. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 12058. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 monthly averaged data on single levels from 1959 to present. Copernic. Clim. Chang. Serv. (C3S) Clim. Data Store (CDS) 2019. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land hourly data from 1981 to present. Copernic. Clim. Chang. Serv. (C3S) Clim. Data Store (CDS) 2019. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lond. Ser. A 1948, 193, 120–146. [Google Scholar]
- Monteith, J.L. Evaporation and Environment. In Proceedings of the 19th Symposium of the Society for Experimental Biology; Cambridge Univ. Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Björnsson, H.; Venegas, S. A Manual for EOF and SVD Analyses of Climate Data; McGill University: Quebec, QC, Canada, 1997. [Google Scholar]
- Navarra, A.; Simoncini, V. A Guide to Empirical Orthogonal Function for Climate Data Analysis; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Voss, H.; Kurths, J. Reconstructionof nonlinear time delay models fromdata by the use of optimal transforma-tions. Phys. Lett. A 1997, 234, 336–344. [Google Scholar] [CrossRef]
- Tacconi, L. Fires in Indonesia: Causes, Costs and Policy Implications; CIFOR Occasional Paper: Bogor, Indonesia, 2003; p. 38. [Google Scholar]
- Purnomo, H.; Okarda, B.; Shantiko, B.; Achdiawan, R.; Dermawan, A.; Kartodihardjo, H.; Dewayani, A. wildfires, toxic haze and local politics in Indonesia. Int. For. Rev. 2019, 21, 486–500. [Google Scholar]
- Kuswanto, H.; Setiawan, D.; Sopaheluwakan, A. Clustering of Precipitation Pattern in Indonesia Using TRMM Satellite Data. Eng. Technol. Appl. Sci. Res. 2019, 9, 4484–4489. [Google Scholar] [CrossRef]
- Aldrian, E.; Susanto, R.D. Identification of three dominant rainfall regions within Indonesia and their relationship to sea surface temperature. Int. J. Climatol. 2003, 23, 1435–1452. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Julianto, M.T.; Septiawan, P.; Rohimahastuti, F. Modelling and analysis impact of El Nino and IOD to land and forest fire using polynomial and generalized logistic function: Cases study in South Sumatra and Kalimantan, Indonesia. Model. Earth Syst. Environ. 2021, 8, 3341–3356. [Google Scholar] [CrossRef]
- Changnon, S.A. Impacts of 1997–98 El Niño–Generated Weather in the United States. Bull. Am. Meteorol. Soc. 1999, 80, 1819–1827. Available online: http://www.jstor.org/stable/26214945 (accessed on 13 July 2022). [CrossRef]
- Byron, N.; Shepherd, G. Indonesia and the 1997-98 EL NIÑO: Fire Problems and Long-Term Solutions. Nat. Resour. Perspect. 1998, 28. [Google Scholar] [CrossRef]
- Hinrichs, A.; Siegert, F. Indonesia: Fire Damages in East Kalimantan in 1997-98 RELATED TO LAND USE—Ers-Sar Inventory Results (Iffn No. 23). Available online: https://gfmc.online/iffn/country/id/id_27.html (accessed on 15 July 2022).
- Lennertz, R.; Panzer, K.F. Preliminary Assessment of the Drought and Forest Damage in Kalimantan Timur; GTZ-TAD Report; DFS German Forest Inventory Service: Feldkirchen Germany, 1983. [Google Scholar]
- Sadli, M. The Indonesian Crisis. ASEAN Econ. Bull. 1998, 15, 272–280. [Google Scholar] [CrossRef]
- Radelet, S.; Sachs, J.D.; Cooper, R.N.; Bosworth, B.P. The East Asian Financial Crisis: Diagnosis, Remedies, Prospects. Brook. Pap. Econ. Act. 1998, 1998, 2534670. [Google Scholar] [CrossRef]
- Yamazawa, I. The Asian Economic Crisis and Japan (PDF). Dev. Econ. 1998, 36, 332–351. [Google Scholar] [CrossRef]
- Badri, M.; Lubis, D.P.; Susanto, D.; Suharjito, D. The Viewpoint of Stakeholders on The Causes Of wildfires in Riau Province, Indonesia. RJOAS 2019, 2, 4–10. [Google Scholar] [CrossRef]
- Kusumaningtyas, S.D.A.; Aldrian, E. Impact of the June 2013 Riau province Sumatera smoke haze event on regional air pollution. Environ. Res. Lett. 2016, 11, 075007. [Google Scholar] [CrossRef]
- McBride, J.L.; Sahany, S.; Hassim, M.E.; Nguyen, C.M.; Lim, S.Y.; Rahmat, R.; Cheong, W.K. The 2014 record dry spell at Singapore: An intertropical convergence zone (itcz) drought. Bull. Am. Met. Soc. 2015, 96, S126–S130. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Septiawan, P. Joint Distribution Analysis of Forest Fires and Precipitation in Response to ENSO, IOD, and MJO (Study Case: Sumatra, Indonesia). Atmosphere 2022, 13, 537. [Google Scholar] [CrossRef]
- Miralles, D.G.; Brutsaert, W.; Dolman, A.J.; Gash, J.H. On the use of the term “evapotranspiration”. Water Resour. Res. 2020, 56, e2020WR028055. [Google Scholar] [CrossRef]
- Van, R.K.; James, A.L.; Alina, C.C.; Nicholas, A.P.; Derek, J.C.; Douglas, F.S.; Jonathan, T.K.; Malcolm, P.N. Water balance and topography predict fire and forest structure patterns. For. Ecol. Manag. 2015, 338, 1–13. [Google Scholar] [CrossRef]
- Reyer, C.; Lasch, P.; Mohren, G.M.J.; Sterck, F.J. Inter-specific competition in mixed forests of Douglas-fir (Pseudotsuga menziesii) and common beech (Fagus sylvatica) under climate change—A model-based analysis. Ann. For. Sci. 2010, 67, 805. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Williams, A.P.; Seager, R.; Macalady, A.K.; Berkelhammer, M.; Crimmins, M.A.; Swetnam, T.W.; Trugman, A.T.; Buenning, N.; Noone, D.; McDowell, N.G.; et al. Correlations between components of the water balance and burned area reveal new insights for predicting forest fire area in the southwest United States. Int. J. Wildland Fire 2015, 24, 14–26. [Google Scholar] [CrossRef]
- Halofsky, J.E.; Peterson, D.L.; Harvey, B.J. Changing wildfire, changing forests: The effects of climate change on fire regimes and vegetation in the Pacific Northwest, USA. Fire Ecol. 2020, 16, 4. [Google Scholar] [CrossRef]
- Price, C.; Rind, D. The impact of a 2 × CO2 climate on lightning caused fires. J. Clim. 1994, 7, 1484–1494. [Google Scholar] [CrossRef]
- Boer, M.; Bowman, D.; Murphy, B.; Cary, G.; Cochrane, M.; Fensham, R.; Krawchuk, M.; Price, O.; Resco de Dios, V.; Williams, R.; et al. Future changes in climatic water balance determine potential for transformational shifts in Australian fire regimes. Environ. Res. Lett. 2016, 11, 065002. [Google Scholar] [CrossRef]
- Venkatesh, K.; Preethi, K.; Ramesh, H. Evaluating the effects of forest fire on water balance using fire susceptibility maps. Ecol. Indic. 2020, 110, 105856. [Google Scholar] [CrossRef]
- Don, A.W.; Francisco, B.-C.; Richard, P.S.; de Arellano, P.R. The effect of wildfire on the structure and water balance of a high conservation value Hualo (Nothofagus glauca (Phil.) Krasser.) forest in central Chile. For. Ecol. Manag. 2020, 472, 118219. [Google Scholar] [CrossRef]
- Moutahir, H.; Touhami, I.; Moghli, A.; Bellot, J. Water Balance Estimation Under Wildfire and Restoration Scenarios in Semiarid Areas: Effects on Aquifer Recharge. In Advances in Sustainable and Environmental Hydrology, Hydrogeology, Hydrochemistry and Water Resources. CAJG 2018, Advances in Science, Technology & Innovation 2019; Chaminé, H., Barbieri, M., Kisi, O., Chen, M., Merkel, B., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Healey, N.C.; Rover, J.A. Analyzing the Effects of Land Cover Change on the Water Balance for Case Study Watersheds in Different Forested Ecosystems in the USA. Land 2022, 11, 316. [Google Scholar] [CrossRef]
- Boisramé, G.F.S.; Thompson, S.E.; Tague, C.; Stephens, S.L. Restoring a natural fire regime alters the water balance of a Sierra Nevada catchment. Water Resour. Res. 2019, 55, 5751–5769. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).