Abstract
Urban canopy models (UCMs) in mesoscale numerical weather prediction models need evaluation to understand biases in urban environments under a range of conditions. The authors evaluate a new drag formula in the Weather Research and Forecasting (WRF) model’s multilayer UCM, the Building Effect Parameterization combined with the Building Energy Model (BEP+BEM), against both in-situ measurements in the urban environment as well as simulations with a simple bulk scheme and BEP+BEM using the old drag formula. The new drag formula varies with building packing density, while the old drag formula is constant. The case study is a strong cold frontal passage that occurred in Houston during the winter of 2017, causing high winds. It is found that both BEP+BEM simulations have lower peak wind speeds, consistent with near-surface measurements, while the bulk simulation has winds that are too strong. The constant-drag BEP+BEM simulation has a near-zero wind speed bias, while the new-drag simulation has a negative bias. Although the focus is on the impact of drag on the urban wind speeds, both BEP+BEM simulations have larger negative biases in the near-surface temperature than the bulk-scheme simulation. Reasons for the different performances are discussed.
1. Introduction
It is important to accurately forecast high-impact weather in urban environments because of the large populations that are at risk. Hazards include local extreme winds, heavy precipitation and flooding, wildfires, urban heat waves, and highly polluted air. Because of the heteorogeneity of surfaces and roughness elements in urban environments, an accurate forecast in the nearby rural environment does not necessarily translate to a good forecast within the urban canopy layer. While many past studies have focused on the urban heat island effect [1], and its direct and indirect effects on urban weather and climate (e.g., [2,3,4,5,6,7]), fewer studies have examined how urbanization affects wind. The urban heat island can indirectly affect wind through an induced secondary circulation [8] and through more vertical mixing, which can mix higher momentum air downward into the city. Additionally, strong wind can occur directly from weather systems such as tropical cyclones, downslope wind storms, frontal systems, winter storms, and sea/land breezes. In quasi-neutral boundary layers, the drag from the enhanced roughness reduces the winds in the city overall, but the wind reductions can be heterogeneous based on the urban morphology. Moreover, although the city-averaged winds are typically reduced, accelerations can occur due to eddies and wind streaks in street canyons. Considering the complexity of winds in the urban environment, and the large populations and infrastructure at risk there, it is critical to observe and forecast them better.
In mesoscale numerical weather prediction models with horizontal grid spacings of O(1 km), buildings are not explicitly resolved and thus their net effects on the grid-scale prognostic variables must be parameterized. In the WRF model, there is a hierarchy of UCMs to accomplish this task, ranging from a simple bulk scheme (urban effects are parameterized by an area of increased aerodynamic roughness, lower vegetation, increased albedo, and increased heat capacity and conductivity) to the multilayer BEP combined with BEM [9,10]. The latter scheme mimics the three-dimensionality of buildings and produces detailed momentum and thermal forcings based on the complex urban morphology (walls, roofs, and roads) and heat exchanges between the interior of buildings and the surrounding environment. The usage of more sophisticated UCMs has generally resulted in better forecasts in the urban environment (e.g., [11,12,13,14]).
In the WRF model version 4.3 (WRFV4.3) [15], a new drag formulation was added to BEP+BEM. The drag coefficient affects the momentum sink caused by vertically oriented surfaces (building walls) as well as the building-induced turbulent kinetic energy (TKE) [9]. The drag from horizontal surfaces (roofs and roads) is based upon Monin–Obukhov similarity theory [16]. Previously, the drag coefficient was set constant at . In WRFV4.3, it was modified to be a function of the building plan area ratio [17,18] since this ratio is known to affect the overall drag in simulations using the Reynolds-averaged Navier–Stokes equations [17]. The building plan area fraction is defined as the ratio of the building plan area to the total surface area of the grid cell [18]. The new drag formula is
wherein is the building plan area ratio, b is the mean building width, and w is the mean street width in a grid cell.
Since this new drag formula was only recently added to WRF, it has not received extensive evaluation under a range of conditions yet. In this work, we evaluate the new drag formula in comparison to the old constant-drag formula during a strong cold frontal passage in Houston. This allows for BEP+BEM to be evaluated in simulations in which the near-surface wind speeds range from 0–15 m s−1 and there are large variations in near-surface water vapor mixing ratio (4–14 g kg−1) and temperature (285–300 K).
2. Case Study
We select a case study of a frontal passage that occurred from 21–24 January 2017 in southeastern Texas, producing high winds and large temperature variations in Houston. A discussion of this high wind event was given by the National Weather Service in Corpus Christi, Texas (available on the website https://www.weather.gov/crp/stormhistory, accessed on 1 August 2022). Although the peak gusts of approximately 24 m s−1 were south of Houston in the Corpus Christi area, sustained winds of 13 m s−1 were present over Houston after the cold front passage. The combination of strong winds and low moisture content contributed to numerous grass fires, and the strong winds resulted in blow-outs of water along bays and waterways. A sequence of synoptic surface maps is shown in Figure 1. Prior to the frontal passage (Figure 1a,b), the surface winds in Houston were from the south to southeast. The evening temperature at 12:00 a.m. UTC 21 January was 67 °F (20 °C). At 12:00 a.m. UTC 22 January (Figure 1c), there was a surface low in the Texas panhandle, and a cold front extended from the north to south over central Texas. Ahead of the cold front, there was a dryline just west of Houston. At that time, the winds had turned southerly to southwesterly. By 1200 a.m. UTC 22 January (Figure 1d), the cold front had passed through southeastern Texas, and stronger near-surface winds [approximately 30 kt (15.4 m s−1)] were from the west with lower temperatures of approximately 50–60 °F (10.0–15.6 °C). The surface low was reasonably deep, with a mean-sea level pressure (MSLP) of 993 hPa at the time. By 12:00 a.m. UTC 23 January (Figure 1e), the surface low had moved over northern Georgia, and the cold front was surging towards Florida. Continued strong west to northwesterly winds existed over southeastern Texas. Finally, by 1200 a.m. UTC 23 January (Figure 1f), the cold front had moved past Florida, and southeastern Texas was quite cool for that time of year (approximately 45–50 °F (7.2–10.0 °C)).
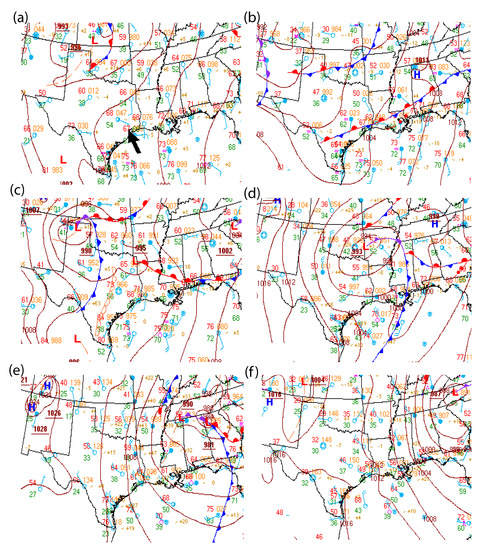
Figure 1.
Surface analyses in the south central U.S. for the 21–24 January cold front passage and wind event in Houston. Panels: (a) 12:00 a.m. UTC 21 January; (b) 12:00 a.m. UTC 21 January; (c) 12:00 a.m. UTC 22 January; (d) 12:00 a.m. UTC 22 January, (e) 12:00 a.m. UTC 23 January, and (f) 12:00 a.m. UTC 23 January. Images are courtesy of the National Weather Service Weather Prediction Center (WPC). Surface observations are given on the standard station model, where red denotes the temperature (°F), green denotes the dewpoint (°F), orange denotes the surface pressure (mb, initial 9 or 10 omitted), and wind barbs denote the wind speed and direction. In (a), the location of Houston is denoted by the black arrow.
3. Numerical Simulations and Observational Data
3.1. Description of Numerical Simulations
The setup of the WRF model numerical simulations is similar to the study by [19], including domain size, grid spacings, nesting strategy, physical parameterizations, and global model data. Three domains with 298 × 298 grid points and respective spacings of 9, 3, and 1 km are used (Figure 2), with the 1-km domain covering Houston and nearby areas. The physical parameterizations are: the WRF single moment 6-class microphysical parameterization [20], rapid radiative transfer model for Global Climate Models (GCMs) [RRTMG] longwave and shortwave parameterizations, the unified Noah land-surface model, and the Yonsei University (YSU) planetary boundary layer (PBL) parameterization [21,22]. On domain 1 (with 9-km grid spacing), the Tiedtke cumulus parameterization [23] is used to help represent the effects of sub-grid-scale convection, while convection is calculated explicitly on the innermost two domains. In the vertical, 60 levels are used between the surface and the model top of 10 hPa, using a stretched grid with finer resolution near the surface. The lowest model level is approximately 26 m above ground level (AGL; varying slightly horizontally due to WRF’s pressure based sigma vertical coordinate), and 15 levels are used below 3 km for high vertical resolution of the boundary layer.
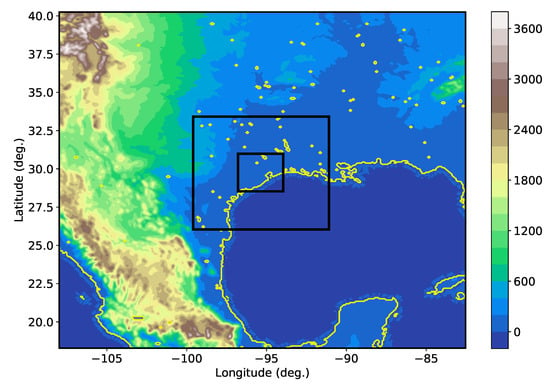
Figure 2.
WRF model’s three nested domains (respective spacings of 9, 3, and 1 km) with resolved topography in color shades. All analysis of the simulations is carried out on the innermost domain.
Three WRF simulations are executed with the model setup above: (i) the bulk urban parameterization, (ii) BEP+BEM using the old , and (iii) BEP+BEM using the new drag formula (Equation (1)). The WRF simulations are initialized at 12:00 a.m. UTC 21 January and integrated until 12:00 a.m. UTC 24 January. The urban parameters for the BEP+BEM simulations are given in Table 1. The simulations are initialized using the National Centers for Environmental Prediction (NCEP) Global Data Assimilation System (GDAS) final analysis at a 0.25° horizontal grid interval, and the lateral boundary conditions are updated at intervals of 3 h. The National Urban Data and Access Portal Tool (NUDAPT-44) dataset is used [24,25] for the urban morphological characteristics of Houston, including urban fraction, impervious fraction, building height histograms, building plan area fraction, building height weighted by footprint plan area, and building surface-area-to-plan-area ratio, among other parameters.

Table 1.
Urban parameters for the YSU BEP+BEM simulations. The values of the parameter for the LIR, HIR, and COI urban classes are in columns 2–4.
In the study by [19], BEP+BEM behaved qualitatively similar in the YSU PBL parameterization as it did in both the Mellor–Yamada–Janjić [26,27] and the Bougeault-Lacarerre [28] PBL schemes. One key quantitative difference is that the YSU scheme does not predict TKE, and thus the building-induced TKE does not contribute to the eddy viscosity coefficient as it does in the latter schemes. In the YSU PBL parameterization, a prescribed functional form in the vertical is used [22]. Another key difference is that the YSU PBL parameterization is a nonlocal scheme, and includes a gradient correction term in the vertical diffusion equation. The amplitudes of the eddy viscosity coefficient and gradient correction terms are directly influenced by the surface heat flux, which contains anthropogenic urban fluxes from BEP+BEM. Thus, nonlocal mixing by large eddies can be enhanced through larger urban surface heat fluxes in the YSU scheme. In the Mellor–Yamada–Janjić and Bougeault–Lacarerre schemes, local vertical mixing is triggered by buoyancy-induced TKE generation during unstable conditions.
3.2. Observational Data
The list of Texas Commission on Environmental Quality (TCEQ) stations used, their locations and altitude AGL, urban classes, and urban fractions are shown in Table 2. The monitors are 6–18 m above ground level, and are located within 30 km of the center of Houston. Of the seven stations, three are in low intensity residential (LIR), two are in high intensity residential (HIR), and two are in commercial and industrial (COI) urban classes. In Figure 3a, the land-use indices are shown in the Houston metropolitan area. The land-use indices are from the 33 Modified International Geosphere-Biosphere Programme (IGBP) Moderate Resolution Imaging Spectroradiometer (MODIS) Noah land use categories (Table 3). The urban area consists of regions of category 31 (LIR), 32 (HIR), and 33 (COI). Away from the urban environment, there are land uses of wetlands, croplands, shrublands, forest, and water. In Figure 3b, the WRF urban fraction is shown with the locations of the TCEQ stations used in the study. The urban fractions at these stations range from 0.3–1.0. Figure 3c shows the resolved building heights weighted by plan area from the NUDAPT dataset and Figure 3d shows the building plan area fraction. C1052 and C1066 are located amidst denser buildings; C169, C1, and C409 are amidst moderate-density buildings; and C1036 and C243 are in areas with fewer buildings. Figure 3e,f show that the new drag formula (1) yields larger drag coefficients in the urban area than the old constant drag formula.

Table 2.
TCEQ air monitoring sites used in study.
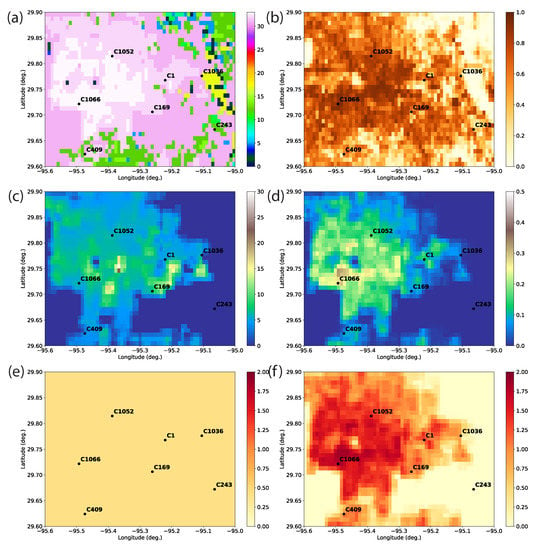
Figure 3.
TCEQ stations collocated on the WRF model’s resolved static data: (a) IGBP MODIS land-use index; (b) urban fraction (); (c) building height weighted by plan area; (d) building plan area fraction (); (e) BEP’s constant drag coefficient, and (f) BEP’s new drag coefficient.

Table 3.
Modified IGBP MODIS Noah land use indices and descriptions.
4. Results
We first examine the evolution of the simulated near-surface winds, temperature, and water vapor in Houston. Next, we carry out time-series analysis of the simulations and TCEQ measurements. Finally, we report on some overall statistical performance measures and simulated variability in the urban sector.
4.1. Near-Surface Forecasts in the Urban Environment
Analysis of the simulations is conducted on the WRF model’s domain 3 (1-km horizontal grid spacing). In the evening prior to the frontal passage (Figure 4), winds are from the south to southwest. The winds are weakest in the urban environment in the BEP+BEM simulations using the new drag formula (minimum of approximately 1 m s−1). The spatial variation in contributes to spatial variability in the winds in the urban sector. The simulation with the old drag formula has slightly stronger winds, and the bulk simulation has the strongest winds in Houston. The urban heat island effect is largest in the simulation with the new drag formula (the center of Houston is 5 K warmer than the rural environment). The urban moisture content did not vary significantly among the simulations; however, the BEP+BEM simulations are slightly drier than the bulk simulation.
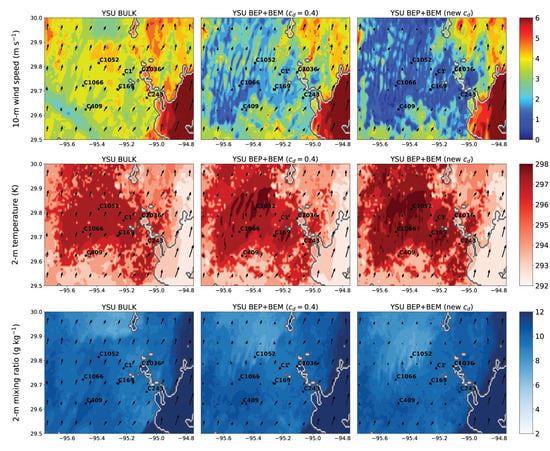
Figure 4.
WRF model’s simulated near-surface fields at 12:00 a.m. UTC 22 January (7:00 p.m. LST). Vectors are shown every 10 model grid points.
Figure 5 depicts the results at the time of peak winds (7:00 p.m. UTC; 1:00 p.m. LST) after the cold front has passed. Strong west to northwesterly winds are evident. Here, the BEP+BEM simulation with the new drag formula has weakest winds again, indicating that it is producing more drag overall in the urban environment. The winds in the rural environment of approximately 15 m s−1 are reduced to approximately 4–6 m s−1 in Houston in that simulation. Near-surface temperatures in both BEP+BEM simulations are slightly cooler than in the bulk simulation at this time. Again, at this time, the water vapor mixing ratios are similar among the simulations.
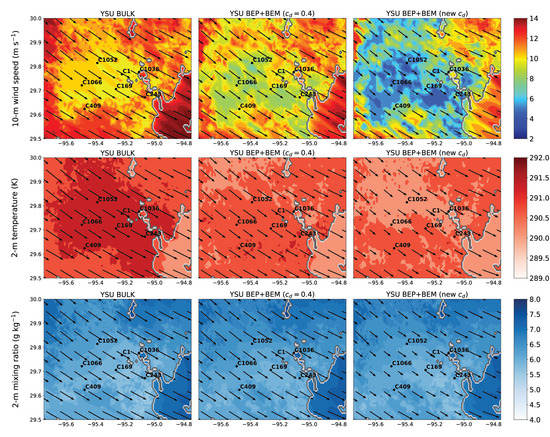
Figure 5.
WRF model’s simulated near-surface fields at 6:00 p.m. UTC 22 January (1:00 p.m. LST). Vectors are shown every 10 model grid points.
Finally, the near-surface fields are shown in the early morning after the frontal passage in Figure 6. The winds are weak in all simulations because the front has passed and vertical mixing is suppressed. The BEP+BEM simulation with new drag formula has the weakest winds as before, and the bulk simulation has the strongest winds. The bulk simulation has the highest temperatures at this time, 5 K warmer than the rural environment in the southeast part of Houston. The contour lines are oriented perpendicular to the winds, illustrating the relationship between temperature advection and the urban surface heat flux. The BEP+BEM simulation with the new drag formula has the second highest temperatures, approximately 3 K warmer than the environment (and maximized in the HIR/COI regions of Houston). The LIR region has similar temperatures as the nearby rural environment. Finally, the BEP+BEM simulation with the new drag formula is slightly moister than both the simulation with the old drag formula and the bulk simulation at this time.
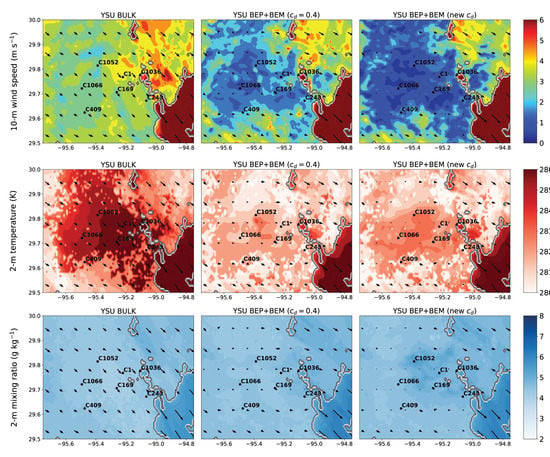
Figure 6.
WRF model’s simulated near-surface fields at 12:00 a.m. UTC 23 January (7:00 a.m. LST). Vectors are shown every 10 model grid points.
To summarize, the new drag formula in BEP+BEM produces more drag in the built-up environment before, during, and after the cold front passage, reducing the near-surface winds there. The near-surface temperatures in the BEP+BEM simulations are more heterogeneous than in the bulk simulation due to the variation in thermal forcing among the LIR, HIR, and COI urban classes. The urban water vapor content does not vary that significantly among the three simulations. The BEP+BEM simulations are slightly drier in the daytime prior to the frontal passage, and slightly moister in the early morning after the front has passed.
4.2. Time Series
In this subsection, we give a quantitative evaluation of the WRF simulations against the TCEQ measurements. To interpolate the simulated values to the TCEQ stations, the inverse distance weighting method is used on the closest four WRF model grid points in the horizontal. Since the TCEQ measurements are not necessarily at the World Meteorological Organization standard measurement levels (10 m AGL for winds, and 2 m AGL for temperature), we linearly interpolate between the WRF diagnosed value at 2 m (for temperature and water vapor) or 10 m (for winds) and the first model level at approximately m. If the TCEQ measurement is below the lowest level of a diagnosed variable, we use the diagnosed value. Time series of WRF model simulations and TCEQ measurements are given in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, for stations C169, C243, C1036, C1, C409, C1052, and C1066, respectively.
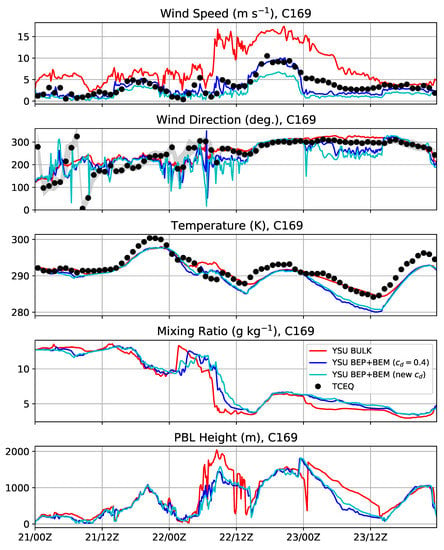
Figure 7.
Measured and WRF model simulation time series at TCEQ station C169 in an LIR region. Measurements are reported as hourly averages (filled black circles), and simulation output is shown at a frequency of 10 min (colored lines). In the wind direction plot, the gray shading denotes the observed standard deviation at the TCEQ station. The stations did not measure water vapor mixing ratio or PBL depth.
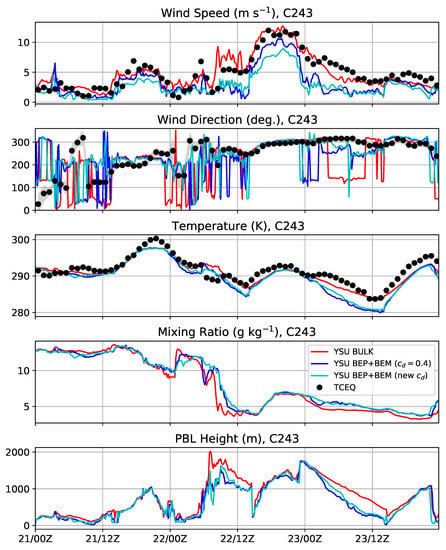
Figure 8.
Same as Figure 7 but at LIR station C243.
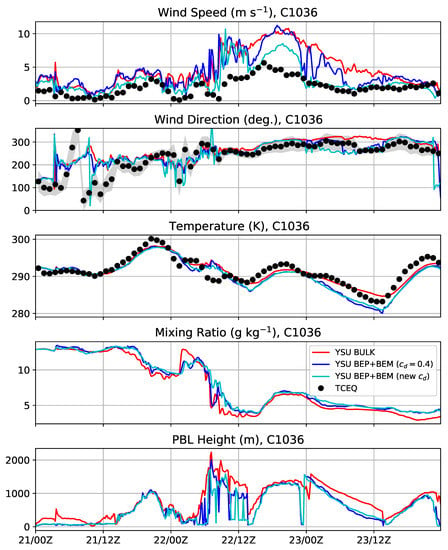
Figure 9.
Same as Figure 7 but at LIR station C1036.
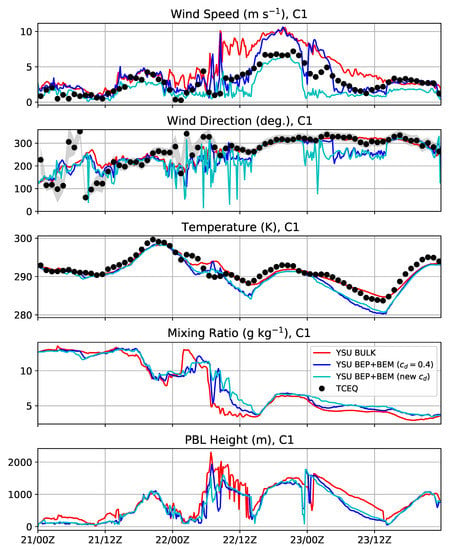
Figure 10.
Same as Figure 7 but at LIR station C1.
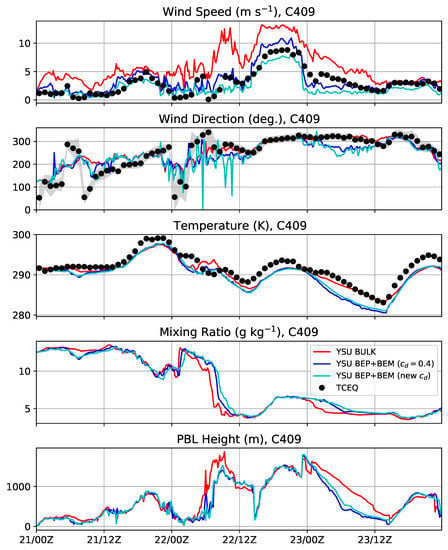
Figure 11.
Same as Figure 7 but at HIR station C409.
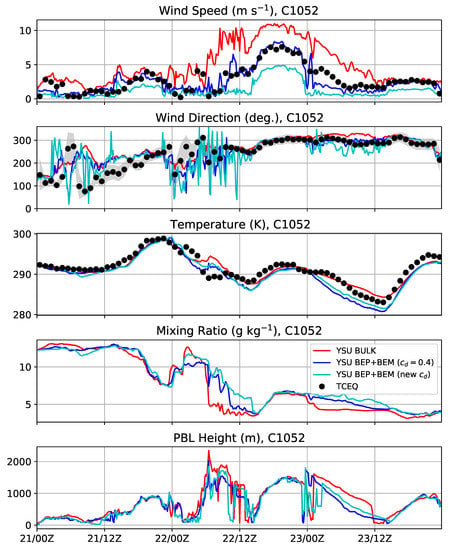
Figure 12.
Same as Figure 7 but at COI station C1052.
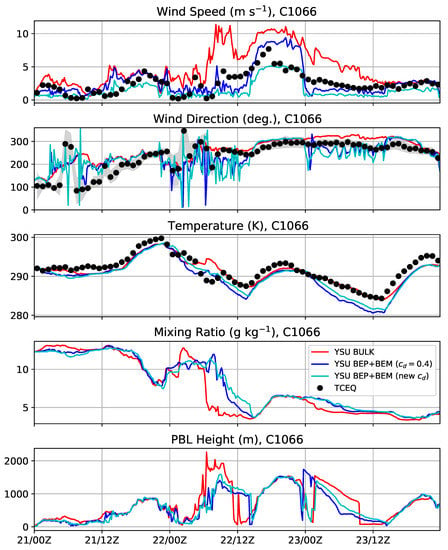
Figure 13.
Same as Figure 7 but at COI station C1066.
We first examine the LIR stations: C169, C243, and C1036. At C169 (Figure 7), which is close to the HIR region, the BULK simulation winds are too strong in comparison to the BEP+BEM simulations. The BEP+BEM simulation with performed best. Wind directions are reasonably well predicted after 12:00 p.m. UTC 21 January. Between 12:00 a.m.–12:00 p.m. UTC 23 January, the bulk simulation has more accurate wind directions than the BEP+BEM simulations. The bulk simulation’s temperature is better predicted than both the BEP+BEM simulations. In particular, the BEP+BEM simulations have temperatures that are too low by 2–3 K in the early mornings (12:00 p.m. UTC 22 January and 12:00 p.m. UTC 23 January). The mixing ratio time series shows a decrease of 7 g kg−1 from before to after that frontal passage. The PBL depth increases with daytime heating and becomes larger during the high wind event after the cold front passes by Houston (between 12:00 p.m. UTC 22 January and 12:00 a.m. UTC 23 January). In the WRF model, the diagnosed PBL depth is determined from the bulk Richardson number, which increased due to the strong vertical wind shear and daytime heating. At C243 (Figure 8) in an LIR location east of the city center, the BULK simulation has the most accurate wind speeds. At C1036 (Figure 9), the final LIR station also east of the center and north of C243, the BEP+BEM simulation with the new drag formulation performed best in terms of wind speed. Although C243 and C1036 are spatially close, the peak measured winds at C243 are 12 m s−1 while the peak measured winds at C1036 are only 5 m s−1. It it likely that, for the measured wind direction of west-northwest at this time, C1036 is more sheltered by the upwind built-up area than C243.
At C1 (Figure 10) in an HIR region, the BEP+BEM simulation with the new drag formulation matched the measured time series best. Both the BULK and BEP+BEM simulation with have peak winds that are 3 m s−1 too high. At C409 (Figure 11), both the BEP+BEM simulations have more accurate peak winds than the BULK simulation near 6:00 p.m. UTC 22 January. Similar behaviors in the other variables are evident at both of these locations as they are at the LIR stations.
Finally, we examine the COI stations C1052 and C1066 (Figure 12 and Figure 13, respectively). At C1052, the BEP+BEM simulation with has the most accurate wind time series (both speed and direction). The BEP+BEM simulation with the new drag formula has winds that are too weak and the BULK simulation has winds that are too strong. Although the BEP+BEM simulation temperatures are too low at night and in the early mornings, the cold bias is less than at the LIR and HIR stations. At C1066, the BEP+BEM simulation performed best with regard to the peak wind, but the overall wind time series in the BEP+BEM simulation with the new drag formula matched better. At this station, the cold biases in the temperature are larger, similar to the LIR and HIR stations. At these two stations, the BULK simulation has a more rapid decrease in the mixing ratio during the frontal passage between 12:00 a.m.–12:00 p.m. UTC 22 January than the BEP+BEM simulations. The reasons for this are not known, nor are there dew point measurements at the TCEQ stations to verify which one is correct.
4.3. Performance Measures
We now examine statistical performance measures. The biases and root-mean-squared errors (RMSE) of the WRF simulations against the TCEQ measurements are calculated for near-surface wind speed, wind direction, and temperature. The bias (or mean error ME) and RMSE are defined, respectively, as
wherein M is the interpolated value from the simulation at the TCEQ station and O is the TCEQ measurement. Overbars denote the mean value of each model simulation or measurement time series. The ME and RMSE are stratified by day versus night (where day is defined as 12:00 p.m.–12:00 a.m. UTC (7:00 a.m.–7:00 p.m. LST) and night is 12:00 a.m.–12:00 p.m. UTC (7:00 p.m.–7:00 a.m. LST)] and by each urban class: LIR, HIR, and COI.
The biases are given in Figure 14. The BULK simulation has positive wind speed biases of approximately 2 m s−1 in Houston, the BEP+BEM simulation with has biases near zero, and the BEP+BEM with the new drag formula has negative biases of approximately −1 to −1.5 m s−1. In all simulations, the wind speed biases at night are worst. Biases are reasonably good for wind direction in all simulations (within ±20°). An exception to this is the BEP+BEM simulations at night, in which the direction is biased more southerly (−40°). This is likely because the winds became weaker at night in the BEP+BEM simulations, and thus more variable. Finally, biases in the near-surface temperature are generally negative in the three WRF simulations. The BULK simulation has better biases than the BEP+BEM simulations, which are negatively biased around −1.5 K. Wind speed biases are larger when the winds are stronger (Figure 15).
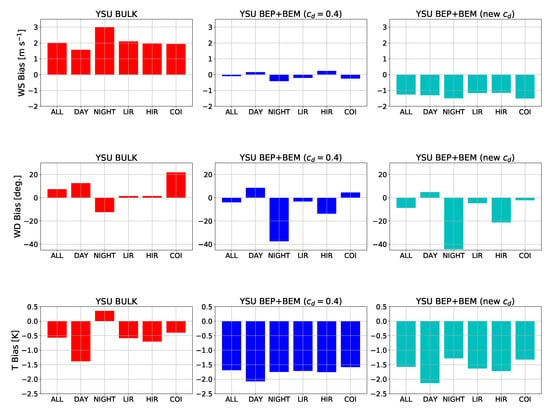
Figure 14.
Biases in near-surface wind speed (WS), wind direction (WD), and temperature (T), in each of the three simulations against the TCEQ measurements. Biases are stratified by day versus night, and for each urban class (LIR, HIR, and COI).
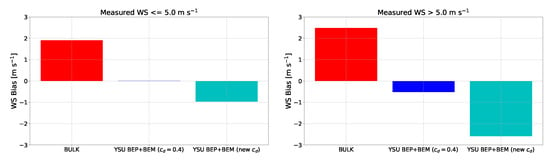
Figure 15.
WS bias stratified by whether the measured WS at the TCEQ station is less or greater than 5 m s−1 for each of the three simulations.
The RMSEs are given in Figure 16. The BEP+BEM simulations have lower wind speed RMSEs (approximately 1–2 m s−1) than the BULK simulation (approximately 3–4 m s−1). The BEP+BEM simulations have lower RMSEs in the HIR and COI regions than the LIR region. Wind direction RMSEs ranged from 20–60° in all simulations, and neither simulation is significantly better than the others. The BULK simulation has lower RMSEs in near-surface temperature (1.5 K) than the BEP+BEM simulations (2–2.5 K).
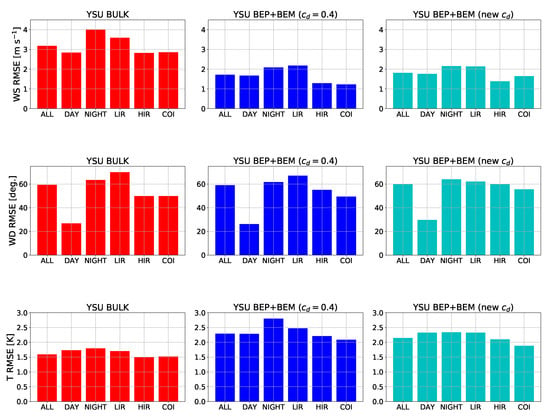
Figure 16.
RMSEs in WS, WD, and T for each of the three simulations against the TCEQ measurements. RMSEs are stratified by day versus night, and for each urban class (LIR, HIR, and COI).
4.4. Variability of Near-Surface Forecasts by Land Use
Finally, we examine variability in the WRF simulations in the urban area and environment. Normalized histograms of wind speed, temperature, and mixing ratio are shown in Figure 17 at 12:00 a.m. UTC 22 January (evening prior to the frontal passage). Clear differences in wind speed are evident between the rural and urban areas due to the enhanced drag from the built-up region in all simulations. Distinct urban heat islands are evident at this time as well. The mixing ratio histograms do not exhibit significant differences between the urban and rural environments. In Figure 18, we show the same histograms after the frontal passage at 6:00 p.m. UTC 22 January, near the time of peak winds after the cold front has passed. The value of BEP+BEM in producing detailed urban forcing is evinced by the separate peaks in the COI, HIR, and LIR urban classes for each variable, but most evident in the wind speed. The temperature histograms are narrower for the BEP+BEM simulations than the BULK simulations at this time. This is likely because advective effects are dominant over surface flux effects in the temperature tendencies at this time due to the strong winds. The value of realistically representing the diversity in near-surface conditions across urban classes is clearly illustrated by these figures.
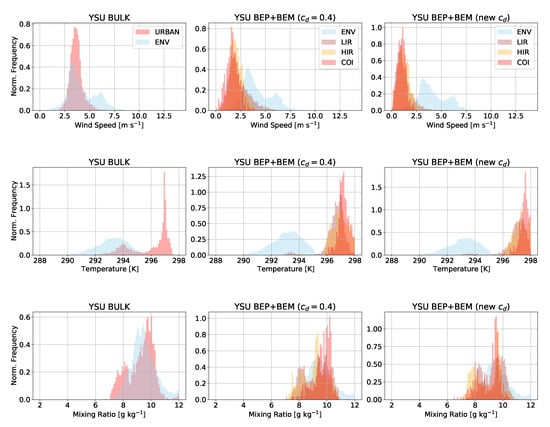
Figure 17.
Normalized histograms from the simulations at 12:00 a.m. UTC 22 January (7:00 p.m. LST), evening in Houston prior to the passage of the cold front. Histograms are 50% transparent so that overlapping histograms can be seen. In the left column, URBAN denotes land-use index 13 (Table 3), and ENV denotes the rural environment (all other land-use indices). In the middle and right columns, the urban area is stratified by the LIR, HIR, and COI land-use indices (31, 32, and 33 from Table 3, respectively), and ENV includes all other land uses.
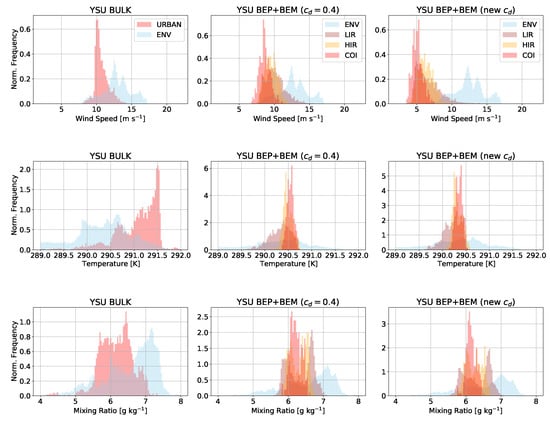
Figure 18.
Same as Figure 17, but at 6:00 p.m. UTC 22 January (1:00 p.m. LST), afternoon in Houston near the time of peak winds after the cold front has passed.
5. Discussion and Conclusions
We evaluated WRF simulations of a strong cold frontal passage against near-surface TCEQ measurements in Houston. This is listed as a significant weather event by National Weather Service in Corpus Christi, Texas. Although the strongest winds were south of Houston near Corpus Christi (approximately 25 m s−1), strong winds of approximately 15 m s−1 impacted Houston and thus this event afforded the opportunity to evaluate how well different urban canopy parameterizations simulate the winds there. Three WRF simulations are evaluated, all using the YSU PBL parameterization, but with variations in the UCM. The first simulation used a simple bulk scheme. The second simulation used the multilayer BEP+BEM UCM using the old constant-drag formula. The third simulation used the the multilayer BEP+BEM simulation with the new drag formula available in WRFV4.3. This event allowed us to comprehensively evaluate these UCMs over a wide range of near-surface conditions that are present when strong cold fronts pass through cities. It also allowed us to further evaluate BEP+BEM coupled to the nonlocal YSU PBL parameterization during a complex synoptic event. BEP+BEM in the YSU scheme has not been evaluated as extensively as in the Mellor–Yamada–Janjić and Bougeault–Lacarerre schemes, since it has only been available in the WRF model since 2021.
Synthesizing all results, a complex picture of the performance of the UCMs emerges. The BEP+BEM simulations have more accurate near-surface wind speeds overall. The average wind speed biases in the bulk, constant-drag BEP+BEM, and new-drag BEP+BEM simulations are approximately 2 m s−1, 0 m s−1, and −1 m s−1, respectively. Both BEP+BEM simulations produced more drag in the built-up region consistent with the TCEQ measurements. Interestingly, the new drag formula of BEP+BEM reduced the urban winds too much, and the simulation performed worse than the constant-drag simulation overall. This result is largely explained by larger drag coefficient resulting from the new formula (1) (Figure 3e,f). Further examination of other cases will shed more light on whether this is a systemic result or related to this one particular case. Although the BEP+BEM simulations performed better for wind speed, they performed worse for near-surface temperature. There are negative biases in these simulations of approximately −1.5 K, while the bulk simulation has a negative bias of approximately −0.5 K. The negative biases in the BEP+BEM simulations are more pronounced at night and in the early morning. This issue deserves further investigation. It is possible that some adjustments to the vertical mixing in stable near-surface layers in the YSU PBL parameterization may be needed when it is coupled with BEP.
We have examined the performances of the UCMs during one event in Houston. Biases and errors for this one event cannot broadly be assumed to apply to other events. Evaluations of the UCMs in the YSU PBL scheme in more cities and under different synoptic conditions will give a more complete picture of their performances, leading to more concrete knowledge of where the UCMs and PBL schemes could be improved.
Author Contributions
Conceptualization, E.A.H. and J.C.K.; methodology, E.A.H. and J.C.K.; software, E.A.H.; validation, E.A.H.; formal analysis, E.A.H.; investigation, E.A.H. and J.C.K.; resources, J.C.K.; data curation, E.A.H.; writing—original draft preparation, E.A.H.; writing—review and editing, E.A.H. and J.C.K.; visualization, E.A.H.; supervision, E.A.H. and J.C.K.; project administration, J.C.K.; funding acquisition, J.C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the National Center for Atmospheric Research (NCAR), which is a major facility sponsored by the National Science Foundation under Cooperative Agreement 1852977. E.A.H. and J.C.K. acknowledge the support from the National Science Foundation (NSF) Prediction of and Resilience against Extreme Events (PREEVENTS) grant 1663978, managed by Justin E. Lawrence, and the U.S. Army Test and Evaluation Command (ATEC) through an Interagency Agreement with the NSF.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The WRFV4.3 model code can be dowloaded here: https://www2.mmm.ucar.edu/wrf/users/download/get_sources_new.php, accessed on 1 August 2022. The static data for the WRF preprocessing system contains the NUDAPT urban dataset for Houston. The NCAR Research Data Archive retains global reanalysis datasets for WRF initial and lateral boundary conditions. The NCEP GDAS final analysis used in the simulations in this manuscript can be downloaded here: https://rda.ucar.edu/datasets/ds083.3/, accessed on 1 August 2022.
Acknowledgments
We thank Yi Wang, Alberto Martilli, Jimy Dudhia, and Hyeyum Shin for helpful discussions. This manuscript was improved by the constructive comments of three anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGL | above ground level |
| BEP | Building Effect Parameterization |
| BEM | Building Energy Model |
| COI | commercial and industrial |
| GDAS | Global Data Assimilation System |
| HIR | high intensity residential |
| IGBP | International Geosphere-Biosphere Programme |
| LIR | low intensity residential |
| LST | local standard time |
| ME | mean error |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MSLP | mean sea level pressure |
| NCAR | National Center for Atmospheric Research |
| NCEP | National Centers for Environmental Prediction |
| NUDAPT | National Urban Data and Access Portal Tool |
| PBL | planetary boundary layer |
| RDA | Research Data Archive |
| RMSE | root mean squared error |
| RRTMG | Rapid Radiative Transfer Model GCMs |
| TCEQ | Texas Commission on Environmental Quality |
| TKE | turbulent kinetic energy |
| UCM | urban canopy model |
| UTC | Coordinated Universal Time |
| WPC | Weather Prediction Center |
| WRF | Weather Research and Forecasting |
| YSU | Yonsei University |
References
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.; Lin, X. Mesoscale observational analysis of isolated convection associated with the interaction of the sea breeze front and the gust front in the context of the urban heat humid island effect. Atmosphere 2022, 13, 603. [Google Scholar] [CrossRef]
- Rozoff, C.M.; Cotton, W.R.; Adegoke, J.O. Simulation of St. Louis, Missouri, land use impacts on thunderstorms. J. Appl. Meteor. Clim. 2003, 42, 716–738. [Google Scholar] [CrossRef]
- Peterson, T.C.; Owen, T.W. Urban heat island assessment: Metadata are important. J. Clim. 2005, 18, 2637–2646. [Google Scholar] [CrossRef]
- Zhong, S.; Yang, X.-Q. Mechanism of urbanization impact on a summer cold-frontal rainfall process in the greater Beijing metropolitan area. J. Appl. Meteor. Clim. 2015, 54, 1234–1247. [Google Scholar] [CrossRef]
- Eastin, M.D.; Baber, M.; Boucher, A.; Bari, S.D.; Hubler, R.; Stimac-Spalding, B.; Winesett, T. Temporal variability of the Charlotte (sub)urban heat island. J. Appl. Meteor. Clim. 2018, 51, 81–102. [Google Scholar] [CrossRef]
- Liu, J.; Niyogi, D. Meta-analysis of urbanization impact on rainfall modification. Sci. Rep. 2019, 9, 7301. [Google Scholar] [CrossRef]
- Vukovich, F.M. Theoretical analysis of the effect of mean wind and stability on a heat island circulation characeteristic of an urban complex. Mon. Weather Rev. 1971, 99, 919–926. [Google Scholar] [CrossRef]
- Martilli, A.; Clappier, A.; Rotach, M.W. An urban surface exchange parametrization for mesoscale models. Bound.-Layer Meteorol. 2002, 104, 261–304. [Google Scholar] [CrossRef]
- Salamanca, F.; Krpo, A.; Martilli, A.; Clappier, A. A new building energy model coupled with an urban canopy parameterization for urban climate simulations—Part I. Formulation, verification, and sensitivity analysis of the model. Theor. Appl. Climatol. 2011, 99, 331–344. [Google Scholar] [CrossRef]
- Wang, J.; Mao, J.; Zhang, Y.; Cheng, T.; Yu, Q.; Tan, J.; Ma, W. Simulating the effects of urban parameterizations on the passage of a cold front during a pollution episode in megacity Shanghai. Atmosphere 2019, 10, 79. [Google Scholar] [CrossRef]
- Holt, T.; Pullen, J. Urban canopy modeling of the New York City metropolitan area: A comparison and validation of single- and multilayer parameterizations. Mon. Weather Rev. 2007, 135, 1906–1930. [Google Scholar] [CrossRef]
- Martilli, A. Numerical study of urban impact on boundary layer structure: Sensitivity to wind speed, urban morphology, and rural soil moisture. J. Appl. Meteor. Climatol. 2002, 41, 1247–1266. [Google Scholar] [CrossRef]
- Salamanca, F.; Martilli, A.; Tewari, M.; Chen, F. A study of the urban boundary layer using different urban parameterizations and high-resolution urban canopy parameters in WRF. J. Appl. Meteor. Climatol. 2011, 50, 1107–1128. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; NCAR Technical Note; NCAR/TN-468+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2021; 88p. [Google Scholar] [CrossRef]
- Louis, J.F. A parametric model of vertical eddies fluxes in the atmosphere. Bound.-Layer Meteorol. 1979, 17, 187–202. [Google Scholar] [CrossRef]
- Santiago, J.L.; Martilli, A. A dynamic urban canopy parameterization for mesoscale models based on computational fluid dynamics Reynolds-averaged Navier–Stokes microscale simulations. Bound.-Layer Meteorol. 2010, 137, 417–439. [Google Scholar] [CrossRef]
- Gutierrez, E.; Martilli, A.; Santiago, J.L.; Gonzalez, J.E. A mechanical drag coefficient formulation and urban canopy parameter assimilation technique for complex urban environments. Bound.-Layer Meteorol. 2015, 157, 333–341. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Knievel, J.C.; Wang, Y. Addition of multilayer urban canopy models to a monlocal planetary boundary layer parameterization and evaluation using ideal and real cases. Bound.-Layer Meteorol. 2020, 59, 1369–1392. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Lim, J.-O. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Hong, S.-Y.; Pan, H.-L. Nonlocal boundary layer vertical diffusion in a Medium Range Forecast model. Mon. Wea. Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y. Projected future changes of tropical cyclone activity over the western north and south Pacific in a 20-km-mesh regional climate model. J. Clim. 2017, 30, 5923–5941. [Google Scholar] [CrossRef]
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modeling system: Development, evaluation, and applications to the urban environmental problems. Int. J. Climatol. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Ching, J.; Brown, M.; Burian, S.; Chen, F.; Cionco, R.; Hanna, A.; Hultgren, T.; McPherson, T.; Sailor, D.; Taha, H.; et al. National Urban Database and Access Portal Tool. Bull. Am. Meteorol. Soc. 2009, 90, 1157–1168. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Janjić, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of orography-induced turbulence in a mesobeta-scale model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).