Abstract
This work investigates extreme weather events such as the onset of medicanes, which can cause severe socioeconomic impacts, along with their predictability. In order to accurately forecast such events, the Weather Research and Forecasting (WRF) model and its state-of-the-art data assimilation modeling framework (WRFDA) were set up to produce high-resolution forecasts for the case study of Medicane Ianos, which affected Greece between 17 and 19 September 2020. Information from weather stations and the satellite precipitation product IMERG was blended with the background model information from the Global Forecast System (GFS) using the 4D variational data assimilation (4D-Var) technique. New fields in an 18 km spatial resolution domain covering Europe were generated and utilized as improved initial conditions for the forecast model. Forecasts were issued based on these improved initial conditions at two nested domains of 6 km and 2 km spatial resolution, with the 2 km domain enclosing Greece. Denial experiments, where no observational data were assimilated in the initial boundary conditions, showed that the temperature fields benefited throughout the forecasting horizon from the assimilation (ranging from a 5 to 10% reduction in the average MAE values), while neutral to slightly positive (ranging from a 0.4 to 2% reduction in the average MAE values) improvement was found for wind, although not throughout the forecast horizon. The increase in spatial resolution did not significantly reduce the forecast error, but was kept at the same small order of magnitude. A tendency of the model to overpredict precipitation regardless of assimilation was observed. The assimilation of the IMERG data improved the precipitation forecasting ability up to the 18th hour of forecast. When compared to assimilation experiments that excluded IMERG data, the assimilation of IMERG data produced a better representation of the spatial distribution of the precipitation fields.
1. Introduction
Weather-related events with poignant societal and economic impacts have long been studied by the scientific community. In order to produce useful weather forecasts, models that realistically represent the atmosphere are needed, and the initial conditions must be known accurately [1]. In this study, beyond the parameterization schemes, the initial conditions of the weather prediction model come into focus. Particular emphasis is placed on assimilating satellite precipitation products, with the goal of improving the forecasting of precipitation fields. Assimilating precipitation comes with its own challenges, with the scientific community utilizing different approaches, including dynamic initialization schemes, nudging techniques, and variational assimilation. Of the aforementioned methodologies, variational assimilation, utilized in this study, offers dynamical consistency, where precipitation data are assimilated directly and the model variables are adjusted to the observed precipitation [2].
The direct assimilation of precipitation using 4D-Var assimilation techniques has been investigated in both global [3] and regional modeling frameworks [2]. Lopez tested 4D-Var precipitation assimilation in the European Centre for Medium-Range Weather Forecasts (ECMWF) at a global scale and demonstrated improved precipitation forecasting ability when utilizing the 6-hour precipitation fields in contrast to the hourly data. The study also found that meteorological data such as geopotential, temperature, moisture, and wind forecast scores generally had a neutral or positive impact on the forecast quality. On a regional scale, with convection-permitting resolutions at 4 km and the WRF modeling system, precipitation assimilation had a positive impact on the model fields—most prominently on low-level moisture [2]. The authors concluded that precipitation assimilation reduced the spin-up time, removed false alarms, and produced precipitation forecasts closer to the observations. Interestingly, they also found that the impact persisted for up to three hours of simulations on average. Both studies used the National Centers for Environmental Prediction (NCEP) stage IV radar and gauge precipitation observations in their assimilation schemes.
The availability of gridded, global, high-resolution satellite precipitation products through the Global Precipitation Measurement (GPM) satellite constellation has made it possible for the scientific community to introduce these data into assimilation schemes under different case studies. Satellite precipitation data from the GPM constellation constitute a valuable source of information, the evaluation of which can give insights into the predictability of weather extremes and the associated behavior of the modeling system. The fact that the IMERG precipitation data cover a 20-year period globally enables the examination of the predictability of a wide range of extreme weather events in the past decades at a local scale when using an appropriate modelling framework. For example, Yi, Zhang, and Wang studied the 4D-Var assimilation of Integrated Multi-satellitE Retrievals for GPM (IMERG) data for heavy precipitation case studies over the Huaihe River Basin in China, with a spatial resolution reaching down to 9 km [4]. They reported that the WRF precipitation predictions were improved at a time interval of 12 h. Another study, also using the WRF modelling system, worked with the observations themselves by logarithmically transforming the precipitation measurements. They found better results when no transformation was applied and, in contrast to previous findings, they reported better performance with 1-hour precipitation products compared to 6-hour precipitation assimilation.
With respect to weather extremes and their predictability, assimilation of satellite precipitation with the WRF modelling system has been investigated for landfalling tropical cyclones (TC) in the Yangtze River Delta in China [5]. The study demonstrated that the assimilation affected the magnitude of WRF’s primary variables, changing the pattern of the TC heavy rain. The comparison with experiments excluding satellite precipitation showed better fraction skill scores (FSSs) when satellite precipitation was included. This was true for a threshold of 10 mm/h, and reversed results were obtained when examining thresholds lower than 5 mm/h.
In this study, the predictability of a Mediterranean tropical-like cyclone (Medicane Ianos) is examined. Intense cyclones occur every year in the Mediterranean basin, producing a broad range of socioeconomic and environmental impacts [6]. The Mediterranean cyclones are mostly created due to baroclinic instability and, similarly to the extratropical cyclones in the mid-latitude storm track, they are affected by diabatic processes. Examining reanalysis data covering a six-decade period, the authors of [7] estimated an average of 1.5 medicanes per year. Their predictability is a challenging task that has been addressed not only in data assimilation concepts but also in terms of the sensitivity of simulations to chosen parameters or forcings [8]. For example, in [9] it was found that for a medicane in the southern Mediterranean the intensity was mainly driven by the boundary/surface layer schemes, its track by the cumulus convection, and its duration by the defined microphysics. The same work concluded that an optimal combination of physical parameterizations simulating all of the characteristics could not be identified. Another study [10] concluded that different convective schemes led to different statistics of the Mediterranean cyclones and that different microphysics were usually affecting the trajectories of the medicanes. A coupling of atmosphere–ocean configuration was able to reproduce more accurate sea surface temperatures and heat fluxes in comparison to a multiphysics ensemble of standalone atmospheric models, as demonstrated in [11].
A systematic investigation of the forecast challenges related to medicanes was also undertaken during the MEDEX-TDS (Targeting Data System) campaign [12]. One of the milestones of the campaign included the identification of sensitive areas where improvements in the type and/or number of observations would be able to reduce the forecast errors. Such sensitivity experiments demonstrated that the benefits were variable and dependent on the relative location of the sensitive areas with respect to the distribution of the operational network of observations, as well as on the predictability characteristics of the case under analysis. In a similar manner, Garcies and Homar [13] verified the utility of the sensitivity products used in the campaign and concluded that there remains the challenge in identifying useful targeting strategies to improve Mediterranean cyclone prediction. Regarding observation assimilation, ensemble Kalman filters for calculating an ensemble of temporally and spatially evolving forecast errors were proposed by Carrió and Homar [14]. This would allow for the construction of a dynamic background error covariance matrix. To this end, a high-resolution ensemble-based assimilation technique (EnKF) was utilized to assimilate in situ conventional and satellite-derived observations to improve the prediction of Medicane Qendresa, which took place on the 7 October 2014 over the Sicilian Channel. Their results revealed an improvement of the short-range forecasts of the trajectory and intensity of Qendresa [15]. Moreover, refs. [13,16] demonstrated that improved analysis metrics—such as temperature, specific humidity, or wind levels—improve the 12–18-hour prediction of small-scale aspects of the cyclone structures.
Improved analysis by assimilating lightning was showcased in [17], leading to a positive impact of the representation of precipitation fields of a Mediterranean cyclone that affected France. This was also the case for [18], in which the impact of lightning data assimilation on the short-term precipitation forecast over the central Mediterranean Sea was investigated. More specifically, the forecasts were compared to the IMERG product and gauge observations, and they revealed a correlation improvement between the predicted and observed precipitation over wide areas of the Ionian Sea and the Adriatic Sea when lightning assimilation was applied.
In [19], the vLAPS model was utilized with a 3D-Var approach to produce the analysis fields as the initial condition for WRF. Sentinel-1 SAR winds were assimilated, and their impacts on the model simulations were examined for 20 cases, including Medicane Numa, which took place in November 2017 and made landfall in Greece, rendering the event the most severe experienced in Greece since 1977. In this work, the authors reported a remarkable improvement of the pressure minimum location of Numa in their simulations. In [20], a 3D-Var assimilation within WRF of the Global Navigation Satellite System (GNSS)’s zenith tropospheric delay (ZTD) was examined, and its impact on several case studies of high-impact rainfall over Greece was studied, including Medicane Zorbas, which impacted Greece between 29 and 30 September of 2018. In this work, the authors found a statistically significant positive impact of ZTD assimilation on the model’s precipitation forecasting ability over Greece.
Considering that the predictability of Medicanes is a multifactor and multiscale challenge, depending on the type of data assimilated and the type of assimilation technique, this work investigated the potential use of satellite precipitation products assimilated via the 4D-Var assimilation technique. More specifically, a 4D-Var assimilation scheme was set up and WRF was utilized to simulate the atmospheric conditions from the onset of the cyclone up to its dissipation. The objective of this work was to identify and quantify the impact of the satellite precipitation data on the quality of the weather predictions by a convection-permitting modelling system.
2. Materials and Methods
Ianos is considered to have been one of the strongest medicanes to have affected the Mediterranean over the last 25 years. In its initial stages, on 15 September 2020, Ianos developed as a thunderstorm cluster in the Gulf of Sidra. Two days later, on 17 September 2020, it evolved into a medicane, heading towards western Greece, before dissipating over the northern coasts of Egypt on 21 September 2020. Over the course of this 7-day period, Ianos followed a path over the Mediterranean area that exceeded 1900 km. During this medicane, extremely intense rainfall events were observed, with daily accumulated amounts exceeding 600 mm and 300 mm in the western and central parts of Greece respectively. As such, the socioeconomic impacts of this phenomenon were grave, leaving a long-lasting mark on the affected communities. Four human casualties and severe damage to various infrastructures were noted due to widespread floods and landslides [21].
To study this atmospheric phenomenon, simulations were conducted using the WRF modelling system and its data assimilation component. For the verification, the Model Evaluation Tools (MET) suite was utilized. A detailed explanation of the setup, the data, and the verification methodology is presented in the following sections.
2.1. Modeling System
The weather forecasts were performed using WRF (WRF-4.2.1), while the data assimilation part was performed with the WRF Data Assimilation model (WRFDA-4.2.1). WRF is able to provide atmospheric simulations suitable for a broad range of applications, while WRFDA provides the analysis—that is, the atmospheric fields taking into account satellite and ground-based observations to be used as initial conditions for WRF. Both models were configured in order to provide a coupled system of analysis/forecasts at high spatial resolutions enclosing Greece.
The WRF model was integrated in time to produce weather forecasts for six simulations in total, with the following initialization times: 00 UTC on 17 September 2022, 12 UTC on 17 September 2022, 00 UTC on 18 September 2022, 12 UTC on 18 September 2022, 00 UTC on 19 September 2022, and 12 UTC on 19 September 2022. The forecast horizon in all of them was 96 h, placing the ending times of each simulation as follows: 00 UTC on 21 September 2022, 12 UTC on 21 September 2022, 00 UTC on 22 September 2022, 12 UTC on 22 September 2022, 00 UTC on 23 September 2022, and 12 UTC on 23 September 2022, respectively. The model output in each case was chosen to have 1-hour intervals for time horizons of 4 days at 18 km spatial resolution covering Europe. This was further downscaled to 6 km spatial resolution covering the Mediterranean regions of Italy, Greece, North Africa, and western Turkey, with a 4-day forecast horizon. Finally, the 6 km spatial resolution domain (“parent”) enclosed Greece, the Aegean, and part of Turkey in a 2 km spatial resolution domain (“child”) that output forecasts for a forecast horizon of 2 days. A detailed depiction of the nests can be found in Figure 1.
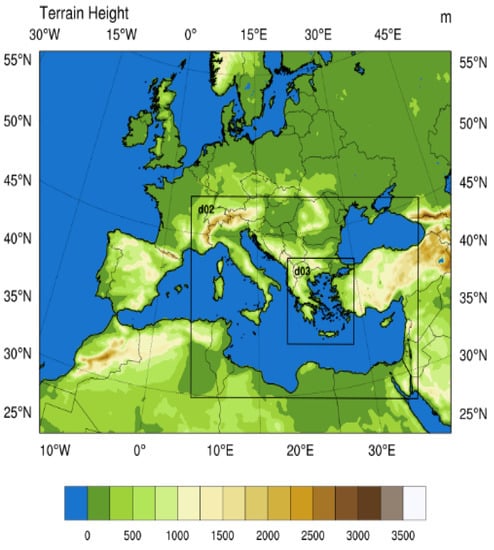
Figure 1.
Integration domains of the modeling system. The outer domain has a spatial resolution of 18 km, down to d02 of 6 km and enclosing Greece with a spatial resolution domain (d03) of 2 km.
The telescoping method was used for the creation of the nests, in which the meteorological information was communicated between the nests. This means that during all simulations the numerical model handled multiple domains at different grid resolutions that were run simultaneously and communicated (one-way) with one another. The 18 km resolution acted as a driver to the 6 km spatial resolution domain which, in turn, acted as a driver to the 2 km spatial resolution domain. The boundary and initial conditions for the model run were provided from the Global Forecast System (GFS) at 0.5 degrees [22]. Considering the importance of sea surface temperatures (SSTs) for the case study in question, the high-resolution Real-Time Global Sea Surface Temperature (RTGSST) dataset was introduced in the initial conditions of the simulations with a spatial resolution of 0.083 degrees [23]. The initial conditions, interpolated into the 18 km domain, were then improved by ingesting observations with the help of the assimilation model. The nest configuration is depicted in Figure 1.
The vertical resolution for each of the domains expanded to 39 eta levels following the terrain, up to 50 hPa. The convection-permitting physics suite utilized was the new Thompson et al. scheme with ice, snow, and graupel processes suitable for high-resolution simulations [24]. For the boundary layer simulation, the Yonsei University (YSU) suite was adopted [25], and the Noah-MP land-surface model was utilized [26]. The surface layer was based on the Monin–Obukhov scheme with a viscous Carlson–Boland sublayer and standard similarity functions from look-up tables [27]. The radiation scheme was based on the new version of the Rapid Radiative Transfer Model (RRTM) shortwave and longwave schemes added in V3.1 and onwards, including the MCICA method of random cloud overlap [28]. Cumulus parameterization was based on the Kain–Fritsch scheme, which is a deep and shallow convection subgrid scheme using a mass flux approach with downdrafts and a CAPE removal timescale [29].
The raw output from the forecasting model was further post-processed with the Unified Post Processor (UPP) in order to produce de-staggered grids and diagnostic variables saved in the common meteorological format GRIdded Binary (GRIB) [30]. For the verification of the results, a state-of-the-art package suite (MET) was configured to calculate the skill scores (detailed explanations in Section 2.3: Methodology). MET was developed by the Developmental Testbed Center (DTC), offering a variety of verification scores [31]. The containerized package suite from DockerHub was used to verify this case study [32].
2.2. Assimilation and Verification of Data
For the assimilation, both ground-based and satellite data were introduced in the outer domain of 18 km and blended in using the 4D-Var assimilation technique. The nested domains benefited from the updated information of the outer domain through the one-way nesting, passing the information from the outer domains to the enclosed domains. The impact of the assimilated observations on the produced forecasts was quantified by denial experiments (excluding observations from the assimilation) compared against reanalysis data. The denial experiments are presented in the Methodology section. First, a detailed description of the datasets follows.
For the ground-based observations, the Meteorological Assimilation Data Ingest System (MADIS) was used [33]. MADIS is a meteorological database of quality-checked observations that covers the globe. Observations from METerological Aerodrome Reports (METAR) were ingested into the assimilation scheme of WRFDA. They provided observations of wind, temperature, and relative humidity. These variables were assimilated in the outer domain of 18 km with the assimilation modelling system, using the two wind components, temperature, and specific humidity as inputs. As explained later, these transformations between what was expected from the assimilation modelling component and what was reported from weather stations were generated by the preprocessing pipelines of the assimilation model. The positions of MADIS stations within the outer simulation domain are depicted in Figure 2. In Figure 3, the locations of stations used to verify the results of the model forecasts are depicted.

Figure 2.
Locations of MADIS stations reporting measured atmospheric data on 18 September 2020 at 00 UTC.
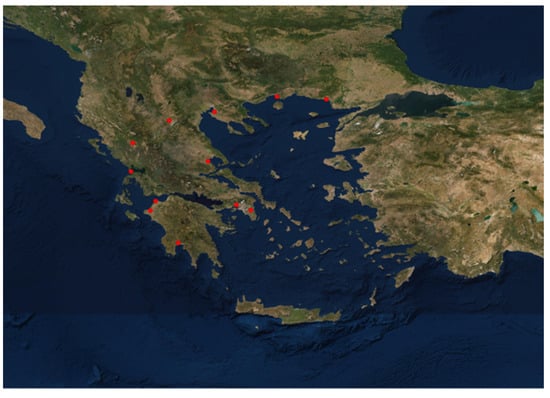
Figure 3.
Locations of stations used for verification purposes.
The datasets were accessed through the MADIS application programming interface (API). The WRFDA system expects the dataset to be in LITTLE-R format, which is an ASCII-based file format. The conversion from MADIS NetCDF files to LITTLE-R was performed via a Fortran routine. In the 4D-Var procedure, a 6-hour assimilation window was defined, in which all available MADIS observations were assimilated. In this time window, despite the dataset itself being quality-controlled, an extra step of preprocessing was performed that removed observations that were outside of the domain borders or had large discrepancies compared to the background model information (see Figure 4).
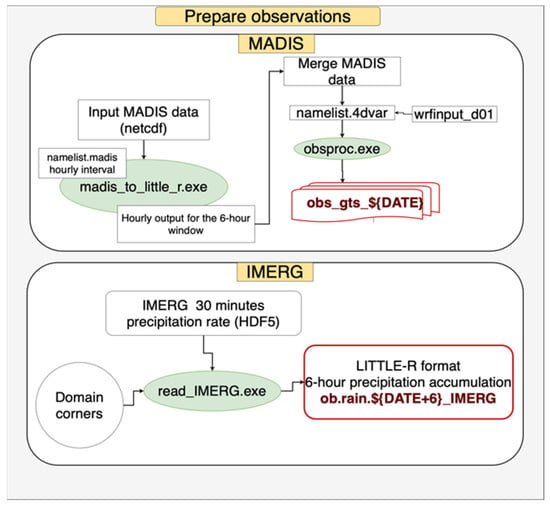
Figure 4.
Flowchart of the preprocessing steps for MADIS and IMERG data. In green are the executed components, and highlighted in red are the final files to be ingested in the WRFDA system.
The space-borne component of precipitation observations was provided from the Global Precipitation Measurement (GPM) constellation. Precipitation estimates from the constellation are made using passive microwave (PMW) sensors that are intercalibrated, merged, and interpolated with microwave-calibrated IR satellite estimates and precipitation gauge analyses. The final product—the Integrated Multi-satellitE Retrievals for GPM (IMERG)—provides 0.1° × 0.1° gridded precipitation fields [34]. Moreover, daily IMERG data are available to support operational weather forecasting, although the quality of the available data increases with time and the applied quality control. There are three types of available IMERG datasets: the early, late, and final runs. They differ in terms of their release time and amount of processing and calibration. The final run has 3.5 months of release latency and is considered to represent research-quality gridded global precipitation estimates with quasi-Lagrangian time interpolation, gauge data, and climatological adjustment. For the purposes of the case study, the 6-hour accumulation of precipitation at the end of the assimilation window was calculated. The multiple observations of 30-minute precipitation rates were converted to 6-hour accumulation in mm. The average value of the observation errors of the 30-minute precipitation rates, converted to mm, was assigned to the observations. The broad strokes of the workflow for the ingestion of these datasets to the initial conditions are depicted in Figure 4.
Regarding the verification, the station data depicted in Figure 3 were used for temperature and wind speed. The ECMWF’s reanalysis data (ERA5-Land) were used for precipitation, and they are available from the Copernicus Data Store (CDS) [35]. The reanalysis data followed the same principle as in the analysis, but at lower resolutions, in order to allow datasets spanning back decades to be included. ERA5 is the fifth-generation ECMWF reanalysis at a 0.25 resolution with global coverage and hourly datasets. It combines model data with observations from around the world into a globally consistent dataset. ERA5-Land is a replay of the land component of the ERA5 climate reanalysis downscaled to a ~12 km spatial resolution.
2.3. Methodology
The forecast/analysis scheme was applied for the three days 17–19 September 2020, during which Medicane Ianos severely affected Greece. In the applied scheme, the forecasts/analyses were initiated twice per day—at 00 and 12 UTC—in order to capture the boundary layer at stable and full growth over the course of the day. In the cycling procedure, the forecasts were initiated using the analysis, and the produced forecasts served as background information in the next cycle for the data assimilation procedure.
During the 4D-Var assimilation, a predefined cost function taking into account the observations and the background information was minimized. A window of six hours to use the available observations was defined, and the initial conditions for which the fit between the model and the observations was optimal were sought.
In order to examine the impact of the assimilated observations on the quality of the forecasts, three experiments were conducted. Experiment 1 (FULL) included the whole observational dataset in the assimilation, experiment 2 (GTS) excluded the IMERG data only, and experiment 3 (NO) had no assimilation procedure (control). Each experiment comprised six forecast/analysis cycles with forecast lengths of 4 days. Each child domain was initialized with a time lag of six hours from its parent domain, in order to provide some relaxation time.
For the comparison between observational data and the forecasts of the three domains at three spatial resolutions, a distance-weighted mean from forecast to the observation location was performed. The forecast value at each grid point was a weighted sum of the values in the interpolation area. The weight given to each forecast point was the reciprocal of the square of the distance (in grid coordinates) from that specific grid point. The weighted sum of the forecast values was normalized by dividing by the sum of the weights [36]. For discrete variables (i.e., precipitation), the nearest neighbors methodology was adopted and performed over a 3-by-3 box centered on each grid point, i.e., over the 9 surrounding grid points closest to the observations (Figure 5).
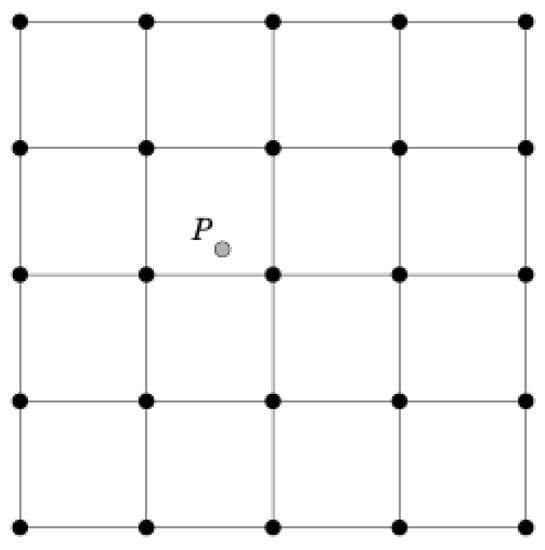
Figure 5.
Illustration of the nearest neighbor interpolation method used for the calculation of the skill scores [36].
Forecast scores for continuous variables included the commonly used mean absolute error (MAE):
where represents the forecasted values, the observed values, and N the total count of the forecast–value pairs.
For the precipitation, the Fraction Skill Score (FSS) is a widespread statistical parameter used for evaluation purposes, and was calculated as follows:
The numerator is the fraction Brier score (FBS), calculated as follows:
The denominator represents the worst case scenario of no overlapping between the forecasts and the observations. is the proportion of grid boxes that have forecast events, while is the proportion of grid boxes that have observed events. The score ranges between 0 and 1, with 0 representing no overlap and 1 representing complete overlap between forecast and observed events.
3. Results
Aggregated Statistics
The forecasts were first evaluated in terms of aggregated statistics over the number of simulations, for which purpose boxplots per forecast hour were plotted as shown in the following figures. As Ianos and its impact on Greece were studied, the time series of the examined scores (i.e., MAE, FSS) for all simulations in Greece for the three experiments (i.e., FULL, GTS, NO) and the three spatial resolutions (i.e., 18 km, 6 km, and 2 km) were plotted. Results are only shown for 00 UTC initializations that were found to outperform the 12 UTC initializations in terms of forecast skill (not shown here).
In Figure 6, the boxplots of the hourly two-meter temperature MAE time series for the simulations of 17–19 September 2020 and initializations at 00 UTC are plotted. First, examining the three types of experiments, there is an obvious improvement in terms of lower temperature MAE values from evening to night hours when comparing the NO experiment against the experiments with data assimilation included (i.e., FULL, GTS). Previous studies reported that the YSU planetary boundary layer in WRF performed worse during night compared to during the day [37]. The assimilation experiments contributed to the reduced MAE during night hours, persisting to a lesser extent to the final hours of the simulations. During the day hours, all experiments were within the same range of MAE, albeit smaller than the MAEs during night hours. An exception to this pattern can be seen for the domain of 2 km spatial resolution in the first 24 h, where we can observe an almost continuous improvement in absolute MAE from day to night (especially in the experiments that included the assimilation of observations). This can be attributed to the enhanced spatial representation of the terrain and the surface–atmosphere interactions at high spatial resolutions.

Figure 6.
Hourly time series of 2 m temperature MAE for the area of Greece. Each panel refers to a specific spatial resolution domain and the scores achieved for each type of experiment (i.e., FULL, GTS, NO). In blue are the boxplots for the FULL experiment; the GTS experiment is depicted in red and the NO experiment is depicted in green.
After the 78th hour of simulations, the benefit from assimilating observations was lost, as is evident from the range of temperature MAE being the same regardless of the experiment. There was clearly greater fluctuation of MAE during the first 54 h of simulations, hinting at the crossing of the phenomenon from the simulation domain. After the 54th hour, the MAE values returned to their expected values for temperature.
In Figure 7, in order to make the experiments’ results clearer, the mean MAE of each experiment per forecast hour is plotted. Contrary to our expectations—especially for the expected improvement in temperature because of the assimilated temperature observations from weather stations in the GTS experiment—we can see that in the first 12 h the NO assimilation experiment outperformed the GTS experiment. One possible explanation could be the fact that stations over land were used for assimilation, while temperature data over sea are vital for the initial boundary conditions as they are drivers of the phenomenon. Nonetheless, there was a 4.97% reduction in the mean temperature MAE for the GTS experiment in the 18 km domain 01 relative to the NO assimilation experiment. This was followed by a 4.44 % reduction for the FULL experiment in the same domain. It is impressive that the FULL experiment achieved a reduction in mean MAE of almost 10% in the domains of 6 km and 2 km spatial resolution, while the GTS experiment remained at the same level of ~5% reduction. The better average scores at higher-resolution domains can be attributed to the spin-up time of 6 h between the nests and, of course, to the better representation of the terrain. The fact that the FULL experiment outperforms the GTS experiment could be attributed to the inclusion of both surface and satellite information in the FULL experiment, as the precipitation fields corrected by the assimilation cause an adjustment of the state variables of the model.

Figure 7.
Hourly time series of 2 m temperature MAE for the area of Greece. Each panel refers to a specific spatial resolution domain and the scores achieved for each type of experiment (i.e., FULL, GTS, NO). The blue lines represent the FULL experiment, the GTS experiment is depicted in red, and the NO experiment is depicted in green.
Following the same analysis as for the two-meter temperature, Figure 8 presents the time series of the hourly MAE for the 10-meter wind speed. In Figure 9, a clear contribution of the assimilation to the improvement in the forecast skill cannot be seen—especially when noting how close the MAE of the three experiments is in all three domains. However, it can be seen that the GTS and NO experiments show a worse MAE than the FULL experiment. An example can be seen between hours of 24–30 and 48–54 h. This was unexpected, as the assimilation of wind, which affects the kinetic energy of the modeling system, should have pushed the system closer to the observations. In terms of spatial resolution, we observed a large improvement in the forecast performance in the high-spatial-resolution domain of 2 km compared to the other two domains. The reduction in MAE of the assimilation experiments relative to the no-assimilation experiment ranged from 0.4 to 2% in the higher-resolution domains. Considering the computational costs of the assimilation, and for wind speed, one would prefer to perform dynamical downscaling to improve the wind speed forecasts in this case than to perform assimilation. Altogether, low wind-speed MAE was achieved throughout the simulation hours as well as for the three integration domains at different spatial resolutions.
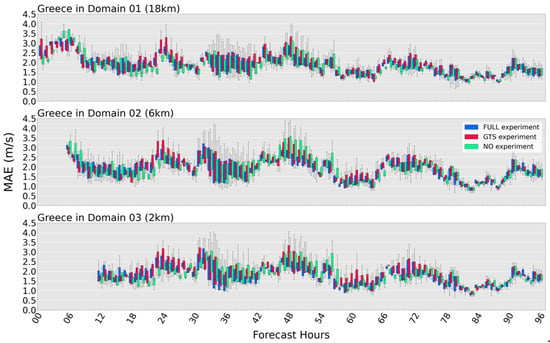
Figure 8.
Hourly time series of 10 m wind speed MAE for the area of Greece. Each panel refers to a specific spatial resolution domain and the scores achieved for each type of experiment (i.e., FULL, GTS, NO). In blue are the boxplots for the FULL experiment; the GTS experiment is depicted in red and the NO experiment is depicted in green.

Figure 9.
Hourly time series of 10 m wind speed MAE for the area of Greece. Each panel refers to a specific spatial resolution domain and the scores achieved for each type of experiment (i.e., FULL, GTS, NO). The blue lines represent the FULL experiment, the GTS experiment is depicted in red, and the NO experiment is depicted in green.
Aside from temperature and wind speed, the focus was also on the precipitation skill scores of the three experiments, with a particular focus on the experiment that included the satellite precipitation from IMERG. It should be noted that in contrast to MAE, larger values for the FSS score denote better performance in predicting the hourly precipitation accumulation. In Figure 10, the hourly precipitation accumulation FSS score for the examined experiments is depicted. Towards a clearer view of the comparison results, Figure 11 showcases the mean FSS score per hour. Clearly, all simulations performed better in the first hours of the simulations, reaching the highest values around the 18th simulation hour. In contrast to the temperature and wind speed results, which showed larger fluctuations of MAE between 0 and 54 h, the precipitation score seemed to have better values in the same time range for all experiments. This means that this modeling system, with and without assimilation, has a good ability to predict precipitation during the passing of the phenomenon from the simulation domain. Among the experiments, the FULL approach seemed to boost the forecast skill between the 24th and 38th simulation hours. After the 38th hour a drop in the skill was noted in all experiments, and after the 60th hour the skill was considered negligible. When comparing between the three spatial resolution domains, no distinct improvement was seen as a result of higher resolutions.

Figure 10.
Hourly time series of precipitation accumulation FSS for the area of Greece. Each panel refers to a specific spatial resolution domain and the scores achieved for each type of experiment (i.e., FULL, GTS, NO). In blue are the boxplots for the FULL experiment, the GTS experiment is depicted in red, and the NO experiment is depicted in green.
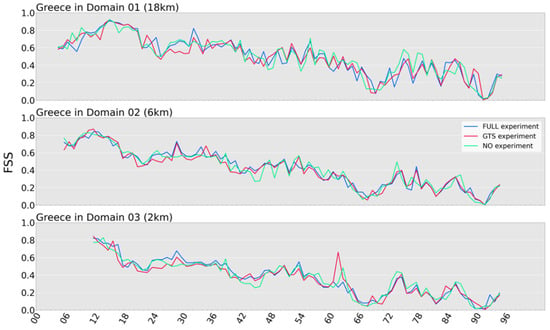
Figure 11.
Hourly time series of precipitation accumulation mean FSS for the area of Greece. Each panel refers to a specific spatial resolution domain and the scores achieved for each type of experiment (i.e., FULL, GTS, NO). The blue lines represent the FULL experiment, the GTS experiment is depicted in red, and the NO experiment is depicted in colors.
As the on-set and impact of Ianos in Greece occurred on the 18th September, the skill scores for this day were examined separately, and focus was also placed on the spatial distribution of precipitation as simulated by the WRF experiments and observed by satellite data.
Ianos—Case Study
Greece was impacted by Ianos, suffering floods, with emphasis on 18 September 2020. For this reason, the analysis minus background (hereafter A_minus_B) for the assimilation taking place on 18 September 2020 at 00 UTC was examined, with the aim of shedding light on the updated initial conditions and their effects on the forecast ability. In Figure 12, the A_minus_B is presented for the 6-hour accumulated precipitation and for the FULL and GTS experiments. The precipitation fields of Medicane Ianos are clearly enhanced (positive A_minus_B) by both experiments, while the FULL experiment places the Medicane’s northern main body in comparison to GTS. This affects the distribution of precipitation in Greece which, as seen later, is better captured in the FULL experiment.
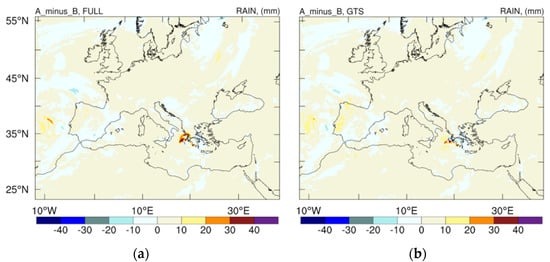
Figure 12.
Analysis minus background for the accumulated 6-hour precipitation in mm between 00 and 06 UTC on 18 September 2020 for (a) the FULL experiment and (b) the GTS experiment.
The 2 m temperature and 10 m wind speed A_minus_B are also presented in Figure 13 and Figure 14, respectively. The 2 m temperature was reduced by 2–3 °C in western Greece, where Ianos was most impactful, compared to the experiments’ backgrounds. This helped to improve the forecast ability by almost 10% in terms of MAE reduction for the 2 m temperature compared to the no assimilation experiments in the high-resolution domains. Between GTS and FULL, there were no substantial spatial differences in 2 m temperature fields, as FULL has the same weather station observations assimilated plus satellite precipitation fields. This is also reflected in the intertwined forecast skill lines for the assimilation experiments of the 2 m temperature depicted in Figure 7 (Greece in domain 01). Regarding the 10 m wind speed, there was an enhancement of the cyclonic speed induced by the assimilation in both the FULL and GTS experiments. Again, there was a northern placement of Ianos by the FULL experiment compared to the GTS. A large positive A_minus_B was seen at the southern counterpart of Ianos in both experiments, showing higher speed in this counterclockwise motion. This large enhancement was more prominent in the FULL experiment, probably due to corrections among the state variables of kinetic energy by the adjustments of the precipitation fields. These corrections did not appear to improve the forecast skill as much in terms of reduced 10 m wind MAE, but they seemed to have contributed to the spatial placement of Ianos.

Figure 13.
Analysis minus background for the 2 m temperature (°C) at 00 on 18 September 2020 for (a) the FULL experiment and (b) the GTS experiment.
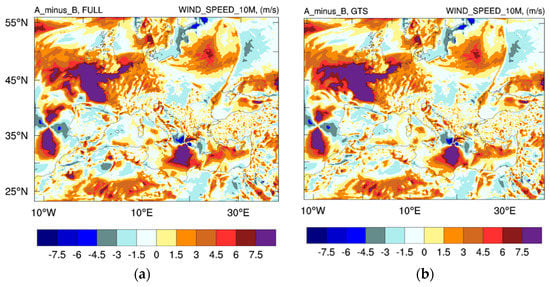
Figure 14.
Analysis minus background for the 10 m wind speed (m/s) at 00 on 18 September 2020 for (a) the FULL experiment and (b) the GTS experiment.
An examination of the FSS score follows for the 2 km domain on the day with the most severe weather phenomena (18 September 2020), and this is presented in Figure 15. The signal of the FULL experiment stood out during the daylight hours. During the nighttime hours although it seems that the exclusion of the IMERG dataset in the GTS experiment resulted in the production of better-performing forecasts. Keeping in mind that higher values of FSS score indicate a better performance, and looking at the first 18 h of the simulations in Figure 15, we can see that when assimilation takes place in the FULL and GTS experiments, it results in better scores than the experiments without assimilation.
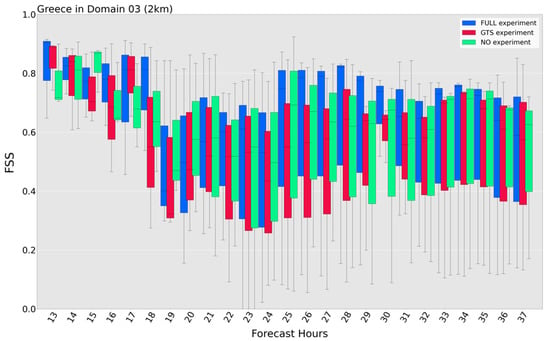
Figure 15.
Hourly time series of precipitation accumulation FSS for 18 September 2020, for the area of Greece, at the 2 km domain. The blue boxplots correspond to the FULL experiment, the GTS experiment is depicted in red, and the NO experiment is depicted in green.
The precipitation accumulation and its spatial distribution in 6 h intervals are given in Figure 16 and Figure 17, respectively. The maps also show ERA5-Land reanalysis data, noting that a comparison was only available over land.

Figure 16.
Spatial distribution of precipitation accumulated from 12 to 18 UTC on 18 September 2022. In (a), the accumulated precipitation as predicted from the FULL simulations is depicted. In (b), the accumulated precipitation as predicted from the GTS simulations is depicted. In (c,d), the accumulated precipitation from the NO simulation and from the reanalysis data ERA5-Land is shown, respectively.
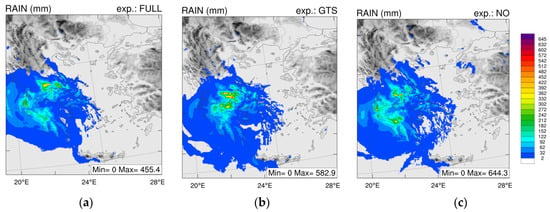
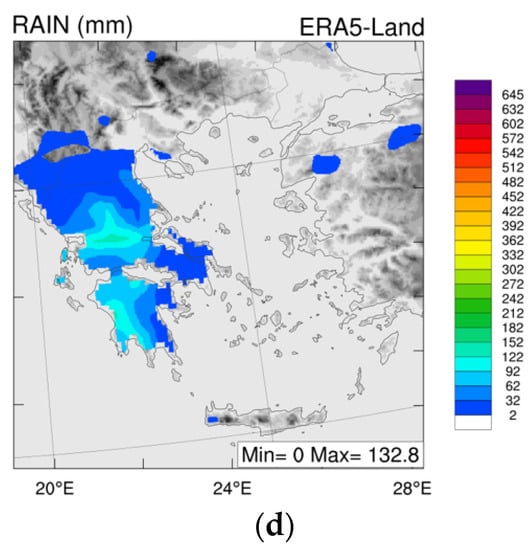
Figure 17.
Spatial distribution of precipitation accumulated from 18 to 24 UTC on 18 September 2022. In (a), the accumulated precipitation as predicted from the FULL simulations is depicted. In (b), the accumulated precipitation as predicted from the GTS simulations is depicted. In (c,d), the accumulated precipitation from the NO simulation and from the reanalysis data ERA5-Land is shown, respectively.
More specifically, in Figure 16, the 2 km spatial resolution domain for Greece depicting the accumulated precipitation in mm from 12 to 18 UTC on 18 September 2020 is presented. The upper three plots (a,b,c) showcase the forecasts produced in each of the three experiments (i.e., FULL, GTS, NO), while the fourth (d) depicts the ERA5-Land reanalysis data for the same time period and geographical area. The maximum precipitation values noted, as can also be seen on the maps, are 367.8 mm for the experiment assimilating both the MADIS and IMERG data, 429.3 mm for the experiment where the IMERG data were excluded from the assimilation, 322.6 mm when no assimilation took place, and 126.9 mm from the gridded reanalysis data. It is clear that the model tends to overpredict the accumulated precipitation, regardless of assimilation. When observations were assimilated from the GTS, the overprediction of precipitation was exaggerated. When on top of the GTS, the IMERG precipitation data were assimilated (FULL experiment), and there was a reduction in the maximum precipitation accumulation, meaning that the assimilation model corrected the precipitation fields towards the IMERG values. Nonetheless, the experiment with no assimilation was found to be closer to the ERA5-Land fields. When it comes to the NO experiment being better than the GTS experiment, this can be explained by the fact that the GTS offers surface observations to be assimilated and does not directly address precipitation fields but, rather, state variables within the model that address the kinetic energy (wind components) and available potential temperature. The direct assimilation of precipitation fields within the 4D-Var context, although it improves the precipitation fields compared to GTS in this case study, does not do better than the no assimilation experiment. The direct assimilation of precipitation is a relatively recent addition within WRFDA and comes with the known issues regarding simplification of condensation and cumulus schemes in the adjoint and tangent linear codes. Only an extensive study, though, could conclusively state if 4D-Var direct precipitation assimilation brings added value to forecast skills.
With regards to spatial distribution, all experiments were able to forecast the intense precipitation cases over land, with the exception of the GTS, where the precipitation over the west Peloponnese is underpredicted. The maximum precipitation values, although overpredicted for the Greek domain, are placed correctly over areas that were indeed flooded in Thessaly.
Figure 17, similarly, presents the accumulated precipitation in mm from 18 to 24 UTC on 18 September 2020 for a 2 km spatial resolution domain of Greece. The upper three plots (a,b,c) showcase the forecasts produced in each of the three experiments (FULL, GTS, NO) and the fourth one (d) the ERA5-Land reanalysis data for the same time and geographical area. The maximum precipitation values noted were 455.4 mm for the experiment assimilating both the MADIS and IMERG data, 582.9 mm for the experiment where the IMERG data were excluded from the assimilation, 644.3 mm when no assimilation took place, and 132.8 mm from the gridded reanalysis data. Similarly, for the results of the 12 to 18 UTC accumulation, the model tended to over-predict the accumulation of precipitation. However, in contrast to the previous results, the experiment with no assimilation is among those farthest away from the ground truth (ERA5-Land), followed by the GTS experiment. When IMERG data were included, the forecast was brought closer to the truth despite the large overprediction. When it comes to the spatial distribution, as discussed previously, GTS seems to produce different precipitation patterns in the Peloponnese.
In addition to the model-reanalysis data comparison, to further quantify the forecast quality during the most extreme day of the medicane, a model satellite data comparison was performed as well, resulting in Figure 18 and Figure 19.

Figure 18.
Bar chart depicting the average spatial values of the accumulated precipitation in mm from 12 to 18 UTC on 18 September 2020 for the high-resolution domain. Green corresponds to the FULL experiment forecasts, yellow to the GTS experiment, red to the NO experiment, and blue to the IMERG precipitation product.
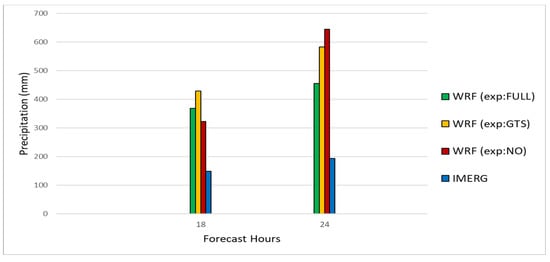
Figure 19.
Bar chart depicting the spatial maximum values of the accumulated precipitation in mm from 18 to 24 UTC on 18 September 2020 for the high-resolution domain. Green corresponds to the FULL experiment forecasts, yellow to the GTS experiment, red to the NO experiment, and blue to the IMERG precipitation product.
For the diagram present in Figure 18, for each of the three experiments and the IMERG data, the spatial average of the precipitation accumulation in the 2 km spatial resolution domain was computed for the two 6-hour periods (12–18 UTC and 18–24 UTC on 18 September 2020). The exclusion of the IMERG precipitation products from the assimilation (GTS experiment) produced the forecasts closest to the actual satellite values, followed closely by the forecasts with no assimilated observations, whereas the inclusion of IMERG in the assimilation produced the most divergent forecasts in terms of spatial averaging.
Similarly, for the diagram in Figure 19, for each of the three experiments and the IMERG data, the spatial maximum of the precipitation accumulation in the 2 km spatial resolution domain was computed for two 6-hour periods: 12–18 UTC and 18–24 UTC on 18 September 2020. As was the case with the model-reanalysis comparison, for the 12–18 UTC period forecasts, with no assimilated observations performed better, in contrast to the 18–24 UTC period where assimilation all available datasets (MADIS, IMERG) helped improve the forecast quality in terms of spatial maximum values.
4. Summary and Discussion
The predictability of impactful weather events, such as medicanes, was examined in this research. The adopted approach targeted temperature, wind speed, and precipitation forecasts at a 4-day forecast horizon. Medicane Ianos, a destructive extreme event to Greece with flooding and loss of life, was selected as our case study. A 4D-Var assimilation scheme was set up to improve the initial conditions. The assimilated data included ground-based observations from weather stations and satellite precipitation products. Three experiments were conducted to investigate the added value of assimilated observations in the final forecasts—the control “NO” experiment where no assimilation took place, the “FULL” experiment where all observations were included, and the “GTS” experiment where the precipitation product was excluded from the assimilation. All experiments were compared in terms of skill scores, with weather stations for temperature and wind speed, while the ERA5-Land reanalysis dataset at ~12 km spatial resolution was utilized to derive the precipitation scores.
Looking at the forecast skill results, better scores for temperature were achieved in the simulations during daylight hours in comparison to night hours. This confirms the results found in [26], where the boundary layer scheme was found to produce this pattern. Clearly, the assimilation smoothed this preference, improving the forecast quality. For the 10-meter wind speed results, low wind-speed MAE was achieved throughout the simulation hours as well as for the three integration domains at different spatial resolutions, although no significant differences were noted in the experiments with assimilated observations. Therefore, considering the computational costs, we would have preferred to perform dynamic downscaling to improve the wind speed forecast for this case, rather than also including the 4D-Var assimilation of observations. The aggregated results revealed that this setup of the modelling framework was able to improve the precipitation skill score up to the 54th simulation hour, in contrast to the wind and temperature skill scores, which suffered during the passing of the phenomenon from the simulation domain.
Due to our interest in the predictability of Medicane Ianos, the focus shifted to the most intense day that impacted Greece. Hence, the results for the high-spatial-resolution domain were examined for the most impactful day in terms of medicane intensity on 18 September 2020. It was found that all simulations, whether with or without assimilation, overpredicted the rainfall amount. The FSS score was found to be higher for the FULL experiment between the 24th and 38th hours of simulations compared to the other two experiments.
Focusing on 6-hour intervals of precipitation accumulation between 12 and 18 UTC, the forecasts with no assimilation seemed to outperform the assimilation experiments in terms of maximum accumulation over the domain. Between the assimilation experiments, the maximum precipitation accumulation was brought closer to the ground truth when the IMERG data were assimilated for the same 6-hour period. Between 18 and 00 UTC, the FULL experiment outperformed all experiments in terms of maximum value, although its results were still far from the ground truth. Moreover, the IMERG assimilation did bring the results closer to the reanalysis data for rainfall and corrected the spatial distribution over the Peloponnese when compared to the GTS experiment. When examining the spatial averages of the domain for the three experiments and for the IMERG satellite data, the findings showed opposite behavior compared to the maximum precipitation accumulation results. It was found that the GTS experiment for the examined day had a spatial average of accumulated precipitation closer to the satellite data results than the FULL experiment, meaning that the inclusion of IMERG data did manage to smooth out extremes but was outperformed by GTS in terms of spatial averaging. This finding should be interpreted carefully, as the spatial distribution of the precipitation was closer to the ground truth when the IMERG data were included. It is possible that the inclusion of GTS data misplaced the precipitation distribution, adding only some extreme values over specific areas while reducing the amount of precipitation in other areas.
In general, the inclusion of observations in the forecasting system can benefit the forecast quality with an appropriate model setup. We found that including precipitation satellite products brought the atmospheric state closer to the truth while also reshaping the spatial distribution of the precipitation closer to the truth. Despite this, the model configuration favored the overprediction of the precipitation patterns regardless of assimilation. The impact of the assimilated observations was found to persist for temperature over the simulation horizon, while precipitation improvement was seen only up to few hours of simulations, consistent with the results of previous studies.
While some benefit can be gleaned from assimilation, there are some points to consider. This research was conducted only for one medicane test case, and no definite conclusions can be drawn. It is possible that with another model setup, altered results could be obtained, but safer conclusions could only be plausible if more test cases could be examined using the same setup. It must be added here that 4D-Var assimilation is computationally expensive, limiting the number of test cases. Moreover, for this case study, the final run of the IMERG product was chosen. The availability of this research-quality product is not suitable for operational assimilation and forecasting. For the operational case, the early run has to be chosen, although with some concerns as to the quality loss of the product. Despite this, IMERG satellite products leave room to investigate possible benefits from all available datasets and possibly computationally cheaper assimilation algorithms.
Author Contributions
P.V., S.K., A.A. and T.M. all contributed equally to the conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing and preparation of the original draft, review and editing, visualization, supervision, project administration, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the European Union’s Horizon 2020 under reSilienT fARminG by Adaptive microclimaTe managEment (STARGATE) project (no. 818187).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All of the data used in this study are available upon request.
Acknowledgments
The authors would like to acknowledge the European Union’s Horizon 2020 and STARGATE project for funding the work, as well as the Copernicus Climate Data Store (https://confluence.ecmwf.int/display/CKB/Use+Case+1%3A+ERA5-Land+hourly+data+from+1950+to+present, accessed on 10 October 2022) for providing the ERA5-Land data used in this study.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ban, J.; Liu, Z.; Zhang, X.; Huang, X.Y.; Wang, H. Precipitation data assimilation in WRFDA 4D-Var: Implementation and application to convection-permitting forecasts over United States. Tellus A Dyn. Meteorol. Oceanogr. 2017, 69, 1368310. [Google Scholar] [CrossRef]
- Lopez, P. Direct 4D-Var assimilation of NCEP stage IV radar and gauge precipitation data at ECMWF. Mon. Weather. Rev. 2011, 139, 2098–2116. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, W.; Wang, K. Evaluation of heavy precipitation simulated by the WRF model using 4D-Var data assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China. Remote Sens. 2018, 10, 646. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Yang, L.; Wang, Q.; Yuan, J.; Wang, Y. Data assimilation of high-resolution satellite rainfall product improves rainfall simulation associated with landfalling tropical cyclones in the Yangtze river Delta. Remote Sens. 2020, 12, 276. [Google Scholar] [CrossRef]
- Flaounas, E.; Davolio, S.; Raveh-Rubin, S.; Pantillon, F.; Miglietta, M.M.; Gaertner, M.A.; Hatzaki, M.; Homar, V.; Khodayar, S.; Korres, G.; et al. Mediterranean cyclones: Current knowledge and open questions on dynamics, prediction, climatology and impacts. Weather. Clim. Dyn. 2022, 3, 173–208. [Google Scholar] [CrossRef]
- Cavicchia, L.; von Storch, H.; Gualdi, S. A long-term climatology of medicanes. Clim. Dyn. 2014, 43, 1183–1195. [Google Scholar] [CrossRef]
- Miglietta, M.M. Mediterranean Tropical-Like Cyclones (Medicanes). Atmosphere 2019, 10, 206. [Google Scholar] [CrossRef]
- Pytharoulis, I.; Kartsios, S.; Tegoulias, I.; Feidas, H.; Miglietta, M.; Matsangouras, I.; Karacostas, T. Sensitivity of a Mediterranean Tropical-Like Cyclone to Physical Parameterizations. Atmosphere 2018, 9, 436. [Google Scholar] [CrossRef]
- Ragone, F.; Mariotti, M.; Parodi, A.; Von Hardenberg, J.; Pasquero, C. A Climatological Study of Western Mediterranean Medicanes in Numerical Simulations with Explicit and Parameterized Convection. Atmosphere 2018, 9, 397. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Barbariol, F.; Benetazzo, A.; Bergamasco, A.; Bonaldo, D.; Cassardo, C.; Falcieri, F.M.; Modugno, G.; Russo, G.A.; et al. Sensitivity of a Mediterranean tropical-like cyclone to different model configurations and coupling strategies. Atmosphere 2017, 8, 92. [Google Scholar] [CrossRef]
- Jansa, A.; Arbogast, P.; Doerenbecher, A.; Garcies, L.; Genoves, A.; Homar, V.; Klink, S.; Richardson, D.; Sahin, C. A new approach to sensitivity climatologies: The DTS-MEDEX-2009 campaign. Nat. Hazards Earth Syst. Sci. 2011, 11, 2381–2390. [Google Scholar] [CrossRef]
- Garcies, L.; Homar, V. Are current sensitivity products sufficiently informative in targeting campaigns? A DTS-MEDEX-2009 case study: Testing DTS-MEDEX-2009 Sensitivity Products. Q. J. Roy. Meteorol. Soc. 2014, 140, 525–538. [Google Scholar] [CrossRef]
- Carrió, D.S.; Homar, V. Potential of sequential EnKF for the short-range pre-diction of a maritime severe weather event. Atmos. Res. 2016, 178–179, 426–444. [Google Scholar] [CrossRef]
- Carrió, D.S. Challenges assessing the effect of AMVs to improve the predictability of a medicane weather event using the EnKF. Storm-scale analysis and short-range forecast. Nat. Hazards Earth Syst. Sci. Discuss. 2022; 1–37, preprint. [Google Scholar]
- Carrió, D.S.; Homar, V.; Wheatley, D.M. Potential of an EnKF Storm-Scale Data Assimilation System Over Sparse Observation Regions with Complex Orography. Atmos. Res. 2019, 216, 186–206. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Kotroni, V.; Defer, E.; Bousquet, O. Study of a heavy precipitation event over southern France, in the frame of HYMEX project: Ob-servational analysis and model results using assimilation of lightning. Atmos. Res. 2013, 134, 45–55. [Google Scholar] [CrossRef]
- Torcasio, R.C.; Federico, S.; Comellas Prat, A.; Panegrossi, G.; D’Adderio, L.P.; Dietrich, S. Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea. Remote Sens. 2021, 13, 682. [Google Scholar] [CrossRef]
- Tiesi, A.; Pucillo, A.; Bonaldo, D.; Ricchi, A.; Carniel, S.; Miglietta, M.M. Initialization of WRF Model Simulations with Sentinel-1 Wind Speed for Severe Weather Events. Front. Mar. Sci. 2021, 8, 573489. [Google Scholar] [CrossRef]
- Giannaros, C.; Kotroni, V.; Lagouvardos, K.; Giannaros, T.M.; Pikridas, C. Assessing the Impact of GNSS ZTD Data Assimilation into the WRF Modeling System during High-Impact Rainfall Events over Greece. Remote Sens. 2020, 12, 383. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Karagiannidis, A.; Dafis, S.; Kalimeris, A.; Kotroni, V. Ianos—A hurricane in the Mediterranean. Bull. Am. Meteorol. Soc. 2022, 103, E1621–E1636. [Google Scholar] [CrossRef]
- Global Forecasting System (GFS). Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ncdc:C00634 (accessed on 7 October 2022).
- NCEP Products Inventory, Sea Surface Temperature (SST) Models. Available online: https://www.nco.ncep.noaa.gov/pmb/products/sst/ (accessed on 23 August 2022).
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Liu, Z.; Berner, J.; Huang, X.-Y.; Wang, W.; Powers, J.G.; Duda, M.G.; et al. A Description of the Advanced Research WRF Version 4; NCAR Tech: Boulder, CO, USA, 2019; Note NCAR/TN-556+STR. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather. Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Xia, Y.; Kumar, A.; Manning, K.; Niyogi, D.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Jimenez, P.A.; Dudhia, J.; Gonzalez–Rouco, J.F.; Navarro, J.; Montavez, J.P.; Garcia–Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Wea. Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long–lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteor. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Development Testbed, Unified Post Processor (UPP). Available online: https://dtcenter.org/community-code/unified-post-processor-upp (accessed on 23 August 2022).
- Development Testbed, Model Evaluation Tools (MET). Available online: https://dtcenter.org/community-code/model-evaluation-tools-met (accessed on 23 August 2022).
- Docker Hub Page for the Official Image of MET. Available online: https://hub.docker.com/r/dtcenter/met (accessed on 23 August 2022).
- Meteorological Assimilation Data Ingest System. Available online: https://madis.ncep.noaa.gov/ (accessed on 7 October 2022).
- NASA Official Website for the Integrated Multi-SatellitE Retrievals for GPM. Available online: https://gpm.nasa.gov/data/imerg (accessed on 23 August 2022).
- ERA5-Land Data Page on Climate Data Store. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=overview (accessed on 23 August 2022).
- MET Software Documentation Concerning the Interpolation/matcing Methods Applied. Available online: https://met.readthedocs.io/en/latest/Users_Guide/point-stat.html?highlight=distance%20weighted%20mean%20#interpolation-matching-methods (accessed on 26 September 2022).
- Hu, X.-M.; Klein, P.M.; Xue, M. Evaluation of the updated YSU planetary boundary layer scheme within WRF for wind resource and air quality assessments. J. Geophys. Res. Atmos. 2013, 118, 10490–10505. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).