Abstract
Precipitation nowcasting is extremely important in disaster prevention and mitigation, and can improve the quality of meteorological forecasts. In recent years, deep learning-based spatiotemporal sequence prediction models have been widely used in precipitation nowcasting, obtaining better prediction results than numerical weather prediction models and traditional radar echo extrapolation results. Because existing deep learning models rarely consider the inherent interactions between the model input data and the previous output, model prediction results do not sufficiently meet the actual forecast requirement. We propose a Modified Convolutional Gated Recurrent Unit (M-ConvGRU) model that performs convolution operations on the input data and previous output of a GRU network. Moreover, this adopts an encoder–forecaster structure to better capture the characteristics of spatiotemporal correlation in radar echo maps. The results of multiple experiments demonstrate the effectiveness of the proposed model. The balanced mean absolute error (B-MAE) and balanced mean squared error (B-MSE) of M-ConvGRU are slightly lower than Convolutional Long Short-Term Memory (ConvLSTM), but the mean absolute error (MAE) and mean squared error (MSE) of M-ConvGRU are 6.29% and 10.25% lower than ConvLSTM, and the prediction accuracy and prediction performance for strong echo regions were also improved.
1. Introduction
Precipitation nowcasting usually refers to the forecasting of precipitation up to 2 h in the future using observed information to predict the evolution of precipitation in a certain area over the short term. The main challenge in nowcasting is currently understanding the evolution and prediction of micro- and meso-scale weather. These types of weather are responsible for the occurrence and development of extreme weather events that rapidly evolve irregularly and non-linearly, which is challenging for existing early warning and forecasting systems to predict. Therefore, how to effectively use observed meteorological information and establish a forecasting method for nowcasting are problems in current meteorological services and research [1].
At present, two methods are mainly used for forecasting weather processes in meteorological services: methods based on the results of numerical weather prediction models and methods based on radar extrapolation [2]. For synoptic-scale weather systems, numerical weather prediction models can describe the continuous change in meteorological elements in time and space through basic atmospheric equations, obtaining reasonably accurate forecast results. However, for micro- and meso-scale weather systems, numerical weather prediction models are not suitable for forecasting severe local weather events in the next few hours because of the low temporal and spatial resolution of the observed data and inability to model the nonlinear processes in meso-scale and micro-scale weather systems [3]. Several studies have further demonstrated that numerical weather forecasting is often ineffective for micro- and meso-scale weather systems [4,5,6]. Radar is the most effective tool for nowcasting [7], and its echoes directly reflect the area and magnitude of current precipitation. Radar extrapolation can predict upcoming weather processes to a certain extent [8,9]. Currently, conventional radar extrapolation methods based on centroid tracking, such as TITAN (Thunderstorm Identification, Tracking, Analysis and Nowcasting) [10] and SCIT (Storm Cell Identification and Tracking) [11], as well as those based on cross-correlation [12] and optical flow methods [13], are widely used in radar-based nowcasting. However, these methods usually only extrapolate the motion vector obtained after simple calculations on the radar echo maps at several moments to predict the changes in the radar echo observations at the next moment. Moreover, they often treat the echo as a rigid body for extrapolation. Obviously, for echoes with a dynamic characteristic, the methods mentioned above have inherent shortcomings, which leads to low accuracy in the prediction results and short prediction time ranges.
As a new branch of machine learning, deep learning has led to great advances in techniques and theory [14], achieving excellent results in many fields, such as machine vision [15,16,17], speech recognition [18,19,20], natural language processing [21,22,23], and autonomous driving [24,25,26]. The success of deep learning has made it an important foundation for innovations and developments in other fields. Since the deployment of a new generation of weather radar networks in China [27], large amounts of historical observation data have been collected, which can be used to help deep learning models fully extract and learn the characteristics of the spatiotemporal evolution of echoes so that these models can be applied to nowcasting.
Recently, researchers have introduced deep learning techniques into the field of meteorological precipitation nowcasting. Nitish et al. [28] extended the sequence-to-sequence framework proposed by Sutskever et al. [29], using an encoder Long Short-Term Memory (LSTM) to map the input sequence to a fixed length vector and then using a decoder LSTM to learn the representation of the video sequence. However, the model proposed by Nitish et al. [28] can only learn the temporal correlations in video sequences. To obtain the spatial characteristics of a video sequence, Shi et al. [30] proposed the ConvLSTM model for precipitation nowcasting. Their results show that the predictions of this model are better than those of the variational optical flow method and the Fully-Connected LSTM (FC-LSTM) [31], which has a fully connected structure and can clearly capture the spatial and temporal characteristics of radar echo maps. Because the recursive convolutional structure in the ConvLSTM model is position invariant, Shi et al. [32] also proposed the Trajectory Gated Recurrent Unit (TrajGRU) model, which has a spatiotemporal variable structure and uses a weighted loss function to optimize the model in order to improve precipitation nowcasting performance. The models mentioned above are based on Convolutional Recurrent Neural Network (ConvRNN) and have made some progress in precipitation nowcasting. Nevertheless, the aforementioned ConvRNN models perform operations separately on the input data, hidden states, and model outputs. This raises the question as to how to make the ConvRNN capture the inherent interaction between input data and hidden state in a single layer.
To learn the inherent interaction between the current input radar echo map and the previous output state of a network (as proposed by Melis et al. [33]) as well as improve the accuracy and timeliness of prediction, this study proposes the addition of a convolution-based preprocessing operation in the Convolutional GRU(ConvGRU) [34] between the current input data and the previous output state to capture the relationship between them. A GRU network performs similarly to LSTM but has lower memory requirements, saving considerable computing time [35]. A six-layer encoder–forecaster framework was adopted in this study to efficiently capture the spatiotemporal characteristics of radar echo sequences. The HKO-7 radar echo map dataset was used to experimentally evaluate the performance and accuracy of the model.
The rest of this paper is organized as follows: in Section 2, we introduced the relative work on spatiotemporal prediction. In Section 3, we introduce the proposed model, M-ConvGRU, in detail. Section 4 presents an evaluation of the model through experiments. Finally, we summarize our work and discuss future work in Section 5.
2. Related Works
ConvLSTM, ConvGRU, and TrajGRU have been proposed to conduct spatiotemporal sequence prediction. They all use convolution operations (two-dimensional) to replace the fully connected operations in the step-by-step transitions between traditional RNN units (one-dimensional). Wang et al. [36] proposed Predictive Recurrent Neural Network (PredRNN) and designed a new spatiotemporal LSTM (ST-LSTM) unit to simultaneously extract and store spatiotemporal features, achieving good results on three video datasets (including radar echo datasets). Sato et al. [37] proposed the Predictive Coding Network (PredNet) model, which introduces a jump connection structure and hollow convolution in the model to improve the prediction performance of short-term forecasts. To solve the problem of blur in extrapolated images, Lin et al. [38] proposed an adversarial ConvGRU model that obtains better experimental results than the ConvGRU model and an optical flow method. Jing et al. [39] proposed a multi-level correlation method that incorporates adversarial training methods so that the prediction results retain more echo details. Agrawal et al. [40] used a U-Net structure for precipitation nowcasting based entirely on a convolutional neural network; its performance was better than that of the NOAA (National Oceanic and Atmospheric Administration) short-term forecast model. Jing et al. [41] proposed the Hierarchical Prediction Recurrent Neural Network (HPRNN) to address the increase in prediction error over time. They verified the effectiveness of the model on short-term to long-term radar echo extrapolation on the HKO-7 (from the Hong Kong Observatory) dataset. Although these methods have surpassed the extrapolation performance of traditional methods to some extent, the accuracy of long-term echo prediction decreases rapidly with time, failing to meet practical forecast requirements. In this paper, we use the convolution operation between input data and hidden state in a single layer and embed it into the ConvGRU to capture the inherent features of the radar echo sequence.
3. Proposed Modified Convolutional Gated Recurrent Unit (M-ConvGRU) Model
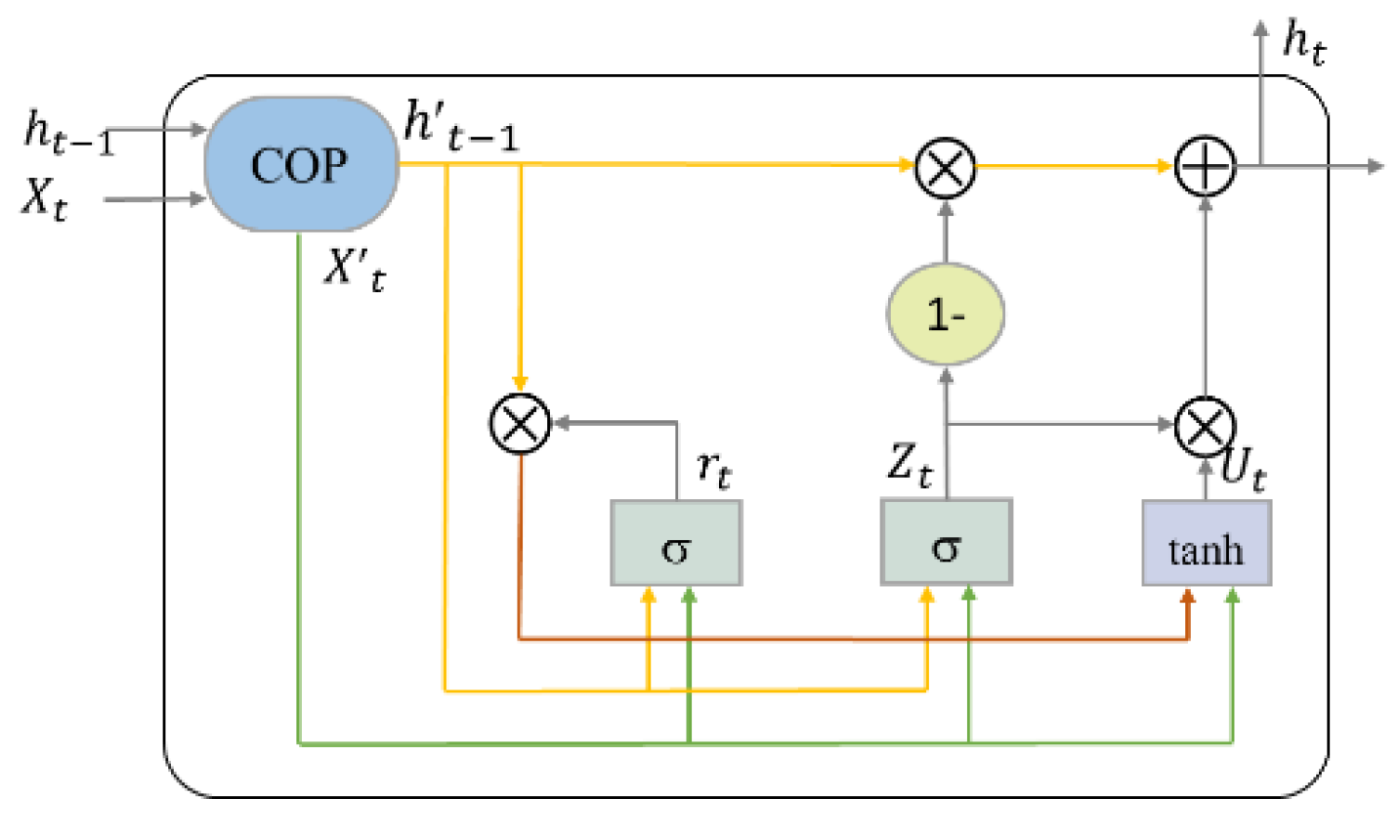
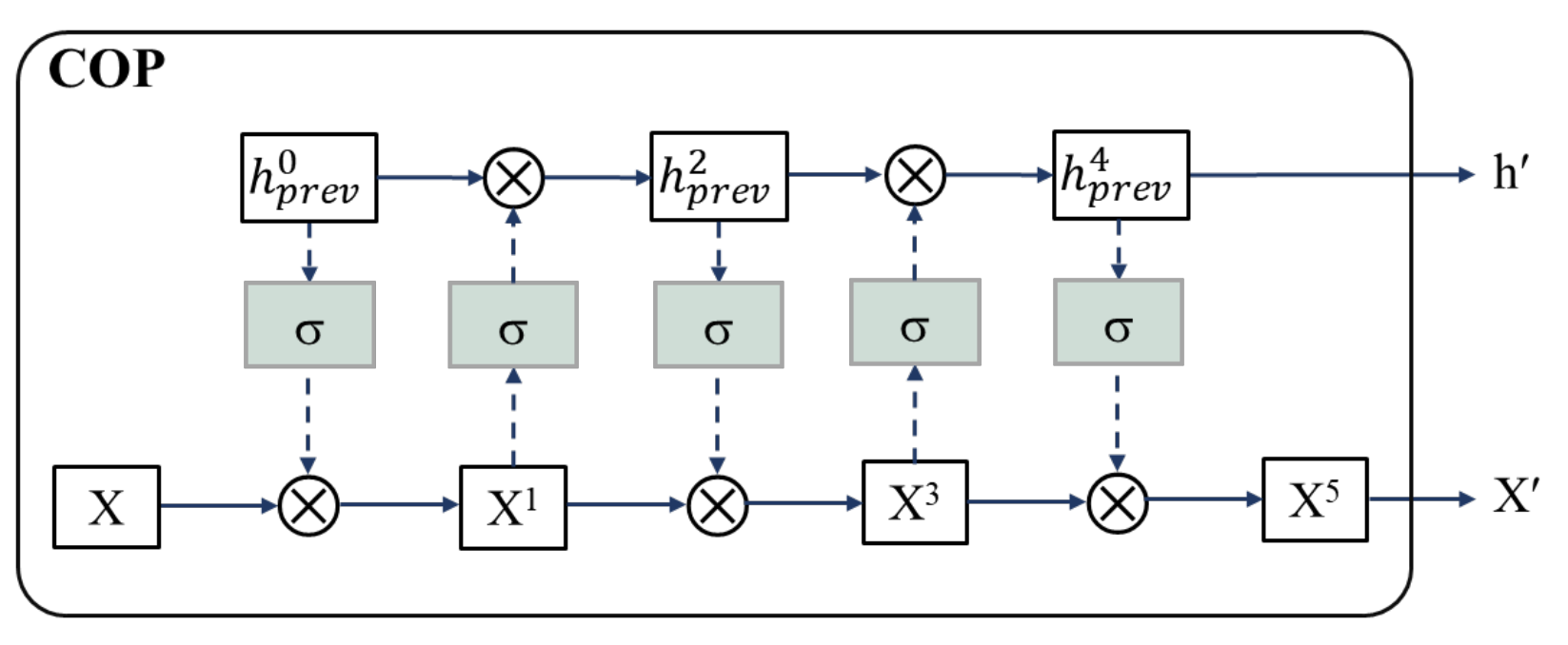
Like ConvLSTM, M-ConvGRU can effectively capture the spatial characteristics of an image while reducing the complexity of the model. Before the current input data and the previous output state of the network are incorporated into the ConvGRU neuron, convolution-based gate preprocessing is performed to capture the contextual relationship between the input data and the previous output of the model. The structure of a single GRU neuron in the model proposed in this study is shown in Figure 1. Figure 2 presents the convolution-based preprocessing between the current input data and the previous output state of the neuron, where COP stands for convolution-based preprocessing.
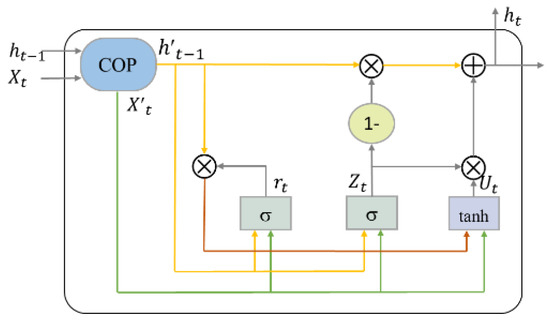
Figure 1.
Structure of a single Gated Recurrent Unit (GRU) neuron in the proposed Modified Convolutional Gated Recurrent Unit (M-ConvGRU) model [32].
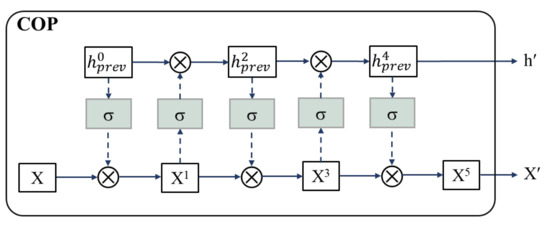
Figure 2.
Convolution-based gate preprocessing of input data and previous output state [33].
The main formula of M-ConvGRU is as follows [32], where “*” is the convolution operation and “” is the Hadamard product:
The bias terms are omitted here for notational simplicity. Here, represent the update gate, reset gate, new information, and memory state, respectively. is the input, and and are the sigmoid function and activation, respectively. and are the height and width, respectively, of the state and input tensors, and are the channel sizes of the state and input tensors, respectively. Whenever there is a new input, the reset gate clears the previous state. The update gate controls the amount of new information written to that state.
As Figure 2 shows, the input X is controlled by the output of the previous step . The gated input is then used similarly to gate the output of the previous time step. After several rounds of mutual gating, the last updated X and are fed into ConvGRU. The updated X and are obtained using the following mathematical formulas [33]:
Hyperparameter is the number of gating operations, where , and the value is set to 5 in this study [33]. By adding operations to the input data and hidden states, the contextual features of the video sequence can be learned, and the inherent interaction of the spatiotemporal sequence can be captured effectively.
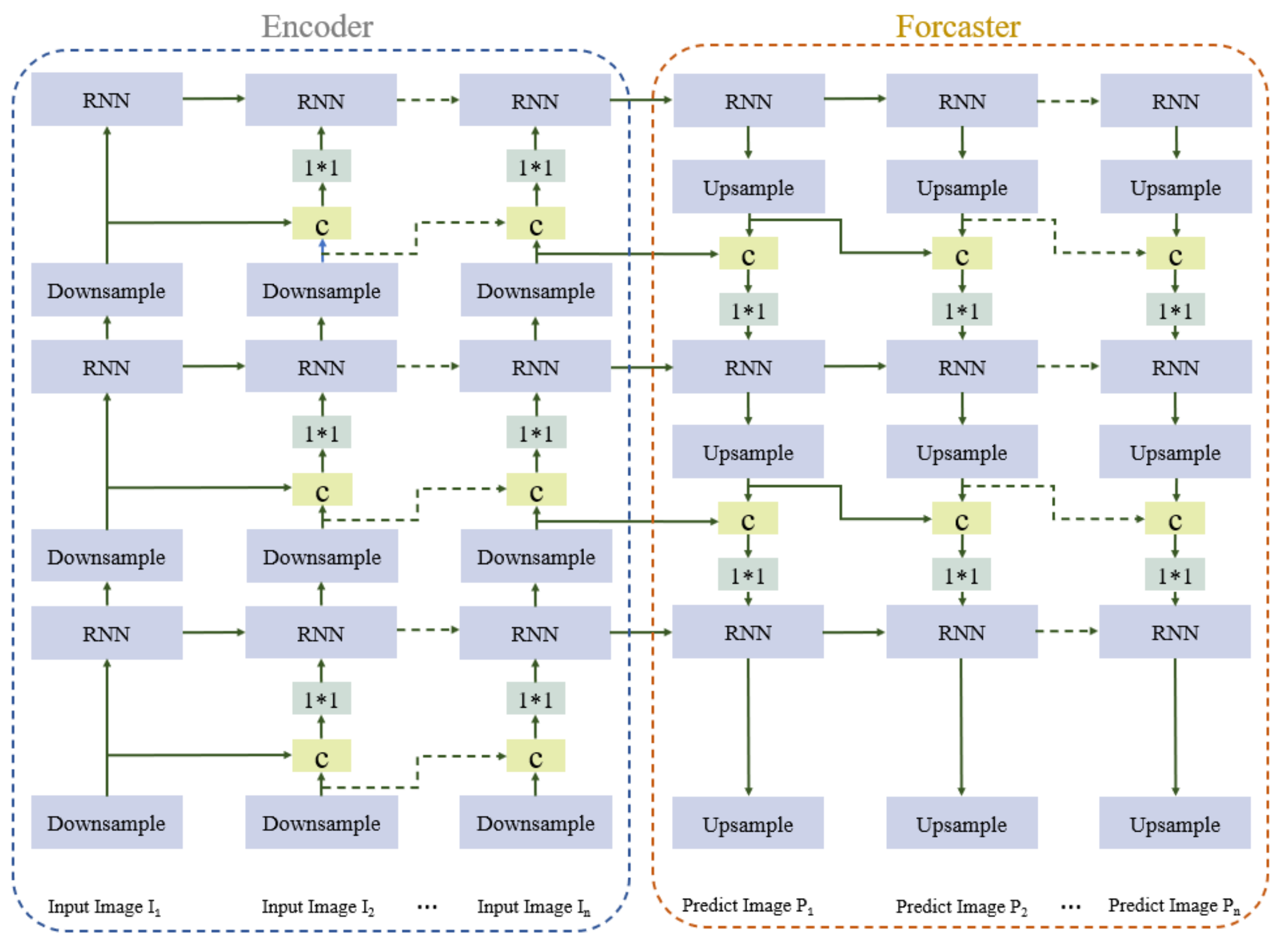
To ensure that the model is able to represent spatiotemporal features well and effectively predict changes in radar echo maps, an encoder–forecaster structure similar to that in Shi et al. [32] is employed to predict spatiotemporal sequences. The architecture of the encoder–forecaster network is shown in Figure 3. The encoder module comprises three downsampling layers and three Recurrent Neural Network (RNN) layers and learns low- to high-dimensional image features. The downsampling layer reduces the size of the feature image. It captures the spatial features of the image through convolution, whereas the RNN layer learns the temporal features of the radar echo sequence. The forecaster module consists of three upsampling layers and three RNN layers and outputs the predicted radar echo maps. The RNN layer learns the image sequence features. The upsampling layer increases the image feature size through deconvolution and guides the update of the low-level state according to the high-level features.
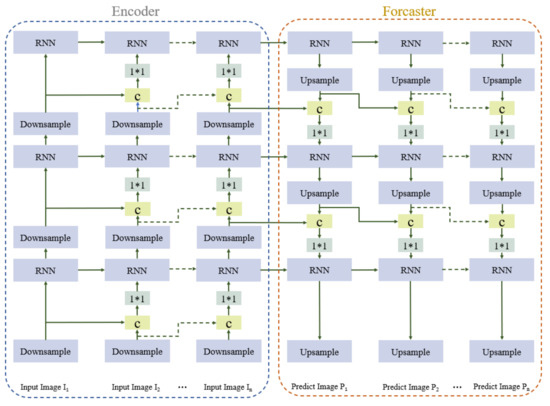
Figure 3.
Architecture of the encoder–forecaster network in the proposed model.
4. Experiments and Results
It is difficult to predict changes in weather radar echoes because convective weather develops non-linearly, irregularly, and continuously merges and splits. To verify the ability of the model to extrapolate radar echoes with such characteristics, we selected the HKO-7 public radar echo dataset, which was collected by the Hong Kong Observatory. This dataset consists of daily radar constant altitude plan position indicator (CAPPI) graphs from 2009 to 2015, of which there are 240 per day (the radar echo data are updated every 6 min). The logarithmic radar reflectivity factors (dBZ) are linearly converted to pixel value through . The image’s resolution is 480 480 pixels, which includes a 512 km 512 km range centered in Hong Kong. The rainfall information was used to select 993 days with rainfall to form the final dataset. Of these, 812 days were used for training, 50 days were used for validation, and 131 days were used for testing. To evaluate the performance of the proposed model, we compared the proposed model, M-ConvGRU, and the ConvLSTM model. In the training process, the batch size of the model was set to four, and the number of iterations was 100,000. The Adam is chosen as the optimizer, and its learning rate is equal to , and betas are set (0.5, 0.999) [32].
In meteorological services, different levels of attention are often given to different precipitation intensities; therefore, the overall performance of the model under different precipitation levels should be used to evaluate the quality of the model. According to the Z–R relationship (the relationship between echo intensity and precipitation) in the HKO-7 dataset, radar reflectivity data can be converted into precipitation (mm/h). Precipitation can be divided into five levels according to the threshold, , values of , , , , and . When evaluating the predictive ability of the model, the ground truth radar and predicted echo pixel values were converted into a precipitation coefficient matrix, and was used to binarize the precipitation coefficient matrix. The metrics TP (prediction = 1, truth = 1), FN (prediction = 0, truth = 1), FP (prediction = 1, truth = 0), and TN (prediction = 0, truth = 0) were calculated. The false alarm rate (FAR), critical success index (CSI), and Heidke skill score (HSS) for each precipitation level were calculated as follows [42]:
The lower the FAR value, the better the prediction effect, and the higher the CSI and HSS values, the better the prediction performance. The traditional mean absolute error (MAE) and mean squared error (MSE) were used to compare the prediction results of the two models. However, because the frequency of different rainfall levels is highly imbalanced, we also used the method in Shi et al. [32] to calculate the balanced mean absolute error (B-MAE) and balanced mean squared error (B-MSE), which use a weighted loss function for heavy rainfall, where a strong echo is given a greater weight. Table 1 shows the sum of MAE, MSE, B-MAE and B-MSE of each pixel pair in the central 240 240 area of the predicted images and the ground truth radar echo maps, respectively. The M-ConvGRU model obtained values that are lower than those of ConvLSTM, indicating that its prediction results are better.

Table 1.
Comparison of the prediction results of the two models. The best results are marked in bold.
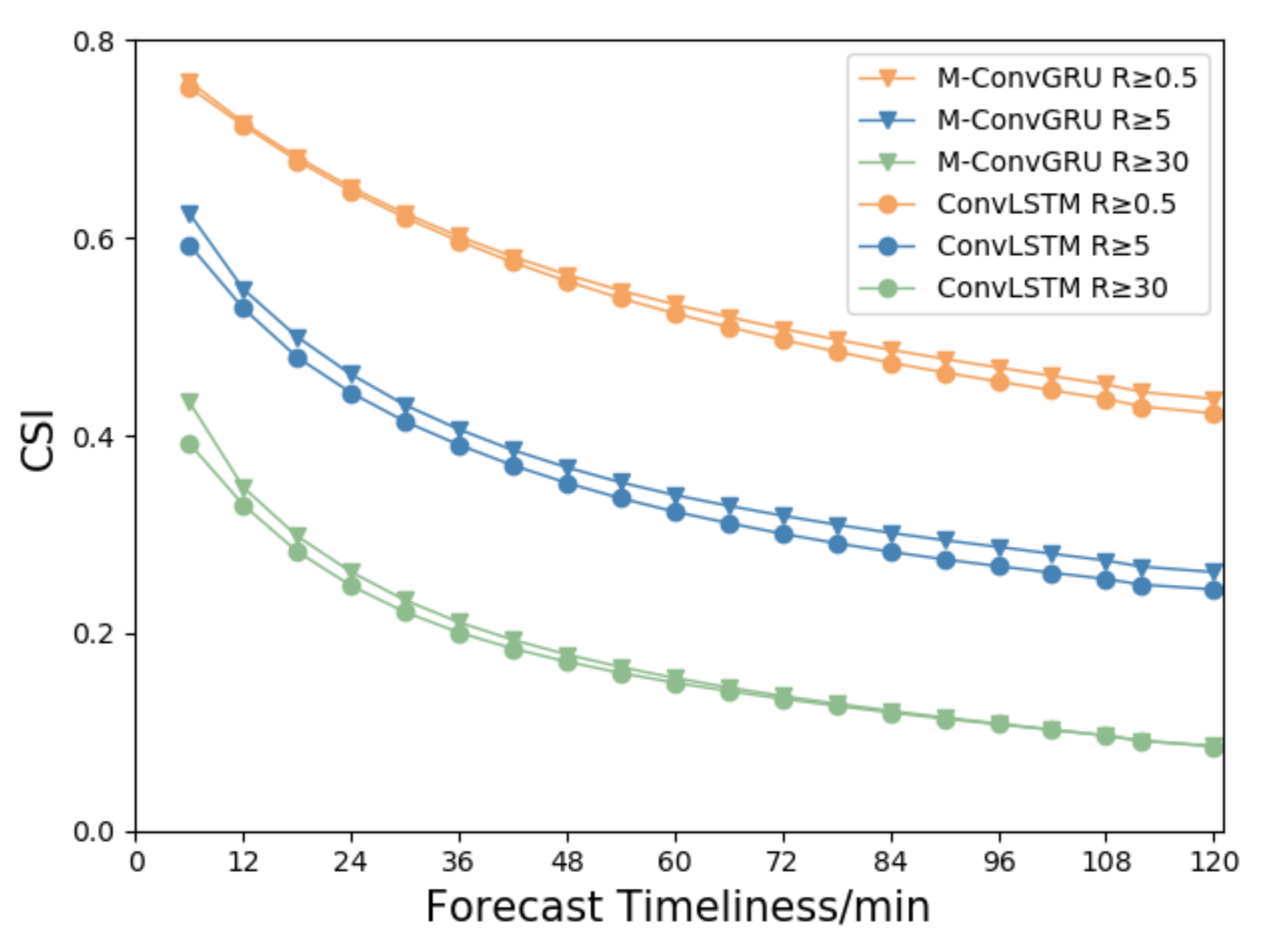
Figure 4 shows the change in CSI scores of the two models with respect to forecast time when the precipitation is greater than 0.5, 5, and 30 mm/h. When the precipitation is greater than 0.5 mm/h, the CSI score of each model is the highest. There is little difference between the scores of the two groups when the forecast is shorter than 30 min. As the prediction time increases, the CSI value of the M-ConvGRU gradually decreases from 0.76 to 0.44, but the CSI value of M-ConvGRU is significantly higher than that of ConvLSTM in later periods. When the precipitation is greater than 5 mm/h, the CSI scores of the M-ConvGRU decreases from 0.62 to 0.26, but the M-ConvGRU score is still higher than that of ConvLSTM for the same forecast period. When the precipitation is greater than 30 mm/h, the CSI scores of the M-ConvGRU decreases from 0.43 to 0.09. Although the CSI score is substantially lower, the score of M-ConvGRU for predictions up to an hour is significantly higher than that of ConvLSTM. This is because both the probability of heavy rainfall and its area are small; therefore, the CSI value of heavy rainfall is also small. A characteristic of the prediction task is that the CSI value decreases with prediction time. The results also have high uncertainty, and this uncertainty increases with time.
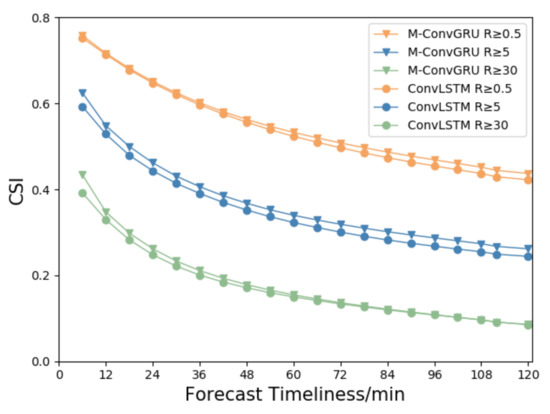
Figure 4.
The critical success index (CSI) scores of the two models at three different precipitation levels with respect to forecast period.
In the experiments, the radar echo map at five consecutive timesteps was used to predict the radar echo map of the next 20 timesteps; that is, the historical 0.5-h data were used to predict the echo data in the next 2 h. Two cases were selected from the test set for analysis so that the prediction performance can be understood more intuitively. These two cases represent the general characteristics of micro- and meso-scale weather; have regions with strong echoes; and include the generation, development, and dissipation stages of the convective process.
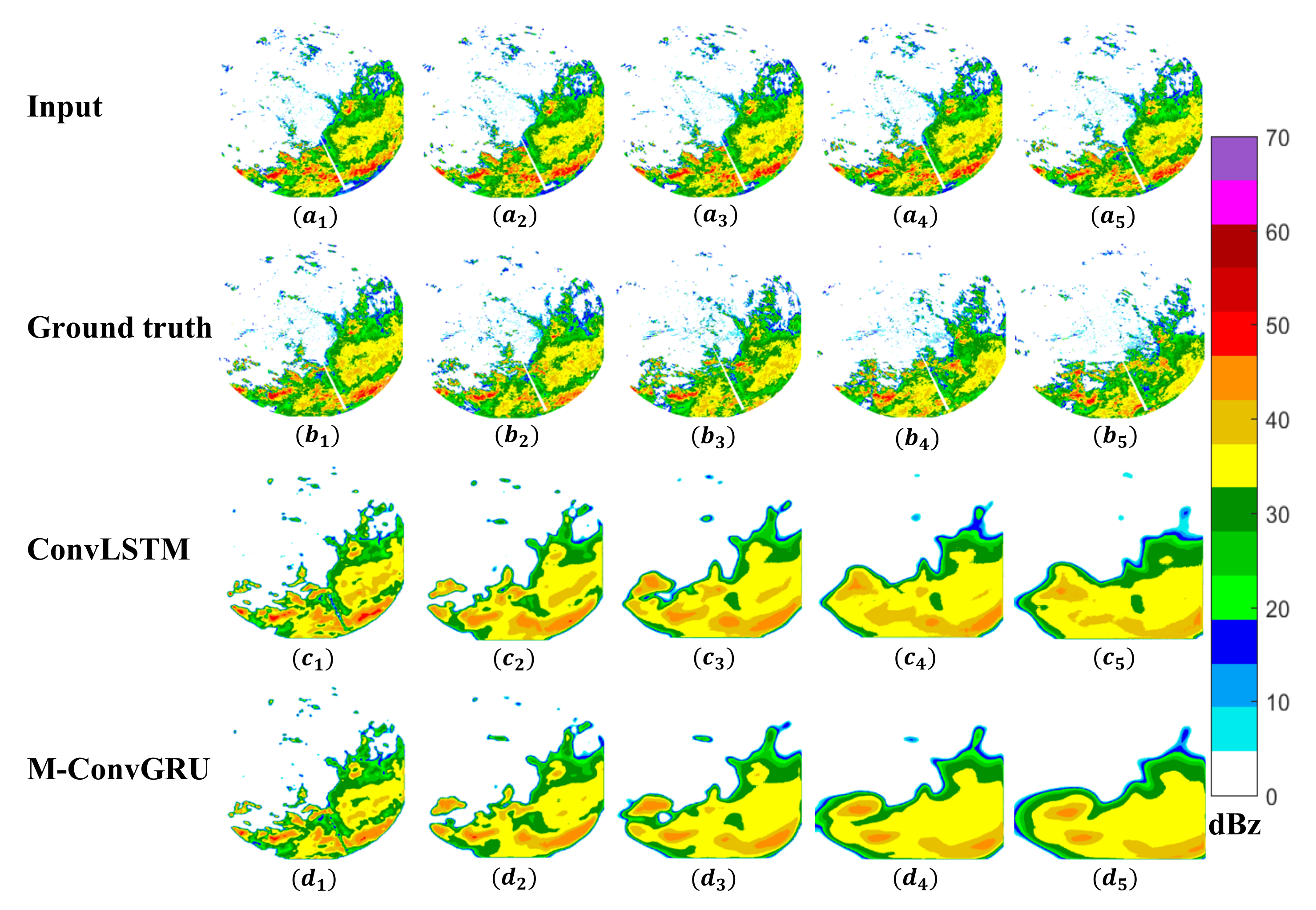
Figure 5 presents the result for the first case. Here, both models predict the development of most echoes at 6 min. Parts of the echo details are lost at 30 min, but the changes in position and movement of the strong echo are still extrapolated. M-ConvGRU predicts the strongest echo regions better than ConvLSTM. After 1 h, because the extrapolation time is too long, the forecast image can only be reconstructed according to the echo characteristics learned by the model. Nevertheless, some strong echo regions can still be extrapolated. When compared with the ground truth, it is clear that the edge details of the echoes at different intensities in the radar echo map predicted by the models are gradually lost, which is consistent with the change in CSI score with respect to forecast time shown in Figure 4.
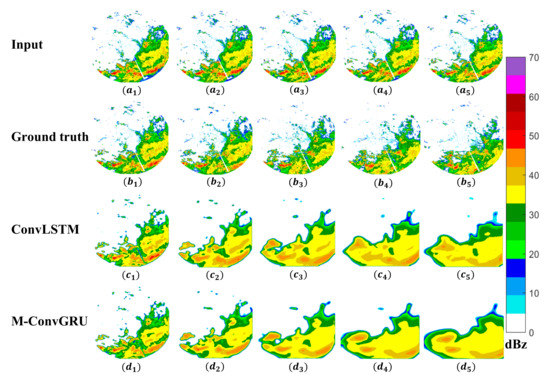
Figure 5.
Visualization results for case 1 ((a1–a5) denotes the model inputs; (b1–b5) denotes the ground truth radar echo maps at 6, 30, 60, 90, and 120 min; and (c1–c5) and (d1–d5)are the corresponding prediction results of ConvLSTM and M-ConvGRU, respectively).
To quantitatively compare the prediction results of case 1, we provide the FAR, CSI, and HSS values of the predicted frames obtained by the two models at 6, 30, and 60 min in Table 2, Table 3 and Table 4, respectively. As the prediction time increases, the CSI and HSS values decrease, and the FAR value increases. The increase in rainfall intensity also shows the same pattern as the forecast time. The scores of M-ConvGRU at 6 min and 30 min are substantially higher than those of ConvLSTM at 60 min; however, a better value is obtained only when . The overall conclusion is that M-ConvGRU can obtain better prediction results than ConvLSTM at different rainfall intensities.

Table 2.
False alarm rate (FAR) values of both models for case 1 at 6, 30, and 60 min. The best results are marked in bold.

Table 3.
CSI values of both models for case 1 at 6, 30, and 60 min. The best results are marked in bold.

Table 4.
Heidke skill score (HSS) values of both models for case 1 at 6, 30, and 60 min. The best results are marked in bold.
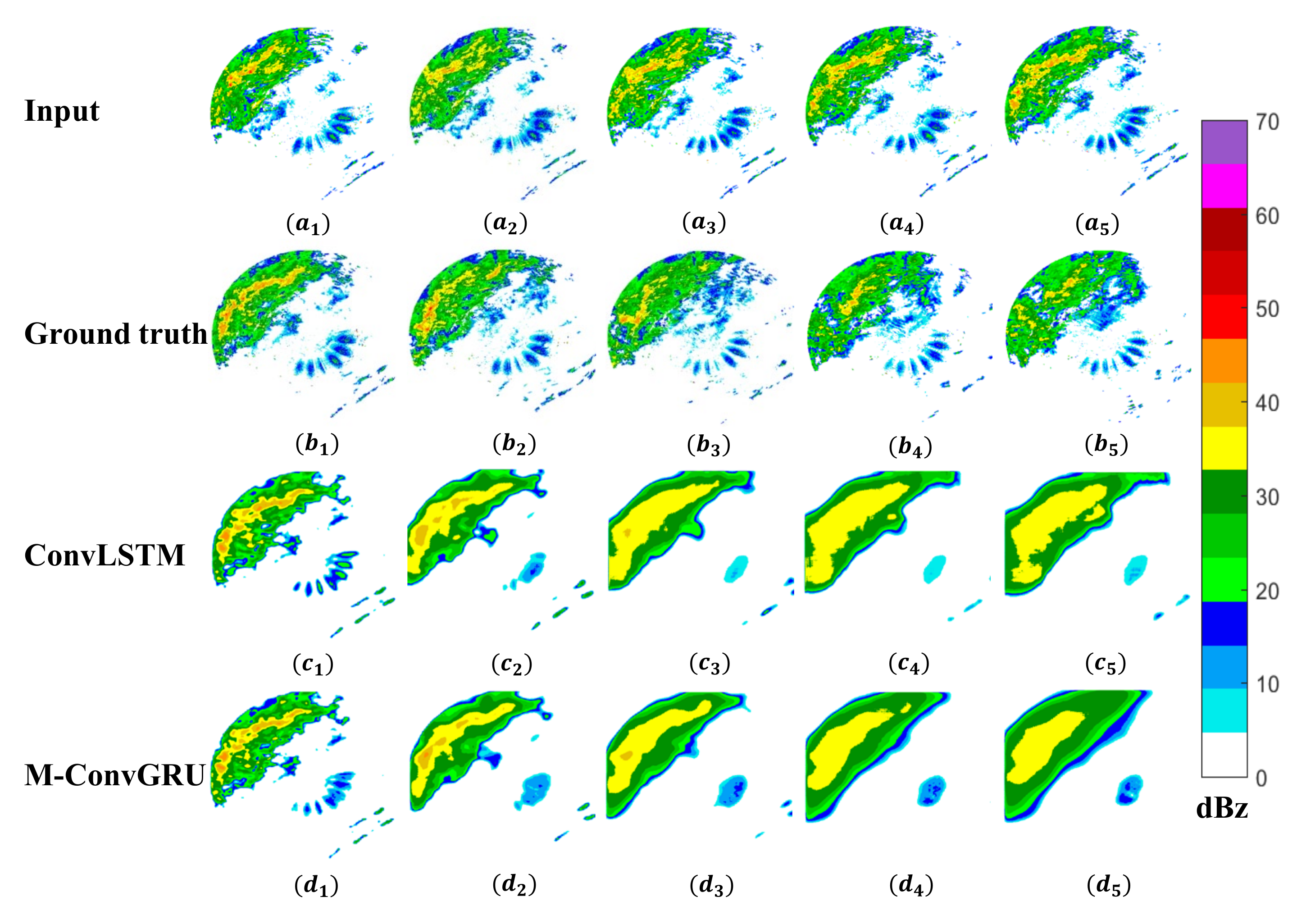
Figure 6 shows the visualization results for case 2. The overall echo intensity in this case is not as strong as that in case 1. Both models accurately predict the location of the strong echo at 6 min. By 30 min, as in case 1, although some echo details are lost, M-ConvGRU still effectively predicts the position of the strongest echo, but ConvLSTM does not. After 1 h, owing to the long extrapolation time, the prediction results have lost more details. The location of the strong echo area in the ground truth map is similar, but it is difficult to distinguish in the predicted maps. In the predicted maps, these regions are merged into a larger echo, resulting in a predicted strong echo area that is significantly larger than that in the ground truth. This problem needs to be addressed in future studies.
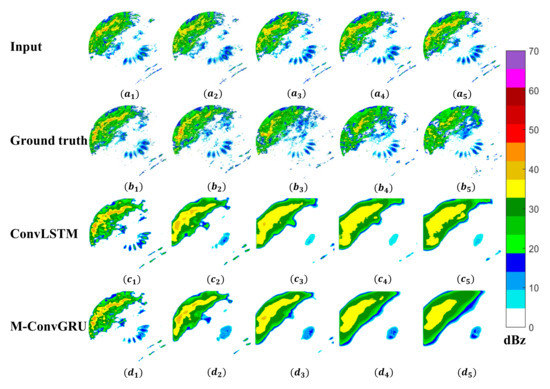
Figure 6.
Visualization results for case 2 ((a1–a5) denotes the model input; (b1–b5) denotes the ground truth radar echo maps of 6, 30, 60, 90, and 120 min; and (c1–c5) and (d1–d5) are the corresponding prediction results of ConvLSTM and M-ConvGRU, respectively).
Table 5, Table 6 and Table 7 respectively show the FAR, CSI, and HSS values of the predicted frames obtained by the two models for case 2 at 6, 60, and 120 min. Some results are missing because the predicted radar echoes from the rain intensity were lower than the currently set threshold as time increased; therefore, the data do not exist. The CSI and HSS values decrease with forecast time and rainfall intensity. By contrast, the FAR value increases with the forecast time and rainfall intensity. Overall, the prediction score of M-ConvGRU at 6, 60, and 120 min is better than that of ConvLSTM.

Table 5.
FAR values of both models for case 2 at 6, 30, and 60 min. The best results are marked in bold.

Table 6.
CSI values of both models for case 21 at 6, 30, and 60 min. The best results are marked in bold.

Table 7.
HSS values of both models for case 2 at 6, 30, and 60 min. The best results are marked in bold.
5. Conclusions and Discussion
This study investigated a deep learning-based echo image extrapolation model used for 0–2 h precipitation nowcasting based on weather radar. The proposed M-ConvGRU model performs a convolution-based operation between the current input and previous output states before being incorporated into the ConvGRU neuron to obtain the contextual relationship between them. The experiment was carried out on the HKO-7 dataset, and the prediction results of ConvLSTM proposed by Shi et al. [30] were compared with those of M-ConvGRU, yielding the following main conclusions:
- The visualization results and quantitative index score analysis of two example cases show that M-ConvGRU can effectively capture the spatiotemporal characteristics of radar echo maps. Moreover, the position and intensity of its predicted radar echoes are closer to the ground truth.
- The test results reveal that the B-MAE and B-MSE of M-ConvGRU are slightly lower than ConvLSTM, but the MAE and MSE of M-ConvGRU are 6.29% and 10.25% lower than ConvLSTM. Moreover, the CSI scores of M-ConvGRU is better than ConvLSTM. These numerical results show that the proposed deep learning model has learned the characteristics of more advanced and abstract spatiotemporal sequences, thereby improving radar echo precipitation nowcasting ability and accuracy to a certain extent.
Although M-ConvGRU improves prediction accuracy, there are still many problems in the later stages of prediction; for example, many details will gradually be lost in the prediction results, and the model cannot guarantee that the input sequence has the best prediction performance for different thresholds at each time. These problems also inevitably appear in the results of ConvLSTM [30], PredRNN [33], and HPRNN [38]. Possible reasons for this are as follows: First, the prediction task itself has the characteristic of great uncertainty. Second, prediction errors will increase exponentially as the extrapolation progresses, and future information will be extrapolated from increasingly inaccurate past information.
Currently, the application of deep learning in meteorology is still in the exploratory stage, and there is still much room for improvement in the combination of the physical concept model of meteorology and extrapolation over time. Based on this work, we will consider incorporating meteorological elements into the radar echo extrapolation model, such as wind speed, temperature, air pressure, etc., in order to fully reflect the convection process’s spatiotemporal characteristics.
Author Contributions
Conceptualization, W.H.; methodology and investigation, W.H., T.X., H.W. and J.H.; software, W.H; experiment, W.H. and X.R.; writing of the original draft, W.H.; editing, W.H., T.X. and H.W.; validation, W.H. and Y.Y.; data analysis, W.H. and L.T.; review and editing, H.W., T.X. and J.H.; supervision, J.H.; formal analysis, H.W. and T.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (2018YFC1506104), Project of Sichuan Department of Science and Technology (22DYF1935), National Natural Science Foundation (41805056), Application of Basic Research of the Sichuan Department of Science and Technology (2019YJ0316), and the Special Funds for the Central Government to Guide Local Technological Development (2020ZYD051).
Data Availability Statement
The HKO-7 dataset used in this study is from the Hong Kong Observatory at https://github.com/sxjscien-ce/HKO-7/tree/master/hko_data (accessed on 20 November 2021).
Acknowledgments
We thank the reviewers for their constructive comments and editorial suggestions that significantly improved the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Juan, S.; Ming, X.; James, W.W.; Isztar, Z.; Sue, P.B.; Jeanette, O.H.; Paul, J.; Dale, M.B.; Li, P.W.; Brian, G.; et al. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar]
- Chen, D.; Xue, J. The present situation and prospect of operational model of numerical weather forecast. J. Meteorol. 2004, 5, 112–122. [Google Scholar]
- Morris, L.W.; Christopher, D.; Wei, W.; Kevin, W.M.; Joseph, B.K. Experiences with 0–36-h explicit convective forecasts with the WRF-ARW model. Weather Forecast. 2008, 23, 407–437. [Google Scholar]
- Cong, W.; Ping, W.; Di, W.; Jinyi, H.; Bing, X. Nowcasting multicell short-term intense precipitation using graph models and random forests. Mon. Weather Rev. 2020, 148, 4453–4466. [Google Scholar]
- Zbyněk, S.; Vojtěch, B.; Petr, Z.; Kateřina, S. Nowcasting of hailstorms simulated by the NWP model COSMO for the area of the Czech Republic. Atmos. Res. 2016, 171, 66–76. [Google Scholar]
- Vojtěch, B.; Zbyněk, S.; Petr, Z. Nowcasting of deep convective clouds and heavy precipitation: Comparison study between NWP model simulation and extrapolation. Atmos. Res. 2017, 184, 24–34. [Google Scholar]
- James, W.W.; Crook, N.A.; Cynthia, K.M.; Juanzhen, S.; Michael, D. Nowcasting thunderstorms: A status report. Bull. Am. Meteorol. Soc. 1998, 79, 2079–2099. [Google Scholar]
- Kao, S.C.; I-An, Y. Improving radar echo Lagrangian extrapolation nowcasting by blending numerical model wind information: Statistical performance of 16 typhoon cases. Mon. Weather Rev. 2020, 148, 1099–1120. [Google Scholar]
- James, W.; Dan, M.; James, P. NWP and radar extrapolation: Comparisons and explanation of errors. Mon. Weather Rev. 2020, 148, 4783–4798. [Google Scholar]
- Michael, D.; Gerry, W. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A radar-based methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar]
- Johnson, J.T.; Pamela, L.M.; Arthur, W.; De Wayne Mitchell, E.; Gregory, J.S.; Michael, D.E.; Kevin, W.T. The storm cell identification and tracking algorithm: An enhanced WSR-88D algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef] [Green Version]
- Dan, C.C.; Alessandro, G.; Luca, M.G.; Jürgen, S. Mitosis detection in breast cancer histology images with deep neural networks. Med. Image Comput. Comput. Assist Interv. 2013, 16, 411–418. [Google Scholar]
- Renzo, B.; Chandrasekar, V. An enhanced optical flow technique for radar nowcasting of precipitation and winds. J. Atmos. Ocean. Technol. 2017, 34, 2637–2658. [Google Scholar]
- Yann, L.C.; Yoshua, B.; Geoffrey, H. Deep learning. Nature 2015, 521, 436–444. [Google Scholar]
- Alex, K.; Ilya, S.; Geoffrey, E.H. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar]
- Karen, S.; Andrew, Z. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Kaiming, H.; Xiangyu, Z.; Shaoqing, R.; Jian, S. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Geoffrey, H.; Li, D.; Dong, Y.; George, E.D.; Abdel-rahman, M.; Navdeep, J.; Andrew, S.; Vincent, V.; Patrick, N.; Tara, N.S.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar]
- Xiong, W.; Droppo, J.; Huang, X.; Seide, F.; Seltzer, M.; Stolcke, A.; Yu, D.; Zweig, G. Achieving human parity in conversational speech recognition. arXiv 2016, arXiv:1609.08144. [Google Scholar]
- Amodei, D.; Ananthanarayanan, S.; Anubhai, R.; Bai, J.; Battenberg, E.; Case, C.; Casper, J.; Catanzaro, B.; Cheng, Q.; Chen, G.; et al. Deep Speech 2: End-to-end speech recognition in English and Mandarin. PMLR 2016, 48, 173–182. [Google Scholar]
- Kai, S.T.; Richard, S.; Christopher, D.M. Improved semantic representations from tree-structured long short-term memory networks. Comput. Sci. 2015, 5, 1556–1655. [Google Scholar]
- Wu, Y.; Schuster, M.; Chen, Z.; Le, Q.V.; Norouzi, M.; Macherey, W.; Krikun, M.; Cao, Y.; Gao, Q.; Macherey, K.; et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv 2016, arXiv:1609.08144. [Google Scholar]
- Ossama, A.; Abdel-rahman, M.; Hui, J.; Li, D.; Gerald, P.; Dong, Y. Convolutional neural networks for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar]
- Chenyi, C.; Ari, S.; Alain, K.; Jianxiong, X. DeepDriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 2722–2730. [Google Scholar]
- Bojarski, M.; Del, T.D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to end learning for self-driving cars. arXiv 2016, arXiv:1604.07316. [Google Scholar]
- Sorin, G.; Bogdan, T.; Tiberiu, C.; Gigel, M. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar]
- Dan, Z.; Junxia, G.; Chunxiang, S. The effective coverage and terrain occlusion analysis of the new generation weather radar network design. Meteorol. Mon. 2018, 44, 1434–1444. (In Chinese) [Google Scholar]
- Nitish, S.; Elman, M.; Ruslan, S. Unsupervised learning of video representations using LSTMs. PLMR 2015, 37, 843–852. [Google Scholar]
- Ilya, S.; Oriol, V.; Quoc, V.L. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Xingjian, S.; Hao, W.; Dit-Yan, Y.; Zhourong, C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Sepp, H.; Jürgen, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Deep learning for precipitation nowcasting: A benchmark and a new model. arXiv 2017, arXiv:1706.03458. [Google Scholar]
- Melis, G.; Kočiský, T.; Blunsom, P. Mogrifier LSTM. arXiv 2019, arXiv:1909.01792. [Google Scholar]
- Nicolas, B.; Li, Y.; Chris, P.; Aaron, C. Delving deeper into convolutional networks for learning video representations. arXiv 2015, arXiv:1511.06432. [Google Scholar]
- Junyoung, C.; Caglar, G.; KyungHyun, C.; Yoshua, B. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Ryoma, S.; Hisashi, K.; Takehiro, Y. Short-term precipitation prediction with Skip-connected PredNet. ICANN Lect. Notes Comput. Sci. 2018, 11141, 373–382. [Google Scholar]
- Lin, T.; Xutao, L.; Yunming, Y.; Pengfei, X.; Yan, L. A generative adversarial gated recurrent unit model for precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2019, 17, 601–605. [Google Scholar]
- Jinrui, J.; Qian, L.; Xuan, P. MLC-LSTM: Exploiting the spatiotemporal correlation between multi-level weather radar echoes for echo sequence extrapolation. Sensors 2019, 19, 3988. [Google Scholar]
- Shreya, A.; Luke, B.; Carla, B.; John, B.; Cenk, G.; Jason, H. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar]
- Jinrui, J.; Qian, L.; Xuan, P.; Qiang, M.; Shaoen, T. HPRNN: A hierarchical sequence prediction model for long-term weather radar echo extrapolation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Robin, J.H.; Christopher, A.T.F.; Ian, T.J.; David, B.S. Equitability revisited: Why the ‘equitable threat score’ is not equitable. Weather Forecast. 2010, 25, 710–726. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).