Abstract
Geostationary satellites can retrieve the cloud droplet effective radius () but suffer biases from cloud inhomogeneities, internal retrieval nonlinearities, and 3-D scattering/shadowing from neighboring clouds, among others. A 1-D retrieval method was applied to Geostationary Operational Environmental Satellite 13 (GOES-13) imagery, over large areas in South America ( N– S; – W), the Southeast Pacific ( N– S; – W), and the Amazon ( N– S; – W), for four months in each year from 2014–2017. Results were compared against in situ aircraft measurements and the Moderate Resolution Imaging Spectroradiometer cloud product for Terra and Aqua satellites. Monthly regression parameters approximately followed a seasonal pattern. With up to 108,009 of matchups, slope, intercept, and correlation for Terra (Aqua) ranged from about 0.71 to 1.17, −2.8 to 2.5 m, and 0.61 to 0.91 (0.54 to 0.78, −1.5 to 1.8 m, 0.63 to 0.89), respectively. We identified evidence for overestimation (underestimation) correlated with shadowing (enhanced reflectance) in the forward (backscattering) hemisphere, and limitations to illumination and viewing configurations accessible by GOES-13, depending on the time of day and season. A proposition is hypothesized to ameliorate 3-D biases by studying relative illumination and cloud spatial inhomogeneity.
1. Introduction
Clouds are the main radiative modulator in the atmosphere [1] and have relevant impacts on climate. In order to adequately describe these impacts, global climate models need constant improvements in the parametrization of cloud properties, and how they respond to changes in atmospheric dynamics and composition. The radiative effect of clouds is influenced by atmospheric aerosol loading [2,3,4,5] and constitutes one of the greatest uncertainties in estimates of climate radiative forcing [6].
Aerosol effects on clouds, at local and global scales, are often modeled as changes in the effective radius of cloud droplets () (e.g., [7,8]), and as the net radiative forcing originating from these changes (e.g., [9]). In case the droplet size is larger than or very close to the incident radiation wavelength, which often happens for warm (i.e., liquid phase) clouds, is defined [10] according to:
where is the number concentration of droplets of radius r per size distribution interval.
Nakajima and King [1] have developed a bispectral method to simultaneously derive and the cloud optical depth . Most of the orbital retrieval methods today employ, in one way or another, the ideas put forward in their seminal paper. The method uses radiance measurements at one water-absorbing wavelength, typically in the near -infrared, and a weakly absorbing wavelength, usually in the visible part of the spectrum. A commonly used strategy is to apply forward modeling to simulate sensor-specific radiance measurements, for a myriad of physical conditions, with 1-D cloud properties, illumination, and viewing angles. A look-up table (LUT) with these results is compiled for use in the inverse problem, i.e., minimizing a cost function defined as the difference between actual radiance measurements and the precomputed LUT solutions.
Assessing over large extents of the globe is only practical if performed using satellite remote sensing retrievals. National Aeronautics and Space Administration (NASA) operates the Moderate Resolution Imaging Spectroradiometer (MODIS) instruments aboard Terra and Aqua satellites, routinely retrieving cloud microphysics [11]. Due to their polar orbits, these satellites can sample cloud properties over the entire globe. However, at surface locations near the Equator, MODIS will have at most one daytime overpass for each satellite, while multiple passes occur near the poles. The instrument has a nominal cross-track swath of 2330 km, which causes gaps between consecutive orbits near the Equator. Therefore, even though MODIS retrievals are considered a worldwide standard, we still lack more frequent, accurate information on cloud microphysics, to better understand cloud development and lifetime cycle, especially in the tropics.
Instruments onboard geostationary satellites, which have been routinely used for weather forecast-related applications, can also be employed for microphysical retrievals. For example, previous works have studied warm cloud retrievals, from radiance measured by the imager sensor on Geostationary Operational Environmental Satellites (GOESs) operated by the National Oceanic and Atmospheric Administration (NOAA). These included retrievals by GOES-8 over the land [12], GOES-8, -10, and -11 also over land [13], GOES-10 over the Southeast Pacific [14], and GOES-13 over the North Atlantic [15]. In all these cases, was retrieved with a repeatability rate of about 30 min, a much higher frequency than possible with polar satellites.
Although useful for gathering a broad perspective on cloud microphysics, retrievals by instruments in polar or geostationary platforms are indirect estimates. They show statistically significant biases when compared to in situ measurements by aircraft (e.g., [14,15,16,17,18,19]), or surface measurements (e.g., [12,13,20]). retrievals also show angular dependence with solar illumination and viewing angles (e.g., [13,21,22,23,24]). The sources of these discrepancies are manifold. Operational retrievals rely on the 1-D LUT approach described above, with biases that are inherent to this methodology (internal biases), and others that are not directly related to it (external). Some general external biases are instrument deviations from calibration, unaccounted above -cloud gaseous absorption, surface albedo contamination [25], and the presence of precipitation [16,26]. Internal biases originate from limitations in the 1-D modeling of cloud properties to accurately describe what in fact are 3-D radiative transfer phenomena. These can be further classified into biases due to resolved and unresolved (subpixel) variability [25]. At the subpixel scale, cloud inhomogeneities (e.g., broken cloud fields) may result in horizontal photon transport that cannot be represented by 1-D modeling [27,28]. Another type of unresolved bias originates from the nonlinear relation between the measured near-infrared radiance and . Due to this nonlinearity, averaging or gridding processes result in a negative bias to the retrieved [25,26]. In addition to this effect, the fact the two wavelengths used to build the LUT have a certain degree of covariance results in an underestimated , associated with averaging radiances at the subpixel scale [29]. Fortunately, a framework has been put forward to mitigate the effects of these unresolved biases [27,29]. Resolved variability refers to enhanced scattering or shadowing effects from nearby 3-D cloud parts, which change the effective radiance measured out of a given cloud section, hence altering the retrieved [25,28,30].
Comparing GOES and surface-derived , McHardy et al. [13] have identified important biases related to 3-D effects The authors analyzed more than 8 years of data, for one specific land site, and concluded that solar and viewing geometries are important factors to be considered in geostationary retrievals. Some other works have analyzed geostationary retrievals in a broader spatial context, however, under a limited temporal domain [12,14,15,16]. This limitation is necessary to avoid technical or practical difficulties related to in situ samplings, but it also restricts the range of accessible illumination and viewing geometries, which are found lacking.
From the operational point of view, 1-D modeling is currently the only option to address retrievals, across broad spatial domains, in a timely manner [28]. Still, the literature has shown the importance of understanding 3-D effects due to cloud inhomogeneity at various levels, and the role of viewing and illuminating geometries in geostationary platforms. This work proposes discussing these issues by using a simple 1-D retrieval methodology and analyzing regressions of GOES-13 against the reference MODIS Terra and Aqua cloud products. We seek to answer how these inter-satellite comparisons change over the seasons and to discuss the role played by geometrical factors. Large areal extents in the tropics are studied over continental South America and the Southeast Pacific. We present our results in the context of previous studies in the Discussion section. The following sections are structured as follows: Section 2.1 presents the datasets used in this study; Section 2.2 discusses the retrieval methodology and assumptions that have been made; Section 2.3 and Section 2.4 describe the strategy used for matching up GOES to MODIS and aircraft datasets; results of matchups are shown in Section 3.1 and Section 3.2; Section 3.3 discusses the influence of illumination on the retrievals; Section 3.4 shows a comparison of some of our retrieval results with in situ aircraft data. We discuss our results in Section 4, with a proposition for moving forward in future studies; our conclusions are discussed in Section 5.
2. Materials and Methods
2.1. Spatial–Temporal Domain and Datasets
The spatial domain for this study was divided into three sections: one designated as the West sector (5° N to 30° S; 70° to 120° W), another as the East sector (5° N to 30° S; 20° to 70° W), and a special quadrant designated as the Amazon sector (2° N to 7° S; 54° to 73° W). The East sector is characterized by a large extent of continental South America, covering a profusion of different surface types, including forests, savannah, grasslands, cities, and mountainous regions over the Andes. The Amazon sector corresponds to mostly forested surfaces and large rivers. The West sector area is dominated by the oceanic surface of the Southeast Pacific, as shown in Figure 1. Over the East sector, many different cloud systems may occur, ranging from small to mid-level cumuli up to deep convective cells, mesoscale convective systems, propagating squall lines, and frontal systems, especially during the austral winter. In the Amazon sector, intense convective activity is often observed, with rapid daily cloud formation, from initial shallow convection to deep convective cells, organization of squall lines, and mesoscale convective systems. In contrast, the West sector is dominated by stratocumuli or stratus cloud decks in the Pacific Ocean, but deeper convective cells may occur closer to the Intertropical Convergence Zone, also subject to seasonal fluctuations. For the sake of this work, we note that these different cloud properties are key to understanding differences in results for each of the regions under study. Statistically, for broken cloud fields and convective cells, under different stages of development in the East and Amazon sectors, shape irregularities on cloud tops are more likely subject to 3-D illumination or shadow casting effects than the more homogeneous conditions in the West sector [25]. Pockets of open cells in the Pacific can be screened out based on their lower average albedo.
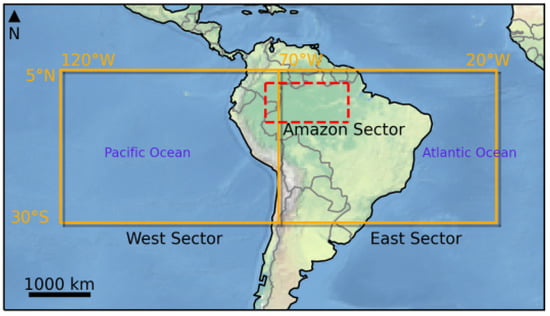
Figure 1.
Spatial domain used in this study: East (5° N to 30° S; 20° to 70° W), West (5° N to 30° S; 70° to 120° W), and Amazon (2° N to 7° S; 54° to 73° W) sectors.
GOES-13 imager, Terra MODIS, and Aqua MODIS data over the three sectors were obtained from online repositories administered by NASA (https://atmosphere-imager.gsfc.nasa.gov/products/cloud, accessed 9 November 2021 12:00 UTC) and NOAA (https://www.avl.class.noaa.gov/saa/products/welcome, accessed 9 November 2021 12:00 UTC). Data from these sensors were retrieved for January, April, July, and October, between 2014 and 2017. Restricting the analyses to these months was motivated by limitations in managing sizable data files, due to the large areal extent in each sector. This constraint does not impact the goals in this work. Only daytime data were used, hence, for each sector, a specific daily time interval was considered. For the East and Amazon sectors GOES and MODIS data were retrieved between 11:00 UTC and 19:59 UTC. For the West sector, this interval was 13:30 UTC to 22:29 UTC. Since the geostationary sensor at 75.2° W has a fixed observation geometry for each given surface pixel, the different months chosen in the study were intended to probe how varying illumination angles along Earth’s orbit would impact GOES vs. MODIS retrieval comparisons. MODIS retrievals have been investigated for biases under inhomogeneous cloud fields, due to 3-D effects arising from the illumination and observation geometries [23]. Horváth et al. [23] have shown that, under observation conditions analogous to the ones used in this work, MODIS retrieval biases due to variations in the sensor view zenith angle, , are minimized. Therefore, such biases do not compromise our results.
Collection 6.1 Terra and Aqua MODIS cloud products (M*D06) [11] were considered as baseline references in this study. Average and sample standard deviation statistics of , from MODIS 3.7 m channel “best quality” pixels, were compared to GOES retrievals in matched-up grid cells. No modification was applied to the regular M*D06 product other than grid averaging. Choosing the MODIS 3.7 m product was motivated by the following: first, this is the closest wavelength to the nominal 3.9 m GOES channel, hence both retrievals should be constrained by similar physical processes, regarding cloud droplet photon scattering and absorption. Secondly, the 3.7 m wavelength vertical photon transport within the cloud is shallower than the shorter 2.2 and 1.6 m wavelengths [31], thus it is less susceptible to variations in the vertical profile of cloud hydrometeor size. Lastly, the 3.7 m MODIS product has shown better resilience against biases due to the presence of precipitation, the occurrence of 3-D effects, and subpixel horizontal photon transport inhomogeneity, and fares better against in situ measurements, when compared to the 2.2 and 1.6 m products [17,23]. Geolocation products (M*D03) were used to assess MODIS viewing geometry, surface type (i.e., land/sea mask), and hydrometeor thermodynamic phase. Only daytime MODIS data were used due to the limitation in the GOES-13 retrieval algorithm, which requires information on the visible (VIS) channel cloud reflectance, as discussed below.
GOES-13 imager raw count data from VIS, infrared (IR), and thermal infrared (TIR) channels, at 0.63, 3.90, and 11.0 m, were converted to calibrated radiances (VIS at 1 km nominal spatial resolution, IR at 4 km), and brightness temperature (TIR at 4 km), according to NOAA’s specifications (https://www.ospo.noaa.gov/Operations/GOES/calibration/index.html, accessed 9 November 2021 21:00 UTC) [32]. GOES-13 “scan coverages” designate specific regions, delimited by latitude–longitude boxes, for which imagery is acquired at regular time intervals. In this study we used the “Full Disk” and the “Northern Hemisphere Extended” scan schedules, resulting in having GOES imagery data typically every 30 min.
2.2. GOES-13 and Phase Retrievals
We describe below the general retrieval strategy used to derive from GOES-13 radiance measurements. This is not intended to be an operational retrieval program, but rather a simple approach anchored in physical processes. The assumptions described below arise from 1-D radiative transfer concepts, and as such need to have their limitations of applicability recognized [26,27]. Yet the same set of concepts constitutes the current core of NOAA’s official retrieval algorithm for GOES-16, as indicated by their Algorithm Theoretical Basis Document (https://www.ospo.noaa.gov/Products/Suites/files/atbd/DCOMP_ATBD_2016_Apr.pdf, accessed 9 November 2021 12:00 UTC).
Pixel-level VIS radiances, , measured by the GOES-13 imager sensor, at 1 km nominal spatial resolution, were expressed in terms of the reflectance function as:
where is the extraterrestrial solar flux at 0.63 m (i.e., integrated over the VIS channel filter function), is the pixel-level cosine of the instantaneous solar zenith angle, and d is the Sun–Earth distance, in astronomical units, for a given day of the year. was used to identify cloudy pixels that could be potential candidates for a retrieval attempt, as explained below.
Planck’s blackbody emission at 3.90 m, , was subtracted from the measured IR radiance to derive , at 4 km spatial resolution, following Kaufman and Nakajima [33]:
where is the extraterrestrial solar flux at 3.90 m [34], and are, respectively, the bidirectional and the upward solar radiation transmission functions at 3.90 m, and is the brightness temperature derived from the TIR channel. Notice that , , , and were specifically derived using the GOES-13 IR channel filter function (https://www.ospo.noaa.gov/Operations/GOES/goes-imager-srfs.html, accessed 9 November 2021 21:00 UTC).
The transmission functions and were parameterized as functions of the pixel-level of a cloudy pixel, using the libRadtran [35] radiative transfer code package. The parameterization is shown in Table 1 and represents the fact that, on average, the lower (i.e., warmer) the cloud, the more water vapor is present in the column above it, hence resulting in lower and . In practice, varies between about 0.6 and 1.0 depending on the cloudy pixel , while Kaufman and Nakajima [33] considered a fixed value of 0.75.

Table 1.
Parameterized transmission functions, according to the pixel-level .
One key issue in this study is what constitutes a cloudy pixel. Our definition is based on a simple threshold method. For small clouds the classification results will deviate from more intricate methodologies, like the one used in the MODIS product chain. In our study GOES-13 pixels were classified as cloudy when having > 0.35 and < 290 K. We reckon this is a rather stringent requirement for the VIS reflectance threshold. It ensures only optically thick clouds ( above 8–10) are selected for subsequent retrievals, and corresponds to a region of approximate orthogonal solutions for and in Nakajima–King type diagrams [33]. The choice does impact the mean GOES-13 retrieval results since it imposes limitations on the subset of cloud regions selected for analysis. In other words, the resulting is constrained to optically thicker clouds, and cannot be identical (i.e., along the 1:1 line) to results intended for broad application, including all types of clouds, such as the MODIS operational product. This does not interfere with the main goal in this study, which is to gather new insights on seasonal variations for the retrievals. In future developments, it will be possible to reevaluate the threshold specifications to admit more demanding cloudy pixel definitions, or to use external ancillary data to improve the cloud selection method.
To avoid inhomogeneous regions near cloud edges, only sections containing at least 8 × 8 km contiguous cloudy pixels were retained for subsequent analysis. This restriction favors the selection of the central core of cloud sections. Avoiding cloud edges [30], and considering clouds with , aims at reducing subpixel and pixel-level variability [26], and the likelihood of having surface scattered radiance diverted toward the sensor field of view. This cloud edge detection routine was performed in the following steps: (1) was resampled to 1 km to match the spatial resolution (these resampled data were used only internally in this routine); (2) an initial cloud mask at 1 km was derived applying the and threshold levels described above, by assigning 0 or 1 to noncloudy or cloudy pixels, respectively; (3) the average of 8 × 8 pixel cloud mask boxes was calculated; if a box showed an average value below unity, none of the corresponding pixels in and arrays were further used by the algorithm. The 8 × 8 km size is arbitrary. We empirically found this to be an adequate compromise in ensuring the screening of inhomogeneous cloud edges and keeping enough statistics for robust results.
The thermodynamic phase of cloudy pixels was determined based on the spectral / signature due to water and ice differential wavelength absorption properties in the VIS and IR. By analyzing the / ratio for cloudy pixels in the water phase (i.e., 0 C) and pixels in the ice phase (40 C), this quantity can identify the thermodynamic phase in hydrometeors and their glaciation temperature [36], for use in future works involving mixed-phase clouds. In this study, only warm water phase pixels were selected.
A LUT with precomputed simulated radiances, under a number of preset conditions, was derived by Mendonça [37] using libRadtran [35]. The LUT was originally developed for tropical atmospheric profile conditions, considering a homogeneous dark surface with 0.09 albedo at 3.90 m, 1-D plane-parallel clouds with constant , considering values from 2.0 to 59.0 m in each simulation, of 10°, 20°, and 30°, solar zenith angles, , ranging from 0° to 75°, relative azimuth angles (sensor view minus solar illumination azimuth: = − ) of 30° and 150°, and ranging from 1.0 to 50. In this work, only the optically thick, asymptotic results for = 50 were used. Surface locations with , , and , respectively, used corresponding LUT solutions for , , and . No retrievals were attempted for locations. No modifications were introduced to account for the fact the nominal wavelength for GOES-13 at 3.90 m differs from the 3.7 m used in MODIS cloud products. The full LUT included calculations for both water droplets and ice particles. Ice phase solutions were based on bulk scattering properties using a general mixture of crystal habits provided by libRadtran [35,38]. Here, only the water phase LUT section was used.
The general GOES-13 retrieval process operated in this fashion: (1) for pixels within a section of at least 8 × 8 km cloudy pixels, the warm water phase was selected by identifying pixels with > 0 °C; (2) for the selected pixels, was determined based on pixel-level latitude, longitude coordinates, day of the year, and the imagery acquisition time. This provided the information to select the LUT subset of solutions in the forward ( > 90°) or backward ( < 90°) scattering hemispheres. Notice that since the LUT uses 1-D calculations, the choice of the scattering hemisphere refers to anisotropic characteristics of the hydrometeor phase function, not related to shading/illumination issues that can only arise in 3-D modeling; (3) considering the particularly observed illumination and viewing geometries, the measured was sought over the LUT; (4) the retrieved solution corresponded to the linear interpolation between the two nearest matching results found in the LUT. Figure 2 illustrates one particular subset of conditions in the LUT, where = 20°, = 150°, and the nonlinear relation between and is evident. This inherent nonlinearity is in itself a potential source of unaccounted subpixel bias in 1-D radiative transfer simulations [25], but mitigating strategies [27,29] can ameliorate this issue. We did not seek to retrieve from the measured VIS reflectance, since our goal is specifically to study retrievals, considered approximately independent of for > 8 clouds.
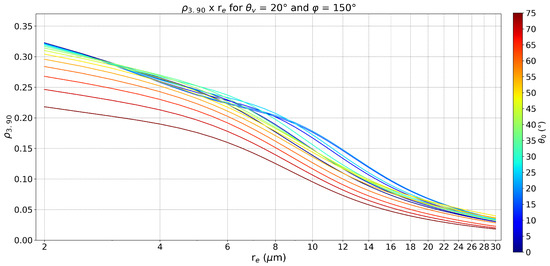
Figure 2.
LUT subsection with solutions for water phase cloud droplets with , m, , and . The curves correspond to the interval .
2.3. MODIS Match Up and Spatial–Temporal Comparison Strategy
GOES-13 imager radiance scans take a regular amount of time to be completed, hence their start times do not directly reflect the instant of acquisition over the region of interest. For instance, a “Full Disk” scan schedule takes about 13 min from the start to get to the eEquator region, while in “Northern Hemisphere Extended” scans the same process takes about 7.5 min. Thus, all GOES-13 retrieval times in this study were adjusted to their equivalent Equator scanning times.
Due to Terra and Aqua polar orbits, MODIS retrievals closer to the Equator can typically have one overpass during daytime for each satellite, while closer to the poles several retrieval occasions can occur each day. To match up these multiple retrieval opportunities, a temporal window of 20 min was established, centered at each GOES-13 Equator scanning time. In this way, any MODIS data granule within this time slot was considered apt for comparison. was limited at below 60° for both MODIS and GOES-13 [39].
To compare the GOES-13 derived to the reference MODIS , both these quantities were bilinearly interpolated over a regular 0.2° latitude/longitude grid, across the spatial domain in each sector, to allow for a direct comparison in coincidentally cloudy pixels. A post-gridding cut-off value of 1.0 m was defined to represent a physical consistency check, i.e., as a lower limit of acceptable gridded values for effective radii. The gridding process can introduce artifacts if a cell contains cloud edges, or if pixels with significantly different end up in the same gridding cell. This can be controlled by excluding from the analysis cells with a relatively large standard deviation (), compared to the gridded value , such as:
where the brackets < > denote the bilinear gridding. Only grid cells with a relative standard deviation below 10% were retained for comparison. Besides excluding gridding artifacts, this also eliminates regions with high variability, arising from other sources of resolved inhomogeneities, such as juxtaposed interfaces with shadowed/illuminated cloud sections [30], or with clouds at different top heights [25]. The computed in each grid cell was further used as an estimate of the uncertainty in regressions, i.e., the larger the in a grid cell, the smaller its weight in computing the regression statistic.
The aim in imposing these series of strict sets of requirements for matchups is assessing the performance of this GOES-13 retrieval algorithm under relatively uniform, although realistic, atmospheric conditions representative of a panoply of environments. In future studies, more challenging cases can be used.
2.4. Aircraft In Situ Match Up and Comparison Strategy
The GOES-13 retrievals were also compared to aircraft in situ measurements collected during the GoAmazon2014/5 experiment [40,41]. During the first GoAmazon2014/5 Intensive Operations Period (IOP1), the US Department of Energy (DOE) Atmospheric Radiation Measurement (ARM) Gulfstream-1 (G-1) aircraft [42] performed 16 research flights near the city of Manaus ( S, W) to measure aerosol, clouds, radiation, and gas-phase chemistry characteristics. The IOP1 took place between February and March 2014, corresponding to the local wet season. During this time of the year, the background atmospheric conditions are rather clean in terms of aerosol pollution due to the frequent rain showers. On the other hand, Manaus emits daily pollution plumes downwind (most often towards the southwest) due in large part to car traffic and urban activities. This creates a contrast between clean and polluted atmospheric conditions, with the respective variety in cloud microphysical properties.
Cecchini et al. [43] have analyzed the statistical differences between clouds affected or not by the pollution plume emitted from Manaus. In this study, the authors organized the 1 Hz Fast Cloud Droplet Probe (FCDP, Spec Inc.) measurements for all G-1 flights, excluding all occurrences of thin clouds with droplet number concentrations below 0.3 cm, or liquid water content below 0.02 g m. Additionally, the data collected during aircraft maneuvers were filtered out. These observations were synchronized with temperature, humidity, pressure, and wind measurements collected by the Aventec Research Inc. Aircraft-Integrated Meteorological Measurement System (AIMSS-20) [44]. For consistency with the warm cloud retrievals presented here, we further excluded all G-1 measurements with temperatures below 0 C. This process resulted in 3068 measurements of with 1 Hz frequency, from which was calculated following Equation (1). With a flight speed of approximately 100 m s, each measurement corresponds to a segment of about 100 m. We refer the reader to Cecchini et al. [43] for further details on the G-1 instrumentation as well as the flight strategies employed during IOP1.
To colocate aircraft measurements with the satellite retrievals the following method was applied: (1) each flight during IOP1 was scrutinized and segmented into flight legs comprising a duration between 120 and 130 s; (2) for each flight leg the average , latitude, longitude, and time coordinates were computed. The selected data points in each leg were also used to compute the standard deviation; (3) each flight leg average time coordinate was used as a reference to search the contemporary GOES-13 imagery, considering a time window of min; (4) the 3 × 3 GOES-13 pixels centered on each flight leg latitude and longitude were used to compute the satellite standard deviation. The GOES-13 retrieved at the central pixel was compared to the aircraft average .
Since the IOP1 measurements were performed during a short period of time, a special GOES-13 comparison strategy was adopted to ensure enough statistics remained for the matchups. The threshold levels to detect cloudy pixels were set as and K during IOP1. These levels were found adequate for the environmental and physical conditions observed during the G-1 flights. The cloud edge detection routine was not applied, i.e., no restrictions were imposed to exclusively retrieve over 8 × 8 contiguous cloudy pixel regions. The relative standard deviation restriction was relaxed to allow up to 50% variation. An additional restriction was implemented, requiring the relative standard deviation to be below 1%.
3. Results
3.1. GOES-13 Imager and MODIS Direct Matchup Results
Representative results of the matchup comparison are shown here, while subsequent sections examine these results in further detail. Comparisons between other geostationary retrievals and MODIS, from previous works, are presented in the Discussion section. In this work, the data were not scrutinized for the influence of precipitation events [16,26], in part due to the relatively shallow vertical photon transport associated with the 3.90 m wavelength [31]. Only statistically significant figures with p-values under 0.05 are presented.
Figure 3 shows an example of regression results and comparison histograms, for January and July in 2014, over the West sector, for water phase droplets over the ocean. Both regressions show a relatively high correlation coefficient, with tens of thousands of matchups in each month. Despite all simplifications involved in the 1-D radiative transfer modeling, the results do capture the essence of MODIS retrievals, explaining 74% to 84% (R²) of variability over a large section in the Southeast Pacific. The sample confidence interval indicates the linear model can explain 95% of individual retrievals within a couple of m. As explained earlier, the retrieved data are not expected to lie at the 1:1 line since our cloudy pixel definition differs from the method used by the operational MODIS product. Most noticeably, the slopes and intercepts change significantly between January and July 2014. While the MODIS value retrieval domain (i.e., Figure 3 projection on the x-axis) does not change considerably between these two months, GOES-13 retrievals undergo a visible change, such that the intercept varies from about +1.5 m to −1.9 m. Even though these regressions show relatively high correlation coefficients, the changing slopes and intercepts show it is not possible to lump all yearly retrievals together to derive a unique comparison. On the contrary, these seasonal differences corroborate the complexities of orbital variations and the relative illumination/viewing geometry [13] in a geostationary platform. Of course, cloud microphysics should change between the two situations in January and July, and therefore can also contribute part of the changes, but the MODIS retrieval domain was not significantly affected.
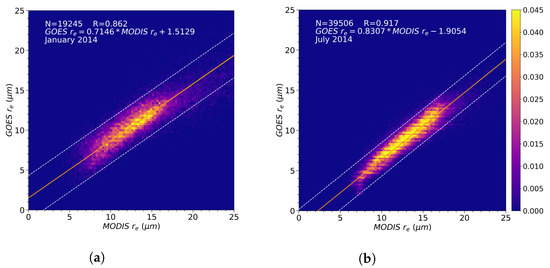
Figure 3.
West sector matchup histograms for the months of (a) January and (b) July in 2014, and regression results for water phase droplets over the ocean. Dashed lines show the 95% sample confidence interval for each regression. Colorbar units are relative density m.
In order to assess the degree of variability, and whether it would impact the comparisons in a consistent fashion, we compared monthly regression results over the ocean, throughout the four years used in this study. Figure 4 shows the regression parameters and correlation coefficients from 2014–2017. In general, similar slope, intercept, and correlation coefficients are obtained for the same months in different years. The yearly repeatability of the regression parameters is an indication that the comparisons are reproducible to a certain degree. Considering the large number of varying physical conditions for cloud formation and development over the region, it is most likely that this cyclic pattern may be related to varying solar illumination conditions, with average 3-D effects related to the illumination and viewing directions, due to shadow casting on irregularly shaped cloud tops [25,30]. Considering our matchup selection method precludes pixels from the shallowest, optically thin clouds, and broken cloud fields, it is unlikely that the pattern shown in Figure 4 reflects seasonal changes in surface properties. The hot spot and glory effects, showing peaking reflectance at the Sun’s backscatter, are other periodic phenomena that can in principle alter cloud reflectivity properties in the region. However, the particular set of geometrical configurations required for illumination and viewing directions makes them rare occurrences [21], that cannot explain the observed yearlong variations shown in Figure 4. These results confirm that each month needs to be treated separately for these inter-instrument comparisons.
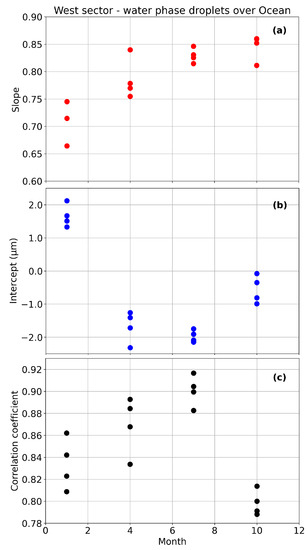
Figure 4.
West sector monthly regression results, for water phase droplets over the ocean, for the months of January, April, July, and October from 2014–2017. (a) Regression slope, (b) intercept, and (c) correlation coefficient. Individual markers correspond to a given month in different years.
We next discuss the particular case for the month of October. Regressions for the monthly 2014–2017 matched-up data are shown in Figure 5. Histograms are shown over the West sector, for oceanic and continental surface types, and the East and Amazon sectors over the land. In the West sector (Figure 5a,b), the number of matchups, N, is much larger over the ocean compared to the land since this sector extends predominantly over the Pacific. The regression results are significantly different over the land and ocean: over the Pacific (Figure 5a) a smaller (absolute) intercept value was obtained, compared to continental matchups (Figure 5). However, the slope of the regression is closer to unity over land than over the ocean. The sample confidence intervals show the regressions can predict 95% of individual data points within about m over the ocean, and within about m over the continental surface. Incidentally, we note the currently operational GOES-16 droplet size retrieval algorithm is required to match MODIS retrievals along the 1:1 line within m (https://www.ospo.noaa.gov/Products/Suites/files/atbd/DCOMP_ATBD_2016_Apr.pdf, accessed 10 November 2021 12:00 UTC).
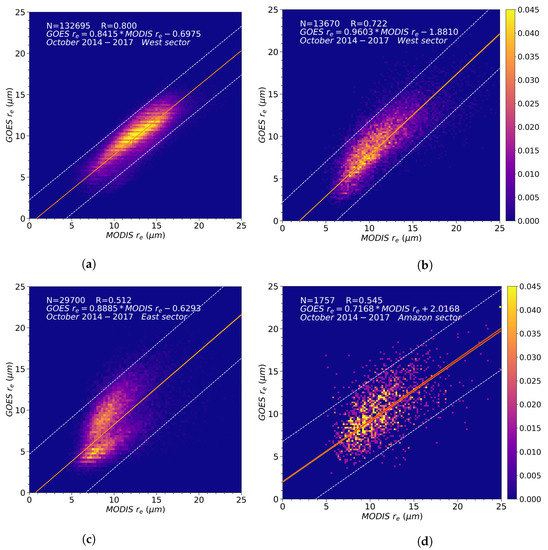
Figure 5.
West sector (a) ocean and (b) land, (c) East sector, and (d) Amazon sector GOES-13 and MODIS Terra and Aqua matchup histograms for the month of October, from 2014 to 2017, and regression results according to surface type. Dashed lines and colorbar units as in Figure 3.
Figure 5c shows East sector matchup and regression results over the land for October 2014–2017. In this sector, there were few matchups for the oceanic surface, which were not statistically significant. Close examination of the bimodal data structure shown in the graph indicated the need to analyze Terra and Aqua matchups separately, as discussed below. Amazon sector results are shown in Figure 5d. In this case the number of water phase matchups is much smaller than identified ice phase pixels. This is mostly due to the prevalence of strong convective activity in this region when compared to the average conditions in the East and West sectors, which favors the frequent occurrence of deep convective clusters with glaciated cloud tops [36].
3.2. GOES-13 Monthly Matchups for MODIS Terra and Aqua
Analyzing East sector matchups over land for October, separately for MODIS aboard Terra and Aqua, allowed a considerable improvement in the regressions as shown in Figure 6a,b (contrast with Figure 5c). Although the methodology was never intended for a 1:1 comparison with MODIS, Figure 6a shows that a slope slightly above unity and intercept of about −0.4 m is a feasible result, even over the land. The correlation coefficient was close to 0.7, with 18,814 observations. However, similar to what occurs over the ocean (Figure 4), land comparisons also show regression parameters that oscillate along the different months of the year. Hence, we interpret the regression in Figure 6a predominantly as the result of a particular set of favorable illumination/viewing conditions, but also due to the average type of clouds observed in October in that region, with less convective activity than in January.
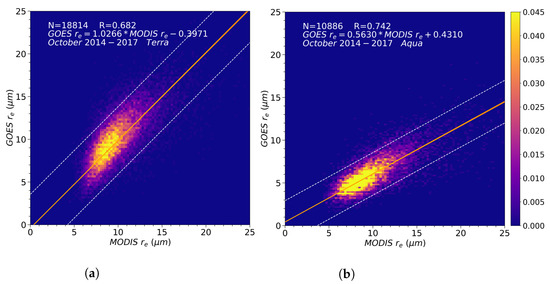
Figure 6.
East sector water phase matchup histograms for MODIS (a) Terra and (b) Aqua, over the land, for October from 2014 to 2017, and regression results. Dashed lines and colorbar units as in Figure 3.
The October regression against MODIS Aqua in Figure 6b indicated a noticeably smaller slope than Terra. Despite the different overpass times for Terra and Aqua, the MODIS retrievals refer essentially to similar environmental conditions, hence the ranges of MODIS retrieved for Terra and Aqua are nearly equivalent (projection onto the x-axis in both graphs). Therefore, the conclusion is that the GOES-13 retrievals in Figure 6b must be subject to particular biases that lead to being underestimated. From the combined analysis with Figure 6a, we propose that this should be related to 3-D illumination/shadowing effects from the geostationary viewpoint, and the particular cloud development stage. Nominally, Aqua overpasses occur at around 1:30 p.m. local time, while for Terra mid-morning overpasses occur at 10:30 a.m. On average, over large areas in continental South America, more convective activity is present close to local noon than by mid-morning, which may contribute to the occurrence of more developed clouds, and therefore be more subject to 3-D shading/illumination effects [25,30].
To assess how the matchups fare against Terra and Aqua overpasses in general, monthly regressions are shown in Table 2 considering each MODIS platform separately. Firstly, analyzing the West sector results over the Pacific, one notices the regressions show consistent similar figures for the correlation coefficients and slopes, for Terra and Aqua, with tens to hundreds of thousands of observations. Intercepts, however, are distinct for the two platforms, with Terra showing larger absolute values than Aqua for all regressions in this sector.

Table 2.
Segregated Terra and Aqua MODIS monthly regressions, such that GOES-13 = Slope × MODIS + Intercept. N: number of matchups; R: correlation coefficient.
On the land surface in the East or the Amazon sectors, GOES-13 vs. Terra slopes approach unity while Aqua regressions show, in general, slopes under 0.6, except for July, with a slightly higher slope of about 0.7 in the East sector. This extends the October analysis discussed above for the other months, such that in the East, Terra and Aqua show robustly different regression results.
Considering Table 2 as a whole, except for two cases in the East sector, all other slopes are below unity. The implication is that, in general, a better agreement with MODIS retrievals is observed for smaller , becoming progressively more distant as increases. The reason for this slope underestimation is still under investigation. Marshak et al. [25] show that subpixel variability induces a reduction in associated with the gridding process. In our case in particular, the same 0.2° gridding is applied to GOES-13 and MODIS. However, the original data have distinct spatial scales, nominally of 1 km for MODIS [11], and 4 km for GOES-13 retrievals, so this can be a possible explanation for slopes smaller than unity. Enhanced illumination at backscattered viewing angles can also act to reduce [30], as discussed in Section 3.3, but it is unlikely this effect alone would act predominantly over clouds with larger to generate smaller slopes. Another possible factor for this would be a positive residual bias in the process of deriving , such as not accounting for droplet size-dependent effective cloud emissivity [45]. We will continue seeking improvements to the GOES-13 retrieval methodology.
The intercepts in Table 2 seem to show a pattern of a relative maximum in January and a minimum in July, except for the Amazon sector that shows a maximum in April. The pattern is not due to any issues concerning the computation of the Sun–Earth distance in Equation (4), which was double-checked to be accurate. The cyclic pattern, though, suggests a global unaccounted effect acting upon the GOES-13 dataset, due to the prevalent scattering conditions and cloud structures in each regression subset. We examine this issue in more detail in the Discussion section. From the results shown in Table 2, it is clear that, statistically, GOES-13 retrievals are subject to different observational artifact levels over oceanic or continental surfaces, that can be due to different illumination/observation geometries, coupled with physically distinct average cloud types, e.g., stratified cloud decks or vertically developed convective clouds.
3.3. Assessing GOES-13 Sensitivity to Illumination and Observation Geometries
Below, we examine the sensitivity of GOES-13 retrievals to geometrical parameters related to the angles of illumination and observation. We compute the relative azimuth angle , as a means to quantify the relative amount of illuminated vs. shaded hemispheres directly accessible to the imager sensor on GOES-13. This methodology was adopted previously to analyze MODIS retrievals’ dependence on [23]. is more sensitive in capturing the variations in illumination observed on the surface of clouds than the scattering angle. While the GOES-13 position relative to a point on the surface is fixed over time, the solar illumination undergoes angular variations during the day and seasonal variations throughout the year. Therefore, since the studied areas include pixels from every view direction to the subsatellite point, it is not immediately obvious how to identify the subset of spatial and temporal domains with scattering regimens best suited for retrievals.
Surface pixels for which correspond to the forward scattering hemisphere and pixels are located in the backscattering hemisphere. In the forward direction, scattering by 3-D cloud structures may cast shadows towards the pixel under analysis, reducing the measured reflectance, therefore inducing an artificial increase in the retrieved [25,30]. In the backscatter hemisphere the opposite effect can happen, with an increased reflectance signal in the field of view, originating from photons scattered by nearby irregularly shaped 3-D clouds [25,30].
In Figure 7 we analyze the measured and retrieved GOES-13 , as a function of for April 2014–2017, during Terra (Figure 7a,b) and Aqua (Figure 7c,d) overpasses. For the oceanic surface in the West sector (Figure 7a) there are retrievals over the whole range, from 0° to 180°, with a predominance of backscattering conditions. This shows that in April, most of the area in the West sector is usually observed by GOES-13 in the backscatter hemisphere at the time Terra flies over the region. and do not show noticeable trends with , but looking closely one notices these two quantities are somewhat anti-correlated: in sections of Figure 7a where decreases with (e.g., for ), there is an increase in . In contrast, Figure 7b shows GOES-13 retrievals over the land, in the Amazon sector, during Terra overpasses. In this case, there are much fewer opportunities for sampling the backscatter hemisphere and the retrievals are largely performed under forward scattering . On average, the measured in Figure 7b is smaller than in Figure 7a, resulting in larger retrieved for clouds over the Amazon, compared to oceanic clouds. This may make sense statistically since it is possible that, by mid-morning during Terra overpasses, deepening cloud clusters might have larger , compared to stratiform cloud decks over the Pacific. However, it is not possible to rule out the occurrence of partial shadowing to explain the Figure 7b results, with thousands of measurements spread over four years.
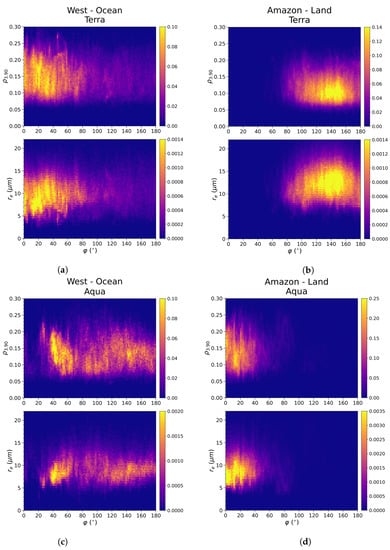
Figure 7.
GOES-13 measurements and retrievals for April 2014–2017, as a function of , for the oceanic surface in the West sector for (a) Terra and (c) Aqua overpass times, and for the land surface over the Amazon sector for (b) Terra and (d) Aqua overpass times. Colorbar units are relative density for plots, and for plots.
Figure 7c shows West sector GOES-13 retrievals over the Pacific during Aqua overpasses for April 2014–2017. There are observations under forward and backward scattering, with a predominance toward backscattering. A section of corresponds to decreasing and increasing , possibly associated with the increased illumination effect that biases the retrievals to smaller . Figure 7d shows that over the land GOES-13 retrievals during Aqua overpasses have very few observations in the forward scattering hemisphere. shows a peak in the backscatter ° associated with reduced that is consistent with the description of the increased illumination effect. Notice that amidst the cases in Figure 7, Figure 7b,c show relatively more retrievals in the forward scattering hemisphere. Figure 7c shows some indication of the shadowing effect for , i.e., a reduction in accompanied by an increase in the retrieved .
We note some of the results described in Figure 7 are contingent on the particular conditions that have been observed in our specific dataset. Namely, 3-D scattering or shadowing effects by neighboring clouds or clusters require that particular configuration to be present [25]. However, the relative position between the satellite and the region of interest (i.e., to the east or west of the subsatellite point), the access to a given range that determines the scattering regimen, and also the typical range of measured values are all key characteristics for the development of a geostationary retrieval algorithm. These need to be taken into account over large spatial domains, either for research concerning GOES-13, or in currently operational applications such as GOES-16 hydrometeor size retrievals.
3.4. GOES-13 In Situ Aircraft Matchups during GoAmazon
Although our focus here is on the multi-year seasonality of GOES vs. MODIS comparisons, it is useful to examine how the GOES-13 algorithm fares against in situ measurements during GoAmazon IOP1 [40]. Figure 8 shows the resulting matchup, using the methodology described in Section 2.4. The data were classified according to to highlight distinctions in the forward or backward scattering regimens.
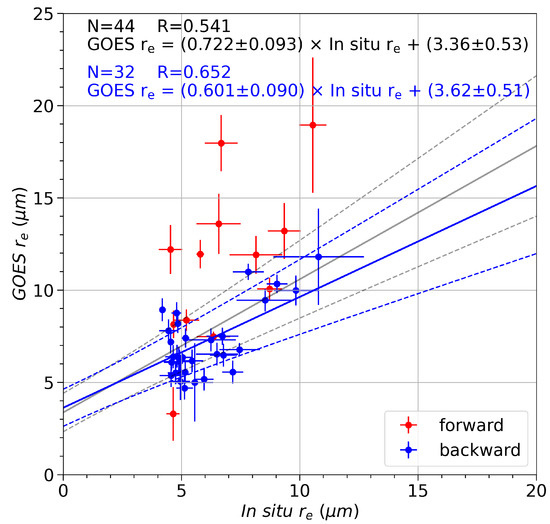
Figure 8.
Colocated comparison between GOES-13 retrievals and GoAmazon in situ aircraft measurements. Forward () and backward () scattering retrievals are shown in red and blue, respectively. Full lines show the linear regression models using all (gray) or only backscattering data (blue). Dashed lines indicate the 95% confidence interval for each regression model. Error bars for in situ are one standard deviation of measurements within 120–130 s time windows. Error bars for GOES are one standard deviation of retrievals in 3 × 3 pixel boxes.
In general, there is a tendency for GOES retrievals to overestimate in situ measurements, similar to those observed in other studies [14,15,16]. It is clear that forward scattering conditions correspond to the highest positive biases in the set. The linear regression with the whole dataset results in a positive correlation of about 0.54. The correlation increases to about 0.65 when considering only GOES retrievals in the backscattering hemisphere. The main reason for the forward scattering overestimation should be related to 3-D shadow casting effects [25]. Note that backscattering retrievals are also overestimated relative to in situ measurements, i.e., they mostly lie above the 1:1 line. In these cases, shadows are less prevalent but other effects contribute to reducing the measured , such as contamination of the detected signal by the surface albedo, the pixel coarsening effect [25], and intrinsic LUT nonlinearities [29]. The altitude inside the cloud at which the aircraft measurements were performed is also important since, on average, is larger closer to cloud tops [15]. Although these results are derived from a limited sample, they provide ground truth equivalence to the algorithm used in this study and clearly show the influence of configurations in the final outcome. The illumination and viewing directions are fundamental pieces of information to determine to what level we can expect GOES retrieved to reproduce direct measurements.
4. Discussion
Previous works have examined the feasibility of retrievals from a geostationary platform, with different objectives from the ones in this study. In general, these works have used operational products to generate , which were compared to in situ aircraft measurements or MODIS retrievals, for limited spatial and/or temporal domains. This work addresses the seasonal variability in regression results, over large spatial scales, while using a simple retrieval strategy. With diverging objectives and methodologies, not all the results are directly comparable. However, it is still interesting to contextualize some key findings in previous works.
Over the North Atlantic, Painemal et al. [15] showed GOES-13 retrievals have a positive bias of about 4.8 m on average compared to in situ aircraft measurements, with a root mean squared error (RMSE) of 5.8 m and . Comparisons with in situ measurements like this are operationally very complex and are fundamental to establishing ground truth equivalence. Against MODIS Terra and Aqua these retrievals showed positive biases of 1.9 and 2.0 m, and , respectively. The study area was situated between 40–60° N, 35–50° W, with an average .
In another study over the Southeast Pacific (10–30° S, 65–90° W), Painemal et al. [14] showed smaller biases for GOES-10 retrievals, compared to the result over the North Atlantic. Against in situ measurements, the retrieval bias was 2.4 m, with and m. Against Terra and Aqua, retrieval biases (RMSE) were 1.15 m (1.2 m), and 0.43 m (0.82 m), respectively.
Kang et al. [16] showed retrievals for the geostationary Himawari-8 satellite for the south of Australia (48–60° S, 138–162° E), with a mean positive bias relative to in situ measurements of 1.88 m and . The authors also reported strong negative biases in cases of heavy precipitation near the cloud tops.
Chen et al. [46] analyzed imagery from the geostationary Feng Yun 4A (FY-4A) satellite, over eastern China (25–35 N, 110–120E), on 30 June 2018, and compared retrievals with MODIS. Both liquid droplet and ice phase retrievals were performed. The authors found an overall similar spatial distribution pattern, with relatively good agreement for small particles but discrepancies for large sizes. The differences were attributed to the disparity in spatial resolution and between the two sensors.
Some other studies highlighted difficulties in comparing retrievals with aircraft and surface-derived measurements. Dong et al. [12] analyzed GOES-8 retrievals over the Southern Great Plains site and found essentially no correlation () with in situ aircraft measurements. At the same location, McHardy et al. [13] derived GOES-8, -10, and -11 retrievals, with data from 1998 to 2006, and also found no correlation () with surface measurements. In this latter study, the authors identified a strong dependence of the retrieved on the solar illumination geometry. They further recognized that it is not possible to probe and study this issue from measurements performed in just one location.
In Figure 8 we show a comparison between GOES-13 retrievals and in situ measurements, for particular GoAmazon conditions. Even with limited statistics, retrievals are markedly dependent on the geometry. These will ultimately determine the regression results, which quantify how retrievals are connected to direct measurements. Considering the wide expanse of the three sectors covered in this study, and the orbital illumination changes throughout the year, many different configurations are accessible. Figure 9 exemplifies typical spatial distribution configurations observed for GOES-13 retrievals during Terra and Aqua overpasses over the East and West sectors, for each of the studied months. Specifically, in Figure 9 we show mid-month days, from the 14th to the 16th, to find convenient GOES-13 imagery examples matching Terra and Aqua overpass times. Some of the examples in the West sector show two foci. One of them corresponds to the GOES-13 subsatellite point on the equatorial line at 75.2° W, and the other corresponds to the instantaneous subsolar point. In the East sector, only the subsolar point is sometimes apparent.
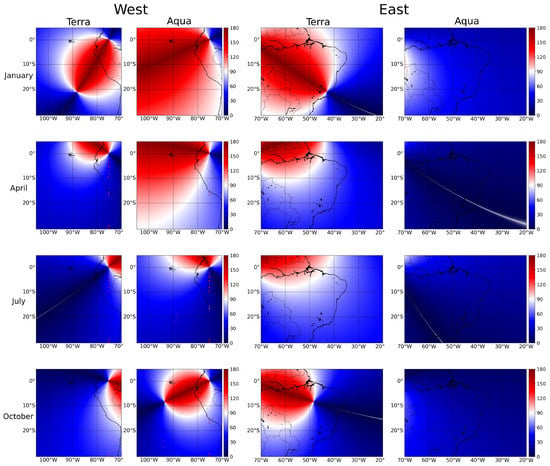
Figure 9.
Typical GOES-13 configurations, in degrees, for the East and West sectors during Terra and Aqua overpass times, for the 14th to 16th day of January, April, July, and October 2014–2017. Forward scattering is shown in red hues, backscattering in blue.
From the distributions in Figure 9, it is clear that relative illumination conditions vary greatly over the spatial domain, and at the same time, not all ranges may be available for validation efforts. For instance, to avoid the enhanced illumination effect in the backscatter hemisphere, one may wish to retrieve under, say, conditions. From Figure 9 we see that Aqua overpasses will rarely have this particular subset of conditions to the east of GOES-13, but will have many such opportunities to the west of the sensor. Likewise, for some months, there are more/fewer occasions for retrievals in the forward/backward scattering hemispheres. In July, for instance, when the sun is in the Northern Hemisphere, there are relatively fewer opportunities for forward scattering observations during both Terra and Aqua overpasses.
In the tropics, the regions on the surface closest to the subsatellite point will see large variations in with changes in the apparent solar position. These changes correspond to illumination constraints that are unique to geostationary platforms, and which need to be properly accounted for in retrievals. However, the quality of these retrievals is also subject to the occurrence resolved and unresolved spatial inhomogeneities [25,26]. Interestingly, Werner et al. [27] have shown it is possible to mitigate subpixel variability and partially compensate for their effects on retrievals. This can be done by applying a framework [29] based on VIS and IR radiance measurements, from two channels with higher spatial resolution than the product. The authors also show that even using a single higher-resolution band with their methodology can improve retrievals [27]. This is important for GOES-13 and other legacy geostationary platforms that only counted with one higher-resolution VIS channel. However, note that the framework implicitly assumes unbiased radiance measurements are used, i.e., not influenced by scattering or shadowing from foreign 3-D cloud structures.
Resolved variability of neighboring cloud structures is a challenging concept to address in single real clouds. It is highly contingent on the type of surrounding clouds, their particular spatial configuration and morphology. In trying to tackle this problem statistically, it is possible to quantify a spatial inhomogeneity index , similar to what has been done before [15,17,23,26]. In one possible definition, corresponds to the ratio between the standard deviation to the average of a variable, such as or . can thus be a proxy quantifying surface roughness for spatial variations at smaller scales, at the same scale, or at coarser resolutions than . The more dissimilar the cloud field in the vicinity of a specific pixel, the higher the values can assume, hence, in general, the higher the potential for the occurrence of 3-D shadowing or enhanced illumination effects.
A possible strategy for future works could begin by seeking to parameterize a function , describing the overall combined effect of the geometrical configuration , with the potential for 3-D effects over a given scene. This would be a statistical parameterization in the sense that it does not address individual clouds, but the average signal from a subdomain. can be computed for each latitude, longitude, and time coordinate, as exemplified in Figure 9. needs to be computed for the specific scene under consideration. The measured can be regressed against a combination of and to derive the effective parameterization function . For instance, with careful study over a stratiform scene, neighboring pixels will have similar = values, but may have different ranges. At the very homogeneous cloud limit (), the measured will respond to and . AsIf the surface inhomogeneity increases to over nearby clouds, we can learn how affects . For instance, Horváth et al. [23] have shown how increasing inhomogeneity changes the retrieved for MODIS. Next, for cloud field sections with similar one can study how the retrieved changes with . For instance, taking low MODIS retrievals over the Southeast Pacific as an benchmark, it can be possible to find stratiform cloud sections with similar MODIS and , but far apart enough to have distinct from the GOES perspective. In such a case, differences in GOES retrievals could then be attributed to variations. The underlying assumption in this type of analysis is that one can find pairs of cloud field sections, with similar microphysical properties, for which only one variable in the space changes significantly. In principle, could be positive or negative, i.e., it can represent an effective enhanced or diminished reflectance added to , to represent the average resolved 3-D variability [25] in a given configuration. The magnitude of should be small compared to unity, but since is nonlinearly related to , the final result on droplet size retrievals can be meaningful. This entire procedure can only make sense if the parameterization is reproducible over time. The periodic regression results shown in Figure 4 indicate that this is possible, i.e., GOES-13 retrievals follow a predictable pattern over months and years, and so it must also be for the signal from which is derived. If proven, this hypothetical procedure could help mitigate enhanced illumination/shadowing effects, to prepare the cloud field scene for applying the aforementioned framework [27,29]. This latter step can further curb cloud subpixel bias due to gridding in retrievals [25] and due to the covariance between and in Nakajima–King diagrams [29]. Other forms of subpixel variability biases, such as horizontal photon transport [17] or precipitation biases [16,26], remain unaddressed.
5. Conclusions
Studying cloud microphysics from geostationary platforms has been hampered by artifacts at subpixel and pixel levels [14,25,28] and geometrical difficulties [13]. We have examined how GOES-13 retrievals, for warm-phase clouds, fare against the reference MODIS cloud product, over large areas in continental South America and the Southeast Pacific Ocean. The retrievals were based on a 1-D LUT developed to simulate radiance measurements at the 3.90 m channel in GOES-13. Despite this simplified approach, we found our results were highly correlated with operational MODIS retrievals, with R between about 0.60 for Aqua and 0.91 for Terra. It is remarkable that over the vast spatial domains analyzed here, combining data from 2014 to 2017, this kind of coherence was observed between MODIS and GOES datasets, with sometimes more than 100,000 matching cloud retrievals (cf. July results for Terra in Table 2).
Over the ocean, there is, in general, a better agreement between GOES and Terra or Aqua, than over the land. The different regression slopes shown in Table 2 indicate that the location of clouds relative to the satellite sensor (i.e., to the east or west of the subsatellite point) and the time of the day the imagery is acquired are critical for the retrievals. The reason for this is twofold. First, cloud formation and development are distinct in both regions, hence the vertical cloud structure will be physically different. These different cloud types have varying degrees of spatial inhomogeneities due to their evolving 3-D structures. Second, the geometrical configuration of illumination and viewing angles are distinct for the two regions, both throughout the day and seasonally. These two factors combined are fundamental in defining the signal from which is directly derived.
We found that GOES vs. MODIS regressions showed a clear seasonal pattern. Regression slopes, intercepts, and R values varied between the ranges shown in Table 2, and exemplified in Figure 4, indicating these retrieval results are reproducible over time. Even though the analyses were performed with varying atmospheric conditions, cloud types, and cloud frequency distributions, the regressions did converge statistically, which allowed combining data from the same months in different years to derive these results.
Evidence for overestimation against in situ measurements is shown in Figure 8, associated with forward scattering conditions. On the other hand, an average underestimation effect, correlated with enhanced in the backscatter hemisphere [25], was exemplified in Figure 7. However, this phenomenon did not always peak at , as shown in Figure 7c. This further highlights how intricate the relationship between illumination/viewing angles and the occurrence of 3-D cloud structures can be, and how they combine to define the retrieved .
There are limitations to the illumination/viewing configurations that can be accessed by GOES-13, as exemplified in Figure 7. Depending on the time of day and season, there will be more or fewer opportunities to sample each scattering hemisphere, for regions to the east or west of the sensor. To define a future retrieval strategy, can be calculated for any given latitude, longitude, time, and day of the year, to predefine a particular scattering regimen of interest. For the sake of geostationary validation efforts, which usually rely on MODIS products, Figure 9 shows typical scattering conditions available throughout the year, at Terra and Aqua overpass times.
We speculate that partial mitigation of pixel-level 3-D illumination/shading effects can be pursued by combining the geometrical information provided by and the inhomogeneity proxy index . This would be a statistical approach to parameterize an average 3-D related effect over subdomains with specific cloud configurations. For instance, Figure 7a,b have different average in April, both measured at Terra overpass times. From Figure 9 we takesee that April Terra scattering over the ocean is mostly in the backscatter hemisphere, while the Amazon is typically in the forward scattering regimen. Under the hypothetical procedure we discussed in this work, part of the average signal in a small subdomain over the ocean (Figure 7a) could, for instance, be quantified as excess illumination in the backscattering due to contributions of nearby clouds. In this case, could be corrected to yield larger retrievals. Similarly, in a subdomain in the Amazon sector, the average (Figure 7b) could be linked to partial shadowing effects since scattering is mostly in the forward hemisphere. In that case, the corrected could yield smaller retrievals. One potential outcome of using this approach could be smaller yearly variations for the intercepts in Table 2. Terra intercepts vary from about to m across different sectors, and such oscillations would be altered if the average signal changes, after implementing the corrections predicted by this procedure.
The complexities of retrieving from geostationary platforms are well known [12,13]. We have discussed new insights from a simple retrieval scheme, and its application over a broad spatial domain, with surprisingly periodic results over four years. The conclusions drawn here are also possibly applicable to other platforms seeking to derive cloud microphysical properties over large geostationary footprints, such as GOES-16, Himawari-8, or FY-4A products.
Author Contributions
A.L.C. initiated the study, analyzed and interpreted the data, and wrote the paper. M.M.M. analyzed and interpreted the data, and modeled the simulation LUT used in the study. T.F.N. and A.C.P. analyzed and interpreted the data, and contributed to the writing. M.A.C. curated, analyzed, interpreted the aircraft data, and contributed to the writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found at NASA: https://atmosphere-imager.gsfc.nasa.gov/products/cloud, accessed on 10 November 2021 12:00 UTC, and NOAA: https://www.avl.class.noaa.gov/saa/products/welcome, accessed on 10 November 2021 12:00 UTC.
Acknowledgments
We thank NOAA GOES and NASA MODIS teams for the datasets used in this study. A.L.C. thanks the Brazilian National Council for Scientific and Technological Development (CNPq) for research grant 421870/2018-4. A.L.C. and M.A.C. thank the Sao Paulo Research Foundation (FAPESP) for research grants SeReNA 2010/15959-3 and 2020/13273-9.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakajima, T.; King, M.D. Determination of the Optical Thickness and Effective Particle Radius of Clouds from Reflected Solar Radiation Measurements. Part I: Theory. J. Atmos. Sci. 1990, 47, 1878–1893. [Google Scholar] [CrossRef]
- Twomey, S. The Influence of Pollution on the Shortwave Albedo of Clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, Cloud Microphysics, and Fractional Cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, D. TRMM observed first direct evidence of smoke from forest fires inhibiting rainfall. Geophys. Res. Lett. 1999, 26, 3105–3108. [Google Scholar] [CrossRef]
- Wang, H.; Dai, T.; Zhao, M.; Goto, D.; Bao, Q.; Takemura, T.; Nakajima, T.; Shi, G. Aerosol Effective Radiative Forcing in the Online Aerosol Coupled CAS-FGOALS-f3-L Climate Model. Atmosphere 2020, 11, 1115. [Google Scholar] [CrossRef]
- Forster, P.; Storelvmo, T.; Armour, K.; Collins, W.; Dufresne, J.L.; Frame, D.; Lunt, D.; Mauritsen, T.; Palmer, M.; Watanabe, M.; et al. Chapter 7: The Earth’s energy budget, climate feedbacks, and climate sensitivity. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Open Access Victoria University of Wellington: Wellington, New Zealand, 2021. [Google Scholar] [CrossRef]
- Feingold, G.; Eberhard, W.L.; Veron, D.E.; Previdi, M. First measurements of the Twomey indirect effect using ground-based remote sensors: Surface remote sensing of the indirect effect. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Zheng, X.; Xi, B.; Dong, X.; Logan, T.; Wang, Y.; Wu, P. Investigation of aerosol–cloud interactions under different absorptive aerosol regimes using Atmospheric Radiation Measurement (ARM) southern Great Plains (SGP) ground-based measurements. Atmos. Chem. Phys. 2020, 20, 3483–3501. [Google Scholar] [CrossRef]
- Sena, E.T.; McComiskey, A.; Feingold, G. A long-term study of aerosol–cloud interactions and their radiative effectat the Southern Great Plains using ground-based measurements. Atmos. Chem. Phys. 2016, 16, 11301–11318. [Google Scholar] [CrossRef]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Platnick, S.; Meyer, K.G.; King, M.D.; Wind, G.; Amarasinghe, N.; Marchant, B.; Arnold, G.T.; Zhang, Z.; Hubanks, P.A.; Holz, R.E.; et al. The MODIS Cloud Optical and Microphysical Products: Collection 6 Updates and Examples From Terra and Aqua. IEEE Trans. Geosci. Remote Sens. 2017, 55, 502–525. [Google Scholar] [CrossRef]
- Dong, X.; Mace, G.G.; Minnis, P.; Smith, W.L.; Poellot, M.; Marchand, R.T.; Rapp, A.D. Comparison of Stratus Cloud Properties Deduced from Surface, GOES, and Aircraft Data during the March 2000 ARM Cloud IOP. J. Atmos. Sci. 2002, 59, 3265–3284. [Google Scholar] [CrossRef]
- McHardy, T.M.; Dong, X.; Xi, B.; Thieman, M.M.; Minnis, P.; Palikonda, R. Comparison of Daytime Low-Level Cloud Properties Derived From GOES and ARM SGP Measurements. J. Geophys. Res. Atmos. 2018, 123, 8221–8237. [Google Scholar] [CrossRef]
- Painemal, D.; Minnis, P.; Ayers, J.K.; O’Neill, L. GOES-10 microphysical retrievals in marine warm clouds: Multi-instrument validation and daytime cycle over the southeast Pacific: Marine clouds microphysics from GOES-10. J. Geophys. Res. Atmos. 2012, 117, 19212. [Google Scholar] [CrossRef]
- Painemal, D.; Spangenberg, D.; Smith, W.L., Jr.; Minnis, P.; Cairns, B.; Moore, R.H.; Crosbie, E.; Robinson, C.; Thornhill, K.L.; Winstead, E.L.; et al. Evaluation of satellite retrievals of liquid clouds from the GOES-13 imager and MODIS over the midlatitude North Atlantic during the NAAMES campaign. Atmos. Meas. Tech. 2021, 14, 6633–6646. [Google Scholar] [CrossRef]
- Kang, L.; Marchand, R.; Smith, W. Evaluation of MODIS and Himawari-8 Low Clouds Retrievals Over the Southern Ocean With In Situ Measurements From the SOCRATES Campaign. Earth Space Sci. 2021, 8, e01397. [Google Scholar] [CrossRef]
- King, N.J.; Bower, K.N.; Crosier, J.; Crawford, I. Evaluating MODIS cloud retrievals with in situ observations from VOCALS-REx. Atmos. Chem. Phys. 2013, 13, 191–209. [Google Scholar] [CrossRef]
- Painemal, D.; Zuidema, P. Assessment of MODIS cloud effective radius and optical thickness retrievals over the Southeast Pacific with VOCALS-REx in situ measurements: MODIS VALIDATION DURING VOCALS-REx. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Noble, S.R.; Hudson, J.G. MODIS comparisons with northeastern Pacific in situ stratocumulus microphysics. J. Geophys. Res. Atmos. 2015, 120, 8332–8344. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, X.; Xi, B.; Song, H.; Ma, P.; Ghan, S.J.; Platnick, S.; Minnis, P. Intercomparisons of marine boundary layer cloud properties from the ARM CAP-MBL campaign and two MODIS cloud products. J. Geophys. Res. Atmos. 2017, 122, 2351–2365. [Google Scholar] [CrossRef]
- Benas, N.; Meirink, J.F.; Stengel, M.; Stammes, P. Sensitivity of liquid cloud optical thickness and effective radius retrievals to cloud bow and glory conditions using two SEVIRI imagers. Atmos. Meas. Tech. 2019, 12, 2863–2879. [Google Scholar] [CrossRef]
- Grosvenor, D.P.; Wood, R. The effect of solar zenith angle on MODIS cloud optical and microphysical retrievals within marine liquid water clouds. Atmos. Chem. Phys. 2014, 14, 7291–7321. [Google Scholar] [CrossRef]
- Horváth, Á.; Seethala, C.; Deneke, H. View angle dependence of MODIS liquid water path retrievals in warm oceanic clouds. J. Geophys. Res. Atmos. 2014, 119, 8304–8328. [Google Scholar] [CrossRef]
- Liang, L.; Di Girolamo, L.; Sun, W. Bias in MODIS cloud drop effective radius for oceanic water clouds as deduced from optical thickness variability across scattering angles. J. Geophys. Res. Atmos. 2015, 120, 7661–7681. [Google Scholar] [CrossRef]
- Marshak, A.; Platnick, S.; Várnai, T.; Wen, G.; Cahalan, R.F. Impact of three-dimensional radiative effects on satellite retrievals of cloud droplet sizes. J. Geophys. Res. 2006, 111, D09207. [Google Scholar] [CrossRef]
- Zhang, Z.; Ackerman, A.S.; Feingold, G.; Platnick, S.; Pincus, R.; Xue, H. Effects of cloud horizontal inhomogeneity and drizzle on remote sensing of cloud droplet effective radius: Case studies based on large-eddy simulations: Heterogeneity and drizzle effect on effective radius retrieval. J. Geophys. Res. Atmos. 2012, 117, 19208. [Google Scholar] [CrossRef]
- Werner, F.; Zhang, Z.; Wind, G.; Miller, D.J.; Platnick, S. Quantifying the Impacts of Subpixel Reflectance Variability on Cloud Optical Thickness and Effective Radius Retrievals Based On High-Resolution ASTER Observations. J. Geophys. Res. Atmos. 2018, 123, 4239–4258. [Google Scholar] [CrossRef]
- Kato, S.; Hinkelman, L.M.; Cheng, A. Estimate of satellite-derived cloud optical thickness and effective radius errors and their effect on computed domain-averaged irradiances. J. Geophys. Res. 2006, 111, D17201. [Google Scholar] [CrossRef]
- Zhang, Z.; Werner, F.; Cho, H.M.; Wind, G.; Platnick, S.; Ackerman, A.S.; Di Girolamo, L.; Marshak, A.; Meyer, K. A framework based on 2-D Taylor expansion for quantifying the impacts of subpixel reflectance variance and covariance on cloud optical thickness and effective radius retrievals based on the bispectral method: Subpixel impact on retrievals. J. Geophys. Res. Atmos. 2016, 121, 7007–7025. [Google Scholar] [CrossRef]
- Vant-Hull, B.; Marshak, A.; Remer, L.A.; Li, Z. The Effects of Scattering Angle and Cumulus Cloud Geometry on Satellite Retrievals of Cloud Droplet Effective Radius. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1039–1045. [Google Scholar] [CrossRef]
- Platnick, S. Vertical photon transport in cloud remote sensing problems. J. Geophys. Res. Atmos. 2000, 105, 22919–22935. [Google Scholar] [CrossRef]
- Weinreb, M.; Jamieson, M.; Fulton, N.; Chen, Y.; Johnson, J.X.; Bremer, J.; Smith, C.; Baucom, J. Operational calibration of Geostationary Operational Environmental Satellite-8 and -9 imagers and sounders. Appl. Opt. 1997, 36, 6895. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, Y.J.; Nakajima, T. Effect of Amazon Smoke on Cloud Microphysics and Albedo-Analysis from Satellite Imagery. J. Appl. Meteorol. 1993, 32, 729–744. [Google Scholar] [CrossRef]
- Platnick, S.; Fontenla, J.M. Model Calculations of Solar Spectral Irradiance in the 3.7-m Band for Earth Remote Sensing Applications. J. Appl. Meteorol. Climatol. 2008, 47, 124–134. [Google Scholar] [CrossRef][Green Version]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Correia, A.L.; Sena, E.T.; Silva Dias, M.A.F.; Koren, I. Preconditioning, aerosols, and radiation control the temperature of glaciation in Amazonian clouds. Commun. Earth Environ. 2021, 2, 168. [Google Scholar] [CrossRef]
- Mendonça, M.M. Estudo de Propriedades de Nuvens no Contexto de Sensoriamento Remoto com satéLites Usando cóDigos de Transferência Radiativa. Mestrado em Física, Universidade de São Paulo, São Paulo, Brazil, 2017. [Google Scholar] [CrossRef]
- Baum, B.A.; Yang, P.; Heymsfield, A.J.; Platnick, S.; King, M.D.; Hu, Y.X.; Bedka, S.T. Bulk Scattering Properties for the Remote Sensing of Ice Clouds. Part II: Narrowband Models. J. Appl. Meteorol. 2005, 44, 1896–1911. [Google Scholar] [CrossRef]
- Maddux, B.C.; Ackerman, S.A.; Platnick, S. Viewing Geometry Dependencies in MODIS Cloud Products. J. Atmos. Ocean. Technol. 2010, 27, 1519–1528. [Google Scholar] [CrossRef]
- Martin, S.T.; Artaxo, P.; Machado, L.A.T.; Manzi, A.O.; Souza, R.A.F.; Schumacher, C.; Wang, J.; Andreae, M.O.; Barbosa, H.M.J.; Fan, J.; et al. Introduction: Observations and Modeling of the Green Ocean Amazon (GoAmazon2014/5). Atmos. Chem. Phys. 2016, 16, 4785–4797. [Google Scholar] [CrossRef]
- Machado, L.A.T.; Calheiros, A.J.P.; Biscaro, T.; Giangrande, S.; Silva Dias, M.A.F.; Cecchini, M.A.; Albrecht, R.; Andreae, M.O.; Araujo, W.F.; Artaxo, P.; et al. Overview: Precipitation characteristics and sensitivities to environmental conditions during GoAmazon2014/5 and ACRIDICON-CHUVA. Atmos. Chem. Phys. 2018, 18, 6461–6482. [Google Scholar] [CrossRef]
- Schmid, B.; Tomlinson, J.M.; Hubbe, J.M.; Comstock, J.M.; Mei, F.; Chand, D.; Pekour, M.S.; Kluzek, C.D.; Andrews, E.; Biraud, S.C.; et al. The DOE ARM Aerial Facility. Bull. Am. Meteorol. Soc. 2014, 95, 723–742. [Google Scholar] [CrossRef]
- Cecchini, M.A.; Machado, L.A.T.; Comstock, J.M.; Mei, F.; Wang, J.; Fan, J.; Tomlinson, J.M.; Schmid, B.; Albrecht, R.; Martin, S.T.; et al. Impacts of the Manaus pollution plume on the microphysical properties of Amazonian warm-phase clouds in the wet season. Atmos. Chem. Phys. 2016, 16, 7029–7041. [Google Scholar] [CrossRef]
- Beswick, K.M.; Gallagher, M.W.; Webb, A.R.; Norton, E.G.; Perry, F. Application of the Aventech AIMMS20AQ airborne probe for turbulence measurements during the Convective Storm Initiation Project. Atmos. Chem. Phys. 2008, 8, 5449–5463. [Google Scholar] [CrossRef]
- Platnick, S.; Valero, F.P.J. A Validation of a Satellite Cloud Retrieval during ASTEX. J. Atmos. Sci. 1995, 52, 2985–3001. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, G.; Cui, C.; Zhang, A.; Wan, R.; Zhou, S.; Wang, D.; Fu, Y. Retrieval of the vertical evolution of the cloud effective radius from the Chinese FY-4 (Feng Yun 4) next-generation geostationary satellites. Atmos. Chem. Phys. 2020, 20, 1131–1145. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).