Impact of Ensemble-Variational Data Assimilation in Heavy Rain Forecast over Brazilian Northeast
Abstract
1. Introduction
2. Materials and Methods
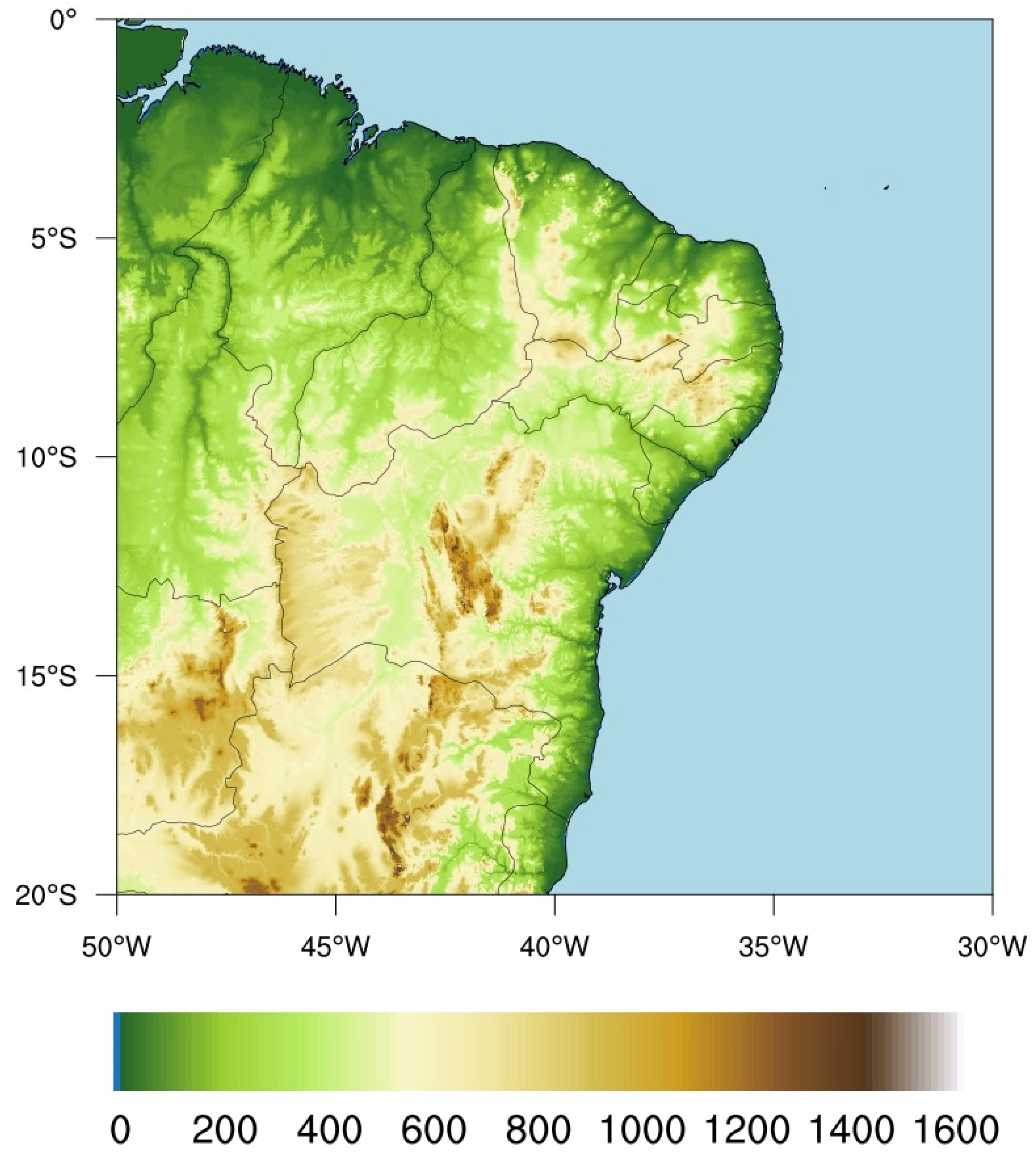
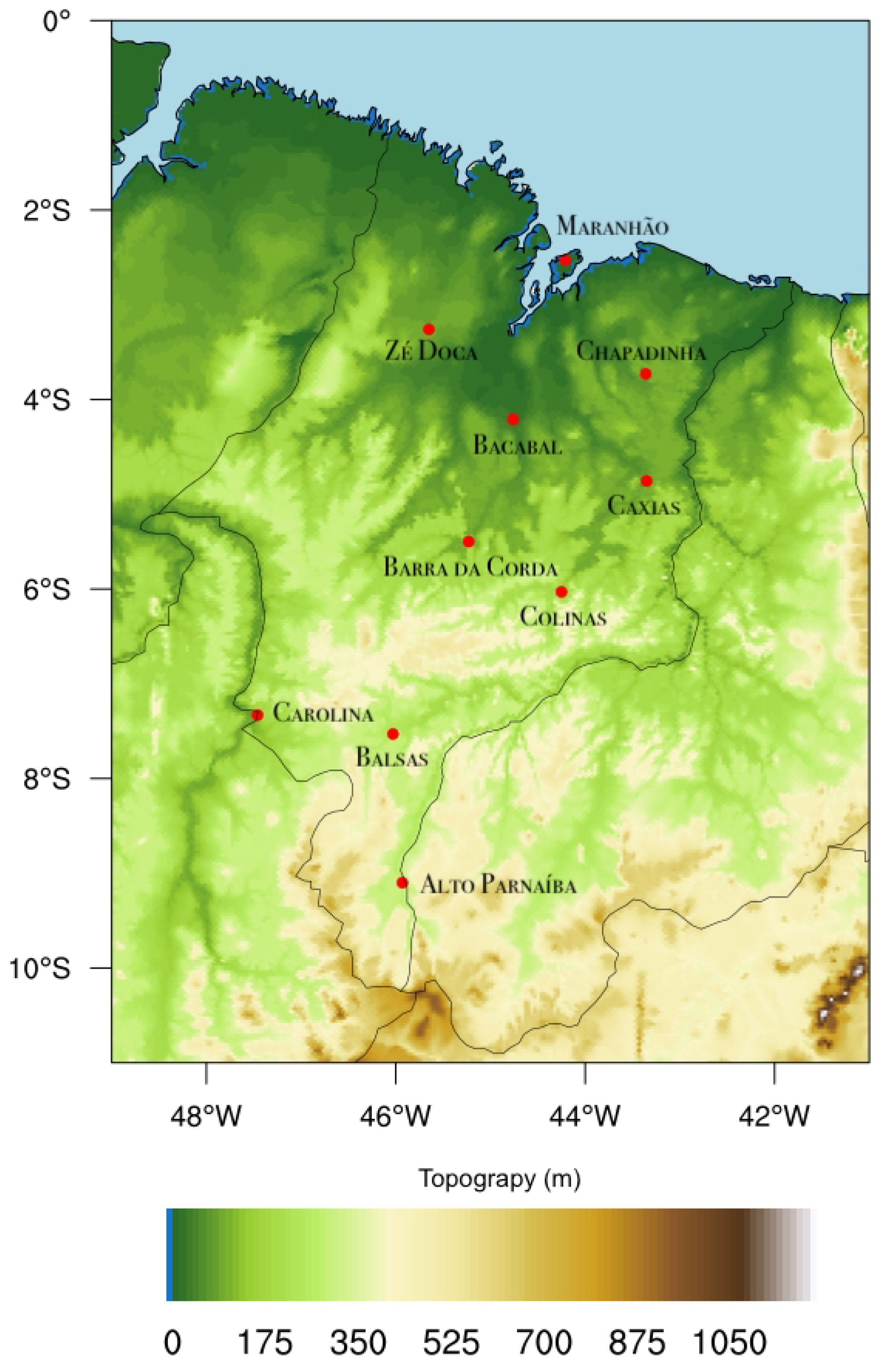
2.1. Location of the Study Area
2.2. Convective Systems Identification
2.3. Rain Events Identification
2.4. WRF Mesoscale Model
2.5. The Gridpoint Statistical Interpolation
2.5.1. Data Assimilated
2.5.2. 3DVar Variational Method
2.5.3. The Ensemble Square-Root Filter
2.5.4. Three-Dimensional Ensemble-Variational
2.6. Statistical Data Analysis
3. Results and Discussion
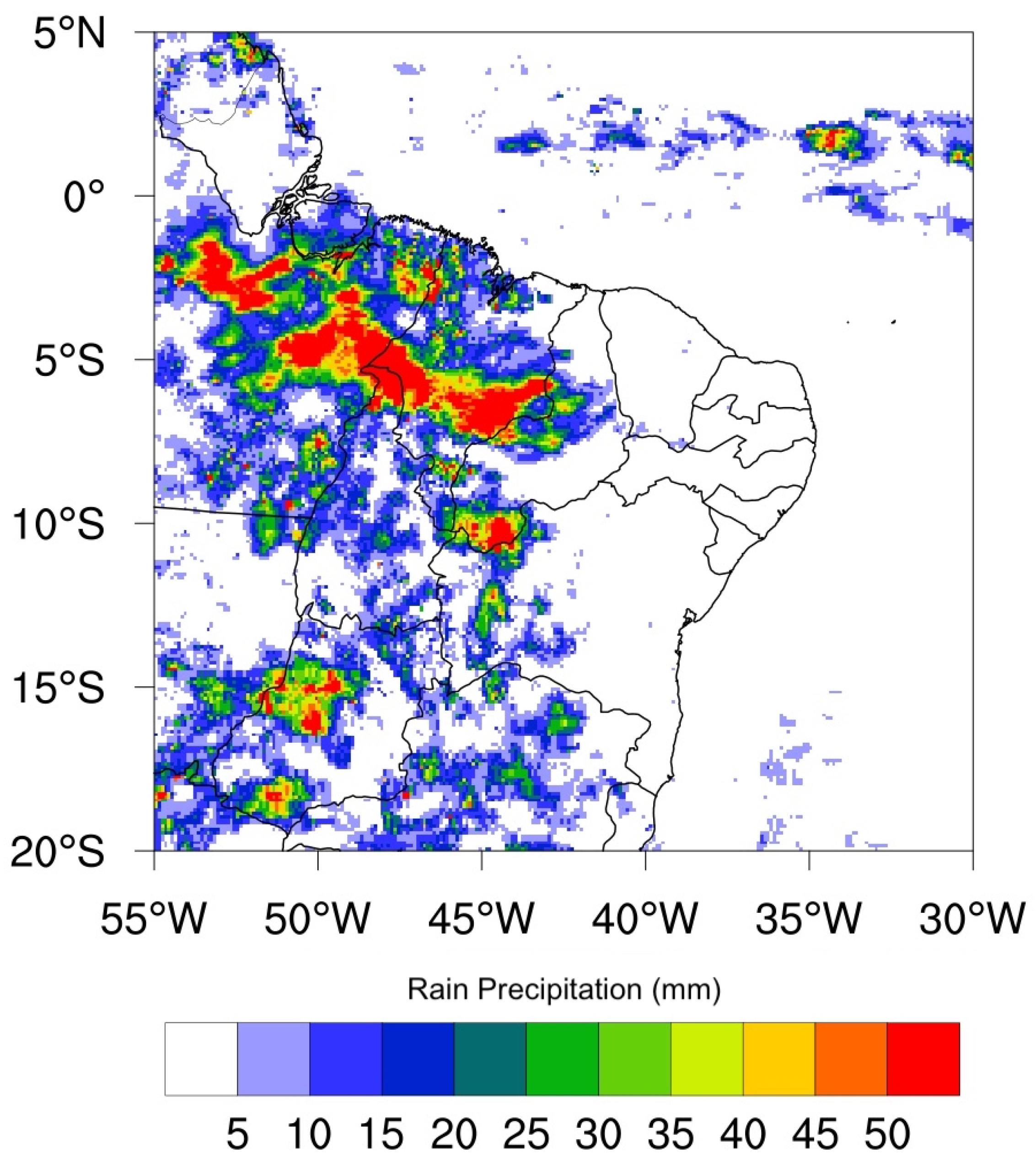
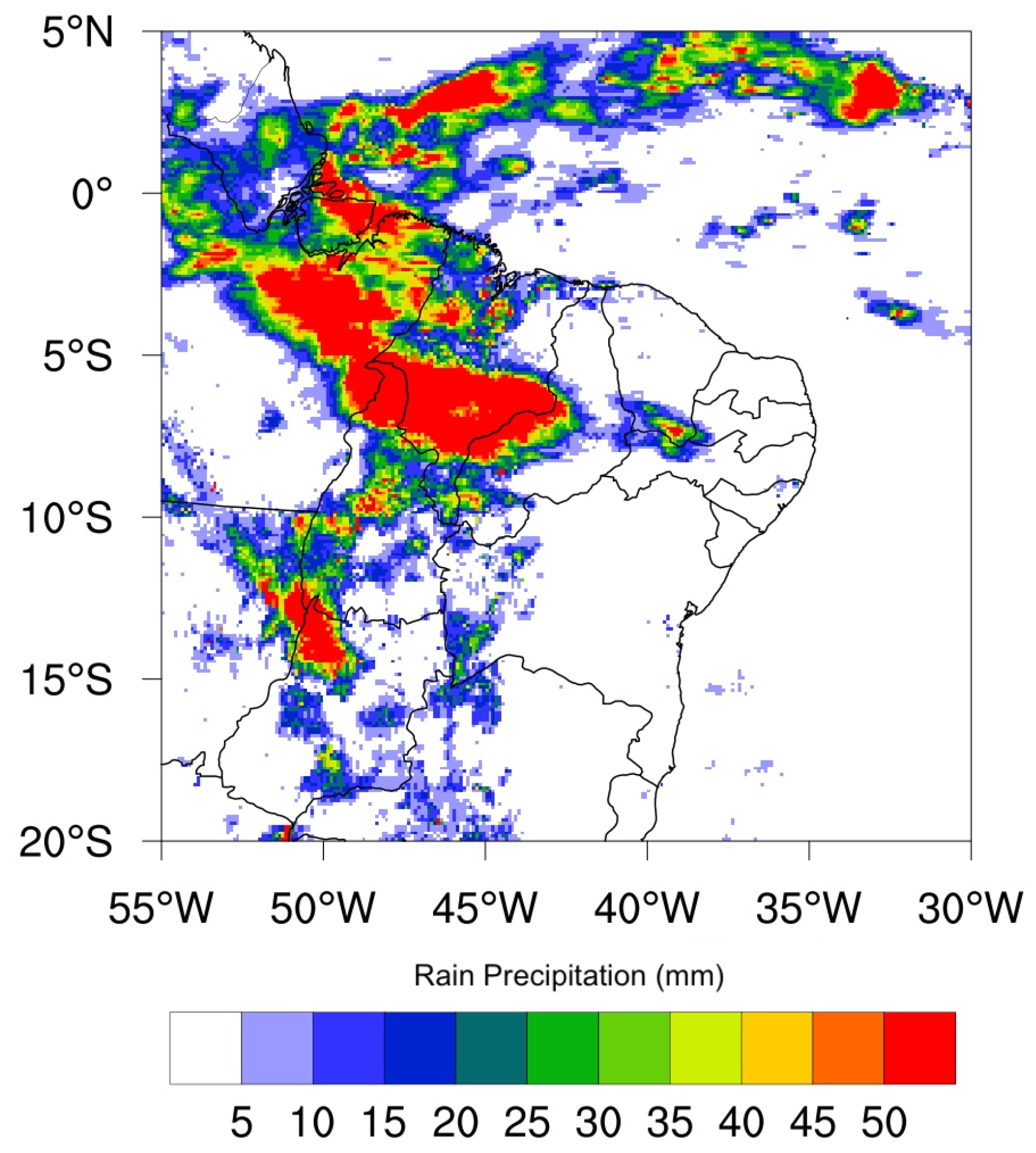
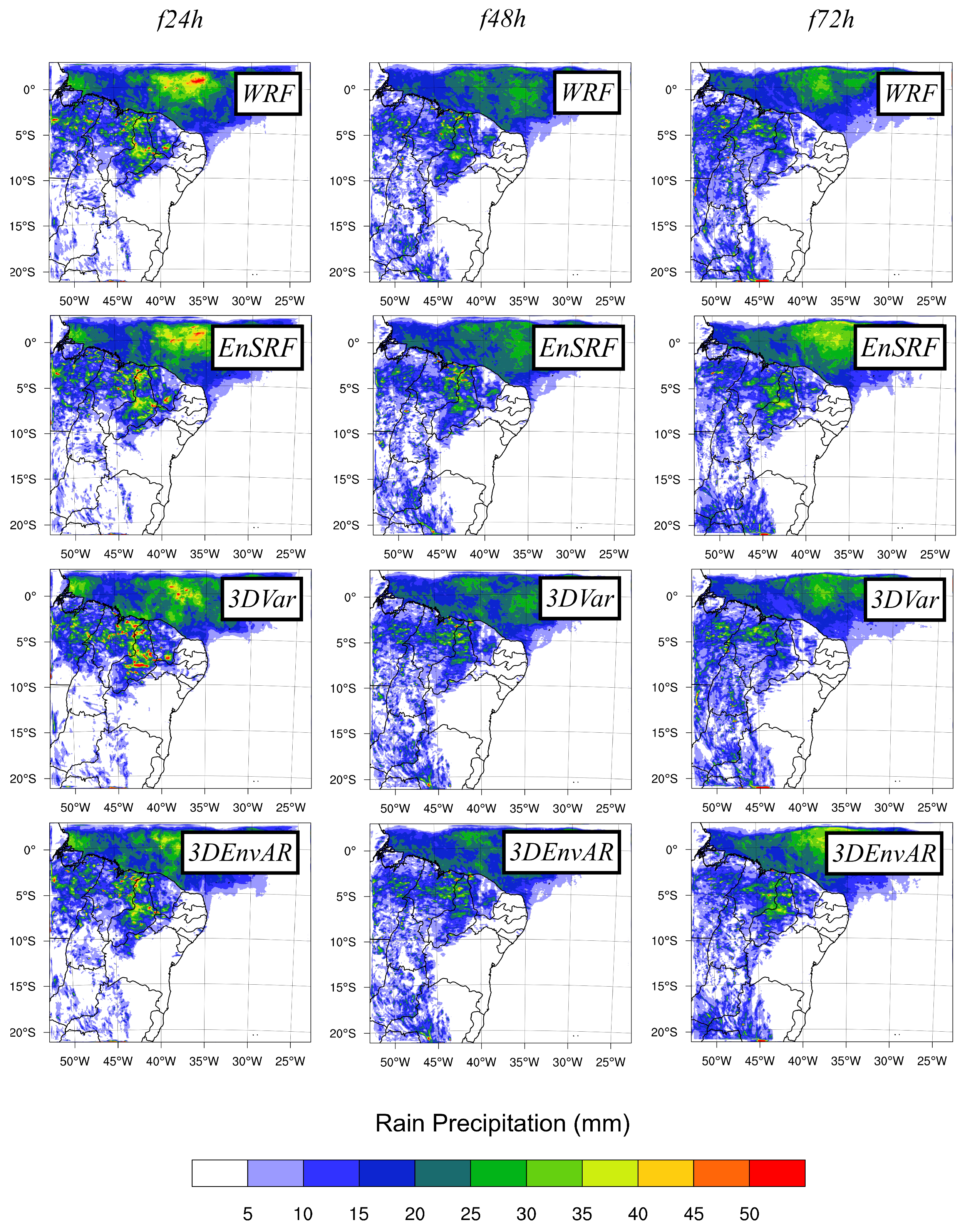
3.1. Convective Rainfall
3.2. Total of Assimilated Data
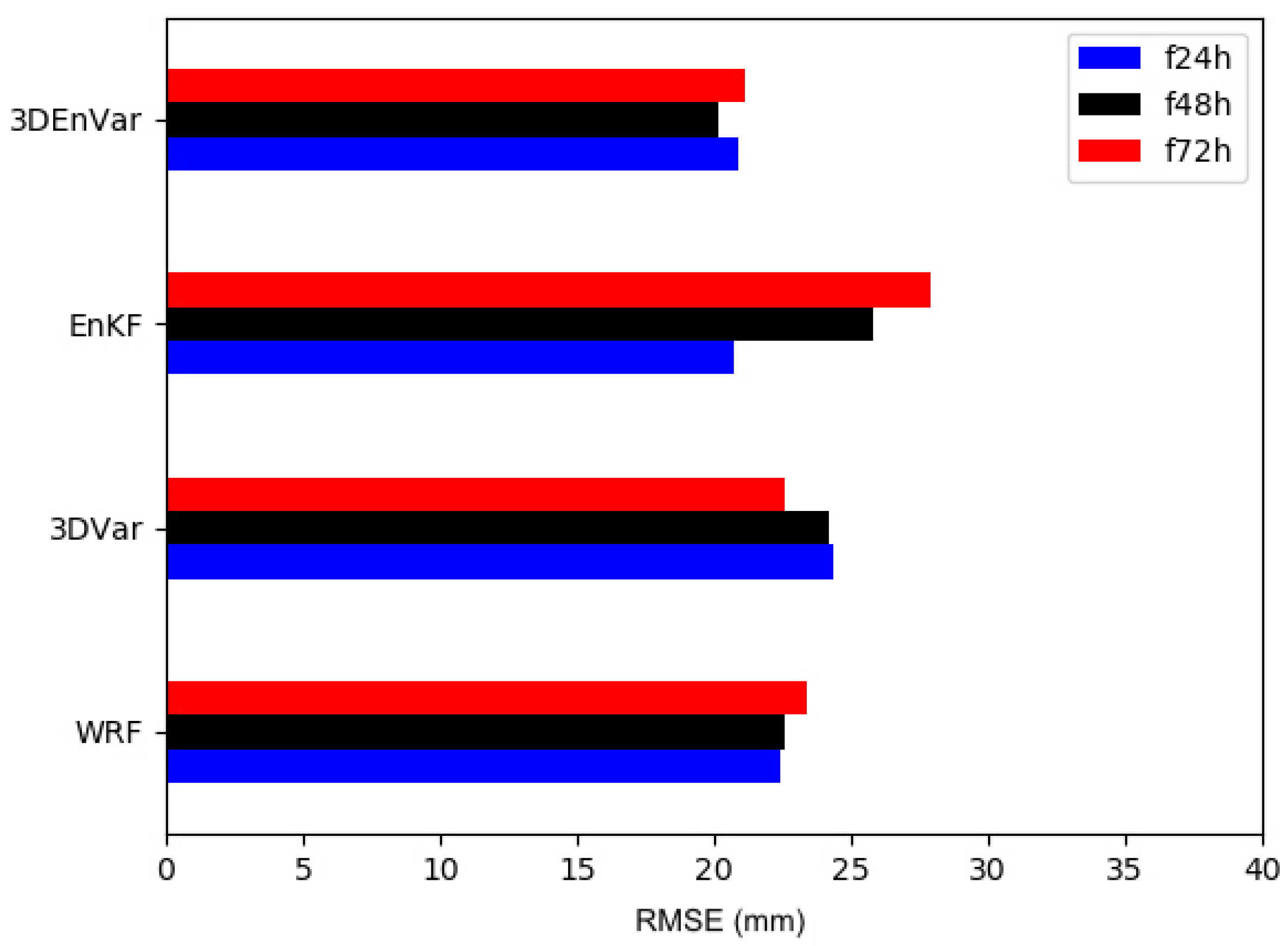
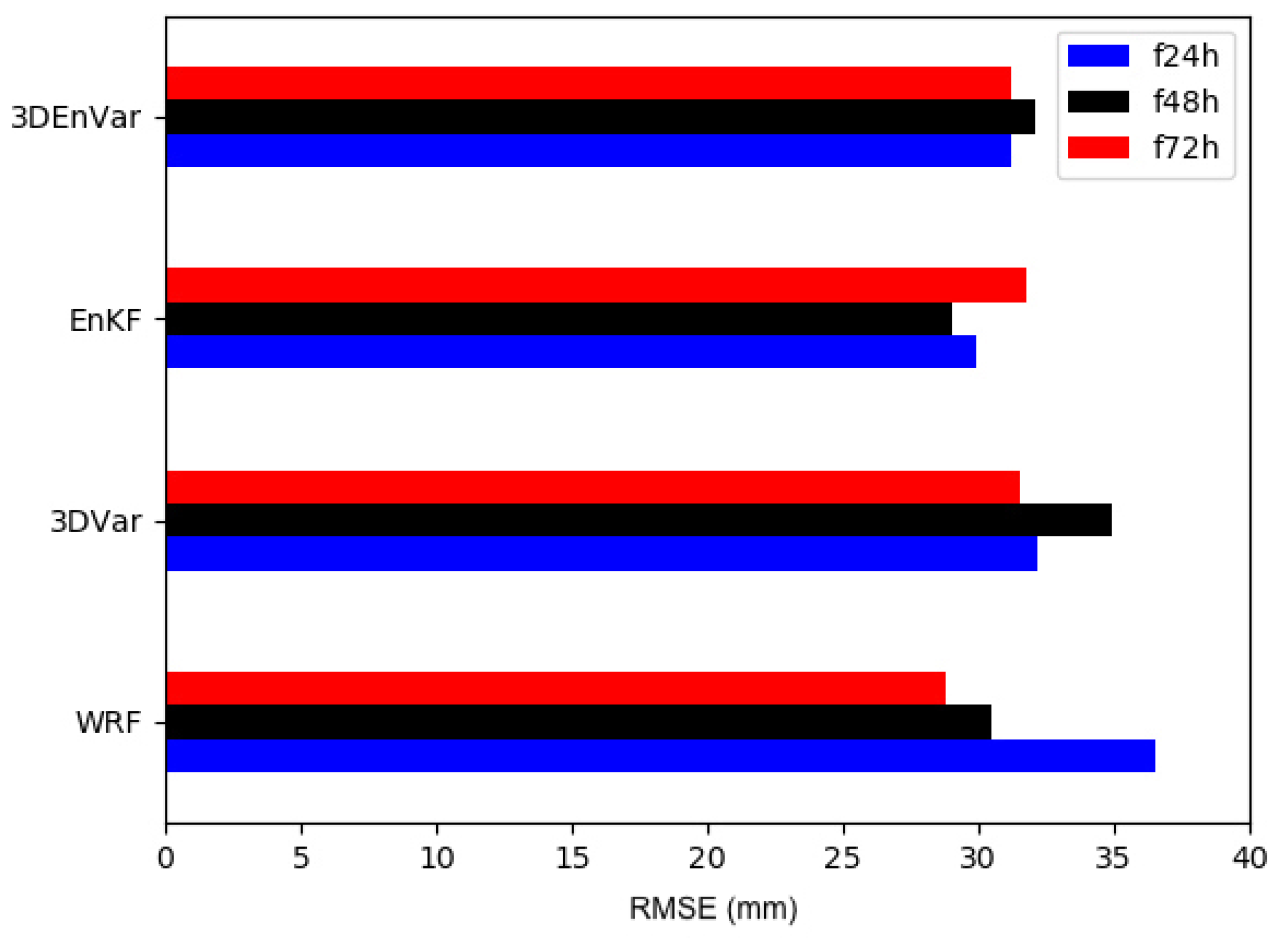
3.3. WRF 24-h Accumulated Precipitation
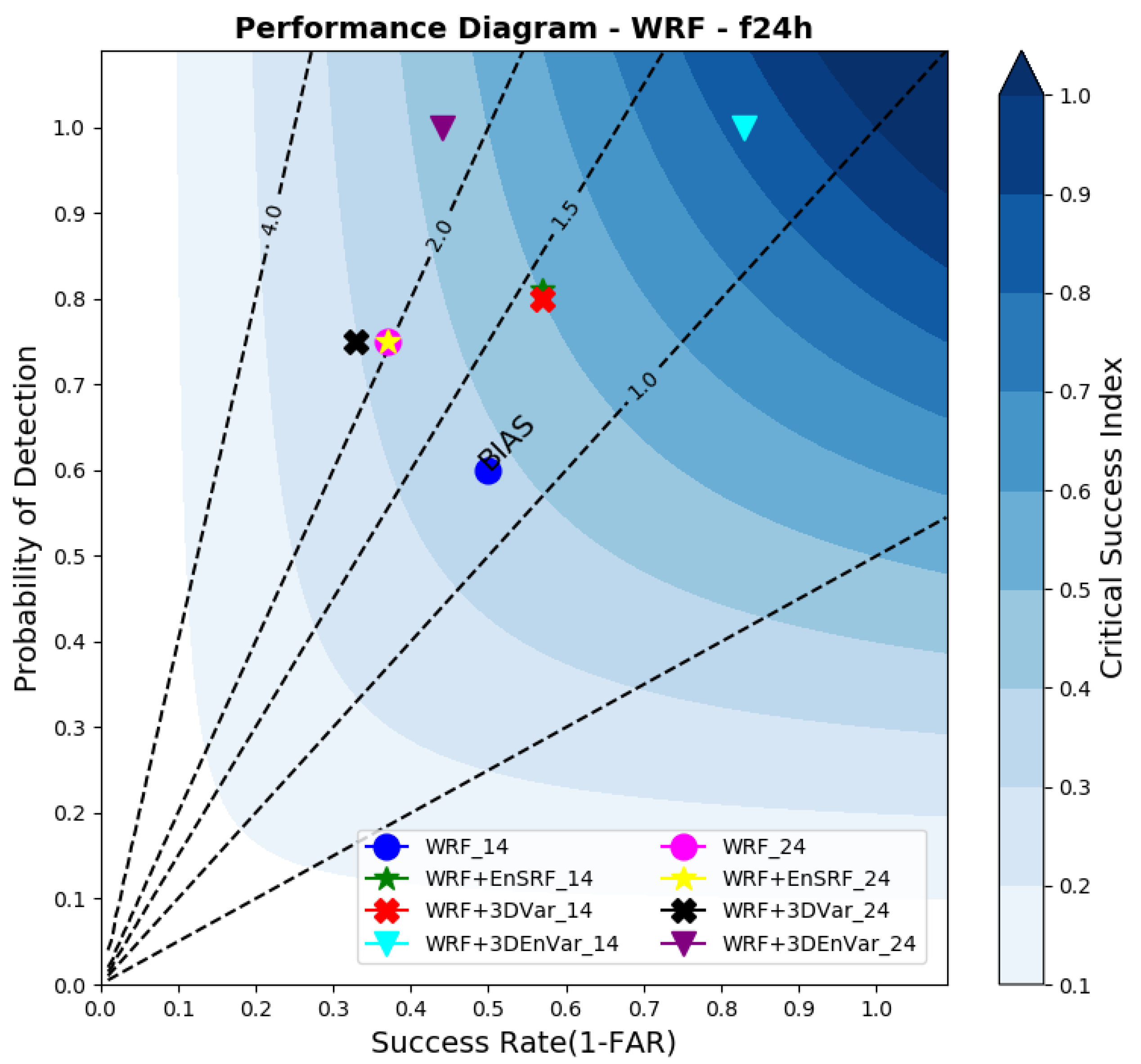
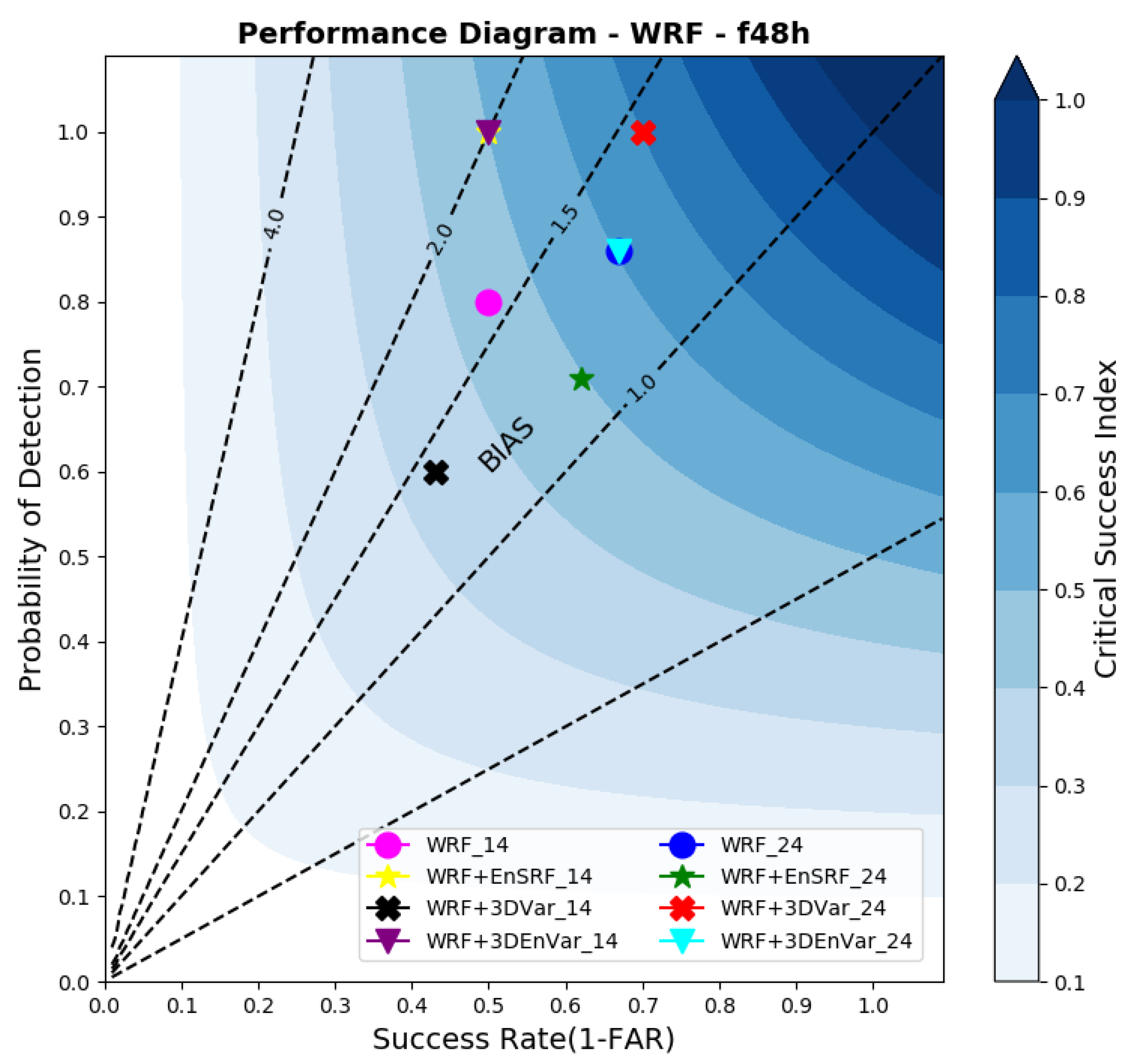
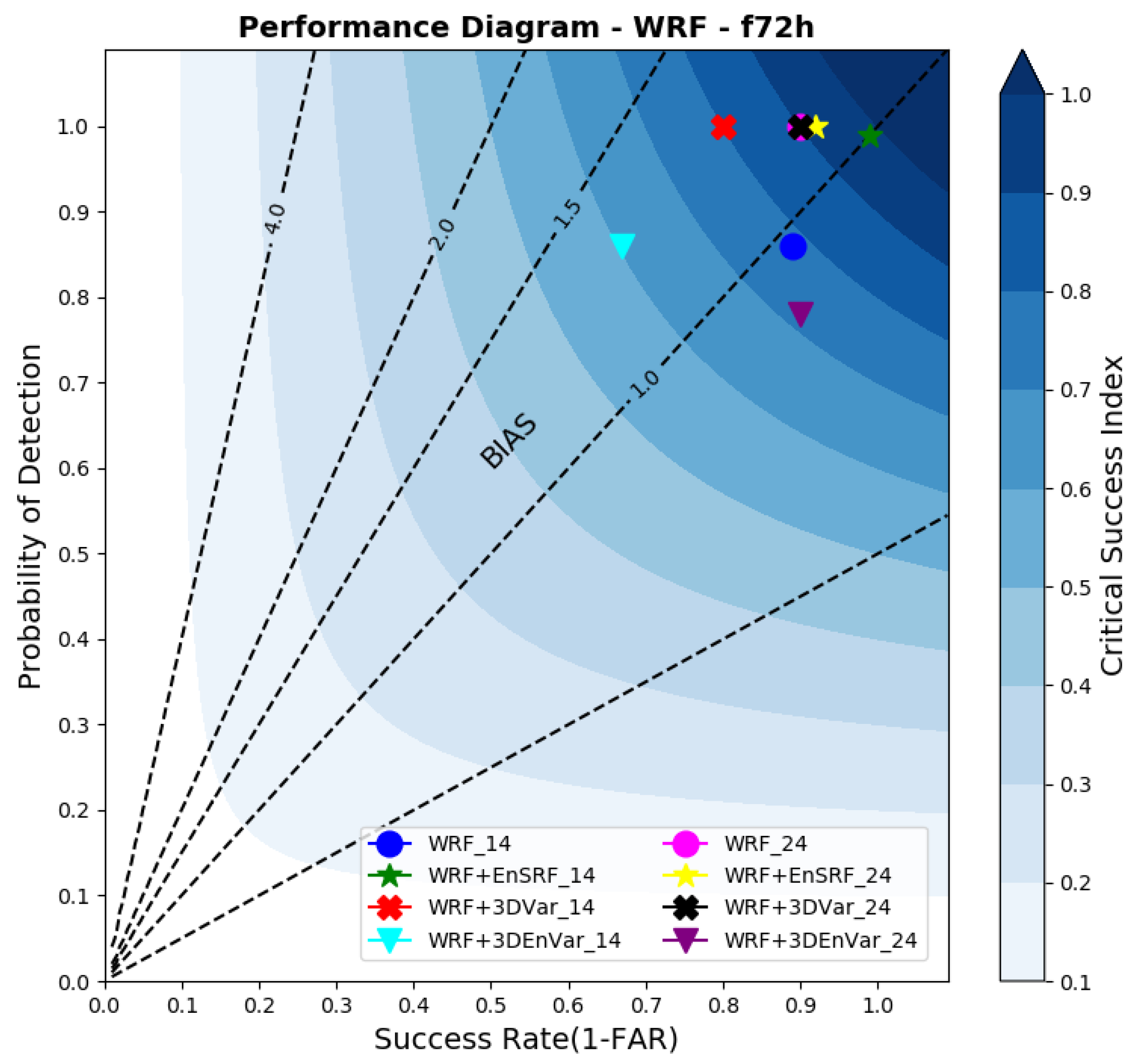
3.4. WRF Rainfall Forecast by Performance Diagram
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3DEnVar | 3D Ensemble Variational; |
| 3DVar | 3D Variational; |
| BNE | Brazilian Northeast; |
| CSI | Critical Success Index; |
| DA | Data Assimilation; |
| EnSRF | Ensemble Kalman Filter; |
| FAR | False Alarm; |
| POD | Probability of Detection; |
| MCS | Mesoscale Convective System; |
| RMS | Regional Modeling System; |
| RMSE | Root Mean Square Error; |
| SR | Success Rate; |
| WRF | Weather Research and Forecasting; |
| GSI | Grid Statistical Interpolation. |
References
- Confederação Nacional dos Municípios. Available online: https://www.cnm.org.br (accessed on 4 January 2021).
- Meteored. Available online: https://www.tempo.com/ (accessed on 2 January 2021).
- Brasseur, P. Ocean data assimilation using sequential methods based on the Kalman filter. Ocean Weather Forecast. 2006, 271–276. [Google Scholar] [CrossRef]
- Gilchrist, B.; Cressman, G.P. An Experiment in Objective Analysis. Tellus 1953, 6, 310–318. [Google Scholar]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability, 1st ed.; Cambridge University Press: New York, NY, USA, 2002; pp. 1–341. [Google Scholar]
- Panofsky, R.A. Objective weather-map analysis. J. Meteorol. 1949, 6, 386–392. [Google Scholar] [CrossRef]
- Bergthórsson, P.; Doos, B.R. Numerical weather map analyses. Tellus 1955, 7, 329–340. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 7, 367–374. [Google Scholar] [CrossRef]
- Eliassen, A. Provisional report on calculation of spatial covariance andautocorrelation of the pressure field. Weather Clim. 1954, 5, 1–10. [Google Scholar]
- Gandin, L.S. The objective analysis of meteorological fields: Israel program for scientific translatinons. Hydrometeoro Press 1963, 5, 1–10. [Google Scholar]
- Sasaki, Y. Some basic formalisms in numerical variational analysis. Mon. Weather Rev. 1970, 98, 875–883. [Google Scholar] [CrossRef]
- Flaterry, T. Spectral models for global analysis and forecasting. Air Weather Serv. Tech. 1970, 242, 42–54. [Google Scholar]
- Talagrand, O. Assimilation of Observations, an Introduction. J. Meteorol. Soc. Jpn. Ser. II 1997, 75, 191–209. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xue, M. Assimilation of Radar Radial Velocity Data with the WRF Hybrid Ensemble–3DVAR System for the Prediction of Hurricane Ike (2008). Mon. Weather Rev. 2012, 140, 3507–3524. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Some Observing System Simulation Experiments with a Hybrid 3DEnVAR System for Storm-Scale Radar Data Assimilation. Mon. Weather Rev. 1963, 142, 3326–3345. [Google Scholar]
- Bastarz, A.B. Assimilação de Dados Global Híbrida por Conjunto-Variacional no CPTEC. Ph.D. Thesis, National Institute for Aerospace Studies, São José dos Campos, Brazil, 2017. [Google Scholar]
- Lyra, M.J.A.; Freitas, I.G.F. Desenvolvimento dos Complexos Convectivos de Mesoescala no Nordeste Brasileiro em 2017. Rev. Bras. Geogr. Física 2019, 2, 2152–2162. [Google Scholar] [CrossRef][Green Version]
- Machado, L.A.T.; Laurent, H. The convective system area expansion over Amazônia and its relationships with convective system life duration and high-level wind divergence. Mon. Weather Rev. 2004, 132, 714–725. [Google Scholar] [CrossRef]
- Rozante, J.R.; Moreira, D.S.; Gonçalves, L.G.G.; Vila, D.A. Combining TRMM and Surface Observations of Precipitation: Technique and Validation over South America. Weather Forecast. 2010, 25, 885–894. [Google Scholar] [CrossRef]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J. The weather research and forecasting model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Institute of Airspace Control. Available online: http://pesquisa.icea.gov.br/ (accessed on 6 July 2014).
- Nobre, J.P.G.; Fedorova, N.; Levit, V.; Santos, A.S.; Lyra, M.A. New Methodology for Evaluation of the Fog Events for the Zumbi dos Palmares Airport, in Maceió (Alagoas). Anuário Inst. Geociências-UFRJ 2019, 42, 527–535. [Google Scholar] [CrossRef]
- Sun, B.Y.; Bl, X.Q. Validation for a tropical belt version of wrf: Sensitivity tests on radiation and Cumulus convection parameterizations. Atmos. Ocean. Sci. Lett. 2019, 12, 192–200. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y. Projected future changes of tropical cyclone activity over the western north and south pacific in a 20-km-mesh regional climate model. J. Clim. 2017, 30, 5923–5941. [Google Scholar] [CrossRef]
- Tiedtke, M.A. A comprehensive mass flux scheme for Cumulus parameterization in larger- scale model. Montly Wearther Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Kain, S.J. The kain—fritsch convective parameterization: An update. J. Appl. Meteorol. Climatol. 2004, 42, 170–181. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.L. Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Weather Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- DOC/NOAA/NWS/NCEP/EMC > Environmental Modeling Center, National Centers for Environmental Prediction, National Weather Service, NOAA, U.S. Department of Commerce. Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ncdc:C00691 (accessed on 25 August 2021).
- NASA Shuttle Radar Topography Mission (SRTM). Shuttle Radar Topography Mission (SRTM) Global. Distributed by OpenTopography. 2013. Available online: https://doi.org/10.5069/G9445JDF (accessed on 25 August 2021).
- Atmospheric and Environmental Research. Available online: http://rtweb.aer.com (accessed on 4 January 2021).
- Hong, S.; Lim, J. The WRF single-moment 6-class microphysics: Song-you hong. J. Korean Meteorol. Soc. 2006, 2, 129–151. [Google Scholar]
- Hong, S.-Y.; Noh, Y.; Dudhia, J.A. New vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Tewari, M.F.; Chen, W.; Wang, J.; Dudhia, M.A.; Lemone, K.; Mitchell, M.E.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the Conference on Weather Analysis and Forecasting, Seattle, WA, USA, 10 January 2004; pp. 11–15. [Google Scholar]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Spectral Statistical-Interpolation Analysis System. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Bierman, G. Factorization Methods for Discrete Sequential Estimation, 1st ed.; Academic Press: New York, NY, USA, 1977; pp. 1–241. [Google Scholar]
- Maybeck, P.S. Stochastic Models, Estimation, and Control, 1st ed.; Academic Press: New York, NY, USA, 1983; pp. 1–423. [Google Scholar]
- Developmental Testbed Center. Available online: https://dtcenter.ucar.edu/com-GSI/users/docs/ (accessed on 18 January 2021).
- Hu, M.; Benjamin, S.G.; Ladwig, T.T.; Dowell, D.C.; Weygandt, S.S.; Alexander, C.R.; Whitaker, J.S. GSI Three-Dimensional Ensemble–Variational Hybrid Data Assimilation Using a Global Ensemble for the Regional Rapid Refresh Model. Mon. Weather Rev. 2017, 145, 4205–4225. [Google Scholar] [CrossRef]
- Da Paz, A.R.; Collischonn, W. Avaliação de estimativas de campos de precipitação para modelagem hidrológica distribuída. Rev. Bras. Meteorol. 2011, 26, 109–120. [Google Scholar] [CrossRef]
- Skamarock, W.C. Evaluating Mesoscale NWP Models Using Kinetic Energy Spectra. Mon. Weather Rev. 2004, 132, 3019–3032. [Google Scholar] [CrossRef]
- Dantas, V.A.; Silva Filho, V.P.; Santos, E.B.; Gandu, A.W. Testando diferentes esquemas da parametrização cumulus do modelo WRF, para a região norte Nordeste do Brasil. Rev. Bras. Geogr. Física 2019, 12, 754–767. [Google Scholar] [CrossRef]


| Parameters | Configurations |
|---|---|
| Model | WRF |
| Horizontal Resolution | 9 km |
| Global Model | GEFS [28] |
| Topographic data | SRTM (30 m) [29] |
| Soil data | MODIS (925 m) |
| Radiation model | RRTMG [30] |
| Vertical levels | 42 sigma-pressure |
| Microphysics | WSM6 [31] |
| Cumulus | New Tiedtke [24] |
| Planetary boundary | YSU [32] |
| Surface model | Noah [33] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves Nobre, J.P.; Vendrasco, É.P.; Bastarz, C.F. Impact of Ensemble-Variational Data Assimilation in Heavy Rain Forecast over Brazilian Northeast. Atmosphere 2021, 12, 1201. https://doi.org/10.3390/atmos12091201
Gonçalves Nobre JP, Vendrasco ÉP, Bastarz CF. Impact of Ensemble-Variational Data Assimilation in Heavy Rain Forecast over Brazilian Northeast. Atmosphere. 2021; 12(9):1201. https://doi.org/10.3390/atmos12091201
Chicago/Turabian StyleGonçalves Nobre, João Pedro, Éder Paulo Vendrasco, and Carlos Frederico Bastarz. 2021. "Impact of Ensemble-Variational Data Assimilation in Heavy Rain Forecast over Brazilian Northeast" Atmosphere 12, no. 9: 1201. https://doi.org/10.3390/atmos12091201
APA StyleGonçalves Nobre, J. P., Vendrasco, É. P., & Bastarz, C. F. (2021). Impact of Ensemble-Variational Data Assimilation in Heavy Rain Forecast over Brazilian Northeast. Atmosphere, 12(9), 1201. https://doi.org/10.3390/atmos12091201






