High-Rate Precipitation Occurrence Modulated by Solar Wind High-Speed Streams
Abstract
1. Introduction
2. Data Sources and Methods
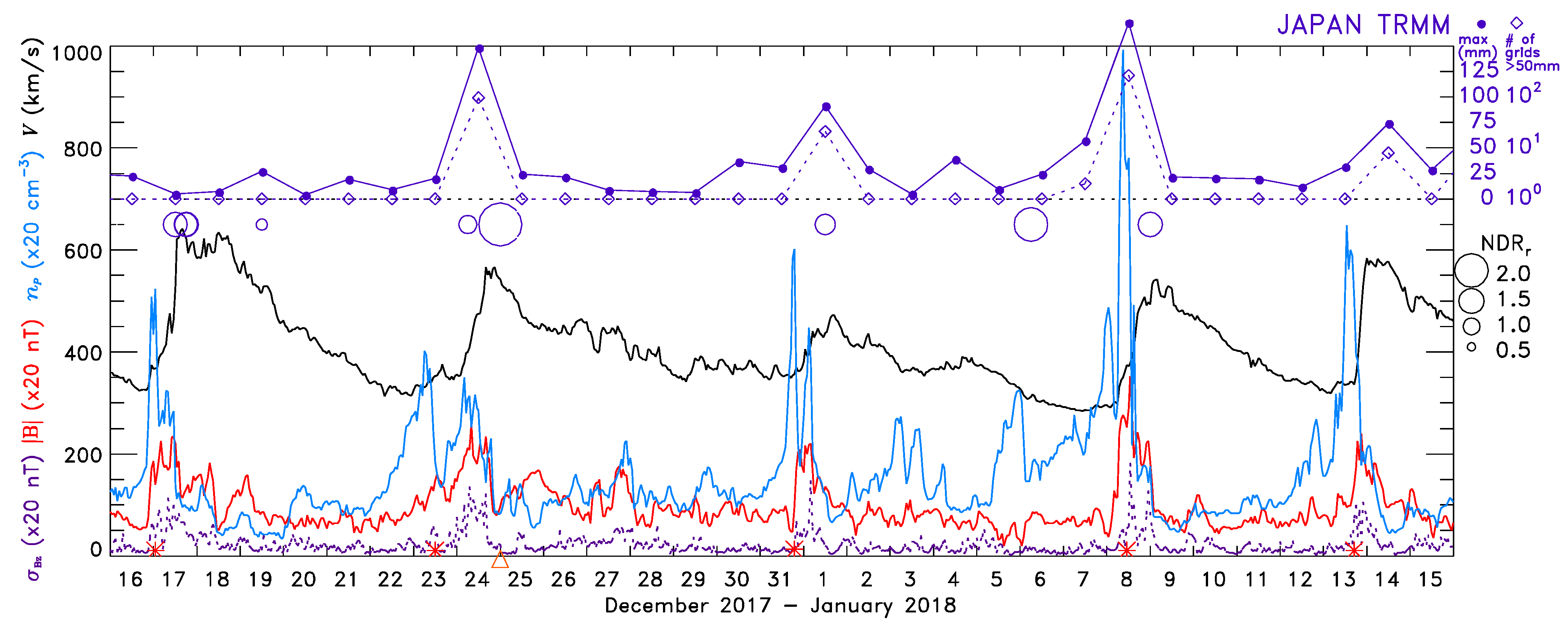
3. High-Rate Precipitation Events in Japan and Solar wind High-Speed Streams
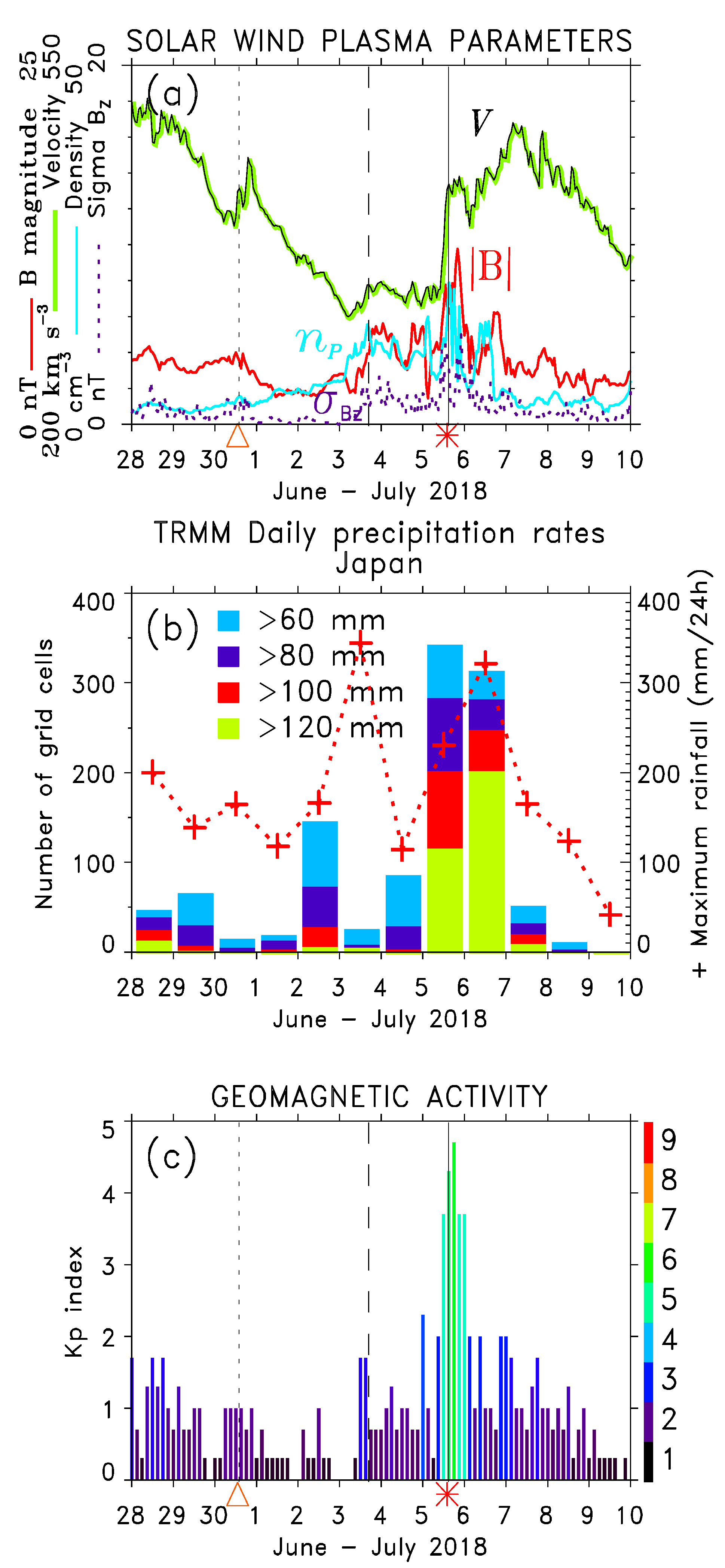
4. Superposed Epoch Analysis Keyed to Heavy Rainfall Events Causing Floods or Flash Floods
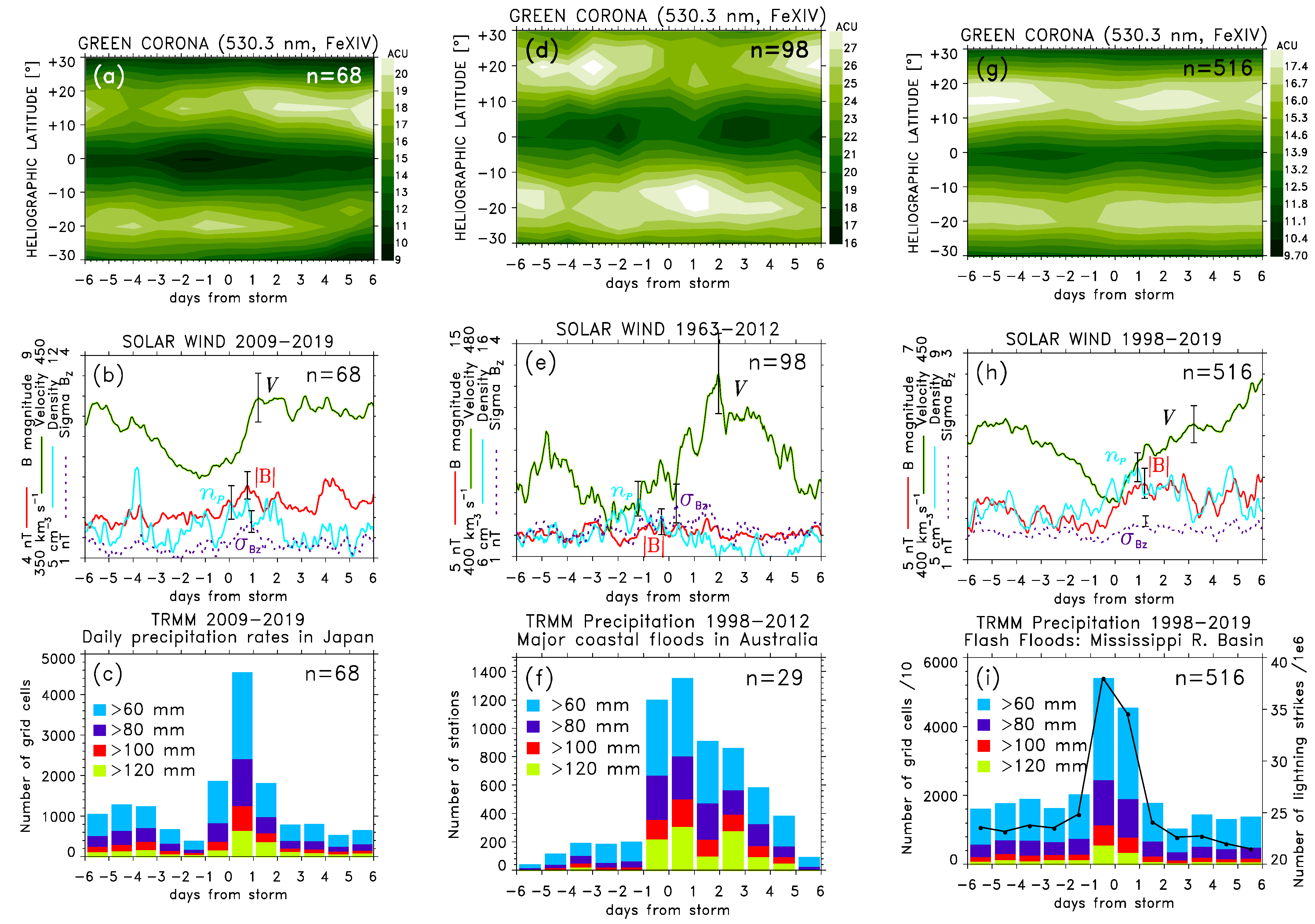
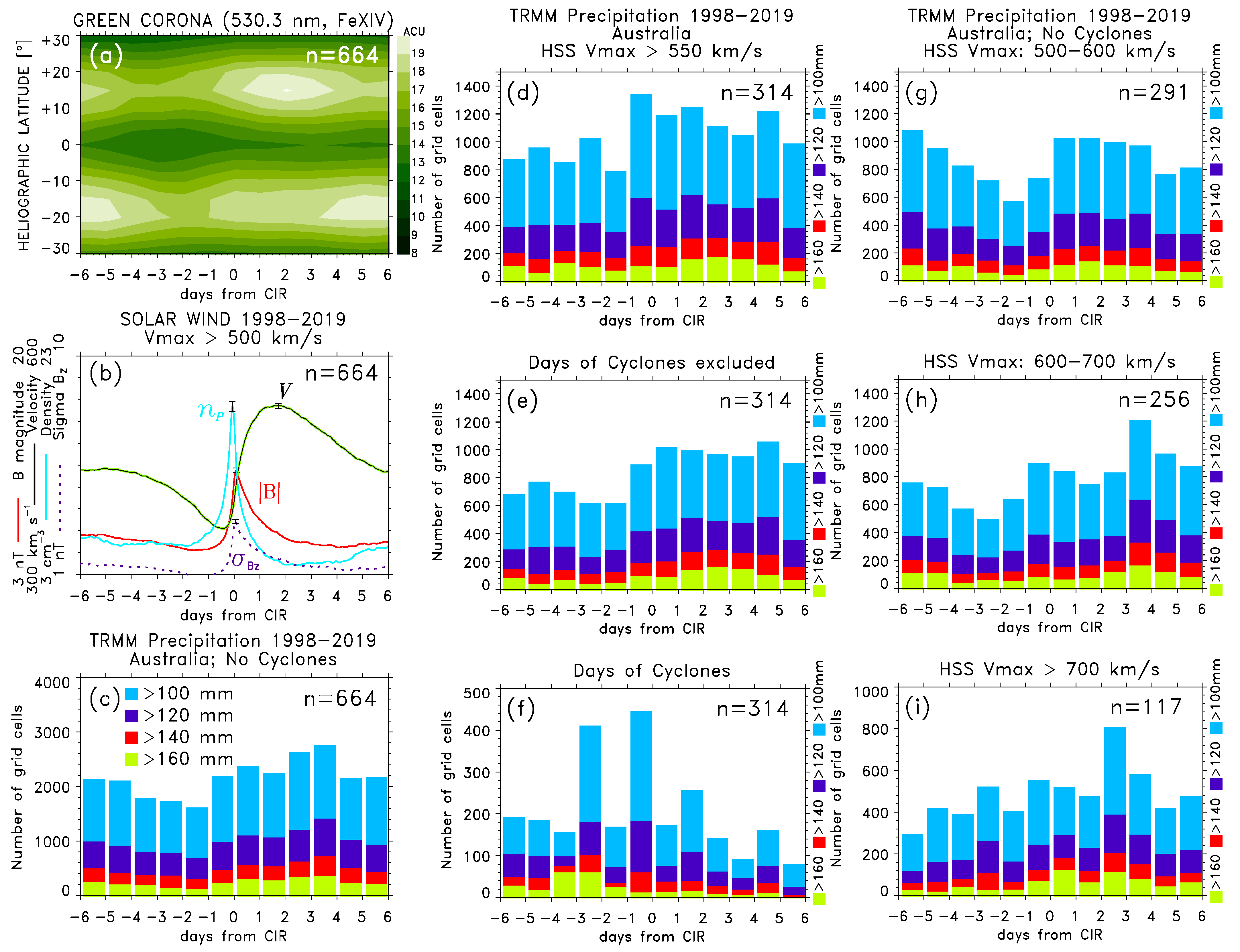
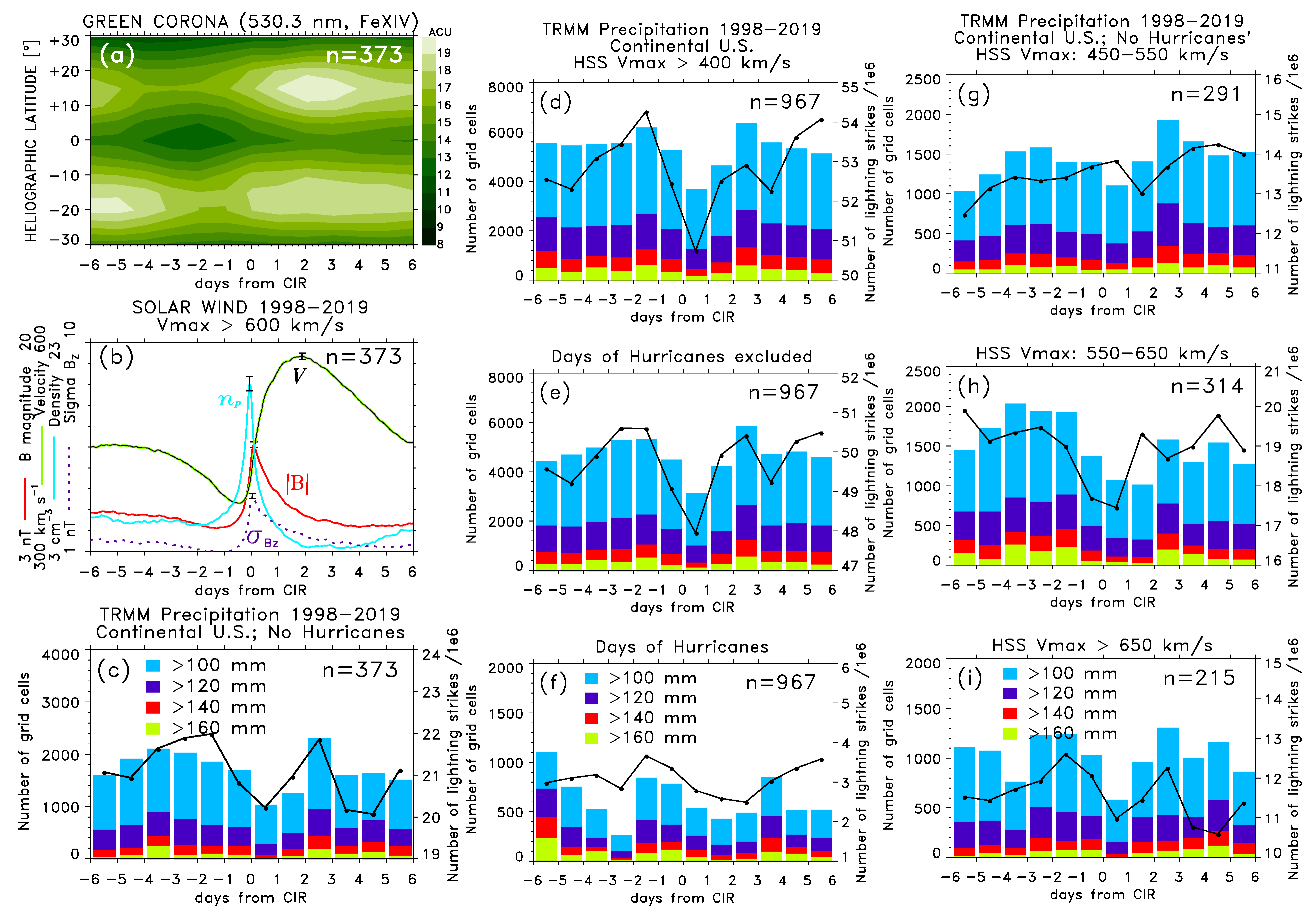
5. Modulation of High-Rate Precipitation Occurrence by High-Speed Streams
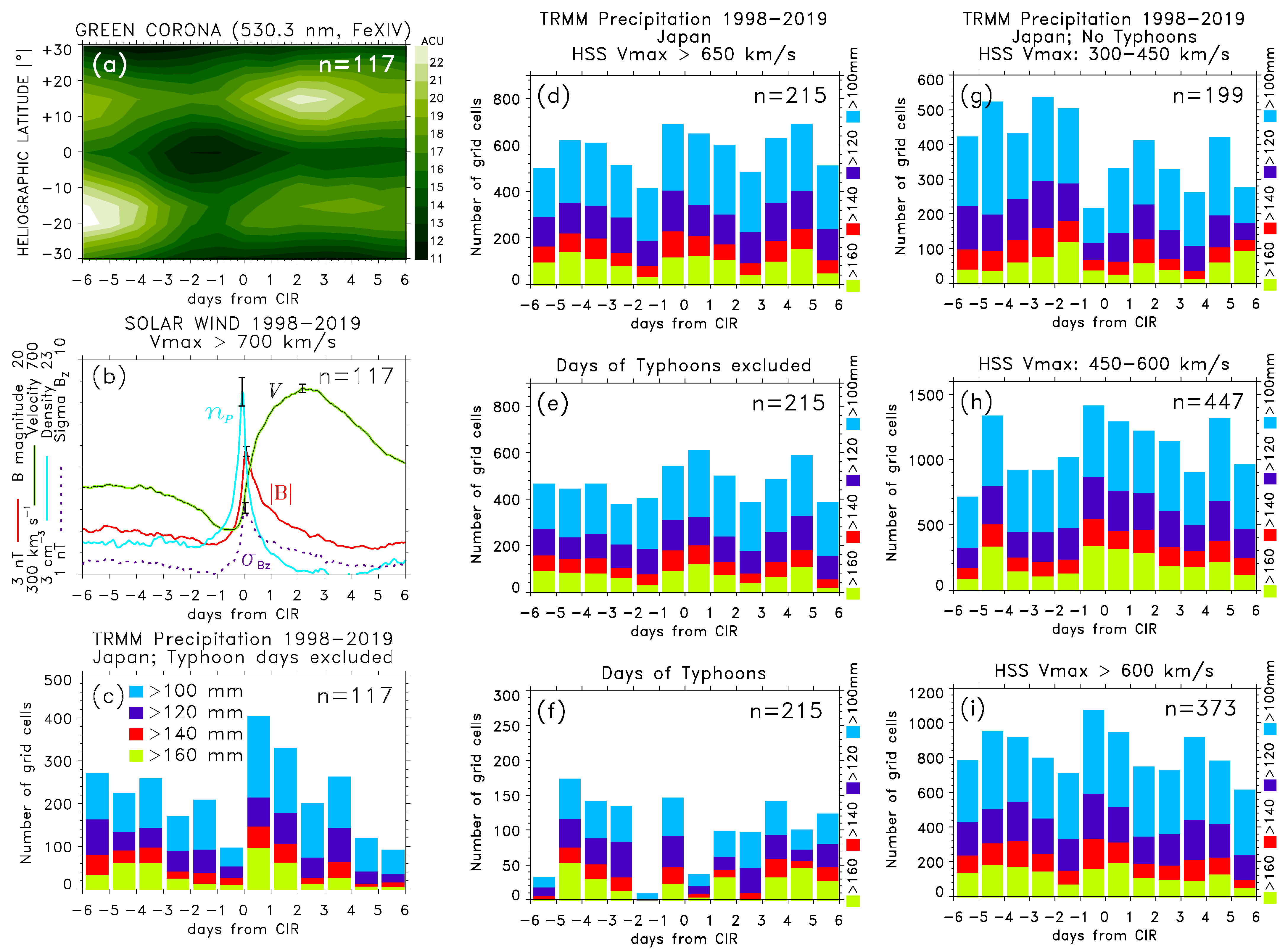
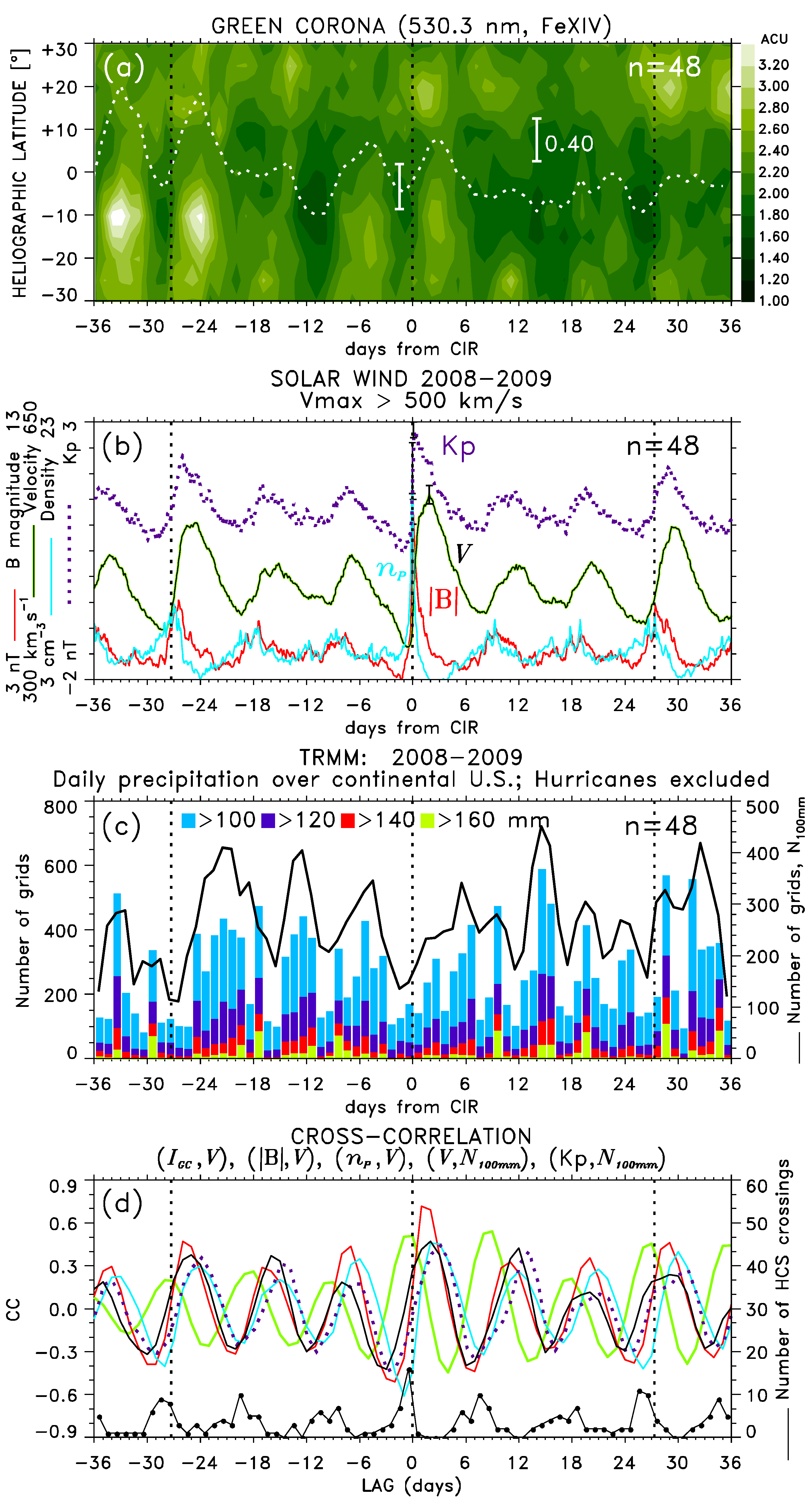
5.1. SPE Analysis Keyed to Arrivals of Major HSS/CIRs
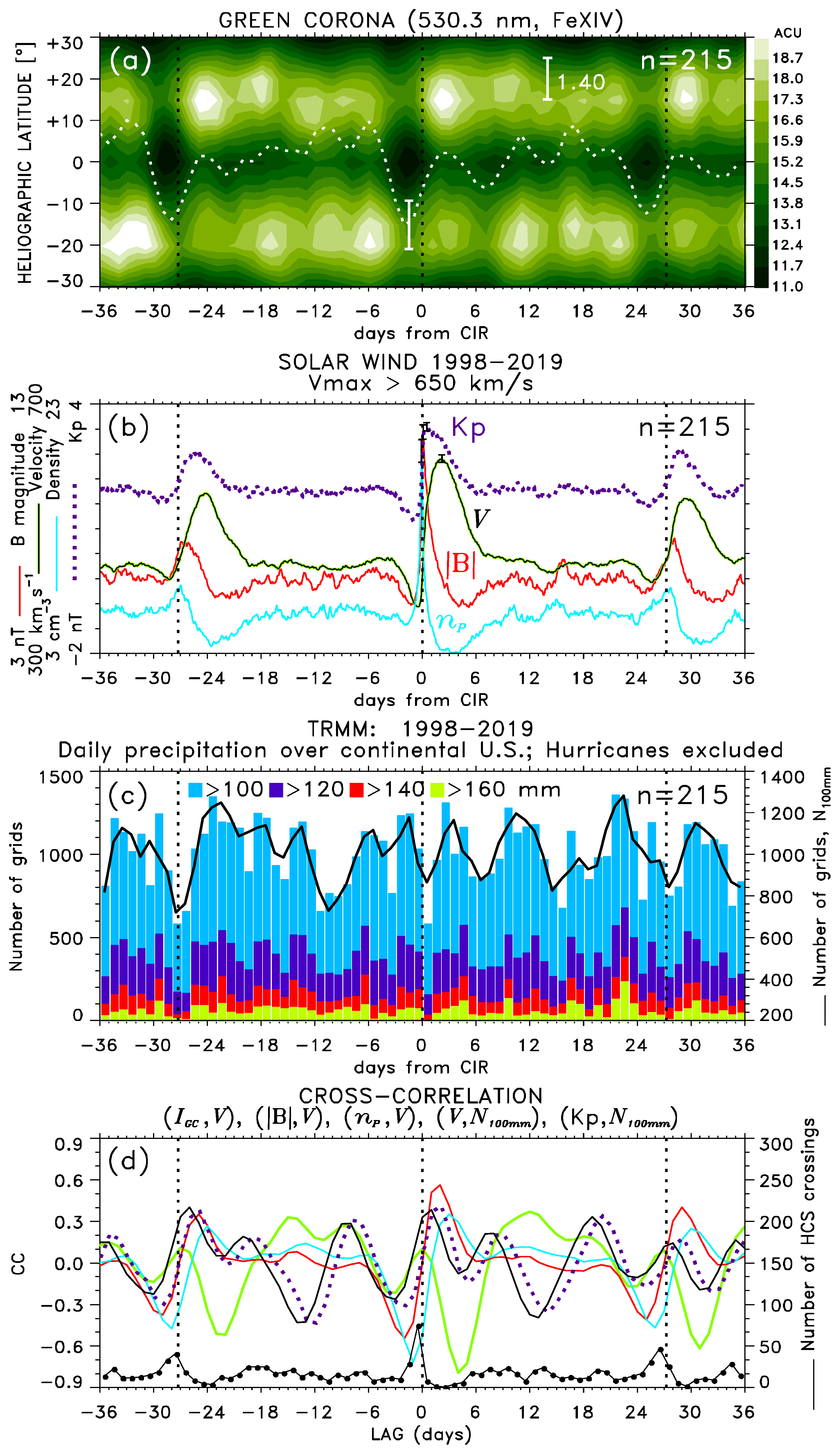
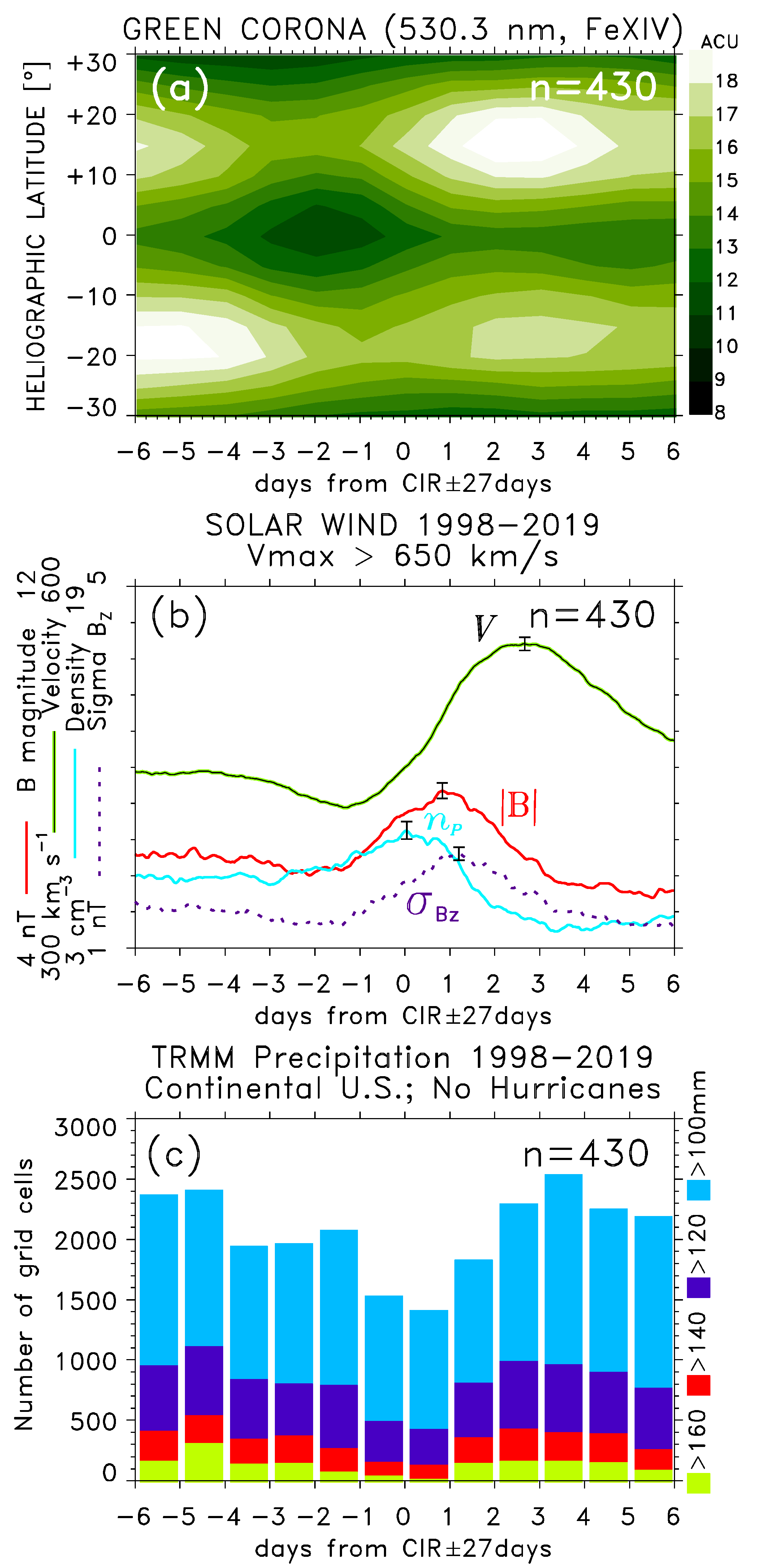
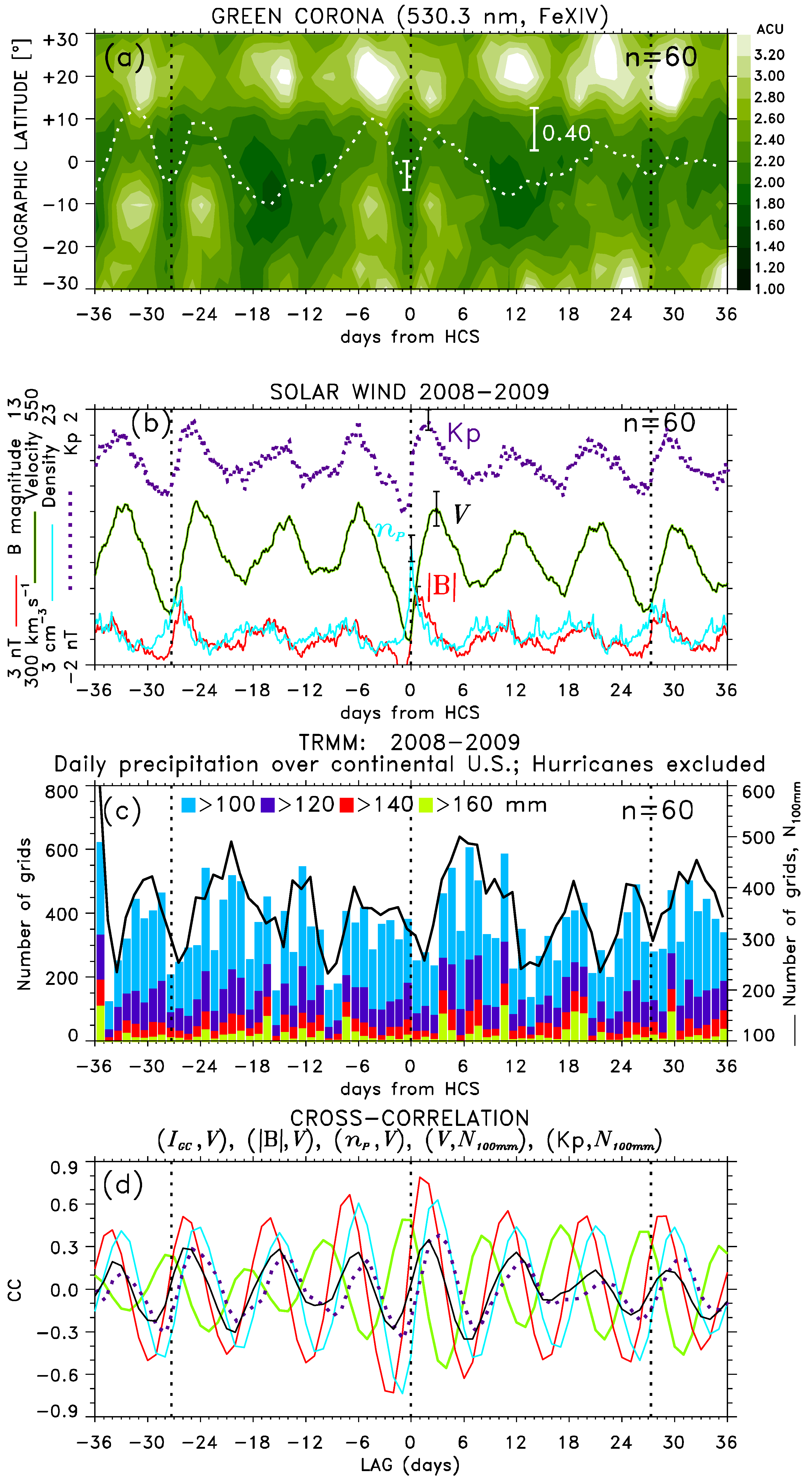
5.2. The SPE Analysis Extended to ±36 Days from Arrivals of Major HSS/CIRs
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MIA | Magnetosphere-Ionosphere-Atmosphere |
| HSS | High-Speed Stream |
| AGW | Atmospheric Gravity Wave |
| CIR | Co-rotating Interaction Regions |
| HCS | Heliospheric Current Sheet |
| ICME | Interplanetary Coronal Mass Ejection |
| ACU | Absolute Coronal Unit |
| SPE | Superposed Epoch |
| NDR | Normalized Deepening Rate |
| CCF | Cross-Correlation Function |
| VAI | Vorticity Area Index |
| HILDCAA | High-Intensity, Long-Duration Continuous Auroral Electrojet Activity |
| ULF | Ultra-Low Frequency |
| TFM | Transfer Function Model |
| SOHO | Solar and Heliospheric Observatory |
| JMA | Japan Meteorological Agency |
| AMeDAS | Automated Meteorological Data Acquisition System |
| APHRODITE | Asian Precipitation Highly Resolved Observational Data Integration towards Evaluation |
| TRMM | Tropical Rainfall Measuring Mission |
| MWRA | Monthly Weather Review—Australia |
| MRB | Mississippi River Basin |
| NOAA | National Oceanic and Atmospheric Administration |
| NWS | National Weather Service |
| CONUS | Continental U.S. |
| NCEI | National Centers for Environmental Information |
| SWDI | Severe Weather Data Inventory |
| NLDN | National Lightning Detection Network |
References
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Bloschl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
- Carlton, E.J.; Eisenberg, J.N.S.; Goldstick, J.; Cevallos, W.; Trostle, J.; Levy, K. Heavy rainfall events and diarrhea incidence: The role of social and environmental factors. Am. J. Epidemiol. 2014, 179, 344–352. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, M.; Borga, M.; Disse, M. Occurrence and characteristics of flash floods in Bavaria (Germany). In Climate Change Management; Leal Filho, W., Nagy, G., Borga, M., Chávez Muñoz, P., Artur, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 293–310. [Google Scholar]
- Du, W.; Fitzgerald, G.J.; Clark, M.; Hou, X.-Y. Health impacts of floods. Prehospital Disaster Med. 2010, 25, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Bandaru, S.; Sano, S.; Shimizu, Y.; Seki, Y.; Okano, Y.; Sasaki, T.; Wada, H.; Otsuki, T.; Ito, T. Impact of heavy rains of 2018 in western Japan: Disaster-induced health outcomes among the population of Innoshima Island. Heliyon 2020, 6, e03942. [Google Scholar] [CrossRef] [PubMed]
- National Academies of Sciences, Engineering, and Medicine. Framing the Challenge of Urban Flooding in the United States; National Academies Press: Washington, DC, USA, 2019; ISBN 978-0-309-48961-4. [Google Scholar]
- Houze, R.A. Mesoscale convective systems. Rev. Geophys. 2004, 42, RG4003. [Google Scholar] [CrossRef]
- Doswell, C.A.; Brooks, H.E.; Maddox, R.A. Flash flood forecasting: An ingredients-based methodology. Weather Forecast. 1996, 11, 560–581. [Google Scholar] [CrossRef]
- Schultz, D.M.; Schumacher, P.N. The use and misuse of conditional symmetric instability. Mon. Weather Rev. 1999, 127, 2709–2732. [Google Scholar] [CrossRef]
- Schumacher, R.S. Heavy rainfall and flash flooding. In Oxford Research Encyclopedia of Natural Hazard Science; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Doswell, C.A.; Bosart, L.F. Extratropical synoptic-scale processes and severe convection. Meteorol. Monogr. 2001, 50, 27–70. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F.; Ntelekos, A.A.; Georgakakos, K.P.; Smith, J.A. Towards probabilistic forecasting of flash floods: The combined effects of uncertainty in radar-rainfall and flash flood guidance. J. Hydrol. 2010, 394, 275–284. [Google Scholar] [CrossRef]
- Gourley, J.J.; Erlingis, J.M.; Hong, Y.; Wells, E.B. Evaluation of tools used for monitoring and forecasting flash floods in the United States. Weather. Forecast. 2012, 27, 158–173. [Google Scholar] [CrossRef]
- Schroeder, A.J.; Gourley, J.J.; Hardy, J.; Henderson, J.J.; Parhi, P.; Rahmani, V.; Reed, K.; Schumacher, R.; Smith, B.; Taraldsen, M.J. The development of a flash flood severity index. J. Hydrol. 2016, 541, 523–532. [Google Scholar] [CrossRef]
- Wilcox, J.M.; Scherrer, P.H.; Svalgaard, L.; Roberts, W.O.; Olson, R.H. Solar magnetic sector structure: Relation to circulation of the Earth’s atmosphere. Science 1973, 180, 185–186. [Google Scholar] [CrossRef]
- Wilcox, J.M.; Scherrer, P.H.; Svalgaard, L.; Roberts, W.O.; Olson, R.H.; Jenne, R.L. Influence of solar magnetic sector structure on terrestrial atmospheric vorticity. J. Atmos. Sci. 1974, 31, 581–588. [Google Scholar] [CrossRef]
- Taylor, H.A. Selective factors in Sun-weather research. Rev. Geophys. 1986, 24, 329–348. [Google Scholar] [CrossRef]
- Lam, M.M.; Tinsley, B.A. Solar wind-atmospheric electricity-cloud microphysics connections to weather and climate. J. Atmos. Sol. Terr. Phys. 2016, 149, 277–290. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Hajra, R.; Tanimori, T.; Takada, A.; Remya, B.; Mannucci, A.J.; Lakhina, G.S.; Kozyra, J.U.; Shiokawa, K.; Lee, L.C.; et al. Heliospheric plasma sheet (HPS) impingement onto the magnetosphere as a cause of relativistic electron dropouts (REDs) via. coherent EMIC wave scattering with possible consequences for climate change mechanisms. J. Geophys. Res. Space Phys. 2016, 121, 130. [Google Scholar] [CrossRef]
- Tinsley, B.A.; Zhou, L.; Wang, L.; Zhang, L. Seasonal and solar wind sector duration influences on the correlation of high latitude clouds with ionospheric potential. J. Geophys. Res. Atmos. 2021, 126, e2020JD034201. [Google Scholar] [CrossRef]
- Prikryl, P.; Rušin, V.; Rybansky, M. The influence of solar wind on extratropical cyclones—Part 1: Wilcox effect revisited. Ann. Geophys. 2009, 27, 1–30. [Google Scholar] [CrossRef]
- Prikryl, P.; Muldrew, D.B.; Sofko, G.J. The influence of solar wind on extratropical cyclones—Part 2: A link mediated by auroral atmospheric gravity waves? Ann. Geophys. 2009, 27, 31–57. [Google Scholar] [CrossRef][Green Version]
- Prikryl, P.; Iwao, K.; Muldrew, D.B.; Rušin, V.; Rybanský, M.; Bruntz, R. A link between high-speed solar wind streams and explosive extratropical cyclones. J. Atmos. Sol. Terr. Phys. 2016, 149, 219–231. [Google Scholar] [CrossRef]
- Prikryl, P.; Bruntz, R.; Tsukijihara, T.; Iwao, K.; Muldrew, D.B.; Rušin, V.; Rybanský, M.; Turňa, M.; Šťastný, P. Tropospheric weather influenced by solar wind through atmospheric vertical coupling downward control. J. Atmos. Sol. Terr. Phys. 2018, 171, 94–110. [Google Scholar] [CrossRef]
- Prikryl, P.; Nikitina, L.; Rušin, V. Rapid intensification of tropical cyclones in the context of the solar wind-magnetosphere-ionosphere-atmosphere coupling. J. Atmos. Sol. Terr. Phys. 2019, 183, 36–60. [Google Scholar] [CrossRef]
- Prikryl, P.; Rušin, V.; Prikryl, E.A.; Šťastný, P.; Turňa, M.; Zeleňáková, M. Heavy rainfall, floods, and flash floods influenced by high-speed solar wind coupling to the magnetosphere-ionosphere-atmosphere system. Ann. Geophys. 2021, 39, 769–793. [Google Scholar] [CrossRef]
- King, J.H. Solar wind spatial scales in and comparisons of hourly wind and ACE plasma and magnetic field data. J. Geophys. Res. Space Phys. 2005, 110, A02104. [Google Scholar] [CrossRef]
- Smith, E.J.; Wolfe, J.H. Observations of interaction regions and corotating shocks between one and five AU: Pioneers 10 and 11. Geophys. Res. Lett. 1976, 3, 137–140. [Google Scholar] [CrossRef]
- Smith, E.J.; Tsurutani, B.T.; Rosenberg, R.L. Observations of the interplanetary sector structure up to heliographic latitudes of 16: Pioneer 11. J. Geophys. Res. Space Phys. 1978, 83, 717–724. [Google Scholar] [CrossRef]
- Hoeksema, J.T.; Wilcox, J.M.; Scherrer, P. The structure of the heliospheric current sheet: 1978–1982. J. Geophys. Res. Space Phys. 1983, 88, 9910–9918. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Gonzalez, A.L.C.; Tang, F.; Arballo, J.K.; Okada, M. Interplanetary origin of geomagnetic activity in the declining phase of the solar cycle. J. Geophys. Res. Space Phys. 1995, 100, 21717–21733. [Google Scholar] [CrossRef]
- Rybanský, M. Coronal index of solar activity. Bull. Astron. Inst. Czechoslov. 1975, 28, 367–370. [Google Scholar]
- Rybansky, M.; Rušin, V.; Minarovjech, M. Coronal index of solar activity—solar-terrestrial research. Space Sci. Rev. 2001, 95, 227–234. [Google Scholar] [CrossRef]
- Rybansky, M.; Rušin, V.; Minarovjech, M.; Klocok, L.; Cliver, E.W. Reexamination of the coronal index of solar activity. J. Geophys. Res. Space Phys. 2005, 110, A08106. [Google Scholar] [CrossRef]
- Dorotovič, I.; Minarovjech, M.; Lorenc, M.; Rybanský, M. Modified homogeneous data set of coronal intensities. Sol. Phys. 2014, 289, 2697–2703. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Adler, R.F. TRMM (TMPA) Precipitation L3 1 Day 0.25 Degree × 0.25 Degree V7; Savtchenko, A., Ed.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2016. Available online: https://disc.gsfc.nasa.gov/datasets/TRMM_3B42_Daily_7/summary (accessed on 9 September 2021).
- Ambrož, P. Statistical method of superposition of epochs. I-Methodical analysis and some criteria of application. Bull. Astron. Inst. Czechosl. 1979, 30, 114. [Google Scholar]
- McPherron, R.L.; Siscoe, G. Probabilistic forecasting of geomagnetic indices using solar wind air mass analysis. Space Weather 2004, 2, S01001. [Google Scholar] [CrossRef]
- Lundstedt, H. Influence of interplanetary interaction regions on geomagnetic disturbances and tropospheric circulation. Planet. Space Sci. 1984, 32, 1541–1545. [Google Scholar] [CrossRef]
- Tsukijihara, T.; Kawamura, R.; Kawano, T. Influential role of inter-decadal explosive cyclone activity on the increased frequency of winter storm events in Hokkaido, the northernmost island of Japan. Int. J. Clim. 2019, 39, 1700–1715. [Google Scholar] [CrossRef]
- Lim, E.-P.; Simmonds, I. Explosive cyclone development in the Southern hemisphere and a comparison with Northern hemisphere events. Mon. Weather Rev. 2002, 130, 2188–2209. [Google Scholar] [CrossRef]
- Knapp, K. Scientific data stewardship of international satellite cloud climatology project B1 global geostationary observations. J. Appl. Remote. Sens. 2008, 2, 023548. [Google Scholar] [CrossRef]
- Kawano, T.; Kawamura, R. Influence of Okhotsk Sea ice distribution on a snowstorm associated with an explosive cyclone in Hokkaido, Japan. SOLA 2018, 14, 1–5. [Google Scholar] [CrossRef]
- Herring, S.C.; Christidis, N.; Hoell, A.; Hoerling, M.P.; Stott, P.A. Explaining extreme events of 2018 from a climate perspective. Bull. Am. Meteorol. Soc. 2020, 101, S1–S140. [Google Scholar] [CrossRef]
- Shimpo, A.; Takemura, K.; Wakamatsu, S.; Togawa, H.; Mochizuki, Y.; Takekawa, M.; Tanaka, S.; Yamashita, K.; Maeda, S.; Kurora, R.; et al. Primary factors behind the heavy rain event of july 2018 and the subsequent heat wave in Japan. SOLA 2019, 15A, 13–18. [Google Scholar] [CrossRef]
- Tsuji, H.; Yokoyama, C.; Takayabu, Y.N. Contrasting features of the july 2018 heavy rainfall event and the 2017 Northern Kyushu rainfall event in Japan. J. Meteorol. Soc. Jpn. 2020, 98, 859–876. [Google Scholar] [CrossRef]
- Zhao, N.; Manda, A.; Guo, X.; Kikuchi, K.; Nasuno, T.; Nakano, M.; Zhang, Y.; Wang, B. A Lagrangian view of moisture transport related to the heavy rainfall of July 2020 in Japan: Importance of the moistening over the subtropical regions. Geophys. Res. Lett. 2021, 48, e2020GL091441. [Google Scholar] [CrossRef]
- Japan Meteorological Agency (JMA). Characteristics of the Heavy Rain of July 2020 and Related Atmospheric Circulation (in Japanese). Press Release on 31 July 2020 of JMA, 2020. Available online: www.jma.go.jp/jma/press/2007/31a/r02gou.pdf (accessed on 9 September 2021).
- Emergency Operations Center of Japan (EOCJ). The Damage Situation during the Heavy Rain of July 2020 (in Japanese); Emergency Operations Center of Japan (EOCJ), Report on 7 August 2020, EOCJ. Available online: http://www.bousai.go.jp/updates/r2_07ooame/pdf/r20703_ooame_33.pdf (accessed on 9 September 2021).
- Burlaga, L.; Sittler, E.; Mariani, F.; Schwenn, R. Magnetic loop behind an interplanetary shock: Voyager, Helios, and IMP 8 observations. J. Geophys. Res. Space Phys. 1981, 86, 6673–6684. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Tang, F.; Akasofu, S.I.; Smith, E.J. Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978–1979). J. Geophys. Res. Space Phys. 1988, 93, 8519–8531. [Google Scholar] [CrossRef]
- Richardson, I.G. The formation of CIRs at stream-stream interfaces and resultant geomagnetic activity. In Recurrent Magnetic Storms: Corotating Solar Wind Streams; Tsurutani, B., McPherron, R., Gonzalez, W., Lu, G., Sobral, J.H.A., Gopalswamy, N., Eds.; American Geophysical Union: Washington, DC, USA, 2006; Volume 167, ISBN 978-0-87590-432-0. [Google Scholar]
- Callaghan, J.; Power, S. Major coastal flooding in southeastern Australia, associated deaths and weather systems. J. South Hemisph. Earth Syst. Sci. 2014, 64, 183–213. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. Aphrodite: Constructing a long-term daily gridded precipitation dataset for asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Smith, E.J.; Pyle, K.R.; Simpson, J.A. Energetic protons accelerated at corotating shocks: Pioneer 10 and 11 observations from 1 to 6 AU. J. Geophys. Res. Space Phys. 1982, 87, 7389–7404. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Gonzalez, A.L.C.; Guarnieri, F.L.; Gopalswamy, N.; Grande, M.; Kamide, Y.; Kasahara, Y.; Lu, G.; Mann, I.; et al. Corotating solar wind streams and recurrent geomagnetic activity: A review. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; McPherron, R.L.; Gonzalez, W.D.; Lu, G.; Gopalswamy, N.; Guarnieri, F.L. Magnetic storms caused by corotating solar wind streams. In Geomagnetically Induced Currents from the Sun to the Power Grid; American Geophysical Union: Washington, DC, USA, 2006; Volume 167, pp. 1–17. [Google Scholar]
- De Toma, G. Evolution of coronal holes and implications for high-speed solar wind during the minimum between cycles 23 and 24. Sol. Phys. 2011, 274, 195–217. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Echer, E.; Gonzalez, W.D. The solar and interplanetary causes of the recent minimum in geomagnetic activity (MGA23): A combination of midlatitude small coronal holes, low IMF BZ variances, low solar wind speeds and low solar magnetic fields. Ann. Geophys. 2011, 29, 839–849. [Google Scholar] [CrossRef]
- Antonucci, E.; Harra, L.; Susino, R.; Telloni, D. Observations of the solar corona from space. Space Sci. Rev. 2020, 216, 1–40. [Google Scholar] [CrossRef]
- Wang, W.; Lei, J.; Burns, A.G.; Qian, L.; Solomon, S.C.; Wiltberger, M.; Xu, J. Ionospheric day-to-day variability around the whole heliosphere interval in 2008. Sol. Phys. 2011, 274, 457–472. [Google Scholar] [CrossRef]
- Harvey, J.; Sheeley, N. Coronal holes and solar magnetic fields. Space Sci. Rev. 1979, 23, 139–158. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D. The cause of high-intensity long-duration continuous AE activity (HILDCAAs): Interplanetary Alfvén wave trains. Planet. Space Sci. 1987, 35, 405–412. [Google Scholar] [CrossRef]
- Belcher, J.W.; Davis, L. Large-amplitude Alfvén waves in the interplanetary medium, 2. J. Geophys. Res. Space Phys. 1971, 76, 3534–3563. [Google Scholar] [CrossRef]
- Dungey, J.W. Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 1961, 6, 47–48. [Google Scholar] [CrossRef]
- Dungey, J.W. Origins of the concept of reconnection and its application to the magnetopause: A historical view, physics of the magnetopause. In Geophysical Monograph Series; Song, P., Sonnerup, B.U.O., Thomsen, M.F., Eds.; AGU: Washington, DC, USA, 1995; Volume 90, pp. 17–19. ISBN 9781118663974. [Google Scholar]
- Mayr, H.G.; Harris, I.; Varosi, F.; Herrero, F.A. Global excitation of wave phenomena in a dissipative multiconstituent medium: 1. Transfer function of the Earth’s thermosphere. J. Geophys. Res. Space Phys. 1984, 89, 10929–10959. [Google Scholar] [CrossRef]
- Mayr, H.G.; Harris, I.; Varosi, F.; Herrero, F.A. Global excitation of wave phenomena in a dissipative multiconstituent medium: 2. Impulsive perturbations in the Earth’s thermosphere. J. Geophys. Res. Space Phys. 1984, 89, 10961–10986. [Google Scholar] [CrossRef]
- Mayr, H.; Harris, I.; Herrero, F.; Spencer, N.; Varosi, F.; Pesnell, W. Thermospheric gravity waves: Observations and interpretation using the transfer function model (TFM). Space Sci. Rev. 1990, 54, 297–375. [Google Scholar] [CrossRef]
- Mayr, H.G.; Talaat, E.R.; Wolven, B.C. Global propagation of gravity waves generated with the whole atmosphere transfer function model. J. Atmos. Sol. Terr. Phys. 2013, 104, 7–17. [Google Scholar] [CrossRef][Green Version]
- Hocke, K.; Schlegel, K. A review of atmospheric gravity waves and travelling ionospheric disturbances: 1982–1995. Ann. Geophys. 1996, 14, 917–940. [Google Scholar] [CrossRef]
- Prikryl, P.; Muldrew, D.B.; Sofko, G.J.; Ruohoniemi, J.M. Solar wind Alfvén waves: A source of pulsed ionospheric convection and atmospheric gravity waves. Ann. Geophys. 2005, 23, 401–417. [Google Scholar] [CrossRef][Green Version]
- Hagiwara, M.; Tanaka, H.L. A theoretical analysis of the atmospheric gravity wave that connects the thermosphere and the troposphere. Tsukuba Geoenviron. Sci. 2020, 16, 1–14. [Google Scholar] [CrossRef]
- Wilcox, J.M.; Svalgaard, L.; Scherrer, P. On the reality of a sun-weather effect. J. Atmos. Sci. 1976, 33, 1113–1116. [Google Scholar] [CrossRef][Green Version]
- Borovsky, J.E.; Steinberg, J.T. The “calm before the storm” in CIR/magnetosphere interactions: Occurrence statistics, solar wind statistics, and magnetospheric preconditioning. J. Geophys. Res. Space Phys. 2006, 111, A07S10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prikryl, P.; Rušin, V.; Prikryl, E.A. High-Rate Precipitation Occurrence Modulated by Solar Wind High-Speed Streams. Atmosphere 2021, 12, 1186. https://doi.org/10.3390/atmos12091186
Prikryl P, Rušin V, Prikryl EA. High-Rate Precipitation Occurrence Modulated by Solar Wind High-Speed Streams. Atmosphere. 2021; 12(9):1186. https://doi.org/10.3390/atmos12091186
Chicago/Turabian StylePrikryl, Paul, Vojto Rušin, and Emil A. Prikryl. 2021. "High-Rate Precipitation Occurrence Modulated by Solar Wind High-Speed Streams" Atmosphere 12, no. 9: 1186. https://doi.org/10.3390/atmos12091186
APA StylePrikryl, P., Rušin, V., & Prikryl, E. A. (2021). High-Rate Precipitation Occurrence Modulated by Solar Wind High-Speed Streams. Atmosphere, 12(9), 1186. https://doi.org/10.3390/atmos12091186






