Study on Air Pollution Behavior of VOCs with Photochemical Monitoring Stations Using EGARCH Model in Southern Taiwan
Abstract
:1. Introduction
2. Methodology
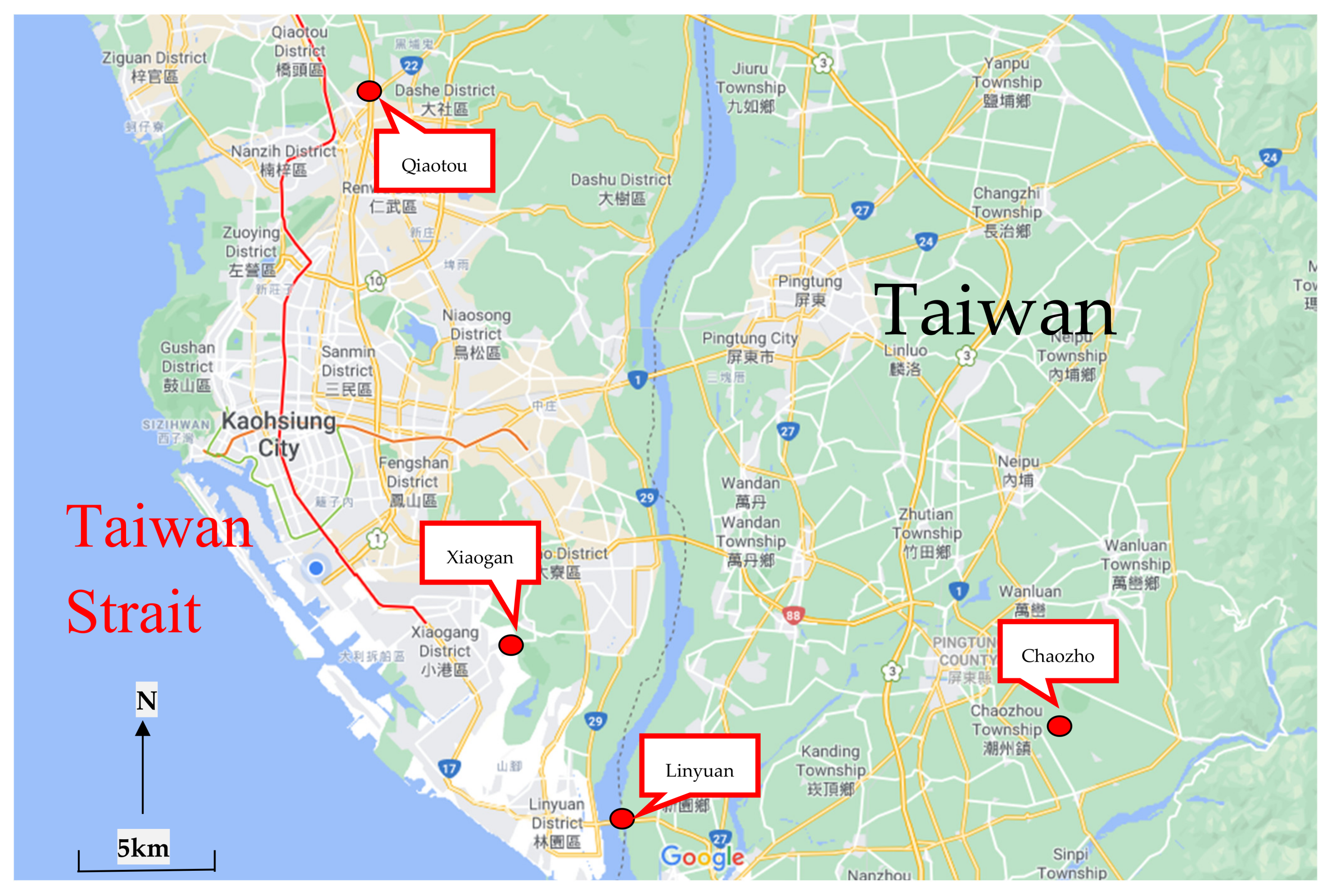
2.1. Selection of Data and Location of PAMSs
2.2. Selection of Influence Factors by Multivariate Analysis
2.3. Development of the VARMA Model
2.4. VARMA-EGARCH Modeling
2.5. Essence of EGARCH Model Development
2.5.1. Fat Tail Test
2.5.2. Ljung–Box Series Examination
2.5.3. Examination of the EGARCH Effectiveness
2.6. Outline of This Research
3. Results and Discussion
3.1. Selection and Standardization of VOCs’ Data
3.2. Discussion on the Effects of the VARMA-EGARCH Model on Mobile Pollution Factor in the Simulation
3.2.1. Fundamental Property Analysis of the Three VOCs
3.2.2. Results of Ljung–Box Serial Examination
3.2.3. Examination of EGARCH Effectiveness
3.3. Selection of the Best Combination for EGARCH
3.4. Simulation Results of Mobile Pollution Factor Using the VARMA(2,1)-EGARCH(1,0) Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pandis, S.N.; Harley, R.A.; Cass, G.R.; Seinfeld, J.H. Secondary organic aerosol formation and transport. Atmos. Environ. Part A Gen. Top. 1992, 26, 2269–2282. [Google Scholar] [CrossRef]
- Karle, M.M.; Mahmud, S.; Sakai, R.; Fitzgerald, R.M. Investigation of the successive ozone episodes in the El Paso–Juarez region in the summer of 2017. Atmosphere 2010, 11, 532. [Google Scholar] [CrossRef]
- Steward, D.; Saunders, E.; Perea, R.; Fitsgerald, R.M.; Campbell, D.E.; Stockwell, W.R. Linking air quality and human health effects models: An application to the Los Angeles air basin. Environ. Health Insights 2017, 11, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Algrim, L.B.; Ziemann, P.J. Effect of the hydroxyl group on yields and composition of organic aerosol formed from OH radical-initiated reactions of alcohols in the presence of NOx. ACS Earth Space Chem. 2019, 3, 413–423. [Google Scholar] [CrossRef]
- Kaipara, R.; Rajakumar, B. Oxidative degradation kinetics and mechanism of two biodiesel constituents (ethyl-2-methyl propionate (E2MP) and ethyl-2,2-dimethyl propionate (E22DMP)) initiated by Cl atoms. ACS Earth Space Chem. 2020, 4, 142–156. [Google Scholar] [CrossRef]
- Shi, X.; Qiu, X.; Cheng, Z.; Chen, Q.; Rudich, Y.; Zhu, T. Isomeric identification of particle-phase organic nitrates through gas chromatography and time-of-flight mass spectrometry coupled with an electron capture negative ionization source. Environ. Sci. Technol. 2020, 54, 707–713. [Google Scholar] [CrossRef] [PubMed]
- Fujita, E.M.; Campbell, D.E.; Stockwell, W.R.; Lawson, D.R. Past and future ozone trends in California’s south coast air basin: Reconciliation of ambient measurements with past and projected emission inventories. J. Air Waste Manag. Assoc. 2013, 63, 54–69. [Google Scholar] [CrossRef] [PubMed]
- Chou, T.G. The research of air quality management in fine particulate matters. In Central Office of Administration, Academia Sinica Research Weekly 1276; Central Office of Administration, Academia Sinica: Taipei City, Taiwan, 2010. (In Chinese) [Google Scholar]
- Gouriou, F.; Morin, J.P.; Weill, M.E. On-road measurements of particle number concentrations and size distributions in urban and tunnel environments. Atmos. Environ. 2004, 38, 2831–2840. [Google Scholar] [CrossRef]
- Chen, W.K.; Li, T.D. The Establishment of Aerosol Control Mode Based on the Photochemical Reaction Mechanism; NSC-1999-EPA-Z-231-001; National Science Council, Executive Yuan: Taipei City, Taiwan, 1999. (In Chinese) [Google Scholar]
- Fu, L.; Hao, J.; He, D.; He, K. Assessment of vehicular pollution in China. J. Air Waste Manag. Assoc. 2001, 51, 658–668. [Google Scholar] [CrossRef] [Green Version]
- Kuo, H.W.; Wei, H.C.; Liu, C.S. Exposure to 16 volatile organic compounds while commuting in Taichung Taiwan. Atmos. Environ. 2000, 34, 3331–3336. [Google Scholar] [CrossRef]
- Geiss, O.; Giannopoulos, G.; Tirendi, S.; Barrero-Moreno, J.; Larsen, B.R.; Kotzias, D. The airmex study-VOC measurements in public buildings and schools/kindergartens in eleven European cities: Statistical analysis of the data. Atmos. Environ. 2011, 45, 3676–3684. [Google Scholar] [CrossRef]
- Cheng, J.H.; Hsieh, M.J.; Chen, K.S. Characteristics and source apportionment of ambient volatile organic compounds in a science park in central Taiwan. Aerosol Air Qual. Resour. 2016, 16, 221–229. [Google Scholar] [CrossRef] [Green Version]
- Wu, E.M.Y.; Kuo, S.L. Air quality time series based GARCH model analyses of air quality information for a total quantity control district. Aerosol Air Qual. Res. 2012, 12, 327–339. [Google Scholar] [CrossRef] [Green Version]
- Wu, E.M.Y.; Kuo, S.L.; Liu, W.C. Generalized autoregressive conditional heteroskedastic model for water quality analyses and time series investigation in reservoir watersheds. Environ. Eng. Sci. 2012, 29, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Nelson, D.B. Conditional heteroscedasticity in asset returns: A new approach. Econometrica 1991, 59, 347–370. [Google Scholar] [CrossRef]
- Brockwell, J.B.; Davis, R.A. Introduction to Time Series and Forecasting; Springer-Verlag Inc: New York, NY, USA, 2002. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications- with R Examples; Springer Science+Business Media, LLC: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ling, S.; McAleer, M. Asymptotic theory for a vector ARMA-GARCH model. Econom. Theory 2003, 19, 278–308. [Google Scholar] [CrossRef] [Green Version]
- Kumar, U.; Prakash, A.; Jain, V.K. A multivariate time series approach to study the interdependence among O3, NOx and VOCs in ambient urban atmosphere. Environ. Modeling Assess. 2009, 14, 631–643. [Google Scholar] [CrossRef]
- Elyasiani, E.; Mansur, I. International spillover of risk and return among major banking institutions: A bivariate GARCH model. J. Account. Audit. Financ. 2003, 18, 303–330. [Google Scholar] [CrossRef]
- Ali, G. Edarch, Gjr-Garch, Tgarch, Avgarch, Ngarch, Igarch and Aparch Models for Pathogens at Marine Recreational Sites. J. Stat. Econom. Methods 2013, 2, 57–73. [Google Scholar]
- Glosten, L.R.; Jagannathan, R.; Runkle, D. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwartz, G.E. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Jiang, W. Using the GARCH Model to Analyze and Predict the Different Stock Market. Master’s Thesis, Statistics Department of Statistics Uppsala University, Uppsala, Sweden, 2012. [Google Scholar]
- Lee, C.L.; Lee, R.K.; Kao, Y.M. Lagrange multiplier optimization synthesis of long-period fiber gratings. In National Tsing Hua University Institutional Repository, Institute of Electrical and Electronics Engineers, EE Conference Papers; Institute of Electrical and Electronics Engineers: Hsinchu City, Taiwan, 2007; p. 826. [Google Scholar]
- Wu, E.M.Y.; Kuo, S.L. VARMA-EGARCH model for air-quality analyses and application in aouthern Taiwan. Atmosphere 2020, 11, 1096. [Google Scholar] [CrossRef]
- Forbes, K.; Rigobon, R. No contagion, only interdependence: Measuring stock market co-movements. J. Financ. 2002, 5, 2223–2261. [Google Scholar] [CrossRef]
| VOC | TU | TB | IB | |
|---|---|---|---|---|
| Parameters | ||||
| Mean | 2.48 | 1.63 | 1.06 | |
| Median | 2.31 | 1.44 | 0.98 | |
| Maximum | 8.16 | 4.03 | 3.92 | |
| Minimum | 0.05 | 0.05 | 0.01 | |
| Std. Dev. | 1.40 | 0.92 | 1.01 | |
| Skewness | 1.23 | 2.46 | 3.55 | |
| Kurtosis | 5.99 | 8.16 | 7.07 | |
| Jarque–Bera | 1517.59 | 1810.24 | 988.54 | |
| Probability | 0.000 | 0.000 | 0.000 | |
| Observations | 12,000 | 12,000 | 12,000 | |
| L–BQ(K) | TU | TB | IB | |
|---|---|---|---|---|
| 1 | 0.43 | 0.86 | 0.38 | 3.84 |
| 2 | 1.09 | 1.69 | 1.09 | 5.99 |
| 3 | 2.38 | 2.29 | 1.87 | 7.82 |
| 4 | 4.87 | 4.67 | 3.35 | 9.49 |
| 5 | 5.52 | 5.16 | 4.43 | 11.07 |
| 6 | 7.69 | 7.03 | 5.60 | 12.59 |
| 7 | 9.46 | 8.45 | 7.59 | 14.07 |
| 8 | 12.01 | 11.64 | 9.56 | 15.51 |
| 9 | 13.97 | 12.50 | 10.74 | 16.92 |
| 10 | 15.88 | 14.62 | 12.76 | 19.68 |
| 11 | 17.94 | 16.58 | 14.92 | 21.96 |
| 12 | 20.60 | 19.41 | 17.40 | 24.05 |
| 16 | 23.95 | 24.47 | 22.79 | 30.30 |
| 20 | 29.66 | 30.79 | 28.74 | 36.41 |
| 24 | 35.51 | 36.17 | 34.33 | 43.42 |
| Q (Lagged Variables) | TU | TB | IB | |
|---|---|---|---|---|
| 1 | 9.15 | 20.59 | 17.20 | 3.84 |
| 2 | 16.47 | 30.65 | 22.54 | 5.99 |
| 3 | 25.66 | 38.91 | 32.68 | 7.82 |
| 4 | 29.71 | 53.06 | 35.89 | 9.49 |
| 5 | 33.73 | 68.56 | 44.57 | 11.07 |
| 6 | 38.49 | 80.34 | 56.40 | 12.59 |
| 7 | 46.72 | 83.67 | 70.63 | 14.07 |
| 8 | 51.64 | 90.48 | 77.85 | 15.51 |
| 9 | 55.67 | 103.26 | 86.71 | 16.92 |
| 10 | 61.08 | 109.60 | 98.45 | 19.68 |
| 11 | 68.58 | 116.82 | 104.68 | 21.96 |
| 12 | 79.40 | 123.60 | 111.12 | 24.05 |
| 16 | 91.55 | 137.02 | 128.19 | 30.30 |
| 20 | 98.78 | 150.16 | 143.06 | 36.41 |
| 24 | 109.56 | 172.44 | 163.47 | 43.42 |
| EGARCH | EGARCH(0,1) | EGARCH(1,1) | EGARCH(1,0) | EGARCH(2,0) | |||||
|---|---|---|---|---|---|---|---|---|---|
| VARMA Types | AIC | SC | AIC | SC | AIC | SC | AIC | SC | |
| VARMA(0,1) | 8.748 | 8.806 | 8.687 | 8.816 | 8.425 | 8.449 | 8.524 | 8.604 | |
| VARMA(0,2) | 8.523 | 8.572 | 8.569 | 8.650 | 8.268 | 8.302 | 8.332 | 8.387 | |
| VARMA(1,0) | 8.466 | 8.505 | 8.382 | 8.505 | 8.343 | 8.387 | 8.359 | 8.442 | |
| VARMA(1,1) | 8.514 | 8.599 | 8.561 | 8.858 | 8.301 | 8.414 | 8.380 | 8.416 | |
| VARMA(2,0) | 8.400 | 8.487 | 8.610 | 8.724 | 8.216 | 8.405 | 8.345 | 8.413 | |
| VARMA(2,1) | 8.621 | 8.669 | 8.659 | 8.772 | 8.179 | 8.306 | 8.317 | 8.445 | |
| VARMA(3,0) | 8.457 | 8.512 | 8.498 | 8.650 | 8.283 | 8.341 | 8.402 | 8.426 | |
| VARMA(3,1) | 8.502 | 8.537 | 8.496 | 8.573 | 8.316 | 8.378 | 8.468 | 8.580 | |
| Parameters | a0 | a1 | a2 | b0 | b1 | b2 | c0 | c1 | c2 | d1 | α0 | α1 | α2 | β1 | γ1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EGARCH Types | ||||||||||||||||
| VARMA(0,1)- | −1.54 | 2.34 | 2.56 | 3.47 | 2.03 | −0.41 | 2.06 | 1.67 | 0.06 | 0.96 | 1.59 | 2.36 | −0.95 | 3.04 | −0.367 | |
| EGARCH(0,1) | 0.92 | 2.42 | 1.04 | −0.22 | 1.56 | 2.39 | 1.98 | −2.48 | 0.42 | 2.51 | 0.67 | 1.19 | 2.01 | −1.14 | 2.52 | |
| VARMA(0,1)- | 0.99 | 3.30 | 1.91 | 3.06 | −0.87 | 0.08 | 2.97 | 3.41 | 1.85 | 3.34 | −2.46 | 1.03 | 2.61 | 0.93 | 1.87 | |
| EGARCH(1,1) | −2.16 | 1.81 | 2.04 | −1.04 | 2.65 | 0.56 | 0.99 | −2.23 | 1.32 | −0.78 | 1.65 | 1.63 | 0.54 | −2.16 | 2.63 | |
| VARMA(1,0)- | 3.55 | −1.23 | 2.20 | 1.98 | 3.06 | 0.95 | 3.34 | 1.15 | −0.90 | 1.55 | 2.06 | −1.09 | 0.87 | −0.53 | −1.53 | |
| EGARCH(1,0) | 1.83 | 0.57 | −0.54 | 2.29 | −0.64 | 1.92 | 2.63 | 0.99 | 2.03 | 1.98 | 3.44 | 1.08 | 2.36 | 0.76 | 3.01 | |
| VARMA(1,1)- | 1.99 | −2.54 | 3.09 | 1.01 | 2.77 | −0.69 | 0.88 | −1.60 | 2.06 | 1.08 | −0.96 | 2.40 | 3.11 | 1.57 | −1.36 | |
| EGARCH(2,0) | 2.77 | 3.06 | 1.78 | 1.46 | −3.26 | 2.33 | −1.48 | 1.98 | −2.08 | 1.35 | 0.59 | 2.69 | 0.97 | −1.43 | 3.04 | |
| VARMA(2,0)- | −0.96 | 1.77 | −0.86 | 3.15 | 1.84 | 0.98 | 2.33 | 0.56 | 3.06 | −1.86 | −1.11 | 3.03 | 1.66 | 3.18 | −0.96 | |
| EGARCH(0,1) | 1.50 | 2.15 | 2.03 | 0.88 | −2.06 | 3.01 | 2.04 | 3.03 | 1.57 | 2.50 | 3.13 | 2.06 | 1.54 | 2.15 | 2.08 | |
| VARMA(2,1)- | 1.81 | 2.06 | 0.87 | −0.49 | 3.03 | 2.88 | −2.01 | 2.34 | 4.03 | 1.69 | 0.89 | −0.87 | 0.96 | 1.19 | −1.01 | |
| EGARCH(1,1) | 2.04 | 1.59 | 3.06 | 1.68 | 1.86 | 2.03 | 1.52 | 1.63 | 2.19 | 2.03 | 1.57 | −1.16 | 2.05 | 2.39 | 2.00 | |
| VARMA(2,1)- | 2.01 | 3.55 | 1.59 | −0.98 | 1.72 | 2.39 | 0.21 | 3.01 | 2.27 | 0.86 | 4.30 | 1.29 | 0.70 | −1.07 | −0.589 | |
| EGARCH(1.0) | 1.56 | 4.14 | 2.67 | −1.03 | 2.31 | 2.80 | 0.64 | 2.32 | 1.99 | 1.55 | 2.66 | −0.98 | 1.58 | 5.55 | 4.43 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, E.M.-Y.; Kuo, S.-L. Study on Air Pollution Behavior of VOCs with Photochemical Monitoring Stations Using EGARCH Model in Southern Taiwan. Atmosphere 2021, 12, 1167. https://doi.org/10.3390/atmos12091167
Wu EM-Y, Kuo S-L. Study on Air Pollution Behavior of VOCs with Photochemical Monitoring Stations Using EGARCH Model in Southern Taiwan. Atmosphere. 2021; 12(9):1167. https://doi.org/10.3390/atmos12091167
Chicago/Turabian StyleWu, Edward Ming-Yang, and Shu-Lung Kuo. 2021. "Study on Air Pollution Behavior of VOCs with Photochemical Monitoring Stations Using EGARCH Model in Southern Taiwan" Atmosphere 12, no. 9: 1167. https://doi.org/10.3390/atmos12091167
APA StyleWu, E. M.-Y., & Kuo, S.-L. (2021). Study on Air Pollution Behavior of VOCs with Photochemical Monitoring Stations Using EGARCH Model in Southern Taiwan. Atmosphere, 12(9), 1167. https://doi.org/10.3390/atmos12091167







