Polyphony of Short-Term Climatic Variations

Abstract

It is widely accepted to believe that humanity is mainly responsible for the worldwide temperature growth during the period of instrumental meteorological observations. This paper aims to demonstrate that it is not so simple. Using a wavelet analysis on the example of the time series of the global mean near-surface air temperature created at the American National Climate Data Center (NCDC), some complex structures of inter-annual to multidecadal global mean temperature variations were discovered. The origin of which seems to be better attributable to the Chandler wobble in the Earth’s Pole motion, the Luni-Solar nutation, and the solar activity cycles. Each of these external forces is individually known to climatologists. However, it is demonstrated for the first time that responses of the climate system to these external forces in their integrity form a kind of polyphony superimposed on a general warming trend. Certainly, the general warming trend as such remains to be unconsidered. However, its role is not very essential in the timescale of a few decades. Therefore, it is this polyphony that will determine climate evolution in the nearest future, i.e., during the time most important for humanity currently.

1. Introduction

The Intergovernmental Panel on Climate Change (IPCC) in its reports has repeatedly warned that global warming will become faster and faster in line with more frequent El Niño, positive phases of the North Atlantic Oscillation (NAO), Pacific Decadal Oscillation (PDO), Arctic Oscillation (AO), etc., whereas in fact, a delay in warming, which was mentioned in the IPCC reports [1], has been observed. For example, [2] argue: “Global temperature continues to increase in agreement with the best estimations of the IPCC, especially if we account for the effects of short-term variability due to the El Niño/Southern Oscillation, volcanic activity and solar variability”. However, many climate scientists have agreed that the recent warming delay was real. It was only stop by a new greatest El Niño event of 2015/16. However, any El Niño is a relatively short-lived phenomenon in climate dynamics, and so prospects for the further evolution of the present-day climate is a mystery in the perspective of the nearest decades.

2. Materials and Methods

Similar to many other researchers, who have published papers about the recent warming delay [3,4,5], the authors considered three time series of the global mean near-surface air temperature over the period of instrumental observations which are created and constantly updated in three climate centers: The Hadley Centre and Climatic Research Unit of the University of East Anglia (HadCRUT3 and HadCRUT4) [6], American National Climatic Data Center (NCDC) [7], and NASA Goddard Institute for Space Studies (GISS) [8]. Although raw station and sea ship temperature observations are processed in slightly different manners in these centers, the resulting global mean temperature time series seem to be very similar to each other. Therefore, for the sake of brevity, and since the main results of the analysis of all of these time series turned out to be almost identical, these results are illustrated for only the NCDC time series.

The choice of the NCDC time series is completely subjective. It is explained by the fact that the scientists of this center use some kind of so-called optimal interpolation to process the original temperature data. It is well known that optimal interpolation is often used to prepare initial meteorological fields to run hydrodynamical models for the goal of numerical weather predictions. The NCDC series is represented as global anomalies of land and ocean temperature, which have data from 1880 to the present. At first, the NCDC series is normalized, then a 12-month running average is performed, and the linear trend is excluded. This is done in order to reduce the edge distortions of the wavelet transform (WT) results that inevitably arise when transforming time series of finite length.

As for the methods of the above analysis of global mean near-surface air temperature time series, temporal autocorrelations and power spectra of the time series themselves and fairly simple cross-correlation of the temperatures with potentially influencing factors (concentration of greenhouse gases in the atmosphere, solar and volcanic activity, and various climatic indices such as (Southern Oscillation Index, NAO, AO, etc.) were used in almost all previously published works [9,10]. The main purpose of these correlations was to understand the contributions of these factors to the general variability of the global temperature. It is essential that these correlations were computed for each factor separately, and only then the contributions of all of these factors were summed. Subtracting such a summed contribution from the observed temperature time series, scientists obtained, as they thought, the net effect of human impact on the climate. An excellent example of using this simple technique is the aforementioned paper [2].

Unfortunately, the analysis of the temperature time series designed in such a manner ignores the fact that the real climate system is nonlinear. As is well known, the principle of superposition does not work in nonlinear systems. Therefore, a sum of contributions of a number of hypothetically affecting factors, computed for each of these factors separately, cannot be equal to the common contribution of these factors to the general temperature variability, if the factors act simultaneously. For example, if a factor affects the temperature in a multiplicative manner, then the cross-correlation analysis is difficult to be used in principle. The multiplicative effect can change not only the amplitudes of the temperature fluctuations but also their frequencies, etc. since it has a nonlinear effect. For this reason, the authors believe that any conclusion drawn on the basis of a sum of individual contributions of potentially affecting factors of the present-day climate change cannot be true.

Rather than such groundless summing, it is proposed to use another technique for the analysis of temperature time series: To allocate a certain range of time scales in the series of interest, and then try to recognize what the factors are, which determine a concrete structure of the temperature variations being extracted inside this time scale range. An excellent tool to do such an analysis is the WT of time series. Note: In contrast to the aforementioned computations of auto- and cross-correlations, WT is applicable to any non-stationary time series, i.e., a series that reveals a trend on the scale of the overall length of this series. It is very important in the case of the current climate change analysis.

In WT-based analysis, the authors limit themselves to studying the inter-annual to inter-decadal temperature variations and exclude the current general warming trend from consideration. It is due to the fact that it was demonstrated recently [10,11] that temperature variations, the periods of which were shorter than about 40 years, led to the respective variations of the atmospheric carbon dioxide concentration in the course of the current warming. Therefore, it seems only “natural” mechanisms must be responsible for the temperature variations of these short-term time scales.

In this study, the authors compute both real and complex WTs of all global temperature time series mentioned above after the 12-month moving average of them. This average excludes the annual cycle from further consideration. In order to extract from the series being transformed temperature variations of a certain range of time scales, at first the smallest WT values are shrunk. Only then, one can compute an inversion of the WT denoised in such a manner. It is known [12] that the procedure of WT shrinkage excludes observational and computational noises from the series. Note also that the WT inversion is additive, i.e., the WT inversions computed for two ranges of time scales, say a1 and a2, being added with each other, are equal to the WT inversion computed for the sum of the scales a1+a2. In other words, the superposition principle is applicable in the frame of WT to any dynamical system, either linear or nonlinear.

How Long Can Delays and Pauses Continue in the Current Climate Warming?

In order to answer this question, let us compute a real WT using the first derivative of Gaussian

$$G(t)=\frac{\sqrt{2}}{\sqrt[4]{\pi }}t \exp \left\{-t^2/2\right\},$$

(1)

where t is the time as the wavelet function. The output of this WT consists of a two-dimensional pattern of the real WT values

$$W{T}_b(a)=a^{-1/2}·{\displaystyle \sum _{t=1880}^{t=2020}T(t) G((t-b)/a)} ,$$

(2)

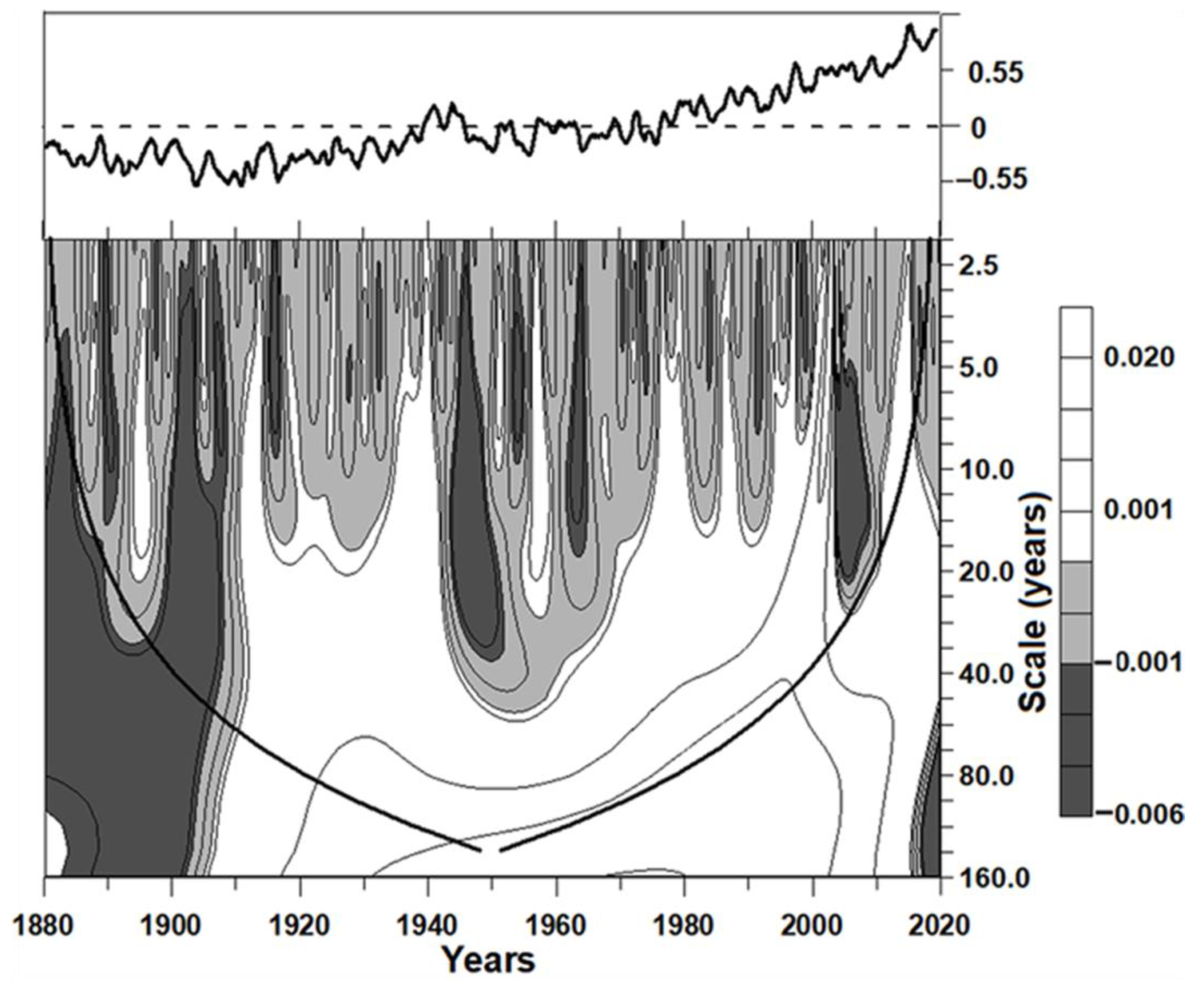
where a is the time scale, and $b\in \left\{1880÷2020\right\}$ are calendar years taken with a monthly resolution and 12-month moving averages, and $a\in \left\{2÷160\right\}$ are wavelet scales in years. The output measures local linear trends in the temperature time series at different time moments b and at different wavelet scales a. This output is shown in Figure 1. The areas of negative warming trends are colored in black, and the areas of positive trends remain white. The areas of unessential WT trends, i.e., the areas of warming pauses as these have been defined by Kerr [13], are colored in grey. Note that since any global temperature series is finite in its length, the WT pattern is slightly disturbed inside of its initial and final parts. The boundaries of the disturbed parts are delimited by parabolic black lines in Figure 1.

It is easy to calculate that 13 warming pauses exist near the 10-year wavelet scale within the undisturbed part of the WT pattern and only four pauses exist near the 15-year scale. Thus, Kerr [13] was right: 10-year long warming pauses are common, but 15-year long ones are rare in the climate dynamics. However, the WT pattern in Figure 1, considered as a whole, reveals that the seldom observed 15-year pauses are grouped in pairs, and account, together with shorter pauses in their beginnings and the ends, for two periods of general climatic cooling, which lasted, in total, approximately 30 years each.

These periods are well known to climatologists. The American meteorologists Schlesinger and Ramankutty were the first who published a paper [14] and a little later another paper [15] about a 65–70-year long climatic oscillation consisting of two equally long cooling periods together with a long warming period in between. These authors attributed this oscillation to the dynamics of the North Atlantic thermohaline circulation. In the development of their ideas, many scientists now call this oscillation the Atlantic Multidecadal Oscillation (AMO).

The recently published paper by Muller [16] indirectly corroborates this point of view indicating that the AMO positively correlates with near-surface air temperatures throughout the world. Taking in mind that cross-correlations do not imply any cause-effect relationship in the nonlinear dynamical system [17], it is possible to suppose that there is a common external driver of both the AMO and worldwide temperature variations of a respective time scale. Assuming that such a driver incessantly affects the global climate system (see supporting evidence of the fact in [18,19], one can believe that the 30-year long delays and pauses have to be present routinely in the climate dynamics.

3. Patterns of Global Temperature Variations

The next computation of WT is done with the Morlet wavelet

$$G(t)={\pi }^{-1/4} \exp \left\{-i \omega t\right\} \exp \left\{-t^2/2\right\}$$

(3)

with $\omega =6.2035$ to provide the exact equality of the wavelet and ordinary Fourier time scales. The goal is to analyze the wave structure of temperature variations over the inter-annual to multidecadal time scales. The Morlet function is complex, i.e., there are two (real and imaginary) components of the WT output: $W{T}_b{(a)}_{re}+i W{T}_b{(a)}_{im}$ in this case. 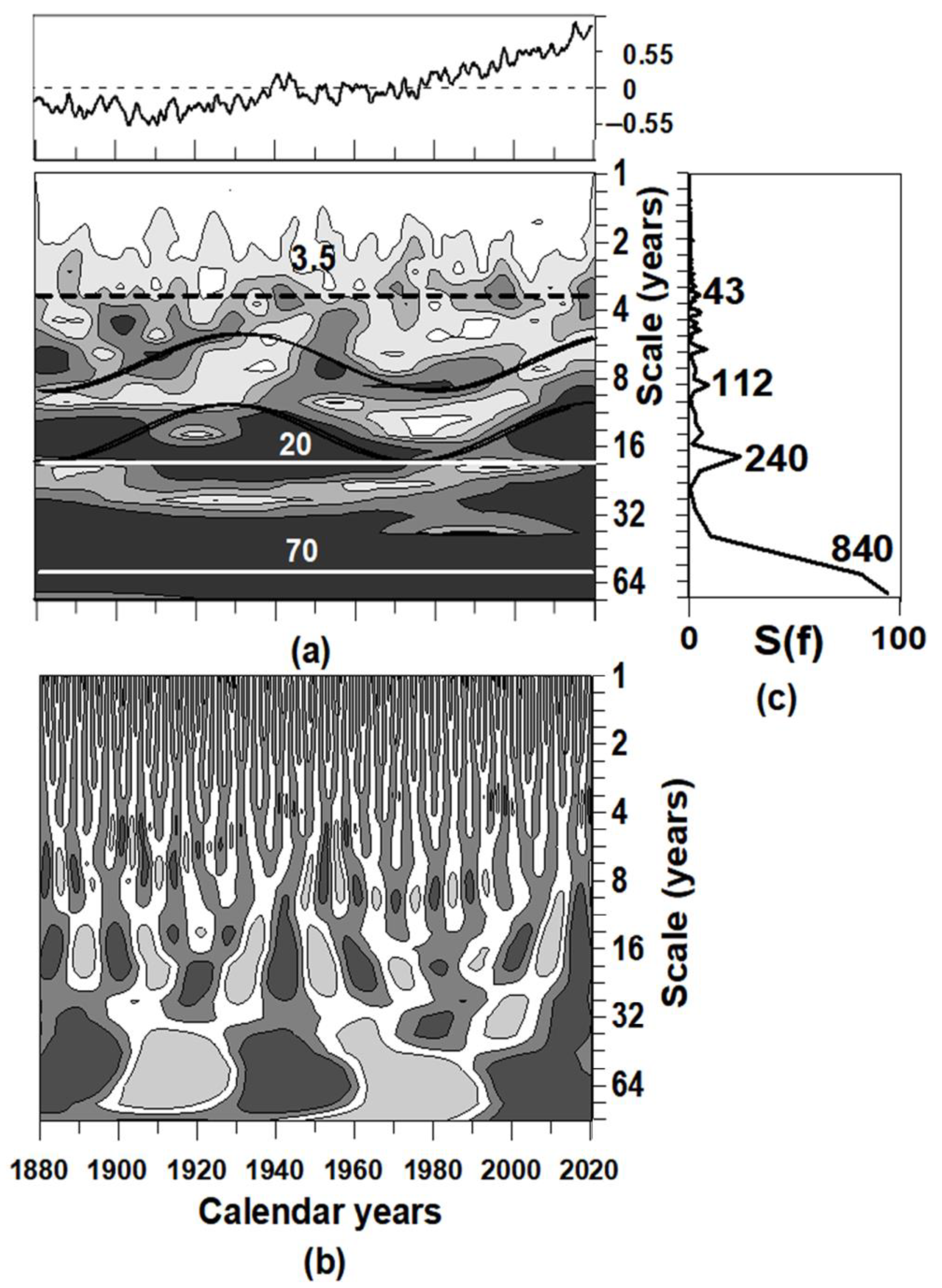The pattern of the WT amplitude $A{M}_b(a)=\sqrt{{\left(W{T}_b{(a)}_{re}\right)}^2+ {\left(W{T}_b{(a)}_{im}\right)}^2}$ is shown in Figure 2a. The areas of different WT amplitudes are shaded proportionally to their values. The pattern of the real component $W{T}_b{(a)}_{re}$ is shown in Figure 2c. The areas of positive (negative) values of the component are colored in shades of dark gray (light gray) in proportion to their WT values. The main focus in Figure 2a is on the areas of locally (in time and scale) maximal WT amplitudes. Considering these areas, one can make sure that the temperature variations of interest consist of four specific wave structures.

3.1. The Structure of the Interannual Temperature Variations

The first wave structure consists of a horizontal strip of slightly increased WT amplitudes near the 3.5-year wavelet scale. It means that a 3.5-year long fluctuation exists of a somewhat larger swing as compared to fluctuations of longer and shorter time scales in the global temperature dynamics. It is quite clear that this structure is nothing but a manifestation of an El Niño Southern Oscillation (ENSO)-like cyclicity in the global temperature dynamics. It is not a manifestation of any direct ENSO influence on the global temperature. It is namely manifestation of a bi-directional coupling between the ENSO and the global temperature as such (see [17] paper already mentioned at the end of the previous section). This coupling is not uniform in time. It is just the reason for the intermittent behavior of fluctuations in the 3.5-year (42 months) strip.

Indeed, considering the real component of the WT-pattern shown in Figure 2c, one can see that the intensities of positive and negative stages of these temperature fluctuations are different. The most intensive positive stages well correspond to El Niño events, and negative ones correspond to La Niña events. Certainly, it is a well-known fact that the global temperature fluctuations of the inter-annual time scales reflect the El Niño/La Niña alternation [20,21]. In spite of the intermittent character of the positive and negative phase alternation, the power spectrum of the NCDC time series shown in Figure 2b reveals a peak at the wavelet scale ~3.5 years (43 months).

Although it is not appropriate to discuss the reasons for the ENSO cyclic behavior with the main period of about 3.5 years, one can mention the following. It was recognized many years ago that the ENSO cyclicity was associated with the annual periodic heating of the atmosphere-ocean system from the Sun [22]. It is only necessary to add to this recognition that the climate system is also influenced by some other periodic external forces. Among these forces, the so-called Chandler wobble in the Earth’s pole motion has been hypothesized [9,23,24,25] to be very important for the ENSO cyclic behavior. Moreover, Serykh and Sonechkin, [24] indicated what a mechanism of the El Niño excitation was, these authors have analyzed satellite sea surface temperature data and the altimetry of the Pacific Ocean surface. They found that the North Pacific Ocean “pole” tide, excited by the Chandler wobbles, after its reflection from the western coast of Central America, excited positive sea-surface temperature and altitude anomalies in the tropics of the Pacific. Thus, this “pole” tide can be considered as a trigger of El Niño.

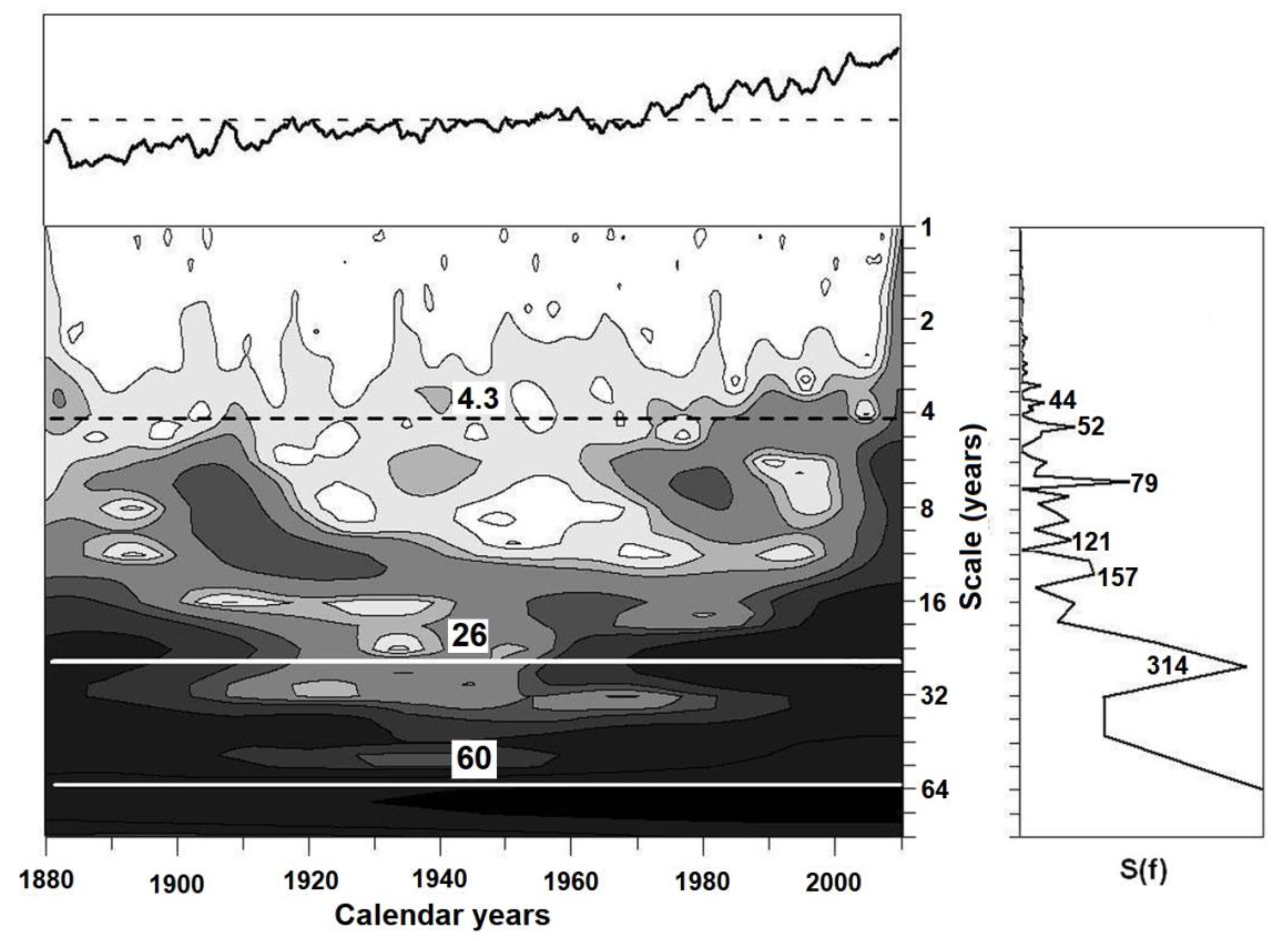
Indirect support for this notion can be seen in the fact that the present-day comprehensive climatic models, which do not take into consideration the Chandler wobble, are unable to reproduce properly the 42-month spectral peak. The authors recently learned this by analyzing long runs of the CMIP5 models. An example of the WT amplitude pattern and the power spectrum of such a run (created by the ECMWF (European Centre for Medium-Range Weather Forecasts) model) is shown in Figure 3. One can see that the main ENSO-related peak exists at the time scale of 52 months (~4.3 years), and another peak at the scale of 44 months. The modeled alternation of the El Niño/La Niña events also is quite different from that seen in the WT amplitude pattern of the real NCDC temperature series (Figure 2a).

If the Chandler wobble is really important, the 42-month period of the ENSO can be explained as a resonance between the semi-annual period of the Intertropical Convergence Zone swinging across the equator in the Pacific (it is very likely to affect the ENSO) and the Chandler wobble main period (14 months): 7 × 6 = 3 × 14. Perhaps, any manifestation of this resonance in the temperature dynamics is a nonlinear phenomenon. It is due to the fact that the 42-month peak exists in the ENSO power spectra, but no such peak is visible in the spectrum of the Chandler wobble itself.

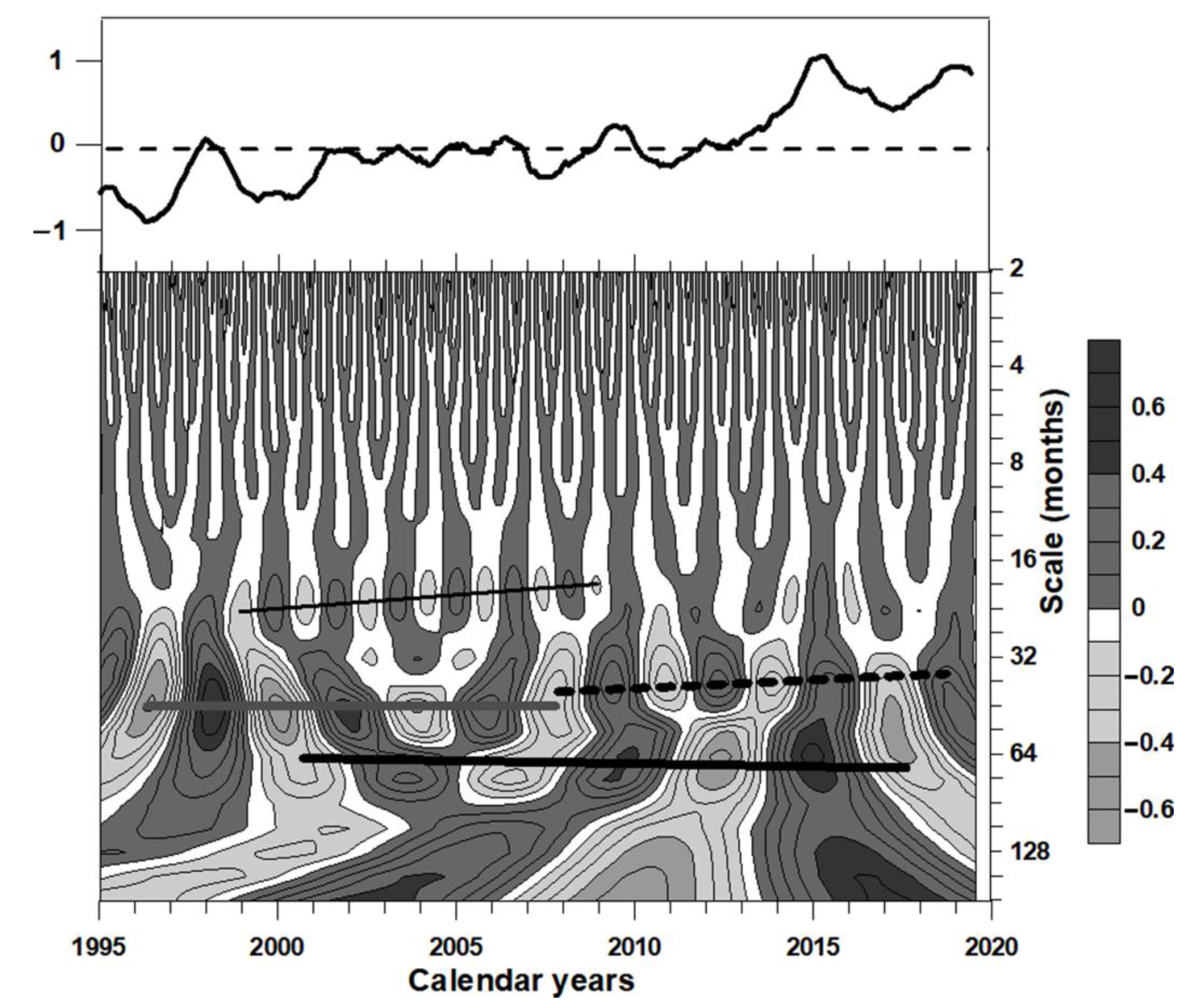
The intermittency of the temperature swings in the 42-month strip is a unique feature of the inter-annual temperature variations seen in the pattern of the real WT values shown in Figure 2c. A zoom of this WT pattern related to the latest calendar years 1995–2020 (Figure 4) reveals that there are several strips of increased WT amplitudes, which exist over finite intervals of calendar years. One of these strips (shown by a bold grey horizontal line) exists within the interval of 1996–2008. The period inherent to this strip is equal to about 45 months (~4 years). This strip disappears after 2008, and instead, the strip (shown by a dotted black line) of about a 36-month period (~3.5 years = the trebled Chandler wobble period) appears. This strip corresponds to the main period of the El Niño rhythms [9,24]. One more strip (a bold black line) exists in the interval of 2001–2018. Its period is equal to about 65 months (~5.5 years = the halved Sunspot cycle). At last, a weak strip (a thin black line) is visible within the interval of 1999–2009. Its period is equal to about 18 months. This strip seems to be responsible for the existence of some El Niño-like conditions which took place in 2002, 2004, 2005–2006, and 2009.

All of the strips mentioned depict an ENSO-like cyclicity of the global temperature. Phases of the real WT components corresponding to these strips do not bind with each other, in general. However, they turn out to be identical in 1997 and 2015/2016 when the two strongest El Niños took place. As a result, the real WT components of all strips are summed which implies two grand maximas of temperature. Note that the distance between El Niños of 1997 and 2015/2016 is exactly equal to the period of the Luni-Solar nutation of the Earth’s rotation axis. This fact can be considered in favor of an important role of this nutation in the short-term climate dynamics.

3.2. The Structure of the Decadal Temperature Variations

The second structure in the multiscale global temperature variations seen in the WT patterns in Figure 2a,c consists of two strips of increased WT amplitudes varying such as sinusoids with a common ~90-year period. Each of the sinusoids envelopes an octave of the time scales: The first octave covers a time scale range of about 5–10 years, and the second one covers a range of about 10–20 years. Both of these sinusoids are nothing other than fingerprints of the frequency modulation of the decadal temperature variations. It is important to indicate that the modeled WT amplitude pattern (Figure 3) does not reveal such a structure. The power spectrum of the NCDC series (Figure 2b) reveals some subtle peaks and spikes in the periods corresponding to maximal and minimal scales of the octaves mentioned. Of course, testing the statistical significance of these peaks relative to the standard null-hypothesis of red noise, one can conclude: All of these peaks are insignificant. However, it is a formal conclusion.

It is well known in the mathematical dynamical system theory that quasiperiodic forced systems are capable of revealing very specific dynamics that are called Strange Nonchaotic (SN). The power spectrum of SN dynamics is discrete in its character, i.e., it has no continuous background, and consists of an infinitely large number of peaks. Moreover, doing a zoom of an SN power spectrum, one can see the same peak re-distribution in a zoomed part of the frequency axis that is inherent to the whole frequency axis of the non-zoomed spectrum. This property of the SN power spectrum is called self-similarity. If the quasiperiodic forces affecting the system of interest become too intensive, the so-called deterministic chaos is excited in the system dynamics. As a result, a continuous background appears in the system power spectrum. However, even in such a case, the power spectrum of the quasiperiodic forced system remains non-smooth, although the number of the peaks seen in the spectrum becomes finite, and their magnitudes are not much higher than the spectral background. For this reason, statistical tests of the peak significance almost for certain give negative results. All of the other peaks turn out to be under the continuous background level. In other words, this kind of deterministic chaos is capable of simulating red noise similar to the “classic” deterministic chaos in autonomous nonlinear dynamical systems.

Any frequency modulation is prominent by not only its modulation frequency but also its carrier frequency. The carrier frequency should be located somewhere between the maximal and minimal frequencies inherent to the sinusoid under consideration. In the considered case, the carrier frequency of the first sinusoid should be located on the wavelet scale of ~7 years, and the second sinusoid carrier frequency—on the scale of ~14 years. However, no spectral peaks can be seen in the power spectrum in Figure 2b at these scales. Rather, spectral gaps are visible there. This could discourage and lead to the conclusion that the frequency modulation does not actually exist in the temperature variations. However, the theory of frequency modulation indicates that the absence of any peak at the carrier frequency is quite possible under the conditions of certain ratios of the external periodic force amplitudes determining both carrier and modulating frequencies.

It is very important to stress that just the frequency modulation of the climate system responses to the solar activity forces is the main reason why the connections between the solar activity cycles and climate dynamics seem to be unstable in time, and so any statistical tests of these connections turn out to be insignificant from the formal statistical point of view.

The modulation period (~90 years) and both carrier periods (~7 and ~14 years) allow for attributing the frequency modulations seen in Figure 2a to the Sun. Indeed, the 90-year period is the 1:2 superharmonic of the known cycle of the ~180-year period of the Sun rotation around the barycenter of the Solar System [26,27,28], and the ~7-year carrier period is a period that arises from the difference between the annual frequency and the frequency of the earlier-mentioned Chandler wobble ($1/12-1/14=1/84 \mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}{\mathrm{h}}^{-1}\equiv 1/7 \mathrm{y}\mathrm{e}\mathrm{a}{\mathrm{r}}^{-1}$). The ~14-year carrier period is just the doubled period. Of course, it is the authors’ supposition that the Sun is responsible for the appearance of the frequency modulation of the decadal temperatures. However, on the one hand, the authors could not find other sources of the external climate system forcing with the periods listed above, and, on the other hand, the deterministic chaos of autonomous (with constant external forces) nonlinear dynamical systems is not in a position to produce peaks in its power spectrum. Only if a system is affected by some periodic or quasi-periodic external forces, some spectral peaks can be found.

3.3. The Structures of the Multidecadal Temperature Variations

The third structure of the global temperature variations seen in Figure 2a consists of a strip of increased WT amplitudes near the time scale of 20 years. A rather strong (but formally insignificant) peak at the scale of 240 months (~20 years) corresponds to this strip in the power spectrum shown in Figure 2b. It should be mentioned that such periodicity has been known to climatologists for many years although its interpretation as evidence of solar magnetic activity is very contradictory in literature. For example, reviews on general aspects of the solar-terrestrial interconnections in [29,30], and more specific considerations of solar-magnetic activity effects in [31,32,33,34,35]. Perhaps, the most careful consideration of this problem and the conclusion about the solar origin of the ~20-year cycle seen in the climate dynamics can be found in [36].

To support the ~20-year peak reality, let us mention that the WT structure corresponding to this peak is similar to a pure harmonic. Its period and amplitude remained almost constant during all 120 calendar years of the instrumental temperature observations considered here. It is clearly seen in Figure 5 where the sequence of the $W{T}_b{(a)}_{re} , a=21, b=1880, \dots , 2010$ values representing this structure is shown (black line 3). The existence of this structure can be treated as evidence of a direct (almost linear) response of the climate system to the Hale solar magnetic activity cycle. Usually, the length of the Hale cycle is indicated as equal to 22 years (two times more than the 11 years of Schwabe’s sunspot cycle). However, the lengths of both Schwabe and Hale cycles actually were shorter during the 20th century (~21 and ~10 years, respectively). The shorter actual length of the Schwabe cycle is confirmed by the presence of a very weak (formally insignificant) peak at the period of 112 months in the spectrum in Figure 2b. Remember that any, even extremely weak, periodic or quasiperiodic external forcing does not pass without leaving a trace for the deterministic chaos. Turning back to Figure 5, one can see that each maximum of the ~21-year long temperature harmonic (black line 3) is preceded by either maxima of an odd Schwabe cycle or minima of an even one (grey line 4). Incidentally, the phase of the ~21-year long oscillation in sea surface temperature constructed on the base of the HadSST time series (grey line 6) slightly precedes that in the global land CRUTEM3 temperature (black line 5) indicating an important role of ocean in the temperature variations of the time scale considered.

Let us stress again that the modeled WT pattern (Figure 3) does not reveal the ~20-year strip of the increased WT amplitudes, as well as the respective peak in its power spectrum. Instead, a rather strong peak can be seen near the period of 314 months (~26 years). However, the WT amplitudes near this time scale are very different. It is rather easy to determine that the ~26-year spectral peak is a result of an overestimation of the volcanic eruption effects on climate in the present-day climatic models. A series of strong volcanic eruptions took place during the instrumental temperature observation period. The apparent periodicity of this series is about 26 years.

The fourth structure in the WT pattern seen in Figure 2a consists of a strip of very increased WT amplitudes near the time scale of 70 years. A strong peak at the scale of 786 months corresponds to this structure in the power spectrum in Figure 2b. Quite similar to the above third structure of the ~20-year long cycle, this structure looks to be perfectly harmonic (black line 7 in Figure 5). It can be treated as evidence of almost linear response of the climate system to the aforementioned Sun rotation cycle. This structure is just the climatic cycle recognized by Schlesinger and Ramankutty [14] and then discussed in the authors’ papers cited above [37]. Many of the more recent publications pointed to the 60-year cycle in the climate dynamics and its dependence on the Sun. As an example, the paper [36] can be mentioned. It seems that nobody currently is doubting in its reality. The present-day climatic models reproduce this oscillation in general. However, the details of this oscillation, such as the character of the oscillation extrema, are reproduced rather badly (see the WT pattern of the modeled global mean temperature time series in Figure 3 in comparison with the respective WT pattern of the real time series in Figure 2). The problem with these details will be discussed in the next section.

4. Discussion

Being summed by means of broadband (see below the range of timescales used) WT inversion, all of the afore-mentioned structures reconstruct a specific shape of the inter-annual to multidecadal temperature variations seen in the global temperature time series. To do this summation, let us use the real WT pattern shown in Figure 2c to compute its inversion by means of the known Morlet inversion formula

$$\widehat{T}(b)={\displaystyle \sum _{a=4}^{a=90}W{T}_b(a) } ,$$

(4)

where $b\in \left\{1880÷2020\right\}$ are calendar years, and the range of wavelet scales under the inversion is 4–90 years. The values in the area of the WT pattern left white in Figure 2c were made zero before the computation (4). Remember that the procedure of preliminary zeroing is called WT shrinkage [12]. This procedure excludes the influences of different kinds of observational and computational noises on $\widehat{T}(b)$.

The curve obtained by means of such a WT inversion (black line 8 in Figure 5) has a specific shape of a cnoidal wave, i.e., a wave with sharp maxima (at the beginning of the 1880s, 1940s, and 2000s) and smooth minima (in between). Interestingly, according to this curve, three maxima of the global temperature were observed in 1884, 1942, and 2002–2003. It means the period of this wave (shrunk from noises!) is equal to ~60 years, i.e., it is almost exactly equal to the 1:3 superharmonic of the Sun rotation cycle discussed above. The maxima of the cnoidal wave are slightly delayed relative to the strongest El Niño of the 20th century (1876, 1941, and 1997–1998).

Incidentally, a similar mismatch between almost simultaneous manifestations of different scale wave processes is known in other branches of geophysics. For example, waves of extreme height are known in oceanology and called “rogue” waves due to their great danger to navigation. Rogue waves are often excited as a result of the combined action of two different physical processes that occurred on the ocean surface: Interference of several waves traveling in different directions (it is a linear process) and nonlinear effects of the stability loss of the wavefield formed by such interference, and (perhaps) some other sources of wave instability that are not known yet.

Contrasts between rather smooth temperature increases observed over the end of the 19th century, as well as over the first and last thirds of the 20th century, and abrupt increases in temperature during the greatest El Niño events mentioned above gave reasons for the ongoing debate. In what year did the global mean temperature reach its highest value? Was it 1997, or some year in the first decade of the 21st century? The formal answer to this question is sensitively dependent on errors and sampling effects of instrumental time series and techniques of data processing. The authors believe that that WT shrinkage used in WT inversion is the best way to diminish such dependence.

Based on this, the authors believe that the grand maximum of the global near-surface air temperature generated by the “natural” factors was reached in the middle of the first decade of the 21st century.

What was said in the previous paragraph allows assuming that El Niño-like variations are specific reactions of the global climate system to its own internal instability. When warming and possibly some other properties of the climate system, which are not recognized yet, reach a certain level, an El Niño-like event is released. Some climatologists have extrapolated the fact and concluded that El Niño will become stronger and stronger in the warming world [38].

However, the reality of the last decades shows that it is not so. With further development of climate warming in the same direction, it seems that El Niño themselves lose their stability. As a result, some El Niño-like conditions were observed in the middle of the first decade of the 21st century only. Contributions of these conditions to the global mean temperature turned out to be much smaller than contributions of the fully developed El Niño observed during a few previous decades.

The found cnoidal wave determines an essential part of the global temperature change over the entire instrumental observation period including almost one half of the temperature trend. The magnetic activity of the Sun and more complex factors connected with the rotation of the Sun around the barycenter of the Solar System seem to be external drivers of this wave.

Taking into account the present-day prospects of solar physics, one can assume one can assume that delays and pauses will repeat in the global climate warming. Moreover, there are some indications [39] that these will develop into a new Little Ice Age during the next several decades. It is in good agreement with some predictions of solar physics investigators (see [40]).

Does everything in this paper mean that anthropogenic carbon dioxide concentration growth in the atmosphere does not influence the current climate warming means? Of course not. However, the paper does not say that. In fact, the direct (linear) part of this influence is limited to longer-term time scales. Specifically, it has been shown [10] that CO₂-concentration growth can directly influence temperature variations with periods of more than 40 years only. This influence began to reveal a sensitive effect approximately from the 1970s. Of course, it is almost certain that there are some indirect CO₂ influences.

It is due to the fact that the direct influence is unstable, and so it must “break down” into smaller-scale (in space and time, as well) temperature variations. Thus, according to the typical scenario of the deterministic chaos onset (look in any textbook for dynamical system theory), noise-like chaos must be created. This chaos differs from the mutually ordered temperature variations created by the external forces mentioned above (the climatic polyphony) since it cannot create any temporal-spatial structures of temperature variations.

Finally, it should be mentioned that the chaos is unpredictable, but the polyphony is predictable, at least partly.

5. Conclusions

It has been confirmed that the Chandler wobble in the Earth’s Pole motion, the Luni-Solar nutation, and the solar activity cycles affect the global climate system in the timescales of years and decades.

It has been found for the first time that responses of the climate system to these external forces are internally ordered, and so they can be seen in the real meteorological observations as a whole structure such as a musical polyphony.

It has been found that the mechanism of the influence of the solar activity cycle consists of frequency modulation. It explains why this influence is difficult to recognize in real meteorological observations.

Of course, even before our paper, there were publications [41,42], in which the problem of modulation of temperature variations was already discussed. However, it was not specified exactly what modulation frequency. Moreover, for the first time in the study of this problem, it is essential what kind of temperature variations are considered. The authors considered time series of the global mean near-surface air temperature. However, the same can be applied to the hemispheric mean near-surface air temperatures.

Finally, the authors believe that the present-day comprehensive climatic models are incapable of reproducing structures of the decadal-centennial variations of the real global temperature.